Adaptive Continuous Non-Singular Terminal Sliding Mode Control for High-Pressure Common Rail Systems: Design and Experimental Validation

Abstract

The High-Pressure Common Rail System (HPCRS) is designed based on fundamental hydrodynamic principles, after which this paper formally defines the key control challenges. The proposed continuous sliding mode control strategy is developed based on a non-singular terminal sliding mode framework, integrated with an improved power reaching law. This design effectively eliminates chattering and achieves fast dynamic response with enhanced tracking precision. Subsequently, a bidirectional adaptive mechanism is integrated into the proposed control scheme to eliminate the necessity for a priori knowledge of unknown disturbances within the HPCRS. This mechanism enables real-time evaluation of the system’s state relative to a predefined detection region. To validate the effectiveness of the proposed strategy, experimental studies are conducted under three distinct operating conditions. The experimental results indicate that, compared with conventional rail pressure controllers, the proposed method achieves superior tracking accuracy, faster dynamic response, and improved disturbance rejection.

1. Introduction

To enhance operational efficiency and curb harmful emissions, high-pressure common rail system (HPCRS) technology has gained widespread adoption in the modern engine systems. As a pivotal part of the engine, the main control objectives of the HPCRS are to regulate fuel injection pressure with high precision, suppress pressure fluctuations, and promote effective fuel atomization [1,2]. However, the HPCRS is inherently nonlinear and subject to significant uncertainties due to the complexities of the fuel delivery and injection dynamics, as well as the fluid’s hydraulic behavior. A critical challenge arises from the intermittent nature of fuel pumping and injection, which makes maintaining a constant injection pressure practically unachievable [3]. This intermittency severely complicates precise pressure control. Additionally, variations in engine operating conditions—such as speed and load—introduce unpredictable external disturbances, further complicating system behavior. These factors collectively render the task of achieving accurate and reliable tracking control for the HPCRS both technically demanding and of considerable engineering value [4,5,6].

A range of advanced control methodologies has been employed in the HPCRS to boost its control performance. In [7], a state-dependent PID control approach, built upon nonlinear feedback, was introduced to achieve precise fuel injection in the HPCRS. Its simple structure is particularly advantageous for practical engineering implementation. In [8], a novel triple-step method, rooted in the traditional PID algorithm, was devised to improve the rail pressure tracking performance. While PID control is extensively utilized in engine control systems owing to its straightforward structure, guaranteeing high control accuracy and robustness becomes a formidable task when faced with a broad spectrum of external disturbances. To address the limitations of the conventional PID controller, numerous studies have explored the integration of advanced theories with PID in the context of HPCRS. For instance, refs. [9,10] employed observer technologies to tackle the uncertainties and disturbances inherent in the HPCRS. However, the convergence performance of these observer-based methods is often constrained by the observer itself. In [11], an active disturbance rejection controller was proposed to manage the erratic fuel flows and pressure fluctuations in the HPCRS. In [4], an innovative, effective model-free controller, based on an intelligent proportional integral algorithm, was designed. Its key advantage lies in alleviating the burden of precise modeling. Furthermore, a plethora of research endeavors have focused on the application of intelligent control techniques in the HPCRS, such as fuzzy logic [12], genetic algorithms [13], and neural networks [14].

Despite the substantial contributions these aforementioned control methods have made to improve the dynamic performance of the HPCRS, a notable disparity persists between theoretical academic research and real-world engineering implementation. As a result, the majority of these methods have undergone testing solely through simulation processes. Additionally, several inherent shortcomings hinder their widespread and practical application within the HPCRS.

As a highly effective nonlinear control technique, sliding mode control (SMC) has garnered substantial interest in engineering applications, primarily due to its notable strengths, including robust performance, rapid response capabilities, and a relatively uncomplicated controller design. Simulations conducted within the AMESim environment have once again underscored the efficiency and superiority of linear SMC (LSMC) in the context of the HPCRS [15]. However, it is important to highlight that LSMC can only guarantee asymptotic stability, and the convergence performance of the closed-loop system may not always be up to par. In the pursuit of faster response times and greater accuracy, the development of finite-time control laws and nonlinear sliding surfaces has emerged as a focal point within the field of SMC. Examples of these include terminal SMC (TSMC) [16], non-singular terminal SMC (NTSMC) [17], and fast NTSMC (FNTSMC) [18]. Nevertheless, these methodologies fall under the umbrella of first-order SMC, and the persistent issue of chattering significantly impedes their practical engineering application in HPCRS. High-order SMC is regarded as an extension of the traditional first-order SMC and stands as one of the primary approaches for mitigating the chattering phenomenon. A comprehensive review of high-order SMC applications across various fields can be found in references [19,20,21], encompassing algorithms such as the twisting algorithm [19], super-twisting algorithm [20], and continuous SMC (CSMC) [21], among others. Typically, the switching gain of the aforementioned SMC is set to a fixed value, determined by the uncertainties and external disturbances that need to be countered. However, in the presence of unknown or highly variable disturbances typical of HPCRS, such fixed-gain approaches may lead to overestimated control efforts and unnecessarily high control magnitudes, thereby degrading overall performance and efficiency.

Building upon the preceding analysis, a novel adaptive continuous sliding mode control strategy incorporating an enhanced reaching law is proposed to improve the control performance of the HPCRS. The core of this method lies in the fusion of continuous NTSMC with a newly designed power reaching law. To address the unknown disturbances and system uncertainties caused by fuel pumping and injection dynamics, a bidirectional adaptive mechanism is also developed. A detailed stability analysis is presented to rigorously verify the theoretical soundness of the proposed approach. The effectiveness of the method is further validated through experiments conducted under three distinct operating scenarios, demonstrating superior response speed and control accuracy compared to conventional control methods.

The remainder of this paper is organized as follows. Section 2 establishes the mathematical model of the HPCRS and defines the control problem. In Section 3, the proposed adaptive NTSMC is introduced, accompanied by a comprehensive stability analysis. Section 4 presents experimental comparisons to evaluate the controller’s performance, and Section 5 concludes the paper with a summary of key findings and insights.

2. HPCRS Modeling and Control Problem Statement

In this section, we begin by providing an overview of the working process and the system architecture of the HPCRS. Subsequently, leveraging the physical principles, we construct a model of the HPCRS. To conclude, we articulate the problem statement and present a simplified control-oriented model.

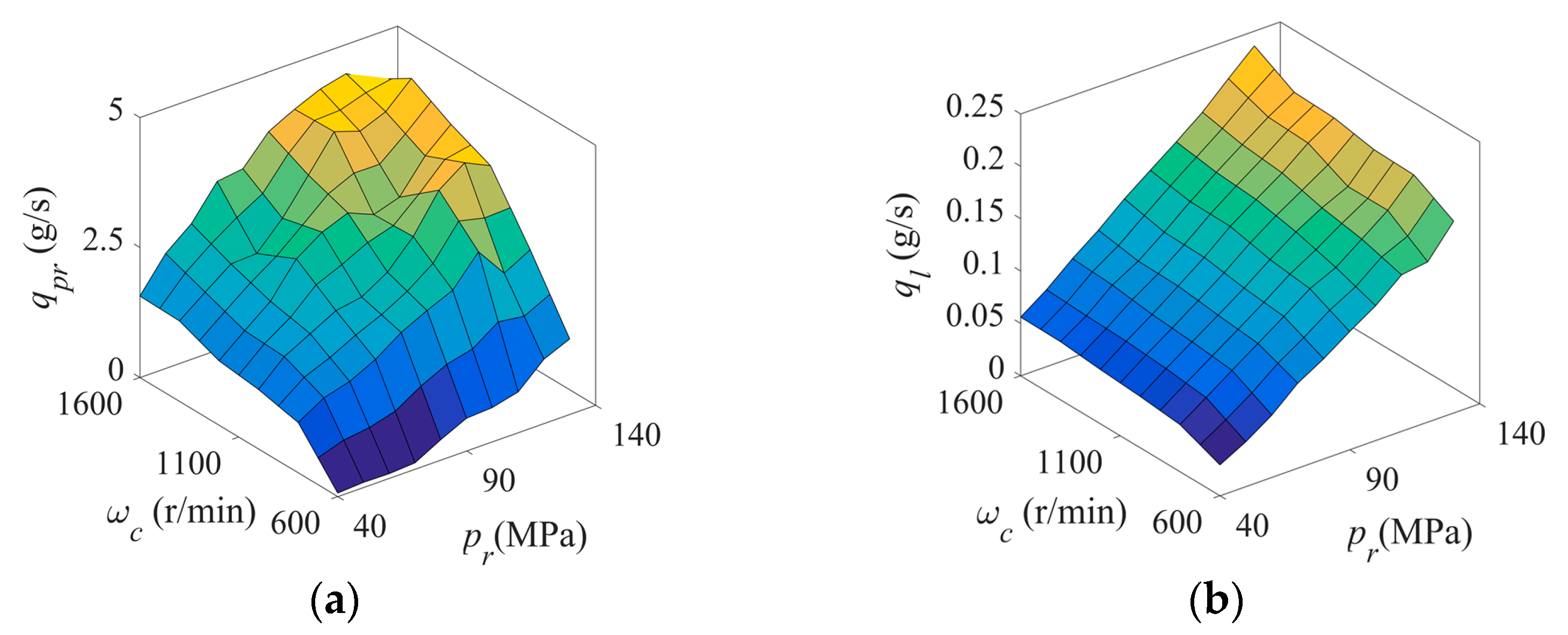
2.1. Problem Statement and Modeling

The HPCRS regulates fuel pressure by adjusting the inlet flow rate to the high-pressure pump. As shown in Figure 1, the HPCRS comprises fuel and electrical subsystems. The fuel subsystem includes the high-pressure pump, common rail, fuel tank, and electronically controlled injectors. The electrical subsystem consists of a pressure sensor, a solenoid valve, and an electronic control unit (ECU). The system operates as follows: fuel from the tank is supplied at low pressure to the high-pressure pump, which compresses it and transfers it to the common rail. The pressurized fuel is then distributed by the rail to individual injectors, which deliver it into the engine cylinders. In the closed-loop control system, the control algorithm is implemented and executed within the Engine Control Unit (ECU). By continuously comparing the reference pressure signal with the actual pressure feedback acquired from the pressure sensor, the ECU dynamically adjusts the fuel flow rate entering the high-pressure pump in real-time. This regulation of fuel flow is accomplished through precise modulation of the solenoid valve opening by the driver module, ultimately ensuring accurate control of the common rail pressure.

To develop an efficient and robust pressure controller, it is imperative to precisely characterize the dynamic behaviors of HPCRS. This system features highly intricate behaviors, including fuel compression, leakage, injection, elastic deformation, and other coupled physical phenomena. In modeling the HPCRS, fuel is treated as a compressible fluid. For a more comprehensive understanding of the modeling principles, readers are referred to [7,15,22,23,24].

Based on the system’s complexity, the following simplifying assumptions are introduced:

• The dynamics of the solenoid valve and temperature-related variations are neglected;
• The fuel dynamics are considered as one-dimensional, unsteady, and laminar flow;
• Pressure wave transmission between the low- and high-pressure circuits is not considered;
• The hydrodynamic phenomena occurring in the connecting pipes are also deemed negligible;
• Since the injection interval is extremely short, the dynamics of the injector are not taken into account.

The high-pressure pump features a straight double-piston configuration, where piston motion is actuated by the engine’s camshaft. During a single fuel supply cycle, its operation can be categorized into three main stages: the suction phase, compression (or pressure buildup) phase, and delivery phase. For a comprehensive and detailed analysis of these processes, readers may refer to [10,25,26,27]. Utilizing the fuel mass balance as a basis, the pressure dynamics of the high-pressure pump are described by the following equation:

$${\dot{p}}_p={\displaystyle \frac{E}{V_p}}\left(-{\displaystyle \frac{d{V}_p}{dt}}-q_{pr}-q_l+q_u\right),$$

(1)

where p_p denotes the fuel pressure within the high-pressure pump; E represents the fuel’s bulk modulus of elasticity; q_pr indicates the outflow rate toward the common rail; q_l corresponds to the leakage flow; q_u refers to the incoming fuel rate; V_p denotes the internal volume of the pump; dV_p/dt is the rate of change of internal volume. In this study, fuel is regarded as a weakly compressible fluid, and its compression behavior is modeled through the bulk modulus E, thereby simplifying system complexity while ensuring model accuracy, which is a widely accepted engineering simplification in HPCRS control. Future research will explore more detailed compressible flow modeling to capture transient and high-frequency pressure dynamics more accurately, whose variation can be described as follows:

$${\displaystyle \frac{d{V}_p}{dt}}=-A_p{\displaystyle \frac{d{h}_p}{dt}}=-A_p{\omega }_c{\displaystyle \frac{d{h}_p}{d\theta }},$$

(2)

where ω_c denotes the engine camshaft speed; h_p represents the instantaneous axial displacement of the piston; and A_p refers to the piston bore, treated as a constant. The term dh_p/dθ characterizes a nonlinear function dependent on the cam profile.

Based on fluid dynamic principles, the expressions for the outlet fuel flow rate q_pr and the fuel leakage flow rate q_l are formulated as follows:

$$q_{pr}=\mathrm{sgn}\left(p_p-p_r\right)c_{pr}{A}_{pr}\sqrt{{\displaystyle \frac{2\left|p_p-p_r\right|}{\rho }}},$$

(3)

$$q_l={\displaystyle \frac{\pi A_l{\delta }^3}{12\eta L}}\left|p_p-p_o\right|,$$

(4)

where p_r and p_l denote the pressures in the common rail and low-pressure circuit, respectively. The parameters c_pr and A_pr refer to the flow coefficient and the effective outlet cross-sectional area, while ρ indicates fuel density. In addition, A_l, δ, η and L are geometric and structural constants related to the plunger–cylinder assembly. Considering that the outlet valve of the high-pressure pump is designed as a check valve, Equation (3) can be reformulated as follows:

$$q_{pr}=\xi c_{pr}{A}_{pr}\sqrt{{\displaystyle \frac{2\left|p_p-p_r\right|}{\rho }}},\xi =\left\{\begin{array}{ll}1& \mathrm{if} p_p>p_r\\ 0& \mathrm{if} p_p\le p_r\end{array}\right.,$$

(5)

Based on Equations (2), (4) and (5), the pressure equation presented in Equation (1) is transformed into the following form:

$${\dot{p}}_p={\displaystyle \frac{E}{V_p}}\left(A_p{\omega }_c{\displaystyle \frac{d{h}_p}{d\theta }}-\xi c_{pr}{A}_{pr}\sqrt{{\displaystyle \frac{2\left|p_p-p_r\right|}{\rho }}}-{\displaystyle \frac{\pi A_l{\delta }^3}{12\eta L}}\left|p_p-p_o\right|+q_u\right),$$

(6)

As a critical element of the HPCRS, the common rail primarily serves to attenuate pressure oscillations. Changes in fuel volume within the rail result from dynamic fuel exchange, namely, the inflow and discharge processes. Based on this mechanism, the corresponding pressure equation can be derived as follows:

$${\dot{p}}_r={\displaystyle \frac{E}{V_r}}\left(q_{pr}-{\displaystyle \sum _{k=1}^6{q}_{ri,k}}\right),$$

(7)

where V_r denotes the internal volume of the common rail pipe. q_ri,k refers to the fuel inflow rate at the k-th injector, where k = 1,…,6. Consequently, upon substituting Equation (4) into Equation (6), Equation (6) can be rephrased as:

$${\dot{p}}_r={\displaystyle \frac{E}{V_r}}\left(\xi c_{pr}{A}_{pr}\sqrt{{\displaystyle \frac{2\left|p_p-p_r\right|}{\rho }}}-q_{ri}\right),$$

(8)

where q_ri is the total outflow of rail common, with $q_{ri}={\displaystyle \sum _{k=1}^6{q}_{ri,k}}$. Its value is contingent upon the engine operating conditions.

2.2. Model Simplification and Problem Statement

The rail pressure controller is developed with the objective of accurately tracking the reference pressure. To ensure high performance, the controller should demonstrate rapid responsiveness, high precision, and strong robustness. However, the full mathematical model of the HPCRS, as described in Equations (5) and (8), is too complex for direct application in controller synthesis. Hence, two simplified cases derived from Equation (5) are considered for control design:

(1)

When ξ = 0, it indicates that the pump pressure is lower than the rail pressure, i.e., p_p ≤ p_r [8]. According to Equations (1)–(8), the dynamics equation of HPCRS in this scenario can become:

$$\left\{\begin{array}{l}{\dot{p}}_p={\displaystyle \frac{E}{V_p}}\left(A_p{\omega }_c{\displaystyle \frac{d{h}_p}{d\theta }}-{\displaystyle \frac{\pi A_l{\delta }^3}{12\eta L}}\left|p_p-p_o\right|+q_u\right)\\ {\dot{p}}_r={\displaystyle \frac{E}{V_r}}\left(-q_{ri}\right)\end{array}\right.,$$

(9)

It can be observed that under this condition, the rail pressure cannot be actively regulated, requiring the design of a control law to shift the system toward the state p_p > p_r. To achieve this, we regulate the inlet fuel flow q_u of the high-pressure pump as suggested in [7]:

$$q_u=q_l-A_p{\omega }_c{\displaystyle \frac{d{h}_p}{d\theta }}-K{\displaystyle \frac{V_p}{V_r}}{q}_{ri},$$

(10)

where K < 1, and a more detailed description and analysis in this case can be found in [7].

(2)

When ξ = 1, it corresponds to the scenario in which the pump pressure exceeds the rail pressure, i.e., p_p > p_r. the dynamics equation of HPCRS can become:

$$\left\{\begin{array}{l}{\dot{p}}_p={\displaystyle \frac{E}{V_p}}\left(A_p{\omega }_c{\displaystyle \frac{dh}{d\theta }}-c_{pr}{A}_{pr}\sqrt{{\displaystyle \frac{2\left(p_p-p_r\right)}{\rho }}}-{\displaystyle \frac{\pi A_l{\delta }^3}{12\eta L}}\left|p_p-p_o\right|+q_u\right)\\ {\dot{p}}_r={\displaystyle \frac{E}{V_r}}\left(c_{pr}{A}_{pr}\sqrt{{\displaystyle \frac{2\left(p_p-p_r\right)}{\rho }}}-q_{ri}\right)\end{array}\right.,$$

(11)

This scenario represents the principal controllable phase within the HPCRS. The variables x₁ and x₂ are designated as the error of rail pressure and its differentiation, respectively, and are mathematically represented as follows:

$$x_1=p_d-p_r\hspace{1em}\hspace{1em}{x}_2={\dot{x}}_1={\dot{p}}_d-{\dot{p}}_r,$$

(12)

where p_d is the reference rail pressure. The control input is selected as the high-pressure pump inflow q_u, i.e., u = q_u, and a new state variable is defined as $z=\sqrt{p_p-p_r}$. Based on Equations (1)–(8), the control-oriented dynamic model of the HPCRS is given by:

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2\hfill \\ {\dot{x}}_2=-a\left(z\right)x_2+b\left(z\right)\left(q_{pr}+q_l-A_p{\omega }_c{\displaystyle \frac{dh}{d\theta }}\right)+a\left(z\right){\dot{p}}_d\\ \hspace{1em}+{\ddot{p}}_d-b\left(z\right)u+d\hfill \end{array}\right.,$$

(13)

where d represents the lumped disturbance, which encapsulates uncertainties in fuel physical properties as well as external perturbations caused by fluctuations in rotational speed, fuel pumping, and injection; the known functions $a\left(z\right)=c_{pr}{A}_{pr}E/\sqrt{2\rho }z{V}_r$ and $b\left(z\right)=a\left(z\right)E/V_p$ describe the system coefficients. This paper focuses on the case of ξ = 1 and proposes a novel adaptive CNTSMC to achieve precise tracking of the reference rail pressure.

Remark 1.

Since the outlet fuel flow q_pr and the fuel leakage flow q_l can be determined by the experiment, the lumped disturbance d exists in the engineering application and involves complex parameter uncertainties and calibration errors of q_pr, q_ri and q_l.

Remark 2.

It is important to note that assuming boundedness of the disturbance d and its derivative $\dot{d}$, i.e., $\left|d\right|\le l_d$ and $\left|\dot{d}\right|\le l_{dd}$, where l_d and l_dd are constants, is a widely accepted simplification for the HPCRS control design [3,4]. Nevertheless, the precise values of these bounds are often difficult to determine in practice. Therefore, an adaptive approach is adopted in this paper to relax the boundedness assumption and improve robustness against external uncertainties in the closed-loop control system.

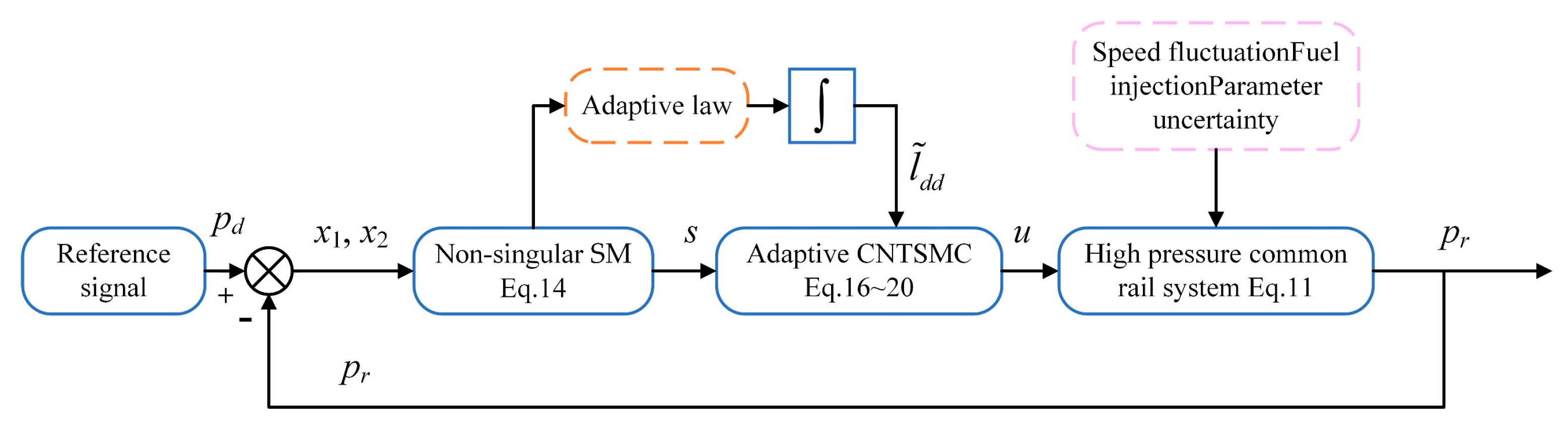
3. Adaptive CNTSMC Design

The primary objectives of rail control in an HPCRS confronted with an unknown disturbance d is to realize precise and resilient tracking control. In this study, we put forward a new adaptive CNTSMC (ACNTSMC) specifically for the HPCRS. This controller amalgamates the idea of nonlinear sliding mode control and incorporates a fast-convergence reaching law. To further mitigate the impact of model uncertainties and external perturbations, an adaptive mechanism is introduced, relying on the system state for compensation.

3.1. Improved CNTSMC Design

For the HPCRS model described by Equation (13), a nonlinear power term is incorporated to ensure finite-time convergence. The corresponding nonlinear manifold is constructed as follows:

$$s=c_1\mathrm{sgn}\left(x_1\right){\left|x_1\right|}^{{\alpha }_1}+c_2\mathrm{sgn}\left(x_2\right){\left|x_2\right|}^{{\alpha }_2}+{\dot{x}}_2,$$

(14)

where c₁ and c₂ are positive design parameters, and the polynomial p² + c₂p + c₁ should satisfy the Hurwitz stability criterion, i.e., its eigenvalues lie in the left-half complex plane; α₁ and α₂ are positive constants and are determined by α₁ = α₂/(2 − α₂).

Once the HPCRS reaches the sliding mode s = 0 in Equation (14), its dynamics will be governed by the following equation:

$${\dot{x}}_2=-c_1\mathrm{sgn}\left(x_1\right){\left|x_1\right|}^{{\alpha }_1}-c_2\mathrm{sgn}\left(x_2\right){\left|x_2\right|}^{{\alpha }_2},$$

(15)

and in finite time, the variables x₁ and x₂ will converge to the equilibrium point where x₁ = x₂ = 0 [28].

To ensure that the HPCRS consistently reaches the sliding mode manifold defined in Equation (14), the CNTSMC law is formulated as follows:

$$u=b^{-1}\left(z\right)\left(u_{eq}+u_n\right),$$

(16)

where u_eq is the equivalent component and u_n indicates the switching component. Following the framework of equivalent control theory [29], the term u_eq is derived as:

$$\begin{array}{cc}{u}_{eq}& =-a\left(z\right)x_2+b\left(z\right)\left(q_{pr}+q_l-A_p{\omega }_c{\displaystyle \frac{dh}{d\theta }}\right)\hfill \\ & +a\left(z\right){\dot{p}}_d+{\ddot{p}}_d+c_1\mathrm{sgn}\left(x_1\right){\left|x_1\right|}^{{\alpha }_1}+c_2\mathrm{sgn}\left(x_2\right){\left|x_2\right|}^{{\alpha }_2}\end{array},$$

(17)

To mitigate the chattering issue, we incorporated an auxiliary control term v, which is defined as follows:

$${\dot{u}}_n+T{u}_n=v,\hspace{1em}\hspace{1em}{u}_n\left(0\right)=0,$$

(18)

where T is a positive constant and v is a constructor using a low-pass filter, given by:

$$v=-\left(k+T\left|u_n\right|\right)\mathrm{sgn}\left(s\right),$$

(19)

where k is a positive design parameter satisfying k > l_dd. Equation (19) employs the constant rate reaching law. To further enhance convergence speed and improve control precision, an improved power reaching strategy is adopted as in [30], resulting in the refined formulation:

$$v=-\left({\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^K+k+T\left|u_n\right|\right)\mathrm{sgn}\left(s\right),$$

(20)

$$D\left(s\right)=\beta +\left(1-\beta \right)e^{-\alpha \left|s\right|},$$

(21)

where k₁, β, K and α are all positive parameters, with 0 < β < 1 and 0 < K < 1.

In the following, we analyze the stability characteristics of the HPCRS under closed-loop operation. Based on Equation (10), by substituting the control input u as defined in Equations (16)–(18) into the nonlinear sliding surface Equation (14), the variable s and its derivative can be deduced as:

$$\begin{array}{ll}s=& -a\left(z\right)x_2+b\left(z\right)\left(q_{pr}+q_l-A_p{\omega }_c{\displaystyle \frac{dh}{d\theta }}\right)+a\left(z\right){\dot{p}}_d+{\ddot{p}}_d+d\\ & -b\left(z\right)u+c_1\mathrm{sgn}\left(x_1\right){\left|x_1\right|}^{{\alpha }_1}+c_2\mathrm{sgn}\left(x_2\right){\left|x_2\right|}^{{\alpha }_2}=d+u_n\end{array},$$

(22)

$$\dot{s}=\dot{d}+{\dot{u}}_n=\dot{d}+v-T\left|u_n\right|,$$

(23)

Taking into account a Lyapunov function V₁ = 0.5 s², we proceed to differentiate V₁ with respect to time. Subsequently, we substitute the expressions from Equations (20) and (21) into the resulting derivative. This yields the following:

$$\begin{array}{c}{\dot{V}}_1=s\dot{s}\hfill \\ \hspace{1em}=s\left(\dot{d}+v-T\left|u_n\right|\right)\hfill \\ \hspace{1em}=s\left(-\left({\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^K+k+T\left|u_n\right|\right)\mathrm{sgn}\left(s\right)-T\left|u_n\right|+\dot{d}\right)\hfill \\ \hspace{1em}=-{\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^{K+1}-k\left|s\right|-T\left|u_n\right|\left|s\right|-T\left|u_n\right|s+\dot{d}s\hfill \\ \hspace{1em}\le -{\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^{K+1}-\left(k-l_{dd}\right)\left|s\right|\hfill \\ \hspace{1em}\le -{\left(\sqrt{2}\right)}^{K+1}{\displaystyle \frac{k_1}{\beta }}{V}_1^{{\displaystyle \frac{K+1}{2}}}-\sqrt{2}\left(k-l_{dd}\right)V_1^{{\displaystyle \frac{1}{2}}}\hfill \end{array},$$

(24)

Given that the parameter k > l_dd, for any non-zero value of s, the system states are capable of reaching the NTSM surface within a finite time frame. It is evident that the convergence speed of Equation (20) surpasses that of the constant rate reaching law, primarily due to the incorporation of the exponential term k₁|s|^K/D(s). Moreover, when the magnitude of |s| is large, the coefficient of the reaching law becomes substantial, thereby expediting the convergence process. Conversely, as |s| approaches zero, the coefficient of the reaching law can asymptotically tend towards l_dd.

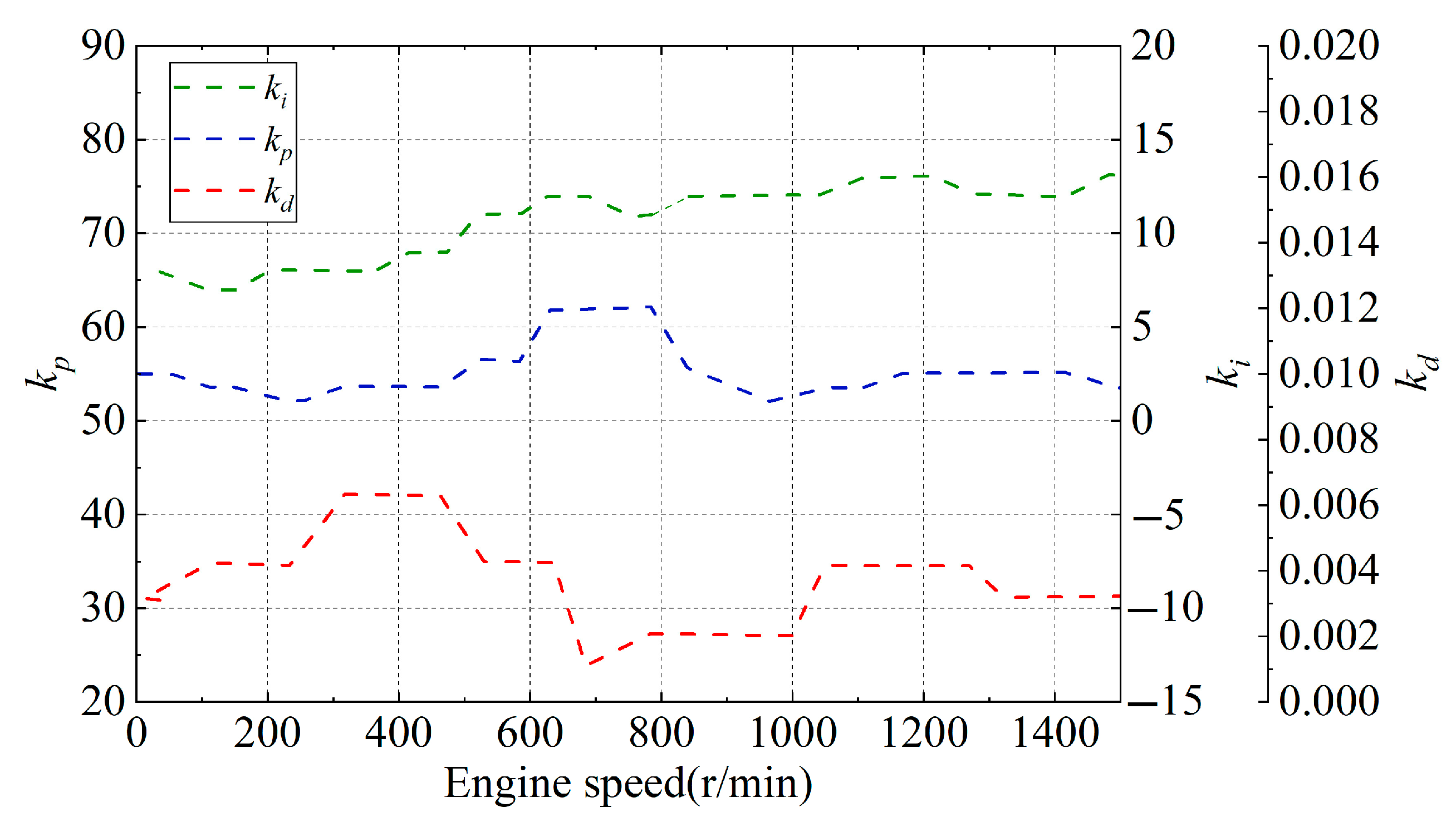
3.2. Adaptive Mechanism Design

Based on Equations (19) and (20), it is evident that to guarantee convergence of the HPCRS, the controller must be initially designed under the assumption that the condition k > l_dd. However, in the practical engineering application of HPCRS, the upper bound of the disturbance is typically unknown and challenging to estimate precisely, and the value of l_dd remains unknown. To circumvent the necessity of prior information of the lumped disturbance d, this paper introduces an adaptive mechanism.

In light of this, the auxiliary control term v in Equation (20) is modified as follows:

$$v=-\left({\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^K+{\tilde{l}}_{dd}+T\left|u_n\right|\right)\mathrm{sgn}\left(s\right),$$

(25)

$${\dot{\tilde{l}}}_{dd}=\gamma \left|s\right|,$$

(26)

where ${\tilde{l}}_{dd}$ is the adaptive parameter and is the estimation of l_dd; γ is a positive constant.

Taking into account a new Lyapunov function V₂ as follows:

$$V_2={\displaystyle \frac{1}{2}}{s}^2+{\displaystyle \frac{1}{2\gamma }}{\left({\tilde{l}}_{dd}-l_{dd}\right)}^2,$$

(27)

The stability assessment of the overall system parallels the approach outlined in Equation (24). By computing the time derivative of the Lyapunov function V₂ and incorporating the expressions from Equations (25) and (26) into this derivative, we obtain the following:

$$\begin{array}{c}{\dot{V}}_2=s\dot{s}+{\displaystyle \frac{1}{\gamma }}\left({\tilde{l}}_{dd}-l_{dd}\right){\dot{\tilde{l}}}_{dd}\hfill \\ \hspace{1em}\le -{\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^{K+1}+\left|s\right|\left|\dot{d}\right|-l_{dd}\left|s\right|-{\tilde{l}}_{dd}\left|s\right|+{\tilde{l}}_{dd}\left|s\right|\hfill \\ \hspace{1em}\le -{\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^{K+1}<-{\left(\sqrt{2}\right)}^{K+1}{\displaystyle \frac{k_1}{\beta }}{V}_2^{{\displaystyle \frac{K+1}{2}}}\hfill \end{array},$$

(28)

Consequently, the condition for Lyapunov stability is satisfied, i.e., ${\dot{V}}_2<0$, and the system states can reach the sliding mode surface s = 0 in finite time. The reaching time t_r can be estimated roughly from (28):

$$t_r<{\displaystyle \frac{2^{K+3}{k}_1}{\left(1-K\right)\beta }}{V}_2^{{\displaystyle \frac{1-K}{2}}}\left(t_0\right),$$

(29)

where V₂(t₀) is the initial value of V₂.

According to Equations (25) and (26), the adaptive parameter ${\tilde{l}}_{dd}$ evolves continuously based on the system state, contributing to overall stability. Ideally, when the state approaches equilibrium, ${\tilde{l}}_{dd}$ should stabilize at a high value and cease to grow. Nevertheless, due to real-world uncertainties in HPCRS applications, reaching a perfectly stable state is often impractical. As a result, ${\tilde{l}}_{dd}$ may keep increasing, potentially degrading control precision and destabilizing the system. To address this issue, an enhanced adaptation strategy is proposed. Specifically, a bounded detection interval is defined to regulate the bidirectional adjustment of ${\tilde{l}}_{dd}$. This interval is expressed as $\left\{s:\left|s\right|\le \epsilon \right\}$, where ε is the positive constant as the size of the region. An improved adaptation mechanism can be designed as:

$${\dot{\tilde{l}}}_{dd}=\left\{\begin{array}{cc}\gamma \left|s\right|\mathrm{sgn}\left(\left|s\right|-\epsilon \right)& \mathrm{if} {\tilde{l}}_{dd}>{\tilde{l}}_{dd}^{\ast }\\ \chi & \mathrm{if} {\tilde{l}}_{dd}\le {\tilde{l}}_{dd}^{\ast }\end{array}\right.,$$

(30)

where ${\tilde{l}}_{dd}^{\ast }$ is the lower bound of ${\tilde{l}}_{dd}$, which is chosen to enhance the HPCRS’s convergence performance and stability, with ${\tilde{l}}_{dd}^{\ast }>0$; χ is a positive parameter and the update law ${\dot{\tilde{l}}}_{dd}=\chi$ is used to maintain the growth of ${\tilde{l}}_{dd}$ when ${\tilde{l}}_{dd}\le {\tilde{l}}_{dd}^{\ast }$. This design allows the adaptive gain to increase when the system deviates from the equilibrium, thus accelerating convergence, and to decrease when approaching the sliding surface, thereby reducing control effort and improving precision. Additionally, we introduce a lower limit parameter χ, ensuring that the adaptive gain ${\tilde{l}}_{dd}$ always remains above a minimum threshold, guaranteeing the responsiveness and stability of the HPCRS.

Considering the Lyapunov function V₂ and improved adaptation mechanism (30), if ${\tilde{l}}_{dd}>{\tilde{l}}_{dd}^{\ast }$ the derivative of V₂ in (28) can be reformulated as:

$$\begin{array}{c}{\dot{V}}_2=s\left(\dot{d}-\left({\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^K+{\tilde{l}}_{dd}+T\left|u_n\right|\right)\mathrm{sgn}\left(s\right)-T{u}_n\right)\hfill \\ \hspace{1em}+\left({\tilde{l}}_{dd}-l_{dd}\right)\left|s\right|\mathrm{sgn}\left(\left|s\right|-\epsilon \right)\hfill \\ \hspace{1em}\le -{\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^{K+1}-\left({\tilde{l}}_{dd}-l_{dd}\right)\left|s\right|+\left({\tilde{l}}_{dd}-l_{dd}\right)\left|s\right|\mathrm{sgn}\left(\left|s\right|-\epsilon \right)\hfill \\ \hspace{1em}\le -{\displaystyle \frac{k_1}{D\left(s\right)}}{\left|s\right|}^{K+1}+\varphi \left|s\right|\hfill \end{array},$$

(31)

$$\varphi =\left(l_{dd}-{\tilde{l}}_{dd}\right)\left(1-\mathrm{sgn}\left(\left|s\right|-\epsilon \right)\right),$$

(32)

According to Lyapunov stability theory, two scenarios must be analyzed depending on whether |s| > ε and |s| ≤ ε: (1) Case 1: when |s| > ε, Equation (32) simplifies to ϕ = 0, ensuring ${\dot{V}}_2<0$, which implies asymptotic convergence. Thus, the state trajectory reaches the sliding manifold s = 0. (2) Case 2: when |s| ≤ ε, the adaptive parameter follows the update rule ${\dot{\tilde{l}}}_{dd}=-\gamma \left|s\right|$, and ϕ ≠ 0 as in Equation (32). Under this condition, the Lyapunov derivative ${\dot{V}}_2$ in Equation (31) cannot be explicitly determined. According to the trajectory-based analysis in [31,32], if ${\dot{V}}_2>0$, the HPCRS state exits Case 2 and returns to Case 1, thereby reinitiating the control cycle. Conversely, if ${\dot{V}}_2<0$ decreases continuously toward its predefined lower bound ${\tilde{l}}_{dd}^{\ast }$, after initially increasing at a rate ${\dot{\tilde{l}}}_{dd}=\chi$ to promote dynamic stability. By integrating the behaviors described in both cases, the proposed adaptive strategy ensures the overall stability of the HPCRS. The control flowchart of the ACNTSMC is illustrated in Figure 2.

4. Experimental Validation and Analysis

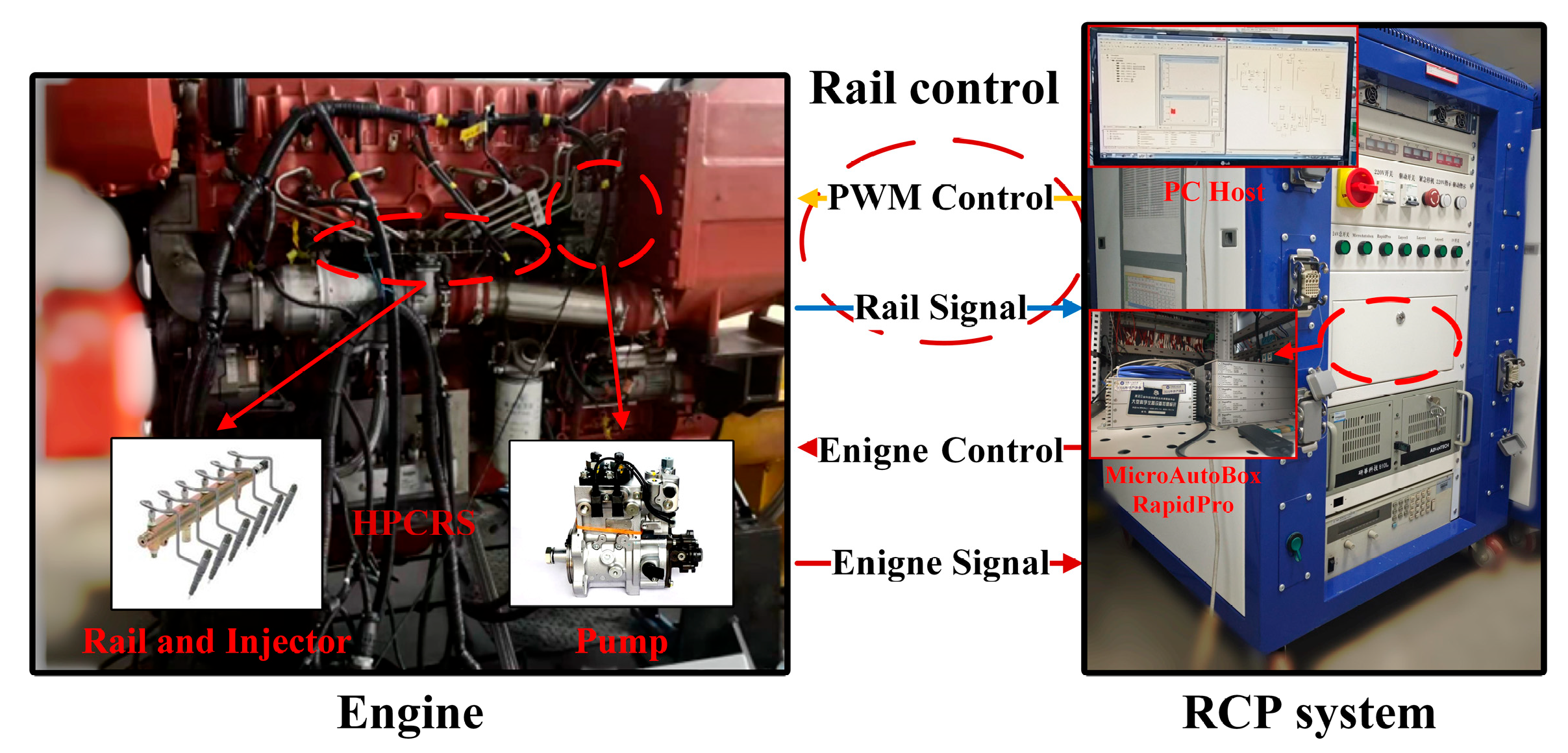
4.1. Engineering Realization

In the engineering application, the sliding variable s in (14) is not available since the derivative of the system state ${\dot{x}}_2$ is not directly measured. In order to calculate ${\dot{x}}_2$, the following robust derivative estimator can be employed [19]:

$$\left\{\begin{array}{l}\dot{w}=g_0\\ {\dot{g}}_0=g_1-{\lambda }_0{\left|w-x_2\right|}^{1/2}\mathrm{sgn}\left(w-x_2\right)\\ {\dot{g}}_1=-{\lambda }_1\mathrm{sgn}\left(g_1-g_0\right)\\ {\widehat{\dot{x}}}_2=g_1\end{array}\right.,$$

(33)

where λ₀ and λ₁ are positive design parameters; ${\widehat{\dot{x}}}_2$ is derivative estimation of the system state ${\dot{x}}_2$.

In practical implementation, the control output u is converted into a command voltage for driving the solenoid valve. This voltage is generated via the ECU and applied to the valve actuator to modulate the fuel inflow in real-time. Moreover, the inflow rate q_u associated with the high-pressure pump is not directly manipulated. Instead, it is modulated by regulating the duty cycle of the PWM signal applied to the solenoid valve, which determines the valve’s opening duration. The governing relationship is given as:

$$q_u=U{c}_{lp}{A}_{lp}\sqrt{2\left|p_p-p_l\right|/\rho }=f\left(u_{PWM}\right)c_{lp}{A}_{lp}\sqrt{2\left|p_p-p_l\right|/\rho },$$

(34)

where c_lp and A_lp are the flow coefficient and the cross-sectional area of the solenoid valve, respectively; U is the opening valve of the solenoid valve; f(·) is a decreasing function measured experimentally.

From Equation (17), the equivalent control component u_eq depends on the fuel leakage rate q_l and the discharge flow q_pr. These two variables are not directly measurable in practical systems and are influenced by engine rotational speed ω_c and the rail pressure p_r. In this study, we constructed a feedforward mapping for q_l and q_pr through experimental calibration. The resulting MAP data is illustrated in Figure 3.

4.2. Experimental Setup

To evaluate the performance and practicality of the proposed AFOSM controller, validation experiments were conducted on a straight-six, four-stroke engine equipped with a second-generation Bosch HPCRS. The experimental arrangement is depicted in Figure 4, and the engine’s technical parameters are summarized in

Table 1. Units for magnetic properties.

Parameters	Specification
Nominal engine speed	1500 r/min
Rated output power	255 kW
Peak injection pressure	1500 bar
Cylinder configuration	6-inline
Compression ratio	16.5:1
Total engine displacement	12.155 L
Piston stroke	155 mm
Cylinder bore diameter	129 mm

.

The rapid control prototyping (RCP) system, which functions as the core hardware platform, consists of two primary modules: the MicroAutoBox and the RapidPro. The MicroAutoBox handles sensor data acquisition and executes control algorithms, operating at a sampling interval of 1 ms. In parallel, the RapidPro facilitates the generation of control signals required for engine management and common rail actuation.

The configuration parameters for the proposed controller used in Equations (14), (25) and (30) are chosen as c₁ = 30, c₂ = 240, α₁ = 11/15, α₂ = 11/13, T = 0.005, β = 0.2, k₁ = 20, α = 2, K = 0.3, γ = 0.4, ε = 50, ${\tilde{l}}_{dd}^{\ast }$ = 40. The final parameter values were obtained through theoretical design principles and experimental calibration under typical operating conditions to ensure balanced performance and robustness. To highlight the practical effectiveness and engineering value of the proposed adaptive NTSMC strategy, the experimental comparison in this study is conducted against the conventional PID controller [2], which remains the most widely adopted solution in current HPCRS due to its simplicity and robustness. Although the proposed method is theoretically derived from and extends the traditional NTSMC framework, its superiority over the basic NTSMC has already been demonstrated through structural design and theoretical analysis. Therefore, the experimental focus is placed on benchmarking against PID control, which better reflects real-world application scenarios and provides a clearer demonstration of the control performance improvements achieved by the proposed method in terms of tracking accuracy, dynamic response, and disturbance rejection. The corresponding tuning values are presented in Figure 5.

To quantitatively evaluate the control strategy, we adopt maximum (MAX) and the root error x₁(i) as the performance indices.

$$\left\{\begin{array}{l}\mathrm{MAX}(e)=\max \left(\left|x_1\left(i\right)\right|\right)\\ \mathrm{RMS}\left(e\right)=\sqrt{{\displaystyle {\sum }_{i=1}^N\frac{x_1^2\left(i\right)}{N}}}\end{array}\right.,$$

(35)

where N is the number of samples.

4.3. Experimental Comparison

Based on practical operating conditions, three experimental scenarios were designed to evaluate the control performance of the proposed control. To comprehensively evaluate the control performance of the proposed ACNTSMC, three experimental cases were conducted. In the first case, the engine operated at 1000 r/min with a load torque of 600 N·m, and a set of step reference rail signals with varying amplitudes was applied to assess the controller’s step response performance. In the second case, the reference rail signal was maintained at a constant value of 70 MPa while the engine speed remained at 1000 r/min; A sudden application of a 600 N·m load torque triggered a rapid fluctuation in engine speed, which served to evaluate the controller’s ability to deal with significant and unknown external disturbances. In the third case, the reference rail signal was designed as a continuously varying ramp signal to evaluate the controller’s dynamic tracking ability under time-varying conditions. A detailed comparison of the operating conditions for the three test cases is provided in

Table 2. Operating conditions for Cases 1, 2, and 3.

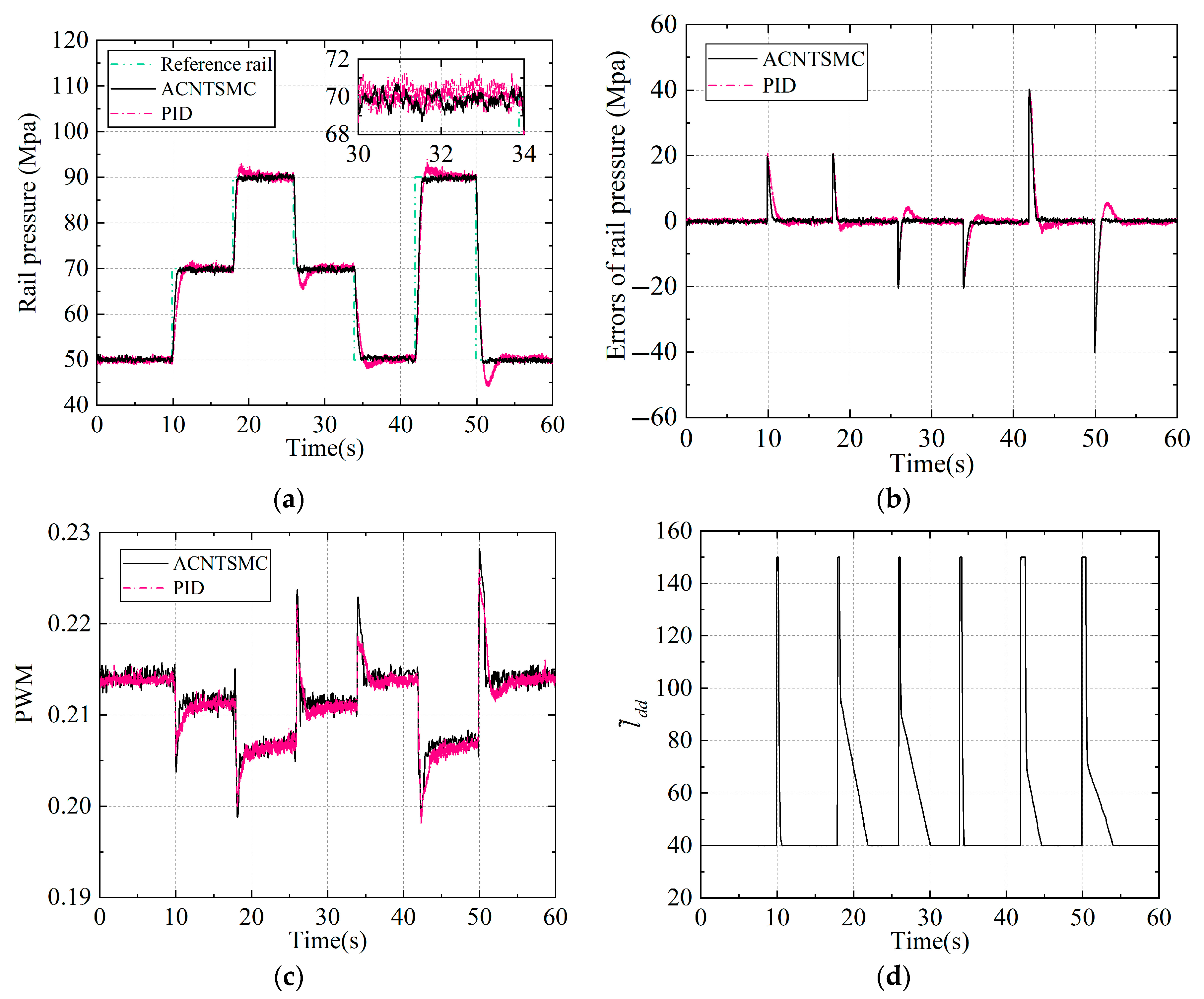
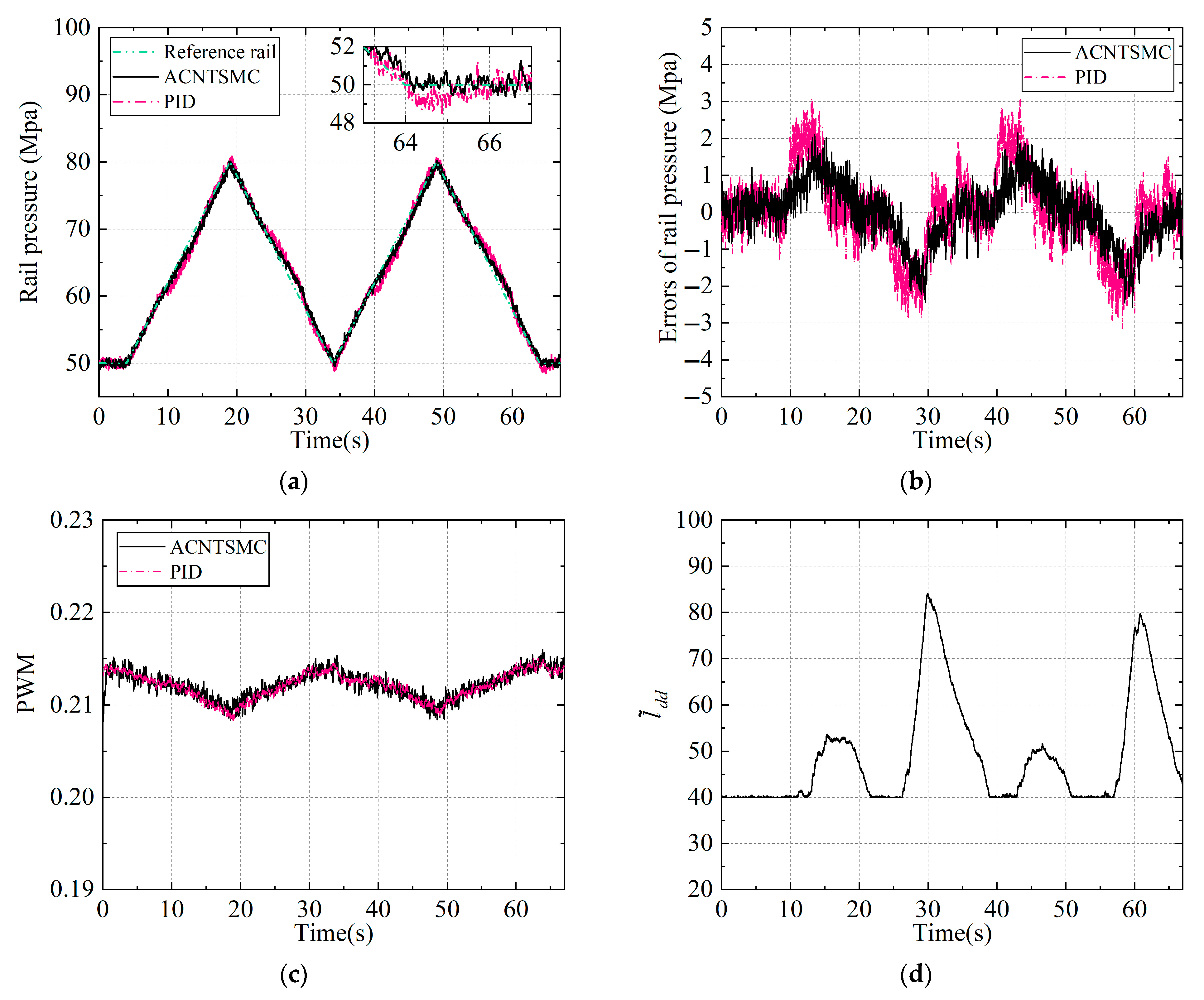
Case	Engine Speed	Load Torque	Reference Rail Pressure	Special Condition
1	1000 r/min	600 N·m	Varying-amplitude step changes 90→50 MPa	Step reference pressure signal with multiple amplitude steps
2	1000 r/min	Sudden 600 N·m torque	Fixed at 70 MPa	Torque disturbance inducing engine speed variation
3	1000 r/min	Not specified	Continuously varying ramp 50→80 MPa linearly	Time-varying ramp reference pressure signal

.

Case 1: Response Performance under Variable-Amplitude Reference Signals

In the first operating condition, the engine operates at a constant speed of 1000 r/min with a 600 N·m load torque. A set of varying-amplitude step reference rail pressure signals is input to comprehensively evaluate the controller’s step response performance under complex working conditions. The experimental results presented in Figure 6 demonstrate detailed comparative analyses from perspectives of control performance, response speed, steady-state accuracy and control smoothness.

As shown in Figure 6a, the PID controller exhibits significant overshoot during multiple step responses, particularly more pronounced in negative steps. For instance, at t = 50 s when the reference rail pressure abruptly decreases from 90 MPa to 50 MPa, the PID controller demonstrates a maximum overshoot of 5.5 MPa, requiring 3.2 s to restore the system within the ±2 MPa steady-state range. In contrast, the ACNTSMC controller completely eliminates overshoot phenomena in all positive/negative steps, achieving a maximum stabilization time of merely 1.0 s, demonstrating remarkable dynamic performance superiority and robustness. Regarding steady-state characteristics, the ACNTSMC controller effectively suppresses rail pressure fluctuations, maintaining steady-state oscillation amplitude within ±1.2 MPa, whereas the PID controller exhibits ±2.0 MPa fluctuations, indicating significantly inferior steady-state precision. The error responses in Figure 6b further validate their steady-state performance differences. During the 50 MPa steady-state phase (t = 36–40 s), the ACNTSMC achieves MAX(e) and RMS(e) values of 1.56 MPa and 0.41 MPa, respectively, compared to 2.77 MPa and 1.07 MPa for the PID controller. This performance superiority primarily originates from the adaptive sliding mode mechanism integrated into the ACNTSMC algorithm, enabling real-time identification and effective compensation of system nonlinearities and disturbances. As depicted in Figure 6c, the ACNTSMC is capable of generating a sharper and faster control input peak at the onset of step transitions, followed by rapid convergence to a steady level. This behavior fundamentally accounts for the superior transient response performance of the proposed algorithm compared to the conventional PID controller. Figure 6d presents the online adaptation process of the adaptive parameter ${\tilde{l}}_{dd}$ in the ACNTSMC controller, which dynamically adjusts sliding mode gain based on system errors. During significant rail pressure variations, ${\tilde{l}}_{dd}$ automatically increases to enhance control intensity, then gradually decreases post-error convergence, achieving optimal balance between rapid response and input suppression. It is worth noting that, due to the design setting of ${\tilde{l}}_{dd}^{\ast }$ = 40, the adaptive gain ${\tilde{l}}_{dd}$ is always maintained above 40 throughout the operation.

This mechanism enables the ACNTSMC to significantly improve control system energy efficiency and stability while maintaining high performance. Under step rail pressure excitations, the ACNTSMC controller demonstrates superior performance compared to conventional PID in response speed, steady-state accuracy, input smoothness, and disturbance rejection capability, validating its engineering adaptability and robustness in HPCRS facing complex dynamic variations.

Case 2: Performance under External Torque-Induced Perturbations

Under the second operating scenario, the engine maintains a constant speed of 1000 r/min while the rail pressure reference is fixed at 70 MPa. At t = 10 s, a sudden torque disturbance of 600 N·m is introduced, inducing rapid engine speed variations and imposing substantial unknown external disturbances. This condition is designed to assess the controller’s disturbance rejection capability and dynamic robustness during steady-state operation. As shown in Figure 7a, following the disturbance onset, the rail pressure regulated by the PID controller exhibits a pronounced deviation of up to 9.8 MPa, taking approximately 5.5 s to return within the ±2 MPa steady-state tolerance. In comparison, the ACNTSMC significantly mitigates the impact, limiting the deviation to 4.3 MPa and achieving recovery within 3.2 s, thereby illustrating its enhanced disturbance handling capability. Further insights are provided by the error metrics in Figure 7b: during the disturbance phase (t = 10~15 s), the ACNTSMC achieves a MAX(e) of 2.1 MPa and RMS(e) of 0.52 MPa, while the PID records 9.2 MPa and 1.83 MPa, respectively. The ACNTSMC’s faster convergence and lower steady-state error confirm its superior adaptability and control precision under disturbance conditions. This performance improvement stems from ACNTSMC’s adaptive gain tuning strategy, which dynamically responds to post-disturbance system deviations by increasing the sliding mode gain to accelerate error correction. As the error subsides, the gain automatically decreases, thus preventing excessive control effort and safeguarding actuator integrity. Figure 7d depicts the real-time evolution of the adaptive gain parameter in the ACNTSMC controller. This parameter increases sharply in response to abrupt disturbances, then gradually decreases as the system stabilizes, enabling a dynamic balance between response aggressiveness and input economy. The lack of such a mechanism in PID control results in persistent oscillatory input signals and degraded transient performance.

Case 3: Performance under Time-Varying Ramp Reference Signals

In the third operating condition, the reference rail pressure signal is designed as a continuously varying ramp profile to evaluate the controller’s dynamic tracking capability under time-varying targets. Such non-constant rail pressure demands frequently occur in practical engine operations, challenging the control system’s continuous regulation capacity and response stability. During experimentation, the reference rail pressure linearly increases from 50 MPa to 80 MPa, requiring real-time, accurate tracking without significant lag or error accumulation. Figure 8a illustrates that the PID controller exhibits notable tracking delay in response to the ramp signal, with the measured rail pressure persistently lagging behind the target. The maximum tracking error reaches 2.1 MPa, and significant deviation occurs during rapid pressure transitions (e.g., t = 40~45 s). In contrast, the ACNTSMC controller closely follows the reference profile with negligible deviation, effectively eliminating lag and avoiding saturation. As depicted in Figure 8a, a quantitative comparison of error profiles during the ramp phase (t = 40~50 s) further supports this observation. The ACNTSMC achieves a maximum tracking error of 2.24 MPa and a root mean square error of 0.46 MPa, outperforming the PID controller’s corresponding values of 3.16 MPa and 1.22 MPa. Throughout the tracking process, the ACNTSMC maintains low-magnitude, stable error dynamics, demonstrating excellent adaptability to time-varying control objectives. Figure 8d shows the trajectory of the adaptive gain parameter in the ACNTSMC. This gain increases proportionally with the rate of pressure change to improve responsiveness and subsequently decreases as tracking error reduces, thereby ensuring a balance between prompt control action and energy efficiency. This real-time gain tuning mechanism enhances the ACNTSMC’s responsiveness and control economy under nonstationary inputs. A detailed comparison of the experimental results of the three cases is provided in

Table 3. The comparative performance results for three cases.

	Controller	MAX (e) (MPa)	RMS (e) (MPa)	Settling Time (s)	Overshoot
Case 1	ACNTSMC	1.56	0.41	1.0	5.5 MPa
	PID	2.77	1.07	3.2	--
Case 2	ACNTSMC	2.1	0.52	3.2	9.8 MPa
	PID	9.2	1.83	5.5	4.3 MPa
Case 3	ACNTSMC	2.24	0.46	--	--
	PID	3.16	1.22	--	--

.

5. Conclusions

This study introduces an innovative adaptive continuous non-singular terminal sliding mode control strategy with an enhanced power reaching law for a HPCRS. Departing from conventional sliding mode control methodologies, the proposed controller effectively suppresses chattering effects through the integration of a low-pass filter, simultaneously improving rail pressure tracking accuracy. The control scheme incorporates a refined power reaching law to accelerate the system’s transient response while maintaining stability. A novel bidirectional adaptive mechanism, dynamically adjusted according to real-time system states, is developed to enhance robustness against inherent HPCRS disturbances and operational uncertainties. For practical engineering implementation, we present an engineering algorithm version that eliminates dependencies on unobservable states and derivative terms, significantly improving applicability in industrial settings. Comparative experimental evaluations against nonlinear PID controllers demonstrate the proposed controller’s superior adaptability and enhanced control performance under various engine operating conditions. Future work will focus on incorporating more detailed compressible fluid modeling to further improve the physical accuracy and adaptability of the system.