Intelligent Deep Learning Modeling and Multi-Objective Optimization of Boiler Combustion System in Power Plants
Abstract
1. Introduction
- (1)
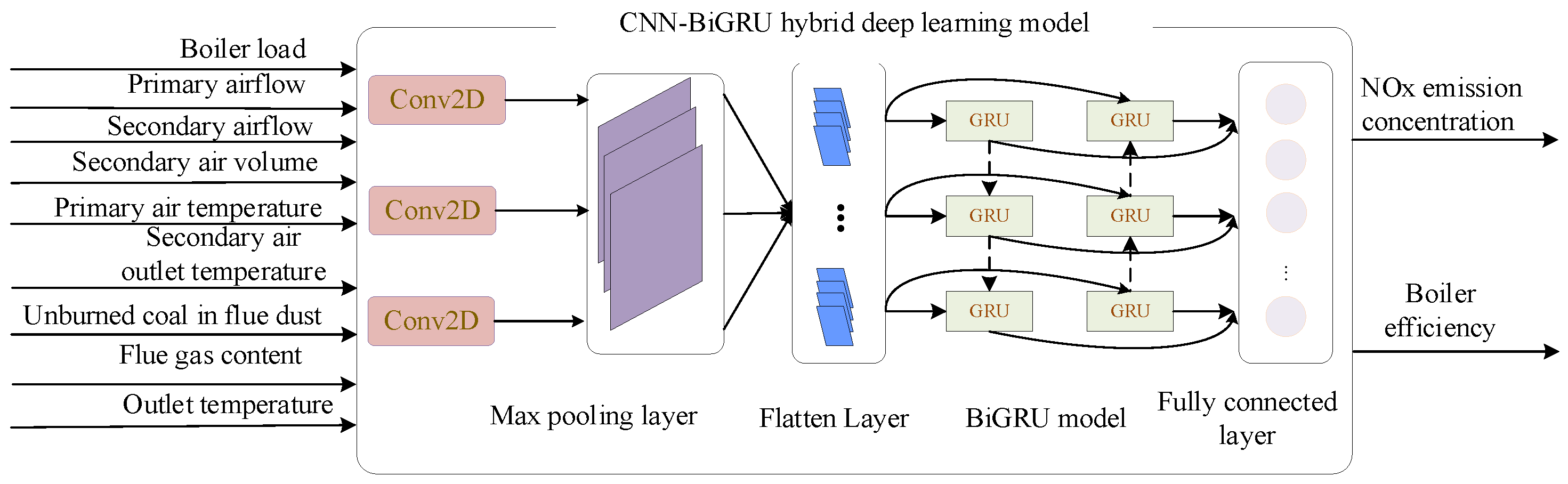
- A hybrid deep learning model, known as CNN-BiGRU, is constructed using historical operational data to accurately predict the NOx emission concentration and to optimize the boiler combustion efficiency of a 300 MW coal-fired boiler. This advanced model integrates convolutional neural networks (CNNs) and bidirectional gated recurrent units (BiGRUs) to capture complex temporal and spatial patterns in boiler combustion. Compared with prior works using LSTM, GRUs, or basic CNN models, the CNN-BiGRU model demonstrates superior prediction accuracy.
- (2)
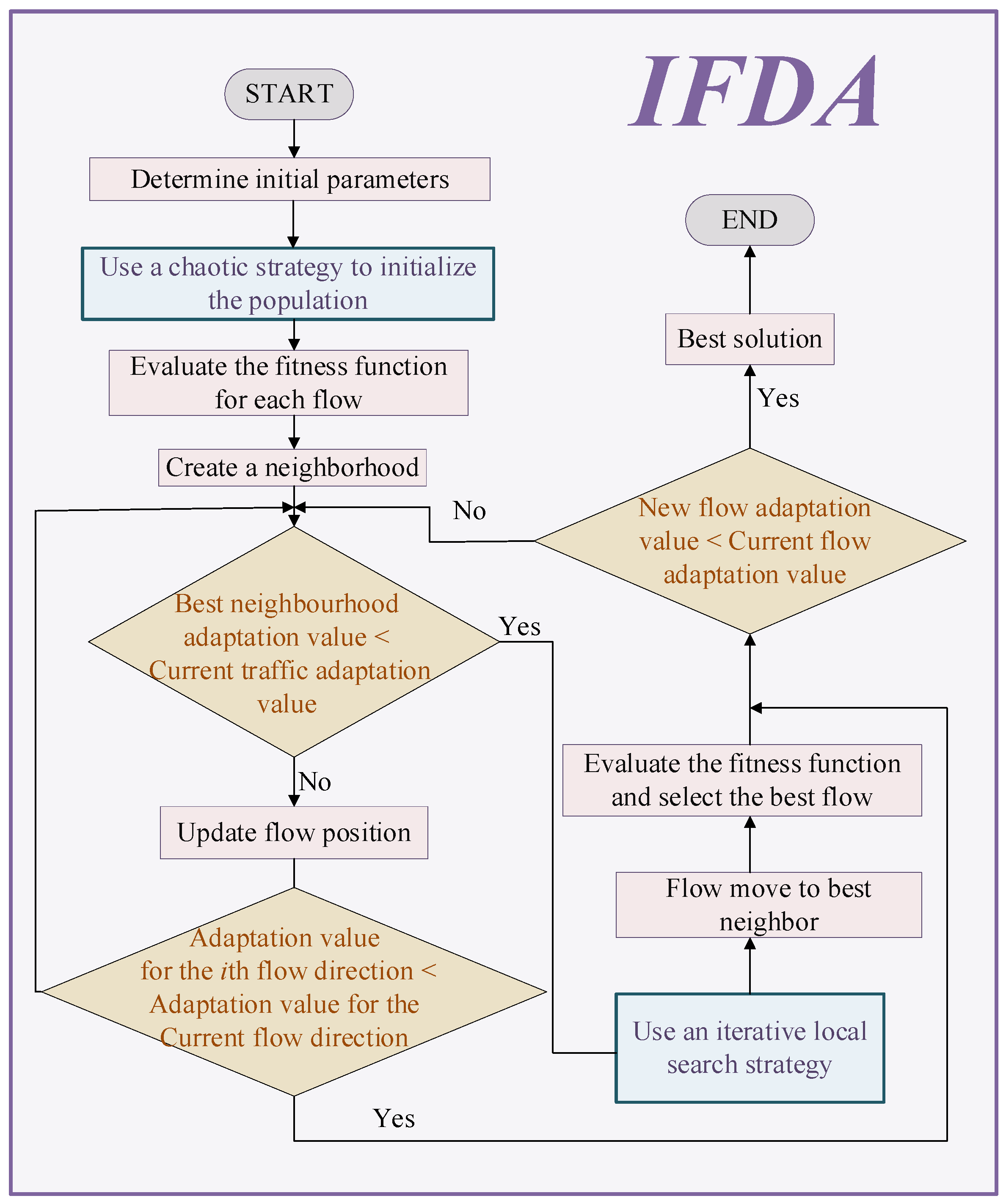
- The NOx emission concentration and boiler combustion efficiency are identified as the optimization objectives. Boiler combustion is optimized with the single goal of using the improved flow direction algorithm (IFDA). The IFDA incorporates iterative local search (ILS) and chaotic initialization to enhance the optimization capabilities, outperforming the original FDA algorithm. The controllable variables and the optimization interval are determined, and the optimal solution is found by continuously adjusting the values of the controllable variables to reduce the NOx emission concentration or to improve the thermal efficiency of the boiler.
- (3)
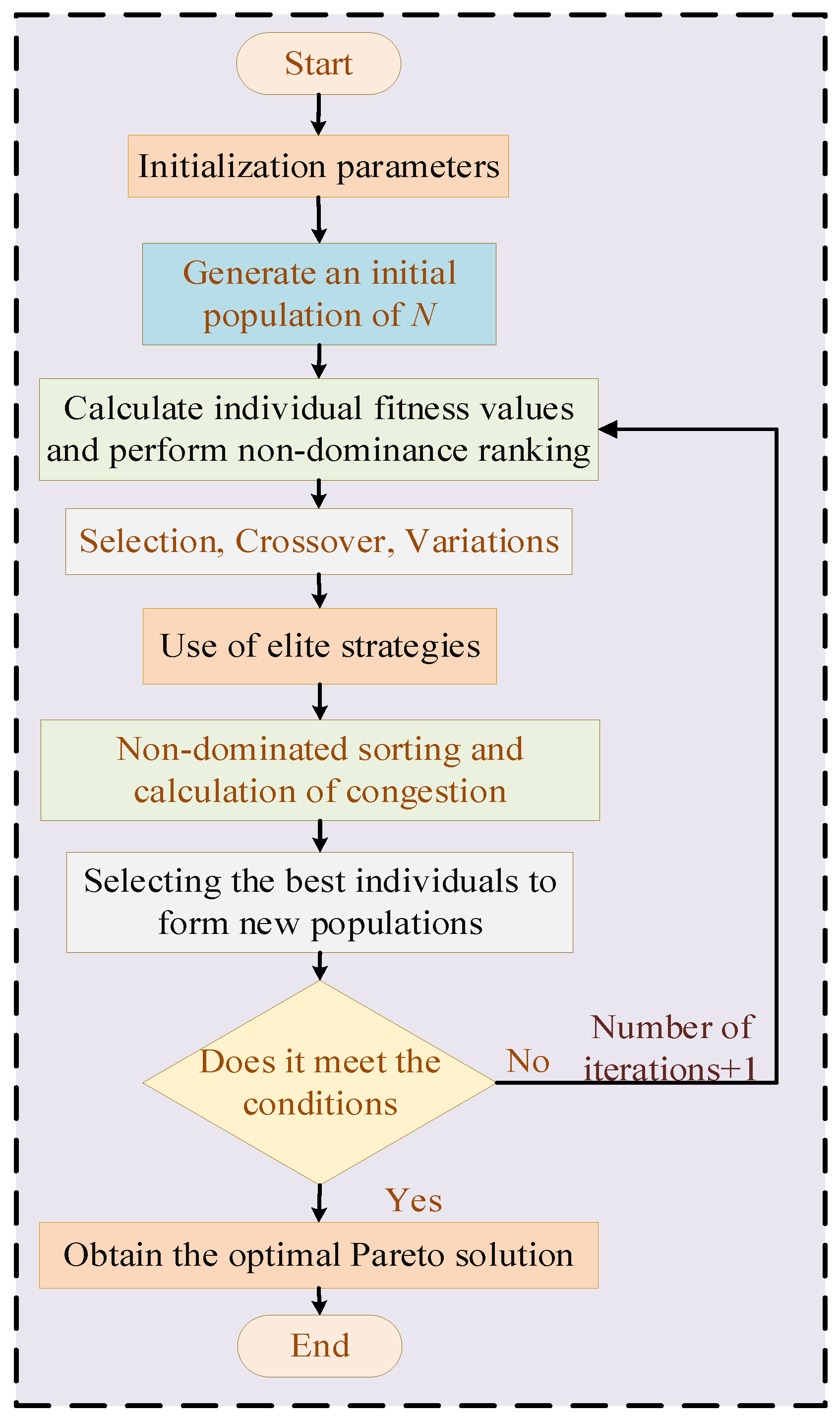
- To optimize the combustion performance of coal-fired boilers, the non-dominated sorting genetic algorithm II (NSGA-II) is employed as a multi-objective optimization tool. The NSGA-II algorithm is utilized to balance NOx emission reduction and boiler efficiency improvement, generating a Pareto optimal front that provides practical solutions for real-world applications. This approach overcomes the limitations of the single-objective optimization methods previously used. The resulting Pareto front is compared against single-objective optimization outcomes, thereby validating the superiority and practicality of the multi-objective approach. The NSGA-II algorithm achieves a significant reduction in NOx emissions and an increase in boiler thermal efficiency, demonstrating the model’s potential for promoting the low-carbon and environmentally sustainable operation of coal-fired boilers.
2. Methods
2.1. Improved Flow Direction Algorithm (IFDA)
2.2. Non-Dominated Sorting Genetic Algorithm-II (NSGA-II)
2.3. The CNN-BiGRU Prediction Model
2.4. Boiler Efficiency Calculations
3. General Flowchart of the CNN-BiGRU and NSCA-II for Boiler Combustion Modeling
- (1)
- Firstly, the study object was identified as a 300 MW circulating fluidized bed boiler, and 3000 samples were selected as the raw data from its historical operation data, of which 70% were classified as the training set and 30% as the test set. There were 25 input variables, while the model output variables mainly involved boiler thermal efficiency and NOx emission concentration.
- (2)
- A CNN-BiGRU-based boiler combustion prediction model was constructed and employed to forecast the concentrations of NOx emissions and the thermal efficiency of the boiler.
- (3)
- A total of five variables, namely the primary airflow rate (y6~y7), secondary airflow rate (y12~y13), and flue gas oxygen content (y20), were selected as controllable variables according to the actual situation, and the optimization interval was determined.
- (4)
- The boiler thermal efficiency and NOx emission concentration were denoted as the optimization objectives.
- (5)
- The NSGA-II algorithm was employed to identify the optimal solution for controllable variables within the defined optimization range, with the best parameter set corresponding to the minimum fitness value achieved by the algorithm.
- (6)
- Simulation analyses were performed to evaluate and compare the outcomes of the IFDA under single-objective and multi-objective optimization scenarios.
4. Case Study
4.1. Data Source and Preprocessing
4.2. Performance Metrics
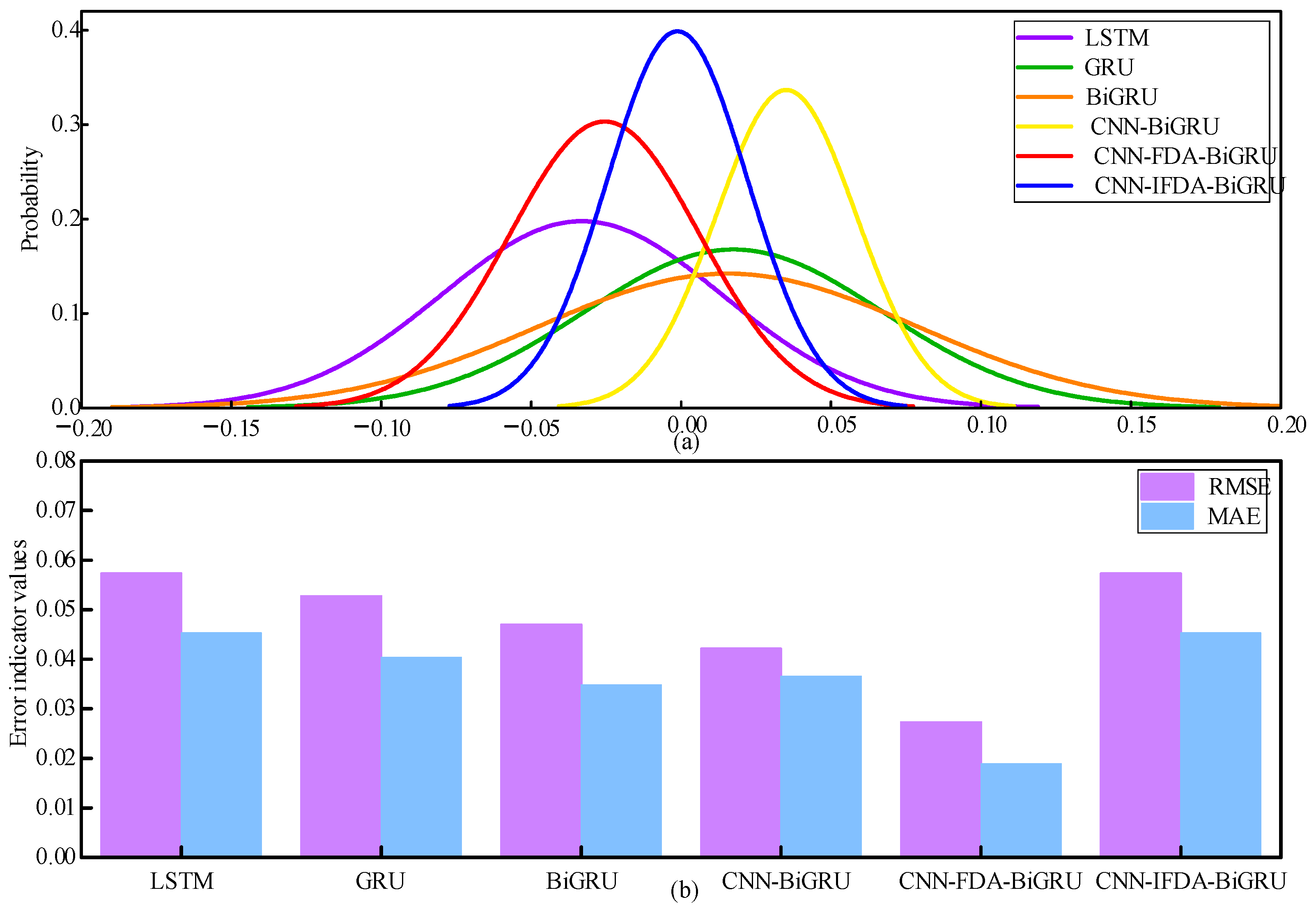
5. Comparison Results
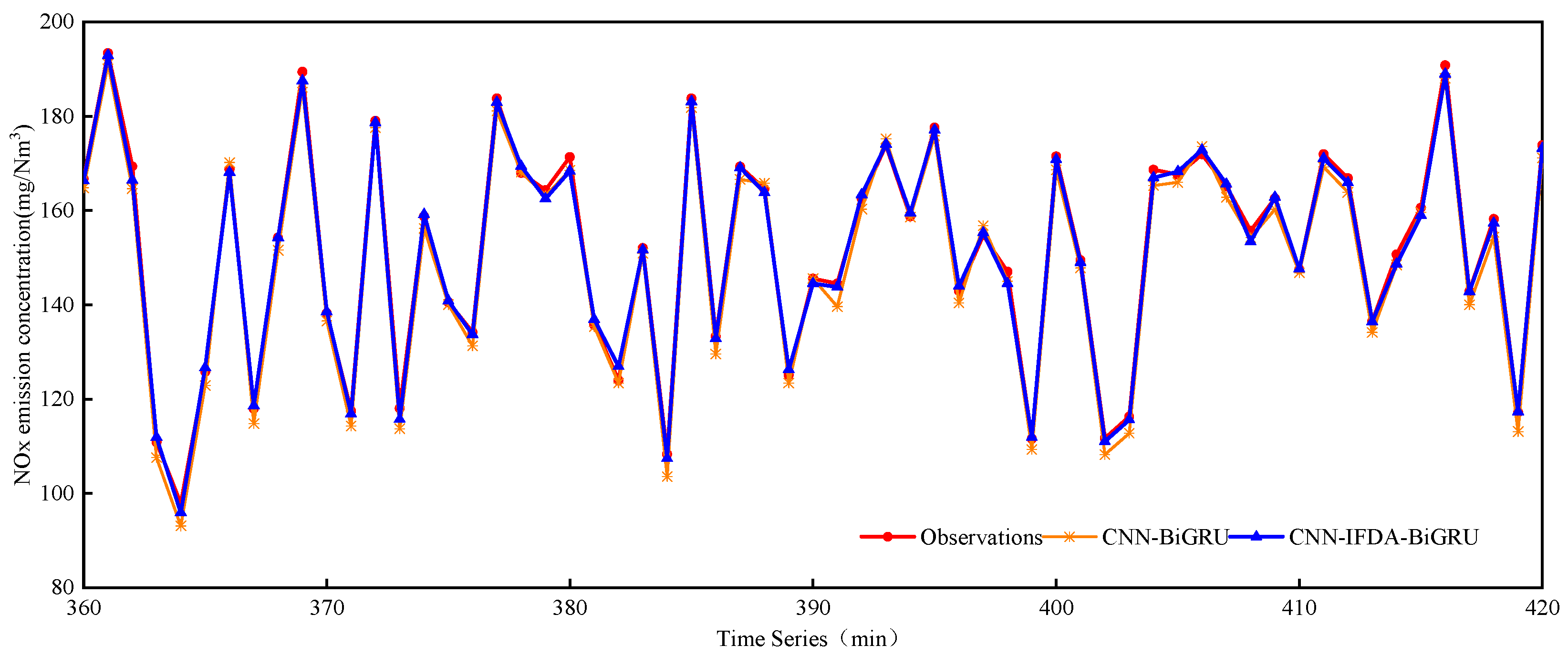
5.1. Analysis of the NOx Prediction Results
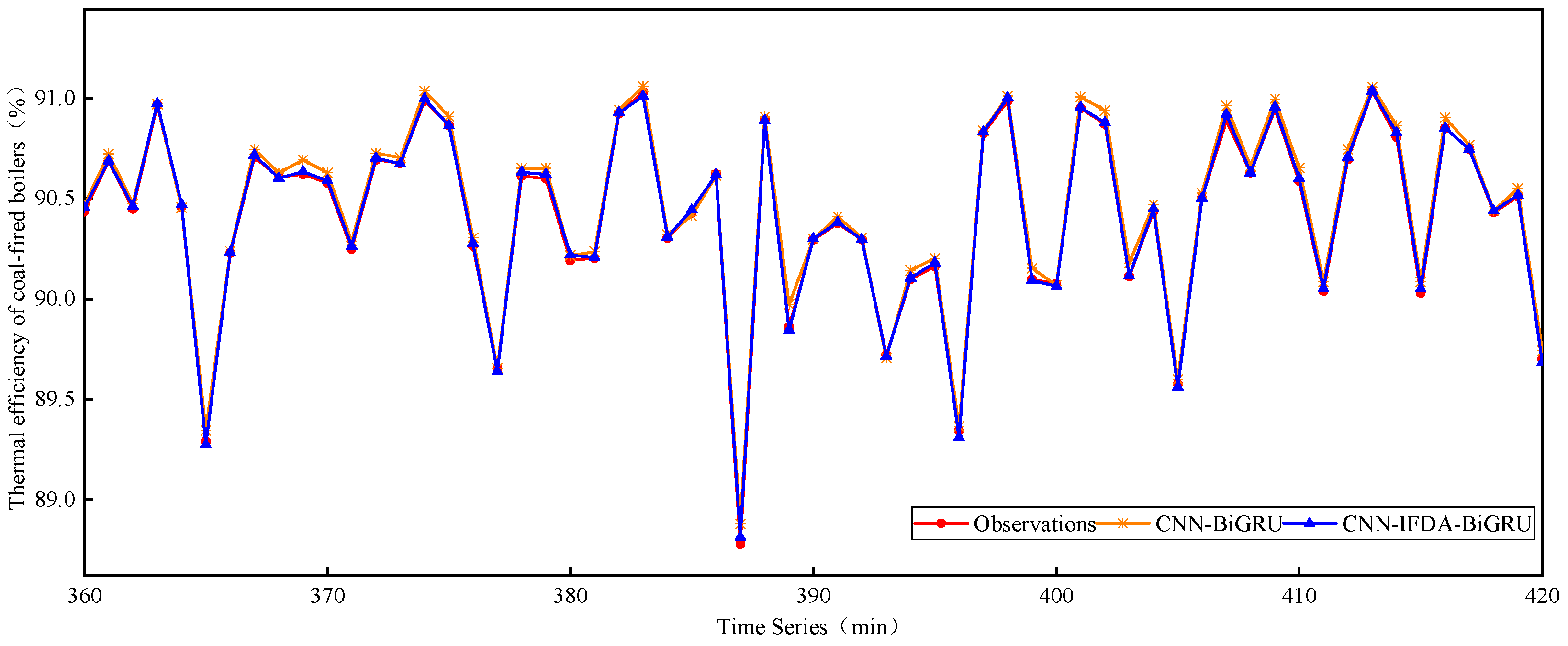
5.2. Analysis of the Thermal Efficiency of Coal-Fired Boilers Prediction Results
5.3. Coal-Fired Boilers with Multiple Objectives
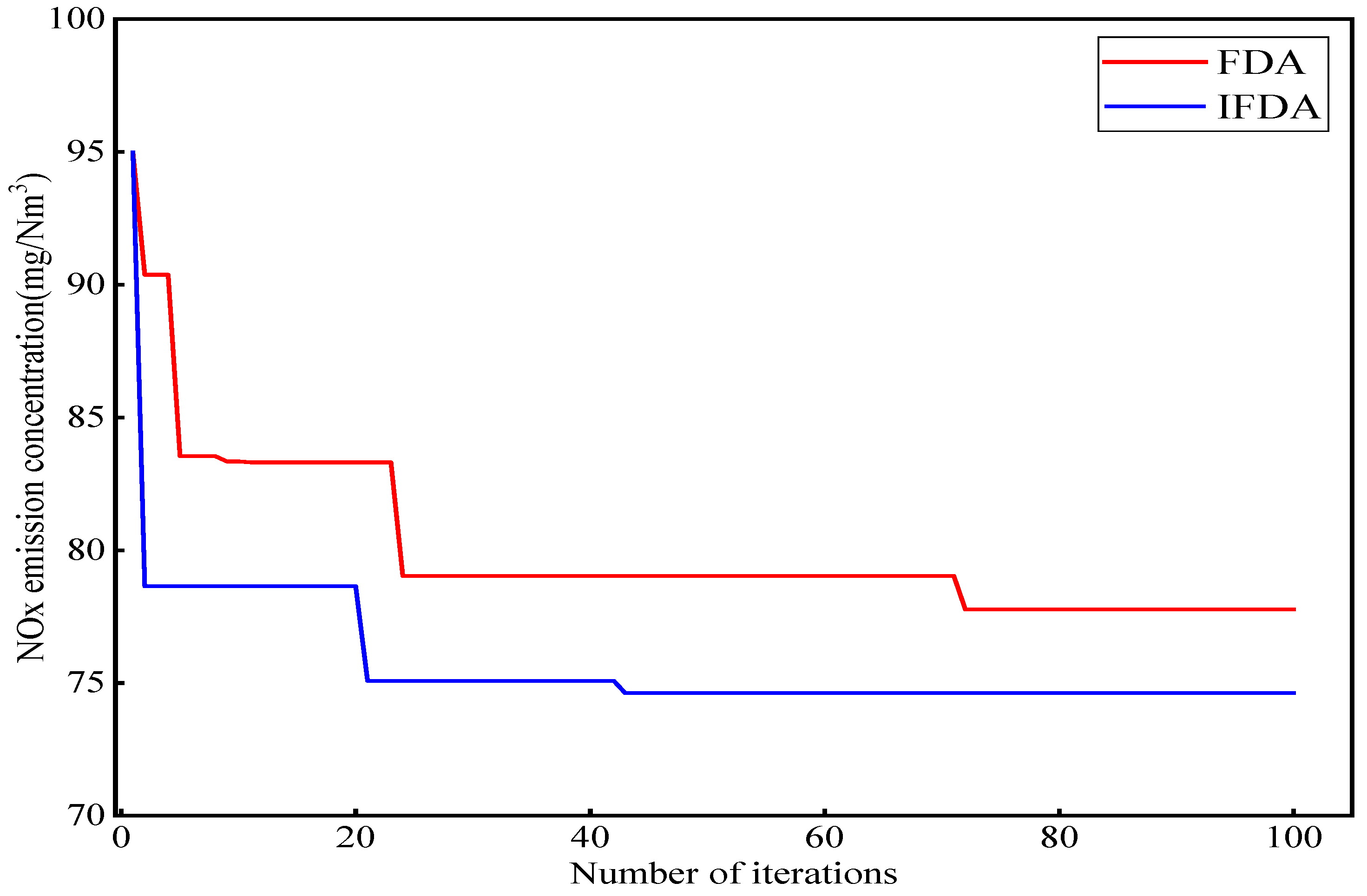
5.3.1. Single-Objective Optimization of NOx Emission Concentrations from Coal-Fired Boilers
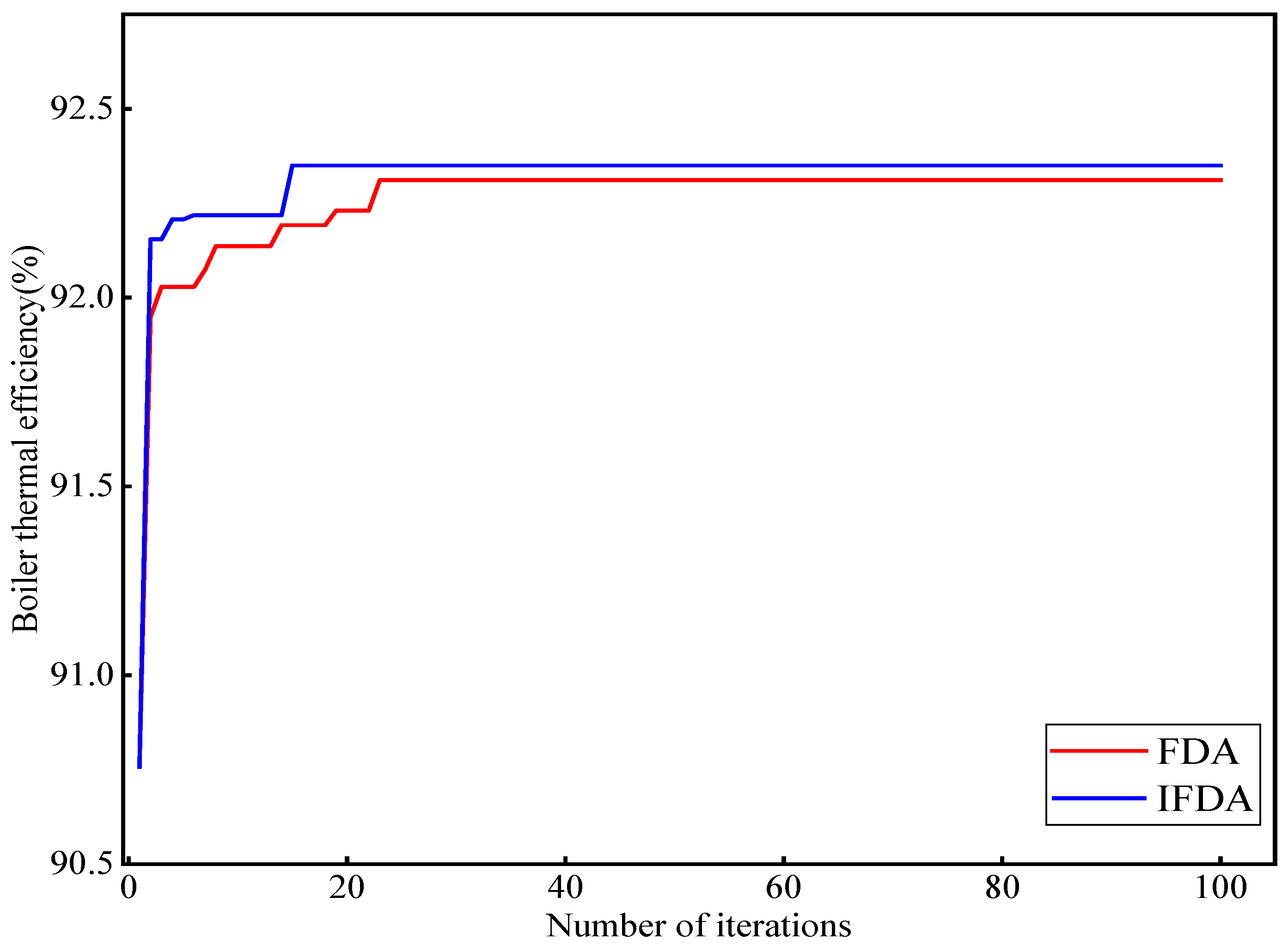
5.3.2. Single-Objective Optimization of Thermal Efficiency in Coal-Fired Boilers
5.3.3. Multi-Objective Optimization for Boiler Combustion
6. Conclusions
- (1)
- A prediction model for the boiler combustion system was developed based on the operating data generated by a 300 MW boiler, which was used to predict the NOx emission concentration and thermal efficiency of the boiler. For the CNN-IFDA-BiGRU model, the MAPE for predicting the NOx emission concentration is 0.78%, while the MAPE for predicting the boiler thermal efficiency is 0.012%.
- (2)
- The boiler combustion system utilizes the FDA and IFDA for single-objective optimization of the boiler thermal efficiency and NOx emission concentration, respectively. Simulation results indicate that the IFDA possesses superior optimization capabilities, effectively achieving the optimization goals of reducing the NOx emission concentration and improving the thermal efficiency of coal-fired boilers separately and efficiently.
- (3)
- The NSGA-II algorithm was employed to optimize the boiler combustion process through an analysis of simulation results. The primary goals were to reduce NOx emission concentrations, improve boiler thermal efficiency, and achieve effective control over the boiler’s combustion system. Utilizing operational data from coal-fired boilers, the proposed approach generated a Pareto optimal front tailored to specific objectives. The findings provide valuable insights for promoting the low-carbon and environmentally sustainable operation of coal-fired boilers. The effectiveness of the NSGA-II algorithm was validated by comparing NOx emission concentrations and boiler thermal efficiencies across various samples before and after optimization, supported by detailed simulation analyses.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ICGO | Improved Chaos Game Optimization | CGO | Chaos Game Optimization |
| BiGRU | Bidirectional Gated Recurrent Unit | PSO | Particle Swarm Optimization |
| NO | Nitric Oxide | NOx | Nitrogen Oxides |
| ML | Machine Learning | ACO | Ant Colony Optimization Algorithm |
| ELM | Extreme Learning Machines | IGOA | Improved Grasshopper Optimization Algorithm |
| SAGA | Simulated Annealing Genetic Algorithm | NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| SVM | Support Vector Machine | MOPSO | Multi-objective Particle Swarm Optimization |
| NO2 | Nitrogen Dioxide | MODE | Multi-objective Differential Evolution |
| RMSE | Root Mean Square Error | ILS | Iterative Local Search |
| CNN | Convolutional Neural Network | MAE | Root Mean Absolute Error |
| ANNSVR | Support Vector Regression Artificial Neural Network | MAPE | Mean Absolute Percentage Error |
| LSTM | Long Short-Term Memory | EMD | Empirical Mode Decomposition |
| RNN | Recurrent Neural Network | R | Correlation Coefficient |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise | LSH | Locality Sensitive Hashing |
| SPS | Steam Power System | FDA | Flow Direction Algorithm |
References
- Yang, G.; Wang, Y.; Li, X. Prediction of the NOx emissions from thermal power plant using long-short term memory neural network. Energy 2020, 192, 116597. [Google Scholar] [CrossRef]
- Resitoglu, I.A.; Keskin, A.; Karaman, B.; Ozarslan, H. Suppressing Calcium Deactivation in Selective Catalytic Reduction of NOx from Diesel Engines Using Antimony. Processes 2025, 13, 1914. [Google Scholar] [CrossRef]
- Ren, M.; Liang, Y.; Chen, J.; Xu, X.; Cheng, L. Fault detection for NOx emission process in thermal power plants using SIP-PCA. ISA Trans. 2023, 140, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Ke, X.; Zhu, S.; Huang, Z.; Zhang, M.; Lyu, J.; Yang, H.; Zhou, T. Issues in deep peak regulation for circulating fluidized bed combustion: Variation of NOx emissions with boiler load. Environ. Pollut. 2023, 318, 120912. [Google Scholar] [CrossRef] [PubMed]
- Bian, C.; Huang, J.; Sun, R. Numerical optimization of combustion and NOX emission in a retrofitted 600MWe tangentially-fired boiler using lignite. Appl. Therm. Eng. 2023, 226, 120228. [Google Scholar] [CrossRef]
- Li, S.; Xu, T.; Hui, S.; Wei, X. NOx emission and thermal efficiency of a 300MWe utility boiler retrofitted by air staging. Appl. Energy 2009, 86, 1797–1803. [Google Scholar] [CrossRef]
- Wen, X.; Li, K.; Wang, J. NOx emission predicting for coal-fired boilers based on ensemble learning methods and optimized base learners. Energy 2023, 264, 126171. [Google Scholar] [CrossRef]
- Qiao, J. A novel online modeling for NOx generation prediction in coal-fired boiler. Sci. Total Environ. 2022, 847, 157542. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Bansal, R.C. Integrating multi-objective optimization with computational fluid dynamics to optimize boiler combustion process of a coal fired power plant. Appl. Energy 2014, 130, 658–669. [Google Scholar] [CrossRef]
- Li, G.; Niu, P.; Ma, Y.; Wang, H.; Zhang, W. Tuning extreme learning machine by an improved artificial bee colony to model and optimize the boiler efficiency. Knowl.-Based Syst. 2014, 67, 278–289. [Google Scholar] [CrossRef]
- Tan, P.; He, B.; Zhang, C.; Rao, D.; Li, S.; Fang, Q.; Chen, G. Dynamic modeling of NOx emission in a 660 MW coal-fired boiler with long short-term memory. Energy 2019, 176, 429–436. [Google Scholar] [CrossRef]
- Liu, X.; Qi, H.; Ren, M.; Cheng, L. A prediction method of NOx in thermal power plants using GC-LSTM neural network. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Wang, Y.; Yang, G. A hybrid NOx emission prediction model based on CEEMDAN and AM-LSTM. Fuel 2022, 310, 122486. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, X.; Cao, S.; Zhou, H.; Fan, S.; Li, K.; Huang, W. NOx emission prediction using a lightweight convolutional neural network for cleaner production in a down-fired boiler. J. Clean. Prod. 2023, 389, 136060. [Google Scholar] [CrossRef]
- Ma, H.; Peng, T.; Zhang, C.; Ji, C.; Li, Y.; Nazir, M.S. Developing an evolutionary deep learning framework with random forest feature selection and improved flow direction algorithm for NOx concentration prediction. Eng. Appl. Artif. Intell. 2023, 123, 106367. [Google Scholar] [CrossRef]
- Li, N.; Lv, Y.; Hu, Y. Prediction of NOx Emissions from a Coal-Fired Boiler Based on Convolutional Neural Networks with a Channel Attention Mechanism. Energies 2023, 16, 76. [Google Scholar] [CrossRef]
- Wan, A.P.; Yang, J.; Miao, X. Boiler Load Forecasting of CHP Plant Based on Attention Mechanism and Deep Neural Network. J. Shanghai Jiao Tong Univ. 2023, 57, 316–325. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000. [Google Scholar] [CrossRef]
- Wei, Z.; Li, X.; Xu, L.; Cheng, Y. Comparative study of computational intelligence approaches for NOx reduction of coal-fired boiler. Energy 2013, 55, 683–692. [Google Scholar] [CrossRef]
- Dirik, M. Prediction of NOx emissions from gas turbines of a combined cycle power plant using an ANFIS model optimized by GA. Fuel 2022, 321, 124037. [Google Scholar] [CrossRef]
- Zhou, H.; Pei Zhao, J.; Gang Zheng, L.; Lin Wang, C.; Fa Cen, K. Modeling NOx emissions from coal-fired utility boilers using support vector regression with ant colony optimization. Eng. Appl. Artif. Intell. 2012, 25, 147–158. [Google Scholar] [CrossRef]
- Song, J.; Romero, C.E.; Yao, Z.; He, B. Improved artificial bee colony-based optimization of boiler combustion considering NOX emissions, heat rate and fly ash recycling for on-line applications. Fuel 2016, 172, 20–28. [Google Scholar] [CrossRef]
- Yao, Z.; Romero, C.; Baltrusaitis, J. Combustion optimization of a coal-fired power plant boiler using artificial intelligence neural networks. Fuel 2023, 344, 128145. [Google Scholar] [CrossRef]
- Wei, L.; Yan, F.; Hu, J.; Xi, G.; Liu, B.; Zeng, J. Nox conversion efficiency optimization based on NSGA-II and state-feedback nonlinear model predictive control of selective catalytic reduction system in diesel engine. Appl. Energy 2017, 206, 959–971. [Google Scholar] [CrossRef]
- Xu, W.; Huang, Y.; Song, S.; Chen, B.; Qi, X. A novel online combustion optimization method for boiler combining dynamic modeling, multi-objective optimization and improved case-based reasoning. Fuel 2023, 337, 126854. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, C.; Liu, D. Data-driven based multi-objective combustion optimization covering static and dynamic states. Expert Syst. Appl. 2022, 210, 118531. [Google Scholar] [CrossRef]
- Xiao, W.; Cheng, A.; Li, S.; Jiang, X.; Ruan, X.; He, G. A multi-objective optimization strategy of steam power system to achieve standard emission and optimal economic by NSGA-II. Energy 2021, 232, 120953. [Google Scholar] [CrossRef]
- Tang, W.J.; Wang, H.T.; Liu, P.J.; Qian, F.L. Combustion Optimization Under Deep Peak Shaving Based on DYNA-A3C With Dynamic Weight. Front. Energy Res. 2023, 10, 953387. [Google Scholar] [CrossRef]
- Karami, H.; Anaraki, M.V.; Farzin, S.; Mirjalili, S. Flow Direction Algorithm (FDA): A Novel Optimization Approach for Solving Optimization Problems. Comput. Ind. Eng. 2021, 156, 107224. [Google Scholar] [CrossRef]
- Chen, H.; Li, W.; Yang, X. A whale optimization algorithm with chaos mechanism based on quasi-opposition for global optimization problems. Expert Syst. Appl. 2020, 158, 113612. [Google Scholar] [CrossRef]
- Gan, C.; Cao, W.; Wu, M.; Chen, X. A new bat algorithm based on iterative local search and stochastic inertia weight. Expert Syst. Appl. 2018, 104, 202–212. [Google Scholar] [CrossRef]
- Kalyanmoy, D. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar]
- Toksari, M.D. A hybrid algorithm of Ant Colony Optimization (ACO) and Iterated Local Search (ILS) for estimating electricity domestic consumption: Case of Turkey. Int. J. Electr. Power Energy Syst. 2016, 78, 776–782. [Google Scholar] [CrossRef]
- Zhang, Q.; Yi, H.; Yu, Z.; Gao, J.; Wang, X.; Lin, H.; Shen, B. Energy-exergy analysis and energy efficiency improvement of coal-fired industrial boilers based on thermal test data. Appl. Therm. Eng. 2018, 144, 614–627. [Google Scholar] [CrossRef]


| Variable Name | Unit | Variable | |
|---|---|---|---|
| Input | Load | % | y1 |
| Ambient pressure | Coal quantity of the coal feeder | t/h | y2–y5 |
| Ambient humidity | Primary airflow of the burner inlet | kNm3/h | y6–y7 |
| Air-filter pressure difference | Primary air temperature of the burner inlet | °C | y8, y9 |
| Gas-turbine exhaust pressure | Primary air fan inlet temperature | °C | y10, y11 |
| Turbine inlet temperature | Distribution flow of the secondary air | kNm3/h | y12, y13 |
| Turbine after temperature | Distribution flow of secondary air | kNm3/h | |
| Compressor discharge pressure | Air preheater secondary air outlet air temperature | °C | y14, y15 |
| Turbine energy yield | Limestone powder conveying motor current | AMP | y16, y17 |
| Carbon monoxide | Flue gas oxygen content | % | y18 |
| Nitrogen oxides | Flue gas temperature | °C | y19 |
| Outlet temperature of slag cooler | °C | Y20–y23 | |
| Output | NOx emission concentration | mg/m3 | |
| efficiency | % |
| NOx Emission Prediction Model | RMSE | MAE | R | MAPE |
|---|---|---|---|---|
| LSTM | 4.7415 | 3.8592 | 0.9953 | 0.0266 |
| GRU | 4.2426 | 3.4098 | 0.9964 | 0.0274 |
| BiGRU | 3.8799 | 3.3472 | 0.9977 | 0.0228 |
| CNN-BiGRU | 2.8784 | 2.4829 | 0.9991 | 0.0199 |
| CNN-FDA-BiGRU | 2.1745 | 1.7395 | 0.9985 | 0.0137 |
| CNN-IFDA-BiGRU | 1.3396 | 1.064 | 0.9992 | 0.0078 |
| Thermal Efficiency Prediction Model | RMSE | MAE | R | MAPE |
|---|---|---|---|---|
| LSTM | 0.0573 | 0.0453 | 0.9935 | 0.00050 |
| GRU | 0.0527 | 0.0404 | 0.9927 | 0.00045 |
| BiGRU | 0.0470 | 0.0348 | 0.9938 | 0.00038 |
| CNN-BiGRU | 0.0421 | 0.0365 | 0.9984 | 0.00040 |
| CNN-FDA-BiGRU | 0.0273 | 0.0189 | 0.9981 | 0.00021 |
| Controllable Variables | Flue Gas Oxygen Content (%a) | Primary Airflow (KNm3/h) | Secondary Airflow (KNm3/h) |
|---|---|---|---|
| Controllable interval | 0.3–3.0 | 1200–1000 | 100–1200 |
| Variables | Primary Airflow | Secondary Airflow | Flue Gas Oxygen Content | ||
|---|---|---|---|---|---|
| y6 | y7 | y12 | y13 | y18 | |
| Observations | 866.15 | 864.27 | 540.70 | 947.79 | 1.06 |
| FDA | 853.03 | 793.89 | 521.58 | 896.28 | 1.01 |
| IFDA | 847.51 | 680.05 | 526.79 | 877.91 | 0.86 |
| Variables | Primary Airflow | Secondary Airflow | Flue Gas Oxygen Content | ||
|---|---|---|---|---|---|
| y6 | y7 | y12 | y13 | y20 | |
| Observations | 866.15 | 864.27 | 540.70 | 947.79 | 1.06 |
| FDA | 896.72 | 868.02 | 560.38 | 952.09 | 1.31 |
| IFDA | 921.51 | 980.05 | 596.79 | 977.91 | 2.09 |
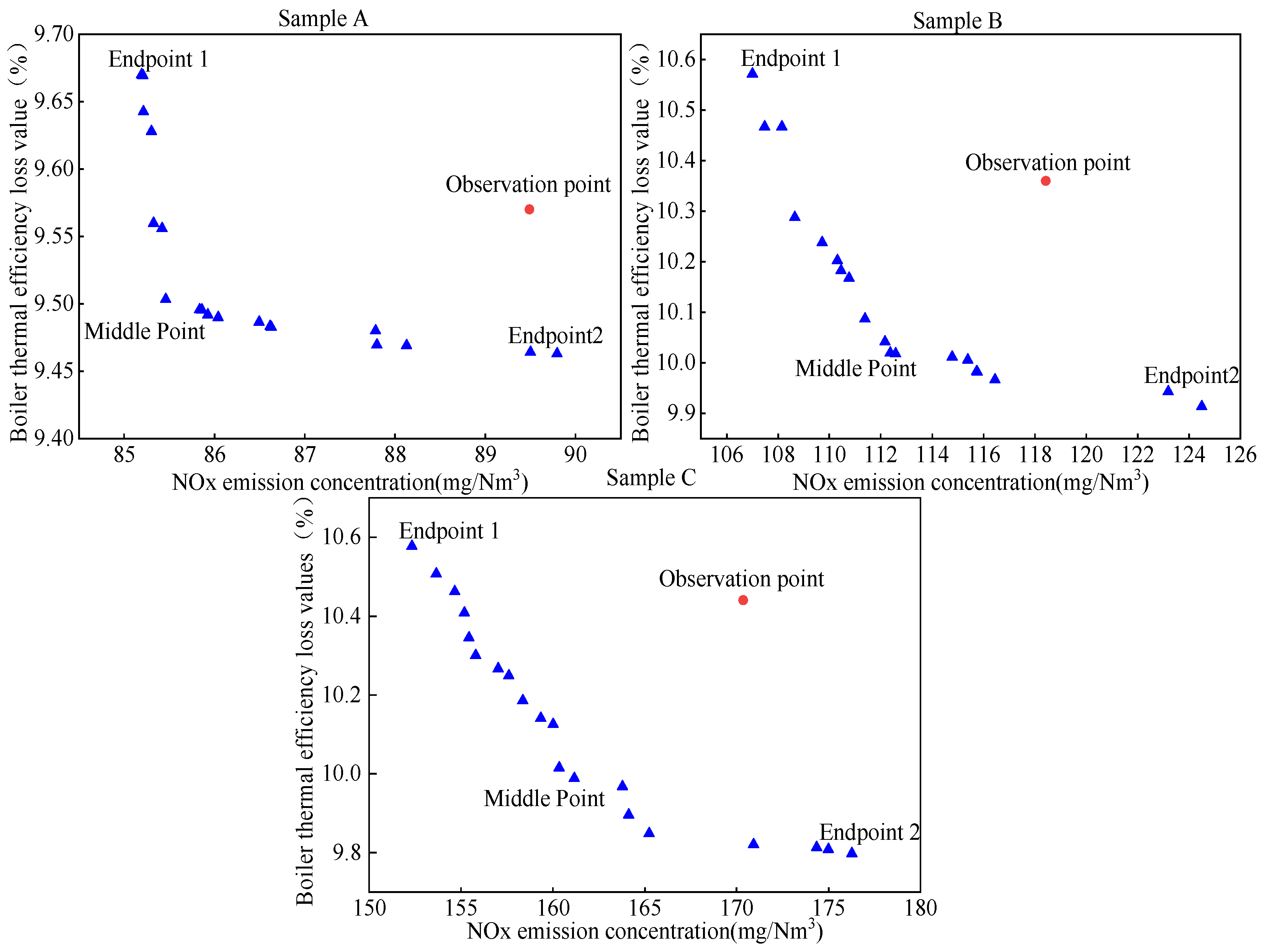
| Sample | Optimization Objectives | NOx Emission Concentration (mg/Nm3) | Thermal Efficiency (%) |
|---|---|---|---|
| Sample A | Observations | 89.49 | 90.43 |
| Endpoints 1 | 85.19 | 90.34 | |
| Endpoints 2 | 89.79 | 90.54 | |
| Middle Point | 85.46 | 90.50 | |
| Sample B | Observations | 118.43 | 89.64 |
| Endpoints 1 | 107.01 | 89.43 | |
| Endpoints 2 | 124.50 | 90.09 | |
| Middle Point | 112.37 | 89.98 | |
| Sample C | Observations | 170.36 | 89.56 |
| Endpoints 1 | 152.33 | 89.42 | |
| Endpoints 2 | 176.27 | 90.20 | |
| Middle Point | 161.17 | 90.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Zheng, Y.; Zhao, H.; Zhu, J.; Fu, Y.; Tang, Z.; Zhang, C.; Peng, T. Intelligent Deep Learning Modeling and Multi-Objective Optimization of Boiler Combustion System in Power Plants. Processes 2025, 13, 2340. https://doi.org/10.3390/pr13082340
Huang C, Zheng Y, Zhao H, Zhu J, Fu Y, Tang Z, Zhang C, Peng T. Intelligent Deep Learning Modeling and Multi-Objective Optimization of Boiler Combustion System in Power Plants. Processes. 2025; 13(8):2340. https://doi.org/10.3390/pr13082340
Chicago/Turabian StyleHuang, Chen, Yongshun Zheng, Hui Zhao, Jianchao Zhu, Yongyan Fu, Zhongyi Tang, Chu Zhang, and Tian Peng. 2025. "Intelligent Deep Learning Modeling and Multi-Objective Optimization of Boiler Combustion System in Power Plants" Processes 13, no. 8: 2340. https://doi.org/10.3390/pr13082340
APA StyleHuang, C., Zheng, Y., Zhao, H., Zhu, J., Fu, Y., Tang, Z., Zhang, C., & Peng, T. (2025). Intelligent Deep Learning Modeling and Multi-Objective Optimization of Boiler Combustion System in Power Plants. Processes, 13(8), 2340. https://doi.org/10.3390/pr13082340






