Abstract
Produced water treatment (PWT) is a critical process in offshore oil and gas production, ensuring compliance with stringent environmental discharge regulations and minimizing environmental impact. This process is characterized by inherent nonlinearities, coupled system dynamics, and the presence of significant disturbances that can impede operational efficiency and separation performance. Effective control strategies are essential to maintain stable operation and high separation efficiency under dynamic and uncertain conditions. This paper presents a comprehensive evaluation of advanced control methods applied to a pilot-scaled PWT facility designed to replicate offshore conditions. Four control solutions are assessed, i.e., (i) baseline approach using PID controllers; (ii) Multi-Input–Multi-Output (MIMO) control; (iii) MIMO Model Predictive Control (MPC); and (iv) MIMO Model Reference Adaptive Control (MRAC). The motivation lies in their differing capabilities for disturbance rejection, tracking accuracy, robustness, and computational feasibility. Real-world operational data were used to assess each strategy in regulating critical process variables, the interface water level in the three-phase gravity separator, and the pressure drop ratio (PDR) in the hydrocyclone, both closely linked to de-oiling efficiency. The results highlight the distinct advantages and limitations of each method. In general, the baseline PID solution offers simplicity but limited adaptability, while advanced strategies such as MIMO , MPC, and MRAC solutions demonstrate enhanced reference-tracking and de-oiling performances subject to diverse operating conditions and disturbances, though different control solutions still exhibit different dynamic characteristics. The findings provide systematic insights into selecting optimal control architectures for offshore PWT systems, supporting improved operational performance and reduced environmental footprint.
1. Introduction
1.1. Motivation
Offshore produced water treatment (PWT) is a crucial process related to sustainable offshore oil and gas production, as it helps mitigate environmental impacts by removing hydrocarbon residuals and other contaminants from the vast produced water before this stream is re-injected into the reservoir (for enhanced oil recovery purposes) or directly discharged to the ocean. This type of process is highly compact and complex due to limited space and weight constraints in offshore applications, as well as inherent nonlinearities, couplings, and diverse and harsh offshore operating conditions. Consequently, different advanced control solutions have been continuously demanded by the relevant industry to comply with increasingly stringent produced water discharge regulations [1,2,3,4].
A central technical challenge in PWT arises from the strong interactions and dynamic couplings between multiple subsystems, particularly the upstream three-phase gravity separator (TPGS) and the downstream de-oiling hydrocyclone. The TPGS subsystem plays a critical role by separating the produced fluid into gas, oil, and water phases based on density differences, which inherently involves complex multiphase flow dynamics. Maintaining a stable water interface level in the TPGS is essential, as fluctuations can propagate downstream and adversely affect the hydrocyclone’s performance in oil removal. Control challenges include dealing with nonlinearities, time-varying disturbances, and operational constraints such as valve saturation and limited sensor accuracy. These difficulties motivate the exploration of robust and adaptive control strategies that can ensure consistent separation efficiency under dynamic offshore conditions.
One of the key challenges is how to effectively handle the potential conflict caused by the functional coupling between the upstream TPGS system and the downstream de-oiling hydrocyclone system, which has been identified as a key factor in determining the de-oiling efficiency of the entire PWT process [5,6,7]. This interconnection introduces multivariable interactions and competing control objectives, making it necessary to apply advanced control solutions capable of managing these complexities while optimizing overall system performance.
To explore the feasibility and effectiveness of different advanced control solutions in real-world applications, this study evaluates four different control solutions, i.e., (i) a baseline PID control, (ii) MIMO control, (iii) MIMO MPC, and (iv) MIMO MRAC, using a laboratory-scale PWT pilot plant that can mimic various real-world PWT conditions.
1.2. State of the Art
By applying the plant-wide control strategy [7], substantial efforts have been made to address the challenges faced in offshore PWT processes. For example, [2] explored several anti-slugging control strategies aimed at stabilizing the multiphase flow through the riser system, thereby mitigating fluctuations caused by slugging inside the TPGS. The study investigated a range of methods, including feedback linearization, gain scheduling, internal model control, and adaptive PI control, highlighting their potential to improve flow stability and overall system performance.
By focusing on the coupled de-oiling hydrocyclone and TPGS systems, a control solution has been proposed in [3], and the system performance is compared against a benchmark PID control. A recent study proposed an -based fault-tolerant control strategy to mitigate disturbance sensitivity under operational constraints in [8]. The work further introduced a differential game framework to address actuator faults and saturation, and developed a reinforcement learning approach with finite-time convergence to enable rapid fault recovery and maintain safety boundaries.
A nonlinear MPC solution has also been studied and tested in [9]. Moreover, in [10], first-principles and gray-box models were developed to describe dynamic relationships, demonstrating suitability for control design and enabling the integration of nonlinear strategies such as feedback linearization and sliding-mode control, thereby enhancing robustness under uncertainty. Moreover, Vallabhan et al. [11] investigated the application of feedforward, cascade, and MPC algorithms for de-oiling hydrocyclones through a comprehensive simulation study, highlighting their potential to improve separation efficiency and operational reliability.
Though all these advanced control solutions showed better performances compared with a benchmark PI control solution, all these solutions are based on the assumption that the de-oiling efficiency is proportional with one of the controlled variables, named as the pressure drop ratio (PDR), and it has been discovered using (online) oil-in-water (OiW) sensors that this linear relationship is only valid for specific operating ranges subject to a static condition [1,12]. It is clear that a reliable evaluation and design of the dynamic de-oiling efficiency cannot be feasible without any real-time OiW monitoring installed in PWT processes. Addressing this need, in [13], nonlinear control-oriented Hammerstein–Wiener models of an offshore PWT hydrocyclone were identified from OiW concentration data via exhaustive search, and PI control was implemented to maintain discharge concentration tracking under varying operating conditions, with improvements in separation efficiency and reductions in oil discharge demonstrated.
Adaptive control is crucial in real-world applications because it dynamically adjusts to uncertainties and disturbances, ensuring reliable and efficient operation despite changing process conditions [14]. In this context, robust MRAC designs have been developed to address practical challenges such as actuator faults, model uncertainties, and external disturbances [15,16,17]. Furthermore, advanced frameworks, such as the decentralized state-feedback MRAC proposed in [18,19,20,21] with time-varying delays, highlight the scalability and robustness of adaptive control in handling complex, distributed industrial processes. Specifically for PWT applications, a robust multivariable MRAC based on output feedback and LDS decomposition was proposed in [4], demonstrating superior tracking and disturbance rejection compared to optimized PI controllers. Collectively, these studies show that adaptive control techniques, particularly MRAC, substantially improve robustness and performance, underscoring their strong potential for real-world applications.
1.3. Key Contributions
The primary objective of this study is to evaluate and compare advanced control strategies for offshore PWT systems under realistic operating conditions. The assessment focuses on regulating key process variables, namely the water interface level within the TPGS and the PDR in the de-oiling hydrocyclone system, while also measuring dynamic de-oiling efficiency using an advanced online OiW monitoring system. A benchmark PID controller is implemented to represent conventional PWT practices, and its performance is compared with three advanced strategies: , MPC, and an MRAC solution. Notably, the proposed MRAC-based control is applied for the first time to a PWT system. Furthermore, this study presents a comprehensive experimental comparison across all controllers, incorporating a broader set of performance metrics than our previous work, to provide deeper insights into which control strategy is best suited for real-world offshore applications. In summary, the key contributions of this paper are as follows:
- Real-world Data Application: The study uses real-world pilot-scale data to evaluate control strategies, offering practical insights into their performance under actual operating conditions.
- First-Time MRAC Application in PWT: The study presents the first implementation of an MRAC strategy for the PWT system and examines how well advanced control strategies, particularly MRAC, handle dynamic feed variations and disturbances, showcasing their adaptability and robustness in real time.
- Comprehensive Control Evaluation: A broader set of performance metrics is applied to systematically compare tracking accuracy, de-oiling efficiency, robustness, and control effort between simulation and experimental results.
- Guidelines for Optimal Control Architecture Selection: Based on the evaluation, the study provides actionable guidelines for selecting the most appropriate control strategy depending on system needs, computational resources, and disturbance handling.
- Practical Implications for Plant-wide Control: This work follows the plant-wide control strategy, highlighting the benefits of coordinated control between the upstream and downstream systems to optimize the overall water treatment process.
The rest of the paper is organized as follows. Section 2 introduces the experimental setup and test conditions used in the study. Section 3 presents the relevant mathematical models used for different control developments and the different control solutions selected for this study. Section 4 discusses the results obtained and the comparative analysis of different control solutions. Finally, Section 5 concludes the paper along with recommendations for future work.
2. Experimental Setup and Testing Conditions
The offshore PWT system examined in this study comprises two-stage separation processes as shown in Figure 1, i.e., an upstream TPGS system and a downstream de-oiling hydrocyclone system. This sequential configuration is designed to efficiently remove hydrocarbons and other dispersed impurities from produced water, to ensure compliance with stringent environmental discharge regulations, or to improve the water purity before re-injection into reservoirs. In some cases, additional separation equipment, such as gas flotation units, may be installed downstream of the hydrocyclone system to further enhance oil and solid removal. The dynamics of the considered system are inherently nonlinear and often subject to fluctuating feed conditions, as well as other external disturbances, necessitating robust and adaptable control strategies to maintain optimal operational performance.

Figure 1.
Simplified P&ID of the considered PWT system illustrated by an upstream TPGS, a downstream de-oiling hydrocyclone, and their relevant control loops.
2.1. PWT Pilot Plant
The pilot-scale experimental setup depicted in Figure 2 is designed to emulate an offshore PWT facility and includes the following key components:

Figure 2.
Picture of the PWT pilot plant at AAU offshore laboratory.
- A multiphase flow generation system to mimic the underground reservoir and production well and pipeline systems. Here the oil and water are mixed, and compressed air is injected to mimic gas flow.
- A set of TPGS systems: The multiphase flow is lifted through a riser pipeline and fed into the TPGS system, where the oil, water, and gas are separated according to their density differences. The gas phase ascends to the top and exits through the gas control valve (), which is regulated by a pressure controller. The oil phase skims over a weir plate into the oil compartment, while the sunken water phase is blocked by the weir plate. The level of the interface between oil and water is monitored by a level transmitter (LT) and controlled by a level controller (LC), which adjusts the underflow control valve () to maintain optimal separation efficiency and stable separator pressure.
- A set of de-oiling hydrocyclone systems: The water separated by the TPGS system is further treated using de-oiling hydrocyclone systems, which employ centrifugal forces to enhance the separation of tiny residual oil from water. Inside the chamber of the hydrocyclone, the dispersed oil is pushed to the axial center, an oil core can be formed subject to proper operating conditions, then the oil core stream exits the hydrocyclone through its overflow port, while the cleaned water is discharged through its underflow port. The de-oiling performance of a hydrocyclone is significantly influenced by its mechanical design and dynamic flow conditions. Achieving optimal separation efficiency requires maintaining a sufficient flow rate to generate a strong centrifugal field within the hydrocyclone. Additionally, an appropriate flow split is essential to ensure effective separation of oil and water phases [22].
- The OiW fluorescence-based Turner designs TD-4100XDC are installed at the inlet and water outlet of the hydrocyclone.
2.2. Testing Conditions
In the experimental test, the system operates with a supply tank that continuously mixes oil and water, while the inlet flow rate, , is regulated by a flow controller . It is worth mentioning that, to mimic the characteristics of PW, non-detergent SAE30 Midland engine oil dispersed in tap water was used. The separator pressure, , is maintained at 7 bar using a PID controller in conjunction with a control valve . An air compressor and a buffer tank supply air at 8 bar to the system. The side-stream flow rates, and , are maintained at 1.5 L per minute using PID controllers to fulfill the OiW monitor’s flow demand. The water level inside the TPGS and the PDR of the hydrocyclone are controlled with reference setpoints of 0.15 m and 2, respectively.
For all experiments, the controller was implemented with a sampling time of s, chosen to provide sufficient temporal resolution while maintaining computational efficiency. Each test scenario lasted 3900 s, with data from the startup and shutdown phases excluded to focus on the main experimental phase and capture both transient and steady-state behavior under the given operating conditions. Raw sensor measurements were filtered using a low-pass filter to suppress high-frequency noise prior to analysis. Subsequent data processing, including normalization and statistical evaluation, was carried out in MATLAB to ensure consistent comparison across control strategies. These settings were selected to support reproducibility and to ensure that the results are representative of practical, industrially relevant operations.
Figure 3 illustrates the feeding (liquid) flow rate to the TPGS system, to mimic a slugging flow pattern between 600 and 3600 s as marked by the vertical lines in Figure 3. It should be noted that the initial 600 s corresponds to the startup phase, while the final 300 s corresponds to the shutdown phase.

Figure 3.
Feeding flow rates (slugging flow pattern) to the TPGS system during different tests subject to different control solutions.
3. Mathematical Models and Control Solutions
3.1. Dynamic Model of TPGS System
The (water interface) dynamic of a TPGS system can be modeled via mass balance analysis. Subject to the assumption of a noncompressible liquid, a simple model describing the water volume inside the TPGS can be formulated as
where and denote the volumetric flow rates entering and leaving the TPGS system, respectively. The flow rate can be determined by using the orifice character of the control valve as
where is the orifice coefficient of the control valve, represents the functional relationship between the opening degree of the underflow valve and its effective opening area, denotes the pressure drop across the control valve, ) is the density of the liquid, and g is the gravitational acceleration.
The water level denoted as in the TPGS system can be used to substitute the liquid volume in Equation (1). Then the dynamic model relevant to the water interface inside the TPGS system can be described as
Under the assumption that the TPGS is a cylinder-shaped vessel, then can be calculated according to the cross-sectional area and the length of the compartment L as [23]
where r represents the radius of the separator.
3.2. De-Oiling Hydrocyclone
One key performance index of the de-oiling hydrocyclone system is the flow split ratio, which is defined as
where represents the volumetric flow rate in the overflow (e.g., the oil-rich stream), and is the volumetric flow rate at the inlet of the hydrocyclone. The flow split ratio needs to be properly controlled, such that ideally all oil residuals are expelled through the overflow stream without too much water accompanying, while the pure water goes through the underflow stream. In reality, the oil compositions in the water effluent need to be limited below 30 ppm to fulfill the compliance [24].
As shown in Figure 1, the common cost-effective approach to realize a flow split control is to implement a PDR control over the hydrocyclone system [6,25]. The PDR is defined as
where , , and indicate the pressures at the inlet, overflow, and underflow ports of the hydrocyclone system, respectively. The relationship between the PDR and the flow split plays a critical role in regulating the flow dynamics within the hydrocyclone system.
An approximately linear relationship between the flow split and PDR has been indicated in [26]. However, this relationship heavily depends on the specific geometric configuration of the deployed hydrocyclone and specific surface characteristics of its inner chamber materials. Nevertheless, the PDR is an essential parameter for fine-tuning flow split control in de-oiling hydrocyclones. Keeping the PDR constant as throughput varies is a reliable strategy to maintain a steady flow split, thereby stabilizing separation performance. In the following experimental work at the pilot plant, the PDR for the hydrocyclones is recommended within a range of 2–3 to balance separation efficiency and operational stability [3].
As shown in Figure 1, the hydrocyclone system’s performance is governed by a PDR control loop, which modulates the overflow valve based on the PDR. This control mechanism ensures efficient separation by maintaining the PDR within desired operational limits. The TPGS and hydrocyclone systems are interconnected through these control loops, enabling coordinated operation to achieve high separation efficiency [3].
3.3. Model of Entire System
A Linear Time-Invariant (LTI) model of the hydrocyclone system was identified in our previous work [3] around a typical operating point with m, , and . This LTI model is combined with the TPGS model to derive a state-space model (7) of the entire considered system, where the two control inputs are opening degrees of the underflow and overflow control valves, and the two outputs are the PDR and water level inside the TPGS system.
here, the state vector of the system is =, where is the interface level, while , , and are the states of the black-box PDR. The control input . The output , represents system disturbances. The detailed matrices of A, B, and C are
3.4. Hydrocyclone’s De-Oiling Efficiency
The de-oiling efficiency, denoted as , of a hydrocyclone system is defined in the following Equation (9). This index is also employed to directly evaluate the de-oiling performance of the system considered.
where , , and represent the volumetric OiW concentrations at the inlet, overflow, and underflow, respectively, and and denote the inlet and underflow flow rate, respectively. In many situations, the overflow rate can be very tiny compared with the inlet flow rate , so the de-oiling efficiency can be approximated using the oil concentration ratio, i.e.,
3.5. Control Solutions
Four different control solutions have been used/developed in the following to perform a systematic comparison.
- Baseline PID control: Two PID control loops, which mimic the actual control loops deployed in one of real-life offshore installations, have been developed as detailed in [3]. As shown in Figure 1, this control solution serves as a baseline control to be compared with other advanced control solutions. The level controller manages the water interface by adjusting the underflow valve () based on feedback from the level transmitter measurements. The PDR is governed by another PID control loop that modulates the overflow valve () to control the flow split.
- control: A MIMO robust control solution is developed using control theory as shown in Figure 4. The objective of this design is to minimize the worst-case transfer function gain from disturbance to output , subject to the condition that the closed-loop system needs to be internally stable. The control is naturally formulated to handle MIMO systems, providing coordinated control actions for both the water interface level and the PDR performances.The LTI-type controller K is achieved by minimizing the norm of the closed-loop system, denoted as via the D-K iteration design method [3].
- MPC control: Based on the same model as used for control design, an MPC solution is also developed similar to [9]. To address the rapid dynamics of the PDR loop, the sampling time was set to s, while the slow TPGS dynamics necessitated a prediction horizon of . The control horizon was tuned to to ensure smooth valve actuation. By solving an optimization problem at each control step, MPC anticipates future disturbances and adjusts control inputs accordingly, effectively handling system constraints and multi-channel interactions.The cost function used in the MPC solution iswhere represents the predicted outputs (level and PDR) at the th step based on the measurement up to the kth step, is the reference trajectory, and and are weighting matrices. The optimization determines future control actions to minimize variations caused by inflow while respecting physical constraints on and . To address the system nonlinearity, the control output is passed through the inverse Hammerstein function given in Equation (12). For more details on the MPC implementation, refer to [9].
- MRAC Control: Different from the robust control strategy, the MRAC solution adapts its control parameters in real time to match a reference behavior provided by a reference model, ensuring robust performance despite impacts due to system uncertainties and external disturbances. An output feedback MRAC is designed in [4,27] as shown in Figure 5. The control signal is described aswhere the adaptive gain matrices are , , , , and , and are filtered input and output signals, i.e., and , where the filter is defined as . Here, is expressed as , and a monic stable polynomial of degree . The parameter presents the observability index of the plant or its upper bound. A diagram of the control system used in this method can be found in Figure 5. Moreover, a more detailed description of this controller can be found in [27].

Figure 4.
Closed-loop control framework.
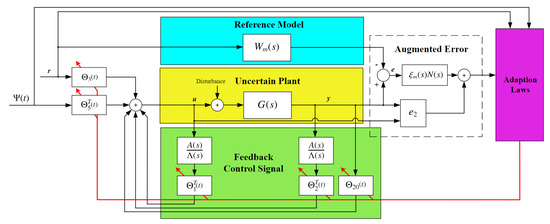
Figure 5.
Closed-loop controlled system using output-feedback output-tracking MRAC.
Each control solution represents one type of distinguished features; for instance, the PID solution is the simplest and easiest in terms of control structure and implementation; the control is a (5th-order) LTI-structured controller with fixed control parameters; the MRAC is a linear type of controller with adaptive control parameters; while the MPC solution represents the most sophisticated control solution which requires online optimization capability.
Table 1 provides a summary of the control solutions implemented for the PWT system, including their key design parameters and the constraints or assumptions considered in their tuning.

Table 1.
Controller design parameters and tuning assumptions.
4. Experimental Results and Discussions
The effectiveness of each control solution is assessed according to the tracking performance of the corresponding closed-loop system. Meanwhile, by using the data from the deployed online OiW sensors, the system’s de-oiling efficiency and the oil discharge (“leakage”) rate are also evaluated. In the rest of this section, a comprehensive evaluation of the controllers across several key performance aspects is performed. First, Section 4.1 focuses on controller performance in terms of system outputs and control inputs. Then, Section 4.2 evaluates the controllers’ behavior under intermittent measurement conditions. Finally, Section 4.3 examines performance with respect to OiW concentration measurements. Together, these analyses provide a clear comparison of each controller’s strengths and limitations under varying operational scenarios.
4.1. Performances in Terms of Outputs and Inputs
The system’s output responses and input signals subject to different control solutions are illustrated in Figure 6. During this period, the considered system sent a slugging feeding flow to the TPGS system as shown in Figure 3. Evaluated from the perspective of (output) tracking performance, the PID and MRAC solutions outperform the control and MPC solutions in terms of water level management. But the PID solution could not make the controlled system track the PDR reference. There are high-frequency oscillations in both the PDR performance and the control input . However, thanks to its flexibility, the MRAC solution still demonstrated a superior PDR performance, although its underflow control signal could respond a little too rapidly for some short periods.
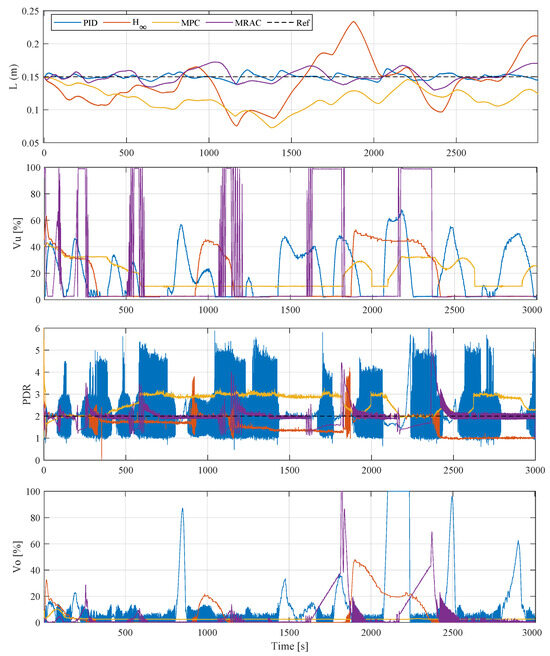
Figure 6.
Dynamic performances of the water interface and the PDR along with the underflow/overflow valve opening degree ()/() subject to different control solutions.
The control solution exhibited its fundamental control principle, i.e., mainly prompted towards the worst scenario while “relaxing” for non-worst scenarios, and thereby, both the output responses and the control signals are the least intensified among all solutions, and this could be beneficial in terms of fatigue loadings to the entire system, thereby prolonging the facility’s lifetime.
The most sophisticated MPC solution did not show superior performance in terms of tracking performance, and even led to the worst case in terms of water level tracking accuracy. However, the MPC solution led to the smoothest behaviors toward both output responses and both control signals. Unlike the solution that exhibited intermittent control reactions, the MPC control took care of the system performance all the time and thereby led to the smoothest behaviors.
Compared to all advanced control solutions, the baseline PID control strategy utilized a two-SISO (decoupled) control structure to manage the water level and PDR performances. It can be observed that this solution is sometimes inadequate in dealing with the inherently coupled dynamics between the water level and PDR control loops.
4.2. Performances in Terms of Intermittent Measurement
All flow rates at the inlet, underflow, and overflow outlets of the hydrocyclone system are also measured using electromagnetic flow-meters/Coriolis flow-meters, though they are often not measured in the actual real-world installations due to the fact that they are just some intermittent variables, and also the high expenses of relevant flow-meters. Hereby, these variables are measured to gain a better understanding of the system’s functionalities. These measured signals are plotted in Figure 7. It can be seen that the inlet flow rate and the underflow rate have quite similar flow patterns, regardless of the control solution applied; this is mainly due to the large difference in the sizes of the underflow and overflow control valves.

Figure 7.
Hydrocyclone’s inlet flow rate (), underflow rate (), overflow rate (), and calculated flow split ().
The dynamic flow split is also plotted in Figure 7. The PID solution led to large high-frequency oscillations in flow split due to its difficulty in maintaining a PDR tracking performance as shown in Figure 6. The MRAC and MPC solutions tried to maintain a constant flow split for most of the operating time, but clearly the MPC solution led to the smoothest performances in terms of both underflow and overflow rates, and thereby the smoothest flow split dynamics as well.
4.3. Performances in Terms of OiW Measurement
The OiW concentrations measured by the OiW sensors installed online and thus the calculated de-oiling dynamic efficiency are plotted in Figure 8. As it has been noted in [6], the decrease in de-oiling efficiency can be attributed to either excessively high or critically low inlet flow rates, both of which disrupt optimal operating conditions.

Figure 8.
Calculated de-oiling efficiency, measured inlet OiW concentrations () and underflow OiW concentrations ().
In general, the MPC solution demonstrated the best steady efficiency among all solutions, which can be confirmed from the concentration measurement at the underflow outlet. The de-oiling efficiencies of the PID and MRAC are more or less at the same level, and their dynamic oscillations have similar size and patterns. The dynamic oscillation of de-oiling efficiency led by the solution is the slowest one, with a clear gradual decline until a low point is reached, followed by the de-oiling efficiency immediately increasing to an upper point (due to the intermittent control reaction). This pattern repeated throughout the testing period.
The oil leakage rate through the underflow stream is calculated based on the online OiW measurement () and the flow rate measurement installed in the underflow by Equation (14):
where denotes the instantaneous underflow OiW concentration, and represents the volumetric flow rate. As illustrated in Figure 9, the MPC solution maintained a relatively constant discharge rate compared to other control solutions. In contrast, the MRAC solution was too proactive during certain periods, e.g., around s. This is possibly due to the fact that this linear MRAC solution did not account for inherent control saturation. In contrast, the MPC control solution is designed by explicitly taking saturation into account, which naturally leads to an advantage in this context.
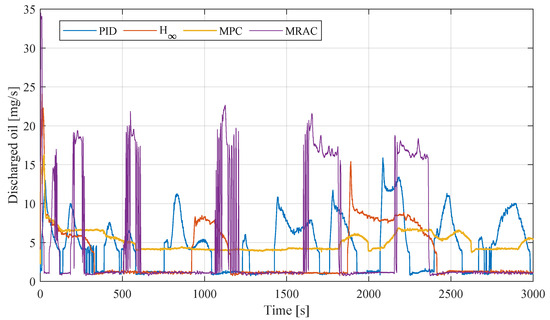
Figure 9.
Oil leakage rates through the underflow stream of the hydrocyclone system.
4.4. Statistical Analysis
The mean values of the hydrocyclone inlet flow rate, underflow rate, overflow rate, flow split, system efficiency, water level tracking error, and PDR tracking error are listed in Table 2. In general, the MPC solution achieved the best mean efficiency of 59.96%. The mean efficiency induced by the MPC is 5.40 p.p. (percentage points) and 13.42 p.p., 7.42 p.p higher than that induced by the PID, , and MRAC solutions, respectively. However, in terms of reference tracking, the MPC approach demonstrated some difficulty in accurately following the water level and PDR, as indicated by its relatively high values.

Table 2.
Means of inlet flow rate, underflow rate, overflow rate, flow split, mean efficiency, water level error, and PDR error.
Figure 10 shows the relative errors in terms of tracking errors and control efforts subject to the four different control solutions. As presented in Equation (15), the relative value for a variable is defined as the ratio of a specific value to the largest value within a predefined set.
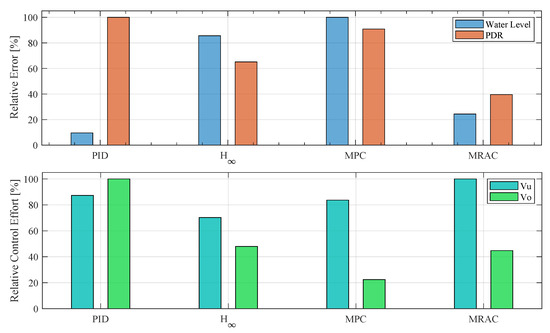
Figure 10.
Comparison of relative errors and control efforts via different control solutions.
It can be observed in Figure 10 that the PID and MPC solutions exhibited the minimum and maximum relative error for water level tracking, respectively. This is also observed in the results shown in Figure 6. In contrast, the MRAC solution showed the best performance for PDR tracking, while PID showed the poorest performance in this regard. In general, the MRAC solution has been proven to be highly effective in tracking references of both the water level and the PDR compared to the other methods. In terms of control effort, and MPC outperform the other control methods, whereas the PID requires significantly high control efforts for manipulating both the underflow and the overflow valves.
Table 3, Table 4 and Table 5 present the test results obtained for the separation process in a hydrocyclone under four control strategies. These results include the total volumes of liquid, oil, and water at different points in the process (inlet, underflow, and overflow), as well as the total mass of oil, the oil mass per liquid volume, and the water-to-liquid volume ratio.

Table 3.
Total volumes of liquid , oil , and water of the hydrocyclone inlet stream, as well as the total mass of oil , total amount of oil mass pr. liquid volume , and total amount of water pr. liquid volume in the hydrocyclone inlet stream.

Table 4.
Total volumes of liquid , oil , and water of the underflow valve, as well as the total mass of oil , total amount of oil mass pr. liquid volume , and total amount of water pr. liquid volume in the underflow valve.

Table 5.
Total volumes of liquid , oil , and water of the overflow valve, as well as the total mass of oil , total amount of oil mass pr. liquid volume , and total amount of water pr. liquid volume in the overflow valve.
The inlet stream data shows that the highest total inlet liquid volume () was achieved by the MPC controller (633.5406 L), followed by the PID (580.1365 L), MRAC (519.1526 L), and (449.2251 L) controllers. Correspondingly, MPC and PID also had a higher total oil mass entering the system, around 41.9 g and 36.7 g, respectively, while the and MRAC had slightly lower oil loads. The oil concentration per unit volume in the inlet was highest for MPC (66.3 mg/L) and MRAC (65.6 mg/L), suggesting that they handled more oil-rich inflows. Despite these differences, all controllers maintained a very high water fraction in the inlet (>0.9999), as expected in de-oiling applications. As noted earlier, achieving optimal separation efficiency in a hydrocyclone relies on maintaining an adequate flow rate to generate a strong centrifugal field. This fact can be seen by comparing the results presented in Table 2 and Table 3, where the MPC controller achieves higher efficiency and higher total liquid volume compared to the other control strategies.
Across controllers, the underflow stream handled most of the separated liquid, with MPC showing the highest total underflow volume (565.1 L), followed by PID (532.2 L), MRAC (474.3 L), and again with the lowest volume (412.7 L). The oil mass removed through the underflow was highest for PID (13.7 g) and MPC (12.7 g), while MRAC and had slightly lower values. The oil concentration in the underflow remained similar across controllers, around 22–24 mg/L, which aligns with the underflow’s role in carrying concentrated oil away. The water fraction here decreased to around 0.89–0.92, reflecting higher oil content relative to the inlet.
As listed in Table 5, the overflow stream consistently carried a smaller liquid volume, with MPC again showing the largest overflow (68.8 L), followed by MRAC (48.4 L), PID (47.9 L), and the lowest (36.4 L). Despite its lower volume, the overflow had a higher oil mass per unit volume, particularly for MPC (27.2 g) and MRAC (21.7 g), resulting in oil concentrations of approximately 40 to 43 mg / L. had the lowest overflow oil mass and concentration (16.0 g and 35.7 mg/L). The water fraction in the overflow was notably lower ( 0.08–0.086), highlighting its role in rejecting more oil relative to water.
4.5. Comparative Analysis
Table 6 summarizes the comparative performance of the four control strategies tested based on experimental results from the pilot-scale offshore PWT system. Moreover, the industrial suitability of each method is also demonstrated by providing some indicators from practical considerations. As mentioned before, the results show that MRAC achieved the highest tracking accuracy, while PID lagged in tracking of PDR due to challenges in handling multivariable interactions. MPC and required the lowest control effort, which could be advantageous for actuator longevity, whereas MRAC and PID demanded higher actuation. From an industrial perspective, PID remains the most practical choice for straightforward applications due to its low implementation cost, ease of tuning, and compatibility with existing hardware, despite offering moderate performance. control, while highly robust and efficient in handling disturbances, is less commonly deployed industrially because of its high tuning complexity and cost. MPC provides a strong balance between high de-oiling efficiency, robustness, and operational feasibility, especially in well-instrumented facilities, though it demands a complex setup and significant resources. MRAC stands out for its excellent tracking accuracy and adaptability at a moderate cost, making it particularly suitable for dynamic offshore environments with varying system parameters. Ultimately, the selection among these methods depends on the specific industrial priorities regarding cost, complexity, and performance requirements.

Table 6.
Comparative summary of control strategies for offshore PWT pilot plant.
Indicators such as cost constraints, desired control performance, ease of tuning, and adaptability to changing conditions vary across applications, guiding the choice between simpler methods like PID and more advanced solutions like MRAC or MPC. Operators prioritizing low cost and simplicity may favor PID, while those requiring high robustness or adaptability might opt for , MPC, or MRAC despite increased complexity or expense. Therefore, aligning control strategy selection with operational goals and resource availability is crucial for successful industrial implementation.
A multi-criteria decision-making (MCDM) approach can be used to identify the optimal method based on operator priorities. In this study, an MCDM procedure through the Weighted Sum Method (WSM) was employed to compare four control strategies based on qualitative performance ratings listed in Table 6. The proposed approach is as follows:
- Step 1: Convert qualitative performance values into numerical scores, on a 1–5 scale. For benefit indicators (e.g., tracking accuracy, robustness), Low and High are scored as 1 and 5, respectively. For cost indicators (e.g., implementation cost, tuning complexity), the scoring is reversed, so that Low is 5 and High is 1.
- Step 2: Apply scenario-specific weighting to each indicator to reflect different operational priorities. The weighted performance for each controller is calculated by multiplying the score of each indicator by its corresponding weight.
- Step 3: Sum the weighted scores across all indicators to obtain a total score for each control strategy in each scenario. The strategy with the highest total score is considered the most suitable for that scenario.where is the converted score for controller i on indicator j and is the weight for that indicator in the given scenario.
Four weighting scenarios were defined to reflect different operational priorities. In Scenario 1, weights of were applied to the seven indicators, prioritizing robustness, low tuning complexity, and low cost. Scenario 2 assigned weights of , giving more emphasis to tracking accuracy, de-oiling efficiency, and robustness. Scenario 3 used weights of , focusing on low control effort, high efficiency, and low cost, while Scenario 4 applied weights of , targeting robustness, low control effort, and adaptability. The total scores for the four methods were 3.3, 2.4, 2.8, and 3.2 in Scenario 1; 2.8, 2.5, 3.2, and 3.5 in Scenario 2; 2.9, 2.5, 3.2, and 3.0 in Scenario 3; and 2.5, 2.9, 3.4, and 3.3 in Scenario 4, for PID, , MPC, and MRAC, respectively.
Figure 11 illustrates the weighted performance comparison of different control strategies under four distinct weighting scenarios. Each radar chart corresponds to a unique prioritization of evaluation criteria, allowing visual identification of the most suitable control method for different operational objectives. The analysis showed that PID is best when simplicity and cost-effectiveness are most important (Scenario 1), MRAC excels when tracking and adaptability dominate (Scenario 2), and MPC leads when efficiency and low control effort are valued (Scenarios 3 and 4). This highlights that the “best” choice of control method is highly dependent on the weighting of performance criteria, and therefore on the specific operational priorities of the end user.
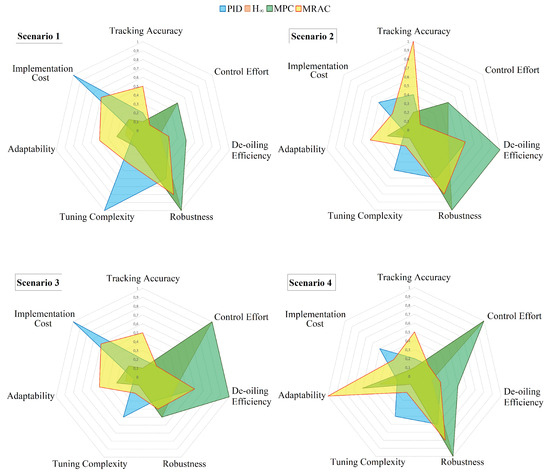
Figure 11.
Scenario-based weighted performance comparison of control strategies for offshore PWT.
5. Conclusions
This study presented a comprehensive evaluation of various control strategies, including PID, , MPC, and MRAC, implemented in a pilot-plant setup at the AAU laboratory. The performance of these control solutions was assessed based on tracking accuracy, efficiency, compliance with operational constraints, and control effort. Among the tested strategies, MRAC demonstrated superior performance in reference tracking, outperforming the other controllers in terms of precision and dealing with the inherent system correlation. However, when considering overall efficiency, MPC emerged as the most effective solution. In terms of control effort, MRAC and PID required higher levels of actuation compared to and MPC. This higher control effort is attributed to the aggressive tuning of the MRAC and PID controllers, which prioritize tracking performance over valve relaxation. In contrast, and MPC exhibited lower control effort, as these controllers allow for the relaxation of control valves while maintaining system stability and efficiency.
Overall, the findings highlight the trade-offs between tracking performance, efficiency, and control effort among different control strategies. MPC, in particular, stands out as a balanced and practical solution for complex industrial applications, combining efficient operation with constraint adherence and minimal control effort. Future research could focus on further optimizing these control strategies and evaluating their applicability to larger-scale industrial systems. In this context, nonlinear system identification using machine learning techniques applied to recorded real-time laboratory data could be investigated to enable more effective control designs and enhance overall system performance. Moreover, the lab-to-industry gap can be addressed through a scalable validation framework combining larger pilot-plant tests, high-fidelity digital twins, and hardware-in-the-loop simulations. This approach enables realistic disturbance testing, safe evaluation of extreme conditions, and gradual progression to limited industrial trials. Such a framework ensures control strategies are robust and practical for full-scale offshore PWT applications.
Author Contributions
Conceptualization, M.K. and Z.Y.; methodology, M.K. and Z.Y.; software, M.K.; validation, M.K., Z.Y. and S.J.; formal analysis, M.K. and Z.Y.; investigation, M.K.; resources, Z.Y.; writing—original draft preparation, M.K.; writing—review and editing, M.K., Z.Y. and S.J.; visualization, M.K.; supervision, Z.Y.; project administration, Z.Y.; funding acquisition, Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Danish EUDP project named OiW Control by 3D spectroscopy, and partially supported by the Danish (DTU) Offshore Technology Center via the DIC project.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the partial support from the Danish Energy Technology Development and Demonstration Programme (EUDP) and the partial support from the Danish (DTU) Offshore Technology Center for this work. Thanks also go to Simon I. Andersen, Isabelle M.A. Viegas, and Benaiah Anabaraonye from Danish Offshore Technology Center, Kristian Nielsen and Kristian Rode from SHUTE Sensing Solutions A/S, for many valuable discussions. Special thanks also goes to Mohsen Sadeghi from AAU Energy for technical assistance during the experimental work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Husveg, T.; Rambeau, O.; Drengstig, T.; Bilstad, T. Performance of a deoiling hydrocyclone during variable flow rates. Miner. Eng. 2007, 20, 368–379. [Google Scholar] [CrossRef]
- Jahanshahi, E.; Skogestad, S. Nonlinear control solutions to prevent slugging flow in offshore oil production. J. Process Control 2017, 54, 138–151. [Google Scholar] [CrossRef]
- Durdevic, P.; Yang, Z. Application of H∞ Robust Control on a Scaled Offshore Oil and Gas De-Oiling Facility. Energies 2018, 11, 287. [Google Scholar] [CrossRef]
- Kashani, M.; Jespersen, S.; Yang, Z. Robust Adaptive Control of the Offshore Produced Water Treatment Process: An Improved Multivariable MRAC-Based Approach. Water 2024, 16. [Google Scholar] [CrossRef]
- Colman, D.A.; Thew, M.T. Correlation of separation results from light dispersion hydrocyclones. Chem. Eng. Res. Des. 1983, 61, 233–240. [Google Scholar]
- Thew, M. FLOTATION | Cyclones for Oil/Water Separations. In Encyclopedia of Separation Science; Wilson, I.D., Ed.; Academic Press: Oxford, UK, 2000; pp. 1480–1490. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Li, S.; Zhang, Y.; Niu, J.; Luo, X.; Wang, J.; Tian, C. Finite-time fault-tolerant H∞ control for offshore de-oiling hydrocyclone systems with input saturation via reinforcement learning. Ocean Eng. 2025, 340, 122188. [Google Scholar] [CrossRef]
- Hansen, L.; Bram, M.V.; Pedersen, S.; Yang, Z. Performance Comparison of Control Strategies for Plant-Wide Produced Water Treatment. Energies 2022, 15, 418. [Google Scholar] [CrossRef]
- Vallabhan, M.; Holden, C. Non-Linear Control Algorithms for De-Oiling Hydrocyclones. In Proceedings of the 2020 28th Mediterranean Conference on Control and Automation (MED), Virtual, 15–18 September 2020; pp. 85–90. [Google Scholar] [CrossRef]
- Vallabhan, M.K.; Matias, J.; Holden, C. Feedforward, cascade and model predictive control algorithms for de-oiling hydrocyclones: Simulation study. Model. Identif. Control 2021, 42, 185–195. [Google Scholar] [CrossRef]
- Vallabhan , K.G.M.; Holden, C.; Skogestad, S. Deoiling Hydrocyclones: An Experimental Study of Novel Control Schemes. SPE Prod. Oper. 2022, 37, 462–474. [Google Scholar] [CrossRef]
- Jespersen, S.; Yang, Z.; Hansen, D.S.; Kashani, M.; Huang, B. Hammerstein–Wiener Model Identification for Oil-in-Water Separation Dynamics in a De-Oiling Hydrocyclone System. Energies 2023, 16, 7095. [Google Scholar] [CrossRef]
- Tao, G. Multivariable adaptive control: A survey. Automatica 2014, 50, 2737–2764. [Google Scholar] [CrossRef]
- Bagherpoor, H.; Salmasi, F.R. Robust model reference adaptive output feedback tracking for uncertain linear systems with actuator fault based on reinforced dead-zone modification. ISA Trans. 2015, 57, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Narendra, K.; Annaswamy, A. Stable Adaptive Systems; Dover Books on Electrical Engineering, Dover Publications: Garden City, NY, USA, 2012. [Google Scholar]
- Guo, J.; Liu, Y.; Tao, G. A Multivariable MRAC Design Using State Feedback for Linearized Aircraft Models with Damage. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 2095–2100. [Google Scholar] [CrossRef]
- Hua, C.C.; Leng, J.; Guan, X.P. Decentralized MRAC for large-scale interconnected systems with time-varying delays and applications to chemical reactor systems. J. Process Control 2012, 22, 1985–1996. [Google Scholar] [CrossRef]
- Song, G.; Tao, G. Partial-state feedback multivariable MRAC and reduced-order designs. Automatica 2021, 129, 109622. [Google Scholar] [CrossRef]
- Wen, L.; Tao, G.; Liu, Y. Multivariable adaptive output rejection of unmatched input disturbances. Int. J. Adapt. Control Signal Process. 2016, 30, 1203–1227. [Google Scholar] [CrossRef]
- Selfridge, J.M.; Tao, G. Multivariable Output Feedback MRAC for a Quadrotor UAV. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 492–499. [Google Scholar] [CrossRef]
- César, S.D.; De Jager, D.; Njoya, M. The role of hydrocyclone and induced gas flotation technologies in offshore produced water deoiling advancements. Pet. Res. 2024, 10, 342–351. [Google Scholar] [CrossRef]
- Backi, C.J.; Skogestad, S. A Simple Dynamic Gravity Separator Model for Separation Efficiency Evaluation Incorporating Level and Pressure Control. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 2823–2828. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, Q.; Zhang, B.; Tian, F. Three-phase hydrocyclone separator—A review. Chem. Eng. Res. Des. 2015, 100, 554–560. [Google Scholar] [CrossRef]
- Meldrum, N. Hydrocyclones: A Solution to Produced-Water Treatment. SPE Prod. Eng. 1988, 3, 669–676. [Google Scholar] [CrossRef]
- Jiang, M.; Zhao, L.; He, J.; Zhou, F. Pressure Drop Ratio–An Important Performance Parameter in Liquid-Liquid Hydrocyclone Separation, Volume All Days. In Proceedings of the International Ocean and Polar Engineering Conference, Montreal, Canada, 24–29 May 1998. [Google Scholar]
- Tao, G. Adaptive Control Design and Analysis; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).