Uncertainty-Aware Economic Dispatch of Integrated Energy Systems with Demand-Response and Carbon-Emission Costs
Abstract
1. Introduction
2. IES Scheduling Framework and Model
2.1. IES Operation Structure
2.2. Distributed Energy Model for the IES
2.3. IES Demand-Response Model
2.4. IES Operation Model
3. Problem Calculation
3.1. Two-Stage Robust Optimization Problem
3.2. Two-Stage Robust Optimization Problem Solving
| Algorithm 1: CCG algorithm solution process. |
| 1: Initialization: LB = −∞, UB = +∞, iteration index n = l, Set error threshold 2: repeat 3: In n-th iteration |
| 4: Solve the main problem according to Formula (19) and update LB. |
| 5: Introducing the KKT conditions, transform Equation (26), solve the subproblem, and update UB. 6: Update the worst-case scenario and add column constraints. 7: Update iteration index: n = n + 1; |
| 8: Until the stopping condition is fulfilled, i.e., LB-UB |
| End |
4. Case Study
4.1. Case Setting
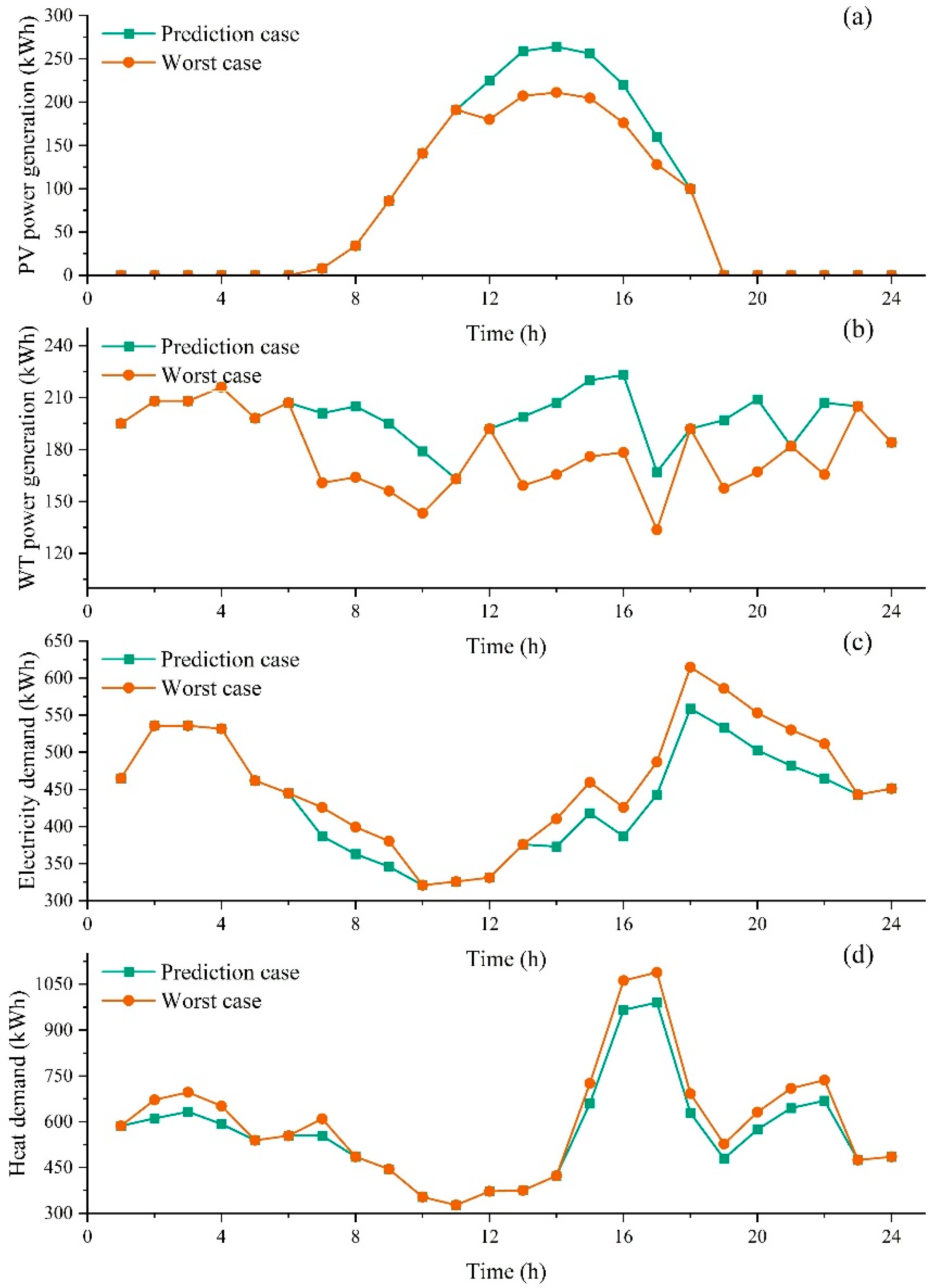
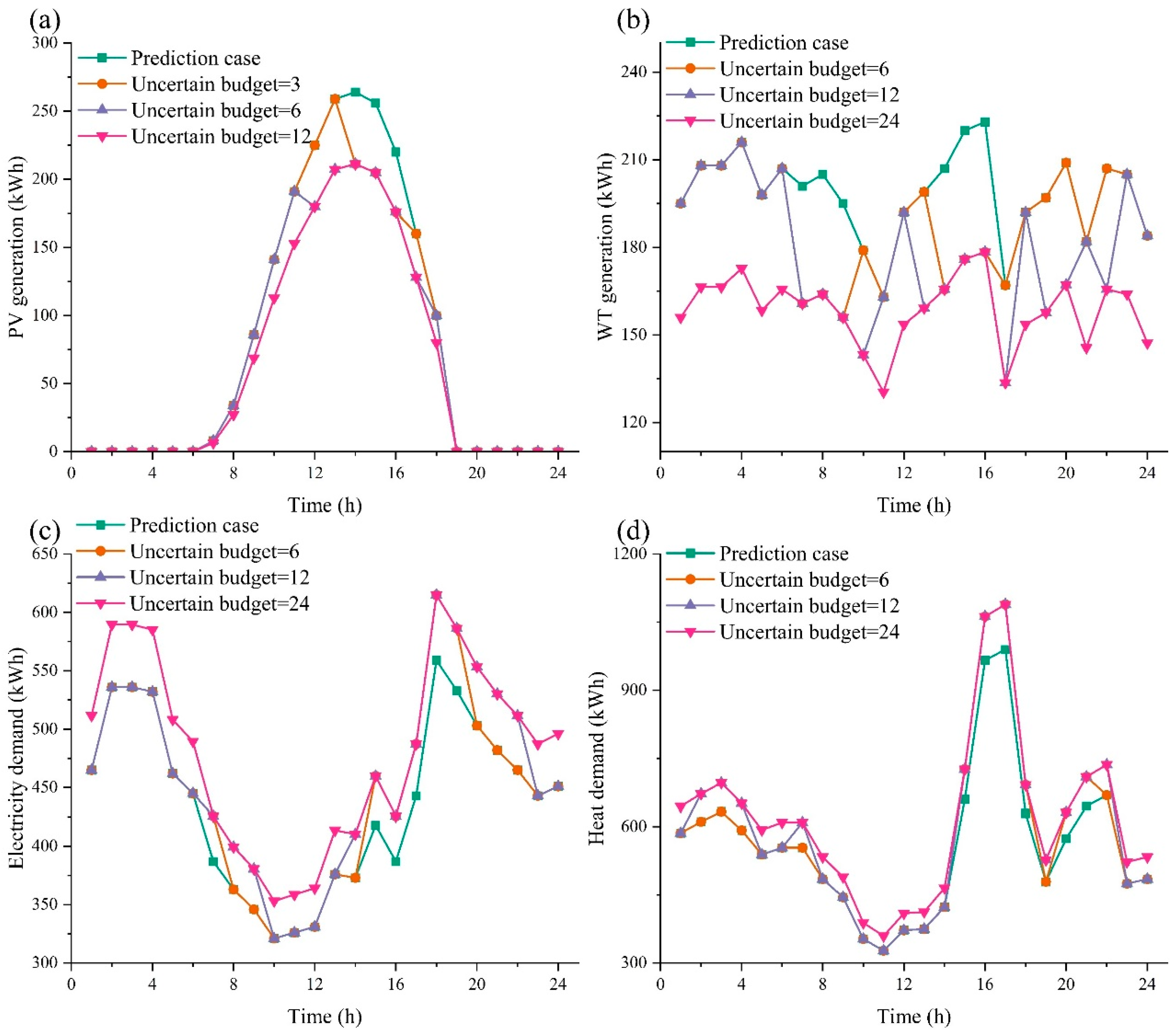
4.2. Uncertainty Analysis
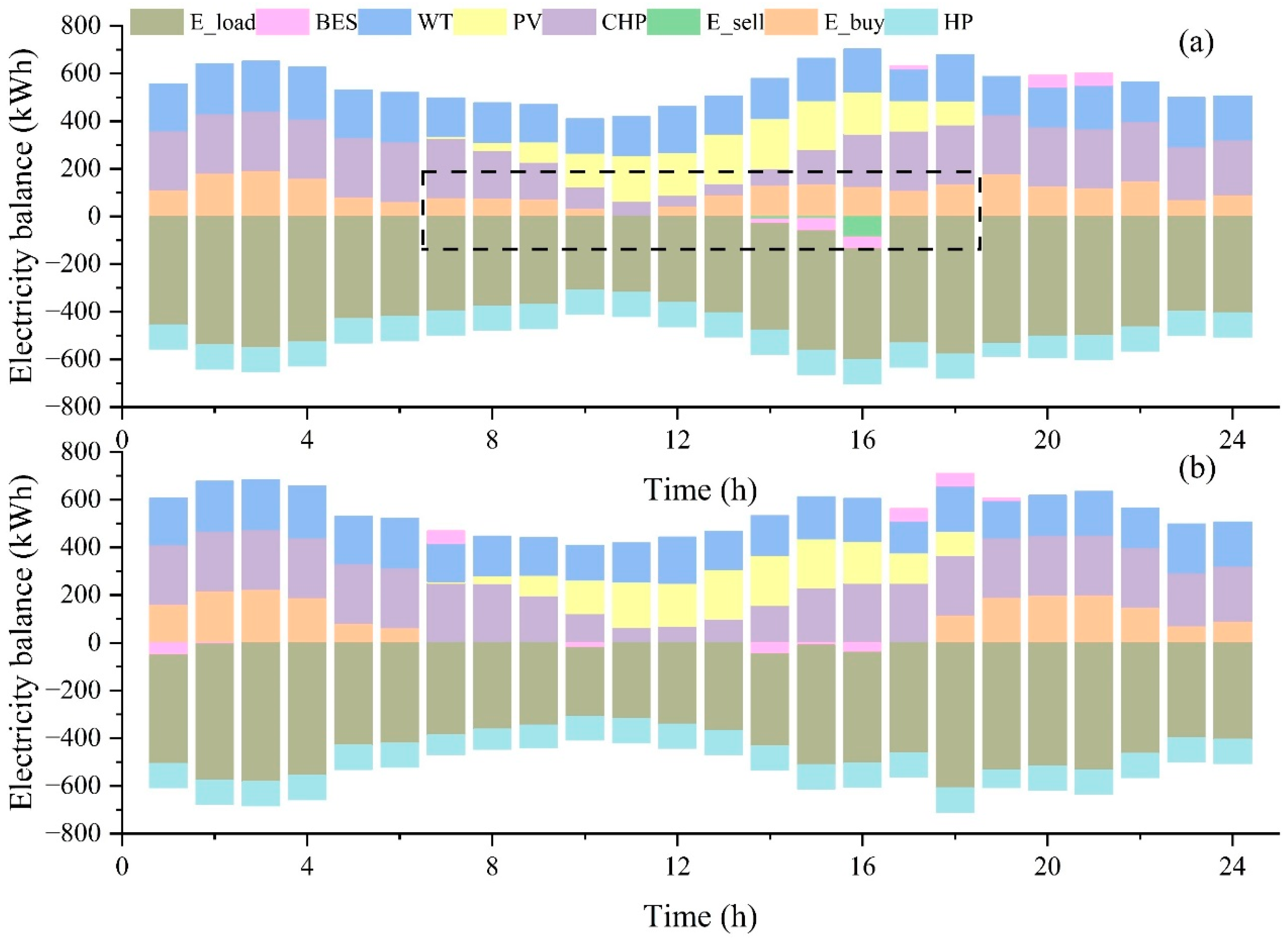
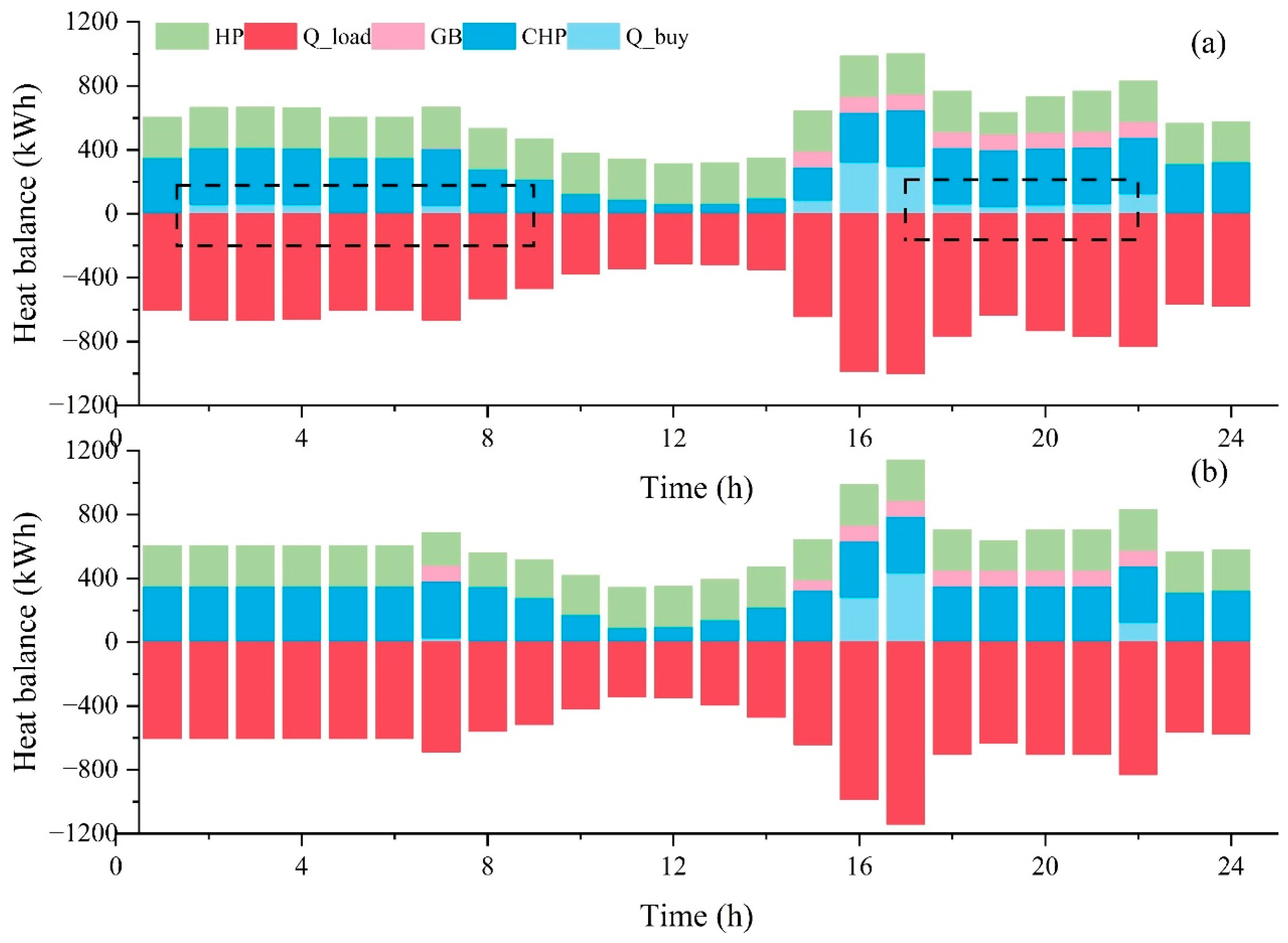
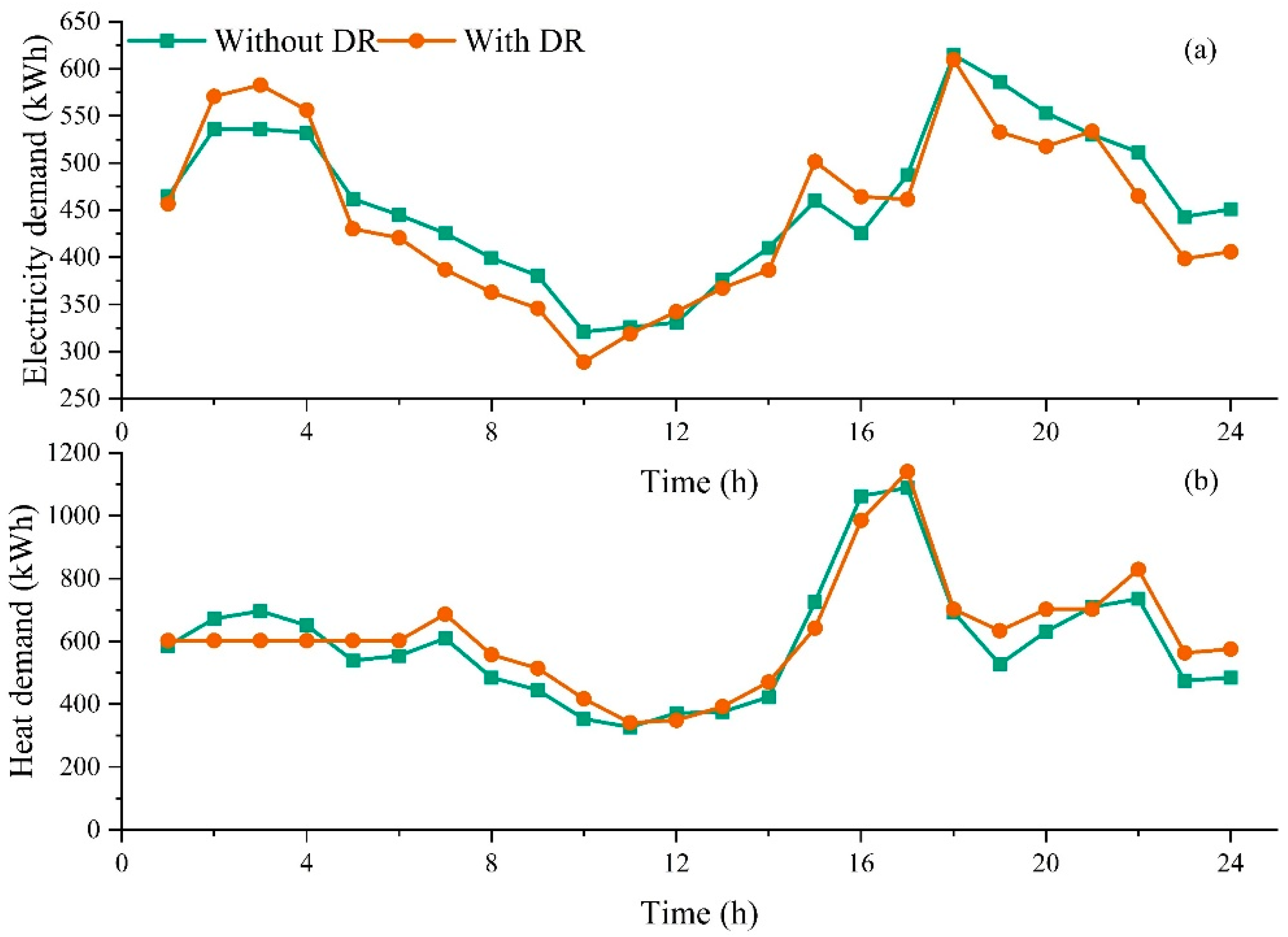
4.3. Scheduling Result Analysis
4.4. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, D.; Hu, W.H.; Zhao, J.B.; Zhang, G.Z.; Zhang, B.; Liu, Z.; Chen, Z.; Blaabjerg, F. Reinforcement Learning and Its Applications in Modern Power and Energy Systems: A Review. J. Mod. Power Syst. Clean Energy 2020, 8, 1029–1042. (In English) [Google Scholar] [CrossRef]
- Cao, D.; Hu, J.X.; Liu, Y.; Hu, W.H. Decentralized Graphical-Representation-Enabled Multi-Agent Deep Reinforcement Learning for Robust Control of Cyber-Physical Systems. IEEE Trans. Reliab. 2024, 73, 1710–1720. (In English) [Google Scholar] [CrossRef]
- Zhao, P.F.; Cao, D.; Hu, W.H.; Huang, Y.H.; Hao, M.; Huang, Q.; Chen, Z. Geometric Loss-Enabled Complex Neural Network for Multi-Energy Load Forecasting in Integrated Energy Systems. IEEE Trans. Power Syst. 2024, 39, 5659–5671. [Google Scholar] [CrossRef]
- Wang, J.; Wen, Y.; Wu, K.; Ding, S.; Liu, Y.; Tian, H.; Zhang, J.; Wang, L.; Cao, Q.; Zhang, Y. Optimization study of wind, solar, hydro and hydrogen storage based on improved multi-objective particle swarm optimization. J. Energy Storage 2024, 93, 112298. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Zhan, Y.; Yan, R.; Mei, J.; Fu, A.; Jiao, F.; Zeng, R. Multi-scenario optimization and performance evaluation of integrated energy system considering co-scheduling of EVs and stationary energy storage. Renew. Energy 2024, 237, 121927. [Google Scholar] [CrossRef]
- Wang, Z.-H.; Ren, X.-Y.; Cui, H.-J.; Wang, W.-Q.; Liu, J.; He, Z.-F. A multi-stage two-layer stochastic design model for integrated energy systems considering multiple uncertainties. Energy 2024, 304, 131729. [Google Scholar] [CrossRef]
- Wang, M.; Wang, M.; Wang, R.; Zhao, Q.; Zheng, X.; Gao, H. Optimization scheduling for low-carbon operation of building integrated energy systems considering source-load uncertainty and user comfort. Energy Build. 2024, 318, 114423. [Google Scholar] [CrossRef]
- Li, H.; Lu, X.; Zhou, K.; Shao, Z. Distributionally robust optimal dispatching method for integrated energy system with concentrating solar power plant. Renew. Energy 2024, 229, 120792. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, J.B.; Hu, J.X.; Pei, Y.S.; Huang, Q.; Chen, Z.; Hu, W.H. Physics-Informed Graphical Representation-Enabled Deep Reinforcement Learning for Robust Distribution System Voltage Control. IEEE Trans. Smart Grid 2024, 15, 233–246. [Google Scholar] [CrossRef]
- Kumar, J.; Hussain, K.; Kannan, S. Positive vs negative economic impacts of tourism development: A review of economic impact studies. In Proceedings of the 21st Asia Pacific Tourism Association Annual Conference, Kuala Lumpur, Malaysia, 14–17 May 2015; pp. 14–17. [Google Scholar]
- Kumar, J.; Hussain, K. A review of assessing the economic impact of business tourism: Issues and approaches. Int. J. Hosp. Tour. Syst. 2014, 7, 49–55. [Google Scholar]
- Qian, J.; Guo, Y.; Wu, D.; Liu, A.; Han, Z.; Liu, Z.; Zhang, S.; Yang, X. Research on multi-time scale optimization of integrated energy system based on multiple energy storage. J. Energy Storage 2024, 102, 113892. [Google Scholar] [CrossRef]
- Wang, J.; Wen, J.; Wang, J.; Yang, B.; Jiang, L. Coordinated scheduling of wind-solar-hydrogen-battery storage system for techno-economic-environmental optimization of hydrogen production. Energy Convers. Manag. 2024, 314, 118695. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, T.; Deng, L.; Song, Z.; Li, T. Research on investment selection of park-level integrated energy system considering electricity-heat-cooling-storage based on matter element extension. Energy 2024, 304, 132054. [Google Scholar] [CrossRef]
- Jia, B.; Li, F.; Sun, B. Knowledge-network-embedded deep reinforcement learning: An innovative way to high-efficiently develop an energy management strategy for the integrated energy system with renewable energy sources and multiple energy storage systems. Energy 2024, 301, 131604. [Google Scholar] [CrossRef]
- Zhu, X.; Hu, M.; Xue, J.; Li, Y.; Han, Z.; Gao, X.; Wang, Y.; Bao, L. Research on multi-time scale integrated energy scheduling optimization considering carbon constraints. Energy 2024, 302, 131776. [Google Scholar] [CrossRef]
- Yan, N.; Zhao, Z.; Li, X.; Yang, J. Multi-time scales low-carbon economic dispatch of integrated energy system considering hydrogen and electricity complementary energy storage. J. Energy Storage 2024, 104, 114514. [Google Scholar] [CrossRef]
- Ye, S.; Wang, J.; Yin, Z.; Kang, J.; Ma, Z. Optimization of a solar-driven community integrated energy system based on dynamic hybrid hydrogen-electric energy storage strategy. J. Energy Storage 2024, 101, 113917. [Google Scholar] [CrossRef]
- Chen, X.; Yang, L.; Dong, W.; Yang, Q. Net-zero carbon emission oriented Bi-level optimal capacity planning of integrated energy system considering carbon capture and hydrogen facilities. Renew. Energy 2024, 237, 121624. [Google Scholar] [CrossRef]
- Dong, F.; Wang, J.; Xu, H.; Zhang, X. A robust real-time energy scheduling strategy of integrated energy system based on multi-step interval prediction of uncertainties. Energy 2024, 300, 131639. [Google Scholar] [CrossRef]
- Kumar, J.; Arora, M.; Bayram, G.E. Research, Innovation, and Industry Impacts of the Metaverse; IGI Global: Hershey, PA, USA, 2024. [Google Scholar]
- Silva, C.A.M.; Bessa, R.J. Carbon-aware dynamic tariff design for electric vehicle charging stations with explainable stochastic optimization. Appl. Energy 2025, 389, 125674. [Google Scholar] [CrossRef]
- Fan, J.; Yan, R.; He, Y.; Zhang, J.; Zhao, W.; Liu, M.; An, S.; Ma, Q. Stochastic optimization of combined energy and computation task scheduling strategies of hybrid system with multi-energy storage system and data center. Renew. Energy 2025, 242, 122466. [Google Scholar] [CrossRef]
- Yan, Y.; Huang, C.; Guan, J.; Zhang, Q.; Cai, Y.; Wang, W. Stochastic optimization of solar-based distributed energy system: An error-based scenario with a day-ahead and real-time dynamic scheduling approach. Appl. Energy 2024, 363, 123099. [Google Scholar] [CrossRef]
- Dong, X.-J.; Shen, J.-N.; Ma, Z.-F.; He, Y.-J. Stochastic optimization of integrated electric vehicle charging stations under photovoltaic uncertainty and battery power constraints. Energy 2025, 314, 134163. [Google Scholar] [CrossRef]
- Duan, F.; Bu, X. Stochastic optimization of a hybrid photovoltaic/fuel cell/parking lot system incorporating cloud model. Renew. Energy 2024, 237, 121727. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, W.; Du, J.; Cao, X.; Bai, C.; Liu, W.; Wang, D.; Chen, Z. Hierarchical distributionally robust scheduling strategy for distributed energy systems in the energy-sharing environment. Appl. Energy 2025, 388, 125639. [Google Scholar] [CrossRef]
- Prome, S.A.; Ragavan, N.A.; Islam, M.R.; Asirvatham, D.; Jegathesan, A.J. Deception detection using machine learning (ML) and deep learning (DL) techniques: A systematic review. Nat. Lang. Process. J. 2024, 6, 100057. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.H.; Zhao, J.B.; Huang, Q.; Chen, Z.; Blaabjerg, F. A Multi-Agent Deep Reinforcement Learning Based Voltage Regulation Using Coordinated PV Inverters. IEEE Trans. Power Syst. 2020, 35, 4120–4123. [Google Scholar] [CrossRef]
- Zhao, P.F.; Hu, W.H.; Cao, D.; Huang, R.; Wu, X.W.; Huang, Q.; Chen, Z. Causal Mechanism-Enabled Zero-Label Learning for Power Generation Forecasting of Newly-Built PV Sites. IEEE Trans. Sustain. Energy 2025, 16, 392–406. [Google Scholar] [CrossRef]
- Emrani, A.; Berrada, A.; Bakhouya, M. Optimal sizing and deployment of gravity energy storage system in hybrid PV-Wind power plant. Renew. Energy 2022, 183, 12–27. [Google Scholar] [CrossRef]
- Cui, J.; Zhu, Z.; Qu, G.; Wang, Y.; Li, R. Demand-side shared energy storage pricing strategy based on stackelberg-Nash game. Int. J. Electr. Power Energy Syst. 2025, 164, 110387. [Google Scholar] [CrossRef]
- Hua, Z.; Li, J.; Zhou, B.; Or, S.W.; Chan, K.W.; Meng, Y. Game-theoretic multi-energy trading framework for strategic biogas-solar renewable energy provider with heterogeneous consumers. Energy 2022, 260, 125018. [Google Scholar] [CrossRef]
- Xu, X.; Wang, B.; Shi, M.; Li, G.; Zhang, Y.; Wang, Q.; Liu, D. Research on hydrogen storage system configuration and optimization in regional integrated energy systems considering electric-gas-heat-hydrogen integrated demand response. Int. J. Hydrogen Energy 2025, 135, 86–103. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Cao, Y. Multi-objective distributed robust cooperative optimization model of multiple integrated energy systems considering uncertainty of renewable energy and participation of electric vehicles. Sustain. Cities Soc. 2024, 104, 105308. [Google Scholar] [CrossRef]
- Wu, Z.; Kang, J.; Mosteiro-Romero, M.; Bartolini, A.; Ng, T.S.; Su, B. A distributionally robust optimization model for building-integrated photovoltaic system expansion planning under demand and irradiance uncertainties. Appl. Energy 2024, 372, 123740. [Google Scholar] [CrossRef]
- Zdraveski, V.; Todorovski, M. A robust optimization model for Optimal Feeder Routing and Battery Storage Systems design. Appl. Energy 2024, 374, 123978. [Google Scholar] [CrossRef]
- Li, L.; Cao, X.; Zhang, S. Shared energy storage system for prosumers in a community: Investment decision, economic operation, and benefits allocation under a cost-effective way. J. Energy Storage 2022, 50, 104710. [Google Scholar] [CrossRef]
- Xiong, K.; Hu, W.; Cao, D.; Zhang, G.; Chen, Z.; Blaabjerg, F. A novel two-level deep reinforcement learning enabled game approach for incentive-based distributed voltage regulation with participation of autonomous photovoltaic inverters. Energy 2025, 324, 135934. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Incentivizing energy trading for interconnected microgrids. IEEE Trans. Smart Grid 2016, 9, 2647–2657. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, W.; Du, J.; Bai, C.; Liu, W.; Chen, Z. Low-carbon optimal operation of distributed energy systems in the context of electricity supply restriction and carbon tax policy: A fully decentralized energy dispatch strategy. J. Clean. Prod. 2023, 396, 136511. [Google Scholar] [CrossRef]
- Kong, X.; Xiao, J.; Liu, D.; Wu, J.; Wang, C.; Shen, Y. Robust stochastic optimal dispatching method of multi-energy virtual power plant considering multiple uncertainties. Appl. Energy 2020, 279, 115707. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, D.; Wang, Y. Optimal operation of integrated energy systems considering energy trading and integrated demand response. Energy Rep. 2024, 11, 3307–3316. [Google Scholar] [CrossRef]
- Li, L.; Yu, S. Optimal management of multi-stakeholder distributed energy systems in low-carbon communities considering demand response resources and carbon tax. Sustain. Cities Soc. 2020, 61, 102230. [Google Scholar] [CrossRef]


| CHP (kW) | GB (kW) | HP (kW) | |
|---|---|---|---|
| IES | 250 | 100 | 150 |
| Time Slot | Electricity/Heat Price (RMB/kWh) | |
|---|---|---|
| Electricity price | Peak (6:00–10:00, 13:00–17:00) | 1.10 |
| Plain (10:00–13:00, 17:00–22:00) | 0.77 | |
| Valley (0:00–6:00, 22:00–24:00) | 0.44 | |
| Heat price | Peak (9:00–12:00, 17:00–21:00) | 0.45 |
| Plain (6:00–9:00, 12:00–17:00) | 0.39 | |
| Valley (0:00–6:00, 21:00–24:00) | 0.33 |
| Scenario 1 | Scenario 2 | Scenario 3 | |
|---|---|---|---|
| Cost (RMB) | 7091.03 | 6589.78 | 6489.18 |
| Carbon emissions (kg) | 6165.57 | 5951.46 | 5732.54 |
| Carbon Tax (RMB/t) | 0 | 50 | 100 | 150 | 200 | 250 |
|---|---|---|---|---|---|---|
| Cost (RMB) | 5896.60 | 6202.55 | 6489.18 | 6774.23 | 7059.23 | 7344.22 |
| Carbon emissions (kg) | 6154.73 | 5732.54 | 5732.54 | 5699.87 | 5699.87 | 5699.87 |
| Uncertain Budget | 6 | 12 | 24 |
|---|---|---|---|
| Cost (RMB) | 5956.46 | 6489.18 | 7232.33 |
| Carbon emission (kg) | 5184.10 | 5732.54 | 6687.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Tian, J.; Guo, Z.; Fu, Q.; Jing, S. Uncertainty-Aware Economic Dispatch of Integrated Energy Systems with Demand-Response and Carbon-Emission Costs. Processes 2025, 13, 1906. https://doi.org/10.3390/pr13061906
Zhang Y, Tian J, Guo Z, Fu Q, Jing S. Uncertainty-Aware Economic Dispatch of Integrated Energy Systems with Demand-Response and Carbon-Emission Costs. Processes. 2025; 13(6):1906. https://doi.org/10.3390/pr13061906
Chicago/Turabian StyleZhang, Yuning, Jiawen Tian, Zhenglin Guo, Qiang Fu, and Shi Jing. 2025. "Uncertainty-Aware Economic Dispatch of Integrated Energy Systems with Demand-Response and Carbon-Emission Costs" Processes 13, no. 6: 1906. https://doi.org/10.3390/pr13061906
APA StyleZhang, Y., Tian, J., Guo, Z., Fu, Q., & Jing, S. (2025). Uncertainty-Aware Economic Dispatch of Integrated Energy Systems with Demand-Response and Carbon-Emission Costs. Processes, 13(6), 1906. https://doi.org/10.3390/pr13061906







