Load Frequency Control of Power Systems with an Energy Storage System Based on Safety Reinforcement Learning

Abstract

Load frequency control (LFC) is a critical component in power systems that is employed to stabilize frequency fluctuations and ensure power quality. As energy storage systems (ESSs) are increasingly integrated into the grid, managing additional constraints has become more challenging. To address these challenges, this paper proposes a safety reinforcement learning-based approach that incorporates ESSs into the LFC framework. By formulating a constrained Markov decision process (CMDP), this approach overcomes the limitations of conventional Markov decision processes (MDPs) by explicitly handling system constraints. Furthermore, a long short-term memory (LSTM)-based cost prediction critic network is introduced to improve the accuracy of cost predictions, and a primal-dual deep deterministic policy gradient (PD-DDPG) algorithm is employed to solve the CMDP. Simulation results demonstrate significant improvements: a 58.2% faster settling time, a 72.5% reduction in peak frequency deviation, and a 68.2% lower mean absolute error while maintaining all operational constraints.

1. Introduction

Load frequency control (LFC) serves as a fundamental mechanism for maintaining power system stability by continuously adjusting generator outputs to mitigate frequency deviations caused by load fluctuations and disturbances [1,2,3]. The integration of energy storage systems into modern grids has opened new avenues for enhancing frequency regulation performance. Unlike conventional generation units, ESS can provide rapid power injection/absorption to counteract frequency anomalies, offering superior dynamic response characteristics [4,5,6]. Among various ESS technologies, flywheel energy storage systems have emerged as particularly promising solutions for LFC applications due to their exceptional power density, ultrafast response capability, and virtually unlimited cycle life.

Recent studies have identified several technical challenges in LFC systems. Research on thermoelectric modules [7] has demonstrated the significant impact of auxiliary system losses on net energy output. Investigations of interior permanent magnet synchronous machines control systems [8] have revealed that conventional approaches often require additional sensors or observers, increasing system complexity. Furthermore, non-intrusive load monitoring studies [9,10] have highlighted the need for advanced adaptive control capabilities to handle spatiotemporal diversity in load patterns. Significant advancements in related fields provide valuable insights for LFC optimization. Impedance analysis of grid-connected converters [11] emphasizes the critical role of accurate modeling for small-signal stability. Developments in sustainable structural batteries [12] and virtual power plant operation [13] demonstrate effective multi-objective coordination for balancing economic and security requirements. Particularly, case studies of battery-integrated renewable energy systems [14] have proven the effectiveness of bi-level optimization frameworks in resolving operational target conflicts.

However, traditional control paradigms face inherent limitations. Conventional LFC approaches are usually developed based on physical dynamic models of power systems and require high real-time computational resources. These methods often rely on linearized models and classical control techniques, which may struggle to handle the increasing complexity of modern power grids. To improve system performance, The authors of [15] proposed a unified PID tuning method for LFC, based on the two-degree-of-freedom internal model control approach, enhancing robustness and adaptability to system variations. The authors of [16] introduced a direct-indirect adaptive fuzzy control method, utilizing local frequency deviations and tie-line power deviations to dynamically adjust control strategies. The authors of [17] employed a full-order generalized state observer in a two-layer active disturbance rejection control framework, integrating equivalent input disturbance compensation to improve disturbance rejection capabilities and ensure high dynamic performance. The authors of [18] developed a robust control scheme for multi-area power systems using second-order sliding mode control combined with an extended disturbance observer, treating load variations and tie-line power deviations as lumped disturbances to enhance system stability. The authors of [19] investigated a model predictive control approach for interconnected power systems, utilizing a simplified Nordic power system model to optimize frequency control while accounting for operational constraints such as tie-line power flow limits and generation rate constraints. The authors of [20] present a comprehensive approach integrating system modeling, simulation, and optimization with advanced control techniques. Their work combines particle swarm optimization with proportional-integral-derivative controllers to enhance LFC system performance. The authors of [21] developed a novel tube-based distributed model predictive control scheme, comprising a nominal MPC component and an ancillary feedback mechanism, to achieve optimal inter-area generation coordination in multi-area power systems. Nevertheless, the growing integration of energy storage systems imposes supplementary operational constraints that are inherently difficult to capture through conventional physical modeling approaches. These emerging constraints (i) substantially elevate the complexity of LFC system design and (ii) pose significant challenges for real-time optimization processes, particularly under high renewable penetration scenarios.

To address these challenges, reinforcement learning (RL), including deep reinforcement learning (DRL), has emerged as a promising solution due to its powerful searching and learning capabilities in uncertain and complex environments. Unlike conventional model-based controllers, RL-based approaches can adaptively learn optimal control policies without requiring an explicit physical model of the system. Notable research efforts in this area have been made. The authors of [22] pioneered a correlated Q($\lambda$) learning algorithm to optimize cooperative equilibrium control strategies in multi-area LFC systems. The authors of [23] developed a hierarchical reinforcement learning architecture featuring dual agent modules (estimator and controller), establishing an intelligent frequency regulator with enhanced uncertainty handling capabilities. The authors of [24] devised a multi-agent reinforcement learning framework employing optimized discretized joint action spaces to achieve precision LFC performance. The authors of [25] introduced a bio-inspired artificial emotional reinforcement learning controller that synergizes mechanical logic with affective computing principles to improve adaptive control. The authors of [26] implemented a deep feature extraction paradigm using stacked denoising auto-encoders, enabling continuous action space optimization for LFC performance enhancement. The authors of [27] incorporated an attention-based critic network to selectively process environmental states, achieving reduction in training time compared to conventional methods. To address challenges including actuator malfunctions, system uncertainties, and limited communication bandwidth, the authors of [28] developed innovative event-triggered LFC strategies with reliability guarantees. In [29], a distributed observer-based framework was established for event-triggered LFC in multi-area power systems vulnerable to cyber threats. The authors of [30] proposed a model-assisted reinforcement learning approach, where an emulator network approximates power system dynamics and zeroth-order optimization enables gradient estimation for control policy generation.

The existing studies predominantly employ direct control strategies, wherein RL agents generate operational commands through real-time frequency signal processing. While these approaches have exhibited satisfactory performance in power system implementations, purely data-driven deep reinforcement learning (DRL) methods encounter fundamental limitations in precisely modeling the nonlinear dynamics of power systems during the training phase. This modeling inaccuracy may consequently yield either suboptimal control decisions or, in severe cases, system instability.

In light of these challenges, this paper proposes a safety reinforcement learning-based approach to enhance LFC performance in power systems integrated with energy storage systems. Specifically, we formulate the problem as a Constrained Markov Decision Process (CMDP), which extends the conventional MDP framework by incorporating explicit constraint handling through a cost function. This formulation enables the proposed method to effectively balance frequency regulation performance with operational constraints. Furthermore, a long short-term memory (LSTM)-based cost prediction critic network is introduced, leveraging supervised learning techniques to improve cost prediction accuracy. To solve the CMDP, we employ a primal-dual Deep Deterministic Policy Gradient (PD-DDPG) algorithm, which efficiently accommodates nonlinear constraints while optimizing frequency control performance. The main novelty of this work lies in its integrated safety reinforcement learning framework for LFC, which fundamentally advances prior approaches through two key innovations: (1) a CMDP formulation that explicitly incorporates operational constraints into the optimization framework, providing provable safety guarantees compared to existing heuristic penalty-based methods, and (2) a PD-DDPG algorithm enhanced with an LSTM-based critic network, which not only solves the CMDP through Lagrangian relaxation but also captures temporal dependencies in cost prediction—addressing critical limitations of standard DDPG implementations and feedforward critics in current literature. This dual innovation enables rigorous constraint satisfaction while achieving superior dynamic performance in renewable-rich power systems.

The rest of the paper is organized as follows. The linearized LFC model and nonlinear behaviors used throughout the paper are introduced in Section 2. Section 3 presents the framework of the proposed method. Section 4 verifies the effectiveness and advantages of the proposed method with simulation results. Finally, the conclusion of this paper is presented in Section 5.

2. Power System Frequency Response Model

This section briefly introduces the linearized LFC model and nonlinear behaviors.

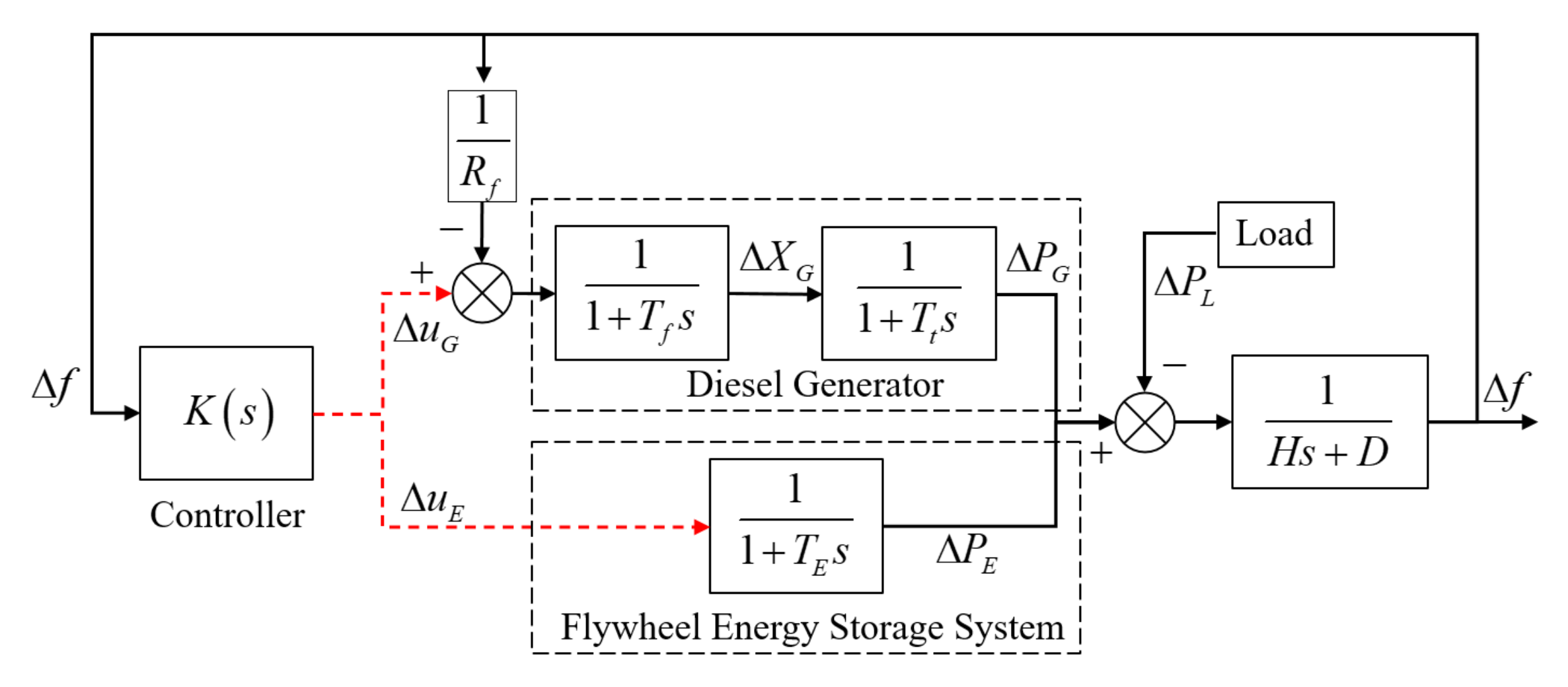
2.1. Linearized LFC Model

In this paper, the microgrid includes a diesel generator and a flywheel energy storage system, with the structure shown in Figure 1.

The whole LFC system is composed of a generator, governor, turbine, and other links involved in the secondary control loop [31]. The system dynamics can be expressed as Equations (1)–(3).

$$\Delta \dot{f}={\displaystyle \frac{1}{H}}\left(\Delta P_G+\Delta P_E-\Delta P_L\right)-{\displaystyle \frac{D}{H}}\Delta f$$

(1)

$$\Delta \dot{P_G}={\displaystyle \frac{1}{T_t}}\Delta X_G-{\displaystyle \frac{1}{T_t}}\Delta P_G$$

(2)

$$\Delta \dot{X_G}={\displaystyle \frac{1}{T_f}}\Delta u_G-{\displaystyle \frac{1}{R_f{T}_f}}\Delta f-{\displaystyle \frac{1}{T_f}}\Delta X_G,$$

(3)

where $\Delta P_G$ and $\Delta u_G$ represent the diesel generator’s output power and control signal, respectively. $\Delta X_G$ is the output signal of the governor. $T_f$ and $T_t$ are the time constants of the governor and the diesel generator, respectively. $R_f$ is the droop coefficient of the diesel generator. $\Delta f$ denotes the frequency deviation of the microgrid. H represents the inertia constant. D represents the generator damping coefficient.

The flywheel energy storage system model is represented as a first-order transfer function, with its dynamic model expressed as Equation (4).

$$\Delta \dot{P_E}={\displaystyle \frac{1}{T_E}}\Delta u_E-{\displaystyle \frac{1}{T_E}}\Delta P_E,$$

(4)

where $\Delta P_E$ and $\Delta u_E$ represent the output power and control signal of the flywheel energy storage system, respectively. $T_E$ is the time constant of the flywheel energy storage system.

2.2. Nonlinear Behaviors

For the sake of the practical application of the proposed method, it is necessary to model nonlinear characteristics of power systems imposed by physical dynamics. This paper considers two nonlinear power characteristics of the diesel generator: the generation rate constraint (GRC) and the power increment change constraint, as shown in Equations (5) and (6).

$$\begin{array}{c}\hfill \Delta P_G=min(\Delta P_{Gmax},max(0,\Delta P_G))+max(\Delta P_{Gmin},min(0,\Delta P_G))\end{array}$$

(5)

$$\begin{array}{c}\hfill \Delta P_G=\int min\left(\delta ,max\left({\displaystyle \frac{d{P}_g\left(t\right)}{dt}}\right)\right)+max\left(-\delta ,min\left({\displaystyle \frac{d{P}_g\left(t\right)}{dt}}\right)\right)dt\end{array},$$

(6)

where $max(x,y)$ represents the maximum value between x and y. $min(x,y)$ represents the minimum value between x and y. $\delta$ and $-\delta$ represent the upper and lower limits of the diesel generator’s power ramp rate, respectively. $\Delta P_{Gmax}$ and $\Delta P_{Gmin}$ represent the upper and lower limits of the power increment, respectively. The power increment constraints of the flywheel energy storage system is also considered, as shown in Equation (7).

$$\begin{array}{c}\hfill \Delta P_E=min(\Delta P_{Emax},max(0,\Delta P_E))+max(\Delta P_{Emin},min(0,\Delta P_E))\end{array}$$

(7)

where $\Delta P_{Emax}$ and $\Delta P_{Emin}$ represent the upper and lower limits of the power increment of the flywheel energy storage system, respectively.

3. Main Results

3.1. Constrained Markov Decision Process

Figure 2 shows the framework of the proposed Primal-Dual DDPG. The LFC model considering the flywheel energy storage system is transformed into a CMDP. In the CMDP, if the control strategy violates the constraints, the agent will receive a negative reward. However, the size of the penalty value is difficult to define. The CMDP extends the MDP with a cost function, which can better balance future discounted rewards with control safety constraints.

In each Markov Decision Process, the agent, at each time step, observes the current state ${\mathbf{s}}_t$ of the power system, performs action $a_t$, obtains a reward value $r_t$ and a cost value $c_t$, and transitions to the next state ${\mathbf{s}}_{t+1}$, until the total control time period is reached. The formulation is as follows. Based on the LFC problem considering the flywheel energy storage system, the CMDP for the time step is constructed as follows:

The state space of the CMDP is defined as Equation (8).

$$s_t=\left[\Delta f_t,\int \Delta fdt,{\displaystyle \frac{d}{dt}}\Delta f\right],$$

(8)

where $\int \Delta fdt$ and $d\Delta f/dt$ represent the integral and derivative of the frequency deviation, respectively.

The action space of the CMDP is defined as Equation (9).

$$a_t=\left[\Delta u_G^t,\Delta u_E^t\right].$$

(9)

The reward function of the CMDP is defined as Equation (10).

$$r_t=\left\{\begin{array}{cc}\alpha \hfill & |\Delta f_t|<0.02Hz\hfill \\ {\xi }_1\Delta f_t^2\hfill & 0.02Hz⩽\Delta f_t<0.05Hz\hfill \\ {\xi }_2\Delta f_t^2\hfill & 0.05Hz⩽\Delta f_t<0.10Hz\hfill \\ {\xi }_3\Delta f_t^2\hfill & 0.10Hz⩽\Delta f_t<0.15Hz\hfill \\ {\xi }_4\Delta f_t^2\hfill & 0.15Hz⩽\Delta f_t⩽0.20Hz\hfill \\ \beta \hfill & \Delta f_t>0.20Hz\hfill \end{array}\right.,$$

(10)

where $\alpha$ is the positive reward value, given only when the frequency deviation is less than 0.02 Hz, with $\alpha >0$. ${\xi }_1,{\xi }_2,{\xi }_3$, and ${\xi }_4$ are the penalty coefficients corresponding to different frequency deviation intervals with ${\xi }_4<{\xi }_3<{\xi }_2<{\xi }_1<0$. The penalty value $\beta$ is applied when the frequency deviation exceeds a certain threshold, and the agent will receive a large penalty.

The cost function of the CMDP is defined as Equation (11).

$$\left\{\begin{array}{cc}{c}_t=\hfill & c_G^t+c_E^t+c_{\delta }^t\hfill \\ c_G^t=\hfill & max(0,\Delta P_G^t-\Delta P_{Gmax})\hfill \\ \hfill & +max(0,\Delta P_{Gmin}-\Delta P_G^t)\hfill \\ c_E^t=\hfill & max(0,\Delta P_E^t-\Delta P_{Emax})\hfill \\ \hfill & +max(0,\Delta P_{Emin}-\Delta P_E^t)\hfill \\ c_{\delta }^t=\hfill & max\left(0,d{P}_G^t/dt-\delta \right)\hfill \\ \hfill & +max\left(0,-\delta -d{P}_G^t/dt\right)\hfill \end{array}\right.,$$

(11)

$C_G^t$ and $C_{\delta }^t$ are the functions representing the violation of the power generation rate and the power increment change of the diesel generator, respectively. $C_E^t$ is the function representing the violation of the power generation rate of the flywheel energy storage system.

The objective function of the CMDP is defined as Equation (12), which builds directly upon the standard CMDP framework established in [32,33].

$$\left\{\begin{array}{cc}{\pi }^{*}=\hfill & \underset{\pi }{argmax}R\left(\pi \right)=\underset{\pi }{\mathbb{E}}\left[{\displaystyle \sum _{t=0}^T{\gamma }^t{r}_t|s_t,a_t}\right]\hfill \\ s.t.\hfill & C\left(\pi \right)=\underset{\pi }{\mathbb{E}}\left[{\displaystyle \sum _{t=0}^T{\gamma }^t{c}_t|s_t,a_t}\right]⩽d\hfill \end{array}\right.,$$

(12)

where $\gamma$ is the discount factor, and $0\le \gamma \le 1$. $\pi$ is the policy mapping from states to actions. $r_t$ is the reward at time t. $c_t$ is the cost at time t. T is the total control time period. The objective is to maximize the future discounted rewards while satisfying the control safety constraints.

3.2. LSTM-Based Cost Critic Network

A cost prediction network based on LSTM is proposed. This network takes the state and action of the frequency control model as inputs to predict the control cost at the current time step, thus realizing a nonlinear mapping from state–action pairs to costs. This method can capture the complex temporal dependencies between states and actions during the system’s operation, effectively improving the accuracy of cost prediction.

In this framework, a PID controller is used to control the LFC model considering the flywheel energy storage system. By collecting real-time information from the power system, a labeled dataset $D=\left\{(s_t,a_t,c_t)\right\}$ is constructed, where the dataset includes the inputs and outputs of the PID controller, i.e., $s_t$ and $a_t$, respectively. Furthermore, the labeled dataset is used to train the LSTM network, thereby establishing a mapping from state and action to cost via supervised learning. During actual control, the cost calculated using Equation (11) is also used as the label for training data. By utilizing the dynamic response data of the flywheel energy storage system, an effective data pair for constructing the LSTM model is formed.

The cost prediction network based on the LSTM architecture is shown in Equation (13). The cost prediction network receives input $x_t$ at time step t and updates the current state through hidden states $h_t$ and memory cells $c_{tLSTM}$. The update equation for the cost prediction network’s state is shown as Equation (13).

$$\left\{\begin{array}{c}{f}_t=\sigma (W_f·[h_{t-1},x_t]+b_f)\hfill \\ i_t=\sigma (W_i·[h_{t-1},x_t]+b_i)\hfill \\ {\tilde{c}}_{tLSTM}=tanh(W_c·[h_{t-1},x_t]+b_c)\hfill \\ c_{tLSTM}=f_t\odot c_{tLSTM}+i_t\odot {\tilde{c}}_{tLSTM}\hfill \\ o_t=\sigma (W_o·[h_{t-1},x_t]+b_o)\hfill \\ h_t=o_t·tanh\left(c_{tLSTM}\right)\hfill \end{array}\right.,$$

(13)

where $f_t$, $i_t$, and $o_t$ are the forget, input, and output gates, respectively, ⊙ represents element-wise multiplication, $\sigma$ is the activation function, $W_f$, $W_i$, $W_o$, and $W_c$ are weight matrices, and $b_f$, $b_i$, $b_o$, and $b_c$ are bias terms.

Once the updated hidden state $h_t$ is obtained, the output of the cost prediction network is mapped to the predicted cost via a fully connected layer, shown as Equation (14).

$$Q_c(s_t,a_t)=h^{\left(n\right)}\left[h^{(n-1)}\left[\cdots h^{\left(1\right)}\left(h_t\right)\right]\right]$$

(14)

where $h^{\left(n\right)}$ is the activation function of the output layer. $Q_c(s_t,a_t)$ is the predicted cost.

The cost prediction network is trained using supervised learning. The training of the cost prediction network aims to minimize the difference between the actual control cost and the cost predicted by the network at each time step, as shown in Equation (15):

$$\underset{{\theta }_c^Q}{min}{∥y-Q_c(s_t,a_t)∥}^2$$

(15)

where ${\theta }_c^Q$ represents the parameter of the cost prediction network. y is the label of the dataset.

3.3. The Proposed Primal-Dual Ddpg

A method based on Primal-Dual DDPG is proposed for solving CMDP. By introducing a Lagrange multiplier, the inequality constraint problem in the objective function is transformed into an unconstrained problem. Additionally, by utilizing a cost prediction neural network, the efficiency of the safe reinforcement learning algorithm is improved, enabling the update of the actor network.

The original CMDP problem is shown in Equation (12). To solve this, we introduce a Lagrange multiplier $\lambda$ and reformulate the problem as an unconstrained min–max optimization shown in Equation (16).

$$\mathcal{L}(\pi ,\lambda )=R\left(\pi \right)-\lambda \left(C\left(\pi \right)-d\right)$$

(16)

The primal-dual optimization then becomes Equation (17):

$$\underset{\pi }{max}\underset{\lambda \ge 0}{min}\mathcal{L}(\pi ,\lambda )$$

(17)

Based on PD-DDPG [34], the Lagrange multiplier is updated to penalize constraint violations, shown in Equation (18).

$$\lambda \leftarrow max\left(0,\lambda -{\eta }_{\lambda }(C\left(\pi \right)-d)\right)$$

(18)

where ${\eta }_{\lambda }$ is the learning rate for $\lambda$. In our method, $C\left(\pi \right)$ is replaced by the LSTM-based cost critic network $Q_c(s_t,a_t)$. The policy $\pi$ is trained to maximize $\mathcal{L}(\pi ,\lambda )$, effectively balancing reward maximization and constraint satisfaction.

A deep reinforcement learning controller is constructed, consisting of the actor network $\mu (a|{\theta }^{\mu })$, the reward critic network $Q_R(s,a|{\theta }_R^Q)$, the target actor network ${\mu }^{\prime }(a|{\theta }^{{\mu }^{\prime }})$, and the target reward critic network $Q_R^{\prime }(s,a|{\theta }_R^{Q^{\prime }})$. The parameters of the actor network ${\theta }^{\mu }$ and the reward critic network ${\theta }_R^Q$ are initialized, and the parameters of both networks are subsequently assigned to their respective target networks.

The interaction experience pool and dual variable $\lambda$ are initialized. Interaction experiences between the actor network and the power system are obtained through simulation experiments to populate the experience pool.

The parameters of the actor network, reward critic network, target actor network, and target reward critic network are optimized based on the interaction experience pool. Specifically, the optimization process includes the following steps based on Equations (19)–(27).

1.

Target reward critic value calculation: K interaction experiences are sampled from the experience pool ${\left\{(s_k,a_k,r_k,c_k,s_{k+1})\right\}}_{k=1}^K$. The target reward critic value $Q_{\mathrm{target},k}$ is computed using the equation:

$$Q_{\mathrm{target},k}=r_k+\gamma Q_R^{\prime }\left(s_{k+1},{\mu }^{\prime }\left(s_{k+1}|{\theta }^{{\mu }^{\prime }}\right)|{\theta }_R^{Q^{\prime }}\right)$$

(19)

where ${\theta }^{{\mu }^{\prime }}$ and ${\theta }_R^{Q^{\prime }}$ denote the parameters of the target actor network and the target reward critic network, respectively. $\gamma$ is the discount factor. $r_k$ is the immediate reward at step k. $s_{k+1}$ is the next state from experience tuple $\{(s_k,a_k,r_k,c_k,s_{k+1})$.

2.

Updating reward critic network: The parameters of the reward critic network are updated by minimizing the loss function ${\mathcal{L}}_R$:

$${\displaystyle {\mathcal{L}}_R=\frac{1}{K}\sum _{k=1}^K\left(Q_{\mathrm{target},k}-Q_R\left(s_k,\mu \left(s_k|{\theta }^{\mu }\right)|{\theta }_R^Q\right)\right)}$$

(20)

3.

Action gradient calculation: Based on Equation (18), the action gradient $d_a$ is computed using

$${\displaystyle d_a=\frac{1}{K}\sum _{k=1}^K\left({\nabla }_{{\theta }^{\mu }}{Q}_R-\lambda {\nabla }_{{\theta }^{\mu }}{Q}_C\right)}$$

(21)

where ${\nabla }_{{\theta }^{\mu }}{Q}_R$ and ${\nabla }_{{\theta }^{\mu }}{Q}_C$ are computed based on chain rule, shown in Equations (22) and (23).

$${\nabla }_{{\theta }^{\mu }}{Q}_R={\nabla }_a{Q}_R\left(s,\mu \left(s\right|{\theta }^{\mu })|{\theta }_R^Q\right){\nabla }_{{\theta }^{\mu }}\mu \left(s|{\theta }^{\mu }\right){|}_{s=s_k}$$

(22)

$${\nabla }_{{\theta }^{\mu }}{Q}_C={\nabla }_a{Q}_C\left(s,\mu \left(s\right|{\theta }^{\mu })|{\theta }_C^Q\right){\nabla }_{{\theta }^{\mu }}\mu \left(s|{\theta }^{\mu }\right){|}_{s=s_k}$$

(23)

where ${\nabla }_a{Q}_R\left(s,\mu \left(s\right|{\theta }^{\mu })|{\theta }_R^Q\right)$, ${\nabla }_a{Q}_C\left(s,\mu \left(s\right|{\theta }^{\mu })|{\theta }_C^Q\right)$, and ${\nabla }_{{\theta }^{\mu }}\mu \left(s|{\theta }^{\mu }\right)$ are derived from the reward critic network, cost prediction network, and actor network, respectively, using the backpropagation algorithm. The parameters of the actor network are updated using gradient descent:

$${\theta }^{\mu }\leftarrow {\theta }^{\mu }-{\eta }_a·d_a$$

(24)

where ${\eta }_a$ is the learning rate of the actor network.

4.

Dual variable gradient calculation: Based on Equation (18), the gradient of the dual variable $\lambda$ is calculated as Equation (25).

$${\displaystyle d_{\lambda }=\frac{1}{K}\sum _{k=1}^K\left[Q_C\left(s_k,\mu \left(s_k\right|{\theta }^{\mu })\right|{\theta }_C^Q)-d\right]}$$

(25)

The dual variable are updated via gradient descent shown in Equation (26).

$$\lambda \leftarrow max\left(0,\lambda -{\eta }_{\lambda }{d}_{\lambda }\right)$$

(26)

where ${\eta }_{\lambda }$ is the learning rate of the dual variable.

5.

Soft update of target networks: The target actor network and target reward critic network are updated using the soft update rule:

$$\left\{\begin{array}{c}{\theta }^{{\mu }^{\prime }}\leftarrow \tau {\theta }^{\mu }+(1-\tau ){\theta }^{{\mu }^{\prime }}\hfill \\ {\theta }_R^{Q^{\prime }}\leftarrow \tau {\theta }_R^Q+(1-\tau ){\theta }_R^{Q^{\prime }}\hfill \end{array}\right.$$

(27)

where $\tau$ is a preset soft update parameter.

4. Case Study

The proposed PD-DDPG LFC method is evaluated on a power system with parameters detailed in

Table 1. Parameters of the power system.

Parameter	Value	Parameter	Value	Parameter	Value
$\Delta P_{Gmax}$ (p.u.)	$0.03$	$T_f$ (s)	10	H (p.u./Hz)	14.22
$\Delta P_{Gmin}$ (p.u.)	$-0.03$	$T_t$ (s)	0.10	D (p.u./Hz)	0
$\Delta P_{Emax}$ (p.u.)	$0.025$	$\delta$ (p.u./s)	0.0017 [36]	R (Hz/p.u.)	0.05
$\Delta P_{Emin}$ (p.u.)	$-0.025$	$T_E$ (s)	1

, which also outlines the system constraints. For the controller updating in simulations, we set the size of the memory replay buffer, learning rate $\eta$, and constant $\tau$ for updating the target network h as 8000, 0.00005, and 0.1, respectively. DDPG [35] is used as a comparison algorithm. DDPG applies different fixed penalty coefficients to penalize actions that violate constraints, with the penalty factor defined as

$$r_p=r_t-\rho c_t$$

(28)

where $\rho$ is the penalty coefficient, set to 0.001 and 0.005, respectively. A PID controller, whose data builds the LFC database, is also used for comparison, and its gains are tuned manually. The memory replay buffer is initialized by the LFC database. Figure 3 shows that the final converged loss of the LSTM-based network is significantly lower than that of the CNN-based network. Figure 4 shows the prediction cost comparison between CNN-based and LSTM-based cost critic networks, demonstrating that the LSTM-based network achieves better prediction cost performance than the CNN-based network.

Step disturbances are applied at the following times: a $0.04p.u.$ disturbance at $t=100$ s, a $-0.06p.u.$ disturbance at $t=250$ s, a $0.05p.u.$ disturbance at $t=400$ s, and a $-0.03p.u.$ disturbance at $t=550$ s. Figure 5 shows the frequency deviation of the power system. It can be observed that, although the DDPG method with a penalty factor ($\rho =0.005$) performs better than the proposed PD-DDPG method when handling positive step disturbances, it performs worse than even the PID controller when facing negative step disturbances. Overall, the proposed PD-DDPG method provides the best control performance, with a smaller overshoot in the frequency deviation and a faster recovery speed, demonstrating its superior ability to regulate frequency. As shown in

Table 2. Performance metrics of different methods.

Method	Settling Time (s)	Peak (p.u.)	Mean Absolute Error (MAE) (p.u.)
Standard PID	131.51	0.0222	0.0022
DDPG [35] with $\rho =0.001$	48.33	0.0104	0.0010
DDPG [35] with $\rho =0.005$	70.50	0.0153	0.0008
Proposed PD-DDPG	55.02	0.0061	0.0007

, the proposed PD-DDPG achieves superior overall performance despite a 13.8% longer settling time (55.02 s) versus DDPG ($\rho$ = 0.001) (48.33 s), delivering 41.4% lower peak deviation (0.0061 p.u.) and 30% reduced MAE (0.0007 p.u.) while maintaining 86.3% faster response than conventional PID. This optimal trade-off ensures enhanced transient stability and robustness, where minimizing overshoots proves more critical than absolute settling time in practical power systems. Figure 6 and Figure 7 show the power output of the diesel generator and the flywheel energy storage system, respectively. It can be observed that, due to different constraint conditions, the power output response curves of the diesel generator and the flywheel energy storage system exhibit distinct characteristics. Under the PD-DDPG control strategy, both the diesel generator and the flywheel energy storage system better account for these constraints during the update process. The proposed method coordinately reduces the power output fluctuations of both diesel generator and flywheel energy storage system, significantly optimizing the amplitude of system frequency deviation fluctuations and effectively improving frequency regulation performance.

5. Conclusions

This paper proposes a safety reinforcement learning framework for load frequency control in modern power systems with energy storage integration, featuring a constrained Markov decision process formulation solved through a novel primal-dual deep deterministic policy gradient algorithm enhanced by an LSTM-based critic network. The proposed approach demonstrates superior constraint-handling capability and frequency regulation performance compared to conventional methods, particularly in renewable-rich power systems, while maintaining strict operational limits, thereby providing an effective solution for next-generation smart grid applications.