Design of Low-Cost Axial-Flow Turbines for Very Low-Head Micro-Hydropower Plants

Abstract

In the Amazon, nearly one million people remain without reliable access to electricity. Moreover, the rural electricity grid is a mostly single-phase, ground-return type, with poor energy quality and high expenses. This study examines very low-head micro-hydropower (MHP) sites in the Amazon, emphasizing the integration of multiple axial-flow turbines. It includes an analysis of flow duration curves and key curves, both upstream and downstream, to design an MHP plant with multiple units targeting maximized energy yield. The presence of multiple turbines is crucial due to the substantial annual flow variation in the Amazon rivers. One contribution of this work is its scalable framework for ultra-low-head and high flow variability in small rivers, which is applicable in similar hydrological configurations, such as those typical of the Amazon. The design applies the minimum pressure coefficient criterion to increase turbine efficiency. Computational Fluid Dynamics (CFD) simulations forecast turbine efficiency and flow behavior. The CFD model is validated using experimental data available in the literature on a similar turbine, which is similarly used in this study for cost reasons, with discrepancies under 5%, demonstrating robust predictions of turbine efficiency and head behavior as a function of flow. This study also explores the implications of including inlet guide vanes (IGVs). We use a case study of a small bridge in Vila do Janari, situated in the southeastern part of Pará state, where heads range from 1.4 to 2.4 m and turbine flow rates span from 0.23 to 0.92 m³/s. The optimal configuration shows the potential to generate 63 MWh/year.

1. Introduction

Brazil possesses an extensive and diversified electrical grid. Nevertheless, remote Amazonian regions experience significant energy poverty, with approximately one million people lacking reliable access to electricity [1]. Nearly one-third of this population resides in isolated communities that rely on polluting diesel generators, which increases public health risks and contributes to environmental degradation [2]. Government programs such as Mais Luz para a Amazônia (MLA), analyzed by [3], aim to achieve universal energy access. However, progress is hindered by geographic isolation, weak governance, and deteriorating infrastructure, particularly the failure of timber bridges, which are essential for people and merchandise transport [4,5]. Paradoxically, the region’s immense hydrography offers untapped opportunities for very low-head micro-hydropower, presenting an interesting renewable power generation alternative to advance socioeconomic equity [6,7].

While conventional hydropower systems are central to Brazil’s energy matrix, they are often impractical in the Amazon due to low topographic heads (<3 m) and significant seasonal variations in river discharge [8,9]. Advances in very-low-head turbines (VLHTs) provide a promising solution in these contexts [10,11]. However, current designs frequently fail to align with broader infrastructure modernization efforts, such as replacing wooden bridges with concrete structures, and often neglect to address hydrological variability. Modular micro-hydropower systems, like those proposed by [12], have achieved up to 73% efficiencies in low-head environments. Nevertheless, standardized design criteria for very-low-head applications remain underdeveloped [13]. Additionally, existing hydrological optimization frameworks often overlook turbine design parameters [14], failing to link flow duration curves to blade geometry—a critical oversight in regions with pronounced seasonal flow fluctuations.

We propose an innovative solution by which the thousands of old wooden bridges in the Amazon are replaced with concrete bridges, integrating ultra-low-head turbines to generate energy. This unique approach is rarely discussed in the literature, considering the specificities of the small rivers in the Amazon. However, it reduces the cost of civil structures for micro-hydropower plants and the cost of construction mobilization. Additionally, an innovative method is used for maximum energy extraction from such rivers using multiple turbines, and the environmental impacts are minimized by providing a fish ladder in the spillway structure. This concept, designated the Ecopontes program, presents a strategic advantage by reducing mobilization and the costs of civil works compared to standalone infrastructure projects, as discussed by Quaranta et al. [11]. In the literature, one similar project on a small dam-bridge was found: the Coimbra dam-bridge small hydro project [12]. However, its power and structure were far greater than that needed for the Ecopontes project.

The rural community of Vila do Janari exemplifies these challenges. Located along the Água Preta River in southeastern Pará (Figure 1), the community depends on a deteriorating wooden bridge for transportation and agricultural logistics, underscoring broader infrastructure vulnerabilities.

To overcome this governance problem, many meetings were held with the local population and community leaders to present and clarify the technical, socioeconomic, and environmental aspects of the project. These community needs were then taken to the municipal government, with the institutional support of the project team at the Federal University of Pará. In parallel, a presentation was given to the Infrastructure Department of the State of Para, detailing the costs associated with the micro-hydropower integration and bridge reconstruction. It is important to note that wooden bridges require routine maintenance, every 3 years on average.

This study proposes a multipurpose dam-bridge system that leverages the Ecopontes initiative, designed to replace wooden bridges with concrete structures, thus reducing mobilization costs, and incorporating fish ladders to protect aquatic biodiversity [15].

The turbine design integrates traditional turbine design methods, such as velocity diagrams [16], and an updated Cordier diagram customized for axial-flow turbines [17] with the minimum pressure coefficient criterion (Cpmin) to enhance hydraulic efficiency [18,19]. The C_p coefficient is defined by Equation (1).

$$C_p={\displaystyle \frac{p-p_0}{0.5\rho w_{\infty }^2}}$$

(1)

where p denotes static pressure on the blade surface, p₀ is the upstream pressure, and w_∞ reference upstream relative velocity. A minimum C_p value must be maintained on the blade’s suction side at the hub section to ensure optimal aerodynamic loading, as established by [18,19,20]. Muis et al. [19] applied this principle to obtain an efficiency of 91% in a very low-head axial flow turbine design.

Adapting such designs to Amazonian contexts requires simplification to suit local machining capabilities [21]. This study addresses the challenge of achieving low-cost fabrication and high efficiency by employing circular flat blades, as demonstrated in previous studies [22,23], to balance performance and feasibility.

Given the critical role of cost in small hydropower development [24], a systematic comparison was conducted between IGV-equipped and non-IGV turbine configurations. IGVs improve flow guidance, reduce swirl losses, and enhance efficiency in low-head applications [25,26]. However, they increase manufacturing complexity and costs. In contrast, non-IGV turbines offer simpler fabrication but lower efficiency [27].

Computational Fluid Dynamics (CFD), a standard tool in VLHT design [28], was used to model a dual-turbine system tailored to the Água Preta River’s hydrology [29]. Simulations employed the k-ω Shear Stress Transport (SST) turbulence model in Ansys CFX to solve the Reynolds-Averaged Navier–Stokes (RANS) equations, validating the results against benchmark experimental data from [30].

The implementation costs for micro-hydro plants were derived from Balarim’s study [31], which proposes expedited methodologies for cost estimation based on parameters such as power capacity (5–100 kW) and hydraulic head (5–60 m), covering civil and electromechanical components. The payback period was compared with the SCABCleuch Micro-Hydro Scheme case study, a Scottish project integrating initial investment data, annual energy generation, and tariff-based revenue [32]. The use of the Ecopontes program presents a strategic advantage by reducing mobilization costs when compared to standalone infrastructure projects [11]. The system is expected to operate seasonally, with an estimated annual generation of approximately 63 MWh, highlighting its operational resilience across both wet and dry seasons.

This work fills a gap between the optimized use of the flow duration curve [14] and high-performance low-head turbine design [13,19], considering the turbine variation’s efficiency as a flow rate function. Additionally, we analyze the use of curved plate blades for both the rotor and stator (guide vanes) to achieve a low-cost design. The presence of guide vanes is also analyzed for off-design operation points.

This analysis highlights the system’s affordability and environmental compatibility. The design mitigates ecological impacts by incorporating fish ladders and aligns with the “energy–ecology nexus” framework [15]. This research proposes a replicable, sustainable energy solution for the Amazon that integrates technical, economic, and environmental challenges.

2. Methods

This methodology outlines a systematic approach for designing and evaluating hydraulic turbines, integrating technical and economic analyses. Figure 2 illustrates the methodology. It begins with a case study to define project scope and collect local hydrological data, followed by key curve analysis to identify critical flow and head scenarios. Turbine configurations are preliminarily selected and designed using the Cordier diagram and Cpmin criteria for high efficiency.

The Cordier diagram demonstrates the good relationship between the inner and outer diameters of the runner. The outer turbine diameter is defined by the turbine flow, considering the compromise of maximum power generation and minimum spillway flow for environmental concerns. Sediment was not considered because the river was clean and small, as is typical in the interior of the Amazon, unlike many large rivers. Finally, to assure good turbine efficiency, the Cpmin criterion defines the solidity cascade and the angle of the runner blade.

CFD simulations validate efficiency and pressure distribution performance metrics. A comparative analysis evaluates trade-offs between IGV-equipped and non-IGV turbines. Subsequently, micro-hydropower plant costs are estimated through literature estimations to assess overall economic viability.

2.1. The Use of Multiple Axial-Flow Turbines in Small Rivers

The turbine flow rates were determined based on the site’s flow (Qriver) duration curve, which indicates the frequency at which specific flow rates occur throughout the year. The smaller turbine (Q2) was designed to operate at Q95% (the flow rate exceeded this 95% of the time), ensuring continuous operation throughout the year.

For the larger turbine (Q1), iterative configurations were tested in increments of 0.5 times the smaller turbine’s flow rate. The total design flow rate (Qp) corresponded to the combined flow rate in each case (Q1 + Q2). The annual energy generated was calculated by integrating the power produced over time, considering the following:

• The exclusive operation of the smaller turbine when Q1 > Qriver > Q95%;
• The exclusive operation of the larger turbine when Qp > Qriver > Q1;
• The combined operation of both turbines when Qriver > Qp;
• The spillage of excess flow when it occurs.

The optimal configuration was selected based on the combination yielding the highest annual energy output. Figure 3 illustrates this concept:

While centrifugal pumps repurposed as turbines (PATs) typically offer cost advantages, axial flow pumps exhibit lower efficiency and higher costs when operated in reverse as turbines. In low-head, high-flow scenarios, axial pumps deviate significantly from their design point, necessitating a specified design, which increases the costs. The inefficiency of these commercial pumps running in pumping mode, compounded by seasonal flow variability, renders axial-flow pumps less economically viable than purpose-built very low-head axial turbines.

2.2. Main Turbine Parameters

A design method for axial-flow turbines operating under very low-head conditions was formulated to maximize hydraulic efficiency. This methodology synthesizes semi-analytical design correlations with the minimum pressure coefficient constraint. The primary rotor geometry was optimized using the Cordier diagram to determine the specific speed N_q (Equation (2)) and rotor diameter, ensuring hydraulic compatibility with low-head applications. Rotational speed and critical design parameters (blade number, hub-to-tip ratio) were subsequently refined using Menny’s empirical models [33] and Quaranta’s dimensionless correlations [34].

$$N_q={\displaystyle \frac{n{Q}^{0.5}}{H^{0.75} }}$$

(2)

where n is the rotational speed (rpm), Q is the flow rate (m³/s), and H is the head (m).

2.3. Low-Cost Blade Design with Linearized Angle Variation

The proposed turbine design employs curved blades fabricated from sheet metal, significantly reducing manufacturing costs compared to CNC-machined or cast blades. The term low-cost in this context prioritizes material accessibility, fabrication simplicity, and scalability for remote regions. Commercial axial-flow turbines typically use CNC-machined or cast blades, which require specialized facilities and incur high production costs. In contrast, the proposed blades are cut and formed from standardized sheet metal, a material widely available even in rural Amazonian communities. This approach reduces blade production costs while remaining compatible with manual forming techniques like grinding and welding tools. The blade angle (β) is defined as a linear function of the radial position (rr) (Equation (3)):

$$\beta \left(r\right)=\beta hub+{\displaystyle \frac{\beta tip-\beta hub}{rtip-rhub}}\cdot \left(r-rhub\right)$$

(3)

where βhub and βtip are the angles at the hub and tip, respectively. This linearization reduces machining complexity and enables mass production using standard sheet metal forming techniques. While this approach introduces a minor efficiency penalty compared to optimized angles, the cost reduction in material and labor justifies its adoption for small-scale hydropower applications.

2.4. Euler’s Equation and Guide Vane Design

The turbine’s hydraulic efficiency hinges on optimizing velocity triangles at the rotor inlet and outlet, governed by Euler’s turbomachinery (Equation (4)):

$$∆Hg=U·(∆Cu)$$

(4)

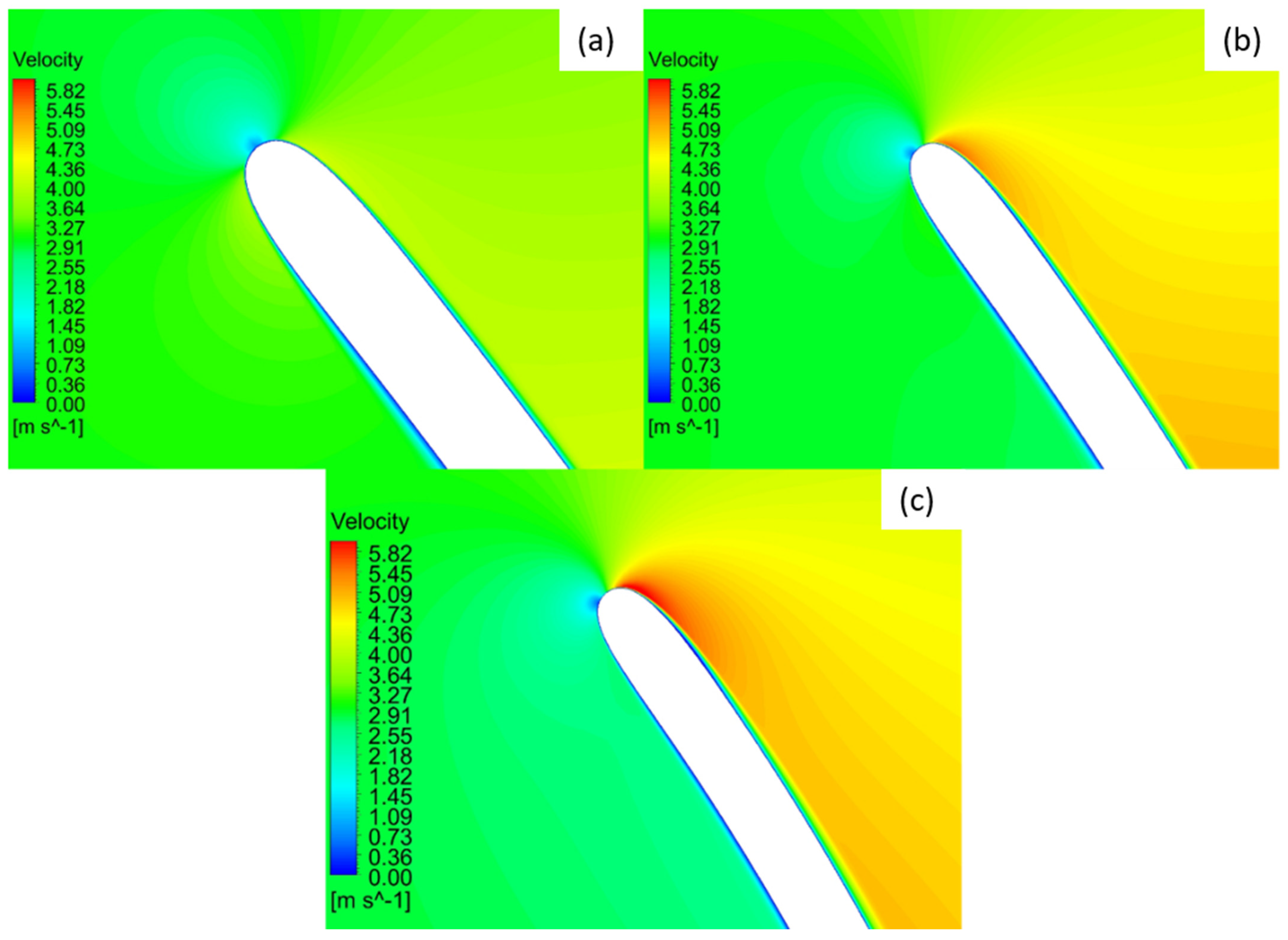
where U is the blade speed and Cu is the difference in tangential components of the absolute velocity at the rotor inlet and outlet. Without an IGV, the incoming flow exhibits higher relative velocity (W) (Figure 4a) and unfavorable incidence angles, leading to excessive aerodynamic loading on the rotor blades. This overload increases separation risks and reduces efficiency. Including an IGV rectifies this issue by imparting pre-swirl (Cu1) to the flow, aligning it with the rotor blade angle and reducing W (Figure 4b). This adjustment ensures smoother energy transfer.

2.5. The Minimum Pressure Coefficient Criterion

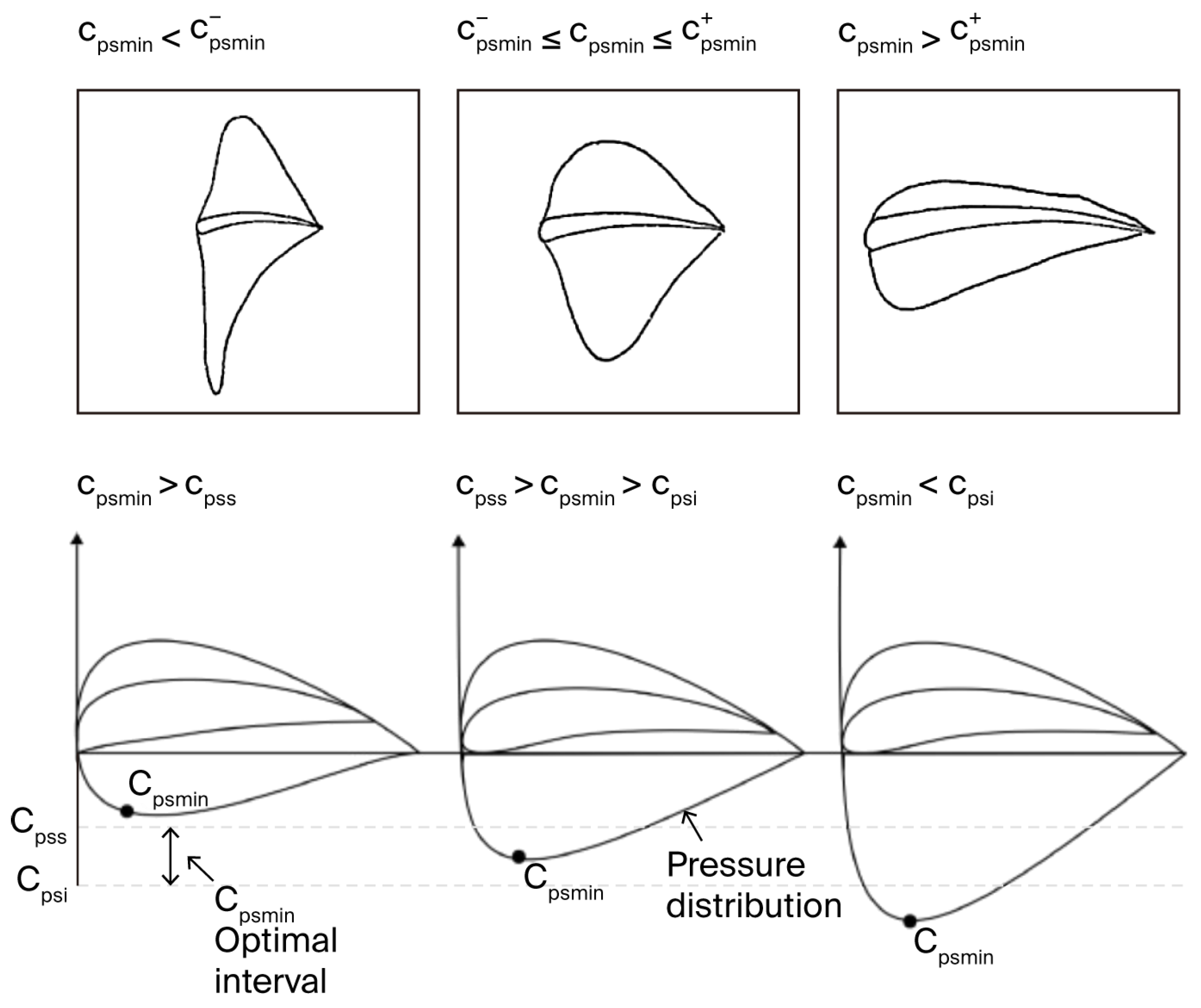
Following the preliminary design phase, the Cpmin criterion is applied to evaluate blade cascade performance at the selected operating point. This analysis focuses on balancing two aerodynamic thresholds:

Cpsi (inferior limit): Below this value, boundary layer separation risks escalate due to excessive pressure loading.

Cpss (superior limit): Above this value, friction losses dominate due to larger wet surfaces.

Recommended Cpmin ranges are specific for each application. For example, Cruz et al. [20] propose a range of from −0.8 to −0.4 for Nq = 278, while Sutikno [18] advocates from −2.25 to −1.25 for Nq = 102. This work selects the applicable range based on numerical validation to balance aerodynamic loading and loss mitigation. This ensures the blade cascade operates within thresholds that minimize boundary layer separation risks and excessive friction losses, as illustrated in Figure 5.

2.6. CFD Analysis

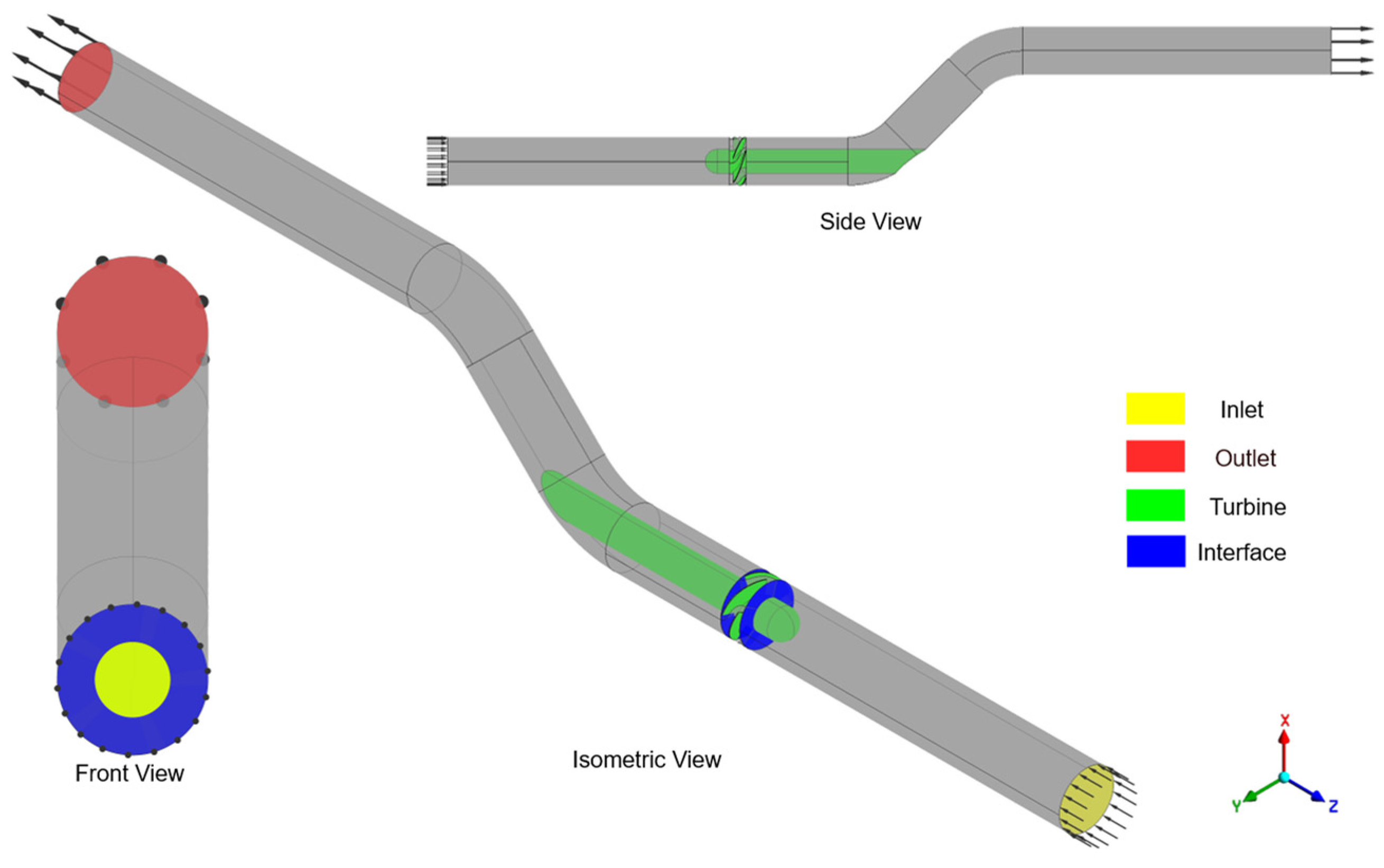
The computational fluid dynamics (CFD) approach used for turbine performance assessment was validated against experimental measurements from an axial-flow turbine (Figure 6), which was tested under various rotation speeds and discharge conditions. Numerical simulations were performed using ANSYS CFX 2024 R2, employing a one-phase flow framework.

2.6.1. Governing Equations

The simulations solved the Reynolds-Averaged Navier–Stokes (RANS) equations to model three-dimensional viscous flow:

• Mass Conservation:

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla ·\left(\rho U\right)=0$$

(5)

2.

Momentum Conservation:

$${\displaystyle \frac{\partial \left(\rho U\right)}{\partial t}}+\nabla ·\left(\rho U\times U\right)=-\nabla p+\nabla ·\mathsf{\tau }+\mathsf{\rho }\mathrm{f}$$

(6)

where τ is the stress tensor, p is pressure, and f includes the Coriolis and centrifugal forces in rotating frames.

2.6.2. Turbulence Modeling and Boundary Conditions

The (SST) k-ω turbulence model was selected for its ability to synergize the k-ω model’s precision in near-wall regions with the k-ϵ model’s reliability in free-stream flows. This hybrid formulation solves adverse pressure gradients and boundary layer separation, critical factors influencing low-head turbine efficiency, where viscous effects dominate performance trends [33].

The boundary conditions were defined as follows:

-

Inlet: Mass flow rate (0.004–0.010 m³/s), turbulence intensity 5%.

-

Outlet: Static pressure set to atmospheric levels (0 Pa gauge).

-

Rotating Domain: The turbine rotor was modeled using a Moving Reference Frame (MRF) approach, and the rotational speed varied from 750 rpm to 1500 rpm. The momentum equation (Equation (7)) in the rotating frame incorporates Coriolis and centrifugal forces.

$$f=-2\omega \times U-\omega \times (\omega \times r)$$

(7)

Interface: A frozen rotor approximation coupled with stationery and rotating domains, preserving relative motion for steady-state performance prediction.

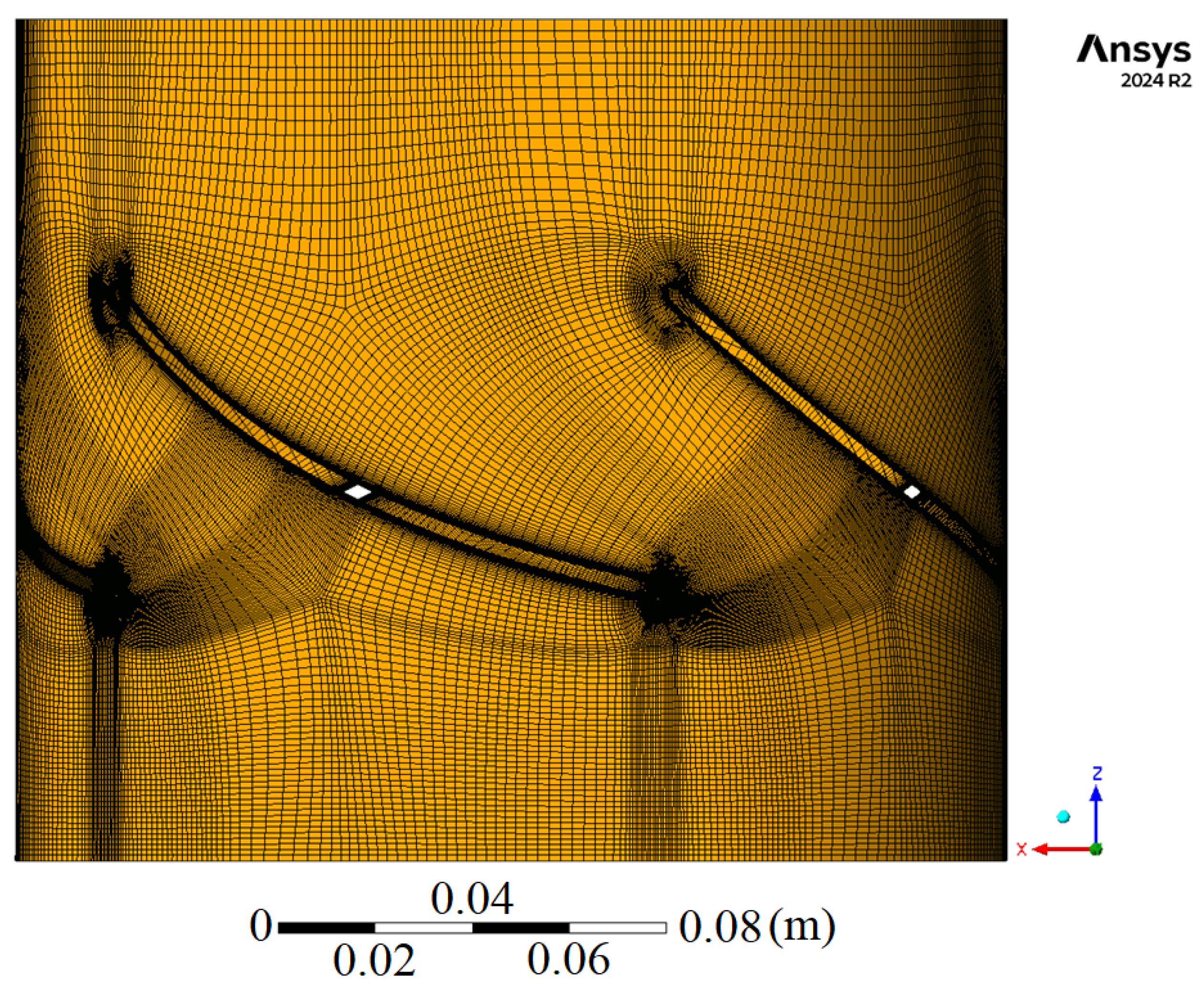
2.6.3. Mesh and Validation

To accurately resolve near-wall turbulence effects, localized mesh refinement was implemented within the boundary layer regions. The initial cell layer height was calibrated to maintain dimensionless wall distances (y+) < 1 across all blade surfaces (Figure 7). A progressive expansion factor of 1.05 between adjacent layers ensured smooth transitions of prism elements while preserving gradient resolution accuracy for the SST k-ω equations. A mesh independence assessment evaluated four configurations (3.4–5.6 million elements) through monitoring of hydraulic efficiency (η) and head (H) (

Table 1. Mesh independence study for the validation case.

Mesh	Efficiency (CFD)	Efficiency (Experimental)	Element Number	GCI (Efficiency)
P1	65.188	65.125	5.60 × 106
P2	65.313	65.125	4.10 × 106	2-1:	0.0057
P3	59.969	65.125	3.40 × 106	3-2:	0.2450
Mesh	Head (CFD)	Head (Experimental)	Element Number	GCI (Head)
P1	0.341	0.34	5.60 × 106
P2	0.342	0.34	4.10 × 106	2-1:	0.0030
P3	0.390	0.34	3.40 × 106	3-2:	0.2305

). The optimal configuration (4.1 million elements) exhibited variations of less than 2% in η and H relative to the finest mesh, satisfying the Grid Convergence Index (GCI) requirements. CFD simulations replicated experimental data with discrepancies of under 5% in both efficiency and pressure distributions, confirming the model’s reliability for ultra-low-head turbine applications.

2.6.4. Numerical Setup

A pressure-based transient solver with second-order spatial discretization was employed to investigate intricate flow separation behaviors and energy dissipation origins across turbine components during nominal and off-design operation.

2.7. Cost Estimation

The cost estimation employs a non-linear regression model proposed by Balarim (1996) [31], developed from historical data of hydroelectric plants constructed by the state-owned Eletrobrás over three decades (1965–1995). The model holistically accounts for nine critical hydropower subsystems: the spillway dam, water intake, adduction channel, surge chamber, penstock, powerhouse, electromechanical equipment, tailrace channel, and distribution transmission lines. These components were statistically correlated to aggregate capital expenditures (CAPEX), including civil works (concrete structures, earthworks) and electromechanical systems (turbines, generators, and transformers), adjusted for inflation to contemporary monetary values. The cost estimation methodology follows the linear regression model proposed by Balarim (1996) [31], expressed as follows:

$$C=\left(A+B·H+{\displaystyle \frac{C}{H}}\right)\times 1000$$

(8)

where H represents the hydraulic head (in meters), A, B, and C are regression constants derived from the rated power capacity (P, in kW) of the hydroelectric plant. These constants encapsulate region-specific cost drivers, including economies of scale, material procurement, and labor intensity, calibrated with historical data from Brazilian hydroelectric projects.

Balarim (1996) [31] emphasizes that this formulation is specifically valid for hydro-power plants within the rated power capacity range analyzed in this study (15 kW), as the regression constants A, B, and C were calibrated to this operational domain. For projects outside this range, the parameters would require recalibration to account for non-linear scaling effects in subsystem costs (disproportionate increases in electromechanical expenses for smaller plants or civil works complexity for larger installations).

The annual revenue from energy generation was calculated using the average regional energy price per kilowatt-hour (kWh) across all states in the North Region of Brazil. This regional average was selected due to the area’s hydrological and infrastructural similarity to the case studied. The derived energy price (USD 0.16/kWh) was then incorporated into the revenue calculation.

3. Results

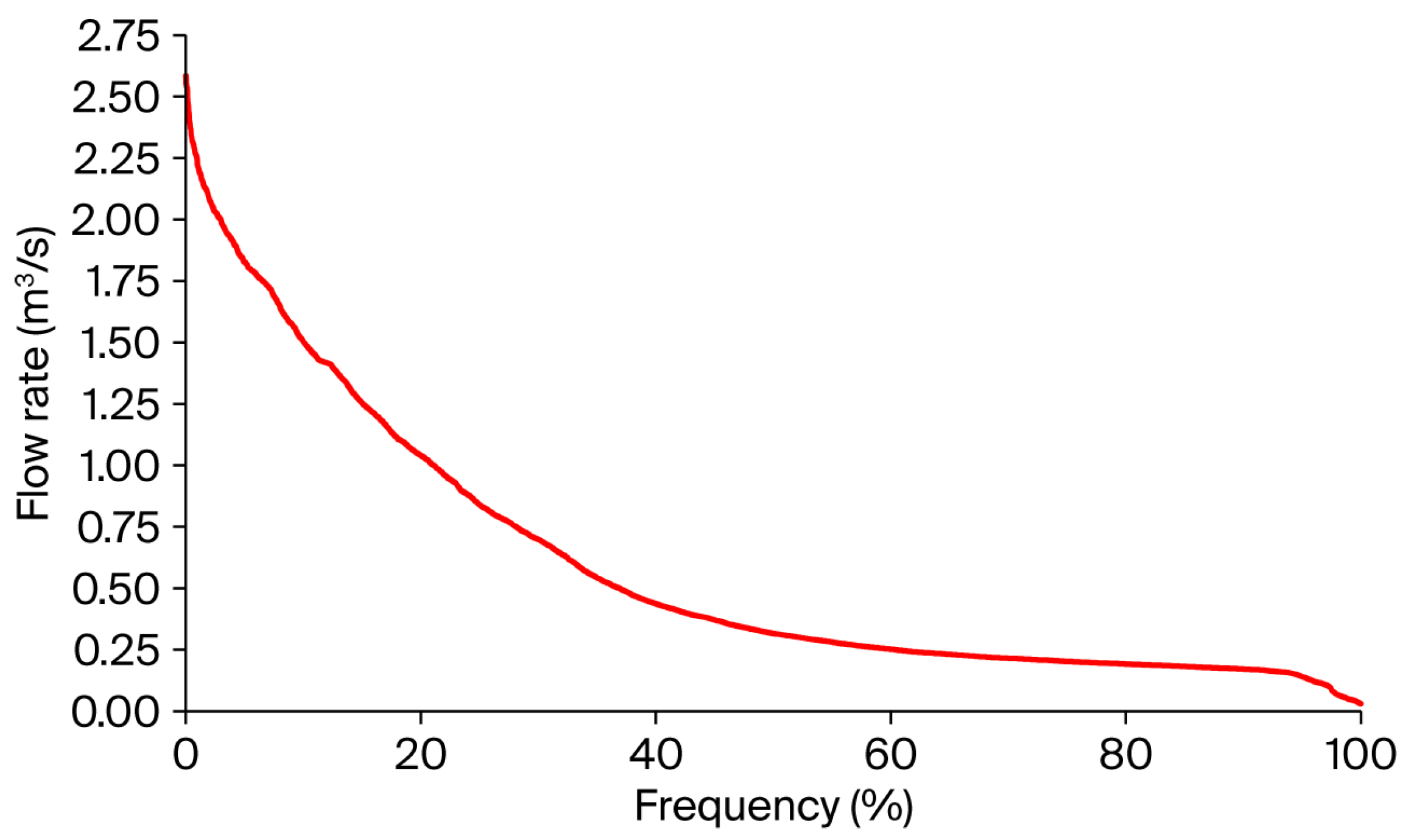
3.1. Key Curve Analysis of the Selected Site

Field inspections were conducted at the small Água Preta River to evaluate its hydraulic dynamics. The findings highlighted substantial flow rate fluctuations and a low hydraulic head. The flow duration curves in Figure 8 and the gross head curve in Figure 9 visually summarize these hydrological patterns.

The data acquired from these assessments directly guided the specification of turbine flow capacities and operational limits explored in this work, as discussed in subsequent sections. By incorporating this site-specific hydraulic information, more accurate boundary conditions were defined for turbine performance analysis, ensuring the design aligns with the site’s distinct hydrological profile.

3.2. Turbine Setup and Flow Rate Definition

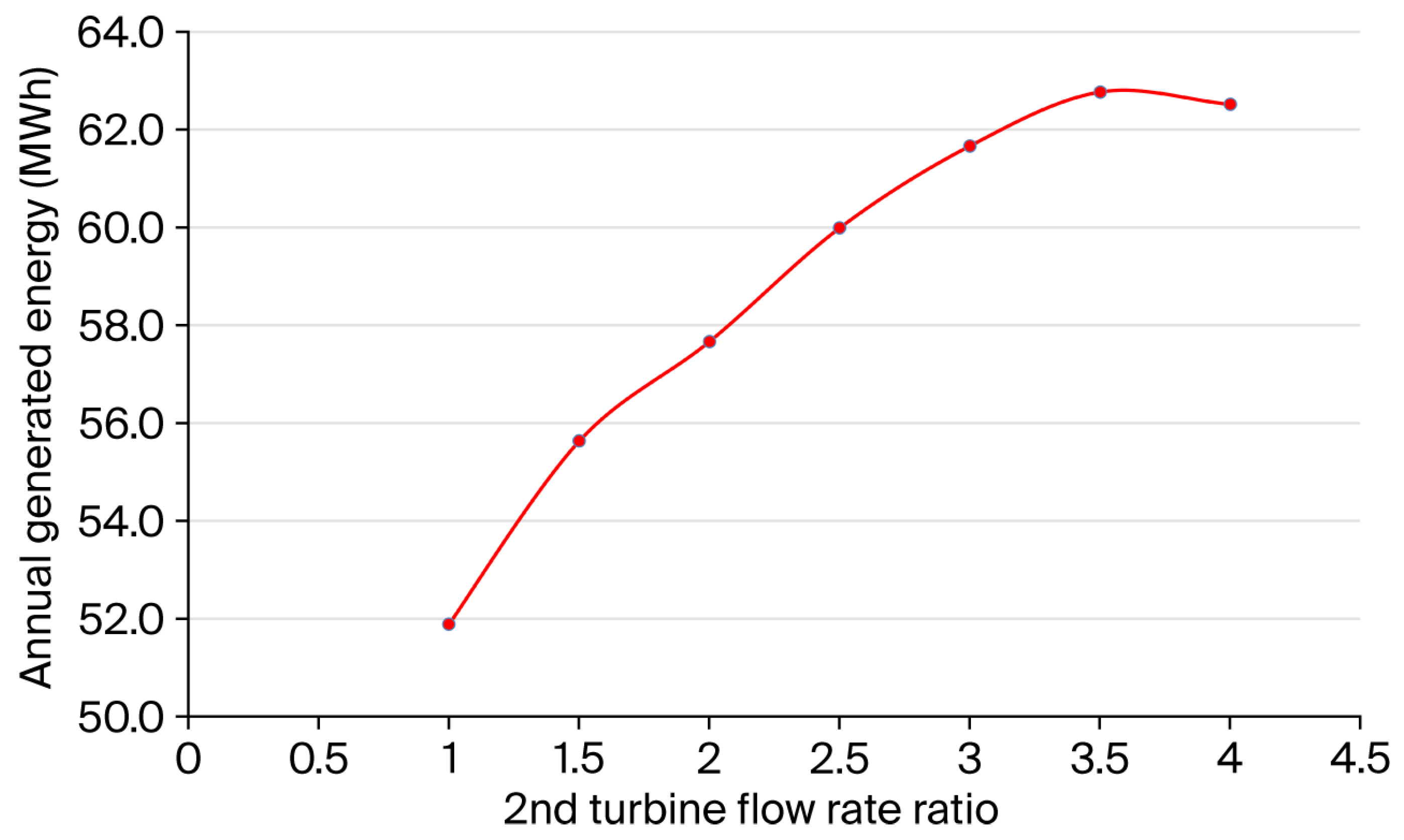
Based on key curve analysis, eight potential turbine setups were screened for hydraulic compatibility. Configurations 1 (1x Q_95%) and 7 (3.5x Q_95%) emerged as superior solutions (Figure 10).

Figure 11 presents the site’s gross head variation as a function of the river flow rate, which is defined by its flow duration curve. Both turbines operate at a constant flow rate, except during the initial starting operation, when the flow rate varies from 80% to 100% of the design flow rate. With the powerhouse configuration, the head losses in the penstock and draft tube can be calculated, giving the net head.

The generated power can be determined using the turbine efficiency curve, provided by the CFD calculation. The annual energy calculation presents an uncertainty related to the flow duration curve. In the Amazon, flow measurement stations for small rivers are rare due to the regionalization of flow estimation from the few existing stations [29], generating uncertainty in the flow estimate. This presents a challenge for the Ecopontes program planning stage. However, the problem can be overcome by measuring the flow rate on site to calibrate the flow rate estimated from the regional flow estimation.

It is also fundamental to consider the control system for energy generation. A control valve must be installed in the penstock to allow for constant load operation and to control the flow rate at head variation. Another control option is variable speed operation using an inverter. Parallel to the present work, studies are considering these issues to identify the most cost-effective control strategy.

3.3. CFD Results of the Validation Case

Experimental data from the literature and simulation results were compared to verify the accuracy of the CFD methodology. Post-processing evaluations showed that the numerically predicted values closely matched the experimentally measured head and efficiency (Figure 12).

The experiments were performed by [30] in an 85 mm tubular turbine without IGV, for different flow rates and rotation speeds. This tangential flow component (Figure 13) generates aerodynamic losses due to non-axial exit flow conditions, directly degrading turbine efficiency.

3.4. Minimum Pressure Coefficient Criterion

Subsequently, an optimized turbine configuration was designed using the validated numerical framework. Three distinct pressure coefficient configurations were simulated to refine aerodynamic performance.

Table 2. Comparison between the reference and proposed turbine.

Value	Reference [30]	Improved
Q	0.0044 m3/s	0.0044 m3/s
H	0.34 m	0.34 m
D	0.085 m	0.066 m
N	750 RPM	1311 RPM

presents comparative analyses between the baseline turbine and the Cordier-optimized design, while

Table 3. Pressure coefficient and cascade geometry comparison.

Machine	Cpmin	Solidity	Camber	Efficiency
a	−0.7881	1.33	7%	85%
b	−0.9292	1.0	7%	86%
c	−2.65	0.66	7%	80%

details the performance variations across the three pressure coefficient-based configurations.

As indicated in Table 3, decreasing the pressure coefficient correlates with reduced efficiency. This occurs because steeper pressure gradients generated at lower pressure coefficients amplify flow separation and turbulence-induced energy losses.

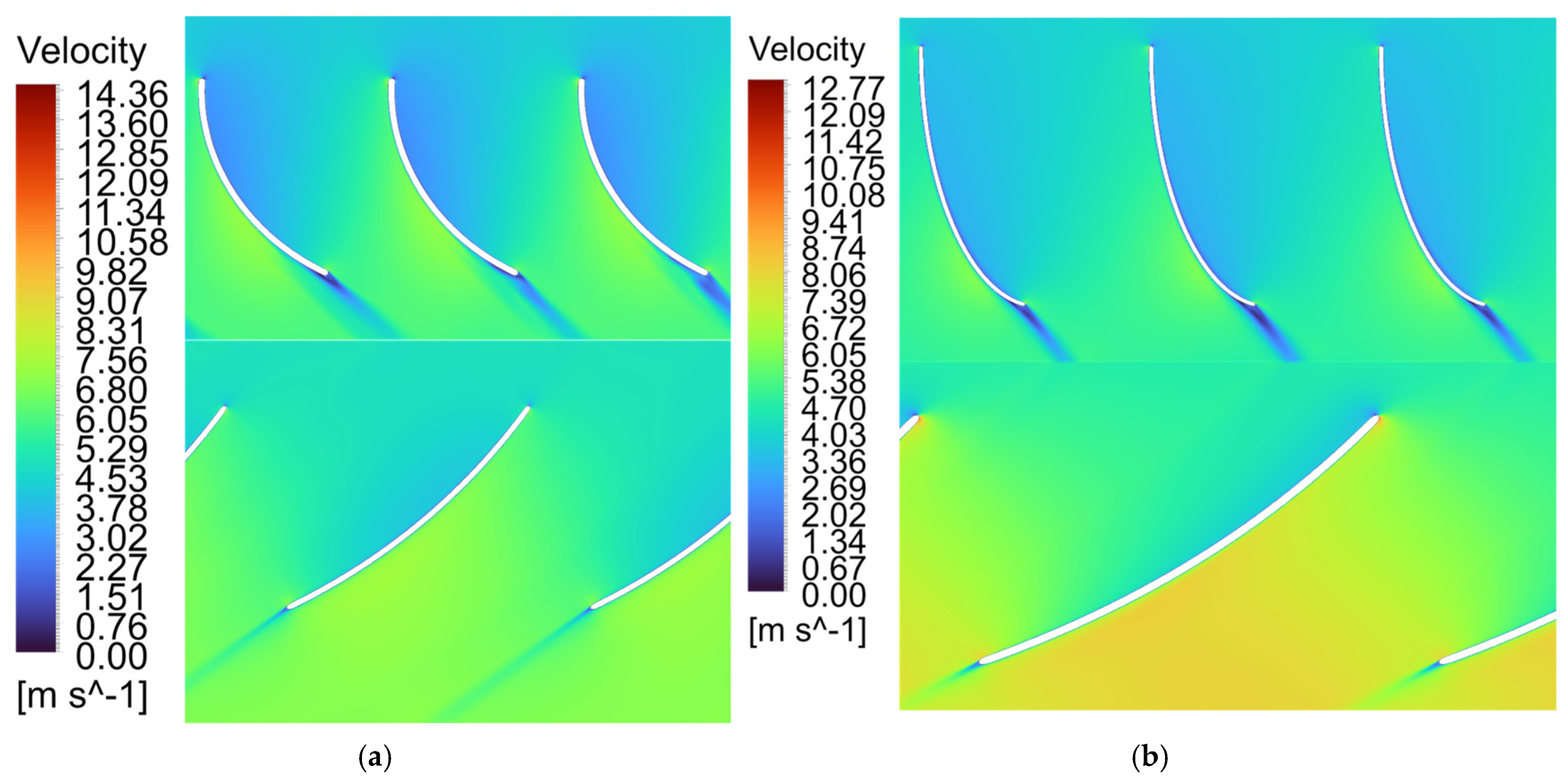
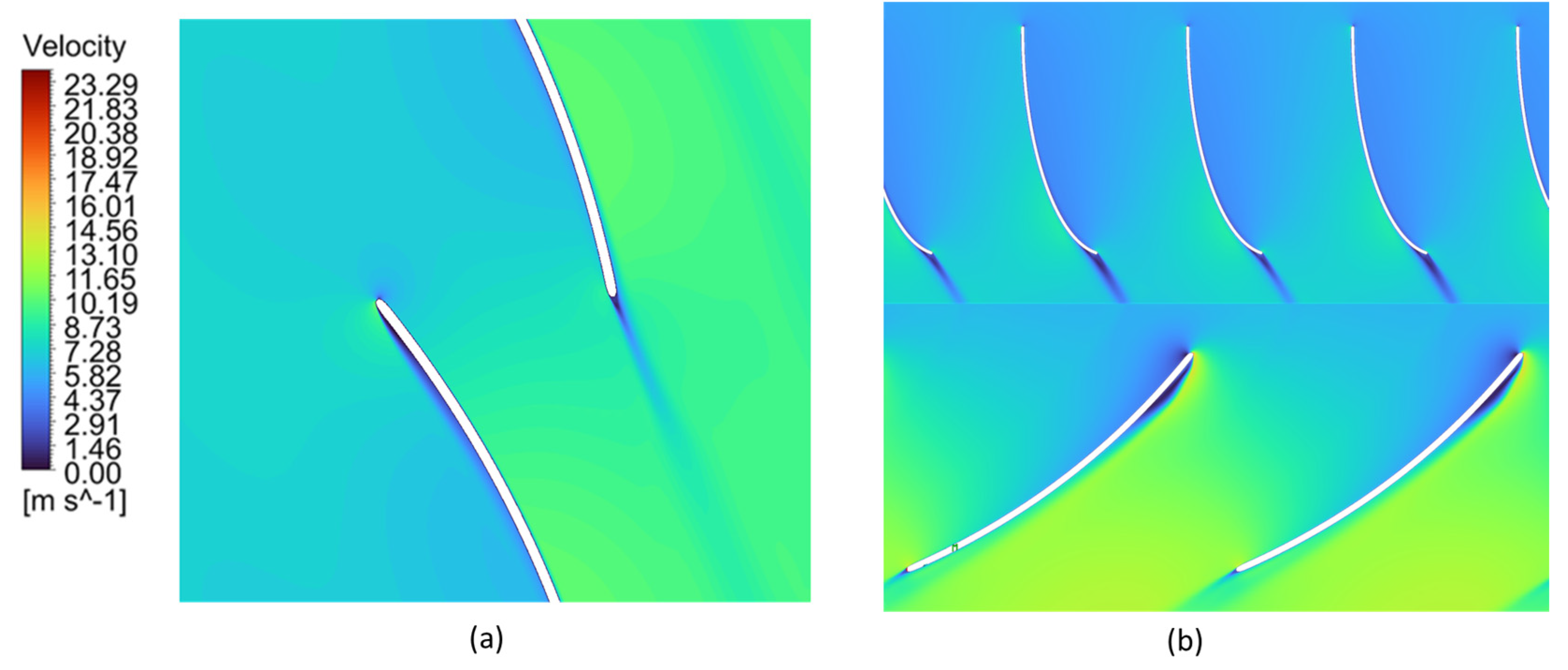
Figure 14 depicts the distinct flow patterns observed across the blade profiles of the three turbine configurations.

Hydraulic loading progressively increases across Machines A–C due to geometric variations. Machine A’s higher solidity (σ = 1.3) maintains attached flow at reduced loading, while Machine C’s compact blade spacing (l/t = 0.66) elevates loading and intensifies suction-side gradients. This trend is quantified by minimum pressure coefficients decreasing from −0.78 (A) to −2.65 (C), indicating stronger adverse gradients and elevated separation risk.

3.5. Machine Design and Performance Comparison: IGV vs. Non-IGV

Two VLHT configurations were developed for the Janari Bridge, addressing site constraints (

Table 4. Operation point of each proposed turbine.

Specifications	Turbine 1	Turbine 7
Flow Rate	0.23 m3/s	0.81 m3/s
Head	2.37 m	1.47 m
Diameter	0.3 m	0.562 m
Rotational Speed	724 RPM	345 RPM
Blade Number	5	4

). Figure 15 details the non-guide-vane design geometry, with Figure 16 showing the IGV-equipped variant.

Cascade parameters and minimum Cp values are tabulated in

Table 5. Minimum pressure coefficient and velocity configuration at the hub section of the blade.

Machine	Cpmin	Solidity	Camber	Relative Velocity (m/s) (IGV)	Relative Velocity (m/s) (no IGV)
Turbine 1	−0.9	1.1	7%	7.94	9.95
Turbine 7	−1.1	1.1	7%	6.29	7.78

. Comparative hub-section flow topologies are shown in Figure 17 (baseline without IGVs) and Figure 18 (IGV-equipped configurations).

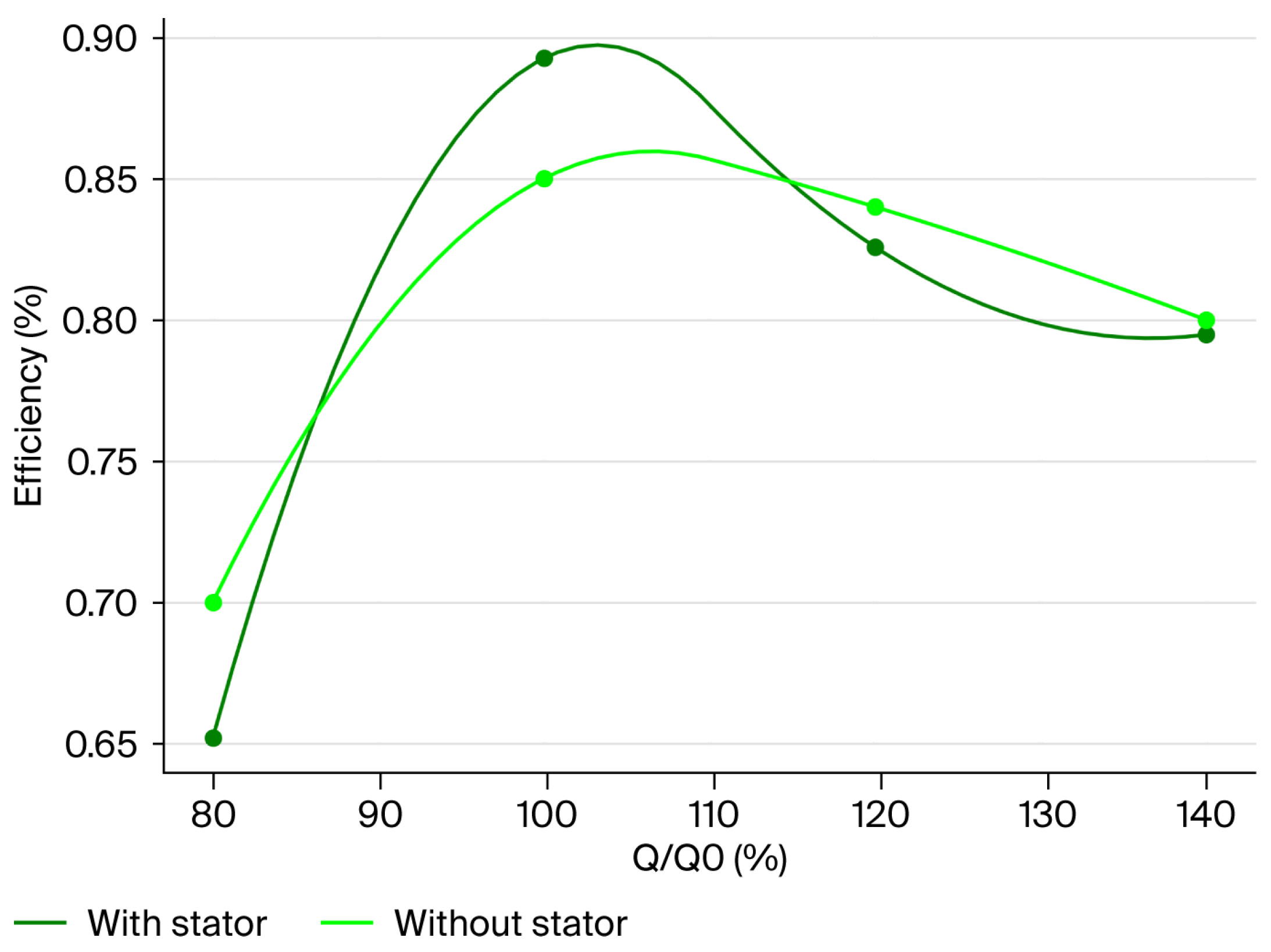
The flow behavior is evident in both the non-IGV (Figure 17) and IGV-equipped (Figure 18) configurations. The main distinction between the two cases is the clear reduction in the machine’s relative flow velocity after IGV implementation. This decrease aligns with the flow-straightening and pre-swirl effects introduced by the guide vanes, which redistribute kinetic energy within the system. Additionally, the efficiency results are displayed in Figure 19 and Figure 20.

Figure 21 and Figure 22 illustrate specific operating points at which the efficiency of the stator-equipped setup is lower than that of the stator-free setup.

This occurrence is linked to unstable flow behavior during off-design operations, which is further evidenced for the IGV-equipped configuration. At these points, the reduced incoming flow creates a mismatch between the absolute velocity from the GV blade and the relative inlet velocity at the blade rotor, leading to boundary layer detachment and loss shock, resulting in diminished power output.

At high flow rates, a difference in behavior is observed between turbines T1 and T7. While turbine T1 has a higher efficiency with the stator than without, the opposite occurs with turbine T7: the efficiency with the stator is lower. This phenomenon can be explained by the fact that the stator of turbine T7 is twice the diameter of turbine T1 and has larger interaction surfaces than those of turbine T1. As a result, head losses and turbulence are generated when turbine T1 operates at conditions far from its design point.

The flow behavior becomes particularly problematic near the hub for both off-design conditions and under- and over-design points. Due to the smaller radius, the blade’s rotational speed is inherently lower. Under reduced flow rates, weak centrifugal forces fail to guide the fluid smoothly along the blade’s surface. Instead, the flow separates, forming vortices and recirculation zones. Visualizations of this phenomenon reveal distorted streamlines and localized low-pressure areas, where the fluid detaches entirely, generating energy losses.

The data show that stator-induced flow guidance becomes less effective outside the design envelope, increasing losses due to unsteady detachment and recirculation zones. These variations highlight the non-linear relationship between stator implementation and system performance, especially when aerodynamic stability is affected.

3.6. Cost Analysis

The total project cost was estimated using Balarim’s (1996) [31] formula, originally developed for small-scale hydropower installations (<15 kW). The cost model is expressed as follows:

$$InvestmentCost=(25.4027+0.0885\cdot H+{\displaystyle \frac{61.5340}{H}})\times 1000$$

(9)

where H = 2 m, and yields a base cost as follows:

$$BaseCost=\left(25.4027+0.177+30.767\right)\times 1000=\mathrm{56,346.70} BRL$$

(10)

To reflect monetary values for 2025, this cost was adjusted for inflation using Brazil’s cumulative inflation rate of 870% (BRL 1 in 1996 = BRL 9.7 in 2025):

$$Cost{2025}_{\left(BRL\right)}=\mathrm{56,346.70}\times 9.7=\mathrm{546,562.99}\hspace{0.17em}BRL.$$

(11)

The final cost in USD was derived using the projected 2025 exchange rate (USD 1 = BRL 5.81):

$$Cost{2025}_{\left(USD\right)}={\displaystyle \frac{\mathrm{546,562.99}}{5.81}}=\mathrm{94,073.15}\hspace{0.17em}\mathrm{U}\mathrm{S}\mathrm{D}$$

(12)

The simple payback method is applied to estimate the period required for a micro-hydropower plant to recover its initial investment through revenues from electricity generation. The total initial investment is estimated at USD 94,073.15. However, due to the simultaneous construction of a bridge at the project site, the overall cost is reduced by 19%, corresponding to the average expenditure related to the mobilization of equipment and personnel, a significant cost component in remote locations. This average was obtained through data obtained from the government for many bridges previously constructed in the region.

$$Adjusted Cost=\mathrm{94,073.15}\times 0.81=USD \mathrm{76,197.25}$$

(13)

The plant is expected to generate approximately 63,000 kWh per year, at a unit sale price of USD 0.1362 per kWh; this price was calculated using the average energy cost in the region for 2024:

$$Gross Annual Revenue=\mathrm{63,000}\times 0.1634=USD \mathrm{10,294.20}$$

(14)

The annual O&M costs for small hydropower are estimated at 1% of the total investment, according to [24]:

$$Annual O\&M Cost=\mathrm{76,197.25}\times 0.01=USD 761.97$$

(15)

The annual net revenue and simple payback were then calculated.

$$Net Revenue=\mathrm{10,294.20}-761.97=USD 9532.23$$

(16)

$$Payback Period \approx 8 years$$

(17)

The estimated costs for the analyzed project align with those reported by Balarim (1996) [31], while the calculated payback period (7–8 years) closely matches the SCABCleuch case study [32] (6–7 years). Minor discrepancies arise from regional variations in labor costs, operational efficiency, and tariff policies. Both cases highlight the economic viability of micro-hydro systems in off-grid communities, demonstrating attractive financial returns within a medium-term horizon.

3.7. Environmental Impact and Dam-Bridge Integration

The constraints associated with power generation and integration into concrete bridge structures include, but are not limited to, the following: (i) the limited space available for the powerhouse, which must nonetheless allow for proper installation and equipment maintenance; (ii) the need for integrated spillway construction, energy dissipation structures, and fish ladders; and (iii) the construction of supporting elements for walls, floors, and other components necessary for equipment operation, without imposing additional mechanical loads on the bridge structure.

The power generation structure is supported by beams and columns not structurally connected to the bridge’s load and stiff elements. Additionally, a modular structure was designed to facilitate the adaptation of the project to other bridges. The first module forms part of the dam and also houses the spillway, energy dissipation structure, and fish lad-der. The second module comprises the dam and the powerhouse, which contains turbines, generators, and control equipment. This module also includes access to the powerhouse. The third module serves to complement the damming function. Figure 23 presents various views of the conceptual design for the dam-bridge structure.

The bridge’s support system on land consists of concrete wing walls, as illustrated in Figure 23a,b. The turbine water intake is equipped with inclined grates, shown in Figure 23c, which are designed to prevent debris from entering that could compromise turbine performance. Their inclination decreases the likelihood of blockage and aids maintenance and cleaning operations.

The lower-capacity turbine is intended for continuous operation under various flow conditions, and the dual-turbine setup reduces the flooded area, leading to lower environmental impact.

The spillway, illustrated in Figure 23d, functions in two scenarios: when both turbines are inactive during low-flow periods, and when only the smaller turbine is running. Still, the flow does not support the larger turbine, and when both turbines operate, they cannot keep the upstream water level below the critical limit. The spillway features an inclined structure for efficient energy dissipation.

To protect the migratory paths of local fish species affected by the bridge, a fish ramp, also depicted in Figure 23d, is included in the design. This ramp has a gentler slope than the spillway, facilitating fish ascension during migration. Consequently, the design helps minimize ecological disruption, particularly regarding the reproductive cycles of aquatic life.

4. Conclusions

This study introduces a robust framework for creating and assessing very low-head axial-flow turbines designed explicitly for the contexts of remote Amazonian community hydrology and infrastructure. The suggested hybrid dam-bridge–turbine system presents a practical, sustainable alternative to diesel-powered generation by combining hydrodynamic principles, cost-effective production methods, and advanced numerical simulations. Circular arc cascades and simplified blade profiles facilitate local manufacturing while ensuring acceptable performance. Additionally, incorporating fish ladders and seasonal operation strategies aligns with ecological preservation goals.

The numerical results indicate a significant correlation between the minimum pressure coefficient and the turbine’s specific speed, suggesting that varying machine designs may exhibit a defined range of minimum pressure values. While the methodology demonstrates robustness in discharge rate fluctuations, its sensitivity to blade angle variations and head changes remains unquantified. These limitations stem from the current focus on nominal operating conditions and fixed geometric parameters. Future studies should incorporate more analyses through blade angle deviations and transient head scenarios to fully characterize the design’s adaptability to real-world uncertainties. The flow patterns also become highly unstable at the low and high ends of the turbine’s operational flow rate. CFD validation confirmed operational robustness for Turbine 7, maintaining <5% efficiency loss across 0.65–1.0 m³/s (80–120% Q₀). However, transient flow phenomena at extreme discharge rates necessitate future transient simulations to mitigate vortex shedding and localized vapor pockets.

Economically, the project’s feasibility hinges on initial investment costs, mainly because constructing bridges to support or integrate turbine infrastructure constitutes a substantial portion of the total expenditure. A cost model was implemented to project capital expenditures, covering electromechanical components and civil works. Additionally, a payback analysis evaluated the return on investment over the expected operational lifespan of the system. Economic viability is demonstrated through a total adjusted project cost of USD 76,197 (19% savings from shared bridge infrastructure) and a simple payback period of 8 years, supported by annual net revenues of USD 9532. The system’s levelized cost of energy (LCOE) is USD 0.12/kWh (63 MWh/year at USD 0.1362/kWh), outperforming regional diesel alternatives (USD 0.28/kWh) and aligning with Brazil’s rural electrification targets.

The linearized blade angle profile was designed to simplify manufacturing while maintaining hydraulic performance at the nominal operating point. The linear variation inherently reduces geometric complexity, but may affect performance under flow angle variations, although this hypothesis requires experimental validation.

The hybrid dam-bridge–turbine system demonstrates a sustainable alternative to diesel generators, achieving peak efficiencies of 88% (Turbine 1: Q = 0.23 m³/s, H = 2.37 m) and 89% (Turbine 7: Q = 0.81 m³/s, H = 1.47 m) under nominal operating conditions. Moreover, the design methodology, considering the site’s flow duration curve and high hydraulic efficiency using the Cpmin criterion, creates a replicable approach for decentralized electrification in other low-head river environments.

This research connects hydropower innovation with regional development strategies by synchronizing energy access initiatives with ongoing infrastructure modernization efforts like that of Ecopontes. The findings advance the broader objective of universal electricity access in the Amazon region of Brazil, demonstrating how tailored technological adaptations can bolster national sustainability and equity goals.