Real-Time Prediction of Wear Morphology and Coefficient of Friction Using Acoustic Signals and Deep Neural Networks in a Tribological System
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Tribological Testing
2.2. Wear Measurement and Finite Element Modeling
2.3. Deep Neural Network Model Development
3. Results
3.1. Surface Roughness Before Wear Testing
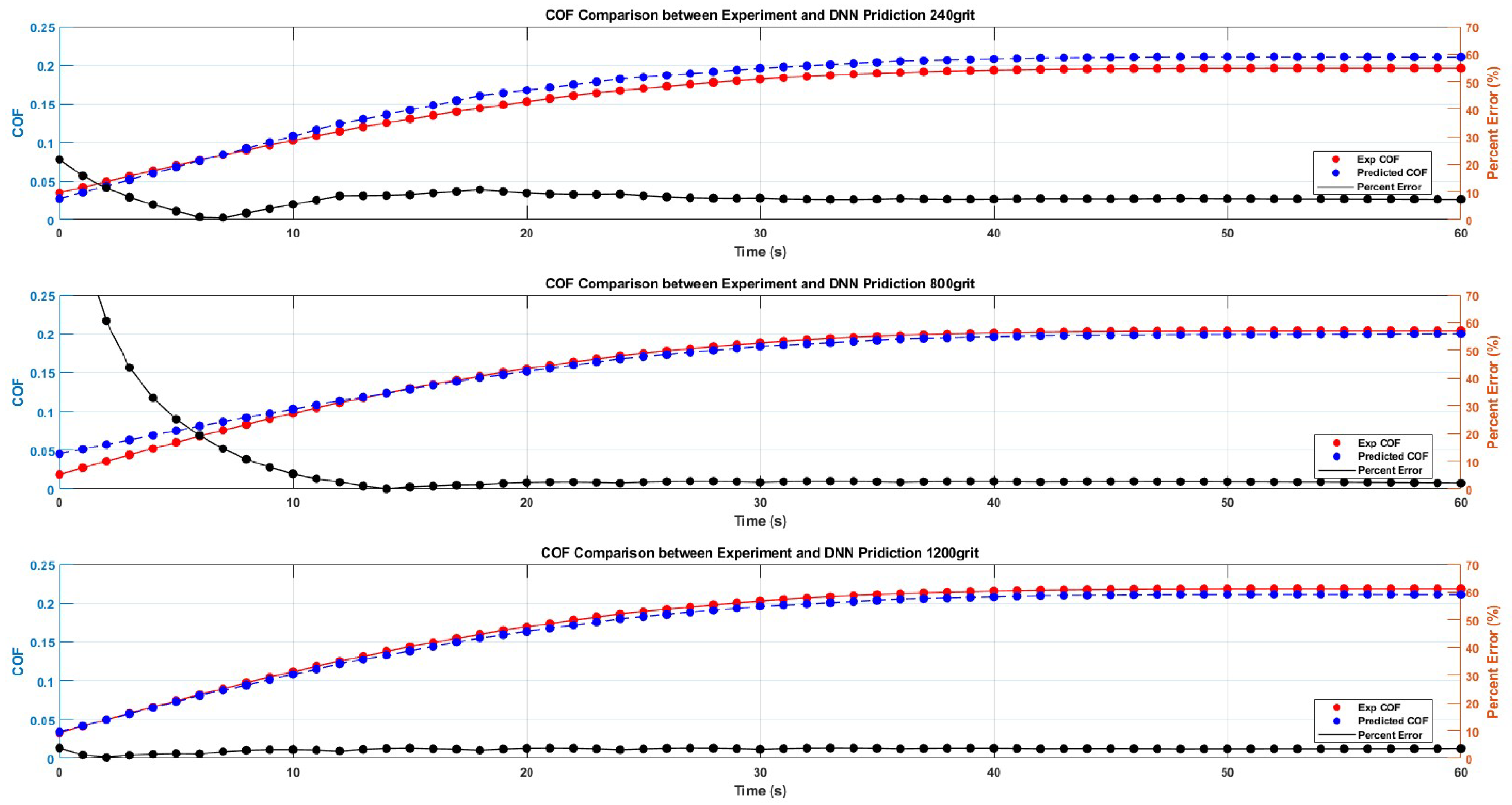
3.2. Coefficient of Friction
3.3. Noise Signal Analysis
3.3.1. Time-Domain Signal (First 1 s)
3.3.2. Power Spectral Density (PSD) Analysis
3.3.3. Spectrogram Analysis
3.3.4. One-Third Octave Band Analysis
3.3.5. Accumulative Average Sound Pressure
3.4. Mesh-Independent Validation and Deep Neural Network Training
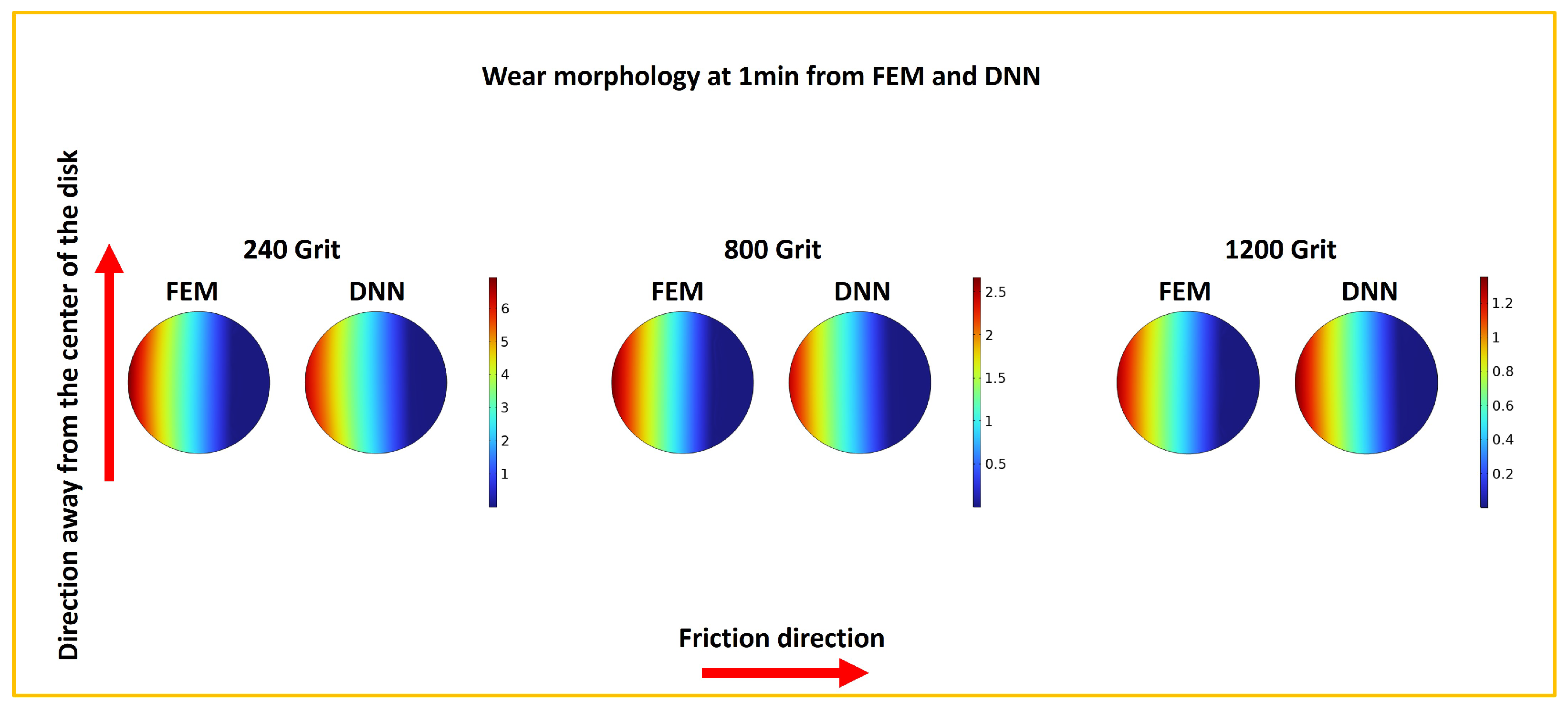
3.5. Wear and COF Prediction
3.6. Strengths and Limitations of the Proposed Approach
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, Y.; Xu, J.; Ma, L.; Jin, Z.; Prakash, B.; Ma, T.; Wang, W. A review of advances in tribology in 2020–2021. Friction 2022, 10, 1443–1595. [Google Scholar]
- Erdemir, A.; Ramirez, G.; Eryilmaz, O.; Narayanan, B.; Liao, Y.; Kamath, G.; Sankaranarayanan, S.K.R.S. Carbon-based tribofilms from lubricating oils. Nature 2016, 536, 67–71. [Google Scholar] [CrossRef] [PubMed]
- Tomanik, E.; Christinelli, W.; Souza, R.M.; Oliveira, V.L.; Ferreira, F.; Zhmud, B. Review of Graphene-Based Materials for Tribological Engineering Applications. Eng 2023, 4, 2764–2811. [Google Scholar] [CrossRef]
- Kasar, A.K.; Menezes, P.L. Synthesis and recent advances in tribological applications of graphene. Int. J. Adv. Manuf. Technol. 2018, 97, 3999–4019. [Google Scholar] [CrossRef]
- Che, Q.; Zhang, G.; Zhang, L.; Qi, H.; Li, G.; Zhang, C.; Guo, F. Switching brake materials to extremely wear-resistant self-lubrication materials via tuning interface nanostructures. ACS Appl. Mater. Interfaces 2018, 10, 19173–19181. [Google Scholar] [CrossRef]
- Wong, V.W.; Tung, S.C. Overview of automotive engine friction and reduction trends–Effects of surface, material, and lubricant-additive technologies. Friction 2016, 4, 1–28. [Google Scholar] [CrossRef]
- Dwyer-Joyce, R.; Rahnejat, H. Special Issue on Automotive Piston–Cylinder Tribology. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2013, 227, 99. [Google Scholar] [CrossRef]
- Miyoshi, K. Aerospace mechanisms and tribology technology: Case study. Tribol. Int. 1999, 32, 673–685. [Google Scholar] [CrossRef]
- Voevodin, A.A.; O’Neill, J.P.; Zabinski, J.S. Nanocomposite tribological coatings for aerospace applications. Surf. Coatings Technol. 1999, 116, 36–45. [Google Scholar] [CrossRef]
- Ralls, A.M.; Kumar, P.; Menezes, P.L. Tribological properties of additive manufactured materials for energy applications: A review. Processes 2020, 9, 31. [Google Scholar] [CrossRef]
- Schmid, S.R.; Saha, P.K.; Wang, J.; Schmitz, T. Developments in tribology of manufacturing processes. J. Manuf. Sci. Eng. 2020, 142, 110803. [Google Scholar] [CrossRef]
- Feng, P.; Borghesani, P.; Smith, W.A.; Randall, R.B.; Peng, Z. A review on the relationships between acoustic emission, friction and wear in mechanical systems. Appl. Mech. Rev. 2020, 72, 020801. [Google Scholar] [CrossRef]
- Tian, Y.; Khan, M.; Yuan, H.; Zheng, B. Wear modeling and friction-induced noise: A review. Friction 2025, 9441124. [Google Scholar] [CrossRef]
- Meng, M.; Wang, X.S.; Li, K.Y.; Deng, Z.X.; Zhang, Z.Z.; Sun, Y.L.; Zhang, S.F.; He, L.; Guo, J.W. Effects of surface roughness on the time-dependent wear performance of lithium disilicate glass ceramic for dental applications. J. Mech. Behav. Biomed. Mater. 2021, 121, 104638. [Google Scholar] [CrossRef]
- Zurek, A.D.; Alfaro, M.F.; Wee, A.G.; Yuan, J.C.-C.; Barao, V.A.; Mathew, M.T.; Sukotjo, C. Wear characteristics and volume loss of CAD/CAM ceramic materials. J. Prosthodont. 2019, 28, e510–e518. [Google Scholar] [CrossRef]
- Ghosh, G.; Sidpara, A.; Bandyopadhyay, P.P. Understanding the role of surface roughness on the tribological performance and corrosion resistance of WC-Co coating. Surf. Coatings Technol. 2019, 378, 125080. [Google Scholar] [CrossRef]
- Briggs, G.A.D.; Briscoe, B.J. Effect of surface roughness on rolling friction and adhesion between elastic solids. Nature 1976, 260, 313–315. [Google Scholar] [CrossRef]
- Zhou, B.; Ma, J.; Yang, Z.; Shi, X. Noise reduction mechanism and analysis of TC4 with dimple textured surfaces. J. Mater. Eng. Perform. 2021, 30, 3859–3871. [Google Scholar] [CrossRef]
- Gurumoorthy, S.; Bhimchand, N.; Bourgeau, A.; Bhumireddy, Y. Effect of Surface Roughness on Tribological and NVH Behaviour of Brake System. In SAE Technical Paper; SAE International: Warrendale, PA, USA, 2024; p. 2024-01-2732. [Google Scholar]
- Sose, A.T.; Joshi, S.Y.; Kunche, L.K.; Wang, F.; Deshmukh, S.A. A review of recent advances and applications of machine learning in tribology. Phys. Chem. Chem. Phys. 2023, 25, 4408–4443. [Google Scholar] [CrossRef]
- Hasan, M.S.; Nosonovsky, M. Triboinformatics: Machine learning algorithms and data topology methods for tribology. Surf. Innov. 2022, 10, 229–242. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Marian, M.; Profito, F.J.; Aragon, N.; Shah, R. The use of artificial intelligence in tribology—A perspective. Lubricants 2020, 9, 2. [Google Scholar] [CrossRef]
- Cheng, K.; Luo, X.; Ward, R.; Holt, R. Modeling and simulation of the tool wear in nanometric cutting. Wear 2003, 255, 1427–1432. [Google Scholar] [CrossRef]
- Shah, R.; Pai, N.; Thomas, G.; Jha, S.; Mittal, V.; Shirvni, K.; Liang, H. Machine learning in wear prediction. J. Tribol. 2025, 147, 040801. [Google Scholar] [CrossRef]
- Gouarir, A.; Martínez-Arellano, G.; Terrazas, G.; Benardos, P.; Ratchev, S.J.P.C. In-process tool wear prediction system based on machine learning techniques and force analysis. Procedia CIRP 2018, 77, 501–504. [Google Scholar] [CrossRef]
- Rajput, A.S.; Das, S. A machine learning approach to predict the wear behaviour of steels. Tribol. Int. 2023, 185, 108500. [Google Scholar] [CrossRef]
- Molinari, J.-F.; Aghababaei, R.; Brink, T.; Frérot, L.; Milanese, E. Adhesive wear mechanisms uncovered by atomistic simulations. Friction 2018, 6, 245–259. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, D.; Sun, Q.; Qin, J.; Chen, L.; Qian, L.; Wang, Y. Atomic-scale wear behaviors of iron oxide through the atom-by-atom attrition and plastic deformation of nano-asperities. Tribol. Int. 2023, 188, 108878. [Google Scholar] [CrossRef]
- Gnecco, E.; Bennewitz, R.; Pfeiffer, O.; Socoliuc, A.; Meyer, E. Friction and wear on the atomic scale. In Springer Handbook of Nanotechnology; Springer: Berlin/Heidelberg, Germany, 2010; pp. 923–953. [Google Scholar]
- Abdelounis, H.B.; Zahouani, H.; Le Bot, A.; Perret-Liaudet, J.; Tkaya, M.B. Numerical simulation of friction noise. Wear 2011, 271, 621–624. [Google Scholar] [CrossRef]
- Lontin, K.; Khan, M.A. Wear and airborne noise interdependency at asperitical level: Analytical modelling and experimental validation. Materials 2021, 14, 7308. [Google Scholar] [CrossRef]
- Basit, K.; Shams, H.; Khan, M.A.; Mansoor, A. Vibration analysis approach to model incremental wear and associated sound in multi-contact sliding friction mechanisms. J. Tribol. 2023, 145, 091201. [Google Scholar] [CrossRef]
- Basit, K.; Shams, H.; Khan, M.A.; Mansoor, A. Empirical modelling of frictional noise and two-point contact using ball-on-disc tribometer. In Proceedings of the TESConf 2020—9th International Conference on Through-life Engineering Services, Cranfield, UK, 3–4 November 2020; p. 3717985. [Google Scholar]
- Tian, Y.; Khan, M.; Deng, H.; Omar, I. Quantifying the interrelationship between friction, wear, and noise: A comparative study on aluminum, brass, and steel. Tribol. Int. 2025, 203, 110403. [Google Scholar] [CrossRef]
- Huang, Z.; Zhu, J.; Lei, J.; Li, X.; Tian, F. Tool wear predicting based on multi-domain feature fusion by deep convolutional neural network in milling operations. J. Intell. Manuf. 2020, 31, 953–966. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, W.; Hu, X.; Liu, Y. A hybrid information model based on long short-term memory network for tool condition monitoring. J. Intell. Manuf. 2020, 31, 1497–1510. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, J.; Mo, R.; Zhang, X. In-process tool condition forecasting based on a deep learning method. Robot. Comput.-Integr. Manuf. 2020, 64, 101924. [Google Scholar] [CrossRef]
- Xu, X.; Wang, J.; Zhong, B.; Ming, W.; Chen, M. Deep learning-based tool wear prediction and its application for machining process using multi-scale feature fusion and channel attention mechanism. Measurement 2021, 177, 109254. [Google Scholar] [CrossRef]
- He, Z.; Shi, T.; Xuan, J.; Li, T. Research on tool wear prediction based on temperature signals and deep learning. Wear 2021, 478, 203902. [Google Scholar] [CrossRef]
- Néder, Z.; Váradi, K. Contact behaviour of the original and substituted real surfaces. Int. J. Mach. Tools Manuf. 2001, 41, 1935–1939. [Google Scholar] [CrossRef]
- Quaglini, V.; Dubini, P. Friction of polymers sliding on smooth surfaces. Adv. Tribol. 2011, 2011, 178943. [Google Scholar] [CrossRef]
- Hsia, F.-C.; Franklin, S.; Audebert, P.; Brouwer, A.M.; Bonn, D.; Weber, B. Rougher is more slippery: How adhesive friction decreases with increasing surface roughness due to the suppression of capillary adhesion. Phys. Rev. Res. 2021, 3, 043204. [Google Scholar] [CrossRef]
- Le Bot, A. Noise of sliding rough contact. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 797, p. 012006. [Google Scholar]
- Yang, C.; Persson, B.N.J. Contact mechanics: Contact area and interfacial separation from small contact to full contact. J. Phys. Condens. Matter 2008, 20, 215214. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Antun, V.; Hansen, A.C. The difficulty of computing stable and accurate neural networks: On the barriers of deep learning and Smale’s 18th problem. Proc. Natl. Acad. Sci. USA 2022, 119, e2107151119. [Google Scholar] [CrossRef] [PubMed]
- Lontin, K.; Khan, M. Interdependence of friction, wear, and noise: A review. Friction 2021, 9, 1319–1345. [Google Scholar] [CrossRef]
- Tian, Y.; Zheng, B.; Khan, M.; He, F. Influence of sliding direction relative to layer orientation on tribological performance, noise, and stability in 3D-printed ABS components. Tribol. Int. 2025, 210, 110762. [Google Scholar] [CrossRef]
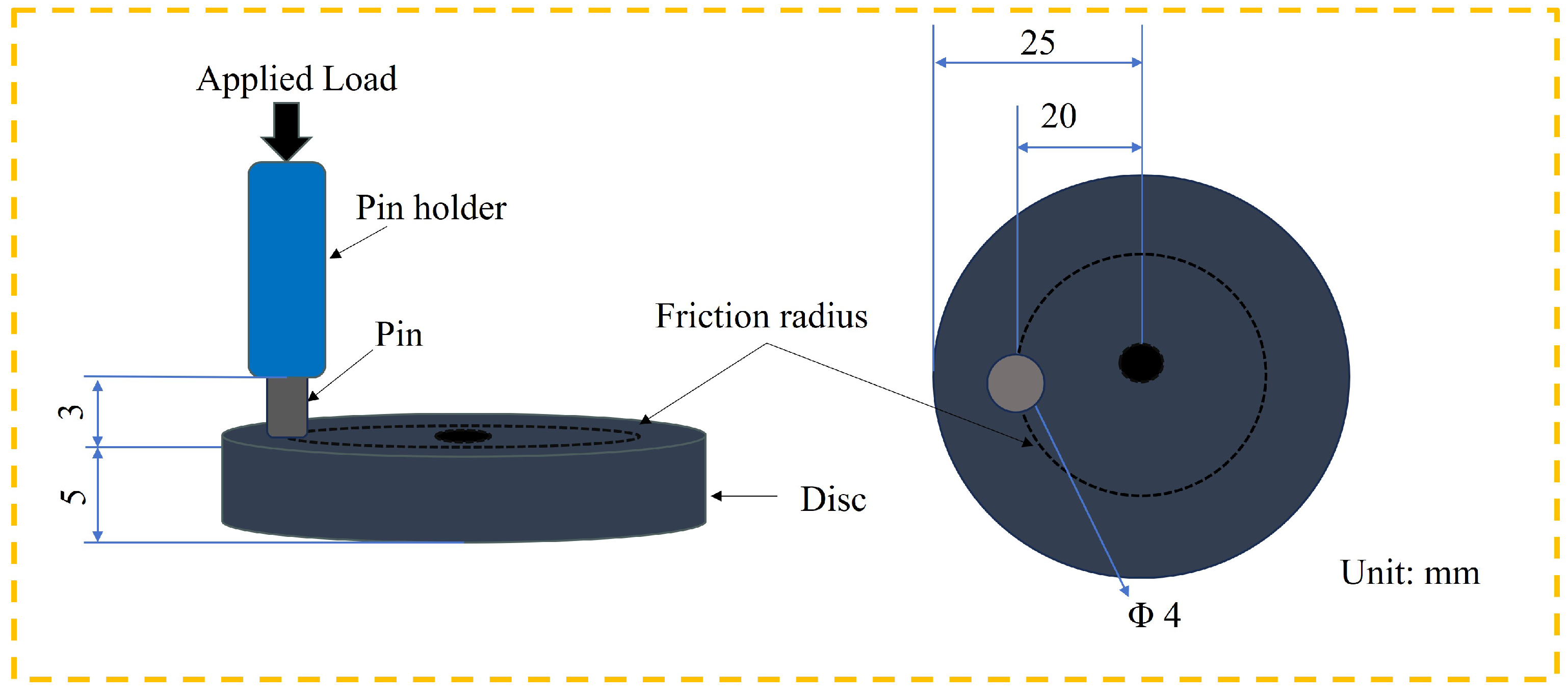

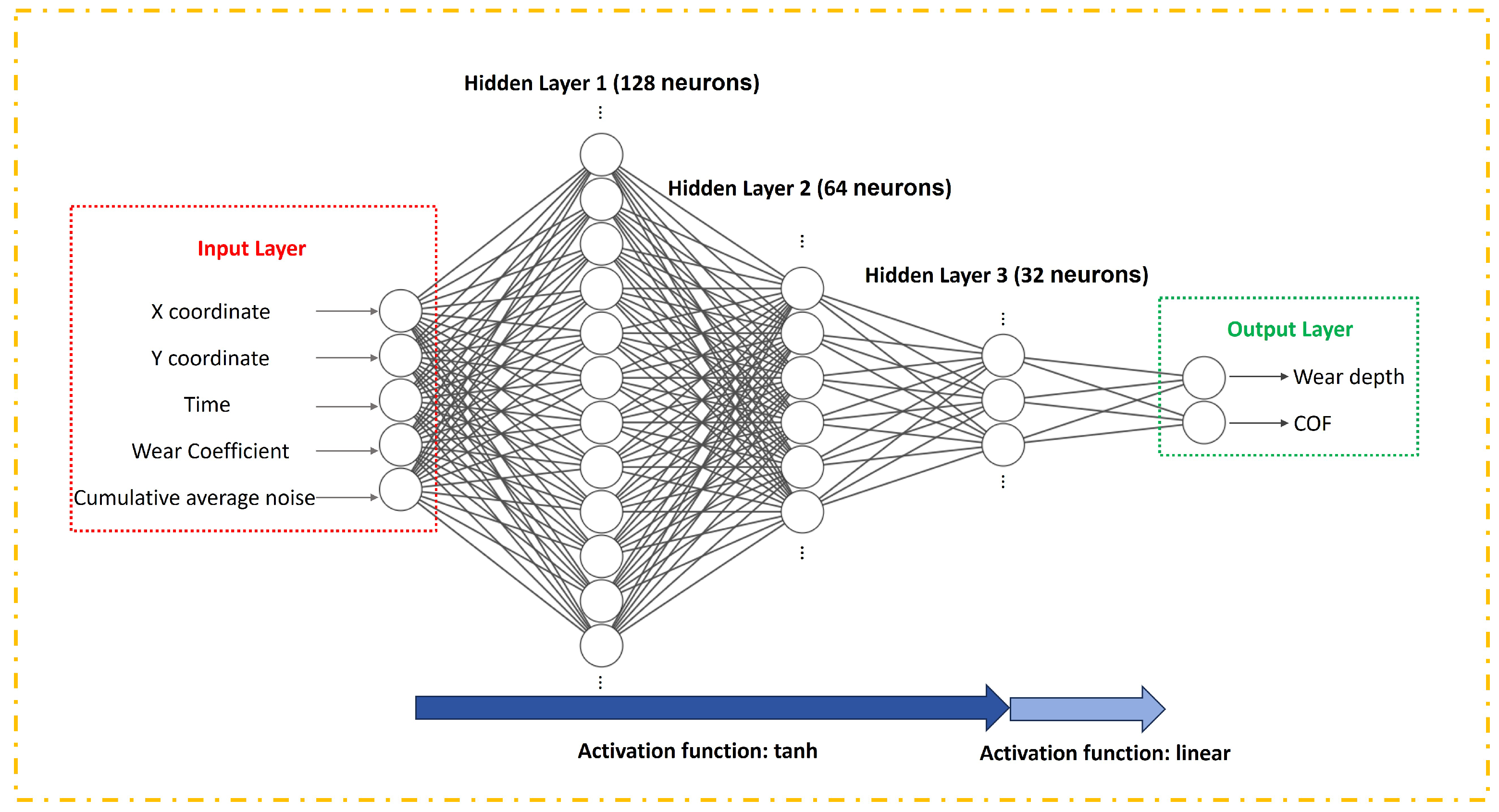



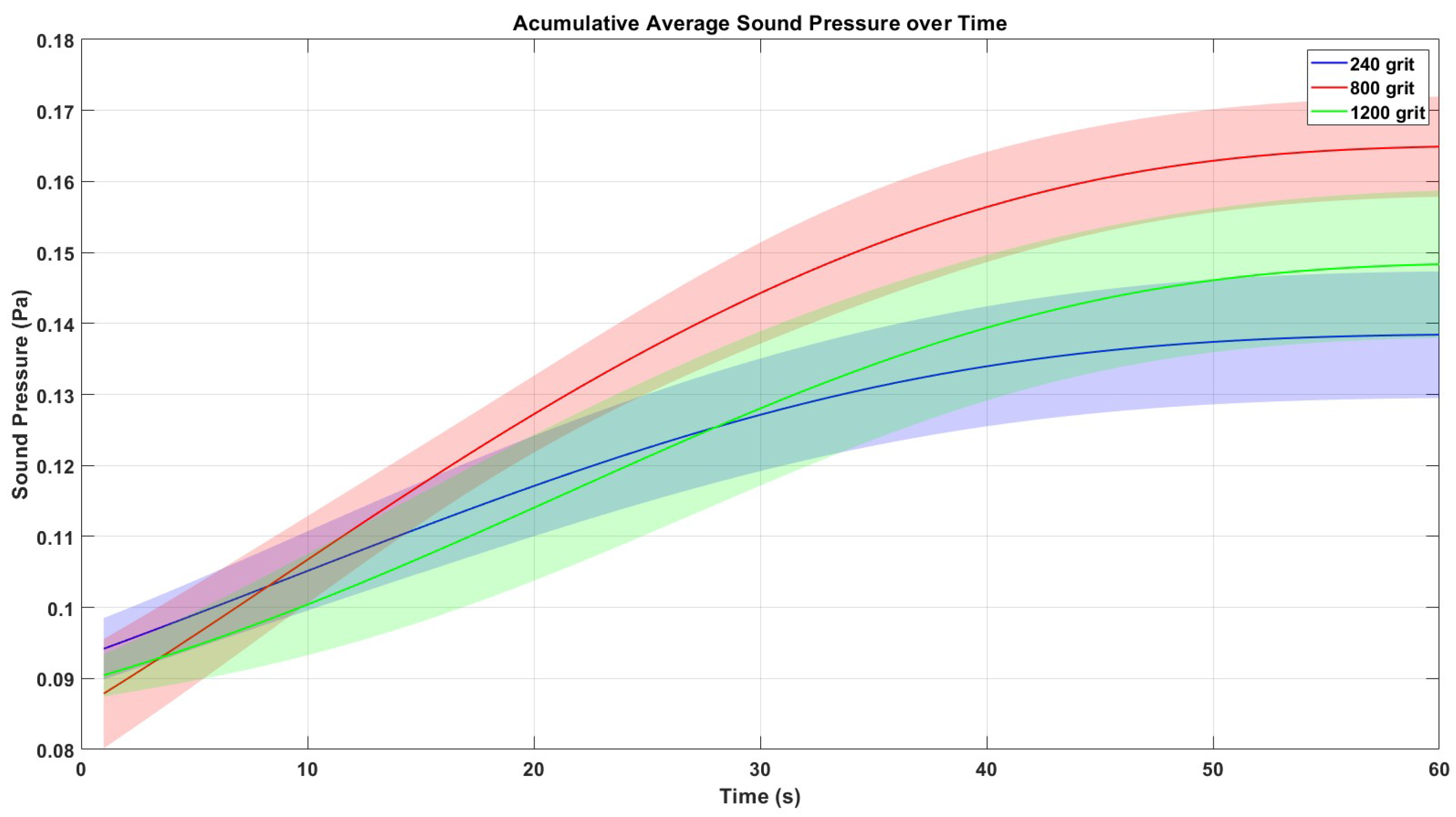
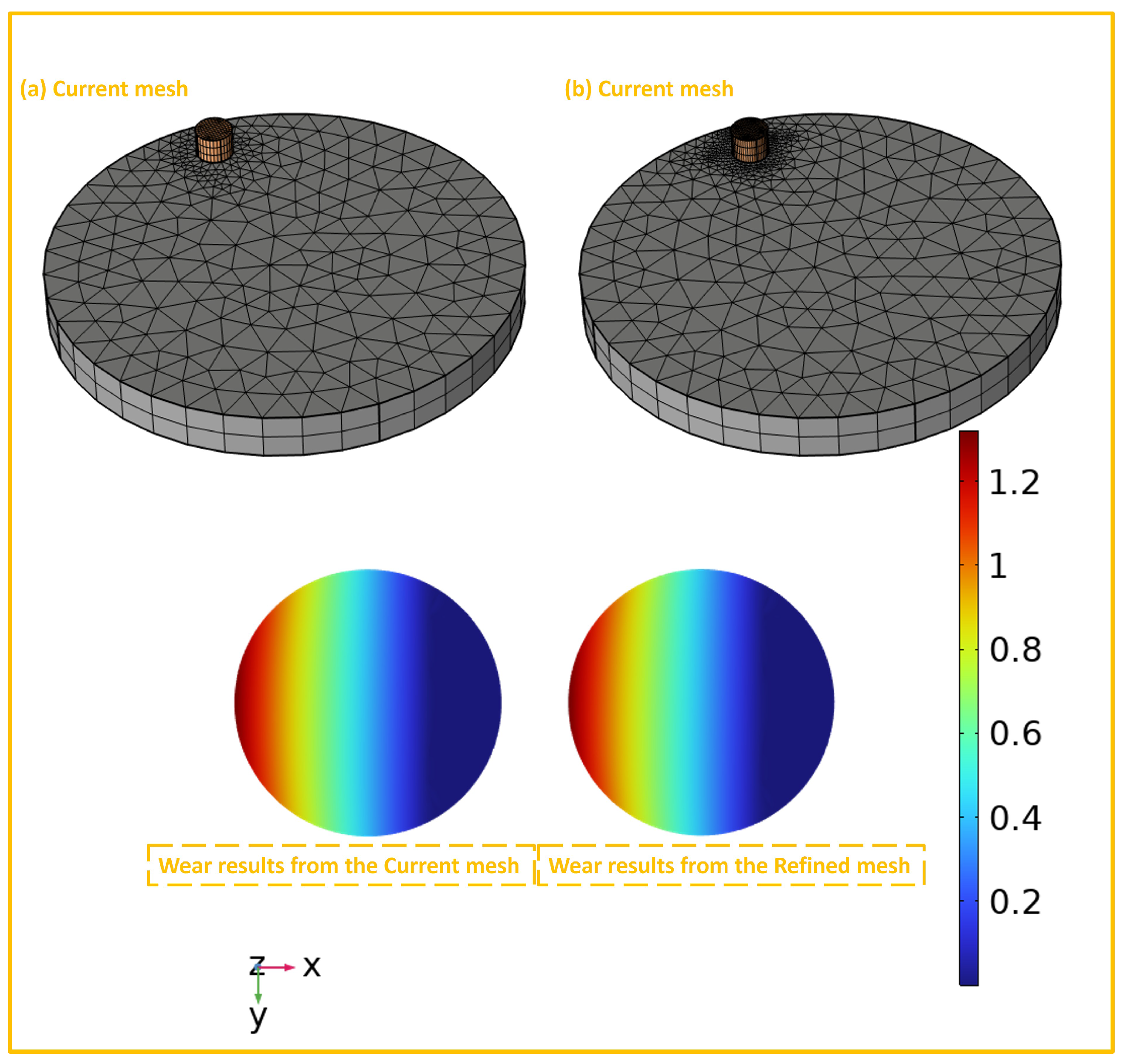



| Material | Density (kg/m3) | Young’s Modulus (Pa) | Poisson’s Ratio |
|---|---|---|---|
| Steel | 7860 | 1.9984 × 1011 | 0.24 |
| Brass | 8469.3 | 9.8 × 1010 | 0.32 |
| Type | Grit Size | (m) | (m) | (m) | Average (m) |
|---|---|---|---|---|---|
| Pin | 240 | 0.4744 | 0.484 | 0.386 | 0.4483 |
| Pin | 800 | 0.207 | 0.245 | 0.366 | 0.2393 |
| Pin | 1200 | 0.0894 | 0.083 | 0.100 | 0.0911 |
| Disc | N/A | 0.7431 | 0.912 | 0.883 | 0.8464 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Zheng, B.; Khan, M.; Yang, Y. Real-Time Prediction of Wear Morphology and Coefficient of Friction Using Acoustic Signals and Deep Neural Networks in a Tribological System. Processes 2025, 13, 1762. https://doi.org/10.3390/pr13061762
Tian Y, Zheng B, Khan M, Yang Y. Real-Time Prediction of Wear Morphology and Coefficient of Friction Using Acoustic Signals and Deep Neural Networks in a Tribological System. Processes. 2025; 13(6):1762. https://doi.org/10.3390/pr13061762
Chicago/Turabian StyleTian, Yang, Bohao Zheng, Muhammad Khan, and Yifan Yang. 2025. "Real-Time Prediction of Wear Morphology and Coefficient of Friction Using Acoustic Signals and Deep Neural Networks in a Tribological System" Processes 13, no. 6: 1762. https://doi.org/10.3390/pr13061762
APA StyleTian, Y., Zheng, B., Khan, M., & Yang, Y. (2025). Real-Time Prediction of Wear Morphology and Coefficient of Friction Using Acoustic Signals and Deep Neural Networks in a Tribological System. Processes, 13(6), 1762. https://doi.org/10.3390/pr13061762






