Comparative Analysis of Ensemble Machine Learning Methods for Alumina Concentration Prediction
Abstract
1. Introduction
2. Prediction Models and Optimization Algorithm
2.1. Neural Network Model Architecture
2.1.1. Long Short-Term Memory Network (LSTM)
2.1.2. Bi-Directional Long Short-Term Memory Network (BiLSTM)
2.1.3. Convolutional Neural Network (CNN)
2.1.4. Attention Mechanism
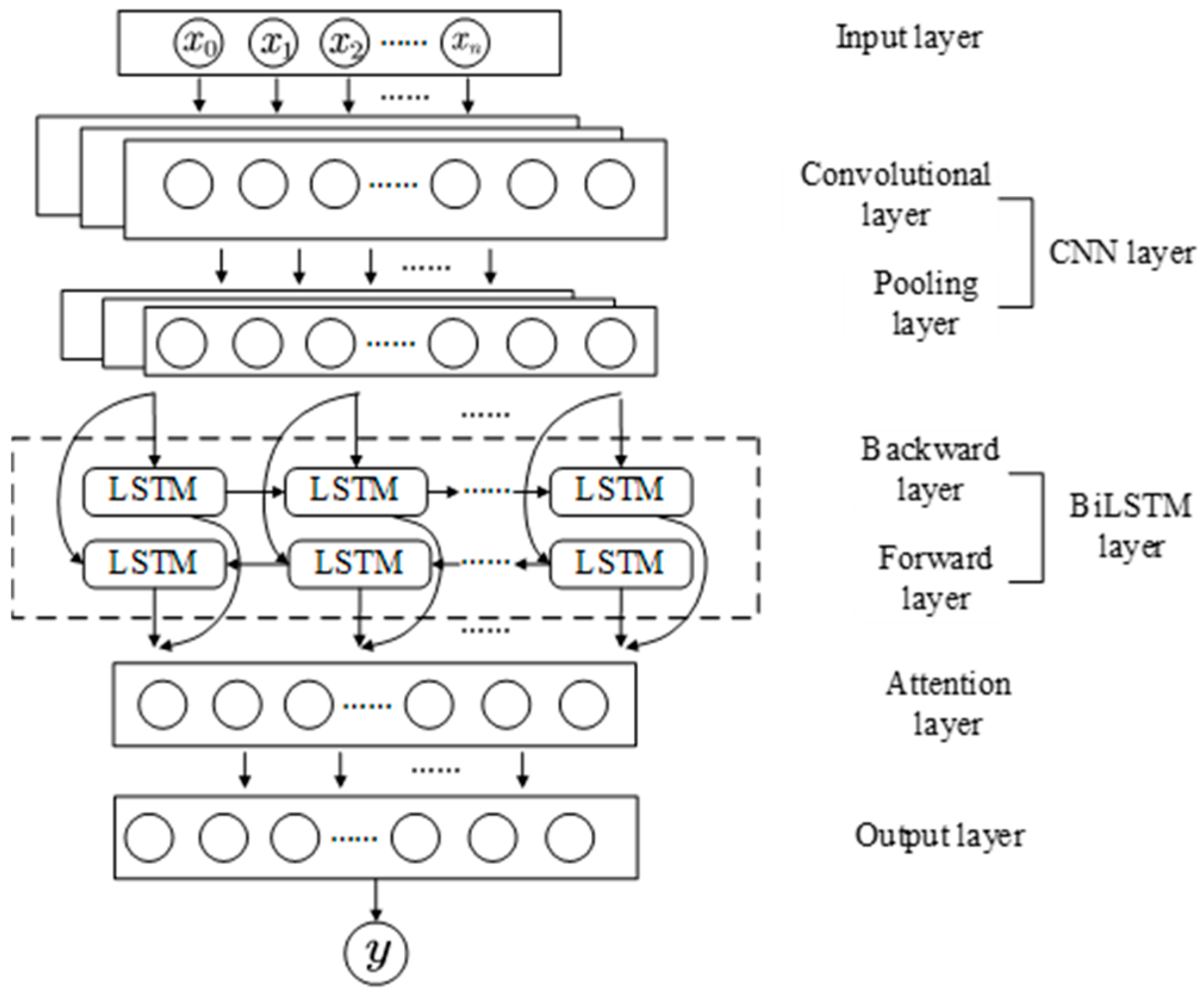
2.1.5. Composition of Hybrid Prediction Models
2.2. Weighted Average Algorithm (WAA)
2.3. Selection of Model Parameters
3. Experimental Simulation
3.1. Aluminum Electrolytic Data
3.2. Model Evaluation Metrics
3.3. Design of the Soft-Sensing Model
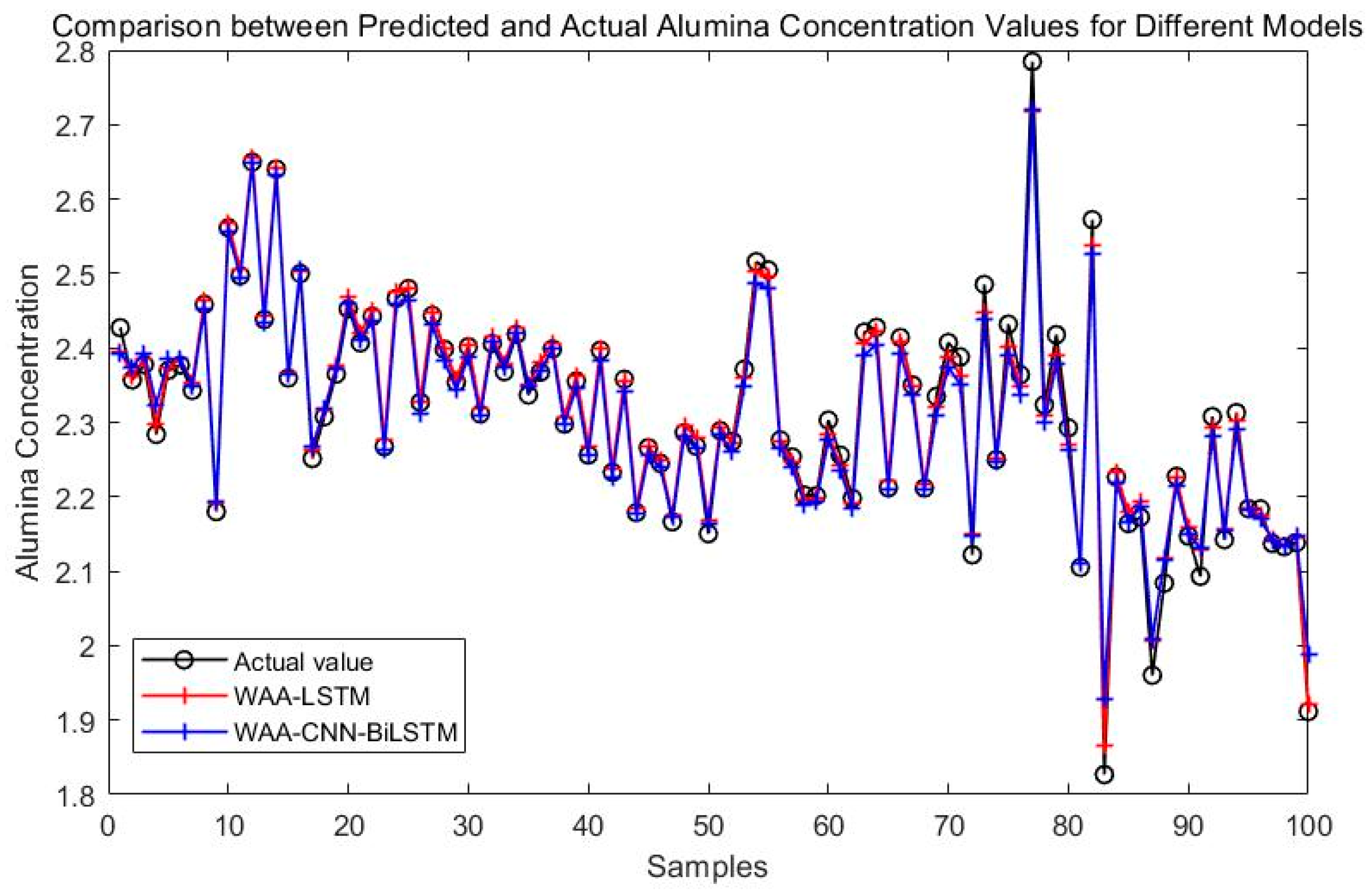
4. Comparative Analysis of Model Results
4.1. Results of Hyperparameter Optimization for Different Models
4.2. Comparison of Simulation Results for Different Models
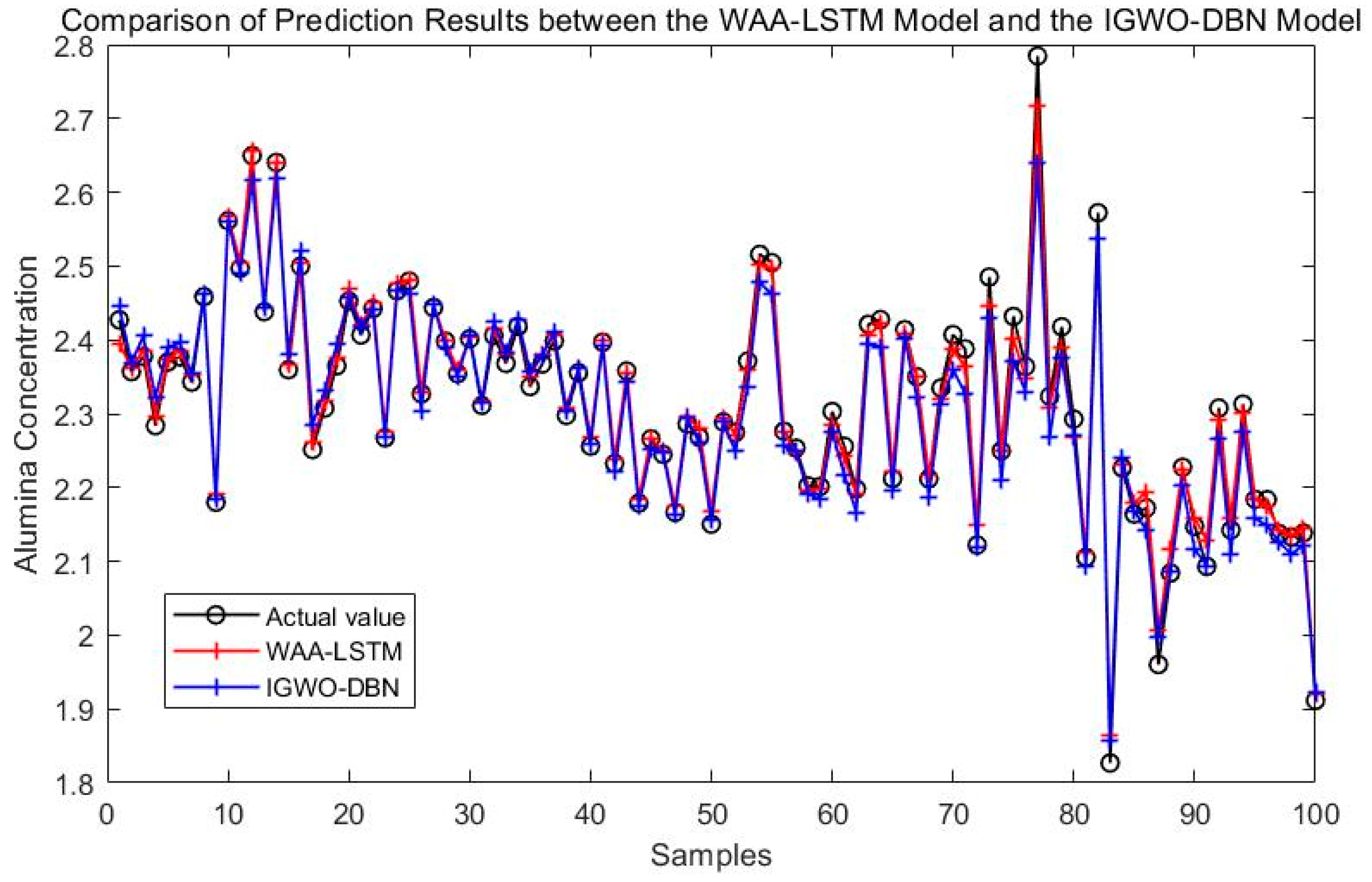
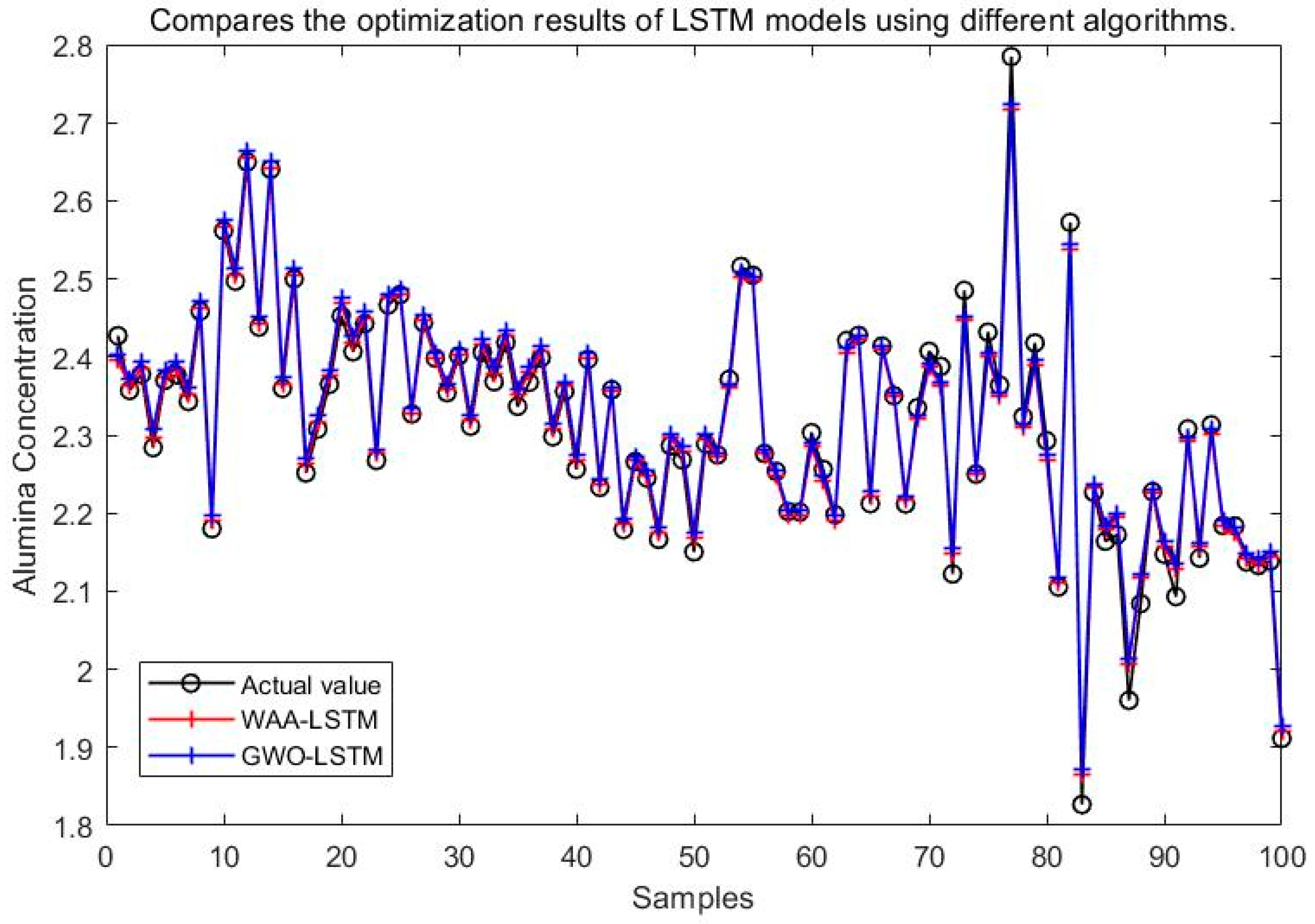
5. Optimization Algorithm Comparison and Analysis
5.1. Parameter Optimization Results of Different Algorithms
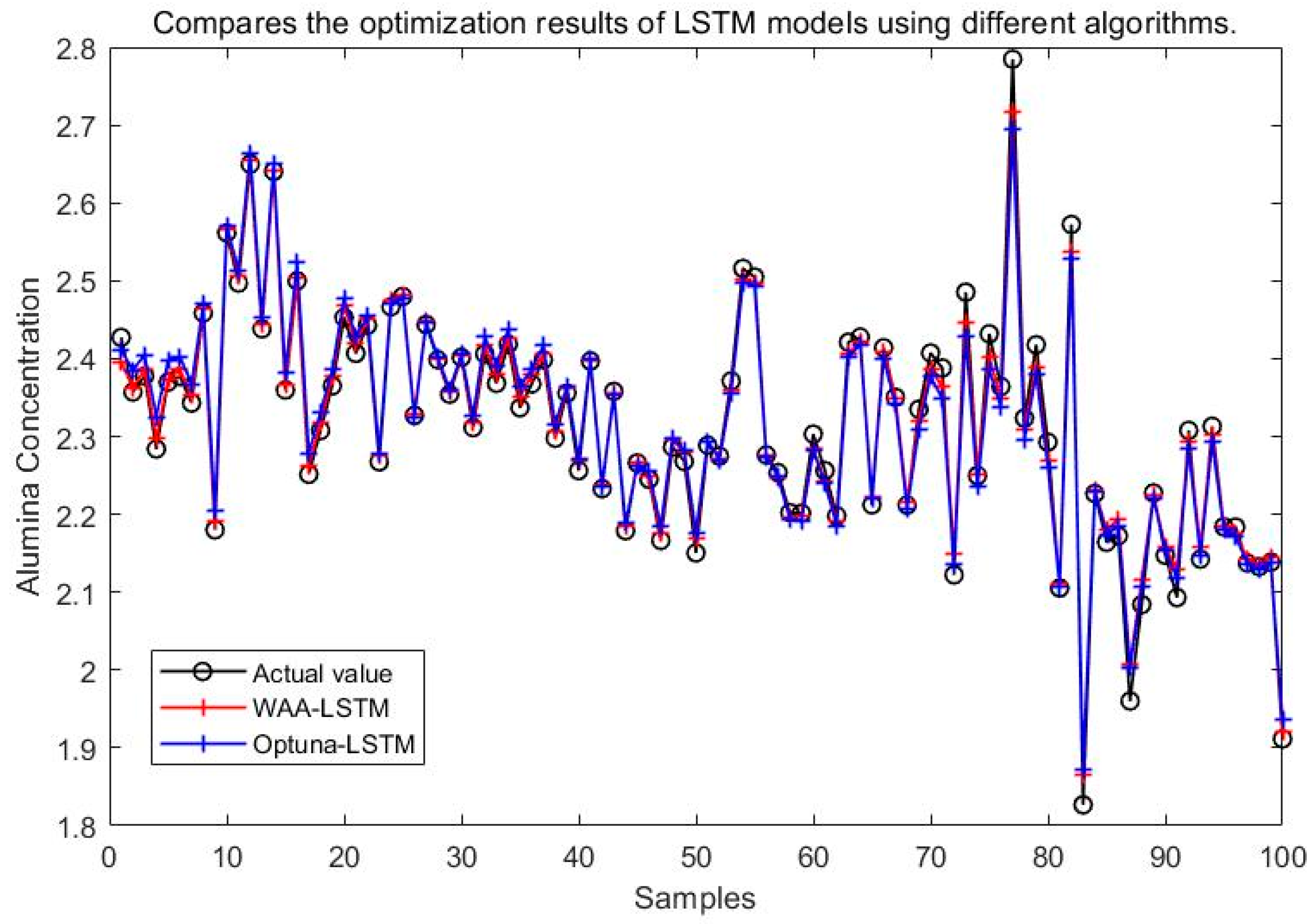
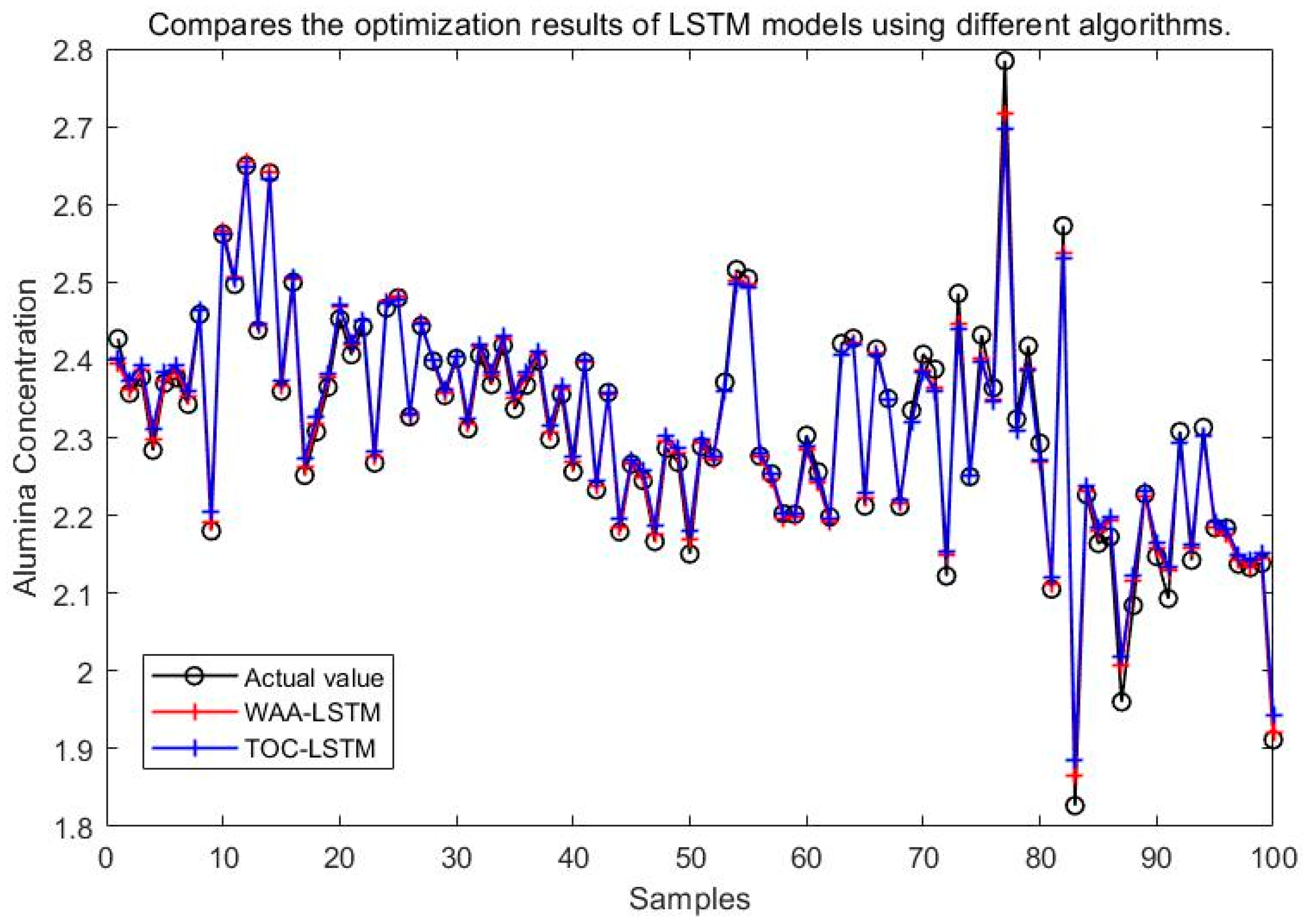
5.2. Comparison of Simulation Results for Different Optimization Algorithms
6. Statistical Analysis and Hypothesis Testing
6.1. Principles of Statistical Hypothesis Testing
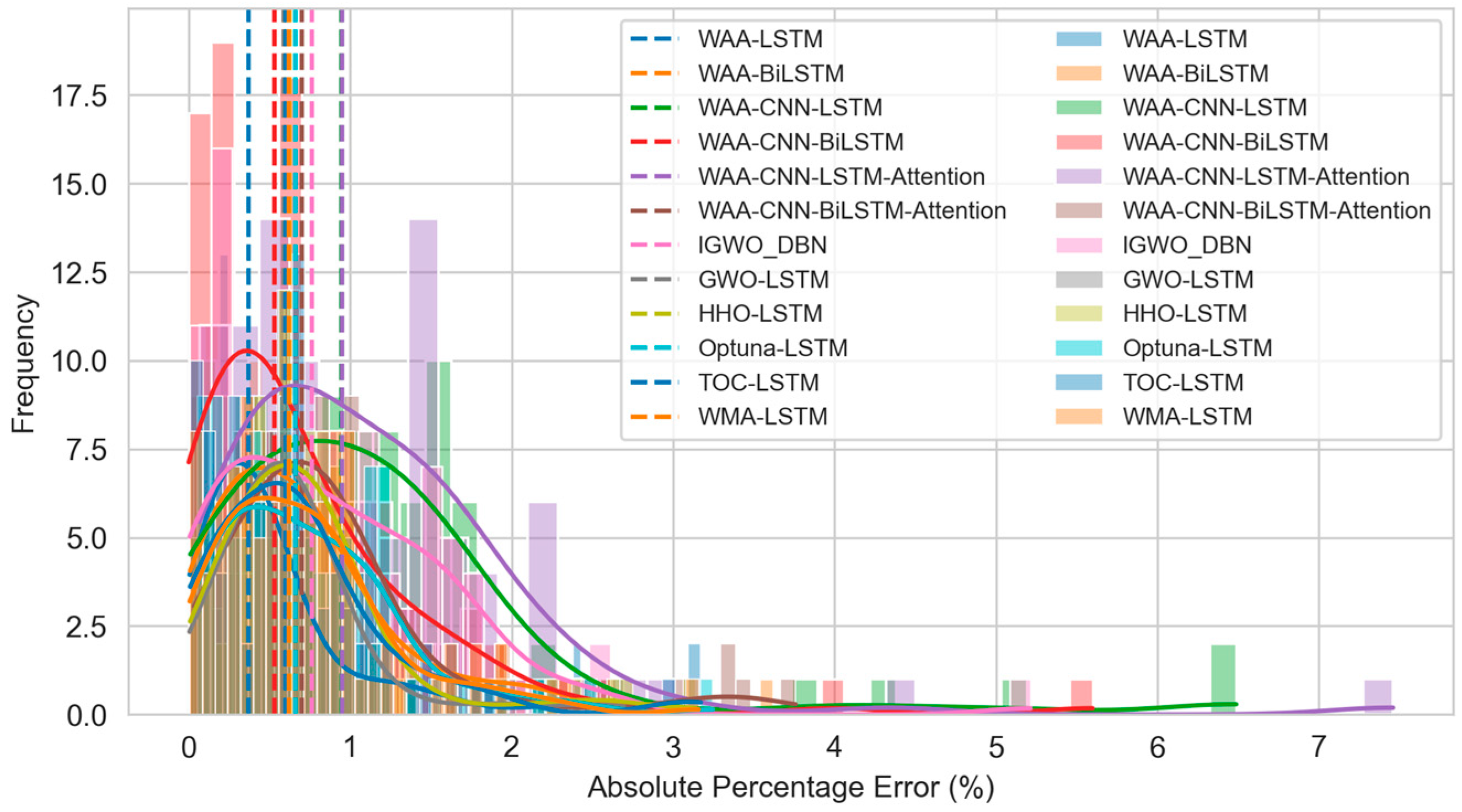
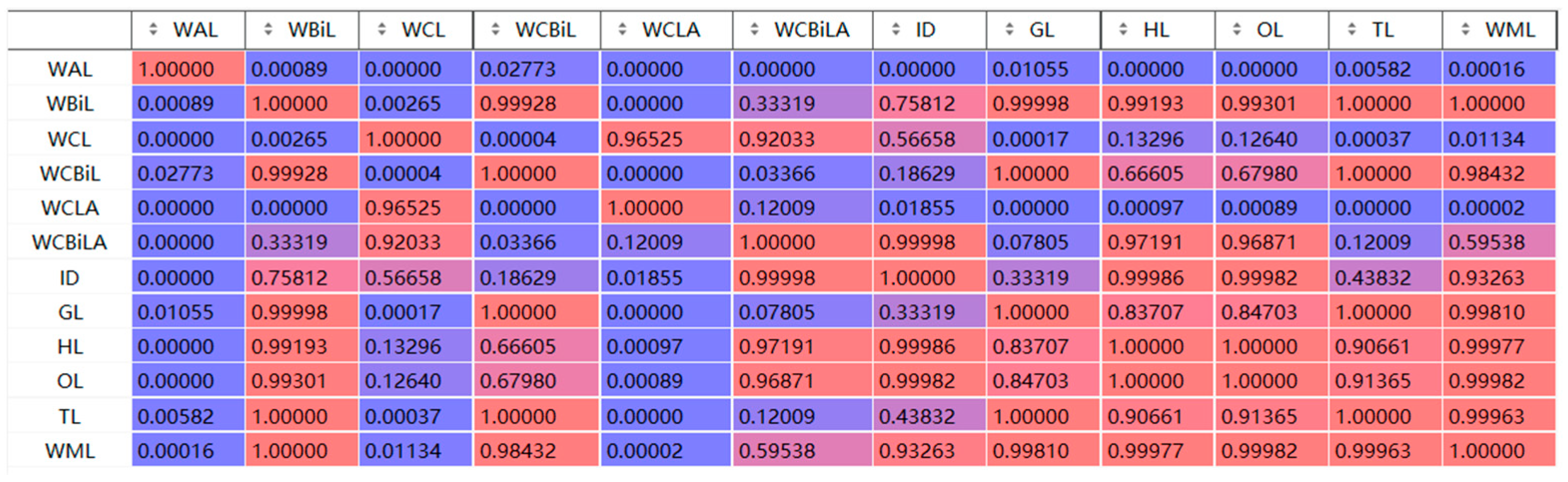
6.2. Results and Visualization
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Yang, Y.; Wang, Z.; Tao, W.; Li, T.; Zhao, Z. CFD modeling of alumina diffusion and distribution in aluminum smelting cells. JOM 2019, 71, 764–771. [Google Scholar] [CrossRef]
- Yao, Y.; Cheung, C.; Bao, J.; Skyllas-Kazacos, M.; Welch, B.; Akhmetov, S. Estimation of spatial alumina concentration in an aluminum reduction cell using a multilevel state observer. AIChE J. 2017, 63, 2806–2818. [Google Scholar] [CrossRef]
- Moxnes, B.; Solheim, A.; Liane, M.; Svinsas, E.; Halkjelsvik, A. Improved cell operation by redistribution of the alumina feeding. In Proceedings of the TMS Light Metals, San Antonio, TX, USA, 15–19 February 2009; pp. 461–466. Available online: https://www.researchgate.net/publication/283249275_Improved_cell_operation_by_redistribution_of_the_alumina_feeding (accessed on 22 July 2025).
- Hou, W.; Li, H.; Mao, L.; Cheng, B.; Feng, Y. Effects of electrolysis process parameters on alumina dissolution and their optimization. Trans. Nonferrous Met. Soc. China 2020, 30, 3390–3403. [Google Scholar] [CrossRef]
- Yan, Q.; Liang, J.; Liu, B.; Cui, J.; Li, Q.; Huang, R. Predictive Control of Alumina Concentration Based on Recursive Subspace. J. Beijing Univ. Technol. 2023, 49, 467–474. [Google Scholar] [CrossRef]
- Geng, D.; Pan, X.; Yu, H.; Tu, G.; Yu, D. Real-Time Automatic Detection of Sodium Aluminate Solution Concentration Based on PSO-BP Neural Network. JOM 2025, 77, 3263–3274. [Google Scholar] [CrossRef]
- Zhu, J.; Xu, Y.; Cao, B.; Cehng, J. Research on Alumina Concentration Prediction in Aluminum Electrolysis Cells Based on PSO-LSTM for the Aluminum Industry. Light Met. 2023, 7, 21–27. [Google Scholar] [CrossRef]
- Du, S.; Huang, Y.; Lu, S.; Shi, J.; Zhang, H. Dynamic Simulation of Alumina Concentration Based on Distributed Sensing. Nonferrous Met. (Extr. Metall.) 2023, 11, 26–32. [Google Scholar] [CrossRef]
- Cao, Z. Research on Alumina Concentration Prediction in Aluminum Electrolysis Cells Optimized by Improved Quantum Genetic Algorithm. Master’s Degree, Central South University, Changsha, China, 2023. [Google Scholar] [CrossRef]
- Li, Y. A Novel Soft Sensor Model for Alumina Concentration Based on Collaborative Training SDBN. In Proceedings of the 2024 IEEE 13th Data Driven Control and Learning Systems Conference (DDCLS), Kaifeng, China, 17–19 May 2024; pp. 1751–1755. [Google Scholar] [CrossRef]
- Ma, L.; Wong, C.; Bao, J.; Skyllas-Kazacos, M.; Welch, B.; Li, W.; Shi, J.; Ahli, N.; Aljasmi, A.; Mahmoud, M. H∞ Filter-based Alumina Concentration Estimation for an Aluminium Smelting Process. IFAC-Pap. 2024, 58, 36–41. [Google Scholar] [CrossRef]
- Ma, L.; Wong, C.; Bao, J.; Skyllas-Kazacos, M.; Shi, J.; Ahli, N.; Aljasmi, A.; Mahmoud, M. Estimation of the Spatial Alumina Concentration of an Aluminium Smelting Cell Using a Huber Function-Based Kalman Filter. In Light Metals 2024; Wagstaff, S., Ed.; TMS 2024—The Minerals, Metals and Materials Series; Springer: Cham, Switzerland, 2024; pp. 464–473. [Google Scholar] [CrossRef]
- Huang, R.; Li, Z.; Cao, B. A Soft Sensor Approach Based on an Echo State Network Optimized by Improved Genetic Algorithm. Sensors 2020, 20, 5000. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, B.; Qian, W.; Rao, G.; Chen, L.; Cui, J. Design of Soft-Sensing Model for Alumina Concentration Based on Improved Deep Belief Network. Processes 2022, 10, 2537. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Zhong, X.; Li, X.; Xia, X.; Liu, B. Design of Soft-Sensing Model for Alumina Concentration Based on Improved Grey Wolf Optimization Algorithm and Deep Belief Network. Processes 2025, 13, 606. [Google Scholar] [CrossRef]
- Choudhary, S.; Kumar, G. Enhancing link prediction in dynamic social networks through hybrid GCN-LSTM models. Knowl. Inf. Syst. 2025. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Cui, J.; Wang, Z.; Ma, L. CNN-LSTM-based Prediction of the Anode Effect in Aluminum Electrolytic Cell. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 4112–4117. [Google Scholar] [CrossRef]
- Pala, M. Graph-Aware AURALSTM: An Attentive Unified Representation Architecture with BiLSTM for Enhanced Molecular Property Prediction. Mol. Divers. 2025. [Google Scholar] [CrossRef] [PubMed]
- Andika, N.; Wongso, P.; Rohmat, F.; Wulandari, S.; Fadhil, A.; Rosi, R.; Burnama, N. Machine learning-based hydrograph modeling with LSTM: A case study in the Jatigede Reservoir Catchment, Indonesia. Results Earth Sci. 2025, 3, 100090. [Google Scholar] [CrossRef]
- Reimers, N.; Gurevych, I. Optimal Hyperparameters for Deep LSTM-Networks for Sequence Labeling Tasks. arXiv 2017. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Wu, T. A novel hybrid model for water quality prediction based on VMD and IGOA optimized for LSTM. Front. Environ. Sci. Eng. 2023, 17, 88. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Xu, C.; Wang, J.; Fang, X.; Xiong, C. BO-STA-LSTM: Building energy prediction based on a Bayesian optimized spatial-temporal attention enhanced LSTM method. Dev. Built Environ. 2024, 18, 100465. [Google Scholar] [CrossRef]
- Li, X.; Lin, J.; Liu, C.; Liu, A.; Shi, Z.; Wang, Z.; Jiang, S.; Wang, G.; Liu, F. Research on Aluminum Electrolysis from 1970 to 2023: A Bibliometric Analysis. JOM 2024, 76, 3265–3274. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2951–2959. Available online: https://proceedings.neurips.cc/paper/2012/hash/05311655a15b75fab86956663e1819cd-Abstract.html (accessed on 22 July 2025).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Xu, G.; Meng, Y.; Qiu, X.; Yu, Z.; Wu, X. Sentiment analysis of comment texts based on BiLSTM. IEEE Access 2019, 7, 51522–51532. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, X. Convolutional neural network based on attention mechanism and bi-lstm for bearing remaining life prediction. Appl. Intell. 2022, 52, 1076–1091. [Google Scholar] [CrossRef]
- Brauwers, G.; Frasincar, F. A General Survey on Attention Mechanisms in Deep Learning. IEEE Trans. Knowl. Data Eng. 2021, 35, 3279–3298. [Google Scholar] [CrossRef]
- Liu, L.; Tian, X.; Ma, Y.; Lu, W.; Luo, Y. Online soft measurement method for chemical oxygen demand based on CNN-BiLSTM-Attention algorithm. PLoS ONE 2024, 19, e0305216. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Waele, W. Weighted average algorithm: A novel meta-heuristic optimization algorithm based on the weighted average position concept. Knowl.-Based Syst. 2024, 305, 112564. [Google Scholar] [CrossRef]
- Chai, Q.; Zhang, S.; Tian, Q.; Yang, C.; Guo, L. Daily Runoff Prediction Based on FA-LSTM Model. Water 2024, 16, 2216. [Google Scholar] [CrossRef]
- Zhu, J. Research on Predicting Alumina Concentration in Electrolytic Cells for Aluminum Industry; Guizhou University: Guiyang, China, 2024. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Nemenyi, P. Distribution-Free Multiple Comparisons; Princeton University: Princeton, NJ, USA, 1963; Available online: https://www.proquest.com/openview/c1f3e8829e8351e9c2a1c5e51778c6cf/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 22 July 2025).















| Full Name | Abbreviation |
|---|---|
| Long Short-Term Memory | LSTM |
| Bi-directional Long Short-Term Memory Network | BiLSTM |
| Convolutional Neural Network | CNN |
| Attention Mechanism | Attention |
| Grey Wolf Optimizer | GWO |
| Harris Hawks Optimization | HHO |
| Tornado Optimization Algorithm | TOC |
| Whale Migration Algorithm | WMA |
| Particle Swarm Optimization | PSO |
| Back Propagation Neural Network | BP neural network |
| Computational Fluid Dynamics | CFD |
| Soft Deep Belief Network | SDBN |
| Improved Genetic Algorithm | IGA |
| Echo State Network | ESN |
| Empirical Mode Decomposition | EMD |
| Deep Belief Networks | DBN |
| Improved Gray Wolf Optimizer | IGWO |
| Variational Mode Decomposition | VMD |
| Improved Grasshopper Optimization Algorithm | IGOA |
| Bayesian Optimization | BO |
| Spatiotemporal Attention | STA |
| Recurrent Neural Networks | RNNs |
| Hyperparameter Name | Lower Bound | Upper Bound |
|---|---|---|
| Number of Neurons | 64 | 512 |
| Number of Layers | 1 | 4 |
| Learning Rate | 0.00001 | 0.1 |
| Batch Size | 16 | 64 |
| Number of Epochs | 50 | 500 |
| No. | X1 | X2 | X3 | Y |
|---|---|---|---|---|
| 1 | 3.658388718 | 7.44300801 | 2.413128337 | 2.551704321 |
| 2 | 3.956737200 | 6.538487214 | 2.636055792 | 2.380336413 |
| 3 | 3.793238259 | 5.883433159 | 1.693218833 | 2.14126837 |
| 4 | 3.782598919 | 6.109309388 | 2.793992135 | 3.02112155 |
| 5 | 3.801940783 | 7.067036763 | 2.506543228 | 2.447662968 |
| 6 | 3.911312398 | 6.210392706 | 2.319062903 | 2.791022997 |
| …… | …… | …… | …… | …… |
| 600 | 3.737352354 | 6.702334075 | 1.574172576 | 1.971260371 |
| Prediction Model | Number of Neurons | Number of Layers | Learning Rate | Batch Size | Number of Epochs |
|---|---|---|---|---|---|
| WAA-LSTM | 230 | 1 | 0.0338 | 16 | 57 |
| WAA-BiLSTM | 160 | 1 | 0.0606 | 16 | 50 |
| WAA-CNN- LSTM | 160 | 1 | 0.0793 | 49 | 54 |
| WAA-CNN- BiLSTM | 160 | 1 | 0.0399 | 34 | 50 |
| WAA-CNN- LSTM-Attention | 64 | 1 | 0.0053 | 17 | 50 |
| WAA-CNN- BiLSTM-Attention | 83 | 3 | 0.1000 | 48 | 119 |
| Prediction Model | MAE | RMSE | R2 | Accuracy (5%) | Accuracy (2%) | Accuracy (1%) |
|---|---|---|---|---|---|---|
| IGWO-DBN | 0.0209 | 0.0285 | 0.9685 | 0.9900 | 0.9500 | 0.6200 |
| WAA-LSTM | 0.0117 | 0.0161 | 0.9883 | 1.0000 | 0.9700 | 0.8700 |
| WAA-BiLSTM | 0.0169 | 0.0228 | 0.9764 | 1.0000 | 0.9500 | 0.7800 |
| WAA-CNN-LSTM | 0.0257 | 0.0344 | 0.9462 | 0.9700 | 0.9100 | 0.5200 |
| WAA-CNN-BiLSTM | 0.0162 | 0.0233 | 0.9753 | 0.9900 | 0.9600 | 0.7700 |
| WAA-CNN-LSTM-Attention | 0.0258 | 0.0326 | 0.9516 | 0.9900 | 0.8800 | 0.5500 |
| WAA-CNN-BiLSTM-Attention | 0.0197 | 0.0252 | 0.9712 | 1.0000 | 0.9400 | 0.7500 |
| Prediction Model | Number of Neurons | Number of Layers | Learning Rate | Batch Size | Number of Epochs |
|---|---|---|---|---|---|
| WAA-LSTM | 230 | 1 | 0.0338 | 16 | 57 |
| GWO-LSTM | 316 | 1 | 0.0319 | 57 | 181 |
| HHO-LSTM | 64 | 1 | 0.0001 | 28 | 149 |
| Optuna-LSTM | 235 | 1 | 0.0047 | 64 | 378 |
| TOC-LSTM | 216 | 2 | 0.0135 | 61 | 224 |
| WMA-LSTM | 230 | 1 | 0.0338 | 16 | 57 |
| Prediction Model | MAE | RMSE | Accuracy (5%) | Accuracy (2%) | Accuracy (1%) | |
|---|---|---|---|---|---|---|
| WAA-LSTM | 0.0117 | 0.0161 | 0.9883 | 1.0000 | 0.9700 | 0.8700 |
| GWO-LSTM | 0.0148 | 0.0181 | 0.9851 | 1.0000 | 0.9700 | 0.8800 |
| HHO-LSTM | 0.0165 | 0.0205 | 0.9809 | 1.0000 | 0.9500 | 0.8300 |
| Optuna-LSTM | 0.0175 | 0.0223 | 0.9775 | 1.0000 | 0.9600 | 0.7100 |
| TOC-LSTM | 0.0157 | 0.0208 | 0.9804 | 1.0000 | 0.9700 | 0.8200 |
| WMA-LSTM | 0.0167 | 0.0215 | 0.9791 | 1.0000 | 0.9700 | 0.8100 |
| Median APE (%) | Mean APE (%) | Std APE (%) | |
|---|---|---|---|
| WAA-LSTM | 0.371339250 | 0.509036785 | 0.483310359 |
| WAA-BiLSTM | 0.587718917 | 0.723661140 | 0.624494207 |
| WAA-CNN-LSTM | 0.946000694 | 1.139855577 | 1.134355742 |
| WAA-CNN-BiLSTM | 0.531563058 | 0.714765792 | 0.809587974 |
| WAA-CNN-LSTM-Attention | 0.950000403 | 1.121347885 | 0.972603571 |
| WAA-CNN-BiLSTM-Attention | 0.700039158 | 0.863990319 | 0.733085291 |
| IGWO_DBN | 0.764104832 | 0.894954675 | 0.766746606 |
| GWO-LSTM | 0.587860957 | 0.647627862 | 0.479657065 |
| HHO-LSTM | 0.624320416 | 0.728598010 | 0.565459009 |
| Optuna-LSTM | 0.659462578 | 0.754129113 | 0.574055374 |
| TOC-LSTM | 0.604570542 | 0.687619493 | 0.609646614 |
| WMA-LSTM | 0.622202965 | 0.715004019 | 0.558122752 |
| Full Name | Abbreviation |
|---|---|
| WAA-LSTM | WAL |
| WAA-BiLSTM | WBiL |
| WAA-CNN-LSTM | WCL |
| WAA-CNN-BiLSTM | WCBiL |
| WAA-CNN-LSTM-Attention | WCLA |
| WAA-CNN-BiLSTM-Attention | WCBiLA |
| IGWO_DBN | ID |
| GWO-LSTM | GL |
| HHO-LSTM | HL |
| Optuna-LSTM | OL |
| TOC-LSTM | TL |
| WMA-LSTM | WL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, X.; Li, X.; Wang, Y.; Li, J. Comparative Analysis of Ensemble Machine Learning Methods for Alumina Concentration Prediction. Processes 2025, 13, 2365. https://doi.org/10.3390/pr13082365
Xia X, Li X, Wang Y, Li J. Comparative Analysis of Ensemble Machine Learning Methods for Alumina Concentration Prediction. Processes. 2025; 13(8):2365. https://doi.org/10.3390/pr13082365
Chicago/Turabian StyleXia, Xiang, Xiangquan Li, Yanhong Wang, and Jianheng Li. 2025. "Comparative Analysis of Ensemble Machine Learning Methods for Alumina Concentration Prediction" Processes 13, no. 8: 2365. https://doi.org/10.3390/pr13082365
APA StyleXia, X., Li, X., Wang, Y., & Li, J. (2025). Comparative Analysis of Ensemble Machine Learning Methods for Alumina Concentration Prediction. Processes, 13(8), 2365. https://doi.org/10.3390/pr13082365






