Abstract
The remanufacturing of end-of-life products is an effective approach to alleviating resource shortages, environmental pollution, and global warming. As the initial step in the remanufacturing process, the quality and efficiency of disassembly have a decisive impact on the entire workflow. However, the complexity of product structures poses numerous challenges to practical disassembly operations. These challenges include not only conventional precedence constraints among disassembly tasks but also sequential dependencies, where interference between tasks due to their execution order can prolong operation times and complicate the formulation of disassembly plans. Additionally, the inherent uncertainties in the disassembly process further affect the practical applicability of disassembly plans. Therefore, developing reliable disassembly plans must fully consider both sequential dependencies and uncertainties. To this end, this paper employs a chance-constrained programming model to characterise uncertain information and constructs a multi-objective sequence-dependent disassembly line balancing (MO-SDDLB) problem model under uncertain environments. The model aims to minimise the hazard index, workstation time variance, and energy consumption, achieving a multi-dimensional optimisation of the disassembly process. To efficiently solve this problem, this paper designs an innovative multi-objective adaptive large neighbourhood search (MO-ALNS) algorithm. The algorithm integrates three destruction and repair operators, combined with simulated annealing, roulette wheel selection, and local search strategies, significantly enhancing solution efficiency and quality. Practical disassembly experiments on a lithium-ion battery validate the effectiveness of the proposed model and algorithm. Moreover, the proposed MO-ALNS demonstrated a superior performance compared to other state-of-the-art methods. On average, against the best competitor results, MO-ALNS improved the number of Pareto solutions (NPS) by approximately 21%, reduced the inverted generational distance (IGD) by about 21%, and increased the hypervolume (HV) by nearly 8%. Furthermore, MO-ALNS exhibited a superior stability, providing a practical and feasible solution for disassembly optimisation.
1. Introduction
Industrial products have significantly enhanced human quality of life and driven societal progress. However, the disposal of large quantities of end-of-life (EOL) products has led to resource shortages and potential environmental pollution. Remanufacturing, as an effective solution to this issue, aims to reduce waste and restore products to desired quality levels through processes such as disassembly, cleaning, sorting, and refurbishment. Disassembly, being the initial step in the remanufacturing chain, involves separating components of EOL products for potential reuse [1,2]. Disassembly sequence planning (DSP) and disassembly line balancing (DLB) problems are two key research areas in this field [3]. However, with technological advancements, the increasing complexity of industrial products has made it more challenging to address intricate disassembly issues through DSP problems alone, prompting researchers to focus more on DLB problems. DLB problems focus on optimally assigning tasks to workstations to improve disassembly line layout and efficiency, thereby enhancing resource utilisation [4,5].
In practice, certain structurally complex and precision-engineered industrial products exhibit disassembly interference between components. This phenomenon prevents workers from employing the most efficient disassembly methods, making task durations highly dependent on the specific disassembly sequence. Consequently, the total disassembly time becomes uncertain, ultimately affecting line balance. Such problems are defined as sequence-dependent disassembly line balancing (SDDLB) problems [6,7]. Research on SDDLB problems not only aligns with real-world disassembly scenarios but also holds significant practical relevance. Moreover, DLB problems without disassembly interference can be viewed as special cases of SDDLB problems where interference times are zero, making the study of SDDLB problems more broadly applicable.
Although existing research has addressed SDDLB problems, models are often based on deterministic assumptions for simplicity, which deviates from the inherent complexity and uncertainty in real-world disassembly processes. In reality, critical factors such as disassembly times are subject to various uncertainties, including operator performance, component degradation, and tool variability [8,9]. Therefore, investigating SDDLB problems under uncertainty has both theoretical and practical significance. By incorporating stochastic factors, more accurate predictions and adaptive strategies can be developed to optimise disassembly sequences and task allocation. To this end, this study introduces chance-constrained programming to enrich research on SDDLB problems. The primary advantage of employing chance-constrained programming lies in its explicit handling of uncertainty through probabilistic constraints. Unlike deterministic approaches that require constraints to hold absolutely, chance-constrained programming allows constraints, such as the workstation cycle time limit, to be satisfied with a specified minimum probability. This enables a more realistic representation of systems where occasional constraint violations due to random fluctuations are tolerable, and it provides decision-makers with a direct mechanism to manage the trade-off between solution robustness and performance by setting the desired reliability level.
Sequence-dependent DLB problems are NP-hard problems whose complexity and scale make exact methods impractical for obtaining solutions within reasonable timeframes [10,11]. Metaheuristics, due to their efficiency and flexibility, have emerged as a promising approach for solving SDDLB problems. These algorithms provide high-quality approximate solutions within acceptable timeframes, particularly for large-scale, complex optimisation problems. While various metaheuristics—such as the hummingbird algorithm [7], the ant colony optimisation algorithm [10], and the artificial bee colony (ABC) algorithm [12]—have been successfully applied to DLB-related problems, the “No Free Lunch” theorem [13] dictates that no single algorithm universally outperforms others. Thus, problem-specific optimisation methods are essential.
Among various metaheuristic algorithms, the adaptive large neighbourhood search (ALNS) algorithm, known for its flexibility and robust local search capabilities, has demonstrated remarkable efficacy in solving complex optimisation problems. ALNS dynamically adjusts combinations of destruction and repair operators to explore new solution spaces while avoiding local optima. Its core mechanism involves partially deconstructing solutions via destruction operators and reconstructing them using repair operators, balancing global exploration and local refinement [14]. Leveraging these advantages, this paper proposes a multi-objective ALNS (MO-ALNS) algorithm to address the proposed MO-SDDLB problem model under uncertain environments. The MO-ALNS algorithm integrates custom-designed destruction and repair operators, simulated annealing for enhanced global search, and local search strategies for solution refinement. Experimental results confirm that the MO-ALNS algorithm significantly outperforms existing algorithms in solution quality.
Against this backdrop, the contributions of this paper are as follows:
- (1)
- A MO-SDDLB model incorporating sequence dependence and uncertainty is developed. Although prior research on SDDLB has generally acknowledged the existence of sequence dependencies, the majority of existing models still rely on deterministic parameters, thereby failing to capture the inherent operational uncertainties prevalent in real-world disassembly environments. This study bridges a critical gap by developing a MO-SDDLB model that incorporates stochastic factors.
- (2)
- A novel MO-ALNS algorithm is proposed. By synergising multiple optimisation strategies, it achieves a superior solution quality. Rigorous experimental analysis demonstrates that the MO-ALNS algorithm consistently outperforms state-of-the-art alternatives in all aspects.
The remainder of this paper is organised as follows: In Section 2, we review the related literature. Section 3 constructs the mathematical model for the MO-SDDLB problem. Section 4 provides a detailed description of the proposed MO-ALNS algorithm. Section 5 examines a case study of end-of-life lithium battery disassembly to analyse the model and algorithm. Section 6 evaluates the performance of the proposed algorithm using various multi-objective evaluation metrics and compares it with other state-of-the-art algorithms. Finally, Section 7 presents the conclusions and suggests future research directions.
2. Literature Review
Relevant to the research undertaken in this paper, this section reviews the literature on the DLB problem (Section 2.1) and the SDDLB problem (Section 2.2). Finally, we provide a summary of these reviewed papers (Section 2.3).
2.1. DLB Problem
The DLB problem aims to allocate disassembly tasks optimally for EOL products to workstations and is a key research area within the circular economy. This problem has garnered significant scholarly attention since its inception. For instance, Li and Janardhanan [15] investigated a profit-orientated U-shaped partial DLB problem. To address this, they formulated a 0–1 integer linear programming model incorporating AND/OR precedence relations and employed an improved discrete cuckoo search algorithm for its solution. Guo et al. [16] studied a U-shaped DLB problem that incorporates human factors. For this specific problem, they developed a mixed-integer linear programming model balancing disassembly profit and worker fatigue index as optimisation objectives and proposed a collaborative resource allocation strategy based on a multi-objective evolutionary algorithm.
Zeng et al. [17] focused on integrating preventive maintenance into the DLB problem. They established a mixed-integer linear programming model aimed at optimising cycle time and minimising task adjustments, and designed an improved genetic simulated annealing algorithm to solve it. Liang et al. [18] addressed the multi-parallel partial DLB problem, with the objectives of optimising the number of shared workstations, workstation load balancing, energy consumption, and profit. They formulated a mixed-integer non-linear programming model for this problem and proposed a hybrid algorithm combining genetic and tabu search. Chen et al. [19] considered the DLB problem under resource and labour constraints. They used a converted AND/OR graph for precedence relations and aimed to minimise the number of workers within a predetermined cycle time, proposing a three-phase heuristic adaptive genetic algorithm for this optimisation task. Zhang et al. [20] investigated the selection of automated disassembly schemes for waste mobile phones, framing it within the context of knowledge reuse and the DLB problem. They established standards for disassembly knowledge and workstation threshold determination, optimising the selection scheme through a quantitative DLB analysis.
Fathollahi-Fard et al. [21] proposed a multi-objective DLB model aimed at simultaneously minimising the idle time rate, smoothness index, labour cost, and energy consumption. For this, they developed a tailored adaptive large neighbourhood search algorithm. Liang et al. [22] studied a multi-objective multi-product DLB problem, considering disassembly profit, energy consumption, and noise pollution. They formulated a multi-objective integer programming model and designed a multi-objective group teaching optimisation algorithm for its solution. Chu and Chen [23] investigated a multi-worker multi-mode DLB for retired power batteries under different operating modes. They explored cost impacts of penalty factors and, addressing real-world unpredictability, proposed a reinforcement learning-based hyper-heuristic algorithm to solve this problem.
Furthermore, recognising the inherent uncertainty in disassembly, some scholars have explored uncertain DLB variants. Wang et al. [24] studied a parallel partial DLB problem with stochastic disassembly time. Their evaluation metrics included workstation count, workload smoothness, and disassembly profit, and they proposed a novel genetic simulated annealing algorithm for optimisation. Zhang et al. [25] introduced a stochastic multi-objective DLB framework. They employed a chance-constrained programming approach for uncertainty and aimed to minimise the workstation idle rate, time variance and energy consumption, proposing a hybrid metaheuristic algorithm. Tian et al. [26] addressed a bucket-chain DLB optimisation problem under uncertainty, using the cloud model for uncertain disassembly times. Their multi-objective approach was tackled with a heuristic method based on the social engineering optimiser. Guo et al. [27] focused on a stochastic multi-product multi-objective DLB problem, aiming to maximise profit and minimise energy consumption and carbon emissions. They proposed a hybrid algorithm combining simulated annealing, stochastic simulation, and a multi-objective discrete grey wolf optimiser. Liang et al. [28] constructed a model for a two-sided DLB problem based on parallel operation constraints and fuzzy theory to handle disassembly time uncertainty. To reduce the balancing loss rate, smoothness index, and energy consumption, they developed a multi-objective planarian algorithm. He et al. [29] studied an integrated stochastic DLB and planning problem where component yields/demands were uncertain and machine characteristics were considered. They constructed a model to minimise the total system cost.
Guo et al. [30] investigated a multi-objective stochastic hybrid production line balancing problem, considering task similarity in assembly and disassembly, with task times as normal random variables. They proposed a hybrid algorithm combining variable neighbourhood search and NSGA-II. Liu et al. [31] tackled a stochastic multi-product DLB problem with labour assignment, assuming only partial distribution information for uncertain task times. Xu et al. [32] used an AND/OR graph for a stochastic multi-product robotic DLB model, considering precedence, cyclic constraints, and failures. To maximise profit and minimise energy consumption, they proposed a Pareto-improved multi-objective brain storm optimisation algorithm with a stochastic simulation. He et al. [33] studied a green-orientated bi-objective DLB problem with stochastic task times. They constructed a mathematical model to minimise the total line configuration cost and pollutant emissions.
2.2. SDDLB Problem
Compared to the DLB problem, the SDDLB problem is a more realistic representation of practical disassembly situations, as it considers the interference between disassembly tasks. Consequently, this problem has garnered significant academic attention and seen considerable research progress since its introduction. For example, Kalayci et al. conducted systematic investigations into the SDDLB problem, employing an artificial bee ABC algorithm to derive solutions and validating its performance through comparisons with six other algorithms [12]. Furthermore, their application of a variable neighbourhood search (VNS) algorithm to the SDDLB problem demonstrated a superior robustness and solution quality [34]. Subsequent research saw them develop a hybrid algorithm combining a genetic algorithm with VNS to address a multi-objective SDDLB problem incorporating workforce, financial, and temporal considerations, thereby offering a novel optimisation approach for complex scenarios [35].
Liu et al. proposed an enhanced discrete ABC algorithm for the SDDLB problem, expanding the methodological scope of this research domain [36]. Yin et al. introduced a partial SDDLB problem from the perspective of cost reduction and operational efficiency improvement, employing a Pareto-discrete hummingbird algorithm solution that was validated across various case scales [37]. Wang et al. developed a hybrid ABC algorithm incorporating novel initialisation rules and dynamic neighbourhood search methods, presenting an innovative solution strategy [7]. Xia et al. formulated a mathematical model for a stochastic mixed-flow partial SDDLB problem, solved through an adaptive hybrid particle swarm genetic algorithm [38].
Çil et al. investigated a two-sided SDDLB problem, proposing two novel mixed-integer linear programming models and a constraint programming model, complemented by a genetic algorithm and an enhanced ABC algorithm for large-scale applications [39]. Li et al. focused on a multi-objective sequence-dependent U-shaped DLB problem, developing an iterated local search algorithm for complex disassembly scenarios [40]. Chen et al. advanced research on a multi-objective sequence-dependent robotic DLB problem through an optimised multi-objective evolutionary algorithm featuring enhanced crossover and mutation operators [41].
2.3. Literature Analysis
Based on the analysis of the literature above, we can draw the following insights:
- (1)
- Existing SDDLB problems predominantly employ deterministic assumptions, neglecting the inherent uncertainties in practical disassembly processes regarding operator conditions and product degradation states. This limitation reduces the practical applicability of current models, necessitating an uncertainty-incorporated SDDLB problems analysis to enhance robustness and operational relevance.
- (2)
- While metaheuristic approaches such as genetic algorithms, ABC algorithms, and VNS algorithms have been extensively applied to SDDLB problems, the potential of an ALNS algorithm remains underexplored. ALNS’s flexible neighbourhood structures and adaptive mechanisms demonstrate exceptional promise for complex combinatorial optimisation, offering a novel solution approach for SDDLB challenges.
To address these gaps, this study introduces a chance-constrained programming method to account for operational uncertainties and develops a MO-ALNS algorithm, providing more realistic and efficient SDDLB solutions.
3. Proposed Model
This section presents our MO-SDDLB model. Section 3.1 provides a detailed description of sequential dependency, and the formulation of our MO-SDDLB problem model is given in Section 3.2.
3.1. Sequential Dependency
Due to the complex structure of some products and the close association of components, there may be mutual interference between tasks without priority relationships during the disassembly process. This interference, referred to as sequential dependency [7], can prevent tasks assigned priority from being disassembled most conveniently, thus leading to an increase in operation time. A disassembly hybrid graph (DHG) provides a visual representation of the relationships between disassembly tasks. Figure 1 illustrates the priority and interference relationships among the disassembly tasks for a product containing 12 components. Solid arrows represent the precedence relationships between disassembly tasks, while dashed arrows indicate the sequential dependency between tasks, with the interference time notated in italics. For example, although disassembly Tasks 10 and 11 have no priority relationship, they interfere with each other. If Task 10 is disassembled before Task 11, it will be obstructed by Task 11, resulting in an additional 4 s of disassembly time for Task 10. Similarly, if Task 11 is disassembled before Task 10, its disassembly time will increase by 6 s. Therefore, the SDDLB problem involves the rational allocation of tasks to various disassembly workstations while considering sequential dependencies, interference times, and precedence relationships, aiming to achieve predefined optimization objectives such as minimizing cycle time, balancing workstation loads, or reducing the total disassembly time.
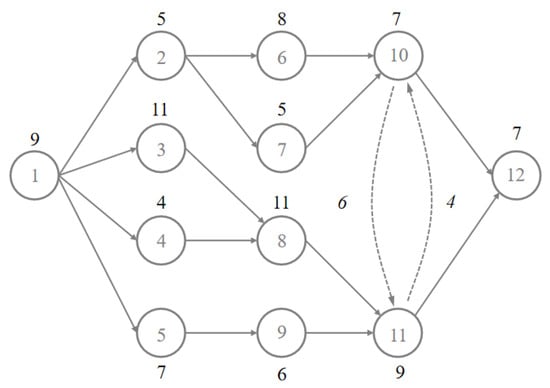
Figure 1.
Product disassembly hybrid graph.
3.2. Proposed MO-SDDLB
As previously established, inherent stochasticity characterises the disassembly process. To rigorously model these uncertainties, this study employs chance-constrained programming, representing disassembly durations, interference times, and energy consumption parameters as stochastic variables. The chance-constrained programming method provides significant advantages for addressing this problem [42]:
- (1)
- Unlike deterministic approaches that require fixed parameters, chance-constrained programming allows constraints to be satisfied with a specified probability level, which better reflects the inherent variability in real-world disassembly operations.
- (2)
- This method enables decision-makers to control the trade-off between solution conservativeness and operational feasibility by adjusting the probability thresholds, ensuring practical applicability while avoiding overly pessimistic scheduling plans.
Based on this method, a corresponding multi-objective optimisation model is constructed. To clearly describe the proposed multi-objective selective disassembly line balancing model, the following notations are defined and used below:
| Indices: | |
| , | Index of disassembly tasks, m,i,, where represents the total number of disassembly tasks |
| Index of workstations,, where represents the maximum number of workstations | |
| Index of disassembly task position, s | |
| Parameters: | |
| Cycle time of disassembly workstations, i.e., the maximum task processing time that a workstation can accommodate | |
| Disassembly time for task | |
| Confidence level | |
| Unit time of the energy consumption of task | |
| Unit time of the energy consumption of workstation standby | |
| Task ’s difficulty coefficient | |
| 1, if task has a hazard attribute, otherwise = 0 | |
| Sequence-dependent time increment influence matrix if task has disassembly interference with task , then the time increment of task is ; = 0 means that task has no disassembly interference with task | |
| 1, if task is a predecessor of task , otherwise, 0 | |
| A sufficiently large number | |
| Decision variables: | |
| 1, if task m is assigned to the position in the disassembly sequence, 0 otherwise | |
| 1, if task is executed before task , otherwise, 0 | |
| 1, if task is disassembled at workstation , otherwise, 0 | |
| 1, if workstation is activated, otherwise, 0 |
Then, the proposed MO-SDDLB model is formulated as follows:
s.t.
Equation (1) represents the minimisation of the hazard index, Equation (2) represents the minimisation of the differences in idle times between workstations, and Equation (3) represents the minimisation of the total energy consumption. In Equations (2) and (3), denotes the expected value. This represents the average value of these respective objectives when considering potential stochasticity, such as variability in task processing times. Constraint (4) ensures that, at the given confidence level, the total task time at each workstation does not exceed the cycle time limit. represents probability, which is used here to quantify the likelihood of this constraint being satisfied. Constraint (5) states that if task is a prerequisite for task , task must be completed before task . Constraint (6) ensures that the execution order of tasks and cannot be mutually exclusive. Constraint (7) specifies that if task is completed before task , task must be assigned to a workstation that is either ahead of task or the same as task . Constraint (8) ensures that each task is assigned to a specific position in the disassembly sequence. Constraint (9) states that each position can only be assigned to one task. Constraint (10) ensures that each task is assigned to one workstation only. Constraint (11) represents the activation sequence of workstations. Constraint (12) ensures that if task is completed before task , task ’s position must be ahead of task ’s position. Constraint (13) ensures that the sequential relationships between tasks are logically transitive. Constraint (14) states that workstations are only activated when tasks are assigned to them, and each workstation can accommodate a maximum of tasks. Constraint (15) defines the decision variables set in the model.
4. Proposed MO-ALNS
The MO-SDDLB problem addressed in this study is a complex assignment task. It involves optimally allocating a series of disassembly operations for EOL products to an ordered set of workstations. This allocation must not only adhere to precedence relationships between tasks but, crucially, also consider sequence dependency. Furthermore, the problem incorporates inherent uncertainties in parameters such as task durations, interference times, and energy consumption. Given the NP-hard nature of the formulated problem, compounded by its multi-objective characteristics and the presence of uncertainty, solving it using exact methods presents significant challenges. Therefore, in this section, we introduce the MO-ALNS algorithm, which we design to solve this problem. Subsequently, we detail the process of generating initial solutions and their representation within the MO-ALNS framework (Section 4.2), and present the customised destruction and repair operators tailored for this study (Section 4.3). Furthermore, we elaborate on the local search strategy (Section 4.4) and the constraint correction method (Section 4.5) designed for MO-ALNS. We also introduce a Monte Carlo simulation technique to address uncertainties in the model (Section 4.6). Finally, we present the complete structure and workflow of the MO-ALNS framework (Section 4.7).
4.1. Multi-Objective Handling Approach
To address the MO-SDDLB problem, this study introduces the concept of Pareto Dominance [24]. Pareto Dominance is used to determine the dominance relationship between two solutions: if a solution is not inferior to another in all objective functions and is superior in at least one objective function, it is referred to as a non-dominated solution. In the MO-ALNS algorithm, all non-dominated solutions are stored in a Pareto solution list. Through iterative optimisation, the algorithm ultimately generates a set of high-quality solutions, providing decision-makers with multiple trade-off options to meet the diverse requirements of practical disassembly scenarios.
4.2. Encoding and Decoding Method
As an efficient metaheuristic algorithm, MO-ALNS selects a solution from the search space as the initial solution in a random and iterative manner during the initialisation phase [43]. This study employs a real-number encoding method to represent the disassembly sequence. Assuming a disassembly process involves tasks, the initial disassembly sequence can be represented as. To generate a feasible disassembly sequence, the algorithm first randomly selects a disassembly task without precedence constraints, removes the constraints associated with that task, and repeats the process until a complete feasible disassembly sequence is generated.
After obtaining the initial feasible disassembly sequence, it needs to be decoded. The core of the decoding process lies in assigning the generated disassembly sequence to various workstations based on disassembly time and task interference time, while ensuring that the workstation cycle time constraints are satisfied, thereby forming a feasible SDDLB solution.
4.3. MO-ALNS Neighbourhood Structures
As a local search algorithm with varied neighbourhood structures, the MO-ALNS broadens the solution search space by integrating numerous destruction and repair operators. Similarly, in response to the proposed problem, three destruction operators and three repair operators are designed in MO-ALNS, which are described as follows:
Suppose the task to be disassembled has points, and the destruction operator randomly selects n of them, where . Let be the location of the point selected by the destruction operator. Here are the three destruction operators:
- Prefix destruction operator : prefix, then, replace the points in the remaining positions with zeroes, and wait for a repair. This step is demonstrated in Figure 2a.
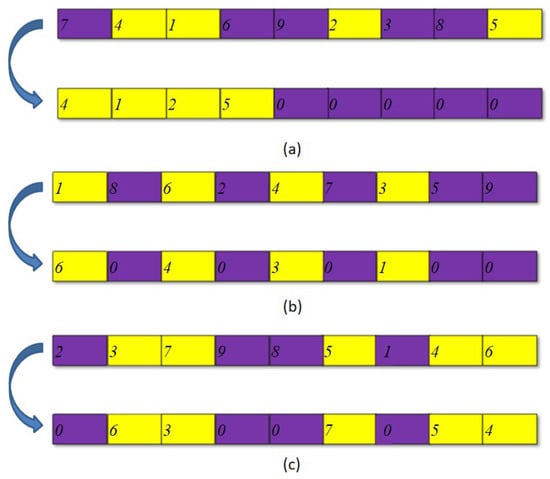 Figure 2. Destruction operators: (a), (b), (c).
Figure 2. Destruction operators: (a), (b), (c). - Forward shifting destruction operator : Take the selected points to be advanced, and place point at the position of point . The remaining points are replaced with zeroes, awaiting repair. The specific implementation is shown in Figure 2b.
- Backward shifting destruction operator : Move the selected points back by one position, advance , followed by reordering. The remaining points are replaced with zeroes in anticipation of repair. The specific implementation is illustrated in Figure 2c.
Assuming that there are points in the disassembly task, the destruction operator randomly selects n points from them, where . Let be the position of the point selected by the repair operator. Here are the three repair operators:
- Random repair operator : Sort the points to be repaired randomly, as shown in Figure 3a below:
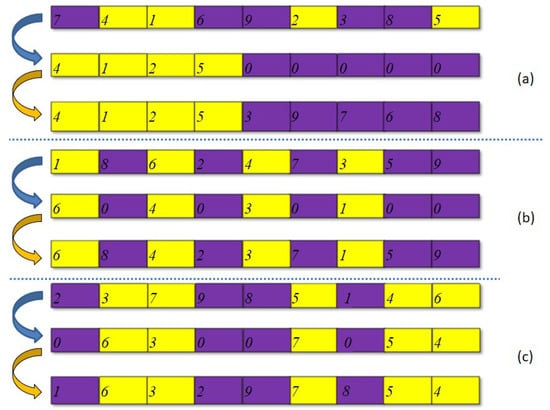 Figure 3. Repair operators: (a), (b), (c).
Figure 3. Repair operators: (a), (b), (c). - Sequential repair operator : The points to be repaired are sequentially placed back into the original sequence, as shown in Figure 3b.
- Push-back repair operator : Move back one position, advance , and return the original sequence, as shown in Figure 3c.
The abovementioned destruction and repair operators are randomly combined to form nine types of neighbourhood structures. Despite the simplicity of these operations, the randomness inherent in the removal of points can significantly expand the search space for solutions and enhance the diversity of the algorithm’s search.
4.4. Local Search
To enhance the algorithm’s ability to avoid local optima, we introduce two new local search operators. These operators are randomly applied to the current best solution during the search process, and by executing iterations of the search, they provide the algorithm with more opportunities to escape local optima, thereby increasing the likelihood of finding global optimal solutions. Specifically, we design the following two operators for the local search algorithm:
- (1)
- Three-point crossover (S1): Three points in the sequence are randomly selected, and a random crossover is performed, as illustrated in Figure 4a.
- (2)
- Four-point crossover (S2): Randomly select two points within the sequence and perform a crossover with the point immediately following each selected point. If a selected point is the last point in the sequence, then perform the crossover with the point immediately preceding it, as depicted in Figure 4b.
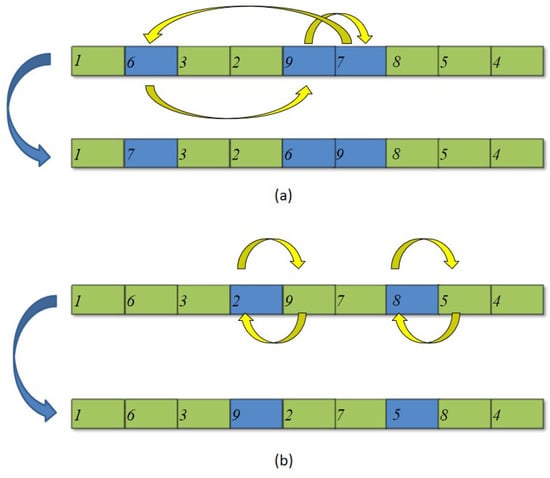
Figure 4.
Chematic diagram of the swap operators for the local search: (a), (b).
4.5. Method for Constraint Correction
In the field of metaheuristic algorithms, newly formulated solutions may sometimes fail to meet predefined constraints. This challenge is also encountered in the proposed MO-ALNS. For each newly generated solution, we perform a validation to determine if the constraints are met. If the generated sequence does not meet the specified conditions, we immediately start searching for alternatives that do. This strategy ensures that our algorithm always adheres to the constraints of the problem throughout the exploration of the solution space.
4.6. Monte Carlo Simulation Method
Recognising the inherent uncertainty in critical operational parameters, this study models disassembly times, task interference times, and energy consumption as stochastic variables. We specifically assume these parameters adhere to uniform distributions, meaning each parameter is uniformly distributed over a specific interval . This selection of the uniform distribution is justified by situations where parameters are understood to fluctuate within defined lower and upper bounds and respectively, yet a precise knowledge of their underlying probability distribution is lacking. Such an approach is a prevalent technique for representing bounded uncertainty and finds application in various uncertainty characterisation contexts [25]. To effectively handle this randomness, we employ the Monte Carlo simulation method. Specifically, for each feasible disassembly sequence, we first generate a set of stochastic variables and construct a SDDLB solution based on these variables. Subsequently, we perform Monte Carlo simulations for this solution. In each simulation, a set of stochastic variables is generated, the corresponding objective function values are calculated, and the solution is checked for constraint satisfaction. Finally, the average of the objective function values from these simulations is taken as the evaluation metric for the solution, while the number of times the constraints are satisfied is recorded. If the number of constraint-satisfying instances does not meet the predefined confidence level, the solution is assigned a significantly large penalty value to ensure that the algorithm prioritises feasible solutions that satisfy the constraints during the optimisation process.
4.7. Algorithmic Framework
In our proposed MO-ALNS, the initial solution is denoted as , and the current solution is . The new solution produced after damage repair and local search is . The optimal solution found in each iteration is designated , where represents the sum of all objective functions, i.e., .
In the first iteration, all the operators are assigned the same weight and score. With three destruction operators and three repair operators , the initial weights are set to 1, and the scores are set to 0 for all. The probability of each operator being selected is as follows [43,44]:
During algorithmic iteration, we select destruction and repair operators according to the roulette wheel selection principle. Operators with higher weights are more likely to be chosen. After each iteration, we assign different scores to the operators based on the quality of the updated solution, and the scores of the three levels are set to . The scoring criteria are as follows:
The operator weights are updated based on operator scores. It is noteworthy that operator weights are not updated in every iteration. Generally, operator weights are set to be updated every generations. The formula for updating operator weights is as follows:
where and refer to the destruction and repair operator weights after the update, indicates the number of times the operator is selected in the past m generations, and represents the cumulative score of the operator over the past m generations. It is important to note that both and are reset to 0 after each update of the operator weights. The term is the weight adjustment coefficient, , which represents the degree of importance of historical weights and operator performance during the operator weight update. Through this formula, the operator weights are linked to historical performance, achieving the purpose of adaptive adjustment of operator weights.
When a high-quality solution emerges from destruction and repair, we replace with and add to the Pareto solution set. If a non-improved solution appears during iteration—meaning that is not superior to —the MO-ALNS algorithm utilises the acceptance criterion of the simulated annealing algorithm to decide whether to accept this non-improved solution with a certain probability. This helps the algorithm avoid falling into local optima. To decide if a non-improved solution should be accepted, we calculate the acceptance probability using the following formula:
In the given algorithm, represents the objective value of the updated solution, and is the objective value of the current solution. The term denotes the temperature of the current generation, which decreases with the iteration count according to the equation , where is the annealing rate. If the non-improved solution is accepted, the current solution is updated to , and is subsequently added to the Pareto solution list.
The termination criterion for the proposed MO-ALNS algorithm is defined by the maximum number of iterations, denoted as . Upon reaching this termination point, the MO-ALNS algorithm organises the list of Pareto solutions to obtain the best non-dominated set.
In summary, the proposed MO-ALNS integrates several critical components, each contributing to its overall performance in tackling the MO-SDDLB problem. The three destruction and three repair operators form the backbone of the search, providing mechanisms for both diversification by exploring new solution structures and intensification by refining existing ones. The roulette wheel selection mechanism, coupled with the adaptive weight adjustment for these operators, intelligently guides the search by prioritising more effective operators over time, thereby enhancing search efficiency and the quality of the solutions found. The simulated annealing strategy plays a vital role in preventing premature convergence by allowing the algorithm to escape local optima, thus fostering a more comprehensive exploration of the solution space. The tailored local search operators further refine solutions. Finally, the Monte Carlo simulation technique directly addresses the uncertainties in problem parameters, leading to more robust and practically applicable solutions.
Integrating these components, Figure 5, below, succinctly encapsulates a review of the proposed MO-ALNS algorithm using a flow chart.
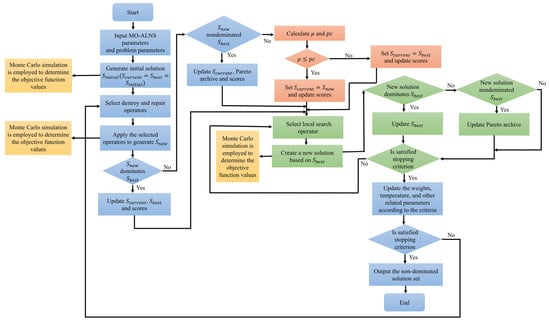
Figure 5.
MO-ALNS flowchart.
5. Case Study
In this section, we conduct analyses of a lithium-ion battery disassembly line comprising 44 disassembly tasks. We begin by performing parameter calibration for the MO-ALNS, followed by presenting and analysing the results. All data and code utilised for the metaheuristic algorithms were executed in MATLAB software version R2013a, running on a 64-bit 2.5 GHz Intel(R) Core(TM) i7 operating system with 8 GB of memory. This specific version is utilised primarily due to its compatibility with existing, validated code modules integral to our experimental setup. While newer versions of MATLAB offer additional features, the core functionalities required for the algorithms and analyses implemented in this work are fully supported by R2013a, ensuring the validity and reproducibility of our results within this established environment. The disassembly information of a lithium-ion battery is shown in Table 1, and its DHG is shown in Figure 6, where denotes hazardous tasks. The parameters for this dataset were gathered and validated through practical disassembly observations and extensive consultations with domain experts in battery recycling and disassembly.

Table 1.
Disassembly information of a lithium battery.
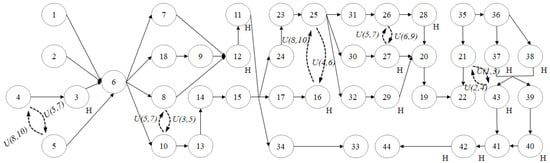
Figure 6.
A DHG of the lithium-ion battery.
Furthermore, the remaining parameters are configured as follows: , , , = 1000, and .
5.1. The Calibration of the MO-ALNS Parameters
The accuracy of the parameters greatly affects the effectiveness of metaheuristic algorithms, and well-tuned parameters can enable a metaheuristic algorithm to exhibit a higher level of efficiency in solving test problems. The metaheuristic algorithm proposed in this paper involves nine parameters. Based on prior experience and thorough research, three candidate values are provided for each of these nine parameters, as shown in Table 2. In addition, the relative percentage deviation () is used as a criterion for determining the optimal level of the parameters [45,46]. The formula for the is as follows:
where represents the average of all the values in the obtained Pareto solutions, and represents the minimum value across all experiments.

Table 2.
MO-ALNS parameter reference values.
Based on the predefined parameter levels, a full factorial experiment would necessitate conducting 39 = 19,683 experimental runs. This number is prohibitively large and impractical due to the significant time and resources required. Therefore, we adopted the Taguchi method for designing the experiments. The Taguchi method achieves efficiency by using Orthogonal Arrays. These arrays select a small, balanced subset of all possible parameter combinations. This balance ensures that the main influence of each parameter can be estimated independently, without needing to test every single combination. Consistent with this method and suitable for our nine parameters each at three levels, we selected the L27 orthogonal array to guide the parameter tuning process, requiring a total of only 27 experiments. Following these experiments, we calculate the average RPD for each parameter at each level, with the final results illustrated in Figure 7.
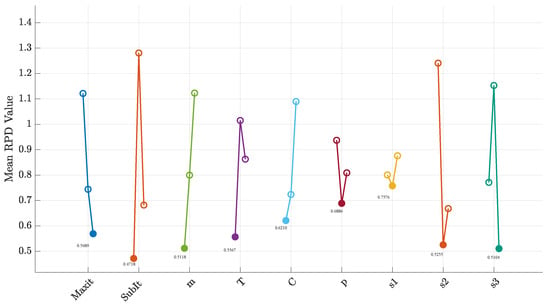
Figure 7.
The behaviour of our MO-ALNS in terms of the RPD metric.
Based on Figure 7, we set the parameters as follows: .
5.2. Results and Discussion
Following the calibration of our MO-ALNS parameters, we implement them in the proposed case study. The execution of the program yields 24 non-dominated solutions, which are presented in Table 3. Following the calibration of our MO-ALNS parameters, we apply them to the proposed case study. Executing the algorithm yields 24 non-dominated solutions, which are presented in Table 3. This table details each solution: the first column provides a solution identifier, the second column outlines the specific DLB scheme obtained, and the final three columns report the corresponding values for our defined objective functions: the minimisation of the hazard index (), the minimisation of the differences in idle times between workstations (), and the minimisation of the total energy consumption ().

Table 3.
Non-dominated solutions for lithium-ion battery disassembly.
As detailed in Table 3, for this case study, Scheme 19 is able to minimise the parts hazard index as much as possible while also having the highest disassembly line smoothness rate. In contrast, Scheme 4 is the preferred option for minimising the disassembly line smoothing rate, but it has a relatively higher hazard index and disassembly energy consumption. In regard to minimising energy consumption, Scheme 11 is the best choice. There is a complex and conflicting relationship between these three goals, and decision makers can choose the best option based on actual needs.
6. Algorithm Performance Analysis
In this section, we first compare the proposed MO-ALNS with other state-of-the-art algorithms (Section 6.1). This is followed by a statistical analysis of the comparison results (Section 6.2). Finally, a sensitivity analysis of the destruction and repair operators within MO-ALNS is conducted (Section 6.3).
6.1. A Comparison with Other Algorithms
To validate the effectiveness of the proposed algorithm, we compare it with other advanced algorithms, including the improved genetic algorithm (IGA) [47], VNS [34], and the social engineering optimiser (SEO) [26], which have been proven to be significantly effective in solving the DLB problem. We use the case study from Section 5 as the evaluation benchmark, and to ensure fairness in the comparison, all algorithms are set to terminate at seconds as the stopping criterion, with their parameters calibrated accordingly. Additionally, all algorithms utilise a uniform individual generation method and constraint verification mechanism. To conserve computational resources, deterministic information is employed for processing.
To assess the quality of the solutions obtained by these methods, we adopt the NPS, IGD, and HV as performance evaluation metrics. The NPS measures the number of non-dominated solutions obtained by the algorithm, with a higher value indicating better performance, directly reflecting the algorithm’s ability to acquire high-quality solutions. The IGD evaluates the proximity of the solution set obtained by the algorithm to the true Pareto front, with a lower value being preferable. The HV measures the convergence and distribution of the solution set, with a higher value being desirable [48,49,50]. For the HV calculation, the reference point is set to (1.1, 1.1, 1.1). As the true Pareto front is often difficult to obtain, the reference front for the IGD metric is constructed by combining the non-dominated solutions obtained from ten independent runs of each of the four algorithms. This consolidated reference front is presented in the Appendix A. Each algorithm is run independently ten times, and the average values of the evaluation metrics are calculated. The final aggregated results are presented in Table 4, and Figure 8 further illustrates the statistical outcomes. According to the results, MO-ALNS comprehensively outperformed the other comparative algorithms across all three key evaluation metrics in terms of average, best, and worst values. More importantly, MO-ALNS exhibited the lowest standard deviation across all metrics, strongly evidencing that the algorithm is not only high-performing but also exceptionally stable and robust, capable of providing reliable and high-quality solutions.

Table 4.
Results of the evaluation metrics over 10 runs (W = Worst, A = Average, B = Best, SD = Standard Deviation).
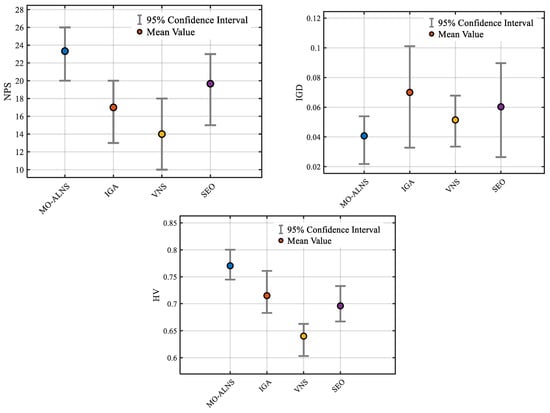
Figure 8.
Interval plots analysing the comparison of the algorithms.
6.2. Statistical Analysis
To further validate the robustness and significance of the observed performance differences among the compared algorithms, this section employs the Wilcoxon rank-sum test. This non-parametric statistical test is utilised to determine if there are statistically significant differences between the results obtained by pairs of algorithms for each of the performance metrics. A significance level of 0.05 is adopted for all tests. A p-value below this threshold indicates a statistically significant difference. The comparison results are illustrated in Figure 9.
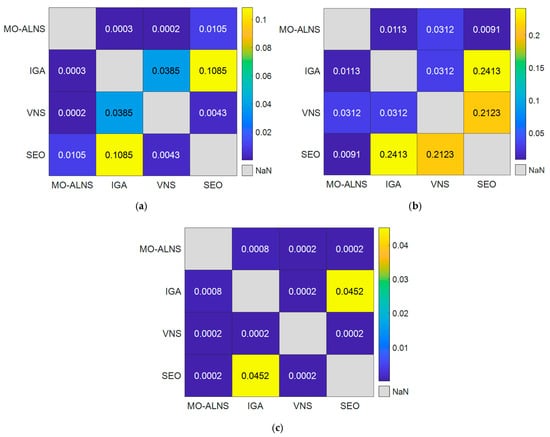
Figure 9.
Wilcoxon rank-sum test results for the pairwise algorithm performance comparison: NPS (a), IGD and (b), HV (c).
Based on the aforementioned results, the MO-ALNS algorithm consistently demonstrates statistically significant superiority over the IGA, VNS, and SEO algorithms across all three metrics. In all pairwise comparisons involving MO-ALNS, the p-values are substantially lower than the 0.05 significance level. This consistent and strong statistical evidence robustly substantiates the effectiveness of the MO-ALNS algorithm in addressing the problem under investigation. It indicates that, compared to the other algorithms, MO-ALNS is capable of identifying a superior set of solutions in terms of quantity, quality, convergence, and diversity.
6.3. A Sensitivity Analysis of the MO-ALNS
The proposed MO-ALNS integrates three destruction operators and three repair operators, thereby constructing nine distinct neighbourhood search mechanisms. Evaluating the individual efficacy of these operator combinations is crucial for understanding the algorithm’s search behaviour and optimising its performance. Consequently, to ascertain the specific contribution of each destruction–repair operator pair to the overall search capability of the algorithm, a quantitative evaluation is conducted based on the aforementioned test instances. The methodology involves independently running the algorithm six times for each operator combination and recording the average performance improvement, defined as the gap between the initial solution and the final optimal solution. The detailed results of this analysis are documented in Table 5. Furthermore, the average performance of each operator is presented in Figure 10.

Table 5.
A sensitivity analysis of destroy and repair heuristics.
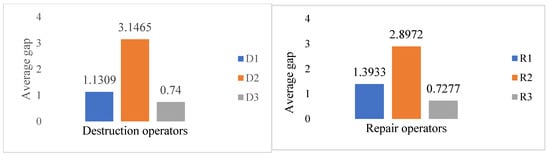
Figure 10.
The average gap in destruction and repair operators.
As illustrated in Table 5 and Figure 10, it is evident that the destruction operator achieves the largest average improvement gap, significantly outperforming both the and operators. This suggests that is particularly effective at escaping local optima and exploring more promising regions of the solution space. Similarly, the repair operator demonstrates a superior performance by yielding the largest average improvement gap compared to and . This indicates that is highly proficient in constructing high-quality solutions from the perturbed states generated by the destruction operators. The combination of and , as seen in Table 5, yields the most substantial improvement, highlighting a strong synergistic effect between these two operators.
7. Conclusions and Future Work
Currently, most modelling approaches for the SDDLB problem are based on deterministic information. This study proposes a MO-SDDLB model, which accounts for multiple disassembly uncertainties, thereby addressing a gap in the literature. Furthermore, a MO-ALNS algorithm is introduced. This algorithm employs three destruction operators and three repair operators, which are randomly combined to form diverse neighbourhood structures and local search operators for solving the MO-SDDLB model. Additionally, the algorithm integrates a simulated annealing strategy and a roulette wheel strategy to adaptively adjust the weights of the operators based on their historical performance, thereby improving the precision and computational efficiency of the solution outputs.
The proposed model and algorithm were validated through a case study on lithium battery disassembly. Subsequently, the performance of MO-ALNS was compared with that of IGA, VNS, and SEO, demonstrating that MO-ALNS yields higher-quality solutions and provides more realistic disassembly plans.
From a managerial perspective, this study offers significant practical value for managing stochastic disassembly operations. The MO-SDDLB model provides a more accurate representation of real-world disassembly scenarios, enabling managers to move beyond simplified deterministic planning. The efficient MO-ALNS algorithm serves as a practical tool to support complex decision-making processes. By generating a diverse set of high-quality solutions, this approach empowers decision-makers to make informed choices regarding different objectives based on their specific operational priorities and risk tolerance.
Despite these contributions, this research is subject to certain limitations which also pave the way for future investigations. Firstly, regarding the evaluation methodology, while the commonly used metrics NPS, IGD, and HV were employed, it is acknowledged that they each possess inherent limitations. Specifically, NPS may not fully capture solution quality and diversity, IGD’s reliance on a known true Pareto front can be problematic for constrained real-world scenarios, and HV is known to be computationally intensive, sensitive to reference point selection, and susceptible to distortion by extreme solutions. Secondly, concerning the scope of the current model and analysis, this study did not account for operational factors such as tool and direction changeover times or energy consumption during the disassembly process. Furthermore, the investigation was confined to straight-line disassembly configurations.
Future research should aim to overcome these limitations. To enhance the evaluation framework, future studies are encouraged to consider alternative or hybrid assessment approaches. This could involve integrating explicit diversity metrics or developing domain-specific indicators that more accurately reflect the complexities of disassembly operations. To broaden the model’s applicability and realism, subsequent research could incorporate the aforementioned operational factors like tool and direction changes, and extend the analysis to more complex configurations such as U-shaped or two-sided disassembly lines. Finally, while MO-ALNS has demonstrated promising performance, further enhancing its constraint handling capabilities presents a valuable research direction. For example, the development of more intelligent repair operators, potentially leveraging problem-specific heuristics or machine learning techniques to more efficiently guide infeasible solutions back to feasibility, could significantly improve performance. This would be especially beneficial for problems with more complex constraint interactions or a larger number of constraints.
Author Contributions
Methodology, D.Z. and X.Z.; Validation, D.Z.; Formal analysis, D.Z.; Data curation, X.H.; Writing—original draft, X.Z., X.H., D.T.P. and C.Z.; Writing—review & editing, D.Z. and D.T.P.; Visualization, D.Z.; Supervision, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
IGD reference points.
Table A1.
IGD reference points.
| Order | |||
|---|---|---|---|
| 1 | 164 | 6768.58 | 1525.46 |
| 2 | 164 | 8815.17 | 1488.18 |
| 3 | 157 | 16,513.11 | 1517.33 |
| 4 | 156 | 11,030.41 | 1539.63 |
| 5 | 167 | 10,668.76 | 1483.60 |
| 6 | 169 | 2890.75 | 1541.24 |
| 7 | 173 | 3538.07 | 1482.66 |
| 8 | 156 | 17,715.46 | 1511.53 |
| 9 | 176 | 7146.59 | 1471.95 |
| 10 | 170 | 5571.07 | 1489.04 |
| 11 | 156 | 17,609.60 | 1519.08 |
| 12 | 156 | 15,459.83 | 1525.12 |
| 13 | 157 | 17,187.21 | 1516.34 |
| 14 | 165 | 6749.50 | 1505.22 |
| 15 | 167 | 4493.28 | 1504.66 |
| 16 | 163 | 7398.66 | 1545.79 |
| 17 | 162 | 7615.51 | 1534.08 |
| 18 | 164 | 8133.84 | 1492.67 |
| 19 | 187 | 5862.76 | 1479.99 |
| 20 | 166 | 4949.13 | 1509.33 |
| 21 | 169 | 3062.02 | 1530.39 |
| 22 | 169 | 2671.85 | 1542.42 |
| 23 | 169 | 3208.93 | 1525.40 |
| 24 | 168 | 3573.95 | 1492.53 |
| 25 | 169 | 5549.99 | 1491.07 |
| 26 | 155 | 16,777.61 | 1530.55 |
| 27 | 157 | 16,837.58 | 1516.69 |
| 28 | 156 | 16,681.27 | 1522.97 |
| 29 | 158 | 15,870.52 | 1505.78 |
| 30 | 156 | 15,284.26 | 1533.99 |
| 31 | 154 | 17,356.98 | 1545.59 |
| 32 | 155 | 20,998.95 | 1504.64 |
| 33 | 159 | 20,665.31 | 1500.58 |
| 34 | 158 | 10,346.10 | 1558.90 |
| 35 | 157 | 14,895.40 | 1526.06 |
| 36 | 158 | 12,801.06 | 1520.32 |
| 37 | 167 | 6715.00 | 1495.08 |
| 38 | 159 | 8361.42 | 1508.94 |
| 39 | 164 | 6563.02 | 1531.60 |
| 40 | 157 | 8579.85 | 1565.45 |
| 41 | 164 | 5468.26 | 1542.35 |
| 42 | 165 | 5880.65 | 1514.01 |
| 43 | 164 | 6788.27 | 1500.18 |
| 44 | 164 | 6768.58 | 1525.46 |
References
- Gao, K.Z.; He, Z.M.; Huang, Y.; Duan, P.Y.; Suganthan, P.N. A survey on meta-heuristics for solving disassembly line balancing, planning and scheduling problems in remanufacturing. Swarm Evol. Comput. 2020, 57, 100719. [Google Scholar] [CrossRef]
- Cappelletti, F.; Rossi, M.; Germani, M. How De-manufacturing Supports Circular Economy Linking Design and EoL-a Literature Review. J. Manuf. Syst. 2022, 63, 118–133. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Gao, L.; Li, P.; Sutherland, J.W. A discrete artificial bee colony algorithm for multiobjective disassembly line balancing of end-of-life products. IEEE Trans. Cybern. 2021, 52, 7415–7426. [Google Scholar] [CrossRef] [PubMed]
- Güngör, A.; Gupta, S.M. Disassembly Line in Product Recovery. Int. J. Prod. Res. 2002, 40, 2569–2589. [Google Scholar] [CrossRef]
- Ding, L.P.; Feng, Y.X.; Tan, J.R.; Gao, Y.C. A New Multi-objective Ant Colony Algorithm for Solving the Disassembly Line Balancing Problem. Int. J. Adv. Manuf. Technol. 2010, 48, 761–771. [Google Scholar] [CrossRef]
- Jia, L.; Shuwei, W. A proposed multi-objective optimization model for sequence-dependent disassembly line balancing problem. In Proceedings of the 2017 3rd International Conference on Information Management (ICIM), Chengdu, China, 21–23 April 2017; pp. 421–425. [Google Scholar]
- Wang, S.; Guo, X.; Liu, J. An efficient hybrid artificial bee colony algorithm for disassembly line balancing problem with sequence-dependent part removal times. Eng. Optim. 2019, 51, 1920–1937. [Google Scholar] [CrossRef]
- Özceylan, E.; Kalayci, C.B.; Güngör, A.; Gupta, S.M. Disassembly line balancing problem: A review of the state of the art and future directions. Int. J. Prod. Res. 2019, 57, 4805–4827. [Google Scholar] [CrossRef]
- Yuan, G.; Liu, X.; Qiu, X.; Zheng, P.; Pham, D.T.; Su, M. Human-robot collaborative disassembly in Industry 5.0: A systematic literature review and future research agenda. J. Manuf. Syst. 2025, 79, 199–216. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Gupta, S.M. Ant colony optimization for sequence-dependent disassembly line balancing problem. J. Manuf. Technol. Manag. 2013, 24, 413–427. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Gao, L.; Garg, A. Partial disassembly line balancing for energy consumption and profit under uncertainty. Robot. Comput. Integr. Manuf. 2019, 59, 235–251. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Gupta, S.M. Artificial Bee Colony Algorithm for Solving Sequence-dependent Disassembly Line Balancing Problem. Expert Syst. Appl. 2013, 40, 7231–7241. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Mara, S.T.W.; Norcahyo, R.; Jodiawan, P.; Lusiantoro, L.; Rifai, A.P. A survey of adaptive large neighborhood search algorithms and applications. Comput. Oper. Res. 2022, 146, 105903. [Google Scholar] [CrossRef]
- Li, Z.; Janardhanan, M.N. Modelling and solving profit-oriented U-shaped partial disassembly line balancing problem. Expert Syst. Appl. 2021, 183, 115431. [Google Scholar] [CrossRef]
- Guo, X.; Wei, T.; Wang, J.; Liu, S.; Qin, S.; Qi, L. Multiobjective U-shaped disassembly line balancing problem considering human fatigue index and an efficient solution. IEEE Trans. Comput. Soc. Syst. 2022, 10, 2061–2073. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, Z.; Wu, T.; Liang, W. Integrated optimization and engineering application for disassembly line balancing problem with preventive maintenance. Eng. Appl. Artif. Intell. 2024, 127, 107416. [Google Scholar] [CrossRef]
- Liang, W.; Zhang, Z.; Yin, T.; Zhang, Y.; Wu, T. Modelling and optimisation of energy consumption and profit-oriented multi-parallel partial disassembly line balancing problem. Int. J. Prod. Econ. 2023, 262, 108928. [Google Scholar] [CrossRef]
- Chen, J.C.; Chen, Y.Y.; Chen, T.L.; Yang, Y.C. An adaptive genetic algorithm-based and AND/OR graph approach for the disassembly line balancing problem. Eng. Optim. 2022, 54, 1583–1599. [Google Scholar] [CrossRef]
- Zhang, M.; Li, L.; Liu, S.; Li, H.; Mu, X.; Yin, F. Selection of disassembly schemes for multiple types of waste mobile phones based on knowledge reuse and disassembly line balancing. J. Manuf. Syst. 2024, 76, 207–221. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Wu, P.; Tian, G.; Yu, D.; Zhang, T.; Yang, J.; Wong, K.Y. An efficient multi-objective adaptive large neighborhood search algorithm for solving a disassembly line balancing model considering idle rate, smoothness, labor cost, and energy consumption. Expert Syst. Appl. 2024, 250, 123908. [Google Scholar] [CrossRef]
- Liang, P.; Fu, Y.; Gao, K. Multi-product disassembly line balancing optimization method for high disassembly profit and low energy consumption with noise pollution constraints. Eng. Appl. Artif. Intell. 2024, 130, 107721. [Google Scholar] [CrossRef]
- Chu, M.; Chen, W. Multi-manned disassembly line balancing problems for retired power batteries based on hyper-heuristic reinforcement. Comput. Ind. Eng. 2024, 194, 110400. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Gao, L.; Li, P.; Gupta, S.M. A genetic simulated annealing algorithm for parallel partial disassembly line balancing problem. Appl. Soft Comput. 2021, 107, 107404. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, G.; Fathollahi-Fard, A.M.; Pham, D.T.; Li, Z.; Pu, Y.; Zhang, T. A chance-constraint programming approach for a disassembly line balancing problem under uncertainty. J. Manuf. Syst. 2024, 74, 346–366. [Google Scholar] [CrossRef]
- Tian, G.; Zhang, C.; Fathollahi-Fard, A.M.; Li, Z.; Zhang, C.; Jiang, Z. An enhanced social engineering optimizer for solving an energy-efficient disassembly line balancing problem based on bucket brigades and cloud theory. IEEE Trans. Ind. Inform. 2022, 19, 7148–7159. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Z.; Qi, L.; Liu, S.; Tang, Y.; Zhao, Z. Stochastic hybrid discrete grey wolf optimizer for multi-objective disassembly sequencing and line balancing planning in disassembling multiple products. IEEE Trans. Autom. Sci. Eng. 2021, 19, 1744–1756. [Google Scholar] [CrossRef]
- Liang, J.; Guo, S.; Zhang, Y.; Liu, W.; Zhou, S. Energy-efficient optimization of two-sided disassembly line balance considering parallel operation and uncertain using multiobjective flatworm algorithm. Sustainability 2021, 13, 3358. [Google Scholar] [CrossRef]
- He, J.; Chu, F.; Dolgui, A.; Zheng, F.; Liu, M. Integrated stochastic disassembly line balancing and planning problem with machine specificity. Int. J. Prod. Res. 2022, 60, 1688–1708. [Google Scholar] [CrossRef]
- Guo, J.; Pu, Z.; Du, B.; Li, Y. Multi-objective optimisation of stochastic hybrid production line balancing including assembly and disassembly tasks. Int. J. Prod. Res. 2022, 60, 2884–2900. [Google Scholar] [CrossRef]
- Liu, X.; Chu, F.; Zheng, F.; Chu, C.; Liu, M. Distributionally robust and risk-averse optimisation for the stochastic multi-product disassembly line balancing problem with workforce assignment. Int. J. Prod. Res. 2022, 60, 1973–1991. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, Z.; Li, Z.; Guo, X.; Qi, L.; Liu, X. Multi-objective discrete brainstorming optimizer to solve the stochastic multiple-product robotic disassembly line balancing problem subject to Disassembly Failures. Mathematics 2023, 11, 1557. [Google Scholar] [CrossRef]
- He, J.; Chu, F.; Zheng, F.; Liu, M. A green-oriented bi-objective disassembly line balancing problem with stochastic task processing times. Ann. Oper. Res. 2021, 296, 71–93. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Polat, O.; Gupta, S.M. A Variable Neighborhood Search Algorithm for Disassembly Lines. J. Manuf. Technol. Manag. 2015, 26, 182–194. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Polat, O.; Gupta, S.M. A hybrid genetic algorithm for sequence-dependent disassembly line balancing problem. Ann. Oper. Res. 2016, 242, 321–354. [Google Scholar] [CrossRef]
- Liu, J.; Wang, S. A hybrid artificial bee colony algorithm for solving sequentially dependent demolition line balancing problem. Control. Decis. 2018, 33, 698–704. [Google Scholar]
- Yin, T.; Zhang, Z.; Jiang, J. A Pareto-discrete hummingbird algorithm for partial sequence-dependent disassembly line balancing problem considering tool requirements. J. Manuf. Syst. 2021, 60, 406–428. [Google Scholar] [CrossRef]
- Xia, X.; Liu, W.; Zhang, Z.; Wang, L. Partial disassembly line balancing problem analysis based on sequence-dependent stochastic mixed-flow. J. Comput. Inf. Sci. Eng. 2020, 20, 061005. [Google Scholar] [CrossRef]
- Çil, Z.A.; Kizilay, D.; Li, Z.; Öztop, H. Two-sided disassembly line balancing problem with sequence-dependent setup time: A constraint programming model and artificial bee colony algorithm. Expert Syst. Appl. 2022, 203, 117529. [Google Scholar] [CrossRef]
- Li, Z.; Kucukkoc, I.; Zhang, Z. Iterated local search method and mathematical model for sequence-dependent U-shaped disassembly line balancing problem. Comput. Ind. Eng. 2019, 137, 106056. [Google Scholar] [CrossRef]
- Chen, Q.; Yao, B.; Pham, D.T. Sequence-dependent robotic disassembly line balancing problem considering disassembly path. In Proceedings of the International Manufacturing Science and Engineering Conference, Cincinnati, OH, USA, 22–26 June 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84263, p. V002T07A019. [Google Scholar]
- Charnes, A.; Cooper, W.W. Chance-constrained programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Liu, W.; Du, N.; Wong, K.Y. Sustainable ridesharing routing and scheduling problem: An efficient multi-objective adaptive large neighborhood search. Ann. Oper. Res. 2025, 1–41. [Google Scholar] [CrossRef]
- Ropke, S.; Pisinger, D. An Adaptive Large Neighborhood Search Heuristic for the Pickup and Delivery Problem with Time Windows. Transp. Sci. 2006, 40, 455–472. [Google Scholar] [CrossRef]
- Mitra, A. The taguchi method. In Wiley Interdisciplinary Reviews: Computational Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; Volume 3, pp. 472–480. [Google Scholar]
- Fathollahi-Fard, A.M.; Tian, G.; Ke, H.; Fu, Y.; Wong, K.Y. Efficient multi-objective metaheuristic algorithm for sustainable harvest planning problem. Comput. Oper. Res. 2023, 158, 106304. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Gao, L.; Li, P. Energy consumption and profit-oriented disassembly line balancing for waste electrical and electronic equipment. J. Clean. Prod. 2020, 265, 121829. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca, V.G. Performance Assessment of Multi-objective Optimizers: An Analysis and Review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Cortés, N.C. Solving multiobjective optimization problems using an artificial immune system. Genet. Program. Evolvable Mach. 2005, 6, 163–190. [Google Scholar] [CrossRef]
- Bader, J.; Zitzler, E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).