Abstract
To advance the optimization of engineering parameters in in-seam borehole predrainage technology, this study developed a comprehensive analytical framework integrating theoretical modeling, numerical simulation, and field validation. Taking Pingdingshan Tian’an Coal Mine No. 1 as a practical case study, we established a gas-bearing coal seam drainage model based on fluid–solid coupling theory. A multifactor optimization scheme was implemented using response surface methodology (RSM) complemented by an evaluation system focusing on the gas extraction efficiency coefficient (K). Numerical simulations through COMSOL Multiphysics 6.0 enabled detailed investigation of single-factor influences and multifactor coupling effects, ultimately identifying field-verified optimal parameters. Key discoveries include the following: (1) Spatiotemporal evolution patterns of gas drainage compliance zones showing stabilized interborehole pressure gradients and enhanced regional connectivity after 300-day extraction; (2) a parameter sensitivity hierarchy for K-value defined as drainage duration (primary) > borehole spacing > borehole diameter > extraction negative pressure; (3) an optimized configuration (4.5 m spacing, 113 mm diameter, 18 kPa pressure) achieving a 54.2% pressure reduction with a 0.98 efficiency coefficient. Field data demonstrated only 2.1% average deviation from model predictions, validating the methodology’s effectiveness for gas control parameter optimization in coal mining operations.
1. Introduction
Coal, serving as China’s primary energy source and ultimate safeguard for energy security, has consistently functioned as the “ballast” and “stabilizer” of national energy infrastructure [1,2,3]. However, most Chinese mining areas exhibit elevated gas pressures and substantial gas content within coal seams, which are characteristics particularly pronounced under deep mining conditions [4,5,6,7]. This geological reality imposes tremendous pressure on frontline gas disaster prevention efforts, severely constraining safe and efficient mine production [8,9,10]. Confronted with these compounded gas challenges, coal seam gas predrainage technology emerges as a fundamental measure to reduce seam gas pressure, decrease gas content, prevent gas-related accidents, and ensure safe and efficient coal mining operations [11,12,13].
As the key factor for evaluating drainage effectiveness, gas extraction efficiency is constrained not only by geological parameters (e.g., seam burial depth, initial gas pressure, in situ permeability) but also critically influenced by engineering parameters (e.g., drainage duration, hole spacing, borehole diameter, and extraction negative pressure). Regarding the influence of engineering parameters on gas extraction effectiveness, extensive research has been conducted by scholars.
Raymond [14] employed subterranean barrier systems integrated with predrainage techniques to mitigate methane emissions, demonstrating through implementation that these engineered partitions effectively delineated drained and undrained zones within the mine workings. Lu et al. [15] developed a predictive model capable of quantitatively evaluating the spatial uniformity of sector-oriented directional borehole distributions. Li et al. [16] identified coal permeability as a critical determinant in coal seam gas predrainage processes. Through physical simulations, they demonstrated that permeability ratio decline rates exhibit a positive correlation with proximity to extraction boreholes. Liu et al. [17] established that gas pressure and coal permeability significantly influence drainage efficiency, with borehole gas emission rates showing direct proportionality to initial gas pressure and fracture permeability coefficients. Xing et al. [18] highlighted three primary optimization parameters for borehole spacing: coal permeability, drainage duration, and negative pressure gradients. Yan et al. [19] developed a Transformer model-based predictive framework to determine optimal drainage durations, emphasizing temporal precision in methane pre-extraction operations. Dong et al. [20] revealed that the dynamic adjustment of extraction negative pressure—specifically, phased reductions during later extraction stages—is essential for maintaining methane recovery efficacy. Shang et al. [21] quantified parameter influence hierarchies on drainage radii, ranking them as follows: initial coal seam permeability > drainage duration > borehole diameter > operational negative pressure.
Effective coal seam gas predrainage typically necessitates the deployment of multiple boreholes to establish robust drainage networks. During concurrent borehole operation, significant interborehole interference phenomena emerge, critically influencing methane production rates and the effective control radius of individual extraction points [22]. While existing research systematically examines singular operational parameters—including drainage duration, borehole spacing, aperture dimensions, and negative pressure intensity—it predominantly neglects to address the multidimensional interactions between these variables and their synergistic effects on overall drainage efficiency.
The Pingdingshan coalfield represents a quintessential example of China’s geologically challenging “three-highs and one-low” coal-bearing formations, which are characterized by elevated in situ stress concentrations, substantial gas reservoir capacities, heightened outburst risks, and restricted permeability characteristics. The No. 1 Mine of Pingdingshan Tianan Coal Mining Co., Ltd. (Pingdingshan, China) serves as a pivotal production facility within the Pingdingshan coalfield, with a certified annual production capacity of 4 million tons. At the No. 1 Mine, where the mining horizon now exceeds 900 m in depth, the multilayered coal system comprises four superimposed workable seams (the Ding, Wu, Ji, and Geng groups), with current operations focused on the structurally stable Ding and Wu formations. This geomechanical environment necessitates advanced predrainage optimization to mitigate gas-driven hazards during deep mining.
This study develops a coupled hydromechanical simulation framework grounded in the geological conditions of Pingdingshan Tianan Coal Mine No. 1, coupling gas transport dynamics with coal matrix deformation mechanisms while employing response surface methodology for multivariate parameterization. Leveraging COMSOL Multiphysics simulations cross-validated against field monitoring data, we implement a dual analytical approach to rigorously characterize (i) single-factor sensitivity indices and (ii) multivariable nonlinear interdependencies. The derived analytical framework facilitates strategic borehole placement optimization that achieves enhanced methane extraction efficiency through pressure-controlled extraction protocols, establishing an engineering design framework for high-yield drainage operations in structurally complex deep coal seams.
2. Fluid–Solid Coupling Extraction Model of Gas-Bearing Coal Body
2.1. Model Assumptions
Based on engineering characteristics of coal seam gas drainage and research objectives, numerical simulation was conducted under the premise of ensuring physical mechanism completeness. Building upon previous studies [23,24,25], the following assumptions were adopted:
(1) Dual-porosity structure: Gas-bearing coal is conceptualized as a fracture–matrix dual-porosity system, where fracture networks dominate seepage processes, while the matrix phase comprises coal skeleton and internal micropores;
(2) Homogeneous isotropy: Geological heterogeneity is neglected, assuming spatially uniform distribution of coal mass with identical mechanical properties in all directions;
(3) Dry medium condition: Moisture effects on adsorption–seepage processes are excluded, postulating absolutely dry states in pore spaces;
(4) Ideal gas behavior: Coalbed methane is simplified as an ideal gas obeying the ideal gas law;
(5) Isothermal constraint: Thermal effects from gas adsorption/desorption are disregarded, establishing a temperature-decoupled isothermal seepage model.
2.2. Stress Field Control Equation
The strain of the coal body is mainly caused by gas adsorption expansion deformation, gas pressure, and external stress. The stress–strain relationship can be expressed as [26]
where G is the shear modulus, ui and uk are the components of displacement in direction i and k respectively, ν is Poisson’s ratio of coal, α and β are Biot coefficients, pf and pm are gas pressures in the fracture and matrix, respectively, K is the bulk modulus of coal, is the change in matrix adsorption strain, and Fi is the body force in direction.
During the formation of predrainage boreholes, the coal body undergoes plastic failure. Therefore, in numerical simulations, the Drucker-Prager (D-P) criterion is often used to characterize the damage and failure of the coal body [27,28].
where J2 is the second principal invariant of the stress deviator tensor, I1 is the hydrostatic stress tensor, C is the cohesion, and φ is the internal friction angle.
2.3. Permeability Evolution Equation
The permeability of the coal seam is one of the key parameters affecting the gas migration law. During the extraction process, the original stress state of the coal body is disrupted, leading to deformation and damage of the coal body, which changes the permeability of the coal body. Considering the Klinkenberg effect, the permeability evolution model is introduced, and the corresponding permeability evolution model is obtained as follows [29]:
where Ke is the effective permeability, is the permeability of the coal body after stress disturbance, bk is the Klinkenberg factor, ϕf0 is the initial fracture porosity, p0 is the initial gas pressure in the coal seam, and ɛL and PL are the bulk Langmuir strain and pressure constants.
2.4. Matrix Gas Diffusion Control Equation
Due to the disturbance caused by borehole drilling, the coal body near the borehole undergoes plastic failure, changing the gas migration path in the coal body. The extraction negative pressure disrupts the gas pressure balance in the coal body, causing the matrix gas to continuously desorb and diffuse into the fracture system. Considering the migration process, the matrix gas diffusion control equation is obtained as follows [30,31]:
where VM is the molar volume of methane at standard conditions, PL is the Langmuir pressure constant, τ is the adsorption time, VL is the Langmuir volume constant, R is the ideal gas constant, T is the coal seam temperature, ρc is the apparent density of the coal body, and ϕm is the porosity of the coal matrix.
2.5. Fracture Gas Seepage Control Equation
The fracture system in the coal body is the storage and migration channel for free gas. Changes in external stress conditions cause gas migration in the coal body. According to the law of mass conservation, the change in gas content in the fracture system per unit coal body is equal to the difference between the mass exchange between the matrix and fractures and the gas flowing into the borehole from the fractures. The fracture gas seepage control equation is defined as follows [32,33]:
where ϕf is the porosity of coal fractures in %; M is the axial constraint modulus; βf is the effective stress coefficient of fractures; βm is the effective stress coefficient of pores; and μ is the dynamic viscosity coefficient of gas.
3. Simulation Scheme and Simulation Results
3.1. Simulation Scheme
3.1.1. Geometric Model and Boundary Conditions
The No. 1 Mine of Pingdingshan Tian’an Coal Mining Co., Ltd., located in the central Pingdingshan Coalfield mainly mines Ding and Wu coal seams. This simulation focuses on the Wu8-31200 working face with a coal seam thickness in the range of 1.6~2.2 m (average 1.9 m), dip angle of 15~18° (average 17°), initial gas pressure of 1.2 MPa, gas content of 6.6 m3/t, firmness coefficient of 0.2~0.5, and permeability coefficient of 0.0053 m2/(MPa2·d).
To investigate gas pressure distribution patterns under adjacent borehole drainage, a simplified 2D geometric model (20.0 m × 10.0 m) was constructed using coal as the primary material (Figure 1). The working face at 920 m depth experiences vertical in situ stress of 22.54 MPa calculated from overburden density (24.5 kN/m3). Key parameters were derived from field measurements and laboratory tests (Table 1).
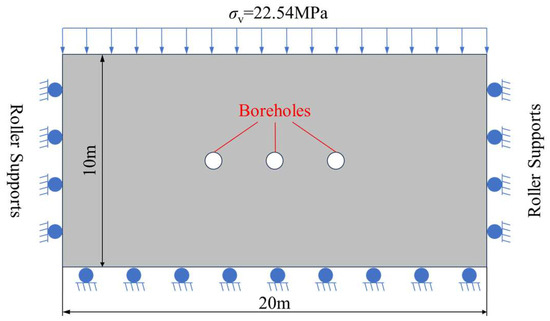
Figure 1.
Illustration of the loading and boundary conditions of the proposed model.

Table 1.
Constant parameters used in the simulation model.
The model employs unstructured free triangular meshes with geometric feature-adaptive refinement, achieving an average mesh quality coefficient > 0.93. Critical zones undergo three-stage mesh independence verification for optimal element sizing. The top edge of the model is subjected to a constant overburden stress. The left, right, and bottom edges are constrained with roller boundary conditions to prevent horizontal displacement [34]. No-flux boundary conditions are imposed on the outer contours of the model. A constant-pressure boundary is applied to the borehole walls to simulate gas extraction operations, mimicking active degasification.
3.1.2. RSM Simulation Scheme
RSM has been widely applied in engineering parameter optimization design due to its advantages of high predictive accuracy, low experimental cost, and capability to resolve multifactor interaction effects [35,36,37,38]. Previous studies have demonstrated that drainage duration, borehole spacing, borehole diameter, and extraction negative pressure exert significant influences on coalbed methane drainage efficiency [39,40,41]. Accordingly, this study employs a four-factor three-level Box–Behnken design (BBD) with coded levels (−1, 0, +1) (Table 2), generating 29 optimization schemes (Table 3).

Table 2.
Range of variation in RSM factor.

Table 3.
Response surface test program and results.
3.1.3. Response Target
In the response surface analysis process, this study innovatively introduces the dimensionless coalbed methane drainage efficiency coefficient K as the core response target. The efficiency coefficient is defined as the ratio between the maximum gas pressure among boreholes and the critical threshold gas pressure, which is mathematically expressed as follows:
where Pm is the maximum gas pressure within the coal mass between boreholes post-drainage, and Pc is critical threshold gas pressure, which is empirically determined as 49% of the original gas pressure (corresponding to 51% pressure reduction [42]).
The efficiency coefficient K comprehensively integrates synergistic effects of key parameters (drainage duration, borehole spacing, extraction negative pressure, borehole diameter) while quantitatively characterizing negative pressure superposition effects during multiborehole collaborative extraction. This coefficient enables precise quantitative evaluation of drainage effectiveness (Figure 2), with the engineering criteria defined as follows:
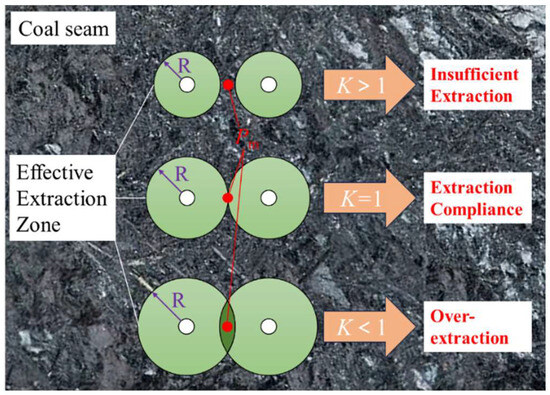
Figure 2.
The schematic diagram of borehole extraction effect.
(1) K < 1: Prematurely meets standards, indicating oversaturated borehole deployment or excessive drainage duration causing redundant boreholes and cost inefficiencies.
(2) K = 1: Optimally meets standards, reflecting the optimal parameter combination.
(3) K > 1: Undrained zones persist, requiring extended drainage periods or adjusted borehole layouts.
3.2. Simulation Results
Taking the engineering parameters corresponding to the code value −1 (borehole spacing of 5 m, borehole diameter of 94 mm, and extraction negative pressure of 13 kPa) as the baseline condition, this study investigates the influence patterns of different pre-extraction durations (200 d, 300 d, and 400 d) on coal seam gas pre-extraction effectiveness through numerical simulations. Figure 3 illustrates the spatial evolution characteristics of gas extraction compliance zones under varying pre-extraction periods.
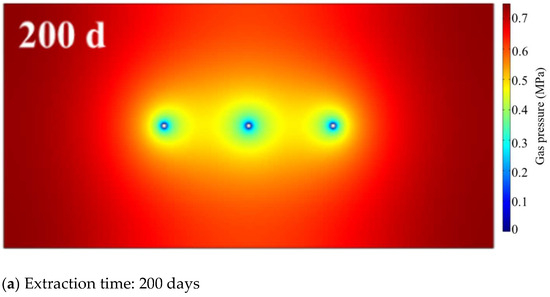
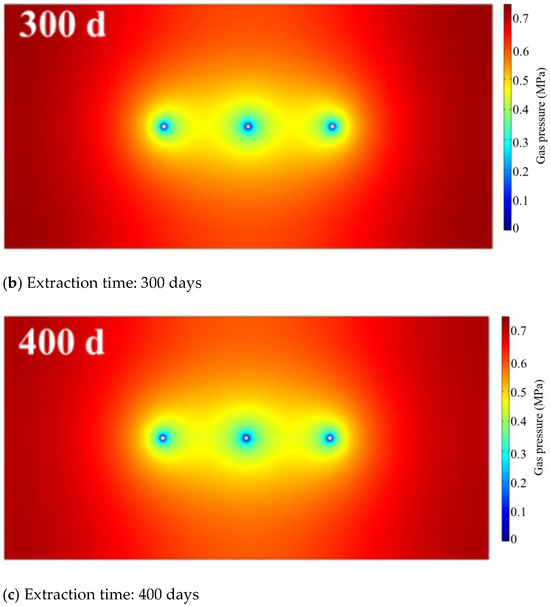
Figure 3.
Gas predrainage effect of in-seam boreholes.
The simulation results indicate that when the pre-extraction duration reaches 200 d, the compliance zones formed by individual boreholes exhibit independent circular distribution patterns, with no effective gas field superposition effects observed between adjacent boreholes (Figure 3a). As the extraction duration extends to 300 d, the diameter of compliance zones around each borehole significantly increases to 4.5~4.8 m, demonstrating initial regional connectivity (Figure 3b). Upon achieving a 400-daypre-extraction period, adjacent compliance zones completely interconnect to form continuous strips, establishing superposition effects between neighboring boreholes (Figure 3c). This spatiotemporal evolution reveals that the expansion of gas extraction compliance zones follows a three-phase development pattern under fixed engineering parameters: “independent development–peripheral contact–complete connectivity”. The temporal–spatial continuity of coal seam gas desorption–seepage processes enhances significantly with prolonged extraction durations, particularly when exceeding 300 d, where superposition effects become dominant in governing the expansion patterns of extraction zones.
3.3. Analysis of Influencing Factors of Coal Seam Gas Pre-Drainage
3.3.1. Influence of Single Factors on Extraction Effect
This study focuses on the critical regulatory role of engineering parameters in coal seam gas pre-extraction effectiveness, employing single-factor sensitivity analysis to systematically reveal the influence mechanisms of various parameters on gas extraction efficiency coefficient K. Through a controlled variable approach, four single-factor level gradients were established for extraction duration, borehole spacing, borehole diameter, and extraction negative pressure, respectively, enabling systematic analysis of the dynamic response characteristics of K-value variations with engineering parameters. The research findings are visually presented through characteristic response curves (Figure 4), which clearly demonstrate the dynamic relationships between engineering parameters and extraction efficiency coefficient K while highlighting significant disparities in parameter-specific impacts on the K value.
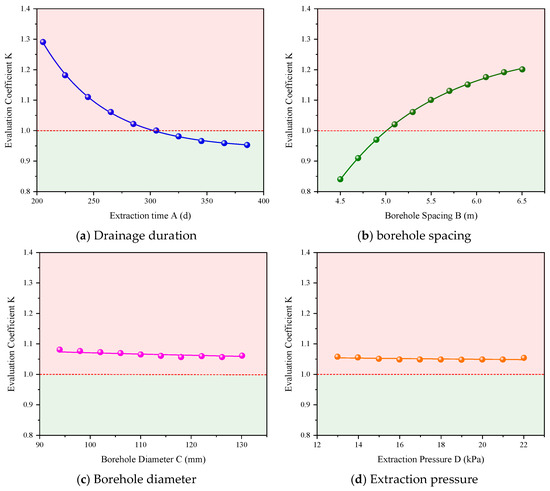
Figure 4.
Influence of single factor on K.
As shown in Figure 4a, under fixed conditions of 5 m borehole spacing, 94 mm borehole diameter, and 13 kPa extraction negative pressure, K exhibits a significant exponential decay pattern with prolonged drainage duration. Specifically, during the extraction period from 205 to 385 days, K decreases from 1.29 to 0.95. The decline rate reaches 17.83% between 205–265 days but reduces to 3.06% during 325–385 days. This nonlinear behavior stems from dual dynamic mechanisms governing gas migration. In the initial extraction phase (<265 days), stress–seepage coupling effects within the borehole disturbance plastic zone significantly enhance coal permeability, promoting rapid desorption of adsorbed gas [43]. During the later phase (>325 days), the depletion of free-state gas reserves leads to attenuated gas pressure gradients, while permeability degradation caused by coal deformation becomes dominant, resulting in substantial efficiency reduction.
Figure 4b reveals a unique nonlinear positive correlation between borehole spacing and K under the baseline conditions of 300-day extraction, 94 mm diameter, and 13 kPa negative pressure. The K values measure 0.84, 1.02, 1.13, and 1.19 at spacings of 4.5 m, 5.1 m, 5.7 m, and 6.3 m, respectively. Over-dense spacing (4.5 m) induces premature extraction compliance through overlapping effective zones, while excessive spacing (≥5.1 m) creates extraction blind areas due to insufficient pressure gradients. This dual control mechanism arises from spacing-dependent superposition effects: Closer spacing (≤4.5 m) enhances interborehole seepage momentum through extraction negative pressure superposition, causing efficiency-reducing zone overlaps [44]. Conversely, larger spacing (≥5.1 m) significantly reduces interborehole pressure gradients, maintaining high residual gas pressures that elevate the K values above 1.
As shown in Figure 4c, under the baseline conditions of 5 m borehole spacing, 300-day extraction duration, and 13 kPa extraction negative pressure, K demonstrates a decreasing trend with increasing borehole diameter, though the variation magnitude remains minor. When the borehole diameter increases from 94 mm to 130 mm, K shows only a 1.7% decrease. The analysis indicates that larger borehole diameters theoretically should enhance gas extraction effectiveness by expanding coal seam exposure areas and intensifying disturbance effects on coal mass. However, constrained by actual geological conditions of coal seams, excessively large borehole diameters may induce borehole collapse while compromising sealing quality [45]. Therefore, to improve gas extraction efficiency, the borehole diameter should be rationally optimized to prevent construction complications caused by oversized apertures.
As shown in Figure 4d, under baseline conditions of 5 m borehole spacing, 300-day extraction duration, and 94 mm borehole diameter, K displays a slight decreasing trend with increasing extraction negative pressure, though the variation magnitude remains minimal. When the extraction negative pressure rises from 13 kPa to 22 kPa, K decreases by only 0.4%. This indicates that gas extraction effectiveness remains essentially consistent across different negative pressure conditions. However, excessively high extraction negative pressures may increase air leakage through sealing sections due to compromised sealing quality [46,47], thereby reducing extraction efficiency and potentially elevating spontaneous combustion risks in coal seams [48]. Therefore, optimization of the extraction negative pressure should holistically consider both sealing integrity and on-site operational conditions to prevent adverse impacts on extraction performance or safety hazards caused by excessive negative pressures.
3.3.2. Influence of Interaction Effects on Gas Predrainage Efficiency
The evolution pattern of K does not result from independent action of single factors but rather manifests as a comprehensive outcome of multifactor coupling effects. This study constructed a three-dimensional K response surface (Figure 5) using Design-Expert 11 software, which visually characterizes the pairwise interaction effects among four parameters—extraction duration, borehole spacing, borehole diameter, and extraction negative pressure—on K variations.
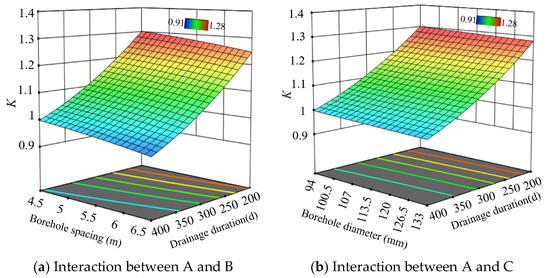
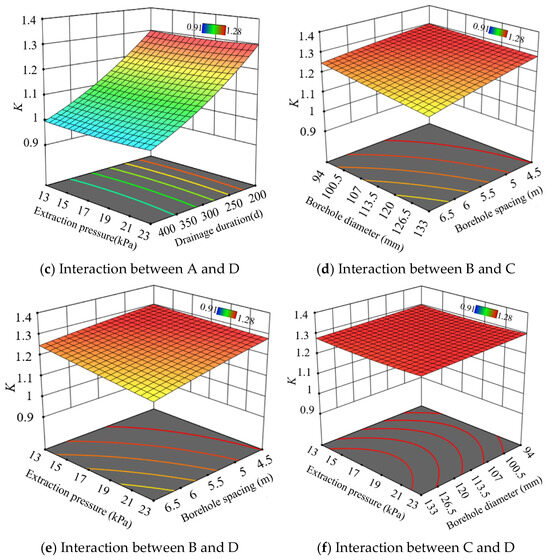
Figure 5.
Influence of various factors’ interaction on K.
The steepness of three-dimensional response surfaces visually reflects the significance of parameter interactions. As illustrated in Figure 5, the pronounced curvature of surfaces Figure 5a–c indicates strong interactive effects between extraction duration and borehole spacing, borehole diameter, and extraction negative pressure, respectively. Conversely, the gentle curvature of the surfaces shown in Figure 5d–f demonstrates weaker interactions among three parameter pairs: borehole spacing–borehole diameter, borehole spacing–extraction negative pressure, and extraction negative pressure–borehole diameter.
Specifically, Figure 5a–c reveal that as the extraction duration increases, the influences of borehole spacing, borehole diameter, and extraction negative pressure on extraction efficiency all exhibit significant enhancement trends. This demonstrates the critical role of optimizing these three parameters in long-term extraction projects: rational borehole spacing configuration improves gas flow efficiency (Figure 5a), increased borehole diameter effectively expands gas migration pathways (Figure 5b), and optimized negative pressure strengthens extraction driving forces (Figure 5c). However, these parameters show relatively lower impact significance in short-term operations. In contrast, the flat surfaces in Figure 5d–f indicate parameter decoupling phenomena between borehole spacing and diameter, borehole spacing and negative pressure, and negative pressure and borehole diameter. This observation suggests that these parameter pairs can be independently optimized in engineering practice, thereby simplifying operational complexity during parameter adjustment.
3.3.3. Regression Model and Parameter Optimization
The experimental results were subjected to multiple regression fitting to obtain a response model with the K value as the response target. The coefficient of determination (R2) reflects the degree of difference between the predicted values, response values, and actual values. The higher the R2, the better the model’s correlation. The error analysis of the response model is shown in Table 4. From Table 4, it can be seen that the coefficient of determination (R2) of the response model is 0.9956, the predicted R2 is 0.9749, and the adjusted R2 is 0.9913. All correlation coefficients are greater than 0.97, and the differences between them are less than 0.2, indicating a high degree of model correlation. The coefficient of variation (C.V) is less than 10%, and the accuracy (A.P) is greater than 4, indicating that the experimental results are highly precise and reliable, and the response model is reasonable.

Table 4.
Error analysis of response model.
The response surface model developed in this study was statistically validated through analysis of variance (Table 5). The results indicate that the quadratic regression model targeting the K value as the response achieves an F value of 228.55 (p = 0.0001), passing significance testing at α = 0.001 confidence level. Statistical inference reveals only 0.01% probability of the model arising from random errors, confirming rigorous nonlinear mapping relationships between input parameters and response targets. Variance contribution analysis demonstrates the following significance hierarchy of four engineering parameters on K: A (extraction duration) > B (borehole spacing) > C (borehole diameter) > D (extraction negative pressure). Notably, Factor A exhibits overwhelming dominance with an F value of 2880.35 (p < 0.001). This statistically proves that the precise regulation of extraction duration serves as the core control variable for optimizing drainage efficiency under dual constraints of eliminating extraction blind zones and suppressing over-extraction.

Table 5.
Response model analysis of variance.
To systematically validate the prediction accuracy of the response model, this study conducted a quantitative analysis by constructing a scatter plot comparing experimental versus predicted K values (Figure 6), with experimental values on the horizontal axis and predicted values on the vertical axis. The spatial distribution characteristics of the data points demonstrate that the experimental and predicted values not only exhibit an ideal linear correlation pattern but also reveal high-fidelity characteristics specific to nonlinear regression models. This pronounced linear correlation not only fully verifies the model’s reliability but also statistically confirms its engineering applicability. Building on the model’s exceptional performance, its application value can be further extended: On one hand, the model effectively supports the quantitative analysis of single-factor interaction effects; on the other hand, it provides a scientific basis for multiparameter design (e.g., borehole spacing, extraction negative pressure, and sealing depth) in in-seam gas drainage engineering, enabling precise optimization of extraction parameters. This achievement delivers critical technical support for advancing gas extraction engineering from empirical design to data-driven scientific design.
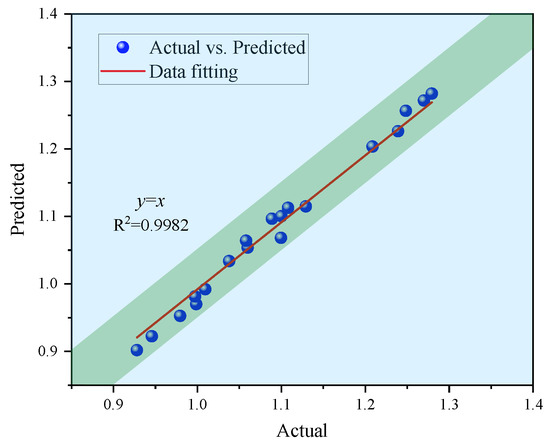
Figure 6.
Actual vs. predicted value comparison for response targets.
4. Engineering Practice
4.1. Construction Parameters
This study established a three-dimensional validation system (Table 4 showing error analysis, Table 5 showing ANOVA, and Figure 6 showing predicted vs. actual value correlation) to achieve closed-loop verification of the theoretical model across three dimensions: mathematical model errors, statistical significance, and engineering consistency. Leveraging this high-confidence response model, typical engineering parameter combinations were selected through experimental design methodology for field validation: 400-day extraction cycle, 4.5 m borehole spacing, 113 mm borehole diameter, and 18 kPa extraction negative pressure.
The test site selection strictly adhered to geological intrinsic condition optimization principles and engineering disturbance minimization criteria: A 10-m section (650–660 m) in the return airway of Panel 31,200 was chosen, representing typical coal seam gas occurrence characteristics while remaining unaffected by mining-induced stress disturbances. The pressure measurement boreholes and extraction boreholes were drilled along the coal seam strike with a dip angle of −16° (negative dip angle denotes downward orientation toward the seam floor), commencing at an elevation of 1.2 m above the roadway floor. Real-time measurement-while-drilling (MWD) systems ensured spatial coupling accuracy with the target seam within 0.5° deviation. The grouting process utilizes a dual-packer injection system to ensure precise sealing integrity and pressure containment during coal seam gas extraction. The gas pressure testing strictly adhered to the Chinese National Standard The direct measuring method of the coal seam gas pressure in mine (KA/T 1047-2007). Pressure measurement boreholes (50 m depth with 35 m sealing length) and extraction boreholes (50 m depth with 15 m sealing length) were deployed according to the layout parameters illustrated in Figure 7.
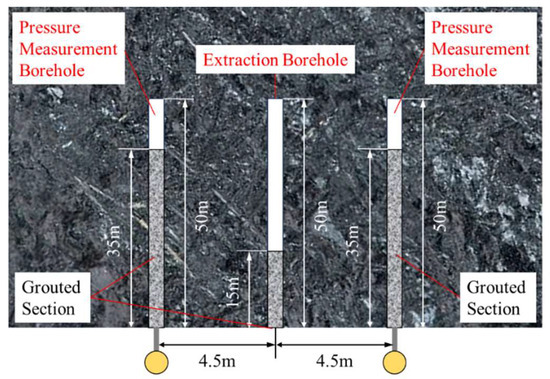
Figure 7.
Borehole layout parameter diagram.
4.2. Field Application
Following the design specifications, boreholes were constructed with continuous pressure monitoring. After pressure stabilization in measurement boreholes, extraction boreholes were connected to the drainage system. Figure 8 illustrates the average gas pressure variations in the monitoring boreholes during extraction via the central drainage pipeline.
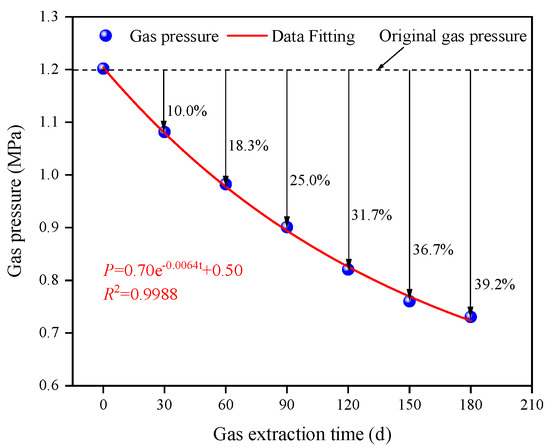
Figure 8.
Gas pressure drop curve of extraction borehole.
The data reveal a continuous decline in coal seam gas pressure with diminishing reduction rates as extraction progressed. At 30-day intervals, pressure reductions reached 10%, 18.3%, 25%, 31.7%, 36.7%, and 39.2% after 30, 60, 90, 120, 150, and 180 days of extraction, respectively, with sequential decrements of 8.3%, 6.7%, 6.1%, 5%, and 2.5%. The pressure evolution followed a characteristic exponential decay pattern mathematically expressed as P(t) = 0.70·e−0.0064t + 0.50. Model extrapolation indicates that the coal seam pressure would decrease to 0.59 MPa (51.0% reduction from initial values) at 323 days, meeting technical compliance thresholds. Extending extraction to 400 days would further reduce the pressure to 0.55 MPa (54.2% reduction), though prolonged operation would induce 0.04 MPa over-extraction beyond design limits.
Response surface methodology optimization demonstrates that under coordinated parameters (400-day duration, 4.5 m spacing, 113 mm diameter, 18 kPa pressure), the gas extraction efficiency coefficient reaches 0.98 within the high-performance range, albeit with mild over-extraction characteristics. The experimental data exhibit a 2.1% deviation rate from model predictions, validating both the accuracy and reliability of the mathematical model. This confirms its practical engineering value for scientifically optimizing coal mine gas control parameters.
5. Conclusions
This study developed a gas extraction numerical model for coal seams based on fluid–solid coupling theory, designed multiparameter optimization schemes using RSM, and established a comprehensive evaluation system centered on the efficiency coefficient K value. The principal findings are as follows:
(1) The development of gas extraction compliance zones exhibits a tri-phase evolution pattern: “isolated nucleation–peripheral contact–full connectivity”. Prolonged predrainage duration exponentially enhances the spatiotemporal continuity of gas desorption–seepage processes. Beyond the 300-day critical threshold, superposition effects dominate the spatial expansion mechanisms of extraction zones.
(2) A hybrid approach combining numerical simulation and response surface methodology was employed to systematically evaluate the influence weights of extraction parameters on the extraction efficiency coefficient K. Sensitivity analysis revealed significant disparities in the parameter impacts: extraction duration > borehole spacing > borehole diameter > extraction negative pressure. Two-factor interaction analysis further identified the extraction duration–borehole spacing combination as having the highest interaction contribution rate to the K value, while the borehole diameter–negative pressure combination showed the lowest.
(3) Field validation demonstrated that the implementation of optimized parameters (4.5 m borehole spacing, 113 mm diameter, 18 kPa negative pressure) resulted in a 54.2% decrease in working face gas pressure and yielded an extraction efficiency coefficient K of 0.98, with 97.9% congruence between measured data and numerical simulations. These outcomes not only confirm the predictive accuracy of the multifield coupling model but also demonstrate its practical applicability, establishing a scientific foundation for designing gas predrainage systems in geologically comparable mining operations.
Author Contributions
Conceptualization, Y.L., Q.L. and C.Z.; methodology, Q.L. and C.Z.; software, Y.W.; validation, Y.L., Q.L. and C.Z.; formal analysis, Y.L. and Q.L.; investigation, Y.L. and Y.W.; resources, Y.L.; data curation, Y.W.; writing—original draft preparation, Y.L.; writing—review and editing, Q.L. and C.Z.; visualization, Y.W.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Q.L. and C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (52174211), Longyan City Wuping County Qimai Science and Technology Innovation Fund Project (2022LYQM007), and Scientific Research Foundation of Longyan University (LB2022004).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
Author Yanhui Li was employed by the company Pingdingshan Tianan Coal Mining Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yue, J.; Xu, J.; Zhang, J.; Shi, B.; Zhang, M.; Li, Y.; Wang, C. Gas Displacement Characteristics During the Water Wetting Process of Gas-Bearing Coal and Microscopic Influence Mechanism. Sci. Total Environ. 2024, 949, 175034. [Google Scholar] [CrossRef]
- Shen, S.; Wang, H.; Ren, T.; Wang, Z. Research on the Pore Structure and Gas Adsorption/Desorption Characteristics of Tectonic Coal in Minor Fault Zone: Implications for Coal and Gas Outbursts. Powder Technol. 2025, 456, 120846. [Google Scholar] [CrossRef]
- Guo, J.; Chen, C.; Liu, Y.; Wen, H.; Quan, Y. Response Characteristics of Molecular Active Structure of Coal of Different Metamorphic Degree to Extractant. Energy 2025, 320, 135372. [Google Scholar] [CrossRef]
- Anani, A.; Adewuyi, S.O.; Risso, N.; Nyaaba, W. Advancements in Machine Learning Techniques for Coal and Gas Outburst Prediction in Underground Mines. Int. J. Coal Geol. 2024, 285, 104471. [Google Scholar] [CrossRef]
- Wang, C.; Liu, L.; Li, X.; Xu, C.; Li, K. Mechanism of Gas Pressure Action During the Initial Failure of Coal Containing Gas and its Application for an Outburst Inoculation. Int. J. Min. Sci. Technol. 2023, 33, 1511–1525. [Google Scholar] [CrossRef]
- Yang, G.; Song, D.; Wang, M.; Qiu, L.; He, X.; Khan, M.; Qian, S. New Insights Into Dynamic Disaster Monitoring through Asynchronous Deformation Induced Coal-Gas Outburst Mechanism of Tectonic and Raw Coal Seams. Energy 2024, 295, 131063. [Google Scholar] [CrossRef]
- Li, M.; Lu, S.; Wei, C.; Li, Z.; Ye, Q.; Zhang, Y. Study on Energy Instability Mechanism of Composite Coal Seam Based on the Coupling Effect of Damage and Unsteady Diffusion. Fuel 2025, 379, 133051. [Google Scholar] [CrossRef]
- Song, D.; Liu, Q.; Qiu, L.; Zhang, J.; Majid, K.; Peng, Y.; Zhao, Y.; Wang, M.; Guo, M.; Guo, T. Experimental Study on Resistivity Evolution Law and Precursory Signals in the Damage Process of Gas-Bearing Coal. Fuel 2024, 362, 130798. [Google Scholar]
- Lei, W.; Chai, J.; Zhang, Y.; Ding, G.; Yao, R.; Chen, Y.; Wang, Z.; Ma, C. Study on Pressure Relief Effect of Upper Protective Coal Seam Mining Based on Distributed Optical Fiber Sensing Monitoring. Opt. Fiber Technol. 2022, 68, 102830. [Google Scholar] [CrossRef]
- Jin, Y.; Tong, X.; Zheng, X.; Li, Y.; Dong, B. Risk Assessment of Coal and Gas Outbursts Driven by the Theory of Three Types of Hazards Coupled with 80 Accident Cases. Safety Sci. 2025, 184, 106771. [Google Scholar] [CrossRef]
- Lou, Z.; Wang, K.; Yao, H.; Zhao, W.; Qin, H.; Wu, Z.; Wei, G. A Novel Dynamic Filling Material for Plugging Fractures Around Underground Gas Extraction Boreholes: Experimental and Engineering Performances. Energy 2025, 314, 134202. [Google Scholar] [CrossRef]
- Zha, W.; Lin, B.; Liu, T.; Liu, T.; Yang, W.; Wang, W. Microscopic Mechanism of Gas-Water Two-Phase Flow Based on Low-Field Nuclear Magnetic Resonance. Gas Sci. Eng. 2025, 134, 205538. [Google Scholar] [CrossRef]
- Yuan, M.; Sun, S.; Liu, Y.; Yang, T.; Li, C.; Niu, Y.; Wen, X. Modeling and Control Method of Coal Instability Around Cavity Under Water Jet Impact Loading. Tunn. Undergr. Sp. Tech. 2025, 161, 106574. [Google Scholar] [CrossRef]
- Johnson, R.L. The Implementation of Subterranean Barriers with Mine Pre-Drainage to Reduce Coal Mine Methane Emissions from Open-Cut and Underground Metallurgical-Coal Mines. Int. J. Coal Geol. 2024, 283, 104402. [Google Scholar] [CrossRef]
- Lu, C.; Wang, H.; Tuo, P.; Zhang, X.; Hu, Q. An Evaluation Model of Distribution Uniformity of Sector Directional Boreholes: Application in Coalbed Gas Extraction. Measurement 2025, 253, 117626. [Google Scholar] [CrossRef]
- Li, Q.; Xu, J.; Yan, F.; Peng, S.; Zhang, C.; Zhang, X. Evolution Characteristics of Reservoir Parameters During Coalbed Methane Drainage Via in-Seam Horizontal Boreholes. Powder Technol. 2020, 362, 591–603. [Google Scholar] [CrossRef]
- Liu, W.; Han, D.; Xu, H.; Chu, X.; Qin, Y. Modeling of Gas Migration in a Dual-Porosity Coal Seam Around a Borehole: The Effects of Three Types of Driving Forces in Coal Matrix. Energy 2023, 264, 126181. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, F. Optimizing Borehole Spacing for Coal Seam Gas Pre-Drainage. J. Geophys. Eng. 2019, 16, 399–410. [Google Scholar] [CrossRef]
- Yan, L.; Wen, H.; Wang, Z.; Jin, Y.; Guo, J.; Liu, Y.; Fan, S. Prediction and Evaluation of Key Parameters in Coalbed Methane Pre-Extraction Based on Transformer and Inversion Model. Eng. Appl. Artif. Intel. 2025, 139, 109661. [Google Scholar] [CrossRef]
- Dong, J.; Cheng, Y.; Jin, K.; Zhang, H.; Liu, Q.; Jiang, J.; Hu, B. Effects of Diffusion and Suction Negative Pressure on Coalbed Methane Extraction and a New Measure to Increase the Methane Utilization Rate. Fuel 2017, 197, 70–81. [Google Scholar] [CrossRef]
- Shang, Y.; Wu, G.; Kong, D.; Wang, Y.; Li, F. Research on Influencing Factors of Effective Gas Extraction Radius in Coal Mine Based on Multiple Linear Regression. Adv. Mater. Sci. Eng. 2022, 2022, 3013647. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, J.; Peng, S.; Li, Q.; Yan, F. Experimental Study of Drainage Radius Considering Borehole Interaction Based on 3D Monitoring of Gas Pressure in Coal. Fuel 2019, 239, 955–963. [Google Scholar] [CrossRef]
- Yuan, M.; Jing, Y.; Lanetc, Z.; Zhuravljov, A.; Soleimani, F.; Si, G.; Armstrong, R.T.; Mostaghimi, P. Modelling Multicomponent Gas Diffusion and Predicting the Concentration-Dependent Effective Diffusion Coefficient of Coal with Application to Carbon Geo-Sequestration. Fuel 2023, 339, 127255. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Xu, C.; Guo, H.; Xu, Z.; Liu, Y.; Dong, H.; Ju, Y. Modeling of Multi-Field Gas Desorption-Diffusion in Coal: A New Insight Into the Bidisperse Model. Energy 2023, 267, 126534. [Google Scholar] [CrossRef]
- Fan, D.; Yang, C.; Sun, H.; Yao, J.; Zhang, L.; Jia, C.; Fu, S.; Sang, Q. A Framework of Parallel Physics-Informed Neural Network with Laplace Transform for Well Testing Interpretation. Phys. Fluids 2025, 37, 14114. [Google Scholar] [CrossRef]
- Liu, T.; Wang, J.; Lin, B.; Wang, X.; Huang, Q.; Li, J. Numerical Simulation on Enhanced Coalbed Methane Extraction by Hot Flue Gas Based on the Ecm-Dfm Model. Comput. Geotech. 2025, 184, 107253. [Google Scholar] [CrossRef]
- Ahamed, M.A.A.; Perera, M.S.A.; Ranjith, P.G. Implementation of an Elastoplastic Constitutive Model to Study the Proppant Embedment in Coal Under Different Pore Fluid Saturation Conditions: A Numerical and Experimental Study. Fuel 2022, 317, 123488. [Google Scholar] [CrossRef]
- Liu, T.; Lin, B.; Fu, X.; Zhao, Y.; Gao, Y.; Yang, W. Modeling Coupled Gas Flow and Geomechanics Process in Stimulated Coal Seam by Hydraulic Flushing. Int. J. Rock Mech. Min. 2021, 142, 104769. [Google Scholar] [CrossRef]
- Sharma, G.; Guria, C. An Improved Klinkenberg Permeability Model for Tight Reservoir Cores: Effects of Non-Linear Gas Slippage to Real Gases. Geoenergy Sci. Eng. 2024, 233, 212477. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, X.; Liu, S.; Zhu, Y.; Liu, A.; Fan, L.; Wang, Y.; Zhang, H. Quantifying and Modeling of Coal Permeability Spatiotemporal Response: Implications for Gas Recovery and Co2 Sequestration. Fuel 2025, 388, 134561. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Xu, C.; Li, X.; Guo, H.; Yi, K. Influence of Gas Diffusion in Coal Matrix on Gas Extraction Process: Modeling, Definition, and Quantitative Analysis. Gas Sci. Eng. 2025, 134, 205545. [Google Scholar] [CrossRef]
- Liu, Z.; Han, J.; Yang, H.; Lv, J.; Dong, S. A New Model for Coal Gas Seepage Based on Fracture-Pore Fractal Structure Characteristics. Int. J. Rock Mech. Min. 2024, 173, 105626. [Google Scholar] [CrossRef]
- Mu, D.; Ma, Q.; Zhang, K.; Zhao, J. A Gas-Mechanical-Damage Coupling Model Based on the Tlf-Sph Method and its Application to Gas Seepage in Fractured Coal. Comput. Geotech. 2024, 171, 106352. [Google Scholar] [CrossRef]
- Saber, E.; Qu, Q.; Aminossadati, S.M.; Zhu, Y.; Chen, Z. Horizontal Borehole Azimuth Optimization for Enhanced Stability and Coal Seam Gas Production. Rock Mech. Bull. 2024, 3, 100100. [Google Scholar] [CrossRef]
- Ng, E.C.J.; Ooi, J.B.; Hung, Y.M. Bicriteria Optimization of Subcooled Flow Boiling in Graphene-Coated Microchannels Using Response Surface Methodology. Int. Commun. Heat Mass. 2025, 164, 108914. [Google Scholar] [CrossRef]
- Yang, X.; Ling Du Lu, X.; Zhang, W. Optimization Design of Hydrogen Storage Reactor Based on Response Surface Methodology and Variable Pressure Hydrogen Charging. Int. J. Hydrogen Energ. 2025, 114, 426–439. [Google Scholar] [CrossRef]
- Xu, S.; Luo, J.; Chen, G.; Zhang, H.; Jia, Z.; Lan, Y.; Jiang, C. Influence and Optimization of Urea Injection Parameters on Scr Characteristics Based on Response Surface Methodology. J. Environ. Chem. Eng. 2025, 13, 116170. [Google Scholar] [CrossRef]
- Davraz, M.; Isildar, N.; Kaplan, A.N. Investigation of the Effects of Steam Curing of Concrete at Different Temperatures on Cost and Compressive Strength by Response Surface Methodology. Constr. Build. Mater. 2025, 470, 140589. [Google Scholar] [CrossRef]
- Yang, H.; Miao, D.; Liu, Z.; Zhao, D.; Zhang, M. Study on the Radial Displacement Law and Permeability Enhancement Effect of Coal Body Around Hydraulic Flushing Drilling. Geofluids 2021, 2021, 5535624. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Z.; Zhao, Y.; Chen, D.; Qiu, Y.; Wei, J. Study on the Design of Gas Extraction Drilling Angle of Crossing Coal Layer Drilling in the Floor Rock Roadway Considering the Boreholes Superposition Effect. Fuel 2024, 378, 132981. [Google Scholar] [CrossRef]
- Fang, H.H.; Zheng, C.S.; Qi, N.; Xu, H.J.; Liu, H.H.; Huang, Y.H.; Wei, Q.; Hou, X.W.; Li, L.; Song, S.L. Coupling Mechanism of Thm Fields and Slg Phases During the Gas Extraction Process and its Application in Numerical Analysis of Gas Occurrence Regularity and Effective Extraction Radius. Petrol. Sci. 2022, 19, 990–1006. [Google Scholar] [CrossRef]
- Yang, F.; Li, P.; Su, W.; Zhang, J.; Wang, L.; Guo, T.; Wang, S. Study on Reasonable Gas Extraction Radius Based on Multi-Index and Multi-Method. Energy Rep. 2022, 8, 287–294. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, Y.; Liu, Q.; Yuan, L.; Dong, J.; Wang, L.; Qi, Y.; Wang, W. A Novel in-Seam Borehole Hydraulic Flushing Gas Extraction Technology in the Heading Face: Enhanced Permeability Mechanism, Gas Flow Characteristics, and Application. J. Nat. Gas Sci. Eng. 2017, 46, 498–514. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Xu, C.; Xu, Z.; Guo, H.; Liu, Y.; Dong, H. Transition of Dominated Factors in Coal Seam Gas Migration: Thermo-Hydro-Mechanical Modeling and Analysis. Int. J. Heat Mass Tran. 2025, 236, 126239. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Ren, P.; Han, H.; Zhang, S. A Fully Multifield Coupling Model of Gas Extraction and Air Leakage for in-Seam Borehole. Energy Rep. 2021, 7, 1293–1305. [Google Scholar] [CrossRef]
- Liu, T.; Lin, B.; Fu, X.; Zhu, C. Modeling Air Leakage Around Gas Extraction Boreholes in Mining-Disturbed Coal Seams. Process Saf. Environ. 2020, 141, 202–214. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Ju, Y.; Dong, H.; Zhao, W.; Du, C.; Guo, Y.; Lou, Z.; Gao, H. Numerical Study on the Mechanism of Air Leakage in Drainage Boreholes: A Fully Coupled Gas-Air Flow Model Considering Elastic-Plastic Deformation of Coal and its Validation. Process Saf. Environ. 2022, 158, 134–145. [Google Scholar] [CrossRef]
- Zhao, Y.; Qi, Q.; Jia, X.; Liu, Y.; Zhang, J. Numerical Simulation of Coal Spontaneous Combustion Around a Borehole Induced by Negative Pressure Gas Drainage. Geofluids 2021, 2021, 3938243. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).