Modeling and Optimization of an Integrated Energy Supply in the Oil and Gas Industry: A Case Study of Northeast China
Abstract
1. Introduction
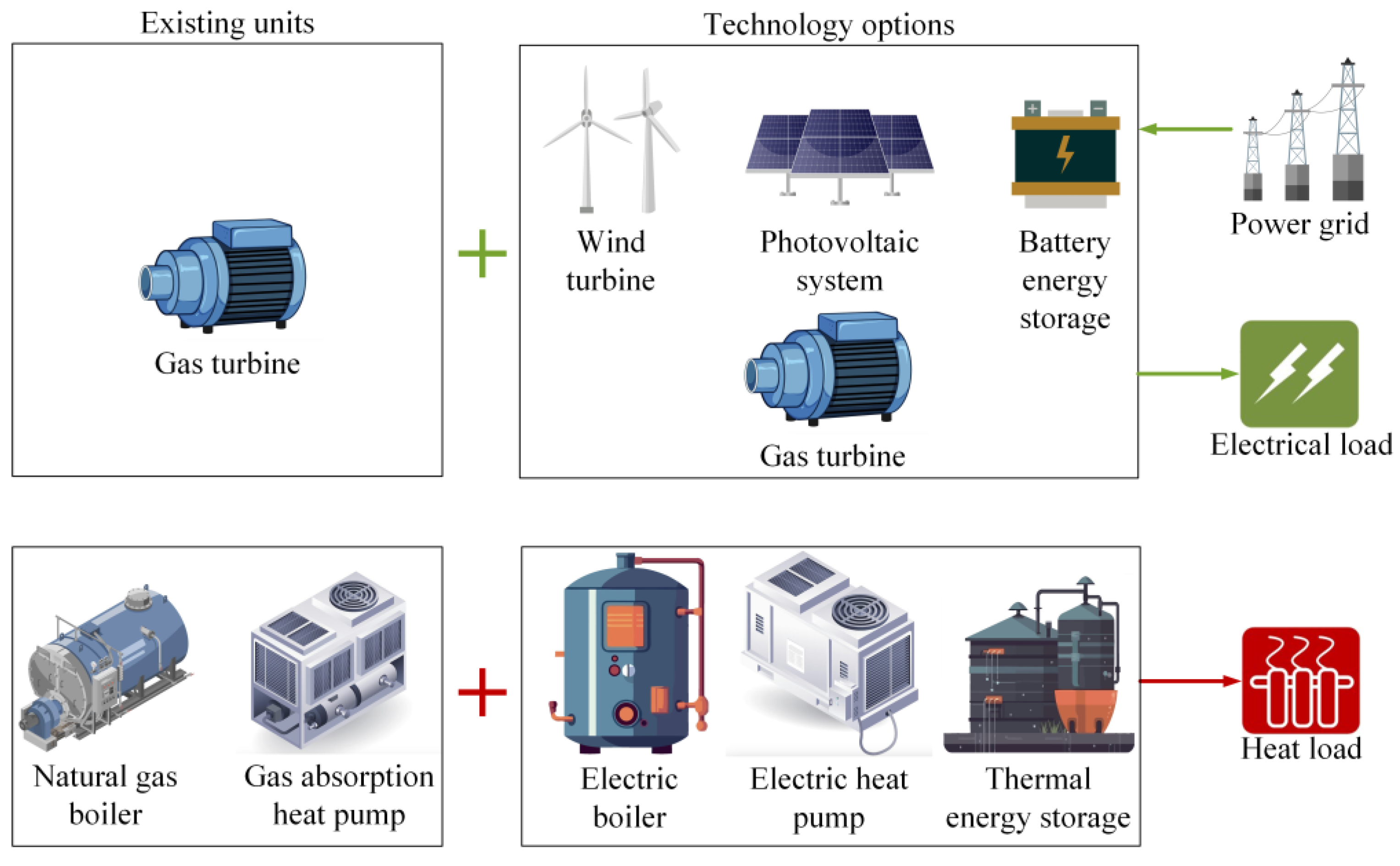
2. System Description
3. Methodology
3.1. Optimization Model with Variable Temporal Resolution
3.1.1. Objective Function
3.1.2. Constraints
- Photovoltaic Module
- 2.
- Wind Turbine
- 3.
- Gas Turbine
- 4.
- Heat Generation Units
- 5.
- Energy Storage System
- 6.
- Power Balance
- 7.
- Heat Balance
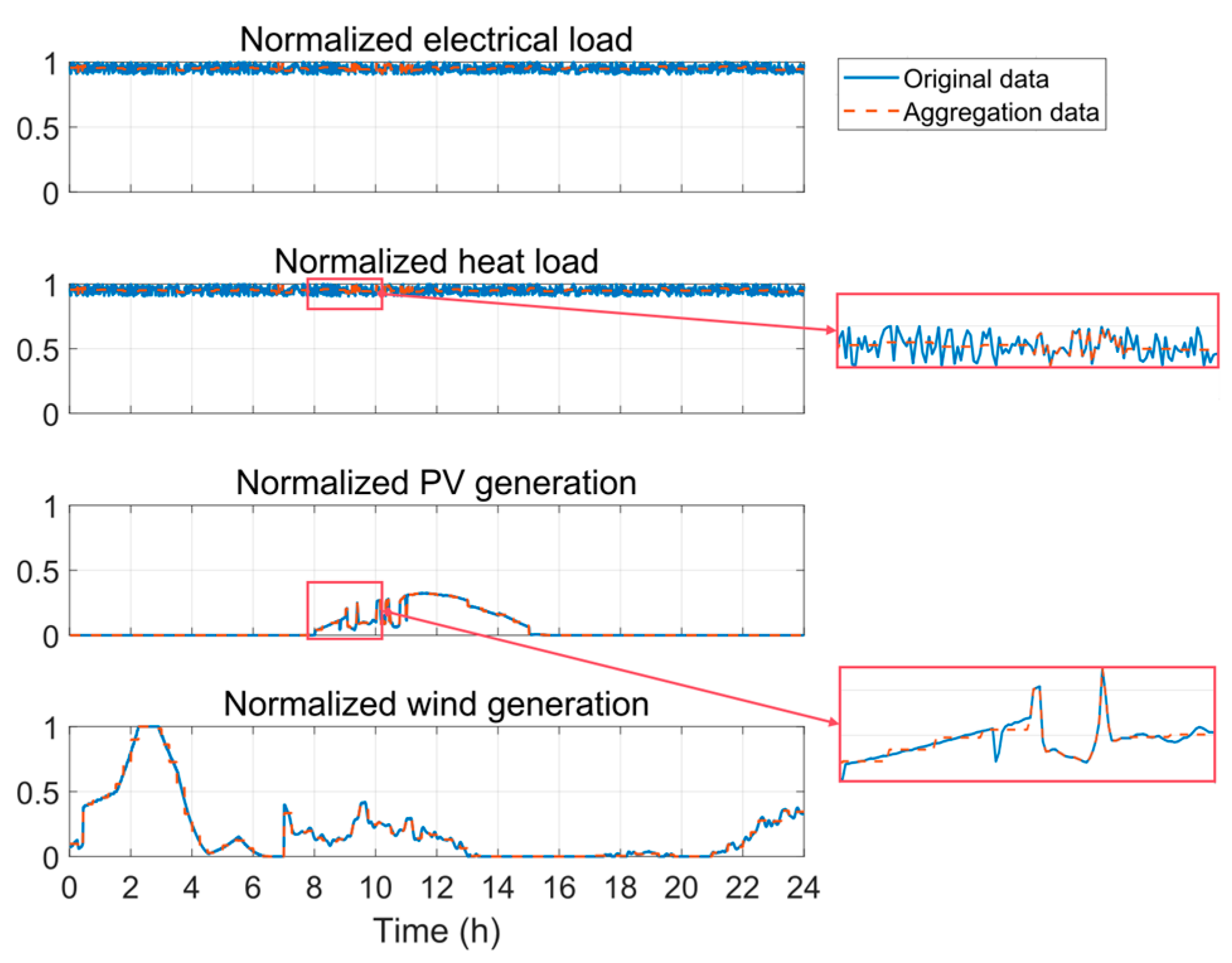
3.2. Adaptive Time-Series Aggregation Algorithm
4. Case Study
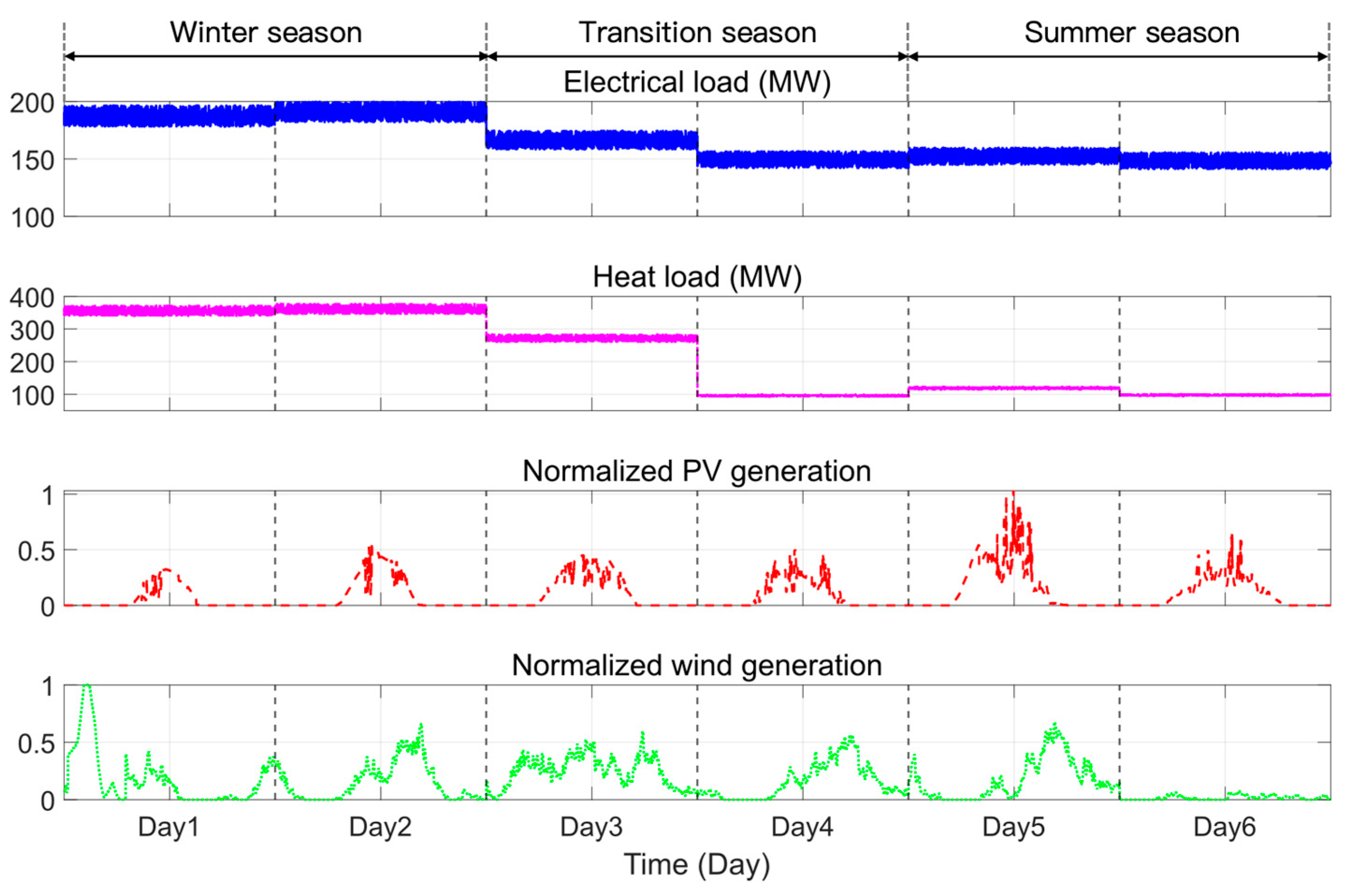
4.1. Model Inputs and Parameter Settings
4.2. Case Setting
- Case 1: Baseline case
- Case 2: Grid-Dependency case
- Case 3: Microgrid case
- Case 4: Heat electrification case
5. Results and Discussion
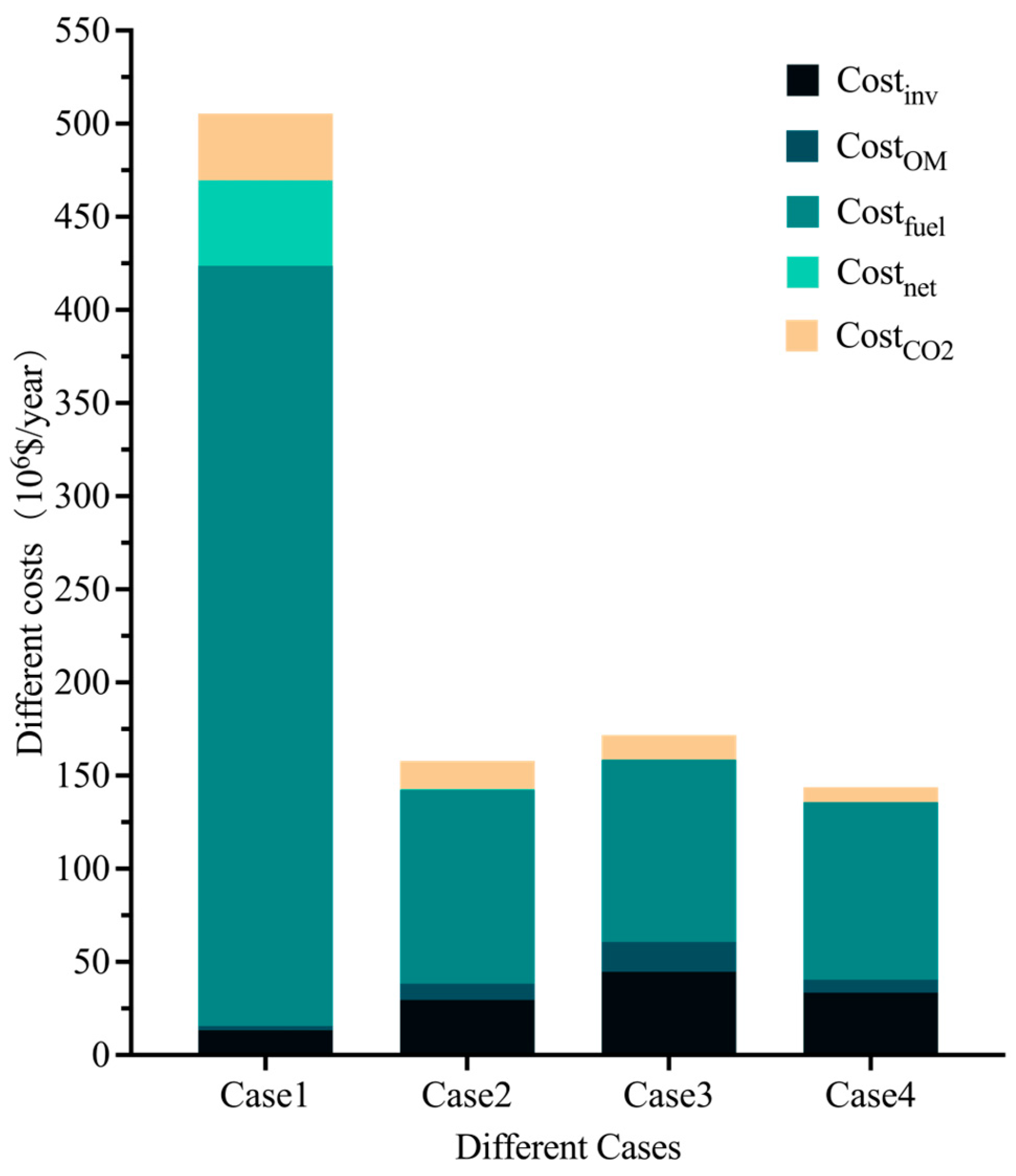
5.1. The Overall Results
5.2. Sensitivity Analysis
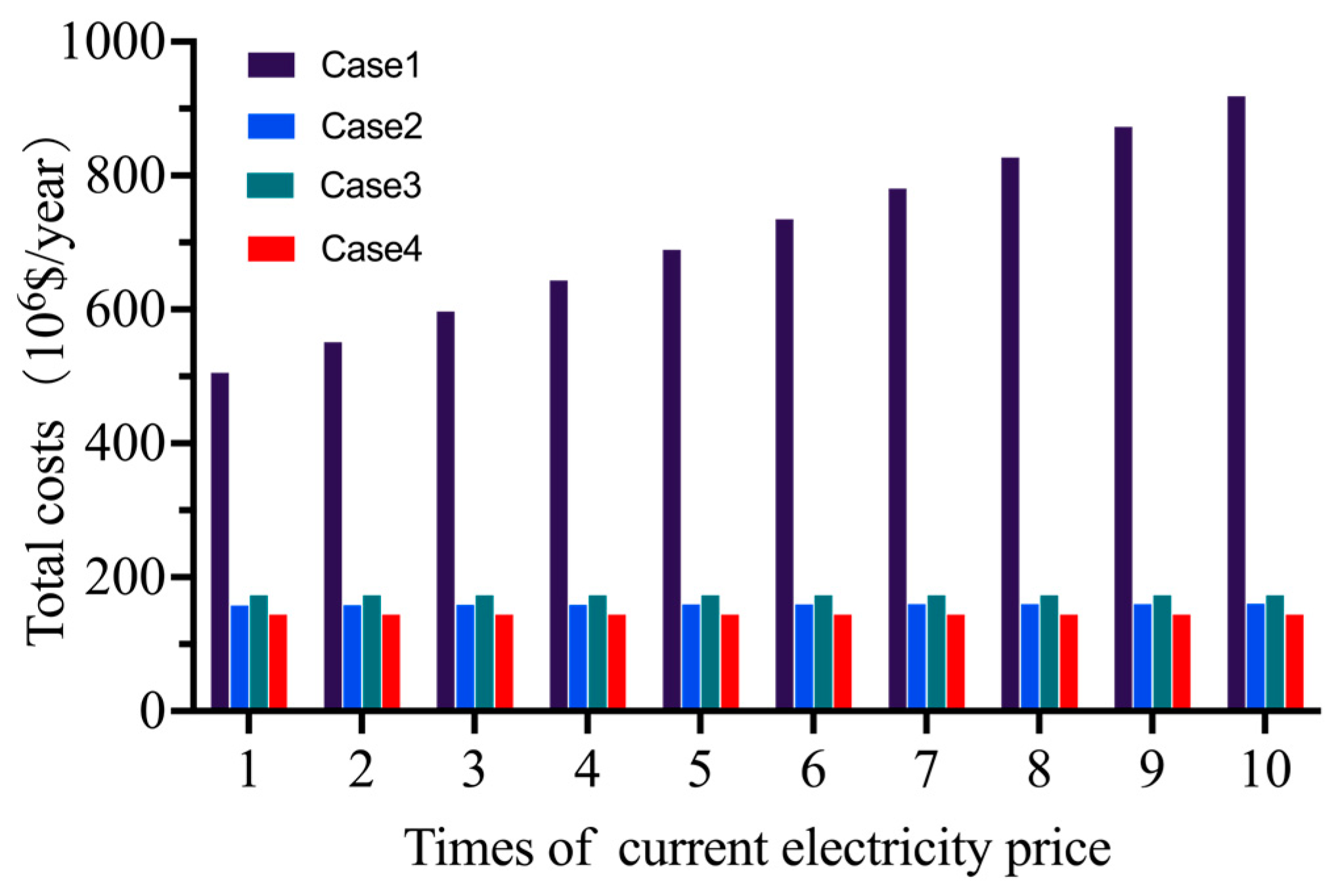
5.2.1. Impacts of the Upper Limit of Electricity Purchase
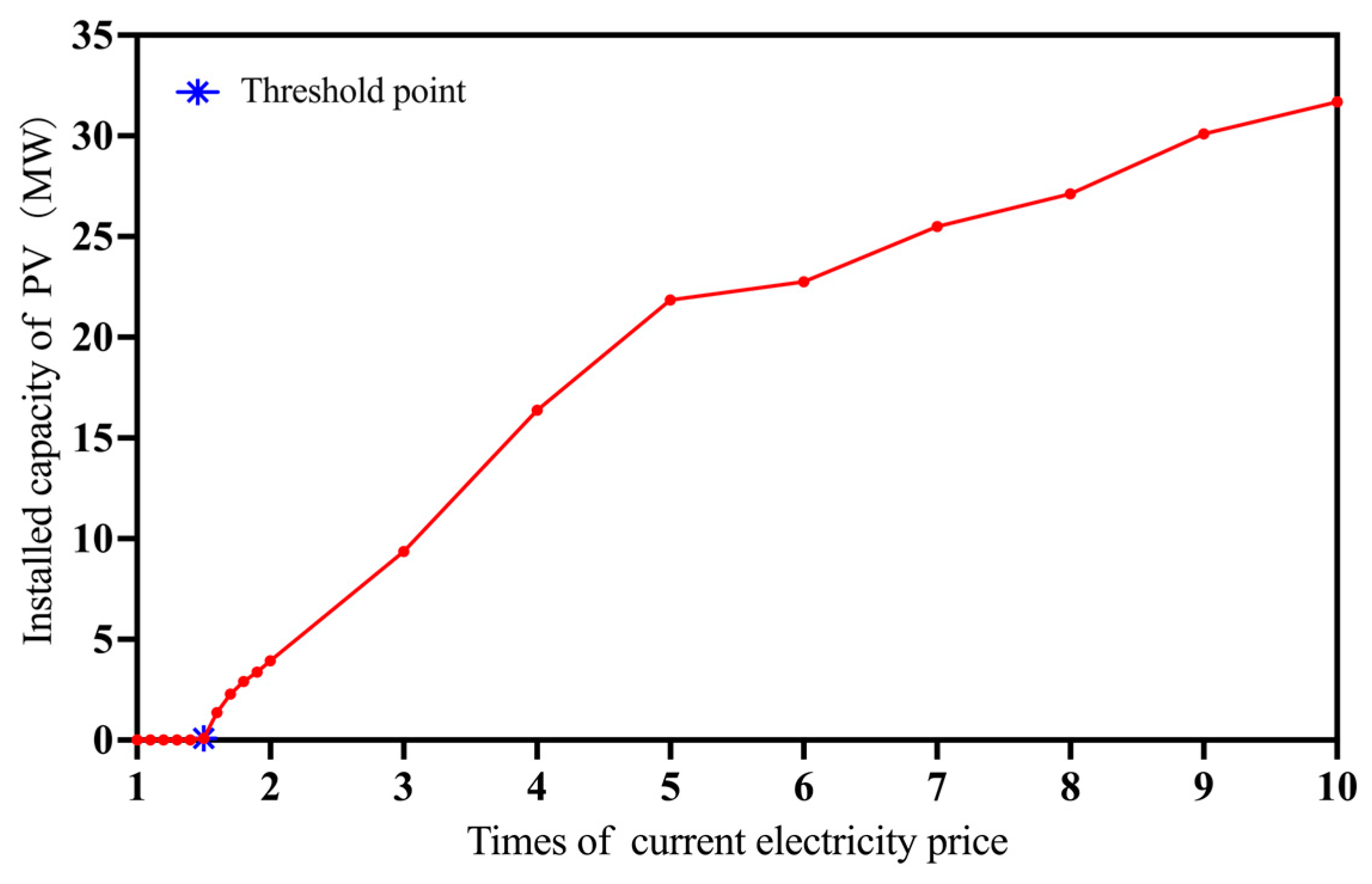
5.2.2. Impacts of Electrical Prices
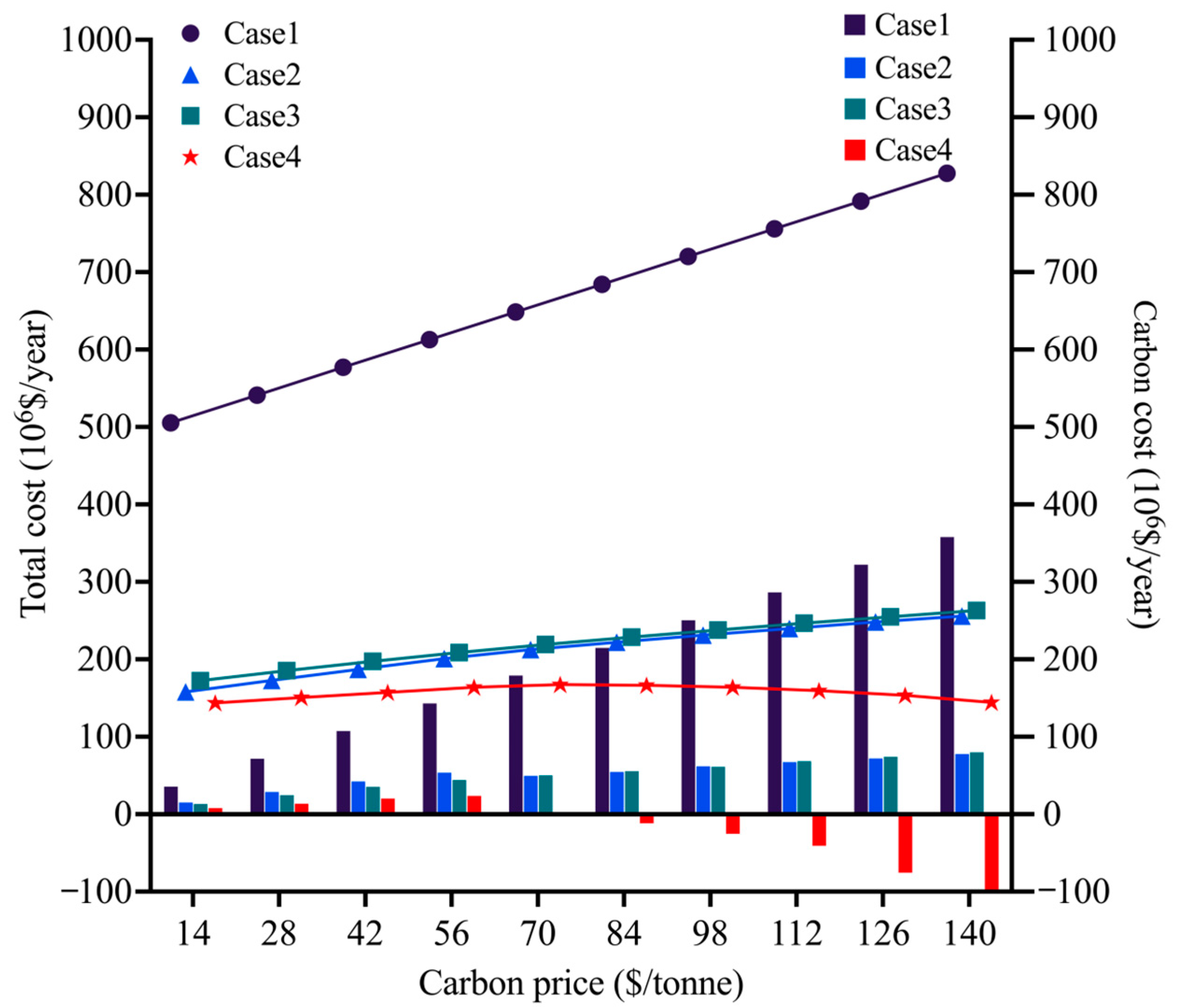
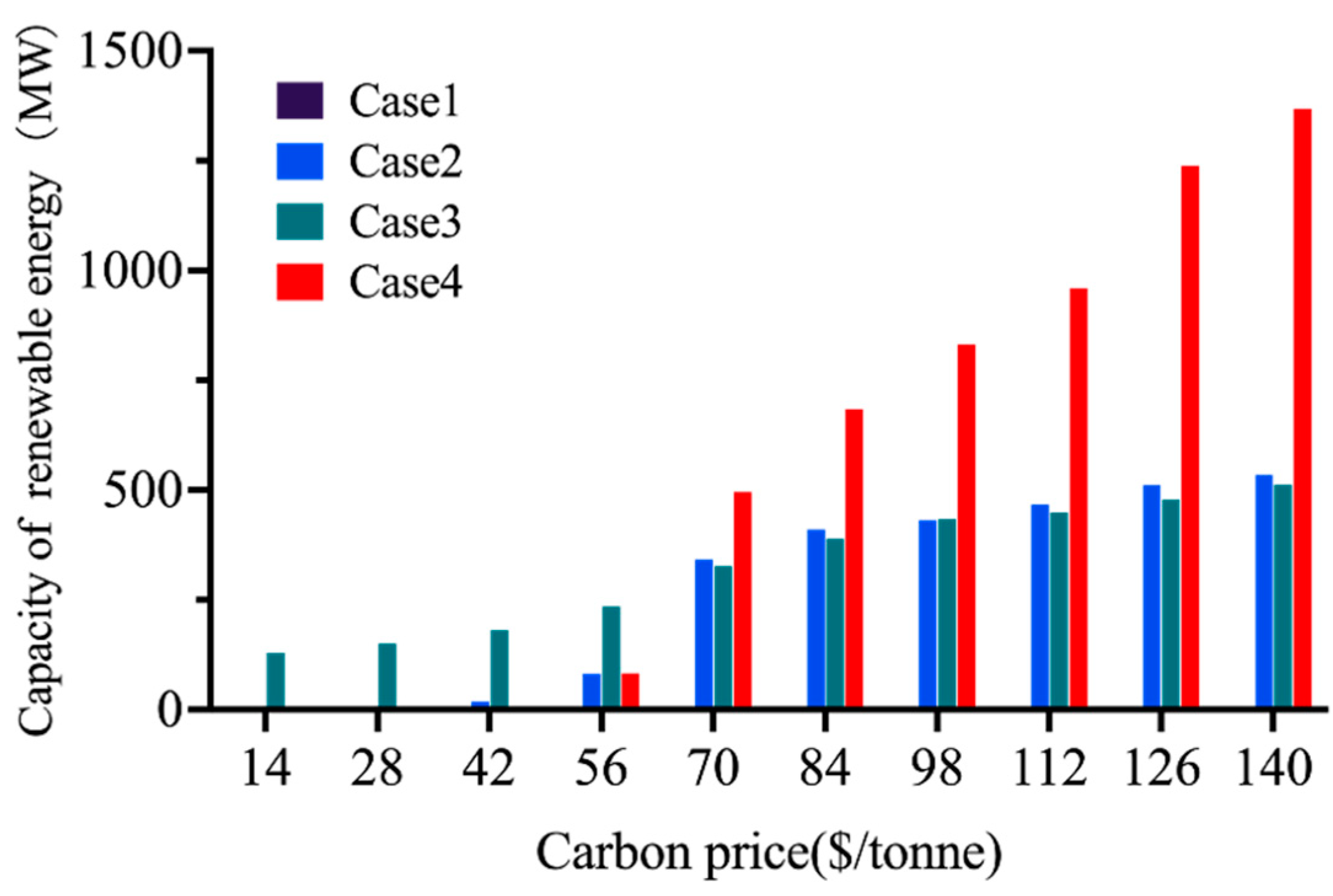
5.2.3. Impacts of Carbon Prices
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Esiri, A.E.; Babayeju, O.A.; Ekemezie, I.O.; Esiri, A.E.; Babayeju, O.A.; Ekemezie, I.O. Implementing sustainable practices in oil and gas operations to minimize environmental footprint. GSC Adv. Res. Rev. 2024, 19, 112–121. [Google Scholar] [CrossRef]
- Esiri, A.E.; Sofoluwe, O.O.; Ukato, A. Aligning oil and gas industry practices with sustainable development goals (SDGs). Int. J. Appl. Res. Soc. Sci. 2024, 6, 1215–1226. [Google Scholar] [CrossRef]
- China ETS carbON PRICE Trends by Instrument 2024. Statista. Available online: https://www.statista.com/statistics/1474955/carbon-prices-in-china-by-ets/ (accessed on 23 January 2025).
- Wang, K.; Lv, C. Global and China Carbon Market Review and Outlook (2025); Center for Energy and Environmental Policy Research, Beijing Institute of Technology: Beijing, China, 2025. [Google Scholar]
- Bartolini, A.; Mazzoni, S.; Comodi, G.; Romagnoli, A. Impact of carbon pricing on distributed energy systems planning. Appl. Energy 2021, 301, 117324. [Google Scholar] [CrossRef]
- Schuldt, H.; Lessmann, K. Financing the low-carbon transition: The impact of financial frictions on clean investment. Macroecon. Dyn. 2021, 27, 1932–1971. [Google Scholar] [CrossRef]
- Boon, M. A Climate of Change? The Oil Industry and Decarbonization in Historical Perspective. Bus. Hist. Rev. 2019, 93, 101–125. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Y.; Bradshaw, M.; Wang, C.; Blondeel, M. Globalization and decarbonization: Changing strategies of global oil and gas companies. Wiley Interdiscip. Rev. Clim. Change 2023, 14, e849. [Google Scholar] [CrossRef]
- Morenov, V.; Leusheva, E.; Buslaev, G.; Gudmestad, O.T. System of Comprehensive Energy-Efficient Utilization of Associated Petroleum Gas with Reduced Carbon Footprint in the Field Conditions. Energies 2020, 13, 4921. [Google Scholar] [CrossRef]
- Veldhuis, A.J.; Leach, M.; Yang, A. The impact of increased decentralised generation on the reliability of an existing electricity network. Appl. Energy 2018, 215, 479–502. [Google Scholar] [CrossRef]
- IER Power Prices Spike in Norway. IER. 2024. Available online: https://www.instituteforenergyresearch.org/regulation/power-prices-spike-in-norway/ (accessed on 11 April 2025).
- Rai, A.; Nunn, O. On the impact of increasing penetration of variable renewables on electricity spot price extremes in Australia. Econ. Anal. Policy 2020, 67, 67–86. [Google Scholar] [CrossRef]
- Heptonstall, P.J.; Gross, R.J.K. A systematic review of the costs and impacts of integrating variable renewables into power grids. Nat. Energy 2021, 6, 72–83. [Google Scholar] [CrossRef]
- Bulut, M.; Özcan, E. Integration of Battery Energy Storage Systems into Natural Gas Combined Cycle Power Plants in Fuzzy Environment. J. Energy Storage 2021, 36, 102376. [Google Scholar] [CrossRef]
- Su, C.; Zhu, J.; Ma, J.; Xu, Y.; Zhao, Y. Thinking and suggestions on integrated development pathways for oil and gas with new energy. Pet. Sci. Technol. Forum 2024, 43, 18. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, W. Thoughts on promoting the integrated development of natural gas and renewable energy in China. World Pet. Ind. 2021, 28, 38–43. [Google Scholar]
- Abraham-Dukuma, M.C.; Dioha, M.O.; Aholu, O.C.; Emodi, N.V.; Ogbumgbada, C. A marriage of convenience or necessity? Research and policy implications for electrifying upstream petroleum production systems with renewables. Energy Res. Soc. Sci. 2021, 80, 102226. [Google Scholar] [CrossRef]
- Xiong, X.; Yun, Q.; Li, B.; Zhu, J. Thinking of clean replacement and re-electrification path for oil and gas production system under carbon peak and carbon neutrality goals. Pet. Sci. Technol. Forum 2023, 42, 21–29. [Google Scholar]
- Ozowe, W.; Ikevuje, A.H.; Ogbu, A.D.; Esiri, A.E. Renewable energy integration in offshore oil and gas installations. Magna Sci. Adv. Res. Rev. 2023, 8, 238–250. [Google Scholar] [CrossRef]
- Ekechukwu, D.E.; Simpa, P. Trends, insights, and future prospects of renewable energy integration within the oil and gas sector operations. World J. Adv. Eng. Technol. Sci. 2024, 12, 152–167. [Google Scholar] [CrossRef]
- Rafiee, A.; Khalilpour, K.R. Chapter 11—Renewable Hybridization of Oil and Gas Supply Chains. In Polygeneration with Polystorage for Chemical and Energy Hubs; Khalilpour, K.R., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 331–372. ISBN 978-0-12-813306-4. [Google Scholar]
- Zhong, M.; Bazilian, M.D. Contours of the energy transition: Investment by international oil and gas companies in renewable energy. Electr. J. 2018, 31, 82–91. [Google Scholar] [CrossRef]
- Hartmann, J.; Inkpen, A.C.; Ramaswamy, K. Different shades of green: Global oil and gas companies and renewable energy. J. Int. Bus. Stud. 2021, 52, 879–903. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, C.; Song, J. Review of Renewable Energy Technologies Utilized in the Oil and Gas Industry. Int. J. Renew. Energy Res. IJRER 2017, 7, 592–598. [Google Scholar]
- World Energy Outlook 2017; International Energy Agency (IEA): Paris, France, 2017.
- Electricity Storage and Renewables: Costs and Markets to 2030; International Renewable Energy Agency (IRENA): Masdar City, Abu Dhabi, 2017.
- Zhou, Z.; Liu, P.; Li, Z.; Ni, W. An engineering approach to the optimal design of distributed energy systems in China. Appl. Therm. Eng. 2013, 53, 387–396. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, P.; Li, Z. Enhancing accuracy of flexibility characterization in integrated energy system design: A variable temporal resolution optimization method. Energy 2024, 288, 129804. [Google Scholar] [CrossRef]
- Murillo-Soto, L.D.; Meza, C. A Simple Temperature and Irradiance-Dependent Expression for the Efficiency of Photovoltaic Cells and Modules. In Proceedings of the 2018 IEEE 38th Central America and Panama Convention (CONCAPAN XXXVIII), San Salvador, El Salvador, 7–9 November 2018; pp. 1–6. Available online: https://ieeexplore.ieee.org/abstract/document/8596458?utm_source=chatgpt.com (accessed on 24 January 2025).
- Saint-Drenan, Y.-M.; Besseau, R.; Jansen, M.; Staffell, I.; Troccoli, A.; Dubus, L.; Schmidt, J.; Gruber, K.; Simões, S.G.; Heier, S. A parametric model for wind turbine power curves incorporating environmental conditions. Renew. Energy 2020, 157, 754–768. [Google Scholar] [CrossRef]
- Huang, Q.; Song, Y.; Sun, Q.; Ren, X.; Wang, W. Integrating Compressed CO2 Energy Storage in an Integrated Energy System. Energies 2024, 17, 1570. [Google Scholar] [CrossRef]
- Dou, X.; Wang, J.; Zhang, Z.; Gao, M. Optimal Configuration of Multitype Energy Storage for Integrated Energy Systems Considering System Reserve Value. CSEE J. Power Energy Syst. 2024, 10, 2114–2126. [Google Scholar] [CrossRef]
- Schittekatte, T.; Stadler, M.; Cardoso, G.; Mashayekh, S.; Sankar, N. The Impact of Short-Term Stochastic Variability in Solar Irradiance on Optimal Microgrid Design. IEEE Trans. Smart Grid 2018, 9, 1647–1656. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, N.; Kirschen, D.S.; Huang, W.; Kang, C. Planning multiple energy systems for low-carbon districts with high penetration of renewable energy: An empirical study in China. Appl. Energy 2020, 261, 114390. [Google Scholar] [CrossRef]
- Renewable Power Generation Costs in 2023; International Renewable Energy Agency (IRENA): Masdar City, Abu Dhabi, 2024.
- Mongird, K.; Viswanathan, V.; Balducci, P.; Alam, J.; Fotedar, V.; Koritarov, V.; Hadjerioua, B. An Evaluation of Energy Storage Cost and Performance Characteristics. Energies 2020, 13, 3307. [Google Scholar] [CrossRef]
- Meteonorm Global Meteorological Database Version 8.2. Software and Data for Engineers, Planers and Education. Available online: https://meteonorm.com/assets/downloads/mn82_software.pdf (accessed on 1 April 2025).
- The Importance of Real-World Policy Packages to Drive Energy Transitions—Analysis. Available online: https://www.iea.org/commentaries/the-importance-of-real-world-policy-packages-to-drive-energy-transitions (accessed on 11 April 2025).


| Technology | Prated (MW) | Pmin (Prated%) | η | rampmax (Prated%/min) | Tschedule (min) |
|---|---|---|---|---|---|
| Gas turbine [28] | 48 | 80% | 0.4 | 5% | 5 |
| Photovoltaic system [28] | - | 10% | - | - | 1 |
| Wind turbine [28] | - | 10% | - | - | 1 |
| Electric boiler [34] | 5 | 20% | 0.9 | 5% | 1 |
| Natural gas boiler [34] | 10 | 30% | 0.8 | 5% | 10 |
| Electric heat pump [34] | 10 | 10% | 3 | 10% | 1 |
| Gas absorption heat pump [34] | 4 | 15% | 1.3 | 10% | 5 |
| Battery energy storage system [34] | - | 0% | 0.92 | - | 1 |
| Thermal energy storage system [34] | - | 0% | 0.95 | - | 15 |
| Technology | Priceinv (105USD/MW) | PriceOM,fid (103 USD/MW/year) | PriceOM,var (USD/(MW·h)) | Lifespan (y) | Maximum Capacity (MW) |
|---|---|---|---|---|---|
| Gas turbine [28] | 4.125 | 5.111 | 2.013 | 30 | - |
| Photovoltaic system [35] | 6.710 | 3.800 | 0.000 | 20 | 1500 |
| Wind turbine [35] | 9.860 | 23.009 | 0.000 | 20 | 1500 |
| Electric boiler [34] | 1.528 | 1.911 | 0.000 | 20 | - |
| Natural gas boiler [34] | 2.083 | 1.389 | 1.875 | 20 | - |
| Electric heat pump [34] | 5.278 | 2.453 | 0.000 | 20 | - |
| Gas absorption heat pump [34] | 6.250 | 2.778 | 2.344 | 20 | - |
| Battery energy storage system [36] | 7.560 | 32.000 | 0.000 | 15 | 10,000 |
| Thermal energy storage system [34] | 0.500 | 0.017 | 0.000 | 20 | 10,000 |
| Time | Electricity Price (USD/kWh) |
|---|---|
| 5:30–7:00 | 0.088 |
| 7:00–8:00 | 0.125 |
| 8:00–9:00 | 0.088 |
| 9:00–11:30 | 0.125 |
| 11:30–12:00 | 0.088 |
| 12:00–14:00 | 0.046 |
| 14:00–15:30 | 0.088 |
| 15:30–20:00 | 0.125 |
| 20:00–23:30 | 0.088 |
| 23:30–5:30 | 0.046 |
| Day 1 | Day 2 | Day 3 | Day 4 | Day 5 | Day 6 | |
|---|---|---|---|---|---|---|
| Original data points | 1440 | 1440 | 1440 | 1440 | 1440 | 1440 |
| Aggregated data points | 202 | 230 | 227 | 300 | 317 | 236 |
| Compression ratio | 0.140 | 0.160 | 0.158 | 0.208 | 0.220 | 0.164 |
| Root mean squared error | 0.959 | 0.942 | 1.081 | 0.930 | 0.934 | 0.955 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Gas turbine | √ | √ | √ | √ |
| Photovoltaic system | × | √ | √ | √ |
| Wind turbine | × | √ | √ | √ |
| Natural gas boiler | √ | √ | √ | √ |
| Electric boiler | × | × | × | √ |
| Gas absorption heat pump | √ | √ | √ | √ |
| Electric heat pump | × | × | × | √ |
| Battery energy storage system | × | √ | √ | √ |
| Thermal energy storage system | × | √ | √ | √ |
| Electricity purchase from the grid | √ | √ | × | × |
| Technology | The Optimal Capacity (MW) | |||
|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 4 | |
| Gas turbine | 96 | 192 | 240 | 288 |
| Photovoltaic system | 0 | 0 | 56 | 2 |
| Wind turbine | 0 | 0 | 74 | 0 |
| Electric boiler | 0 | 0 | 0 | 15 |
| Natural gas boiler | 360 | 90 | 90 | 60 |
| Electric heat pump | 0 | 0 | 0 | 290 |
| Gas absorption heat pump | 12 | 276 | 276 | 24 |
| Battery energy storage system | 0 | 0 | 2 | 0 |
| Thermal energy storage system | 0 | 53 | 53 | 158 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Daily Average Carbon Emissions (t) | 8518.38 | 5369.86 | 4989.92 | 4858.00 |
| Renewable Energy Utilization Rate | - | - | 0.93 | 0.97 |
| Renewable Energy Capacity Share | - | 0.00 | 0.35 | 0.01 |
| Renewable Energy Generation Share | - | 0.00 | 0.10 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Li, J.; Liu, P.; Zhang, G.; Liu, H. Modeling and Optimization of an Integrated Energy Supply in the Oil and Gas Industry: A Case Study of Northeast China. Processes 2025, 13, 1512. https://doi.org/10.3390/pr13051512
Zhu Y, Li J, Liu P, Zhang G, Liu H. Modeling and Optimization of an Integrated Energy Supply in the Oil and Gas Industry: A Case Study of Northeast China. Processes. 2025; 13(5):1512. https://doi.org/10.3390/pr13051512
Chicago/Turabian StyleZhu, Yujie, Jinze Li, Pei Liu, Guosheng Zhang, and He Liu. 2025. "Modeling and Optimization of an Integrated Energy Supply in the Oil and Gas Industry: A Case Study of Northeast China" Processes 13, no. 5: 1512. https://doi.org/10.3390/pr13051512
APA StyleZhu, Y., Li, J., Liu, P., Zhang, G., & Liu, H. (2025). Modeling and Optimization of an Integrated Energy Supply in the Oil and Gas Industry: A Case Study of Northeast China. Processes, 13(5), 1512. https://doi.org/10.3390/pr13051512







