An Enhanced Logic-Based Bender’s Decomposition Algorithm with Proximity Principle for Simulator-Based Distillation Process Optimization
Abstract
1. Introduction
2. Materials and Methods
2.1. Problem Statement and Logic-Based Bender’s Decomposition Algorithm
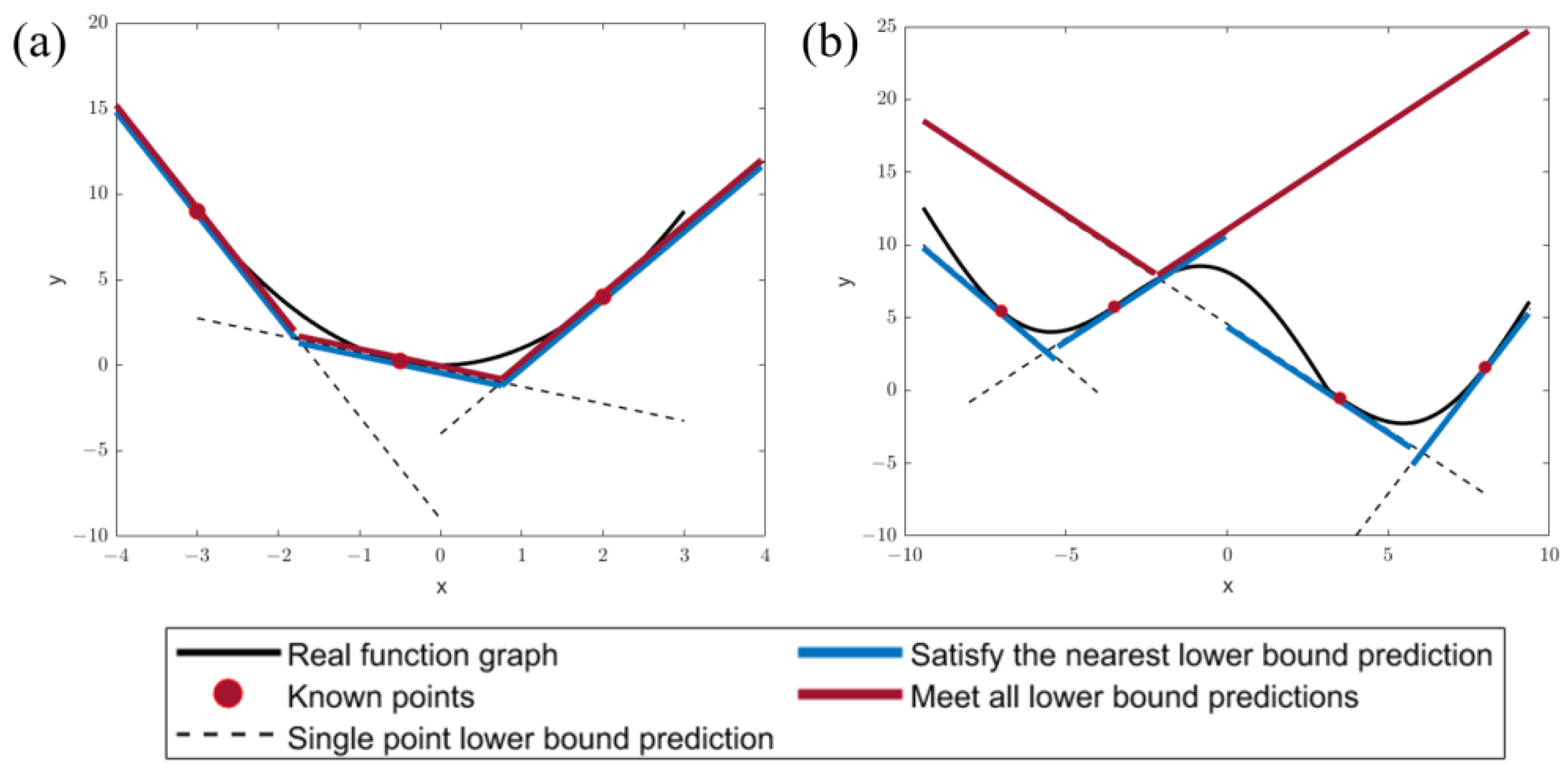
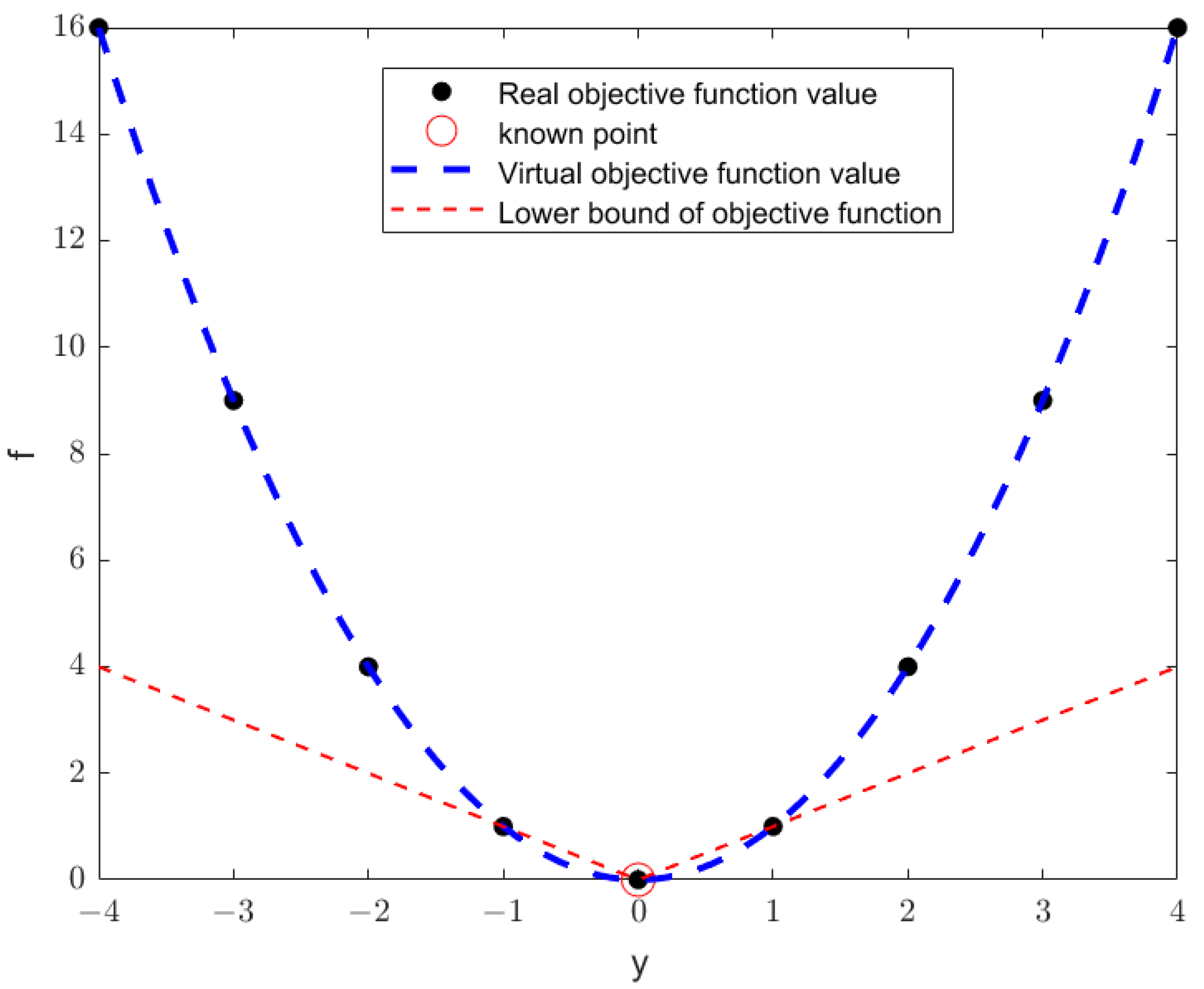
2.2. Proximity Principle and Logic-Based Proximity Principle Bender’s Decomposition Algorithm
2.3. Delayed Convergence Strategy and Multi-Start Points Strategy
2.4. Solver and Simulator Configuration
3. Results and Discussion
3.1. Case 1—Numerical Experiment
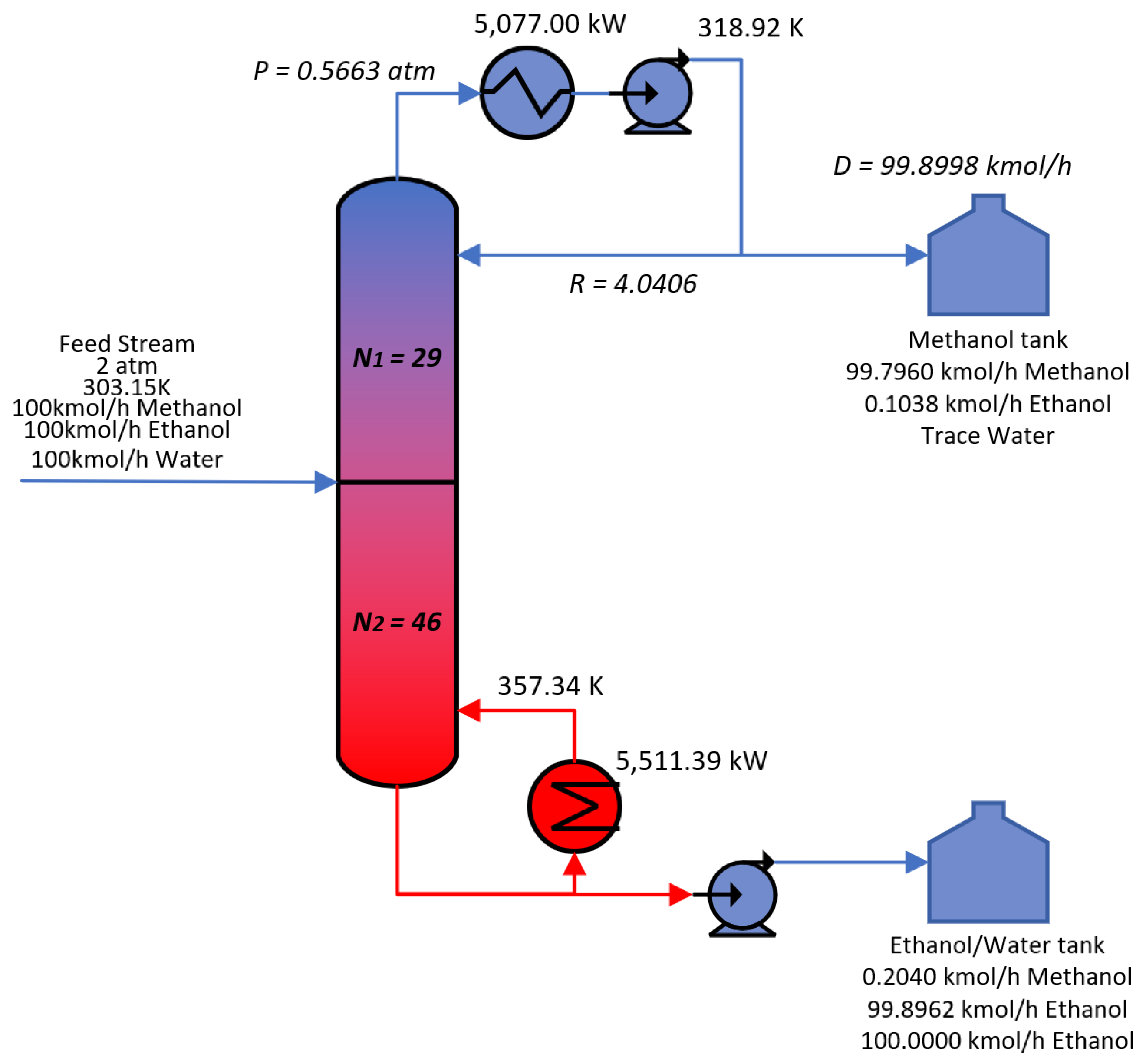
3.2. Case 2—Single Column Case of Methanol Distillation
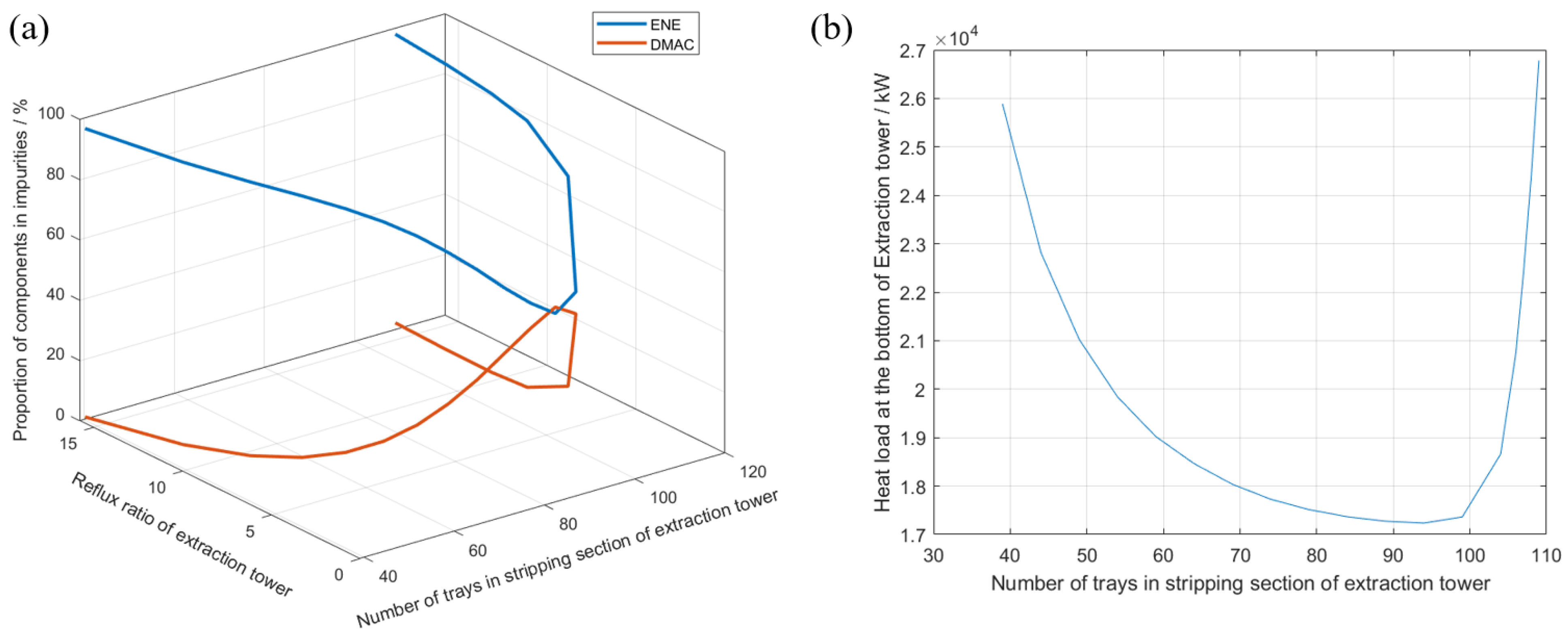
3.3. Case 3—Extraction Distillation Case of Cyclohexane/Cyclohexene
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Roman symbols | |
| The relaxation variable for the objective function | |
| The relaxation variable for the constraint function | |
| letters | |
| ANE | Cyclohexane |
| Integer variable selection logic-based flag in MILP Bottoms rate in distillation column | |
| Distillate rate in distillation column | |
| Makeup rate of extractant | |
| DMAC | Dimethylacetamide |
| ENE | Cyclohexene |
| Objective function | |
| Constraint inequality system for programming | |
| Constraint inequality for programming | |
| Hyper parameter of multi-start points strategy | |
| Hyper parameter of delayed convergence strategy | |
| LB-OA | Logic-based outer approximation algorithm |
| LB-BD | Logic-based Bender’s decomposition |
| LB-PBD | Logic-based proximity principle Bender’s decomposition |
| A sufficiently large number | |
| MILP | Mixed-integer linear programming |
| MINLP | Mixed-integer nonlinear programming |
| Neighborhood vector | |
| Number of trays for a specific section | |
| NLP | Nonlinear programming |
| Condenser pressure in distillation column | |
| Reflux ratio in distillation column | |
| SPDDE | Synchronously Population-Distributed Differential evolution |
| Total annualized cost | |
| Outlet temperature of heat exchanger | |
| Equation system of the simulator | |
| Dependent variable vector in simulator | |
| Independent variable vector with continuous values | |
| Independent variable vector with integer values | |
| Independent variable with integer value | |
| Selection flag for known integer combinations in MILP | |
| superscripts | |
| Lower bound value | |
| Upper bound value | |
| A fixed variable for the current programming | |
| subscripts | |
| The index of the constraint function | |
| The index of the known integer combinations in MILP | |
| The index of elements in an integer vector | |
| The index of elements in a set of logic-based flag |
Appendix A

References
- Sorensen, E. Principles of Binary Distillation. Distillation: Fundamentals and Principals; Elsevier: Amsterdam, The Netherlands, 2014; pp. 145–185. [Google Scholar] [CrossRef]
- David, S.S.; Ryan, P. Lively. Seven chemical separations to change the world. Nature 2016, 532, 435–437. [Google Scholar] [CrossRef]
- Boukouvala, F.; Misener, R.; Floudas, C.A. Global optimization advances in Mixed-Integer Nonlinear Programming, MINLP, and Constrained Derivative-Free Optimization, CDFO. Eur. J. Oper. Res. 2016, 252, 701–727. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glo. Opt. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hu, Z.; Li, P.; Liu, Y. Enhancing the Performance of Evolutionary Algorithm by Differential Evolution for Optimizing Distillation Sequence. Molecules 2022, 27, 3802. [Google Scholar] [CrossRef] [PubMed]
- Clerc, M.; Kennedy, J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comp. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Liang, M.; Song, J.; Zhao, K.; Jia, S.; Qian, X.; Yuan, X. Optimization of dividing wall columns based on online Kriging model and improved particle swarm optimization algorithm. Comp. Chem. Eng. 2022, 166, 107978. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, UK, 1976. [Google Scholar] [CrossRef]
- Zhang, D.; Zeng, S.; Li, Z.; Yang, M.; Feng, X. Simulation-assisted design of a distillation train with simultaneous column and sequence optimization. Comp. Chem. Eng. 2022, 164, 107907. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, L.; Cui, C.; Sun, J. A self-adaptive multi-objective dynamic differential evolution algorithm and its application in chemical engineering. Appl. Soft Comp. 2021, 106, 107317. [Google Scholar] [CrossRef]
- Xu, Z.; Ding, Y.; Ye, Q.; Li, J.; Wu, H.; Pan, J. Investigation of side-stream extractive distillation for separating multi-azeotropes mixture based on multi-objective optimization. Chem. Eng. Proce. Proc. Inten. 2024, 200, 109793. [Google Scholar] [CrossRef]
- Aspen OOMF—Script Language Reference Manual; AspenTech: Knowledge Base; Aspen Technology, Inc.: Bedford, MA, USA, 2011.
- López, C.A.M.; Telen, D.; Nimmegeers, P.; Cabianca, L.; Logist, F.; Van Impe, J. A process simulator interface for multiobjective optimization of chemical processes. Comp. Chem. Eng. 2018, 109, 119–137. [Google Scholar] [CrossRef]
- Milán-Yañez, D.; Caballero, J.A.; Grossmann, I.E. Rigorous design of distillation columns: Integration of disjunctive programming and process simulators. Ind. Eng. Chem. Res. 2005, 44, 6760–6775. [Google Scholar] [CrossRef]
- Lawler, E.L.; Wood, D.E. Branch-and-Bound Methods: A Survey. Oper. Res. 1966, 14, 699–719. [Google Scholar] [CrossRef]
- Geoffrion, A.M. Generalized Benders decomposition. J. Optim. Theory Appl. 1972, 10, 237–260. [Google Scholar] [CrossRef]
- Duran, M.A.; Grossmann, I.E. An outer-approximation algorithm for a class of mixed-integer nonlinear programs. Math. Prog. 1986, 36, 307–339. [Google Scholar] [CrossRef]
- Tapio, W.; Frank, P. An extended cutting plane method for solving convex MINLP problems. Comp. Chem. Eng. 1995, 19, 131–136. [Google Scholar] [CrossRef]
- Ugray, Z.; Lasdon, L.; Plummer, J.; Glover, F.; Kelly, J.; Martí, R. Scatter Search and Local NLP Solvers: A Multistart Framework for Global Optimization. INFORMS J. Comput. 2007, 19, 328–340. [Google Scholar] [CrossRef]
- Trespalacios, F.; Grossmann, I.E. Review of Mixed-Integer Nonlinear and Generalized Disjunctive Programming Methods. Chem. Ingen. Tech. 2014, 86, 991–1012. [Google Scholar] [CrossRef]
- Su, L.J.; Grossmann, I.E.; Tang, L.X. Computational strategies for improved MINLP algorithms. Comp. Chem. Eng. 2015, 75, 40–48. [Google Scholar] [CrossRef]
- Franke, M.B. Mixed-integer optimization of distillation sequences with Aspen Plus: A practical approach. Comp. Chem. Eng. 2019, 131, 106583. [Google Scholar] [CrossRef]
- Javaloyes-Antón, J.; Kronqvist, J.; Caballero, J.A. Simulation-based optimization of distillation processes using an extended cutting plane algorithm. Comp. Chem. Eng. 2022, 159, 107655. [Google Scholar] [CrossRef]
- Bergamini, M.L.; Aguirre, P.; Grossmann, I.E. Logic-based outer approximation for globally optimal synthesis of process networks. Comp. Chem. Eng. 2005, 29, 1914–1933. [Google Scholar] [CrossRef]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. 2024. Available online: https://www.gurobi.com (accessed on 22 February 2025).
- Chia, D.N.; Duanmu, F.; Sorensen, E. Optimal Design of Distillation Columns Using a Combined Optimization Approach. Comp. Aided Chem. Eng. 2021, 50, 153–158. [Google Scholar] [CrossRef]
- Liñán, D.A.; Contreras-Zarazúa, G.; Sanchez-Ramírez, E.; Segovia-Hernández, J.G.; Ricardez-Sandoval, L.A. A hybrid deterministic-stochastic algorithm for the optimal design of process flowsheets with ordered discrete decisions. Comp. Chem. Eng. 2024, 180, 108501. [Google Scholar] [CrossRef]
- Caballero, J.A. Logic hybrid simulation-optimization algorithm for distillation design. Comp. Chem. Eng. 2015, 72, 284–299. [Google Scholar] [CrossRef]
- Trespalacios, F.; Grossmann, I.E. Lagrangean relaxation of the hull-reformulation of linear generalized disjunctive programs and its use in disjunctive branch and bound. Euro. J. Oper. Res. 2016, 253, 314–327. [Google Scholar] [CrossRef]
- Corbetta, M.; Grossmann, I.E.; Manenti, F. Process simulator-based optimization of biorefinery downstream processes under the Generalized Disjunctive Programming framework. Comp. Chem. Eng. 2016, 88, 73–85. [Google Scholar] [CrossRef]
- Liñán, D.A.; Ricardez-Sandoval, L.A. A Benders decomposition framework for the optimization of disjunctive superstructures with ordered discrete decisions. AICHE J. 2023, 69, 18008. [Google Scholar] [CrossRef]
- Lyu, H.; Cui, C.; Zhang, X.; Sun, J. Population-distributed stochastic optimization for distillation processes: Implementation and distribution strategy. Chem. Eng. Res. Des. 2021, 168, 357–368. [Google Scholar] [CrossRef]
- Lyu, H.; Li, S.; Yu, X.; Sun, J. Superstructure modeling and stochastic optimization of side-stream extractive distillation processes for the industrial separation of benzene/cyclohexane/cyclohexene. Sep. Purif. Technol. 2021, 257, 117907. [Google Scholar] [CrossRef]
- Duran, M.A.; Grossmann, I.E. A mixed-integer nonlinear programming algorithm for process systems synthesis. AICHE J. 1986, 32, 592–606. [Google Scholar] [CrossRef]
- Rathore, R.N.S.; Vanwormer, K.A.; Powers, G.J. Synthesis of distillation systems with energy integration. AICHE J. 1974, 20, 940–950. [Google Scholar] [CrossRef]
- William, L. Plantwide Dynamic Simulators in Chemical Processing and Control, 1st ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar] [CrossRef]
- Seider, W.D.; Lewin, D.R.; Seader, J.D.; Widagdo, S.; Gani, R.; Ng, K.M. Product and Process Design Principles: Synthesis, Analysis and Evaluation, 4th ed.; John Wiley & Sons: New York, NY, USA, 2019. [Google Scholar]
- Luyben, W.L. Principles and Case Studies of Simultaneous Design, 1st ed.; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Luyben, W.L. Capital cost of compressors for conceptual design. Chem. Eng. Proce. Proce. Inten. 2018, 126, 206–209. [Google Scholar] [CrossRef]






| The logic-based proximity principle Bender’s decomposition algorithm for mixed-integer nonlinear programming. | |
| S1. Initialization (multi-start points strategy with hyperparameter ) | |
| Initialize fixed integer combinations , and their neighborhood and , solve the nonlinear programming subproblem (Formulas (4)–(6)) for each fixed integer combinations with objective function value , and , constraint function value , and , and the optimal objective function value . Set and . | |
| S2. Mixed-integer linear programming master problem | |
| Solve mixed-integer linear programming master problem (Formulas (13)–(15) and (24)–(31) with all solution of nonlinear programming subproblem (Formulas (4)–(6)). The result of solution is with optimization objective function value , if , set and continue with S4, else set and continue with S3. | |
| S3. Nonlinear programming subproblem | |
| solve the nonlinear programming subproblem (Formulas (4)–(6)) for each fixed integer combinations and their neighborhood and , with objective function value , and , constraint function value , and , and optimal objective function value , if , set . Then set and continue with S2. | |
| S4. Convergence judgment (delayed convergence strategy with hyperparameter ) | |
| If , end the algorithm, the global optimal solution is the independent variable corresponding to . Else, set and continue with S3. | |
| Hyperparameter h | Average CPU Consumption (Excluding NLP Consumption)/s | Average Number of Iterations | Average Number of NLP Solved | Theoretical Number of NLP Solved Increases |
|---|---|---|---|---|
| 1 | 39.70 | 32.9 | 164.4 | - |
| 5 | 42.23 | 30.3 | 171.7 | (5 − 1) × 5 |
| 15 | 60.63 | 26.5 | 202.7 | (15 − 1) × 5 |
| Hyperparameters | LB-PBD () | LB-PBD () | LB-BD |
|---|---|---|---|
| 28/30 | 9/30 | 0/30 | |
| 30/30 | 20/30 | 0/30 | |
| 30/30 | 22/30 | 0/30 | |
| 30/30 | 30/30 | 0/30 | |
| 30/30 | 28/30 | 0/30 | |
| 30/30 | 30/30 | 0/30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, C.; Zhang, X.; Lan, Y.; Sun, J. An Enhanced Logic-Based Bender’s Decomposition Algorithm with Proximity Principle for Simulator-Based Distillation Process Optimization. Processes 2025, 13, 977. https://doi.org/10.3390/pr13040977
Tian C, Zhang X, Lan Y, Sun J. An Enhanced Logic-Based Bender’s Decomposition Algorithm with Proximity Principle for Simulator-Based Distillation Process Optimization. Processes. 2025; 13(4):977. https://doi.org/10.3390/pr13040977
Chicago/Turabian StyleTian, Chenshan, Xiaodong Zhang, Yang Lan, and Jinsheng Sun. 2025. "An Enhanced Logic-Based Bender’s Decomposition Algorithm with Proximity Principle for Simulator-Based Distillation Process Optimization" Processes 13, no. 4: 977. https://doi.org/10.3390/pr13040977
APA StyleTian, C., Zhang, X., Lan, Y., & Sun, J. (2025). An Enhanced Logic-Based Bender’s Decomposition Algorithm with Proximity Principle for Simulator-Based Distillation Process Optimization. Processes, 13(4), 977. https://doi.org/10.3390/pr13040977







