Experimental and Simulation Study of Particle Deposition Characteristics and Pressure Drop Evolution in Pleated Filter Media
Abstract
1. Introduction
2. Experiment and Numerical Simulation
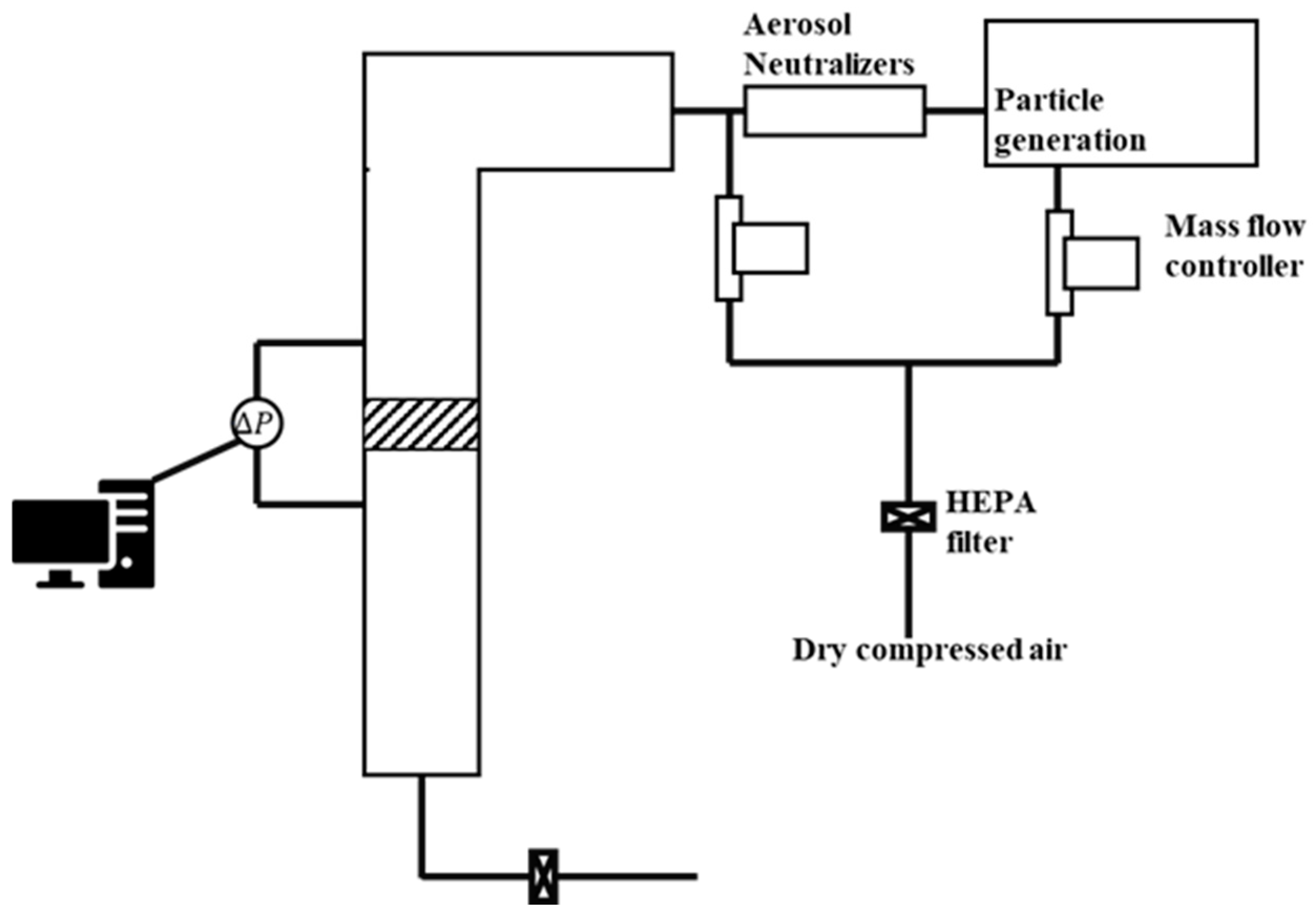
2.1. Experimental System and Preparation of Pleated Filter Element
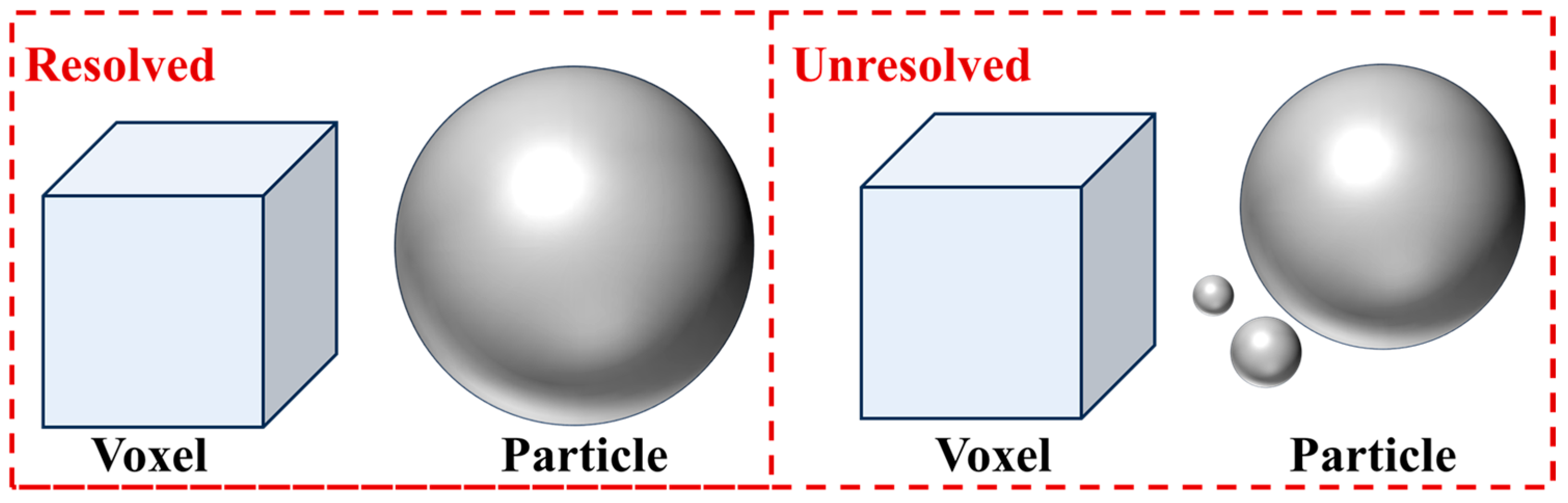
2.2. Numerical Simulation
- Precise calculation of the flow field information.
- Particle loading at the inlet, with particle trajectories computed based on the flow field.
- Particles are captured and deposited according to their trajectories.
- New flow field information is calculated based on the structure after particle deposition.
2.2.1. Geometric Parameters of Pleated Filter Media and Boundary Conditions
2.2.2. Fluid Flow Calculation
2.2.3. Particle Movement
3. Results and Discussion
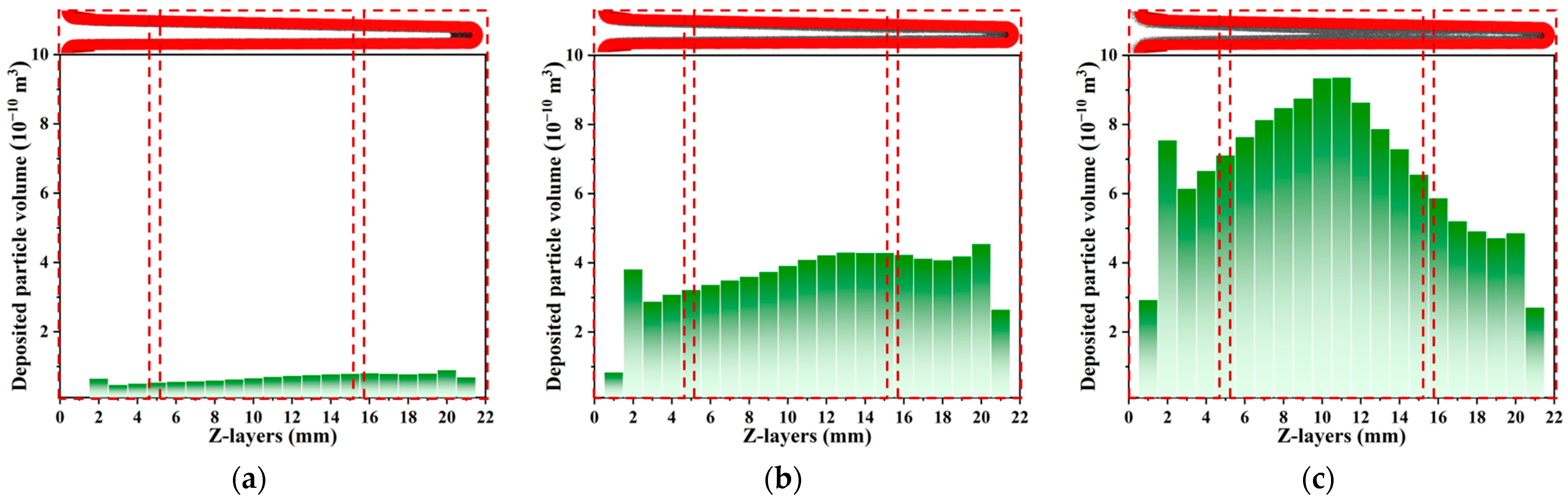
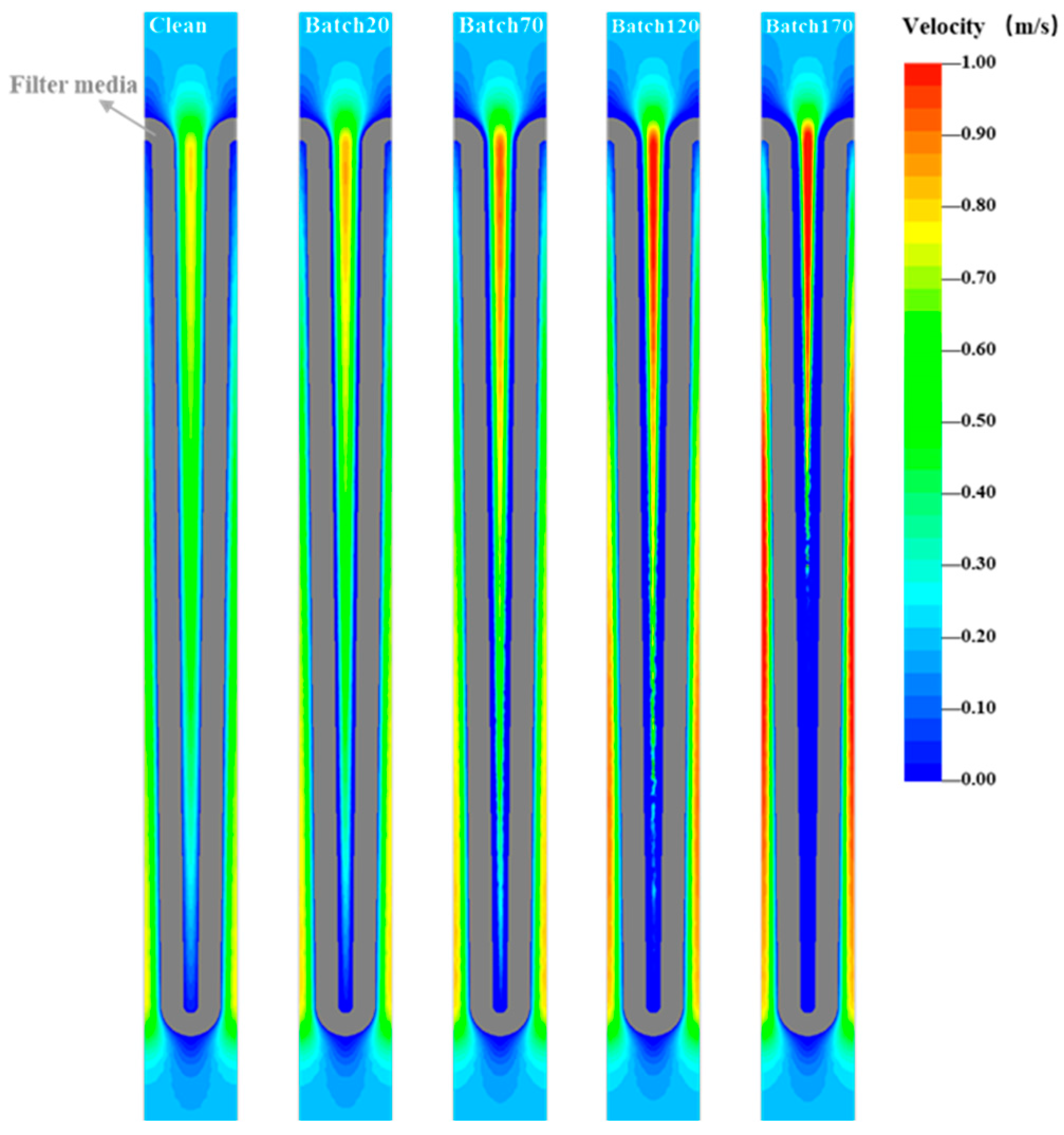
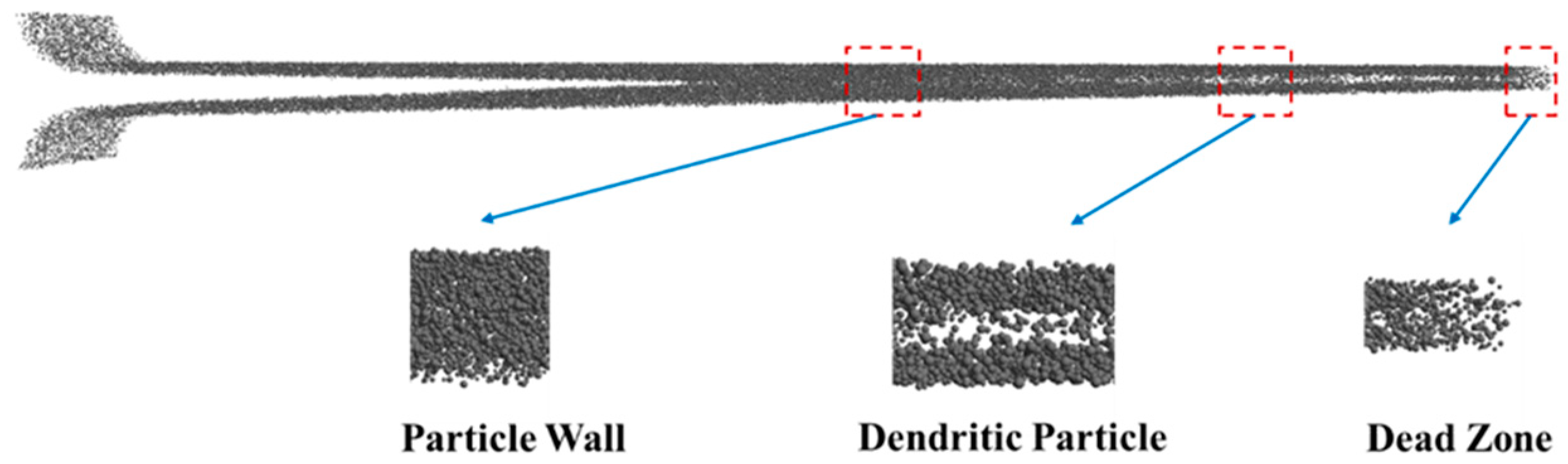
3.1. Particle Deposition Characteristics of Pleated Filter Media
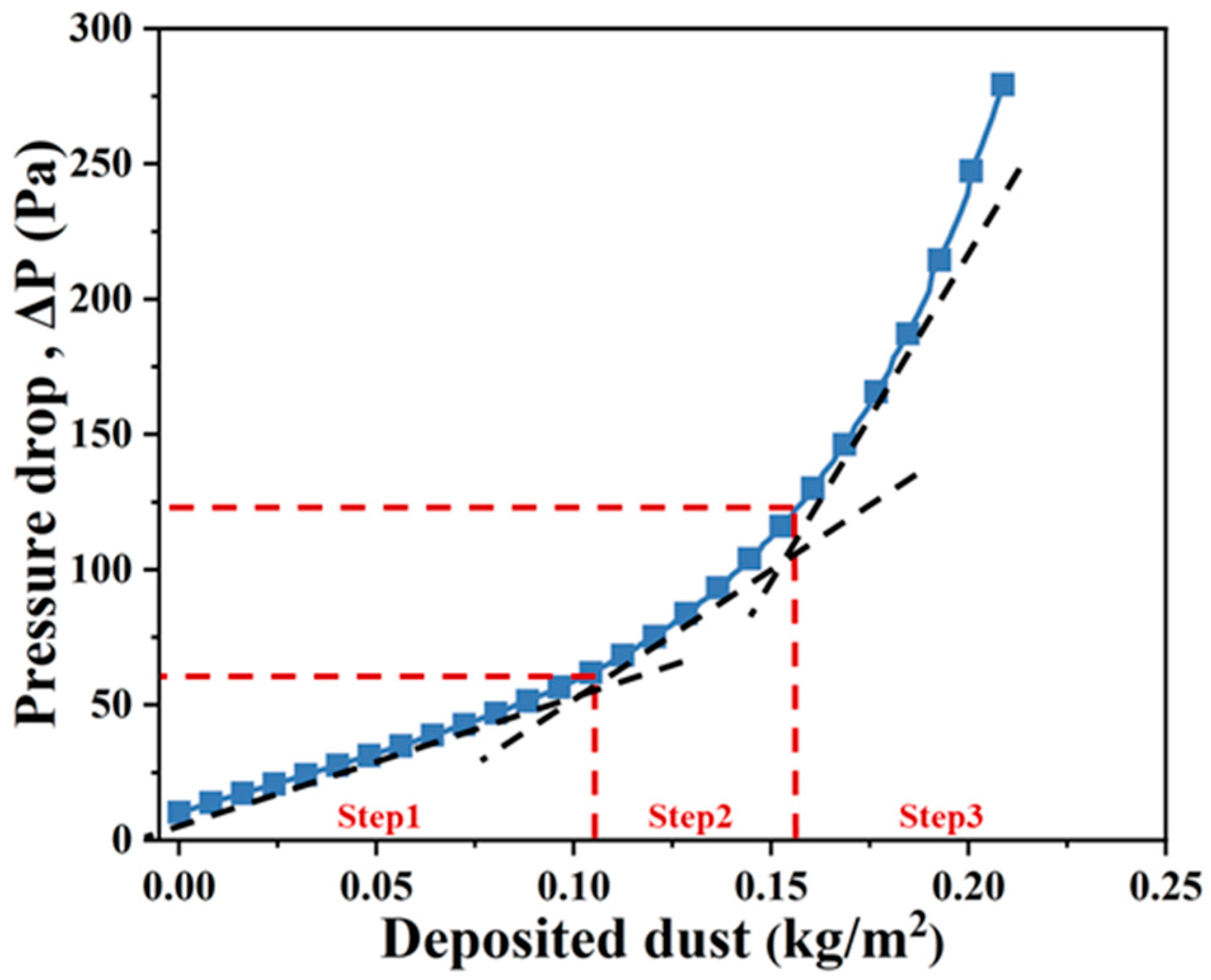
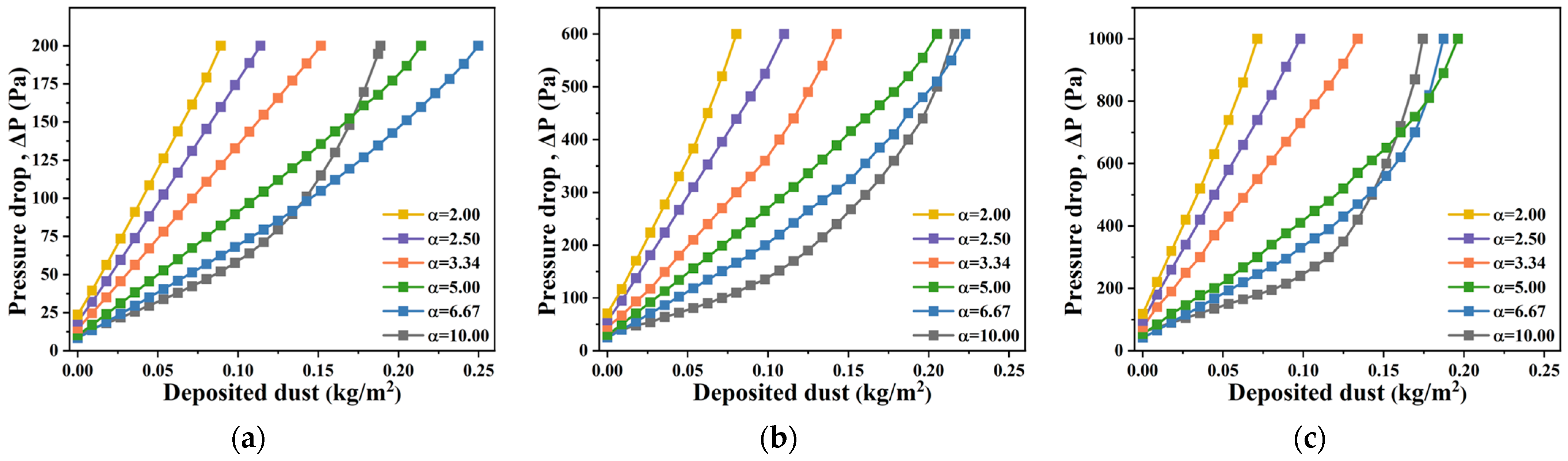
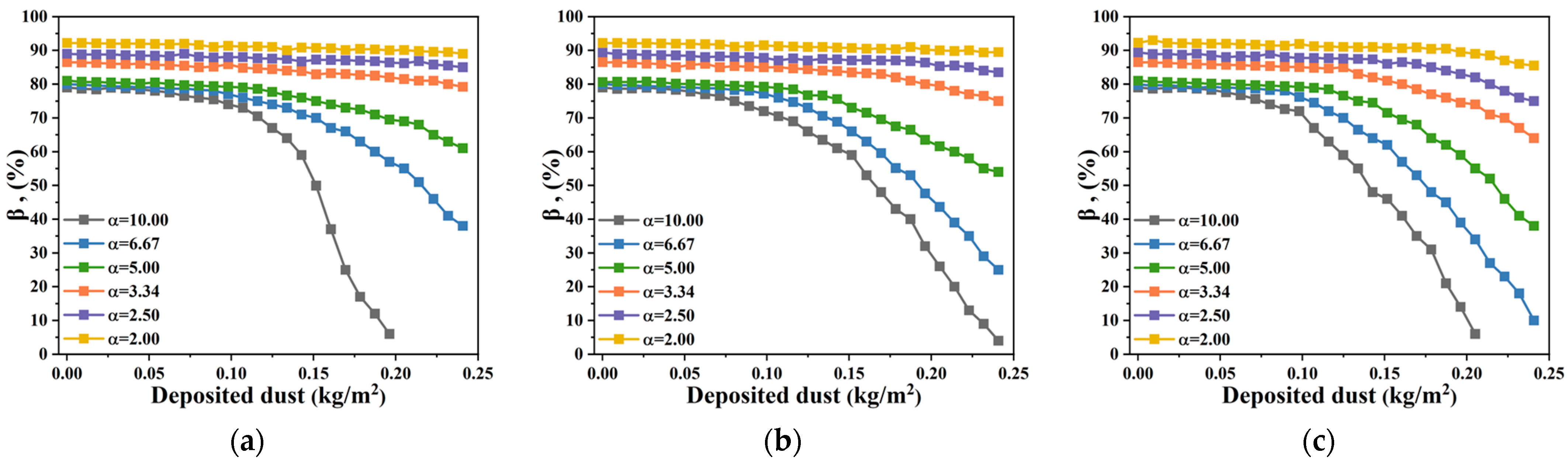
3.2. Effect of the Pleating Ratio on the Dust-Holding Performance of Pleated Filter Media
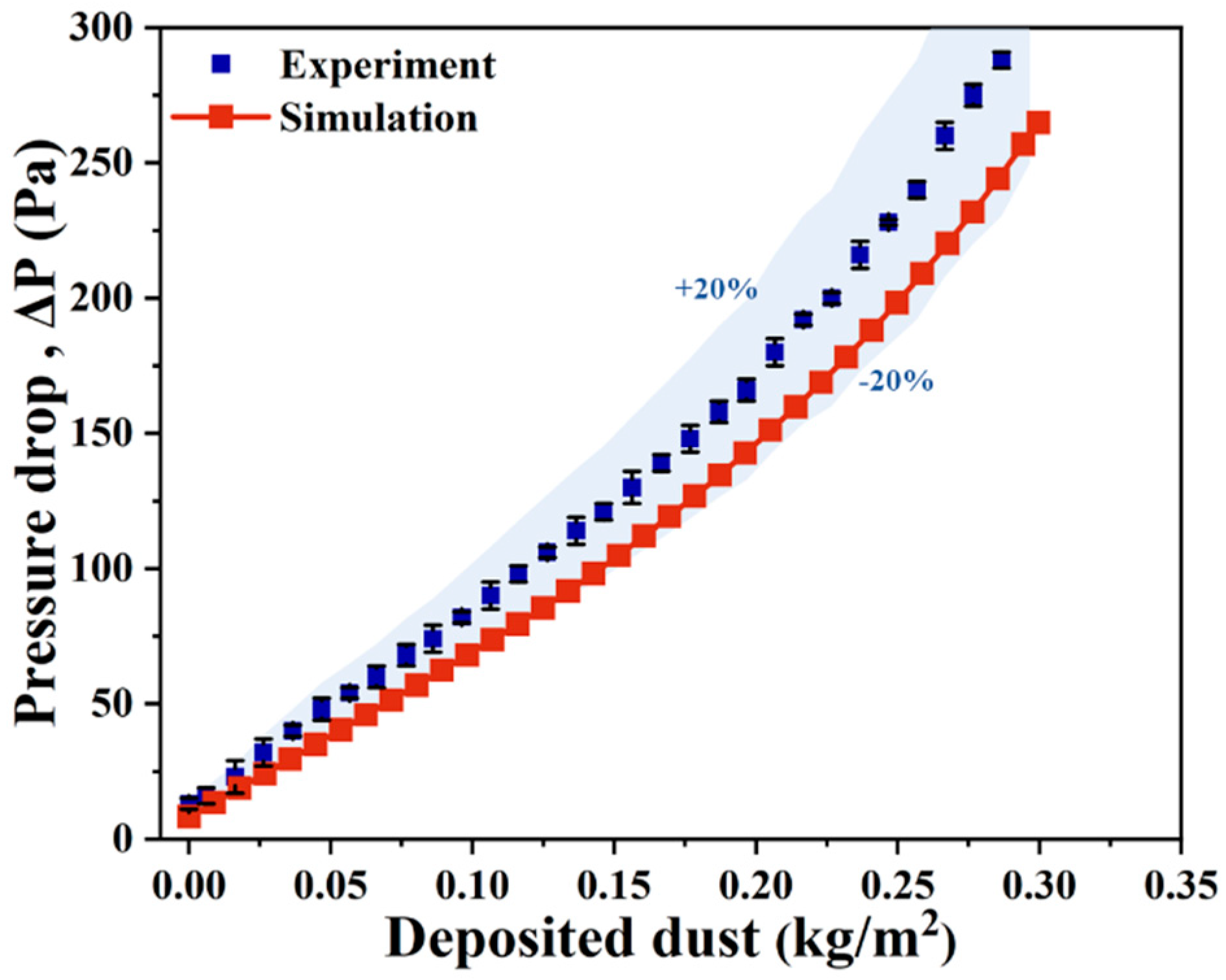
3.3. Experimental Verification of Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ivaneev, A.; Brzhezinskiy, A.; Karandashev, V.; Fedyunina, N.; Ermolin, M.; Fedotov, P. Nanoparticles of Dust as an Emerging Contaminant in Urban Environments. Environ. Geochem. Health 2024, 46, 367. [Google Scholar] [CrossRef]
- Fu, C.; Kuang, D.; Zhang, H.; Ren, J.; Chen, J. Different Components of Air Pollutants and Neurological Disorders. Front. Public Health 2022, 10, 959921. [Google Scholar] [CrossRef]
- Hahad, O.; Lelieveld, J.; Al-Kindi, S.; Schmitt, V.H.; Hobohm, L.; Keller, K.; Röösli, M.; Kuntic, M.; Daiber, A. Burden of Disease in Germany Attributed to Ambient Particulate Matter Pollution. Herz 2025, 50, 42–50. [Google Scholar] [CrossRef]
- Ammons, S.; Aja, H.; Ghazarian, A.A.; Lai, G.Y.; Ellison, G.L. Perception of Worry of Harm from Air Pollution: Results from the Health Information National Trends Survey (HINTS). BMC Public Health 2022, 22, 1254. [Google Scholar] [CrossRef] [PubMed]
- Morantes, G.; Jones, B.; Molina, C.; Sherman, M.H. Harm from Residential Indoor Air Contaminants. Environ. Sci. Technol. 2024, 58, 242–257. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zhang, Q.; Huang, G.; Huang, J.; Zhang, H. The Impact of PM2.5 on Kidney. J. Appl. Toxicol. 2023, 43, 107–121. [Google Scholar] [CrossRef]
- Pham, L.; Roach, T. Particulate Pollution and Learning. Econ. Educ. Rev. 2023, 92, 102344. [Google Scholar] [CrossRef]
- Lippi, G.; Mattiuzzi, C. Particulate Matter Pollution and Lung Cancer: A Worldwide Perspective. Clin. Respir. J. 2020, 14, 179–180. [Google Scholar] [CrossRef]
- Akduman, C.; Demirel, V.; Tezcan, F. Filter Life Comparison of Different Levels of Nanofiber Coated Cleanable-Surface Filter for Gas Turbine. J. Appl. Polym. Sci. 2021, 138, 50820. [Google Scholar] [CrossRef]
- Ma, S.; Zhou, Y.; Sun, Z.; Gu, H.; Wang, Y.; Yu, X. Numerical Simulation Study on the Filtration Performance of Metal Fiber Filters. Progress Nucl. Energy 2024, 171, 105169. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, Y.; Zhang, C.; Zhou, Y.; Yu, D.-G. Electrospun Nanofiber as Building Blocks for High-Performance Air Filter: A Review. Nano Today 2024, 55, 102161. [Google Scholar] [CrossRef]
- Luo, T.; Zhang, J.; Wang, J.; Shi, H.; Hong, Y.; Zhao, R. Sustainable Pollution Treatment System through Fiber Filter Materials. Sustain. Mater. Technol. 2024, 42, e01168. [Google Scholar] [CrossRef]
- Li, X.; Ba, X.; Dai, Y.; Feng, Y.; Yan, S.; Zhang, Q.; You, R. Silk Nanofibrillar Aerogel as Sustainable Filters for Environmental Purification. Small 2025, 2500226. [Google Scholar] [CrossRef]
- Kalani, S.; Jubinville, D.; Mekonnen, T.H. Nano-Porous Melt-Blown Poly(Lactic Acid) Fiber Mat Air Filters for High Efficiency Particulate Capture. Adv. Sustain. Syst. 2025, 202400898. [Google Scholar] [CrossRef]
- Jin, H.; Li, S.; He, S.; Hu, S.; Yuan, L.; Zhou, F. The Pressure Drop of Fibrous Surface Filters for Gas Filtration: Modeling and Experimental Studies. Sep. Purif. Technol. 2024, 350, 127981. [Google Scholar] [CrossRef]
- Zhao, X.; Bai, Y.; Fan, G.; Guo, H.; Shi, P.; Cui, W.; Jin, X.; Liu, Y.; Wang, R.; He, J. Large-Scale Fabrication of 3D Gradient Hierarchical Fibrous Filter Materials with Micro-Submicro-Nanofibers for Efficient and Long-Duration Air Filtration. Sep. Purif. Technol. 2025, 362, 131867. [Google Scholar] [CrossRef]
- Lin, X.; Sun, W.; Lin, M.; Chen, T.; Duan, K.; Lin, H.; Zhang, C.; Qi, H. Bicomponent Core/Sheath Melt-Blown Fibers for Air Filtration with Ultra-Low Resistance. RSC Adv. 2024, 14, 14100–14113. [Google Scholar] [CrossRef]
- Liao, J.; Nie, J.; Sun, B.; Jiao, T.; Zhang, M.; Song, S. A Cellulose Composite Filter with Multi-Stage Pores Had High Filtration Efficiency, Low Pressure Drop, and Degradable Properties. Chem. Eng. J. 2024, 482, 148908. [Google Scholar] [CrossRef]
- Sawatdee, S.; Botalo, A.; Noinonmueng, T.; Posoknistakul, P.; Intra, P.; Pongchaikul, P.; Charnnok, B.; Chanlek, N.; Laosiripojana, N.; Wu, K.C.W.; et al. Fabrication of Multilayer Cellulose Filters Isolated from Natural Biomass for Highly Efficient Air Filtration for Replacement of Synthetic HEPA Filters. Process Saf. Environ. Prot. 2025, 194, 216–230. [Google Scholar] [CrossRef]
- Chagas, P.A.M.; Lima, F.A.; Yamanaka, V.; Medeiros, G.B.; Guerra, V.G.; Oliveira, W.P.; Aguiar, M.L. Short Cellulose Acetate Nanofibers: A Novel and Scalable Coating for Enhancing Nanoparticles Filtration Efficiency of Filter Media. Sep. Purif. Technol. 2025, 358, 130315. [Google Scholar] [CrossRef]
- Ma, S.; Zhou, Y.; Sun, Z.; Gu, H.; Yuan, H.; Cao, S. Numerical Simulation Study on Depth Filtration Performance of Metal Fiber Pre-Filters with Different Pleat Structures. Nucl. Eng. Des. 2024, 425, 113337. [Google Scholar] [CrossRef]
- Cuiping, Y.; Wanlan, H.; Feng, X.; Junzhe, F.; Yang, L.; Yuyan, P.; Yunduan, W.; Ruizhi, M. The Effect of Pleat Ratio on the Effective Filtration Area of the Large-Diameter Pleated Filter Cartridge. Part. Sci. Technol. 2024, 42, 1031–1042. [Google Scholar] [CrossRef]
- Wu, J.; Lin, B.; Zhou, H.; Rao, Y.; Xu, C.; Zhou, Q.; Feng, S.; Zhong, Z.; Xing, W. Effect of Pleat Structure on the Air Purification Performance of a Polytetrafluoroethylene/Poly(Ethylene Terephthalate) Composite Membrane Filter. Ind. Eng. Chem. Res. 2023, 62, 16048–16057. [Google Scholar] [CrossRef]
- Park, B.H.; Lee, M.-H.; Jo, Y.M.; Kim, S.B. Influence of Pleat Geometry on Filter Cleaning in PTFE/Glass Composite Filter. J. Air Waste Manag. Assoc. 2012, 62, 1257–1263. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhou, Y.; Wang, Z.; Gu, H.; Sun, Z.; Li, Y.; Ma, S. Research on the Filtration Performance of Pleated Filters with Rectangular and Triangular Structures through Developed CFD Code. Progress Nucl. Energy 2022, 153, 104413. [Google Scholar] [CrossRef]
- Feng, Z.; Long, Z. Modeling Unsteady Filtration Performance of Pleated Filter. Aerosol Sci. Technol. 2016, 50, 626–637. [Google Scholar] [CrossRef]
- Cheng, K.; Zhu, J.; Qian, F.; Cao, B.; Lu, J.; Han, Y. CFD–DEM Simulation of Particle Deposition Characteristics of Pleated Air Filter Media Based on Porous Media Model. Particuology 2023, 72, 37–48. [Google Scholar] [CrossRef]
- Teng, G.; Shi, G.; Zhu, J. Influence of Pleated Geometry on the Pressure Drop of Filters during Dust Loading Process: Experimental and Modelling Study. Sci. Rep. 2022, 12, 20331. [Google Scholar] [CrossRef]
- Choi, P.; Santos, C.A.; Kim, M.K.; Jung, H.; Hong, D.Y.; Koo, J. Pressure Drop and Optimization Meta-Models for Arbitrary Low-Height Pleated Filter Shapes and Flowrates. J. Mech. Sci. Technol. 2021, 35, 5007–5022. [Google Scholar] [CrossRef]
- Dziubak, T. Experimental Studies of PowerCore Filters and Pleated Filter Baffles. Materials 2022, 15, 7292. [Google Scholar] [CrossRef]
- Théron, F.; Joubert, A.; Le Coq, L. Numerical and Experimental Investigations of the Influence of the Pleat Geometry on the Pressure Drop and Velocity Field of a Pleated Fibrous Filter. Sep. Purif. Technol. 2017, 182, 69–77. [Google Scholar] [CrossRef]
- Fotovati, S.; Hosseini, S.A.; Vahedi Tafreshi, H.; Pourdeyhimi, B. Modeling Instantaneous Pressure Drop of Pleated Thin Filter Media during Dust Loading. Chem. Eng. Sci. 2011, 66, 4036–4046. [Google Scholar] [CrossRef]
- Shu, Z.; Qian, F.; Fang, C.; Zhu, J. Numerical Simulation of Particle Spatial Distribution and Filtration Characteristic in the Pleated Filter Media Using OpenFOAM. Indoor Built Environ. 2021, 30, 1159–1172. [Google Scholar] [CrossRef]
- Kim, Y.; Kwon, M.; Lee, M. Optimized Pleat Geometry at Specific Pleat Height in Pleated Filters for Air Purification. Indoor Air 2022, 32, e13135. [Google Scholar] [CrossRef]
- Saleh, A.M.; Fotovati, S.; Vahedi Tafreshi, H.; Pourdeyhimi, B. Modeling Service Life of Pleated Filters Exposed to Poly-Dispersed Aerosols. Powder Technol. 2014, 266, 79–89. [Google Scholar] [CrossRef]
- Li, S.; Hu, S.; Xie, B.; Jin, H.; Xin, J.; Wang, F.; Zhou, F. Influence of Pleat Geometry on the Filtration and Cleaning Characteristics of Filter Media. Sep. Purif. Technol. 2019, 210, 38–47. [Google Scholar] [CrossRef]
- ISO 12103-1:2024; Road Vehicles—Test Contaminants for Filter Evaluation. Part 1: Arizona Test Dust. ISO: Geneva, Switzerland, 2024.
- Fotovati, S.; Tafreshi, H.V.; Pourdeyhimi, B. A Macroscale Model for Simulating Pressure Drop and Collection Efficiency of Pleated Filters over Time. Sep. Purif. Technol. 2012, 98, 344–355. [Google Scholar] [CrossRef]
- Iliev, O.; Laptev, V. On Numerical Simulation of Flow Through Oil Filters. Comput. Vis. Sci. 2004, 6, 139–146. [Google Scholar] [CrossRef]
- Song, Y.; Shim, E. High-Fidelity 3D Simulation of Dust-Loading Behavior and Clogging Process of Coarse Nonwoven Filter Media Considering Collision Effect. Sep. Purif. Technol. 2024, 344, 127046. [Google Scholar] [CrossRef]
- Becker, J.; Cheng, L.; Kronsbein, C.; Wiegmann, A. Simulation of Cake Filtration for Polydisperse Particles. Chem. Eng. Technol. 2016, 39, 559–566. [Google Scholar] [CrossRef]
- Linden, S.; Wiegmann, A.; Hagen, H. The LIR Space Partitioning System Applied to the Stokes Equations. Graph. Models 2015, 82, 58–66. [Google Scholar] [CrossRef]
- Chen, L.; Hu, W.; Xu, Y.; Qian, F.; Li, H.; Zheng, Z. The Study of Dust-Holding Characteristics of Pleated Non-Uniform Porous Media: Macroscale Simulations. Sep. Purif. Technol. 2025, 362, 131719. [Google Scholar] [CrossRef]
- Glowinski, R.; Pironneau, O. Finite Element Methods for Navier-Stokes Equations. Annu. Rev. Fluid. Mech. 1992, 24, 167–204. [Google Scholar] [CrossRef]
- Kang, S.; Lee, H.; Kim, S.C.; Chen, D.-R.; Pui, D.Y.H. Modeling of Fibrous Filter Media for Ultrafine Particle Filtration. Sep. Purif. Technol. 2019, 209, 461–469. [Google Scholar] [CrossRef]
- Cheng, L.; Rief, S.; Wiegmann, A.; Techno, F.-I. Nano Filtration Media—Challenges of Modelling and Computer Simulation. Available online: https://www.math2market.com/fileadmin/Showroom/Presentations/2001-2010/2009FiltechWiesbadenNanoChengPaper.pdf (accessed on 19 March 2025).
- Crowe, C.T.; Crowe, C.T. (Eds.) Multiphase Flow Handbook; CRC Press: Boca Raton, FL, USA, 2005; ISBN 978-0-429-12657-4. [Google Scholar]
- Pan, Z.; Ou, Q.; Romay, F.J.; Chen, W.; You, T.; Liang, Y.; Wang, J.; Pui, D.Y.H. Study of Structural Factors of Structure-Resolved Filter Media on the Particle Loading Performance with Microscale Simulation. Sep. Purif. Technol. 2023, 304, 122317. [Google Scholar] [CrossRef]
- Teng, G.; Shi, G.; Zhu, J.; Qi, J.; Zhao, C. Research on the Influence of Pleat Structure on Effective Filtration Area during Dust Loading. Powder Technol. 2022, 395, 207–217. [Google Scholar] [CrossRef]
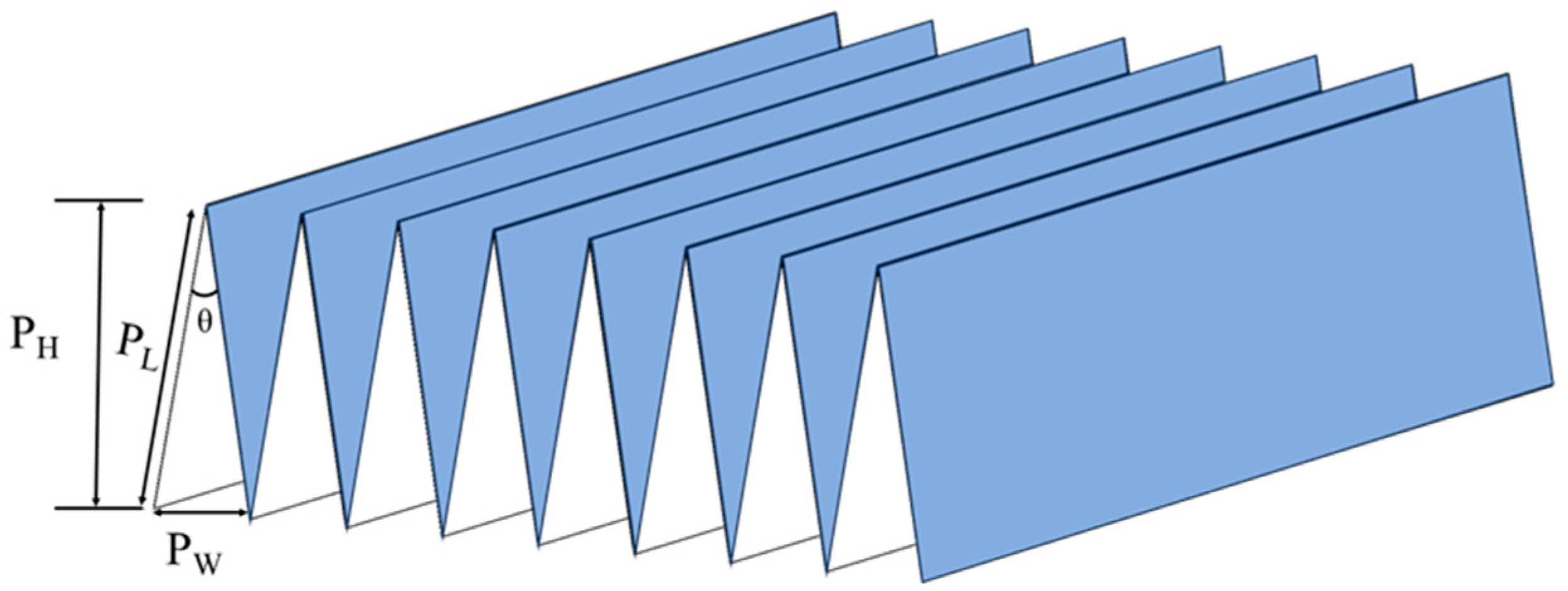








| Parameters | Type 1 | Type 2 | Type 3 | Type 4 | Type 5 | Type 6 |
|---|---|---|---|---|---|---|
| Pleat height (PH, mm) | 20 | 20 | 20 | 20 | 20 | 20 |
| Pleat width (PW, mm) | 2 | 3 | 4 | 6 | 8 | 10 |
| Pleat length (PL, mm) | 20.04 | 20.07 | 20.10 | 20.23 | 20.40 | 20.62 |
| Pleat ratio (α, PH/PW) | 10.00 | 6.67 | 5.00 | 3.34 | 2.50 | 2.00 |
| Angle (θ, °) | 5.85 | 8.77 | 11.71 | 17.50 | 23.14 | 28.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Kang, J.; Wang, D.; Liang, Y.; Wang, L.; Xu, G.; Wang, H.; Tang, M. Experimental and Simulation Study of Particle Deposition Characteristics and Pressure Drop Evolution in Pleated Filter Media. Processes 2025, 13, 975. https://doi.org/10.3390/pr13040975
Guo C, Kang J, Wang D, Liang Y, Wang L, Xu G, Wang H, Tang M. Experimental and Simulation Study of Particle Deposition Characteristics and Pressure Drop Evolution in Pleated Filter Media. Processes. 2025; 13(4):975. https://doi.org/10.3390/pr13040975
Chicago/Turabian StyleGuo, Changzeng, Jian Kang, Desheng Wang, Yun Liang, Lingyun Wang, Guilong Xu, Hao Wang, and Min Tang. 2025. "Experimental and Simulation Study of Particle Deposition Characteristics and Pressure Drop Evolution in Pleated Filter Media" Processes 13, no. 4: 975. https://doi.org/10.3390/pr13040975
APA StyleGuo, C., Kang, J., Wang, D., Liang, Y., Wang, L., Xu, G., Wang, H., & Tang, M. (2025). Experimental and Simulation Study of Particle Deposition Characteristics and Pressure Drop Evolution in Pleated Filter Media. Processes, 13(4), 975. https://doi.org/10.3390/pr13040975






