Abstract
This study investigates the impact of injection depth on CO2 plume migration dynamics in saline aquifers, a critical aspect of secure and efficient carbon capture, utilization, and storage (CCUS). While CCUS offers a vital pathway for mitigating greenhouse gas emissions, challenges such as buoyancy-driven flow, salinity effects, and potential leakage threaten long-term CO2 containment. Using compositional reservoir simulation (CMG GEM 2021.10, Calgary, Canada) and Illinois Basin Decatur Project (IBDP) data, we modeled CO2 injection into a 10,000 ppm salinity aquifer, evaluating the effects of single- and multi-depth injection (5370 to 5385 ft). The results demonstrate that multi-depth injection significantly enhances CO2–brine contact area, promoting dissolution trapping and mitigating buoyancy-driven migration. This enhanced dissolution and residual trapping improves horizontal containment and overall storage security in the modeled salinity environment. The work provides valuable insights for optimizing injection strategies to maximize CO2 storage efficiency and minimize leakage risks.
1. Background
Carbon capture and storage (CCS) has become a key method to lower atmospheric CO2 levels as the need for solutions to decrease greenhouse gas emissions grows globally. Geological sequestration is regarded as a feasible long-term strategy for storing CO2 because of its extensive storage capabilities and accessibility, especially in deep saline aquifers. A significant amount of anthropogenic CO2 emissions could be stored in saline aquifers, which are thought to have a worldwide storage capacity of 1000–10,000 gigatons [1,2]. The effectiveness of CO2 storage in saline aquifers depends on multiple factors, including reservoir salinity, temperature, depth, and permeability. Among these factors, salinity plays a particularly important role as it influences the solubility of CO2 in the formation water, the density and viscosity of brine, and the physical and chemical interactions between CO2 and the reservoir matrix [3]. These parameters, in turn, affect the CO2 plume migration dynamics, which are critical to ensuring safe and effective storage. Drilling and fracturing operations, integral to accessing some reservoirs, have also been shown to enhance CCUS potential by increasing permeability and reducing migration barriers. For instance, hydrates formed as by-products during CO2 leakage can play a role in preventing further leakage [4]. Horizontal migration of the CO2 plume is a particularly relevant aspect of storage as it determines the extent of horizontal spread and impacts the risk of leakage, containment integrity, and storage efficiency. According to earlier research, higher salinity tends to decrease CO2 solubility, which lowers the dissolved phase and restricts the reservoir’s storage capacity. This mechanism, called the “salting-out effect”, promotes the formation of a free gas phase, which has a higher capacity for migration, and limits the solubility of CO2 in extremely saline settings. The main factors influencing the horizontal migration of CO2 are buoyant forces, pressure gradients, and the formation’s permeability; in this study, these factors are controlled by injection depth and salinity levels [5].
2. Literature Review
2.1. CO₂ Sequestration in Saline Aquifers
Due to their extensive availability and high storage capacities which are expected to be between 1000 and 10,000 gigatons worldwide saline aquifers, which are large porous formations filled with brine, are among the most promising choices for CO2 storage [2]. Because they provide a variety of CO2 trapping mechanisms, such as structural, residual, solubility, and mineral trapping, these aquifers are ideal for geological sequestration [6]. Early in the injection phase, structural and residual trapping processes are involved because CO2 takes up pore spaces and becomes immobile in trapped pockets. Mineral trapping enables CO2 to react with minerals to generate stable compounds that permanently sequester CO2, whereas solubility trapping happens when CO2 dissolves into brine over time [5].
The high salinity of these aquifers, however, can impact CO2 storage efficiency. CO2 solubility in brine decreases as salinity increases, which can reduce the amount of CO2 that can be securely stored in dissolved form [7,8]. This salting-out effect highlights the importance of understanding how different salinity levels affect CO2 plume behavior.
2.2. CO₂ Storage Mechanisms in Saline Aquifers
Multiple trapping methods that hold CO2 in various phases and guarantee its long-term containment within the geological formation are used to store CO2 in saline aquifers. From short-term physical trapping to long-term geochemical trapping, each mechanism has a unique function over different periods. The following are the main trapping mechanisms:
- Structural and Stratigraphic Trapping
Structural and stratigraphic trapping are the primary and immediate mechanisms for CO2 storage in saline aquifers. In structural trapping, CO2 is physically held beneath an impermeable caprock or geological barrier, which prevents its upward migration due to buoyancy. Stratigraphic trapping, on the other hand, occurs in reservoirs with complex sedimentary layers, where CO2 becomes confined within certain strata due to variations in rock properties [7]. These mechanisms provide the initial containment for injected CO2 and are particularly effective in formations with domes, anticlines, or faulted structures.
Stratigraphic trapping are especially effective for CO2 storage in saline aquifers with well-defined caprocks [2]. The effectiveness of this mechanism depends on the integrity and thickness of the caprock and the structural features of the formation.
- Residual Trapping
Residual trapping occurs when CO2 is immobilized within the pore spaces of the rock through capillary forces as it migrates through the aquifer. As CO2 moves, small amounts become trapped in pore throats, where it remains even after the primary plume migrates onward. This mechanism provides a stable form of storage since trapped CO2 becomes disconnected from the main plume, preventing it from migrating further [9].
The effectiveness of residual trapping is influenced by the aquifer’s pore structure, capillary pressure, and the degree of CO2 saturation. Research has shown that residual trapping can account for a significant proportion up to 30% of CO₂ storage capacity in saline aquifers, as CO2 is effectively immobilized in small clusters throughout the [10].
- Solubility Trapping
In solubility trapping, CO2 dissolves into the brine within the aquifer, forming a homogeneous solution that is less buoyant than free-phase CO2 and thus less likely to migrate. This dissolution process occurs gradually, and while it is a slower form of trapping compared to structural or residual trapping, it significantly enhances storage security over time [3]. The extent of solubility trapping is influenced by factors such as aquifer salinity, pressure, and temperature, with lower salinity levels allowing greater CO2 dissolution due to the salting-out effect [11].
As CO2 dissolves in brine, it creates a density contrast that can drive convective mixing, further enhancing dissolution rates. This convective mixing effect can accelerate the process of solubility trapping and improve CO2 storage efficiency in saline aquifers with high permeability [5].
- Mineral Trapping
Since CO2 is transformed into solid minerals by geological processes with the surrounding rock matrix, mineral entrapment is the most stable and long-lasting method of storing CO2. Carbonic acid, which is created when CO2 dissolves in brine, can react with aquifer minerals to generate carbonate minerals, thereby trapping CO2 in a solid state. Because the CO2 is trapped in crystalline form, this method offers the most secure form of storage over extended durations, frequently hundreds to thousands of years [12].
2.3. Aquifer Salinity in Louisiana
Saline aquifers in Louisiana show a range of salinity levels that affect their potential for CO2 sequestration. According to the U.S. Geological Survey (USGS), Louisiana’s coastal lowlands aquifer system holds approximately 16,300 million acre-feet of saline water, categorized as slightly to moderately saline (1000 to 10,000 mg/L dissolved solids) and very saline (10,000 to 35,000 mg/L dissolved solids) (Figure 1) [13]. These varying salinity levels influence CO2 storage dynamics, as salinity impacts the solubility of CO2 in brine, as well as the viscosity and density of formation water factors that govern CO2 plume migration and containment within these aquifers.
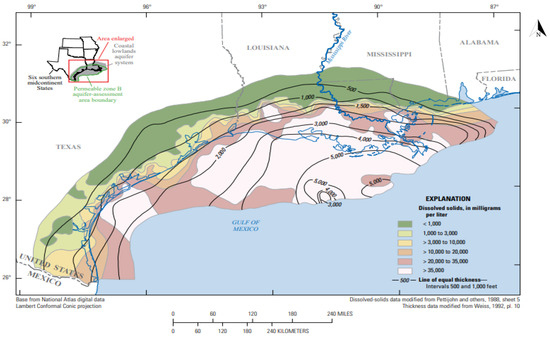
Figure 1.
Dissolved solid concentrations and thickness in the Gulf Coast Regional Aquifer System [13].
2.4. Impact of Injection Depth on CO₂ Migration
Injection depth plays a critical role in CO2 migration dynamics. Deeper injections expose CO2 to higher pressure and temperature conditions, which help maintain CO2 in a supercritical state with higher density and lower viscosity, reducing the tendency for buoyant migration. Conversely, shallower injection depths result in less dense CO2, enhancing buoyancy and increasing the risk of upward migration and horizontal spread [14,15]. Research [15] emphasizes that understanding the influence of injection depth is essential for predicting CO2 migration patterns and designing effective containment strategies, particularly for horizontal migration, where the plume may spread across wide areas under certain depth conditions. As an example, the Illinois Basin Decatur Project (IBDP) involves injecting CO2 at a depth of approximately 2100 m (6890 feet) into the Mount Simon Sandstone Formation, a geologically stable saline aquifer. This depth was strategically chosen to ensure that the CO2 remains securely stored, as the overlying shale layers provide an effective caprock for containment. Since its inception, the IBDP has successfully stored over one million metric tons of CO2, offering valuable insights into the viability of large-scale carbon storage and the geomechanical behavior of deep saline formations under CO2 injection [16].
2.5. Horizontal vs. Vertical Migration of CO₂ Plumes
While buoyancy forces often drive CO2 to migrate vertically within an aquifer, horizontal migration is equally important to consider, especially in sloping or heterogeneous formations [17]. Horizontal migration extends the horizontal reach of the plume and can impact surrounding areas within the aquifer. This horizontal spread is particularly affected by reservoir heterogeneity, pressure gradients, and capillary forces, all of which can vary across different aquifer layers [3].
Horizontal migration is critical for effective containment, as it can influence both the spatial distribution of CO2 and the potential for interaction with faults or other geological features. Research [5] highlights that horizontal migration distances are significantly affected by permeability contrasts within the aquifer, where high-permeability zones enhance horizontal spread and lower-permeability zones restrict plume movement. Understanding these dynamics is crucial for selecting aquifer sites and designing monitoring strategies that ensure effective containment over the long term.
3. Methodology
Using characteristics taken from the Illinois Basin Decatur Project, this work simulates the injection of CO2 into a saline aquifer under realistic conditions that are typical of deep (onshore Louisiana) saline deposits using CMG GEM. The model is intended to study the horizontal migration of CO2 plumes, looking at the effects of injection depth on containment, plume dynamics, and overall storage efficiency over a 200-year period (2024 to 2224) represented by the horizontal axis of graph profiles.
3.1. Model Setup and Grid Configuration
The model consists of a 3D grid with dimensions of 50 × 30 × 4 along the X, Y, and Z directions, respectively, with a width of 10 ft in all directions built with CMG 2021.10 software (Figure 2). This grid size was chosen to provide a sufficiently large area for observing horizontal migration patterns while maintaining a manageable number of cells for computational efficiency. The grid depth to the top is set at a depth of 5365 ft to reflect the conditions typical of the Illinois Basin Decatur Project’s geological setting. The four vertical layers in the grid allow CO2 injection at varying depths (5370 ft, 5375 ft, 5380 ft, and 5385 ft), enabling an assessment of how injection depth influences the horizontal spread and trapping of CO2 within the aquifer.

Figure 2.
Grid model.
3.2. Reservoir Properties
Reservoir PVT, rock, and rock/fluid property (Figure 3) data are based on the Illinois Basin Decatur Project’s parameters, ensuring that the model closely resembles real-world CO2 storage conditions. The horizontal permeability (kx and ky) is set to 200 millidarcies (mD) to permit significant horizontal CO2 migration, while vertical permeability (kz) is set to 20 mD, which restricts vertical movement and promotes horizontal dispersion of the plume. The uniform porosity of 30% across the grid cells reflects the average porosity observed in the Illinois Basin, contributing to consistent storage ability within the bearing saline formation. Additionally, the reservoir temperature is set at 112 °F, the reference pressure is 3205 psi, and the rock compressibility is 3.2 × 10−6 1/psi.
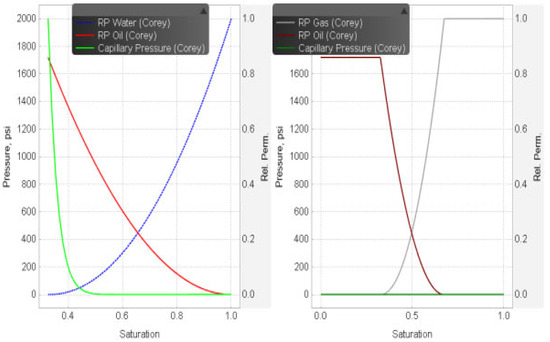
Figure 3.
Relative permeability curve from the IBDP (EDX 2021).
3.3. Aquifer Salinity Level and Aqueous Phase Components
These salinity levels correspond to the concentration of dissolved salts, primarily in the form of ions such as Na⁺ (sodium) and Cl⁻ (chloride). The simulator allows the following components to participate in the aqueous reactions:
H2O ⟷ H+ + OH−
CO2 + H2O ⟷ H+ + HCO−3
NaHCO3 ⟷ HCO−3 + Na+
NaCl(s) ⟷ Na+ + Cl−
CaCO3(s) + H+ ⟷ Ca2+ + HCO−3
3.4. CO₂ Injection Parameters
Supercritical CO2 was injected at a constant rate of 35,000 scf/day for three years to ensure a controlled comparison of injection performance at varying depths. Injection occurred at four discrete depths, 5370 ft, 5375 ft, 5380 ft, and 5385 ft, corresponding to the center of each of four distinct grid layers (Figure 4). This relatively small depth variation was selected to evaluate the influence of initial pressure and temperature conditions on CO2 migration while maintaining the CO2 in a dense, supercritical state to minimize buoyancy effects. Following the injection period, each simulation included a post-injection monitoring phase to track residual CO2 migration and assess long-term containment dynamics as the plume stabilized and interacted with the brine.
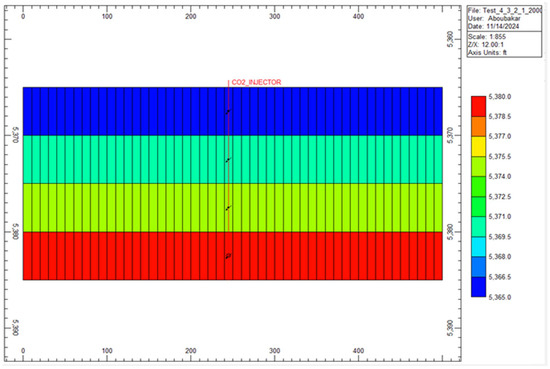
Figure 4.
Vertical profile and injection depths.
Table 1 summarizes the model parameters.

Table 1.
Model parameter summary.
3.5. Simulation Process and Data Collection
The simulation of CO2 injection and migration in saline aquifers incorporates multiple equations; these equations collectively simulate how CO2 interacts with brine, migrates within the aquifer, and undergoes various trapping mechanisms. The following are the key equations and processes used during simulation and data collection:
- Steady-state Aquifer:
This model assumes that the pressure at the external boundary of the aquifer does not change.
Then, the rate of water influx is
where CA = total compressibility of the aquifer, = pressure at the external boundary of the aquifer, and = average pressure at the aquifer–reservoir interface.
- Well Model:
The well model is an extension of the approach proposed by Peaceman [18,19] for both square and non-square gridblocks. The treatment of mobility adheres to the method suggested by Chappelear and Williamson [20]. Furthermore, the geometric factor enables the calculation of the equivalent radius based on the gridblock’s geometry and the well’s position within it. The injection well model establishes a relationship between the reservoir flow rate of phase , the wellbore pressure , and the pressure at the grid point as follows:
where = flow rate of phase j (j = g,w) at reservoir conditions (ft3/day), = well injectivity index, = total mobility of the fluid in the well block, = bottomhole pressure (kPa | psia), = pressure of th gridblock containing the well (kPa | psia), = fraction of completion of the well in the gridblock, = effective permeability in the plane perpendicular to the well direction, = gridblock thickness in the well direction (m | ft), = well fraction governed by areal geometry, = effective radius (m ft), = wellbore radius (ft), and S = skin factor.
- Pressure Loss Equation:
The wellbore model is an adaptation of the method by Aziz et al. [21], incorporating modifications that utilize an EOS to determine the phase behavior and fluid properties of the flowing fluid. The equation that describes the pressure variation along the flow direction in the wellbore model is
where is the hydrostatic pressure, is the kinetic energy gain, and is the friction gain. Here, ρ = density of the flowing “in situ” mixture, = acceleration due to gravity, f = fanning friction factor, = average velocity of the mixture, = inside pipe diameter, and = − = pressure drop over the length .
- Partial Molar Volume Equation:
For CO₂, an internally developed correlation that aligns with the experimental data from Duan and Sun [22,23] is applied:
where T is the temperature in °C.
- Effect of Salinity:
The salting-out coefficient used is defined by the following relationship between Henry’s constant in pure water and in brine [24]:
where = Henry’s constant of component in brine (salt solution), = Henry’s constant of component at zero salinity, = salting-out coefficient for component , and = molality of the dissolved salt (mol/kg H2O).
Bakker [25] provides the following correlations for the salting-out coefficients of CO₂ and CH₄, based on the data from Cramer [24]:
where is the temperature in °K.
- Darcy’s Law for Multiphase Flow:
Darcy’s Law governs the flow velocities of each phase (CO2 and brine) through the porous media of the saline aquifer, based on the formation’s permeability, viscosity, and pressure gradients:
where = absolute permeability of the formation, = relative permeability of phase (varies with saturation), = viscosity of phase (affected by salinity and temperature), ∇Pα = pressure gradient of phase , and = density of phase .
- Peng–Robinson Equation of State (EOS) for Phase Behavior:
The Peng–Robinson EOS is used to model the phase behavior of CO2 under high-pressure, high-temperature conditions, allowing the simulator to account for CO2 properties in the supercritical and gaseous states:
where = 8.314 J/mol. K, = molar volume of CO2 or brine phase, a = attraction parameter, and = repulsion parameter.
4. Results and Discussion
4.1. CO2 Plume Migration in Layer 4 (Bottom Layer)
With the largest CO2 mole fractions concentrated close to the wellbore (around 0.99), the plume in this instance exhibits a radial spread centered around the injection site, progressively declining outward (Figure 5). According to this gradient, dissolution trapping becomes increasingly important toward the edges of the plume, whilst CO2 is mostly in a supercritical phase close to the injection site. The sustained saturation levels in the outer plume regions are a result of increased dissolution trapping caused by the reduced salinity, which also increases CO2 solubility in brine. A significant amount of CO2 has changed into a dissolved state, stabilizing the horizontal spread of the plume, as evidenced by the trapping mechanisms graph, which displays a consistent increase in dissolved CO2 over time.
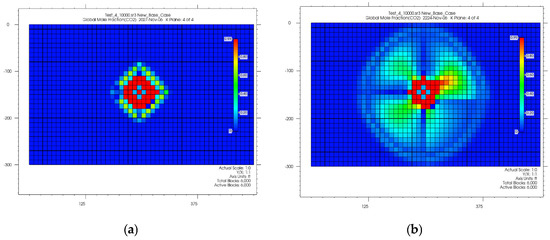
Figure 5.
Plume migration in layer 4 from shut-in (a) to the end of the simulation (b).
The residually trapped CO2 continues to increase steadily after 2007 days, reaching a peak of 84,854 moles. This can be attributed to the dissipation of the pressure buildup created during the injection phase once injection ceases. As the pressure decreases, brine from surrounding areas flows back toward the injection site, and this backflow effectively traps the CO2 in the pore throats of the reservoir. When mineral and dissolution trapping mechanisms take effect, residual trapping starts decreasing, reaching 66,080 moles at the end of the simulation period. The supercritical CO2 fraction starts high at approximately 2.2 million moles but decreases gradually, reflecting a phase transition or dissolution into the aqueous phase, reaching about 1.4 million moles. Conversely, the CO2 dissolved in the formation shows a significant increase, starting at zero and rising to over 1.56 million moles, highlighting the active role of solubility trapping in long-term storage. The decreasing slope of the dissolved CO2 curve over time may result from the brine gradually reaching saturation with CO2, which limits the rate of further dissolution. In addition, the salting-out effect may limit CO2 solubility due to increased ionic strength in the brine.
The well bottomhole pressure (BHP) starts at 4037 psi and shows a slight but consistent decrease, reaching 3998 psi, suggesting effective pressure dissipation in the reservoir. The interplay between trapped, supercritical, and dissolved CO2 emphasizes the reservoir’s capacity to transition between different trapping mechanisms, ensuring effective and secure CO2 storage. These trends confirm the reservoir’s ability to immobilize CO2 securely, with a balance between residual and solubility trapping (see Figure 6). The total trapped CO2 in this case is 1.63 million moles.
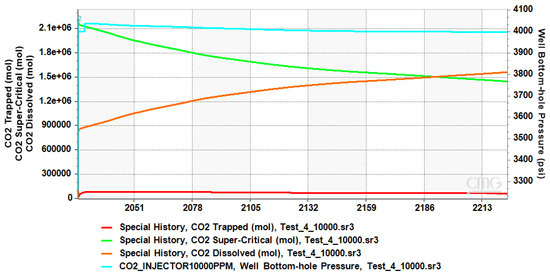
Figure 6.
Trapped, supercritical, dissolved, and BHP profile of CO2 in layer 4.
4.2. CO2 Plume Migration in Layers 3 and 4
Because of the combined pressure fields from each injection point, the simulation results show a compact, merged plume structure with CO2 injectors operating at injection depths of 5380 and 5385 feet (layer 3 and 4), see Figure 7. Effective confinement through dissolution trapping is suggested by the plume image’s high CO2 mole fraction concentrated close to the injection zone, approaching 0.99, which progressively drops outward. The comparative salinity of 10,000 ppm improves this trapping by making CO2 more soluble, which permits more CO2 to dissolve into the brine as it spreads out from the injection point. A consistent CO2 distribution is produced at 5380 and 5385 feet. This is characterized by the overlapping pressure fields at both depths, stabilizing the plume boundary and reducing both vertical and horizontal migration. The graph of the trapping mechanisms supports this containment: the dissolved CO2 steadily rises and plateaus, indicating near-saturation in the brine, while supercritical CO2 declines as it transitions into more stable dissolved and trapped states. Residual trapping, shown in the graph, is low but stable, adding to long-term containment by immobilizing CO2 in pore spaces.
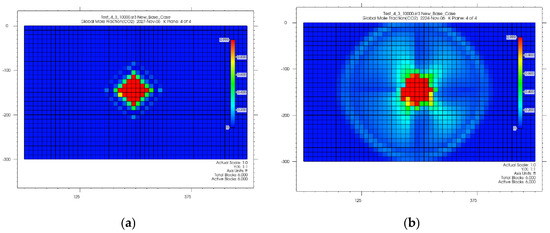
Figure 7.
Plume migration in layer 3 and 4 from shut-in (a) to the end of the simulation (b).
The efficiency of residual trapping mechanisms is demonstrated by the amount of CO2 trapped, which starts at 0 mol and climbs gradually during the simulation before stabilizing at about 134,000 moles. After beginning at a high value of more than 2.4 million moles, the supercritical CO2 progressively drops to about 1.68 million moles, signaling a switch to different trapping methods such as solubility trapping. The predominant long-term storage mechanism, solubility trapping, is highlighted by the fact that dissolved CO2 rises quickly, eventually surpassing supercritical CO2 and reaching 1.7 million moles. This is 200,000 more moles of dissolved CO2 than in the previous case. The BHP decreases from about 4216 psi to 4208 psi, suggesting slow pressure dissipation in the reservoir. This modest reduction is possibly due to CO2 migration and trapping mechanisms balancing the injection rates (see Figure 8). In this case, the total trapping mechanisms trapped 1.83 million moles of CO2.
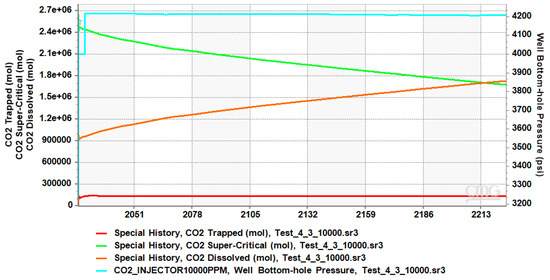
Figure 8.
Trapped, supercritical, dissolved, and BHP profile of CO2 in layers 3 and 4.
4.3. CO2 Plume Migration in Layers 2, 3, and 4
Compared to the prior completion options, the plume shows larger horizontal migration (Figure 9), where CO2 is injected in layers 2 to 4, at depths of 5385, 5380, and 5375 feet. This is because the combined pressure from several depths causes the plume to extend horizontally. A more uniform horizontal distribution generated by cumulative pressure across the three injection spots is indicated by the plume image’s high CO2 mole fraction of 0.99 near the injection area, which tapers to about 0.2–0.4 at the edges. As the CO2 plume encounters a larger volume of brine, the graph shows that the dissolved CO2 rises to about 1.8 million moles, a steeper rise than in the case of injecting in only layers 3 and 4. These results highlight improved dissolution trapping. Supercritical CO2, tracked by the green line, decreases from about 2.3 million moles initially to around 1.4 million moles, suggesting that the broader horizontal spread facilitates the transition of CO2 into dissolved and residually trapped states.
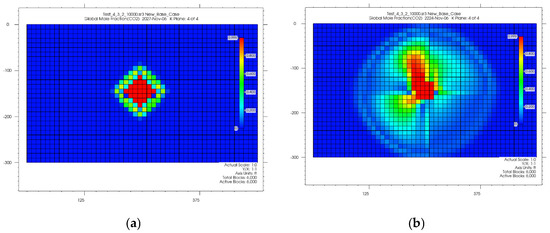
Figure 9.
Plume migration in layers 2, 3, and 4 from shut-in (a) to the end of the simulation (b).
The sensitivity analysis of CO2 trapped and bottomhole pressure (BHP) over the simulation period reveals key insights into reservoir behavior. The CO2 residual trapped starts at 60,731 moles and steadily increases throughout the simulation, reaching a maximum of 107,112 moles in 2027. It then decreases, reaching a minimum of 98,700 moles in 2224, demonstrating effective residual and mineral trapping mechanisms. Meanwhile, the BHP begins at 4184 psi; toward the end of the simulation, the BHP decreases slightly, stabilizing at 4166 psi, indicating slight pressure dissipation within the reservoir. We noticed a total of 1.78 million moles of CO2 dissolved, 80,000 more moles than in the previous case. The supercritical CO2 dropped to reach 1.46 million moles, a decrease of 220,000 moles compared to the previous case (see Figure 10), leading to a total sequestration of 1.88 million moles of CO2.
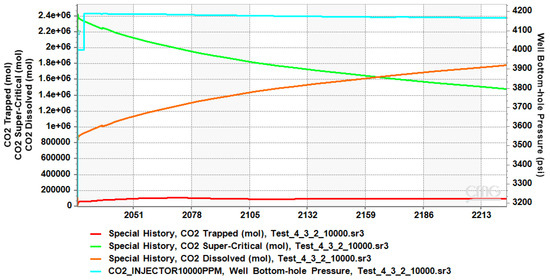
Figure 10.
Trapped, supercritical, dissolved, and BHP profile of CO2 in layers 2, 3, 4.
4.4. CO2 Plume Migration in Layers 1 Through 4
The horizontal movement of the plume is more noticeable with CO2 injected in layers 1 through 4 (Figure 11). The pressure field is expanded both horizontally and vertically by the additional injection point at 5370 feet, which promotes the spread of CO2. With CO2 mole fractions progressively dropping from a peak of 0.99 close to the injection locations to roughly 0.04 at the outside borders, the plume propagation figure displays a wider horizontal spread. A larger, more cohesive pressure field produced by the additional injectors pushes CO2 farther outward, lowering the concentration gradient and enabling more extensive interaction between the CO2 and the surrounding brine. This is demonstrated by the enlarged horizontal migration. The greater brine contact area and higher dissolution trapping effectiveness over the larger containment zone are reflected in the graph, which supports this improved horizontal spread as the amount of dissolved CO2 reaches 1.9 million moles. The total residually trapped CO2 is 69,080 moles. This horizontal movement causes additional CO2 to go into dissolved phases, as evidenced by the amount of supercritical CO2 dropping from 2.4 million moles to 1 million moles.
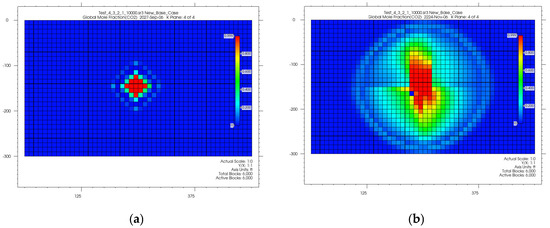
Figure 11.
Plume migration in layer 1 through 4 from shut-in (a) to the end of the simulation (b).
The well bottomhole pressure stabilizes at around 4000 from 4031 psi, maintaining a stable containment field across the larger horizontal area but allowing for greater horizontal distribution than in the three-injector case, where the plume was more compact. Completing layers 1 through 4 maximizes horizontal migration, enhancing CO2 trapping across a broader area while achieving a stable containment field with a reduced likelihood of vertical migration (see Figure 12). In our last case, we had a total of 1,969,080 moles of trapped CO2.
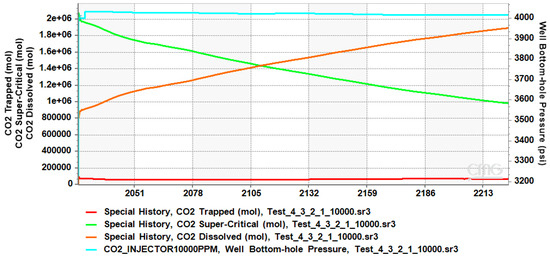
Figure 12.
Trapped, supercritical, dissolved, and BHP profile of CO2 in layer 1 through 4.
Multi-layer completion significantly enhances CO2 sequestration compared to single-layer injection. Simultaneous injection at four depths (5370 ft, 5375 ft, 5380 ft, and 5385 ft) maximized CO2 storage, achieving approximately 2 million moles, with dissolution trapping accounting for 96% of the total during the simulation period. This multi-layer approach resulted in a 1.2-fold increase in sequestration capacity relative to single-depth injection. The improvement is attributed to the increased interfacial contact area between CO2 and brine, which promotes dissolution and reduces the volume of buoyant supercritical CO2. The relatively high CO2 solubility in the 10,000 ppm brine further facilitates dissolution and minimizes the potential for lateral or upward plume migration. The observed deviation from a perfectly circular plume is attributed to vertical migration, likely influenced by the relatively low vertical permeability (20 mD). This result is consistent with previous research by Hassan et al. [26], which demonstrated that multi-layer injection in idealized aquifer systems enhances CO2 storage capacity by distributing the injected fluid across multiple zones, increasing the CO2–brine contact area and promoting dissolution trapping.
Despite these promising results, several potential limitations and uncertainties in the study warrant consideration. First, the results rely on specific assumptions about reservoir properties, such as permeability, porosity, and brine salinity. Variations in these parameters could significantly impact CO2 storage efficiency, plume behavior, and dissolution rates. Conducting sensitivity analyses in future studies would help quantify the effect of these parameter variations on the outcomes. Then, this study assumes homogeneous aquifer properties, such as uniform permeability (along the X and Y directions) and salinity. In reality, aquifers are often highly heterogeneous, which can lead to more complex CO2 plume behavior and storage dynamics. Incorporating reservoir heterogeneity into the simulation framework could provide more accurate and realistic predictions. Finally, the boundary conditions used in the model might not perfectly represent the extent of the reservoir or its interaction with neighboring formations. Simplifying the reservoir boundaries could lead to deviations between simulated results and actual field performance. Considering more complex boundary conditions and scaling effects would enhance the model’s applicability to real-world scenarios.
5. Conclusions
This study investigated multi-layer CO2 injection for enhanced sequestration in a 10,000 ppm salinity saline aquifer. The results demonstrate that simultaneous injection at four depths (5370–5385 ft) maximized CO2 storage, achieving approximately 2 million moles, with dissolution trapping accounting for 96% of the total during the simulation. This multi-layer approach yielded a 1.2-fold increase in sequestration capacity compared to single-depth injection, attributed to increased CO2–brine contact, and promoted dissolution, consistent with the findings of Hassan et al. [26]. However, the study relies on simplifying assumptions regarding reservoir properties (e.g., homogeneity, constant permeability, and salinity) and boundary conditions, which could impact the accuracy of predictions. Future work should prioritize sensitivity analyses, incorporate reservoir heterogeneity, and consider more complex boundary conditions to enhance the model’s applicability to real-world scenarios.
Author Contributions
Methodology, F.B. and R.T.; Software, A.K.; Validation, F.B.; Formal analysis, F.B.; Investigation, A.K. and H.T.; Writing—original draft, A.K.; Visualization, A.K.; Supervision, F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Jackson, C.; Krevor, S. The feasibility of reaching gigatonne scale CO2 storage by mid-century. Nat. Commun. 2024, 15, 6913. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Birkholzer, J.T.; Tsang, C.F.; Rutqvist, J. A method for quick assessment of CO2 storage capacity in closed and semi-closed saline formations. Int. J. Greenh. Gas Control 2008, 2, 626–639. [Google Scholar] [CrossRef]
- Fominykh, S.; Stankovski, S.; Markovic, V. Analysis of CO2 migration in horizontal saline aquifers during carbon capture and storage process. Sustainability 2023, 15, 8912. [Google Scholar] [CrossRef]
- Li, Q.; Han, Y.; Liu, X.; Ansari, U.; Cheng, Y.; Yan, C. Hydrate as a by-product in CO2 leakage during the long-term sub-seabed sequestration and its role in preventing further leakage. Environ. Sci. Pollut. Res. 2022, 29, 77737–77754. [Google Scholar] [CrossRef]
- Jing, J.; Yang, Y.; Cheng, J.; Ding, Z. Exploring the influences of salinity on CO2 plume migration and storage capacity in sloping formations: A numerical investigation. Energy 2024, 309, 133160. [Google Scholar] [CrossRef]
- Sun, X.; Cao, Y.; Liu, K. Effects of fluvial sedimentary heterogeneity on CO2 geological storage: Integrating storage capacity, injectivity, distribution, and CO2 phases. J. Hydrol. 2023, 617, 128936. [Google Scholar] [CrossRef]
- Al-Khdheeawi, E.; Vialle, S.; Barifcani, A.; Sarmadivaleh, M.; Zhang, Y.; Iglauer, S. Impact of salinity on CO2 containment security in highly heterogeneous reservoirs. Greenh. Gases Sci. Technol. 2017, 8, 1723. [Google Scholar]
- Al-Khdheeawi, E.; Vialle, S.; Barifcani, A.; Sarmadivaleh, M.; Zhang, Y.; Iglauer, S. Influence of injection well configuration and rock wettability on CO2 plume behaviour and CO2 trapping capacity in heterogeneous reservoirs. J. Nat. Gas Sci. Eng. 2017, 3, 16. [Google Scholar]
- Kumar, S.; Foroozesh, J.; Edlmann, K.; Rezk, M.; Lim, C. A Comprehensive Review of Value-Added CO2 Sequestration in Subsurface Saline Aquifers. J. Nat. Gas Sci. Eng. 2020, 81, 103437. [Google Scholar] [CrossRef]
- Okwen, R.T.; Stewart, M.T.; Cunningham, J.A. Analytical solution for estimating storage efficiency of dissolved and residual CO2 in saline aquifers. Int. J. Greenh. Gas Control 2010, 4, 102–107. [Google Scholar] [CrossRef]
- Liu, E.; Lu, X.; Wang, D.A. Systematic Review of Carbon Capture, Utilization and Storage: Status, Progress and Challenges. Energies 2023, 16, 2865. [Google Scholar] [CrossRef]
- Xu, T.; Apps, J.A.; Pruess, K.; Yamamoto, H. Numerical modeling of injection and mineral trapping of CO2 with H2S and SO2 in a sandstone formation. Chem. Geol. 2007, 242, 319–346. [Google Scholar] [CrossRef]
- Osborn, N.I.; Smith, S.J.; Seger, C.H. Hydrogeology, Distribution, and Volume of Saline Groundwater in the Southern Midcontinent and Adjacent Areas of the United States. US Geol. Surv. 2013, 15, 16–17. [Google Scholar]
- Yang, D.; Liu, N.; Gu, Y. Enhanced mass transfer for CO2 sequestration in saline aquifers. Ind. Eng. Chem. Res. 2005, 44, 2164–2174. [Google Scholar]
- Yang, Y.; Xu, T.; Wang, F.; Zhao, N. Impact of inner reservoir faults on migration and storage of injected CO2. Int. J. Greenh. Gas Control 2021, 72, 14–25. [Google Scholar] [CrossRef]
- Hovorka, S.D.; Meckel, T.A.; Treviño, R.H. Monitoring a large-volume injection at Cranfield, Mississippi Project design and recommendations. Int. J. Greenh. Gas Control 2013, 18, 345–360. [Google Scholar] [CrossRef]
- Rathnaweera, T.D.; Ranjith, P.G. Effect of salinity on effective CO2 permeability in reservoir rock determined by pressure transient methods. Rock Mech. Rock Eng. 2023, 48, 2093–2110. [Google Scholar] [CrossRef]
- Peaceman, D. Interpretation of well-block pressures in numerical reservoir simulation. In Proceedings of the 52nd Annual Fall Technical Conference and Exhibition, Denver, CO, USA, 9–12 October 1977. [Google Scholar]
- Peaceman, D. Interpretation of well-block pressures in numerical reservoir simulation with non-square grid blocks and anisotropic permeability. Soc. Pet. Eng. J. 1983, 23, 531–543. [Google Scholar] [CrossRef]
- Chappelear, J.; Williamson, A.E. Representing Wells in Numerical Reservoir Simulation: Part I—Theory Part II—Implementation. Soc. Pet. Eng. J. 1981, 21, 323–344. [Google Scholar] [CrossRef]
- Aziz, K.; Govier, G.W.; Schowalter, W.R. The Flow of Complex Mixtures in Pipes. ASME J. Appl. Mech. 1973, 2, 404. [Google Scholar]
- Duan, Z.; Sun, R.; Zhu, C.; Chou, I.M. An improved model for the calculation of CO2 solubility in aqueous solutions containing Na+, K+, Ca2+, Mg2+, Cl−, and SO₄²−. Mar. Chem. 2006, 98, 131–139. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Cramer, S. The Solubility of Methane, Carbon Dioxide, and Oxygen in Brines from 0 to 300 C; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1982. [Google Scholar]
- Bakker, R. Computer programs for analysis of fluid inclusion data and for modelling bulk fluid properties. Chem. Geol. Chem. Geol. 2003, 194, 3–23. [Google Scholar] [CrossRef]
- Hassan, W.; Jiang, X. Numerical Investigation of Multi-layer CO2 Injection in Deep Saline Aquifers with Improperly Abandoned Wells. Energy Procedia 2014, 61, 160–163. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).