Effects of Liquid Nitrogen on Mechanical Deterioration and Fracturing Efficiency in Hot Dry Rock
Abstract
1. Introduction
2. Experiment and Simulation
2.1. Thermal Treatments and Mechanical Property Experiments
2.2. Numerical Simulation of Liquid Nitrogen Fracturing
2.2.1. Governing Equations
2.2.2. Model Descriptions
3. Mechanical Property Deterioration
3.1. Crack Initiation Stress
3.2. Crack Damage Stress
3.3. Peak Stress
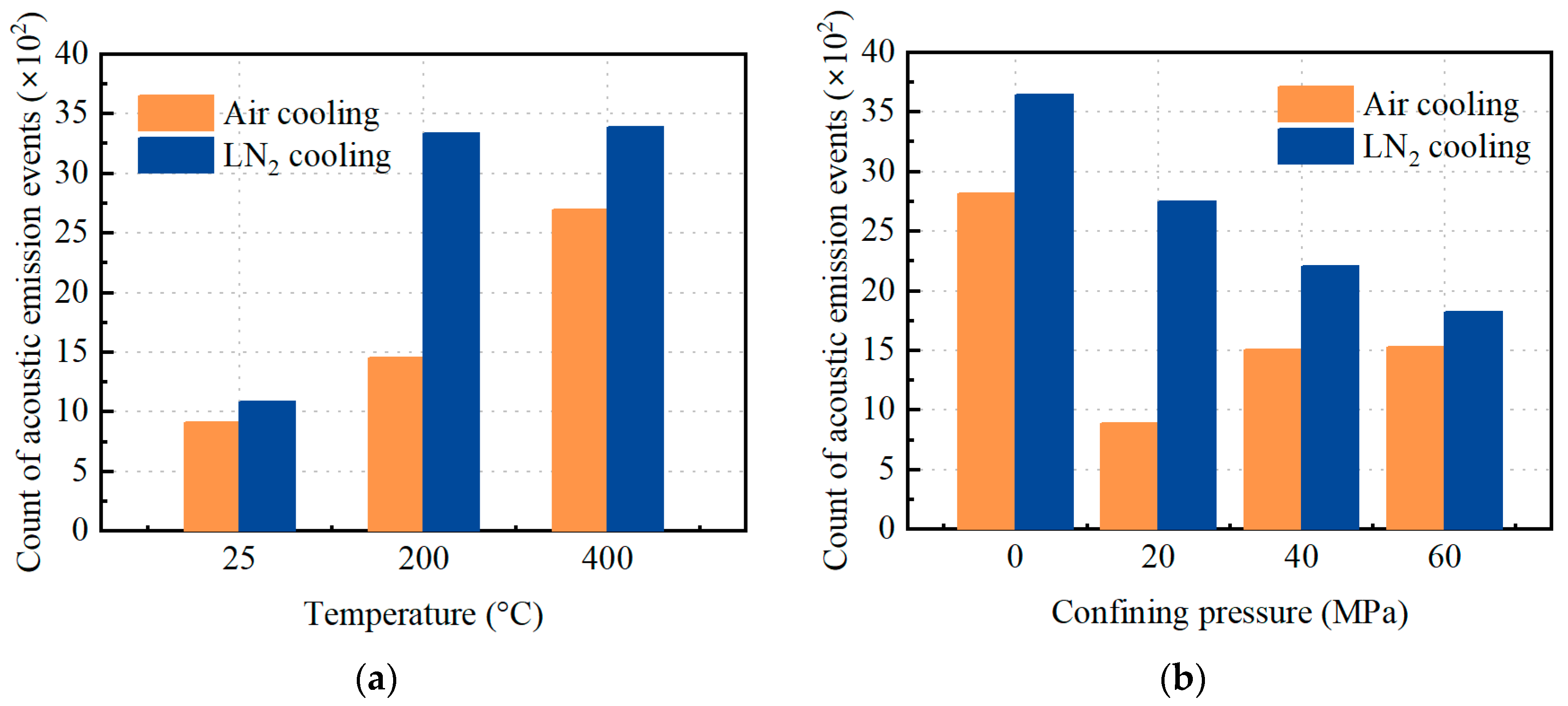
4. Acoustic Emission Event Statistics
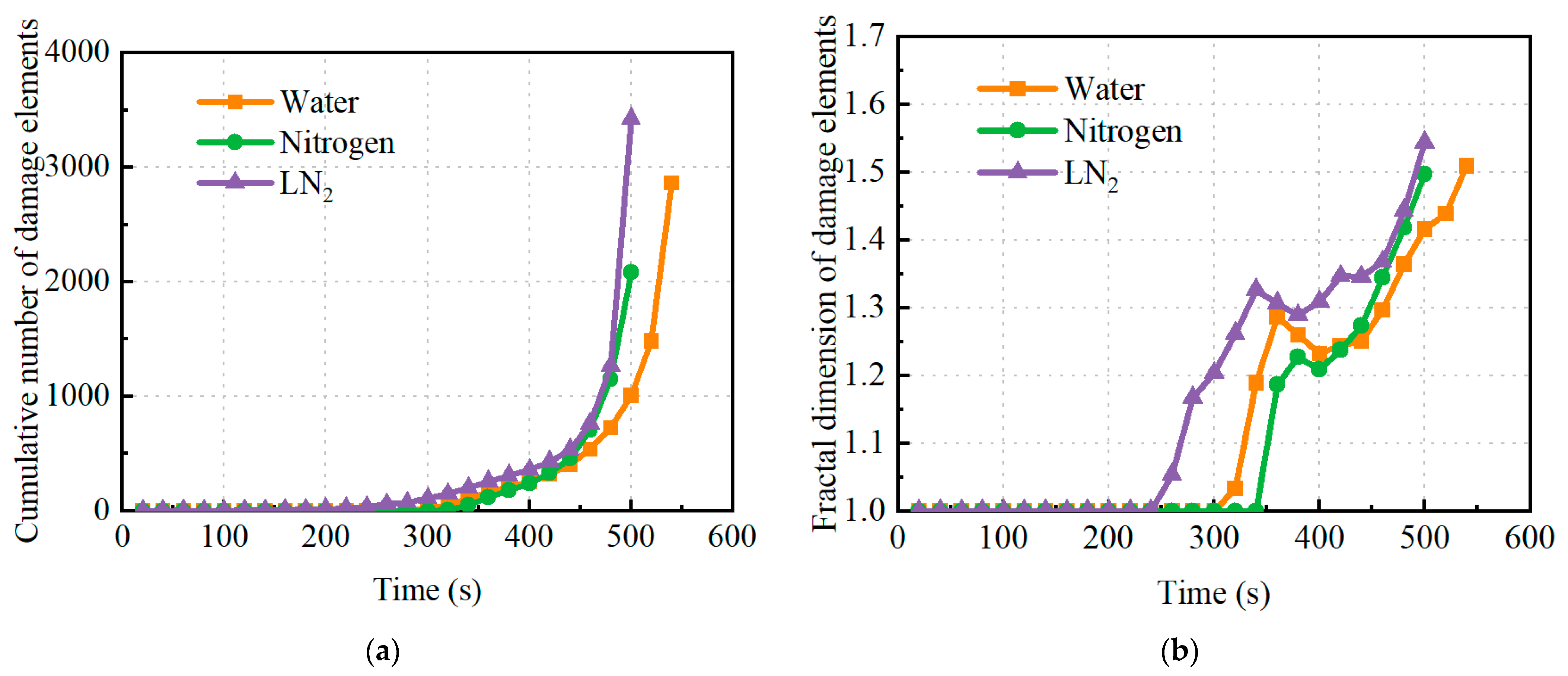
4.1. Event Count
4.2. Fractal Dimension
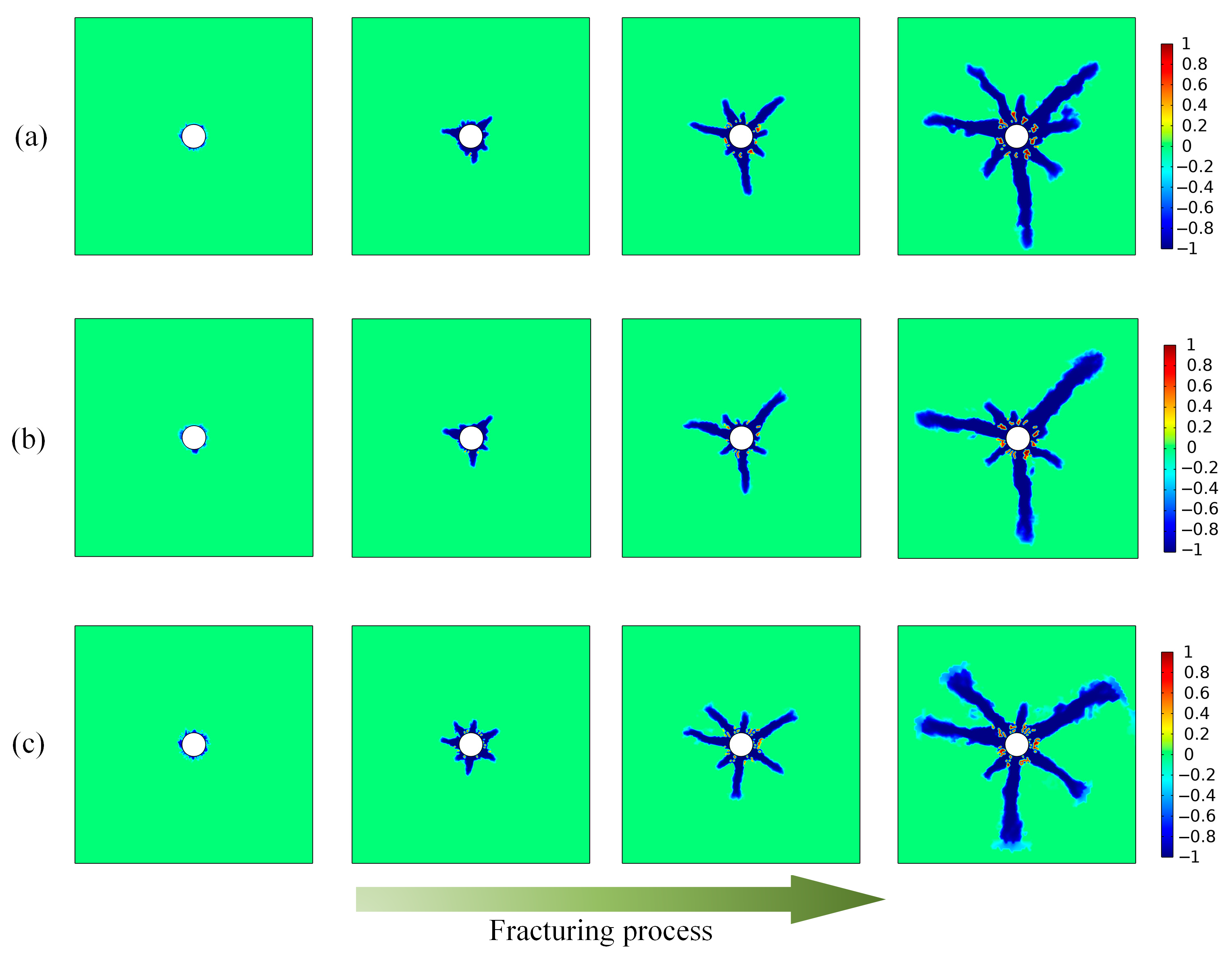
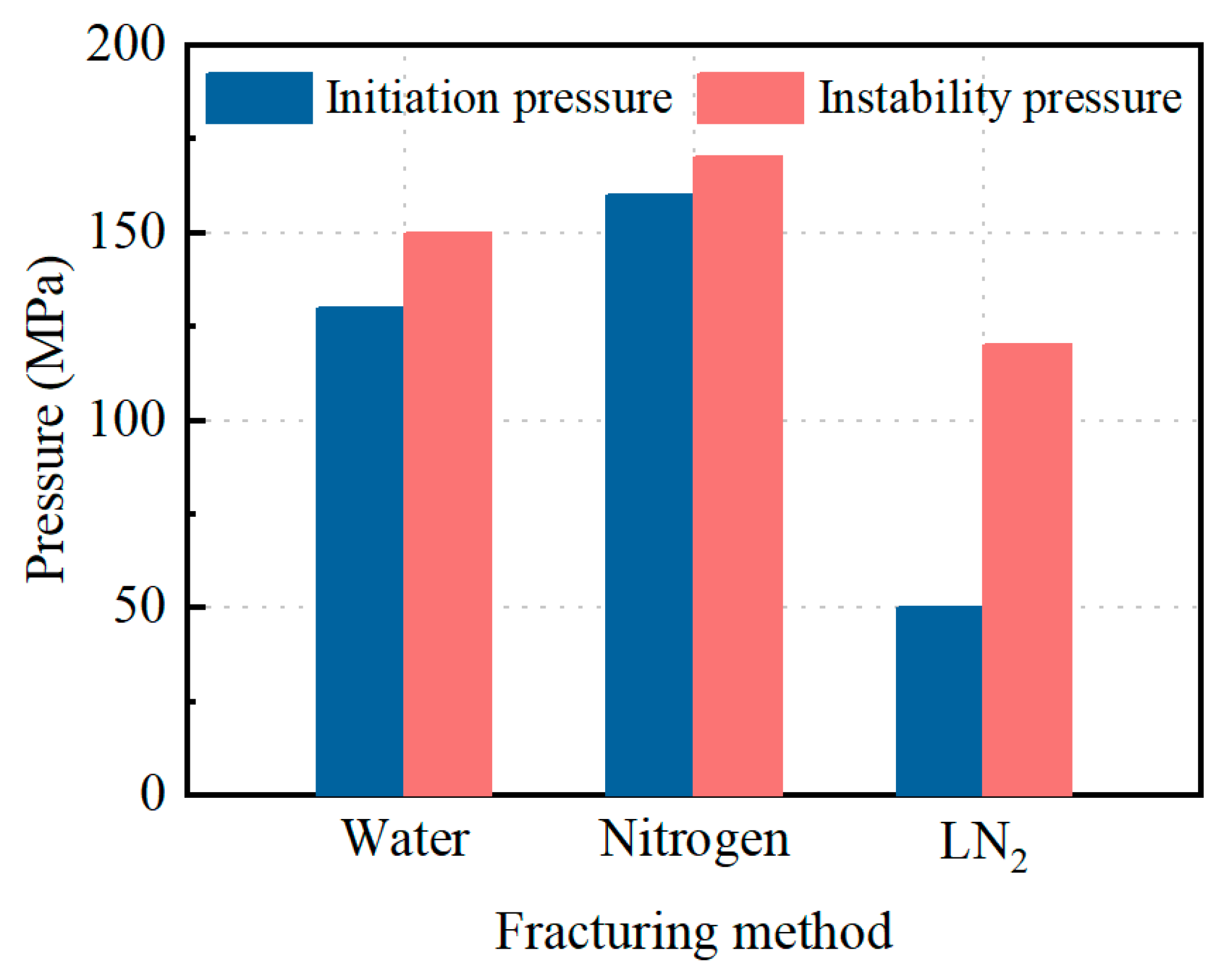
5. Comparison of Liquid Nitrogen Fracturing and Conventional Fracturing
6. Conclusions
- (1)
- Confining pressure mitigated the effect of temperature on crack initiation stress, crack damage stress, and peak stress. It also reduced the deterioration effect of LN2 cooling on these stress parameters.
- (2)
- LN2 still reduced stress parameters under high confinement pressures. From 20 to 60 MPa, the reduction rates of crack initiation stress, crack damage stress, and peak stress induced by LN2 cooling were 7.73–18.51%, 3.46–12.15%, and 2.51–8.50%, respectively.
- (3)
- Cryogenic LN2 increased the counts and fractal dimensions of AE events during sample failure under different conditions.
- (4)
- LN2 fracturing led to a greater number and complexity of fractures and reduced the breakdown pressures. Compared with water and nitrogen fracturing, the initiation pressures of LN2 fracturing decreased by 61.54% and 68.75%, while the instability pressures of LN2 fracturing decreased by 20.00% and 29.41%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, H.; Li, C.; Zhou, T.; Chen, J.; Liao, J.; Ma, J.; Li, B. Conceptualization and evaluation of the exploration and utilization of low/medium-temperature geothermal energy: A case study of the Guangdong-Hong Kong-Macao Greater Bay Area. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 18. [Google Scholar] [CrossRef]
- Kong, G.; Wu, D.; Wei, Y. Experimental and numerical investigations on the energy and structural performance of a full-scale energy utility tunnel. Tunn. Undergr. Space Tech. 2023, 139, 105208. [Google Scholar] [CrossRef]
- Chen, R.; Wu, D.; Zhang, T.; Kong, G.; Fang, J. Thermo-mechanical behavior of energy piles equipped with PCM tubes. Comput. Geotech. 2025, 179, 107005. [Google Scholar] [CrossRef]
- Martin, C.D.; Chandler, N.A. The progressive fracture of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Li, C.; Xie, H.; Wang, J. Anisotropic characteristics of crack initiation and crack damage thresholds for shale. Int. J. Rock. Mech. Min. 2020, 126, 104178. [Google Scholar] [CrossRef]
- Yang, R.; Hong, C.; Liu, W.; Wu, X.; Wang, T.; Huang, Z. Non-contaminating cryogenic fluid access to high-temperature resources: Liquid nitrogen fracturing in a lab-scale Enhanced Geothermal System. Renew. Energ. 2021, 165, 125–138. [Google Scholar] [CrossRef]
- Tomac, I.; Sauter, M. A review on challenges in the assessment of geomechanical rock performance for deep geothermal reservoir development. Renew. Sustain. Energy Rev. 2018, 82, 3972–3980. [Google Scholar] [CrossRef]
- Pan, S.; Gao, M.; Shah, K.J.; Zheng, J.; Pei, S.; Chiang, P. Establishment of enhanced geothermal energy utilization plans: Barriers and strategies. Renew. Energ. 2019, 132, 19–32. [Google Scholar] [CrossRef]
- Li, B.; Xie, H.; Sun, L.; Gao, T.; Xia, E.; Liu, B.; Wang, J.; Long, X. Advanced exergy analysis and multi-objective optimization of dual-loop ORC utilizing LNG cold energy and geothermal energy. Renew. Energ. 2025, 239, 122164. [Google Scholar] [CrossRef]
- Su, X.; Zhou, L.; Li, H.; Lu, Y.; Song, X.; Shen, Z. Effect of mesoscopic structure on hydro-mechanical properties of fractures. Environ. Earth Sci. 2020, 79, 146. [Google Scholar] [CrossRef]
- McClure, M.W.; Horne, R.N. An investigation of stimulation mechanisms in Enhanced Geothermal Systems. Int. J. Rock. Mech. Min. 2014, 72, 242–260. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, S.; Yang, R.; Wu, X.; Li, R.; Zhang, H.; Hung, P. A review of liquid nitrogen fracturing technology. Fuel 2020, 266, 117040. [Google Scholar] [CrossRef]
- Wang, L.; Yao, B.; Cha, M.; Alqahtani, N.B.; Patterson, T.W.; Kneafsey, T.J.; Miskimins, J.L.; Yin, X.; Wu, Y. Waterless fracturing technologies for unconventional reservoirs-opportunities for liquid nitrogen. J. Nat. Gas. Sci. Eng. 2016, 35, 160–174. [Google Scholar] [CrossRef]
- Cai, C.; Tao, Z.; Ren, K.; Liu, S.; Yang, Y.; Feng, Y.; Su, S.; Hou, P. Experimental investigation on the breakdown behaviours of sandstone due to liquid nitrogen fracturing. J. Petrol. Sci. Eng. 2021, 200, 108386. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, Z.; Huang, P.; Wu, X.; Xiong, C.; Zhang, C. Numerical and experimental analysis of hot dry rock fracturing stimulation with high-pressure abrasive liquid nitrogen jet. J. Petrol. Sci. Eng. 2018, 163, 156–165. [Google Scholar] [CrossRef]
- Wu, X.; Huang, Z.; Song, H.; Zhang, S.; Cheng, Z.; Li, R.; Wen, H.; Huang, P.; Dai, X. Variations of physical and mechanical properties of heated granite after rapid cooling with liquid nitrogen. Rock. Mech. Rock. Eng. 2019, 52, 2123–2139. [Google Scholar] [CrossRef]
- Kang, F.; Jia, T.; Li, Y.; Deng, J.; Tang, C.; Huang, X. Experimental study on the physical and mechanical variations of hot granite under different cooling treatments. Renew. Energ. 2021, 179, 1316–1328. [Google Scholar] [CrossRef]
- Sha, S.; Rong, G.; Chen, Z.; Li, B.; Zhang, Z. Experimental evaluation of physical and mechanical properties of geothermal reservoir rock after different cooling treatments. Rock. Mech. Rock. Eng. 2020, 53, 4967–4991. [Google Scholar] [CrossRef]
- Wu, X.; Huang, Z.; Li, R.; Zhang, S.; Wen, H.; Huang, P.; Dai, X.; Zhang, C. Investigation on the damage of high-temperature shale subjected to liquid nitrogen cooling. J. Nat. Gas. Sci. Eng. 2018, 57, 284–294. [Google Scholar] [CrossRef]
- Wu, X.; Huang, Z.; Zhang, S.; Cheng, Z.; Li, R.; Song, H.; Wen, H.; Huang, P. Damage analysis of high-temperature rocks subjected to LN2 thermal shock. Rock. Mech. Rock. Eng. 2019, 52, 2585–2603. [Google Scholar] [CrossRef]
- Hou, P.; Su, S.; Zhang, Y.; Gao, F.; Gao, Y.; Liang, X.; Ding, R.; Cai, C. Effect of liquid nitrogen thermal shock on structure damage and brittleness properties of high-temperature marble. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 69. [Google Scholar] [CrossRef]
- Su, S.; Hou, P.; Gao, F.; Liang, X.; Ding, R.; Cai, C. Changes in mechanical properties and fracture behaviors of heated marble subjected to liquid nitrogen cooling. Eng. Fract. Mech. 2022, 261, 108256. [Google Scholar] [CrossRef]
- Wu, X.; Huang, Z.; Cheng, Z.; Zhang, S.; Song, H.; Zhao, X. Effects of cyclic heating and LN2-cooling on the physical and mechanical properties of granite. Appl. Therm. Eng. 2019, 156, 99–110. [Google Scholar] [CrossRef]
- Rong, G.; Sha, S.; Li, B.; Chen, Z.; Zhang, Z. Experimental investigation on physical and mechanical properties of granite subjected to cyclic heating and liquid nitrogen cooling. Rock. Mech. Rock. Eng. 2021, 54, 2383–2403. [Google Scholar] [CrossRef]
- Ge, Z.; Sun, Q.; Yang, T.; Luo, T.; Jia, H.; Yang, D. Effect of high temperature on mode-I fracture toughness of granite subjected to liquid nitrogen cooling. Eng. Fract. Mech. 2021, 252, 107834. [Google Scholar] [CrossRef]
- Yang, R.; Hong, C.; Huang, Z.; Wen, H.; Li, X.; Huang, P.; Liu, W.; Chen, J. Liquid nitrogen fracturing in boreholes under true triaxial stresses: Laboratory investigation on fractures initiation and morphology. Spe J. 2021, 26, 135–154. [Google Scholar] [CrossRef]
- Span, R.; Lemmon, E.W.; Jacobsen, R.T.; Wagner, W.; Yokozeki, A. A reference equation of state for the thermodynamic properties of nitrogen for temperatures from 63.151 to 1000 K and pressures to 2200 MPa. J. Phys. Chem. Ref. Data 2000, 29, 1361–1433. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Jacobsen, R.T. Viscosity and thermal conductivity equations for nitrogen, oxygen, argon, and air. Int. J. Thermophys. 2004, 25, 21–69. [Google Scholar] [CrossRef]
- Zhou, C.; Su, S.; Liang, X.; Xue, Y.; Cai, C.; Gao, F. Liquid nitrogen pre-injection assisted fracturing in hot dry rock reservoirs. Phys. Fluids 2025, 37, 012007. [Google Scholar] [CrossRef]
- Guo, T.; Tang, S.; Liu, S.; Liu, X.; Zhang, W.; Qu, G. Numerical simulation of hydraulic fracturing of hot dry rock under thermal stress. Eng. Fract. Mech. 2020, 240, 107350. [Google Scholar] [CrossRef]
- Xia, T.; Zhou, F.; Liu, J.; Kang, J.; Gao, F. A fully coupled hydro-thermo-mechanical model for the spontaneous combustion of underground coal seams. Fuel 2014, 125, 106–115. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, C.H. Numerical simulation on mining-induced water inrushes related to geologic structures using a damage-based hydromechanical model. Environ. Earth Sci. 2011, 62, 43–54. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Guo, T.; He, J.; Zhang, L.; Chen, S.; Qu, Z. Study on the cracking mechanism of hydraulic and supercritical CO2 fracturing in hot dry rock under thermal stress. Energy 2021, 221, 119886. [Google Scholar] [CrossRef]
- Zhu, W.C.; Tang, C.A. Micromechanical model for simulating the fracture process of rock. Rock. Mech. Rock. Eng. 2004, 37, 25–56. [Google Scholar] [CrossRef]
- Tang, C.A.; Yang, W.T.; Fu, Y.F.; Xu, X.H.; Pusch, R. A new approach to numerical method of modelling geological processes and rock engineering problems; continuum to discontinuum and linearity to nonlinearity. Eng. Geol. 1998, 49, 207–214. [Google Scholar] [CrossRef]
- Wang, J.; Elsworth, D.; Wu, Y.; Liu, J.; Zhu, W.; Liu, Y. The Influence of fracturing fluids on fracturing processes: A comparison between water, oil and SC-CO2. Rock. Mech. Rock. Eng. 2018, 51, 299–313. [Google Scholar] [CrossRef]
- Wu, X.; Huang, Z.; Dai, X.; Song, H.; Zhang, S. Thermo-coupled FSI analysis of LN2 jet impinging on hot dry rock. Appl. Therm. Eng. 2020, 165, 114621. [Google Scholar] [CrossRef]
- Hou, P.; Su, S.; Gao, F.; Liang, X.; Wang, S.; Gao, Y.; Cai, C. Influence of Liquid Nitrogen Freeze–Thaw Cycles on Mechanical Behaviors and Permeability Properties of Coal Under Different Confining Pressures. Rock. Mech. Rock. Eng. 2024, 57, 2625–2644. [Google Scholar] [CrossRef]
- Alameedy, U.; Al-Behadili, A. An Overview of How the Petrophysical Properties of Rock Influenced After Being Exposed to Cryogenic Fluid. J. Eng. 2023, 29, 1–16. [Google Scholar] [CrossRef]
- Lu, Y.L.; Elsworth, D.; Wang, L.G. Microcrack-based coupled damage and flow modeling of fracturing evolution in permeable brittle rocks. Comput. Geotech. 2013, 49, 226–244. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| ) (m2) | 4 × 10−19 |
| Average value of the coefficient of thermal expansion (K−1) | 8 × 10−6 |
| Average value of modulus of elasticity (GPa) | 45 * |
| Average compressive strength (MPa) | 400 * |
| Average compressive strength/average tensile strength | 16 |
| Internal friction angle (°) | 54 |
| Heterogeneity coefficient (m) | 4 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Hu, Y.; Luo, N.; Zhou, C.; Cai, C. Effects of Liquid Nitrogen on Mechanical Deterioration and Fracturing Efficiency in Hot Dry Rock. Processes 2025, 13, 696. https://doi.org/10.3390/pr13030696
Wang H, Hu Y, Luo N, Zhou C, Cai C. Effects of Liquid Nitrogen on Mechanical Deterioration and Fracturing Efficiency in Hot Dry Rock. Processes. 2025; 13(3):696. https://doi.org/10.3390/pr13030696
Chicago/Turabian StyleWang, Hu, Yong Hu, Na Luo, Chunbo Zhou, and Chengzheng Cai. 2025. "Effects of Liquid Nitrogen on Mechanical Deterioration and Fracturing Efficiency in Hot Dry Rock" Processes 13, no. 3: 696. https://doi.org/10.3390/pr13030696
APA StyleWang, H., Hu, Y., Luo, N., Zhou, C., & Cai, C. (2025). Effects of Liquid Nitrogen on Mechanical Deterioration and Fracturing Efficiency in Hot Dry Rock. Processes, 13(3), 696. https://doi.org/10.3390/pr13030696





