MILP-Based Multistage Co-Planning of Generation–Network–Storage in Rural Distribution Systems

Abstract

A multistage coordinated expansion-planning framework for distribution systems is developed to jointly optimize investments in the network, distributed generation (DG), and energy storage systems (ESS). Network reinforcements select from multiple feeder and transformer candidates, while DG installations consider conventional and photovoltaic (PV) options. In this study, a set of candidate buses are considered for the installation of PVs and energy storage systems. Therefore, the expansion plan can determine the optimal installation locations and timing of these candidate assets. The objective minimizes total cost in net-present-value terms, covering investment, maintenance, generation, and operating components. Representative hourly load profiles are incorporated to capture ESS dispatch behavior and PV output variability; operating costs are modeled via piecewise linearization. To preserve connectivity and preclude islanding in the presence of DG and ESS, modified radiality constraints are imposed. The formulation is a mixed-integer linear program solvable efficiently by commercial optimizers, and numerical studies confirm the method’s effectiveness.

1. Introduction

Driven by decarbonization and decentralization, electric power systems are witnessing a continued rise in the share of distributed renewables—most notably photovoltaic and wind resources [1,2]. The inherently intermittent and stochastic behavior of these resources elevates operational uncertainty in rural distribution networks [3]. Key manifestations include voltage deviations, tighter adequacy at peak periods, and constrained operational flexibility. In many rural contexts, the rapid deployment of DERs has exposed structural limits of legacy AC distribution infrastructures in accommodating multi-source integration, supporting flexible scheduling, and sustaining efficient operation. These observations motivate sustained investigation into coordinated planning across generation, network, and storage. Energy storage systems (ESS), endowed with bidirectional charge–discharge capability, are widely recognized as pivotal for enhancing flexibility and buffering DER-induced uncertainty [4,5]. Consequently, under security and economic constraints, it is essential to optimize the siting, sizing, and deployment timing of distribution assets, generation facilities, and ESS within existing networks, and to devise staged expansion and capacity-allocation policies that advance high-quality, low-carbon development of rural power systems.

Expansion planning for distribution systems has been widely investigated [6,7,8,9,10]. Within this line of work, several studies focus on networks with distributed resources. Reference [11] formulated a multi-objective PV planning model that jointly considers active power loss, voltage deviation, total harmonic distortion, and static voltage-stability indices. In microgrid contexts. Reference [12] proposed an effective DG siting framework aided by a new voltage-regulation metric for screening candidate interconnection points; yet joint expansion where the candidate set spans both DG units and network assets (feeders, transformers, substations) remains relatively underexplored. Variability in PV and wind output is explicitly modeled in Reference [13], which develops a DG siting/sizing approach to reduce operational risk. Reference [14] analyzed DG impacts on network structure and optimizes line routing together with DG siting and capacity, but does not fully capture coordinated DG–network interactions. By contrast, Reference [15] addressed DG uncertainty and incorporates DG–network coordination in the grid-structure configuration process. Reference [16] proposed a novel model suitable for multi-stage planning of distribution systems, which not only jointly considers the construction sequence, siting, and capacity determination of distribution assets and distributed power sources but also explicitly introduces structural constraints of radial system operation in the modeling. Reference [17] proposed a two-layer optimization model for the multi-stage expansion of active distribution grids. The upper-layer model aims to minimize the present value of total costs borne by the DSO in network asset investment, maintenance, and operation processes; the lower-layer model models the participation behavior of distributed energy resource (DER) owners and demand aggregators through local energy market settlement to achieve social welfare maximization. Despite these advances, most models still rely on annual peak or representative yearly loads, overlooking intra-day load chronology and the time-dependent nature of PV output. This omission is particularly consequential when ESS participates in operations, since charge–discharge strategies hinge on the hour-by-hour sequence of net load and generation. Without such chronological modeling, the operational value and optimal sizing of storage cannot be assessed reliably. In addition, the recent literature has further emphasized data-driven analysis and coordinated multi-energy operation in active distribution networks. Reference [18] developed an FFRLS-based voltage security assessment method, demonstrating the value of data-driven approaches for enhancing situational awareness in distribution grids. Reference [19] presented a coordinated control strategy for integrated engine–grid–load–storage systems, highlighting the increasing importance of multi-energy collaborative operation. These studies reinforce the growing trend toward coordinated, data-driven methods in modern distribution system analysis.

Energy storage systems (ESS) serve as flexible resources in distribution networks, providing bidirectional regulation—absorbing energy during charging and supplying power during discharging. By mitigating renewable-output variability, deferring network reinforcements, improving supply reliability, and strengthening the response to load swings and contingencies, ESS materially enhance operational flexibility. At the planning layer, a broad set of optimization models targets ESS siting and sizing. Reference [17] proposes a two-layer optimization structure based on representative daily and annual loads, coupling energy storage deployment with distribution network expansion planning to achieve coordinated decision-making across layers. Reference [20] proposed incorporating energy storage scheduling as a stochastic planning variable within a transmission-distribution coordination framework, comprehensively considering intra-day uncertain photovoltaic output and load fluctuations to improve voltage security constraints and enhance system resilience. The above studies mainly focus on operational coordination and uncertainty modeling, while another important research direction concerns the long-term reliability of energy storage assets. Numerous studies have investigated the impacts of battery degradation and lifetime constraints on investment decisions and operational optimization outcomes. Reference [21] conducted a comprehensive review on considering degradation effects—particularly the influence of ambient temperature—in energy storage system planning, and pointed out that factors such as state of charge (SOC), depth of discharge (DOD), cycle number, and temperature jointly determine battery lifetime and should be incorporated into planning optimization models. Reference [22] pointed out that if battery deterioration limits are considered in the model, the overall annual power cost reduction from PV and storage systems decreases by approximately 5–12%. However, there remains relatively limited attention on joint multi-stage expansion planning problems that simultaneously incorporate distributed power generation units, lifetime-aware energy storage, and distribution equipment (such as feeders, transformers, and substations) as candidate assets.

From a modeling standpoint, mixed-integer linear programming (MILP) has been widely adopted for distribution expansion planning. References [23,24,25,26] constructed MILP frameworks that effectively captured the discrete and continuous variable characteristics in distribution network investment decisions, but did not address the simultaneous expansion of distribution networks and distributed power sources. Reference [27] proposed a MINLP model, which was input into a commercially available software without guaranteeing global optimality. To improve the solution quality, reference [28] proposed an approximate solution strategy based on a genetic algorithm for this model; References [29,30] further applied an evolution-inspired heuristic algorithm—the evolutionary particle swarm algorithm—to solve the mixed-integer nonlinear programming model for joint optimization expansion planning. However, such MINLP methods generally suffer from difficulties in feasible domain characterization, high computational costs, and unproven optimality. To address these shortcomings, references [31] employs piecewise linear approximation and integer algebraic techniques to reconstruct nonlinear terms into linear expressions, thereby transforming the original MINLP model into a MILP model, enabling it to be efficiently processed by commercial MILP solvers. MILP models, with their ability to converge to optimal solutions within a finite number of steps and their explicit optimality gap assessment capabilities, are increasingly becoming the more engineering-practical modeling choice for joint planning problems in energy systems [32].

Based on the aforementioned research, the main contributions and innovations of this paper are as follows:

(1)

A battery energy storage lifetime model is incorporated into the planning framework, which captures the impact of degradation on long-term decision-making;

(2)

The proposed multi-stage expansion planning framework realizes the coordinated optimization of substation construction or replacement, feeder construction or replacement, and new energy storage deployment, thereby effectively promoting the integrated development of generation, grid, and storage.

2. Multi-Stage Coordinated Expansion Planning Model for Rural Distribution Systems

To systematically describe the proposed joint expansion planning model, this section presents the complete mathematical formulation. The model considers both investment and operational decisions over a multistage planning horizon, jointly optimizing distribution network assets and distributed generation units—including conventional generators and photovoltaic units—while incorporating energy storage systems to enhance system flexibility. All relevant sets, parameters, decision variables, and constraints are explicitly defined.

2.1. Objective Function and Cost-Related Terms

$$c^{TPV}={\displaystyle \sum _{y\in Y}\left[{(1+i)}^{-y}\left(c_y^I+c_y^M+c_y^E+c_y^R\right)\right]}$$

(1)

Equation (1) represents an optimization model that aims to minimize the present value of total costs, which include five major expenses: investment costs, maintenance costs, energy production costs, operating costs. All cost items are aggregated by planning year y and discounted using the discount factor ${(1+i)}^{-y}$ based on the annual discount rate i to convert the costs of each year into a uniform present value at a benchmark time point, thereby reflecting the actual impact of costs at different stages on the total system cost under the time value of money. This present value treatment ensures the equivalence and comparability of investment and operating costs at different periods within the planning cycle in economic assessments.

The total cost in (1) comprises amortized investment, maintenance, production, operating costs, and is expressed as:

$$\begin{array}{l}{c}_y^I={\displaystyle \sum _{l\in \{\mathrm{NRF},\mathrm{NAF}\}}R}{R}^l{\displaystyle \sum _{k\in K^l}{\displaystyle \sum _{(s,r)\in {{\rm Y}}^l}{C}_k^{I,l}}}{\mathcal{l}}_{sr}^l{x}_{srky}^l+R{R}^{SS}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{SS}}{C}_s^{I,SS}}{x}_{sy}^{SS}+R{R}^{NT}{\displaystyle \sum _{k\in K^{NT}}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{SS}}{C}_k^{I,NT}}}{x}_{sky}^{NT}\\ +{\displaystyle \sum _{p\in P}R}{R}^p{\displaystyle \sum _{k\in K^p}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^p}{C}_k^{I,p}}}pf{\overline{G}}_k^p{x}_{sky}^p+R{R}^{ESS}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{ESS}}{C}^{I,ESS}{x}_{sy}^{ESS}},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall y\in Y\end{array}$$

(2)

$$c_y^M={\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K^l}{\displaystyle \sum _{(s,r)\in {{\rm Y}}^l}{C}_k^{M,l}}}}\left(y_{srky}^l+y_{rsky}^l\right)+{\displaystyle \sum _{tr\in TR}{\displaystyle \sum _{k\in K^{tr}}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{SS}}{C}_k^{M,tr}}}}{y}_{sky}^{tr}+{\displaystyle \sum _{p\in P}{\displaystyle \sum _{k\in K^p}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^p}{C}_k^{M,p}}}}{y}_{sky}^p,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall y\in Y$$

(3)

$$c_y^E=N^{\mathrm{day}}{\displaystyle \sum _{b\in B}{p}_b\cdot }pf\left(\begin{array}{l}{\displaystyle \sum _{t\in T}{\displaystyle \sum _{tr\in TR}{\displaystyle \sum _{k\in K^{tr}}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{SS}}{C}_b^{SS}{P}_{skybt}^{tr}}}}}+{\displaystyle \sum _{t\in T}{\displaystyle \sum _{p\in P}{\displaystyle \sum _{k\in K^p}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^p}{C}_k^{E,p}{P}_{skybt}^p}}}}\\ +{\displaystyle \sum _{t\in T}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{ESS}}{C}^{E,ess}(P_{sybt}^{ch}+P_{sybt}^{dch})}}\end{array}\right),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall y\in Y$$

(4)

$$c_y^R=N^{\mathrm{day}}{\displaystyle \sum _{b\in B}{p}_b}{C}_b^{SS}pf\left[\begin{array}{l}{\displaystyle \sum _{t\in T}{\displaystyle \sum _{tr\in TR}{\displaystyle \sum _{k\in K^{tr}}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{SS}}{Z}_k^{tr}}}}{\left(P_{skybt}^{tr}\right)}^2}+{\displaystyle \sum _{t\in T}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K^l}{\displaystyle \sum _{(s,r)\in {{\rm Y}}^l}{Z}_k^l}}}{\mathcal{l}}_{sr}^l{\left(P_{srkybt}^l+P_{rskybt}^l\right)}^2}\\ +{\displaystyle \sum _{t\in T}{\displaystyle \sum _{p\in P}{\displaystyle \sum _{k\in K^{pv}}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{pv}}{C}_k^{pv\_AB}{P}_{skybt}^{pv\_AB}}}}}\end{array}\right], \forall y\in Y$$

(5)

The capital recovery rate is calculated as: $R{R}^l={\displaystyle \frac{i{(1+i)}^{{\eta }^l}}{{(1+i)}^{{\eta }^l}-1}}, \forall l\in \{\mathrm{NRF},\mathrm{NAF}\}$; $R{R}^{NT}={\displaystyle \frac{i{(1+i)}^{{\eta }^{NT}}}{{(1+i)}^{{\eta }^{NT}}-1}}$; $R{R}^p={\displaystyle \frac{i{(1+i)}^{{\eta }^p}}{{(1+i)}^{{\eta }^p}-1}}, \forall p\in P$ $R{R}^{SS}={\displaystyle \frac{i{(1+i)}^{{\eta }^{SS}}}{{(1+i)}^{{\eta }^{SS}}-1}}$; $R{R}^{ESS}={\displaystyle \frac{i{(1+i)}^{{\eta }^{ESS}}}{{(1+i)}^{{\eta }^{ESS}}-1}}$.

In Equation (2), the investment costs for each phase are composed of the following items: (1) replacement and addition of feeders; (2) reinforcement of existing substations and construction of new ones; (3) installation of new transformers; (4) installation of distributed generation (DG); (5) installation of energy storage. The investment cost of substations includes only the costs of upgrading or constructing new infrastructure, excluding the maintenance cost of transformers, which is considered separately in the third term of Formula (3). Equation (3) models the maintenance costs of feeders, transformers, and photovoltaic systems at each stage. It is important to note that, for each time stage, a single binary variable per conductor of the feeder connecting nodes s and r is used to represent the corresponding investment decision, denoted as $x_{srkt}^l$. Additionally, two binary variables, $y_{srkt}^l$ and $y_{rskt}^l$, as well as two continuous variables, $f_{srktb}^l$ and $f_{rsktb}^l$, are introduced to represent the minimum and maximum power flow on each feeder, allowing the model to capture its utilization status and operational conditions. A critical constraint is that when the power flow at both ends of a feeder is equal to zero, the corresponding investment variable must also be zero; otherwise, the investment would be invalid.

The production costs associated with substations and distributed photovoltaic and energy storage systems are described in Equation (4). Operating costs in transformers and feeders, as well as curtailment costs, are modeled as quadratic terms in Equation (5). The motivation for minimizing operating costs is to avoid unintended increases in operating caused by improper installation of distributed generation devices. The nonlinear costs of operating can be accurately approximated using a set of tangents. This approximation method generates a piecewise linear function, and in practical applications, as long as a sufficient number of segments are used, it is virtually indistinguishable from the nonlinear model.

The quadratic terms representing the operating costs in transformers and feeders in Equation (5) are approximated using a piecewise linear approach. Therefore, Equation (5) can be reformulated as:

$$\begin{array}{l}{c}_y^R=N^{\mathrm{day}}{\displaystyle \sum _{b\in B}{p}_b}{C}_b^{SS}pf\left[{\displaystyle \sum _{t\in T}{\displaystyle \sum _{tr\in TR}{\displaystyle \sum _{k\in K^{tr}}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{SS}}{\displaystyle \sum _{\nu =1}^{n_{\nu }}{M}_{k\nu }^{tr}{\delta }_{skyb\nu t}^{tr}}}}}}\right.\\ +{\displaystyle \sum _{t\in T}{\displaystyle \sum _{p\in P}{\displaystyle \sum _{k\in K^{pv}}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{pv}}{C}_k^{pv\_AB}{P}_{skybt}^{pv\_AB}}}}}\\ +\left.{\displaystyle \sum _{t\in T}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K^l}{\displaystyle \sum _{(s,r)\in {{\rm Y}}^l}{\displaystyle \sum _{\nu =1}^{n_{\nu }}{M}_{k\nu }^l{\mathcal{l}}_{sr}\left({\delta }_{srkyb\nu t}^l+{\delta }_{rskyb\nu t}^l\right)}}}}}\right];\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall y\in Y\end{array}$$

(6)

2.2. Constraints

(1)

Investment Cost Constraints

$$\begin{array}{c}{\displaystyle \sum _{l\in \{NRF,NAF\}}{\displaystyle \sum _{k\in K^l}{\displaystyle \sum _{(s,r)\in {{\rm Y}}^l}{C}_k^{I,l}}}}{\mathcal{l}}_{sr}^l{x}_{srky}^l+{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{SS}}{C}_s^{I,SS}}{x}_{sy}^{SS}+{\displaystyle \sum _{k\in K^{NT}}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{SS}}{C}_k^{I,NT}}}{x}_{sky}^{NT}\\ +{\displaystyle \sum _{p\in P}{\displaystyle \sum _{k\in K^p}{\displaystyle \sum _{s\in {\mathrm{\Omega }}^p}{C}_k^{I,p}}}}pf{\overline{G}}_k^p{x}_{sky}^p+{\displaystyle \sum _{s\in {\mathrm{\Omega }}^{ESS}}{C}^{I,ESS}{x}_{sy}^{ESS}}\le I{B}_y,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall y\in Y\end{array}$$

(7)

Equation (7) imposes a budget constraint on the investment cost at each planning stage.

(2)

Investment Status Constraints

The investment status constraints indicate whether feeders, transformers, distributed generation (DG), and energy storage systems (ESS) are invested/commissioned over the planning horizon; for each asset at each candidate location, at most one investment option may be selected in each period.

$${\displaystyle \sum _{y\in Y}{\displaystyle \sum _{k\in K^l}{x}_{srky}^l}}\le 1;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall l\in \{\mathrm{NRF},\mathrm{NAF}\},\forall (s,r)\in {{\rm Y}}^l$$

(8)

$${\displaystyle \sum _{y\in Y}{x}_{sy}^{SS}}\le 1,\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^{SS}$$

(9)

$${\displaystyle \sum _{y\in Y}{\displaystyle \sum _{k\in K^{NT}}{x}_{sky}^{NT}}}\le 1,\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^{SS}$$

(10)

$${\displaystyle \sum _{y\in Y}{\displaystyle \sum _{k\in K^p}{x}_{sky}^p}}\le 1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall p\in P,\forall s\in {\mathrm{\Omega }}^p$$

(11)

$${\displaystyle \sum _{y\in Y}{x}_{sy}^{ESS}\le 1},\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^{ESS}$$

(12)

$$x_{sky}^{NT}\le {\displaystyle \sum _{\tau =1}^y{x}_{s\tau }^{SS}},\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^{SS},\forall k\in K^{NT},\forall y\in Y$$

(13)

According to Equations (8)–(12), each system component and location can be reinforced, replaced, or newly installed at most once over the entire planning horizon. Furthermore, Equation (13) ensures that new transformers can only be installed at substations that have already been reinforced or newly constructed.

(3)

Power Flow Constraints of the Distribution Network

$$\begin{array}{l}{\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K^l}{\displaystyle \sum _{r\in {\mathrm{\Omega }}_s^l}\left(P_{srkybt}^l-P_{rskybt}^l\right)}}}={\displaystyle \sum _{tr\in TR}{\displaystyle \sum _{k\in K^{tr}}{P}_{skybt}^{tr}}}+{\displaystyle \sum _{p\in P}{\displaystyle \sum _{k\in K^p}{P}_{skybt}^p}}-{\mu }_{bt}{D}_{sy}-P_{skybt}^{pv\_AB}\\ +P_{sybt}^{dis}-P_{sybt}^{ch},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^N,\forall y\in Y,\forall b\in B,\forall t\in T\end{array}$$

(14)

$$\begin{array}{c}{y}_{srky}^l\left[Z_k^l{\mathcal{l}}_{sr}^l{P}_{srkybt}^l-\left(v_{sybt}-v_{rybt}\right)\right]=0\\ \forall l\in L,\forall s\in {\mathrm{\Omega }}_r^l,\forall r\in {\mathrm{\Omega }}^N,\forall k\in K^l,\forall y\in Y,\forall b\in B,\forall t\in T\end{array}$$

(15)

$$\underset{\_}{V}\le v_{sybt}\le \overline{V};\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^N,\forall y\in Y,\forall b\in B,\forall t\in T$$

(16)

Based on the linearized network model, Equations (14) and (15) reflect the operational impacts of the distribution network. This linearized model is an enhanced version of the DC power flow model commonly used in transmission systems, established under the assumptions:

• The per-unit voltage drop across each branch is equal to the difference in voltage magnitudes at the two end nodes of that branch.

The assumption allows Kirchhoff’s Voltage Law (KVL) for each active feeder to be represented as a linear expression linking current magnitudes, nodal voltage magnitudes, and branch impedance parameters.

Equation (15) extends this formulation to account for the utilization status of each feeder by incorporating binary variables representing feeder investment decisions. Additionally, Equation (16) enforces upper and lower bounds on the voltage magnitudes at all nodes.

The nonlinear expression in (15) can be equivalently represented in the following linearized form:

$$\begin{array}{c}-H(1-y_{srky}^l)\le Z_k^l{\mathcal{l}}_{sr}^l{P}_{srkybt}^l-(v_{sybt}-v_{rybt})\le H(1-y_{srky}^l),\\ \forall l\in L,\forall s\in {\mathrm{\Omega }}_r^l,\forall r\in {\mathrm{\Omega }}^N,\forall k\in K^l,\forall y\in Y,\forall b\in B,\forall t\in T\end{array}$$

(17)

(4)

Feeder-Related Constraints

$$0\le P_{srkybt}^l\le y_{srky}^l{\overline{F}}_k^l;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall l\in L,\forall s\in {\mathrm{\Omega }}_r^l,\forall r\in {\mathrm{\Omega }}^N,\forall k\in K^l,\forall y\in Y,\forall b\in B,\forall t\in T$$

(18)

$$y_{srky}^{EFF}+y_{rsky}^{EFF}\le 1,\hspace{0.33em}\hspace{0.33em} \forall (s,r)\in {{\rm Y}}^{EFF},\forall k\in K^{EFF},\forall y\in Y$$

(19)

$$y_{srky}^l+y_{rsky}^l\le {\displaystyle \sum _{\tau =1}^y{x}_{srk\tau }^l},\hspace{0.33em}\hspace{0.33em} \forall l\in \{\mathrm{NRF},\mathrm{NAF}\},\forall (s,r)\in {{\rm Y}}^l,\forall k\in K^l,\forall y\in Y$$

(20)

$$y_{srky}^{ERF}+y_{rsky}^{ERF}\le 1-{\displaystyle \sum _{\tau =1}^y{\displaystyle \sum _{\kappa \in K^{NRF}}{x}_{sr\kappa \tau }^{NRF}}},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall (s,r)\in {{\rm Y}}^{ERF},\forall k\in K^{ERF},\forall y\in Y$$

(21)

$$P_{srkybt}^l={\displaystyle \sum _{\nu =1}^{n_{\nu }}{\delta }_{srkyb\nu t}^l}; \forall l\in L,\forall s\in {\mathrm{\Omega }}_r^l,\forall r\in {\mathrm{\Omega }}^N,\forall k\in K^l,\forall y\in Y,\forall b\in B,\forall t\in T$$

(22)

$$0\le {\delta }_{srkyb\nu t}^l\le A_{k\nu }^l,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall \nu =1\dots n_{\nu }, \forall l\in L,\forall s\in {\mathrm{\Omega }}_r^l,\forall r\in {\mathrm{\Omega }}^N,\forall k\in K^l,\forall y\in Y,\forall b\in B,\forall t\in T$$

(23)

Equation (18) defines the upper and lower bounds of line currents, where the upper limit of feeder ${\overline{F}}_k^l$ may be set below its rated capacity to reserve operational margin under emergency conditions. Equations (19)–(21) describe the feeder utilization status. The feeder status variable $y_{srky}^l$ can take the value of 1 only when $x_{srkt}^l$ = 1, indicating that the feeder is activated and available for operation; otherwise, the feeder status variables are 0. Only when the feeder-status variables equal 1, the value of the power flow variable $P_{srkybt}^l$ is not 0; otherwise, the power flow through the feeder is constrained to be zero. This ensures the required logical relationship that there exists power flow through the feeder only when the feeder is both invested and activated in the network. Equations (22) and (23) are associated with the linearization of operating within feeders.

(5)

Transformer-Related Constraints

$$0\le P_{skybt}^{tr}\le y_{sky}^{tr}{\overline{G}}_k^{tr};\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall tr\in TR,\forall s\in {\mathrm{\Omega }}^{SS},\forall k\in K^{tr},\forall y\in Y,\forall b\in B,\forall t\in T$$

(24)

$$y_{sky}^{NT}\le {\displaystyle \sum _{\tau =1}^y{x}_{sk\tau }^{NT}},\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^{SS},\forall k\in K^{NT},\forall y\in Y$$

(25)

$$P_{skybt}^{tr}={\displaystyle \sum _{\nu =1}^{n_{\nu }}{\delta }_{skyb\nu t}^{tr}}; \forall tr\in TR,\forall s\in {\mathrm{\Omega }}^{SS},\forall k\in K^{tr},\forall y\in Y,\forall b\in B,\forall t\in T$$

(26)

$$0\le {\delta }_{skyb\nu t}^{tr}\le A_{k\nu }^{tr},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall \nu =1\dots n_{\nu }, \forall tr\in TR,\forall s\in {\mathrm{\Omega }}^{SS},\forall k\in K^{tr},\forall y\in Y,\forall b\in B,\forall t\in T$$

(27)

Equation (24) imposes upper and lower bounds on the injection current of transformers, where the upper limit of transformer ${\overline{G}}_k^{tr}$ may be set below its rated capacity to reserve operational margin under emergency conditions. The utilization of newly installed transformers is modeled in Equation (25). Equations (26) and (27) are associated with the linearization of operating in transformers.

(6)

Distributed Generator-Related Constraints

$$y_{sky}^p\le {\displaystyle \sum _{\tau =1}^y{x}_{sk\tau }^p},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall p\in P,\forall s\in {\mathrm{\Omega }}^p,\forall k\in K^p,\forall y\in Y$$

(28)

$$0\le P_{skybt}^{PV}\le y_{sky}^{PV}\cdot \min \left\{{\overline{G}}_k^{PV},{\widehat{G}}_{skyb}^{PV}\right\},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^{PV},\forall k\in K^{PV},\forall y\in Y,\forall b\in B,\forall t\in T$$

(29)

$$P_{skybt}^{pv\_AB}\le P_{skybt}^{PV},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^{PV},\forall k\in K^{PV}, \forall y\in Y,\forall b\in B,\forall t\in T$$

(30)

The use of new distributed photovoltaic power generation is modeled separately in Equation (28). The upper limit of photovoltaic power generation output is modeled as the smaller value between the rated capacity of the photovoltaic modules and the maximum power that can be generated under the corresponding illumination conditions at that moment. That is, photovoltaic output is subject to dual constraints of installed capacity and solar resource availability, as shown in Equation (29). Equation (30) indicates that curtailed power generation cannot exceed photovoltaic power generation.

(7)

Energy Storage System (ESS) Constraints

The logical relationship between the investment status of energy storage systems and their charging/discharging states is defined by Equations (31) and (32), ensuring that charging and discharging operations are permitted only when the storage system is installed.

$$y_{sybt}^{ch}\le {\displaystyle \sum _{\tau =1}^y{x}_{s\tau }^{ESS}},\hspace{0.33em}\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(31)

$$y_{sybt}^{dch}\le {\displaystyle \sum _{\tau =1}^y{x}_{s\tau }^{ESS}},\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(32)

The energy of the energy storage system at time t is determined by its energy at time t − 1 as well as the charging and discharging power at time t, and is constrained by the minimum and maximum energy limits, as defined in Equations (33) and (34).

$$S_{sybt}^{oc}=S_{syb(t-1)}^{oc}+\left(P_{sybt}^{ch}{\eta }^{ch}/E_{cap}^b-P_{sybt}^{dch}/{\eta }^{dch}{E}_{cap}^b\right){\mathrm{\Delta }}_t;\forall s\in {\mathrm{\Omega }}^{ESS},\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(33)

$$x_{sy}^{ESS}{S}_{sybt}^{\min }\le S_{sybt}^{oc}\le x_{sy}^{ESS}{S}_{sybt}^{\max };\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(34)

The charging and discharging power of the energy storage system is constrained as specified in Equations (35) and (36).

$$0\le P_{sybt}^{ch}\le y_{sybt}^{ch}{\overline{G}}^{ch};\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(35)

$$0\le P_{sybt}^{dch}\le y_{sybt}^{dch}{\overline{G}}^{dch};\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(36)

The charging and discharging state logic constraint, as defined in Equation (37), ensures that the energy storage system cannot simultaneously operate in both charging and discharging modes.

$$y_{sybt}^{ch}+y_{sybt}^{dch}\le 1 ;\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(37)

To ensure the sustainable operation of the energy storage system, the state of charge at the beginning and end of the scheduling horizon must be equal, as specified in Equation (38).

$$S_{syb24}^{oc}=x_{sy}^{ESS}{S}_{syb0}^{oc} ,\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B$$

(38)

Building upon the existing ESS operational constraints (30)–(37), this paper further introduces lifetime constraints. By incorporating the concept of equivalent cycle depth, the degradation under different depths of discharge is converted into equivalent full cycles. An upper bound on the total equivalent cycles is then imposed over the entire scheduling horizon to reflect the impact of battery lifetime degradation on planning and operation decisions.

$$N_{sybt}^{\mathrm{eq}}\hspace{0.33em}=\hspace{0.33em}{(d_{sybt}^{\mathrm{b}})}^{k_p};\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(39)

$$d_{sybt}^{\mathrm{b}}\hspace{0.33em}=(1-S_{sybt}^{oc})y_{sybt}^{ch};\forall s\in {\mathrm{\Omega }}^{ESS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(40)

$${\displaystyle \sum _{y\in Y}{\displaystyle \sum _{b\in B}{\displaystyle \sum _{t\in T}{N}_{sybt}^{\mathrm{eq}}}}}\hspace{0.33em}\le \hspace{0.33em}{N}^{\max };\forall s\in {\mathrm{\Omega }}^{ESS}$$

(41)

For a charging and discharging process under different depths of discharge, it can be converted into an equivalent number of cycles at 100% depth of discharge (also referred to as equivalent full cycles) according to Equation (39). The calculation of the depth of discharge is given in Equation (40), where the sum of the state of charge and the depth of discharge equals one if and only if =1. To mitigate the lifetime degradation of the energy storage system, the total number of equivalent full cycles during the entire load recovery process is constrained, as expressed in Equation (41).

The lifetime degradation of the energy storage system is jointly determined by the coupling relationships among SOC, DOD, partial cycles, and equivalent full cycles. Equation (33) describes the temporal evolution of the SOC, while Equation (40) defines the DOD based on the SOC. Using the DOD, Equation (39) converts each partial discharge process into an equivalent number of full cycles, reflecting the impact of different discharge depths on battery degradation. Equation (41) then imposes a cumulative limit on the equivalent full cycles over the planning period, ensuring that the energy storage system satisfies its lifetime constraint. Therefore, Equations (33)–(41) form a complete modeling chain—from SOC → DOD → cycle depth → lifetime consumption—that accurately captures the long-term degradation characteristics of the energy storage system in a multi-stage planning context.

(8)

Radial and Connectivity Constraints

The proposed model incorporates the following conventional radiality constraints:

$${\displaystyle \sum _{l\in L}{\displaystyle \sum _{s\in {\mathrm{\Omega }}_r^l}{\displaystyle \sum _{k\in K^l}{y}_{srky}^l}}}=1,\hspace{0.33em}\hspace{0.33em} \forall r\in {\mathrm{\Omega }}_y^{LN},\hspace{0.33em}\forall y\in Y$$

(42)

$${\displaystyle \sum _{l\in L}{\displaystyle \sum _{s\in {\mathrm{\Omega }}_r^l}{\displaystyle \sum _{k\in K^l}{y}_{srky}^l}}}\le 1,\hspace{0.33em}\hspace{0.33em} \forall r\notin {\mathrm{\Omega }}_y^{LN},\hspace{0.33em}\forall y\in Y$$

(43)

Constraint (42) stipulates that each load node can have only one incoming current, while constraint (43) limits all other nodes to at most one incoming current. In the absence of distributed generation (DG), this modeling approach ensures that the distribution network maintains a tree-shaped (radial) structure, even with the presence of relay nodes. However, when DG is incorporated, constraints (42) and (43) alone are insufficient to prevent the formation of isolated areas powered solely by DG units, disconnected from all substations in terms of topology. To address this issue, an additional set of radiality constraints can be introduced as follows:

$${\displaystyle \sum _{l\in L}{\displaystyle \sum _{k\in K^l}{\displaystyle \sum _{r\in {\mathrm{\Omega }}_s^l}\left(P_{srkybt}^{l,im}-P_{rskybt}^{l,im}\right)}}}=W_{sybt}^{SS}-{\tilde{D}}_{sybt},\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^N,\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(44)

$$0\le P_{srkybt}^{EFF,im}\le M,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}_r^{EFF},\hspace{0.33em}\forall r\in {\mathrm{\Omega }}^N,\hspace{0.33em}\forall k\in K^{EFF},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(45)

$$0\le P_{srkybt}^{ERF,im}\le M\left(1-{\displaystyle \sum _{\tau =1}^y{\displaystyle \sum _{\kappa \in K^{NRF}}{s}_{sr\kappa \tau }^{NRF}}}\right),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall (s,r)\in {{\rm Y}}^{ERF},\hspace{0.33em}\forall k\in K^{ERF},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(46)

$$0\le P_{rskybt}^{ERF,im}\le M\left(1-{\displaystyle \sum _{\tau =1}^y{\displaystyle \sum _{\kappa \in K^{NRF}}{s}_{sr\kappa \tau }^{NRF}}}\right);\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall (s,r)\in {{\rm Y}}^{ERF},\hspace{0.33em}\forall k\in K^{ERF},\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(47)

$$0\le P_{srkybt}^{l,im}\le M{\displaystyle \sum _{\tau =1}^y{s}_{srk\tau }^l},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall l\in \{NRF,NAF\},\hspace{0.33em}\forall (s,r)\in {{\rm Y}}^l,\hspace{0.33em}\forall k\in K^l,\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(48)

$$0\le P_{rskybt}^{l,im}\le M{\displaystyle \sum _{\tau =1}^y{s}_{srk\tau }^l};\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall l\in \{NRF,NAF\},\hspace{0.33em}\forall (s,r)\in {{\rm Y}}^l,\hspace{0.33em}\forall k\in K^l,\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(49)

$$0\le W_{sybt}^{SS}\le M;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^{SS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(50)

$$W_{sybt}^{SS}=0;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \forall s\in {\mathrm{\Omega }}^N\backslash {\mathrm{\Omega }}^{SS},\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(51)

Equations (45)–(51) can be used to avoid the existence of isolated generators. These formulas construct a virtual system that includes virtual loads. At load nodes that are candidates for DG installation, the virtual load is set to 1 p.u., while the virtual load at other nodes is set to 0. Mathematically, this is expressed as:

$${\tilde{D}}_{sybt}=\left\{\begin{array}{l}1;\hspace{1em}\forall s\in \left(\left({\mathrm{\Omega }}^{PV}\cup {\mathrm{\Omega }}^{ESS}\right)\cap {\mathrm{\Omega }}_y^{LN}\right),\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T\hfill \\ 0;\hspace{1em}\forall s\notin \left(\left({\mathrm{\Omega }}^{PV}\cup {\mathrm{\Omega }}^{ESS}\right)\cap {\mathrm{\Omega }}_y^{LN}\right),\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T\hfill \end{array}\right.$$

(52)

The load of these virtual nodes can only be supplied by virtual substations located at the original substation nodes, which inject virtual energy through actual feeders. Constraint (44) represents the virtual current balance equation of the node. Constraints (45)–(49) limit the virtual power flow in the feeders. Constraints (50) and (51) set the upper limit of the current injected by the virtual substation.

(9)

Agricultural greenhouse Load

$$\begin{array}{c}{P}_{sybt}^{\mathrm{gh}}={\displaystyle \sum _{p=1}^n{d}_{sybt}^{\mathrm{water}}{P}_{sybtp}^{\mathrm{water}}}+{\displaystyle \sum _{p=1}^m{d}_{sybt}^{\mathrm{w}}{P}_{sybtp}^{\mathrm{w}}}+{\displaystyle \sum _{p=1}^k{d}_{sybt}^{\mathrm{light}}{P}_{sybtp}^{\mathrm{light}}}+{\displaystyle \sum _{p=1}^s{d}_{sybt}^{\mathrm{mac}}{P}_{sybt}^{\mathrm{mac}}}, \\ \forall s\in {\mathrm{\Omega }}^N,\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T\end{array}$$

(53)

Equation (53) characterizes the instantaneous electricity demand of an agricultural greenhouse at any given time, which is obtained by summing the products of the rated power of various electrical devices—such as ventilation fans, water pumps, motors, and supplemental lighting and their corresponding operational status variables.

In cloudy or rainy weather, additional lighting is typically required to promote crop growth; whereas, in the summer with clear skies and high temperatures, shading measures are necessary to regulate the greenhouse environment. The lighting constraints for supplementary lighting are shown in (54) and (55).

$$\left\{\begin{array}{l}{T}_s^{\mathrm{light}}{\displaystyle \frac{P_{syb}^{\mathrm{light}}}{S_{syb}^{\mathrm{light}}}}+{\displaystyle \sum _{t\in {\mathrm{\Omega }}^{\mathrm{T}}}{P}_{sybt}^{\mathrm{sun}}}\ge P_{syb}^{\mathrm{crop},\min }\\ {\displaystyle \sum _{t=1}^{24}{d}_{sybt}^{\mathrm{light}}}\ge T_s^{\mathrm{light}}\end{array}\right., \forall s\in {\mathrm{\Omega }}^N,\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(54)

$$\left\{\begin{array}{l}{d}_{sybt}^{\mathrm{mac}}=1, T_{sybt}^{\mathrm{out}}\ge T_s^{\mathrm{gh},\max }\\ 0\le d_{sybt}^{\mathrm{mac}}\le 1, T_s^{\mathrm{gh},\mathrm{req}}\le T_{sybt}^{\mathrm{out}}\le T_s^{\mathrm{gh},\max }\\ d_{sybt}^{\mathrm{mac}}=0, T_{sybt}^{\mathrm{out}}\le T_s^{\mathrm{gh},\mathrm{req}}\end{array}\right., \forall s\in {\mathrm{\Omega }}^N,\hspace{0.33em}\forall y\in Y,\hspace{0.33em}\forall b\in B,\forall t\in T$$

(55)

3. Solution Strategy

AMPL is a modeling language designed for describing and solving large-scale complex mathematical programming problems. It does not directly solve optimization problems itself, but rather relies on external solvers (such as CPLEX, MINOS, GUROBI, and SNOPT) to handle the computational process.

In this study, the proposed open configuration optimization model is formulated as a mixed-integer linear programming (MILP) problem. Accordingly, the model is solved using the GUROBI solver within the AMPL platform. The solution process employs the branch-and-bound algorithm to handle integer variables and explore the solution space efficiently.

4. Case Study

4.1. Parameter Settings

In this study, the proposed method is validated using the IEEE 24-node distribution system as a case study. The system comprises 20 load nodes, 4 substation nodes, and 33 distribution lines. The network topology is illustrated in Figure 1 The hourly load variation trends under different typical days are depicted in Figure 2 The system operates at a voltage level of 20 kV, with the substation node voltage set at 1.05 p.u., and the voltage limits for load nodes constrained between 0.95 p.u. and 1.05 p.u. Based on the solar irradiance data provided in

Table 1. Solar irradiance across different stages (W/m²).

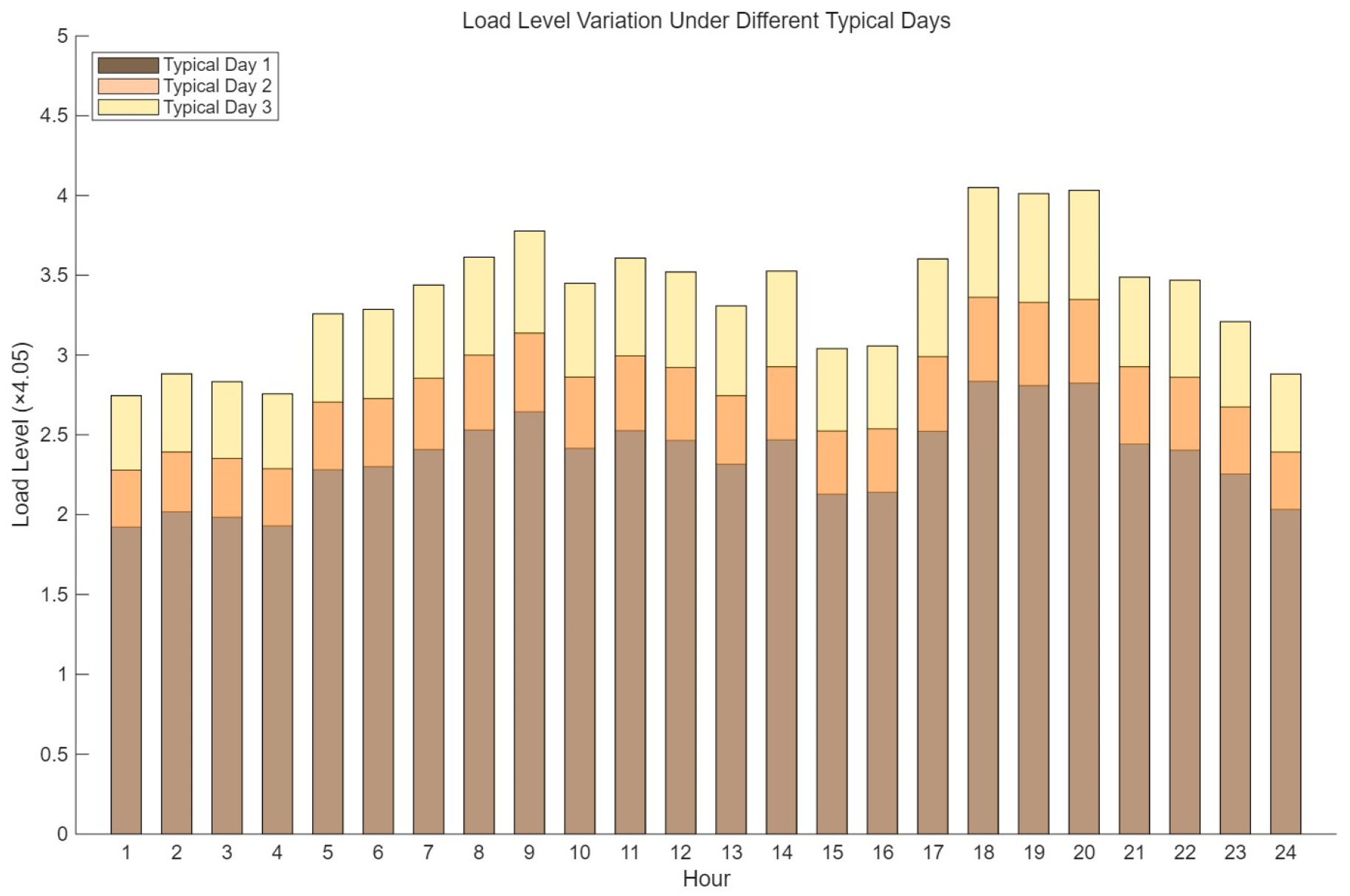
Zones	Load Level
	1	2	3
A	400	700	900
B	350	600	850
C	300	500	800

, the system is divided into three regions. For simplicity, it is assumed that the solar irradiance levels in each region remain constant throughout the entire planning horizon.

The simulations are performed on the AMPL platform using an Intel Core i5 quad-core CPU with 16 GB RAM, and solved by Gurobi 12.0.2. The stopping criterion is an optimality gap of 1%, and the total solution time is 2271 s.

The planning horizon is set to three years, divided into annual stages. The annual discount rate is assumed to be 4.9%, with a total investment budget of $6 million. To reflect the uncertainty in system loads, three typical operating scenarios are considered, corresponding to load levels of 70%, 83%, and 100%, respectively.

Line parameters are provided in

Table 2. Line lengths of the 24-node distribution system.

Line		Length (km)	Line		Length (km)	Line		Length
s	r		s	r		s	r
1	5	2.67	4	9	1.20	7	23	0.90
1	9	1.27	4	15	1.60	8	22	1.90
1	14	1.27	4	16	1.30	10	16	1.60
1	21	2.67	5	6	2.40	10	23	1.30
2	3	2.00	5	24	0.70	11	23	1.60
2	12	1.10	6	13	1.20	14	18	1.00
2	21	1.70	6	17	2.20	15	17	1.20
3	10	1.10	6	22	2.70	15	19	0.80
3	16	1.20	7	8	2.00	17	22	1.50
3	23	1.20	7	11	1.10	18	24	1.50
4	7	2.60	7	19	1.20	20	24	0.90

. The lines are categorized into existing lines and candidate new lines. Among the existing lines, two types are defined: one is fixed single-feeder lines that cannot be modified, represented by solid lines in the figure; the other is replaceable single-feeder lines, depicted as double solid lines, which can be adjusted or replaced during planning. Candidate lines for new feeders are illustrated with dashed lines. The capacity of existing feeders is 3.94 MVA, and the unit impedance is 0.732 Ω/km. Conductor options for branch replacements and new candidate branches are listed in

Table 3. Candidate conductor data for the 24-node distribution system.

Types		NRF	NAF
Candidate 1	${\overline{F}}_1^l$ (MVA)	6.29	3.98
	$Z_1^l$ (Ω/km)	0.557	0.734
	$C_1^{I,l}$ ($/km)	19,140	15,020
Candidate 2	${\overline{F}}_2^l$ (MVA)	9.23	6.33
	$Z_1^l$ (Ω/km)	0.458	0.557
	$C_2^{I,l}$ ($/km)	29,870	25,030

, with two alternative conductor types available for each branch. The annual operation and maintenance cost of all feeders is $450, and the service life is assumed to be 30 years.

In terms of the substation expansion, two types of investment decisions are considered: (1) increasing capacity by adding transformers at existing substation sites, and (2) constructing new substations at candidate locations. Given that substations typically have a much longer service life than other distribution equipment, they are not modeled for periodic replacement. All substations are assumed to have the same unit supply cost, with electricity prices set at $57.7/MWh, $70.0/MWh, and $85.3/MWh under low, medium, and high load levels, respectively. The existing substations are located at nodes 21 and 22, each equipped with a 7.5 MVA transformer with an impedance of 0.25 Ω and an annual maintenance cost of $1000. Nodes 23 and 24 are designated as candidate substation locations. The expansion costs for sub-stations at nodes 21 through 24 are $100,000, $100,000, $140,000, and $180,000, respectively. Based on [26], candidate transformer specifications are listed in

Table 4. Candidate Transformer Data for the 24-Node Distribution System.

Replacement Option 1	${\overline{G}}_1^{NT}$ (MVA)	12
	$Z_1^{NT}$ (Ω)	0.16
	$C_1^{M,NT}$ ($)	2000
	$C_1^{I,NT}$ ($)	750,000
Replacement Option 2	${\overline{G}}_2^{NT}$ (MVA)	15
	$Z_2^{NT}$ (Ω)	0.13
	$C_2^{M,NT}$ ($)	3000
	$C_2^{I,NT}$ ($)	950,000

, with two types of transformers available for each substation. All candidate transformers are assumed to have a service life of 25 years.

Two candidate DG options are considered. In Option 1, the PV unit has a capacity of 0.91 MVA, with an investment cost of $1.85 million per MW and zero operation and maintenance cost. In Option 2, the PV unit has a capacity of 2.05 MVA, with an investment cost of $1.84 million per MW, and also zero maintenance cost. The service life for all technical options is uniformly set to 25 years, and the power factor is assumed to be pf = 0.9. Parameters related to the energy storage system are listed in

Table 5. Energy Storage System Parameters.

$C^{I,ESS}$ ($)	$C^{E,ess}$ ($/MWh)	$\overline{E}$ (MVA)	${\overline{G}}^{ch}$ (MW)	${\overline{G}}^{dch}$ (MW)
150,000	180	50	1.5	1.5

. The ESS data are obtained from Anhui Mingsheng Hengzhuo Technology Co., Ltd., Hefei, China; however, due to confidentiality agreements, the original data cannot be disclosed, and modified representative values are adopted in this study.

To comprehensively evaluate the impact of PV and ESS integration on distribution network expansion planning, a stepwise resource integration approach is adopted for modeling and analysis. In the first stage, only feeders, substations, and transformers are considered as candidate investment assets. In the second stage, DG units are incorporated. In the final stage, energy storage systems are introduced. The investment structure and operational performance of the system are then compared across different planning scenarios.

4.2. Results and Analysis

4.2.1. Analysis of Planning Schemes

Figure 3, Figure 4 and Figure 5 illustrate the line planning schemes under different resource configurations, while

Table 6. PV and ESS Planning under Different Schemes.

Scheme		Stage 1	Stage 2	Stage 3
No PV, No ESS	—	—	—	—
PV Only	Installation Node	PV: 9, 4	PV: 1, 9, 4, 17	PV: 1, 7, 9, 15, 18, 4, 17
	Installed Capacity	8.10 MWh	16.20 MWh	28.35 MWh
PV + ESS	Installation Node	PV: 3, 9, 4 ESS: 1, 5, 9, 16	PV: 1, 3, 9, 4, 5 ESS: 1, 3, 4, 5, 9, 13, 15, 16	PV: 1, 3, 9, 15, 16, 18, 4, 5 ESS: 1, 3, 4, 5, 9, 13, 15, 16, 18, 20
	Installed Capacity	PV: 12.15 MWh ESS: 6.00 MWh	PV: 20.25 MWh ESS: 12.00 MWh	PV: 28.35 MWh ESS: 13.50 MWh

presents the planning results of PV and ESS under various configurations. In the figures, hollow circles denote non-load nodes, solid circles represent load nodes; solid squares indicate existing substations, and dashed squares indicate candidate substations that have not yet been constructed. The asterisk “*” marks equipment that is newly installed or replaced in the current planning stage. It can be observed that the network topology of the distribution system varies significantly across different planning stages. The integration of energy storage systems exerts a notable impact on system expansion paths and investment strategies, leading to more optimized substation expansion decisions.

As shown in Figure 3, in response to the gradually increasing load demand, the system activates the substation at node 23 as early as Stage 1. Subsequently, new substations are added at node 24 in Stage 2. This evolution path indicates a heavy reliance on the expansion of traditional supply capacity to meet load growth, resulting in high upfront investment intensity. In addition, to ensure the reliability of the main network structure, multiple feeders must be replaced or newly constructed, leading to a more complex system topology in later stages and reduced operational flexibility. As depicted in Figure 4, to accommodate the growing load demand, new substations at nodes 23 and 24 are introduced in Stages 2 and 3, respectively, alleviating the capacity limitations of the existing substations. Simultaneously, multiple DG units are deployed to support the increased load and reduce operating costs. However, due to the absence of energy storage systems, the system must rely solely on additional substation infrastructure to address peak demand and localized power shortages. This leads to higher overall investment costs and a more intricate network topology. In contrast, Figure 5 shows that with the integration of ESS, the system follows a notably different expansion trajectory. The substation at node 24 is not commissioned until Stage 3, and only a single transformer is installed, indicating that the ESS effectively contributes to load regulation and peak shaving in Stages 1 and 2. This defers substation expansion and reduces total investment costs. Moreover, due to the effective alleviation of power supply pressure in later stages through the synergy between distributed PV and energy storage, the substation originally planned at Node 23 was not commissioned in any of the three optimization stages, leading to additional savings in investment costs. Although some feeder replacements are still required in Stage 3, the overall network structure remains more compact compared to the extensive transformer upgrades and line reconstructions seen in Figure 3, indicating a more controlled and cost-effective development scale.

4.2.2. Economic Comparison of Planning Schemes

Table 7. Annual Costs Under Different Planning Schemes (10⁶ $).

		Investment Cost	Maintenance Cost	Generation Cost	Operating Cost
No PV, No ESS	Stage 1	0.1230	0.0094	8.9088	0.1576
	Stage 2	0.1136	0.0141	14.7659	0.2960
	Stage 3	0.0046	0.0150	25.0827	0.5729
PV Only	Stage 1	0.3920	0.0766	8.1593	0.0708
	Stage 2	0.4457	0.2021	13.1885	0.1474
	Stage 3	0.4747	0.3785	22.0204	0.2647
PV + ESS	Stage 1	0.6293	0.2581	7.1162	0.1424
	Stage 2	0.4871	0.4326	11.7879	0.1849
	Stage 3	0.4342	0.5554	20.7891	0.2761

presents the annual cost composition across different planning stages for the three typical planning schemes. The costs include investment, operation and maintenance, generation, operating costs. A comparison reveals that the system configuration has a significant impact on the cost structure and its dynamic evolution.

In the traditional expansion scheme without PV and ESS, investments are primarily concentrated in Stage 1 and Stage 2, together accounting for approximately 96% of the total investment over the entire planning horizon, with substation and feeder expansions representing the main expenditures. Although this high proportion of upfront investment ensures adequate supply capacity in the early stages, the system approaches its capacity limit by Stage 3. As a result, the share of generation costs increases by about 80% compared with Stage 1, while the share of operating costs rises by more than 260%, leading to a marked decline in operational efficiency and revealing the limitations of this strategy in terms of sustainability and resilience. In the PV-only scheme, the investment share increases to approximately 3–5% and is more evenly distributed across the three stages. The introduction of PV reduces the share of generation costs in all stages by about 8–12% compared with the no-PV scenario, and the share of operating costs decreases by around 10–20%, with a significantly slower growth rate in generation costs. However, due to the non-dispatchable nature of PV output, the system must still rely on conventional generation and additional infrastructure to address peak–valley mismatches, resulting in relatively high investment and maintenance cost shares in the later stages.

In the coordinated PV and ESS scheme, the investment share is the highest (approximately 5–7%), and the maintenance share also increases. Nevertheless, ESS plays a vital role in peak shaving and load balancing during the planning stages, reducing the share of generation costs by about 15–20% and the share of operating costs by approximately 20–25% compared with the no-PV scenario. Moreover, both cost components experience the smallest growth rates across the planning horizon among the three schemes. This indicates that, although the capital investment is higher, the scheme can effectively flatten the operational cost curve, significantly enhancing the system’s long-term economic performance and operational flexibility.

Table 8. Present Value of Total Costs Under Different Planning Schemes (10⁶ $).

Cost Component	No PV, No ESS	PV Only	PV + ESS
Investment Cost	3.0652	16.0713	19.2337
Maintenance Cost	0.2053	4.8949	7.4375
Generation Cost	329.1814	289.5051	272.1906
Operating Cost	7.4394	3.4452	3.6841
$c^{TPV}$	339.894	313.9165	302.5459

presents the present values of various cost components under the three typical planning schemes. Notably, the coordinated scheme integrating distributed PV and ESS reduces the total system cost by approximately 11.0% compared with the scheme without PV and ESS, and by about 3.6% compared with the PV-only scheme. This result further confirms the economic viability and effectiveness of the “PV + ESS” strategy in distribution network expansion planning.

In the third stage, to further evaluate the impact of ESS integration, the PV accommodation rate is compared before and after ESS installation. As shown in

Table 9. PV accommodation rate before and after ESS integration.

Case	PV Accommodation Rate (%)
Without ESS	83.5
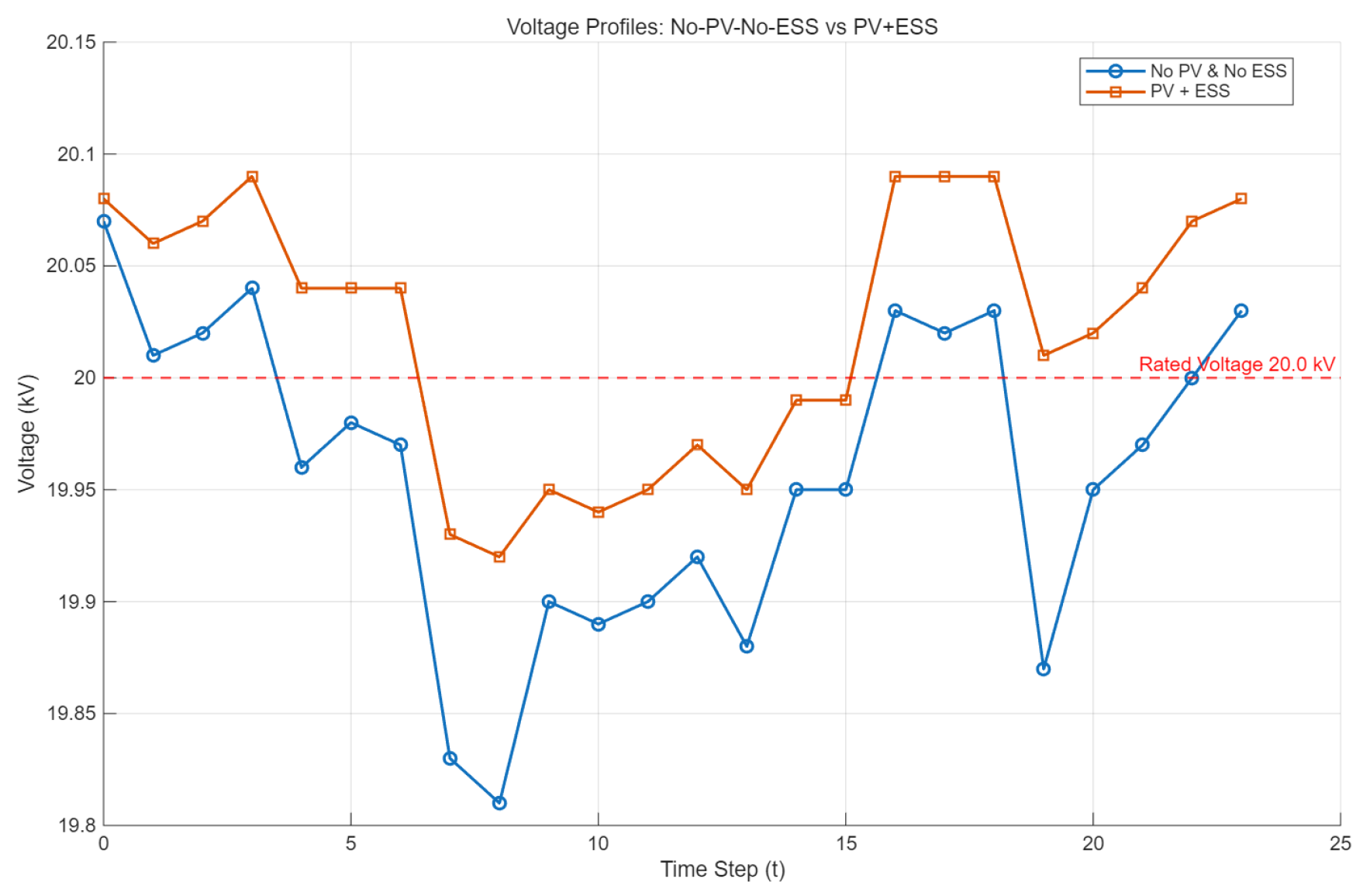
With ESS	92.8

, the accommodation rate increases from 83.5% to 92.8% with ESS integration, which verifies the effectiveness of storage in mitigating PV curtailment.

Figure 6 presents the nodal voltage profiles with and without PV and ESS integration. In the base case without PV and ESS, the voltage drops to around 19.85–19.95 kV during several time steps, approaching the lower bound of the acceptable range and exhibiting noticeable fluctuations along the day. After integrating PV and ESS, the voltage is significantly improved and maintained within 19.98–20.10 kV, remaining very close to the rated 20 kV level. The fluctuation range becomes smaller and the voltage curve becomes smoother by employing the PV and ESS, indicating an enhanced voltage-support capability provided by the coordinated PV–ESS operation.

4.2.3. Effect of Lifetime Constraints on Energy Storage Planning Schemes

To further evaluate the impact of battery lifetime modeling on system operation, the storage locations and capacities obtained from Table 3 are fixed, and two operational cases are compared:

• Case 1 (With lifetime model): the equivalent cycle constraint is considered in the optimization model, limiting the depth and frequency of charge–discharge cycles to reflect degradation effects on dispatch behavior.
• Case 2 (Without lifetime model): the equivalent cycle constraint is not considered in the optimization model, allowing unrestricted cycling during operation.

By comparing the average state of charge (SOC) and total system cost between the two cases, the influence of lifetime modeling on storage behavior and overall economic performance can be quantitatively assessed. The corresponding results are presented in

Table 10. Comparison between cases with and without battery lifetime modeling.

Case	Average SOC	Total Cost (106 $)
Without lifetime model	0.74	303.4059
With lifetime model	0.82	302.5459

:

As shown in Table 10, incorporating battery lifetime modeling significantly affects system operation and economic performance under fixed storage locations and capacities. When the lifetime constraint is neglected (Case 1), the storage unit performs frequent and deep charge–discharge cycles to pursue short-term economic optimality, resulting in a lower average SOC (0.74) and a higher total system cost (303.41 × 10⁶ $). In contrast, when the lifetime model is included (Case 2), the equivalent cycle constraint smooths the charging and discharging behavior, yielding a higher average SOC (0.82) and a lower total system cost (302.55 × 10⁶ $). These results demonstrate that lifetime modeling effectively prevents excessive cycling, enhances long-term reliability, and improves the overall economic sustainability of the distribution system.

4.2.4. Sensitivity Analysis of PV Output and ESS Performance

Table 11. Sensitivity Analysis of Total System Cost Under PV and ESS Uncertainty Scenarios.

Changes in PV Generation and ESS Capacity		Total Cost (106 $)
PV	ESS
−10%	0%	305.5037
0%	0%	302.5459
+10%	0%	298.4785
0%	−10%	304.8923
0%	+0%	302.5459
0%	+10%	301.3278

presents the variation in the total cost under different deviation levels of PV output and ESS performance. It is seen from Table 11 that as the PV generation and ESS capacity increase, the total cost decreases. Therefore, more PV generation and larger ESS capacity are beneficial to reducing the economic benefit of the planning solutions.

5. Conclusions

This paper proposes a comprehensive multistage expansion planning model for rural distribution systems, jointly optimizing the location, sizing, and timing of feeders, substations, PV, and ESS. By integrating typical-day time series load and PV profiles, the model accurately captures the operational value of ESS and the spatiotemporal flexibility of PV resources. A piecewise linear formulation is employed to linearize operating expressions, enabling the entire problem to be cast as a MILP model solvable by commercial solvers.

Numerical results show that incorporating distributed generation and energy storage investment decisions into distribution system planning significantly reduces total system cost compared to traditional network-only expansion strategies. Furthermore, the coordinated integration of PV and ESS defers costly substation upgrades by leveraging the flexible dispatch of energy storage. Although the computational effort increases due to the multistage nature and integrated asset modeling, the solution time remains acceptable for practical planning applications using commercial MILP solvers. These results demonstrate that the proposed model provides an effective and scalable framework for future rural distribution system planning under high renewable energy penetration. In future research, the proposed framework can be extended by explicitly incorporating N–1 security criteria to improve the reliability of the multi-stage planning decisions.