Machine Learning-Based Prediction of Coagulant Dosing in Drinking Water Treatment Plants Using Polynomial Regression with Lasso Regularization

Abstract

Coagulation is a critical unit process in drinking water treatment plants (DWTPs), where accurate dosing of coagulants such as polyaluminum chloride (PAC) and polyaluminum hydroxide chloride silicate (PACS) directly determines turbidity removal and operational stability. However, nonlinear interactions among water-quality variables complicate dosage prediction, and jar tests or operator heuristics cannot support real-time control. This study presents a scientifically interpretable and operationally transferable framework based on polynomial multiple linear regression (PMLR) with Lasso regularization, which was specifically developed for full-scale DWTP environments. While conventional PMLR rapidly overfits beyond polynomial degrees of 4–5, the Lasso-regularized model maintained stable generalization even at a degree of 10 by automatically pruning redundant terms and suppressing multicollinearity, thereby minimizing the need for manual hyperparameter tuning. Using 8303 hourly operational records from a full-scale DWTP in Korea, the Lasso-PMLR achieved R² = 0.951, RMSE = 0.120, and MAPE = 7.02%, outperforming traditional linear regression (R² = 0.896; MAPE = 8.64%). This proportional stability across increasing polynomial degrees, demonstrated directly using long-term real-world data, is particularly valuable for practical deployment because it ensures robustness without complex model-selection procedures. The transparent coefficient structure enables operators—who typically rely on jar tests—to understand and adjust dosing behavior, offering a field-ready and interpretable alternative to black-box models and supporting more efficient coagulant use, reduced sludge production, and sustainable automation in DWTP operation.

1. Introduction

Coagulation in drinking water treatment plants (DWTPs) is a key process for removing colloids, natural organic matter, and turbidity-causing particles through the addition of chemical coagulants. Its effectiveness directly influences downstream treatment performance, as improper dosing can result in residual turbidity, excessive chemical consumption, increased sludge production, and higher operational costs [1]. In many regions, seasonal fluctuations and climate-driven variability further complicate this challenge by inducing rapid changes in raw-water quality. Such conditions make accurate and stable coagulant dosing essential for maintaining both technical reliability and economic sustainability.

The operational data used in this study were obtained from a full-scale DWTP with a treatment capacity of approximately 200,000 m³/day, which treats surface water through a conventional process train consisting of coagulation, flocculation, sedimentation, sand filtration, and final disinfection. Online sensors measuring turbidity, pH, electrical conductivity (EC), temperature, and color are installed immediately upstream of the coagulation stage, providing continuous monitoring of raw-water conditions that directly influence chemical dosing decisions. This operational context is crucial for understanding the dataset and assessing the practical applicability of the proposed model; further details on data acquisition and quality control are provided in Section 2.1.

Although automation in DWTPs has advanced considerably, determining the optimal coagulant dosage in real time remains difficult because of the highly nonlinear interactions among multiple water-quality parameters and operational variables [2]. Such complexity limits the reliability of empirical dosing formulas or operator heuristics, which remain widely used in practice. In this study, the applied coagulant was polyaluminum hydroxide chloride silicate (PACS), a widely adopted agent known for strong turbidity-removal performance and stable operation under variable influent conditions. However, PACS dosage is still commonly determined using jar-test lookup tables or operator experience, both of which struggle to respond to rapid influent fluctuations and are therefore unsuitable for real-time control [3].

To address these limitations, recent studies have explored advanced statistical and machine-learning (ML) approaches for predicting coagulant demand [4,5,6]. Given the nonlinear relationships between influent characteristics and dosage, fuzzy inference systems (FIS) [5,6,7,8,9] and artificial neural networks (ANN) [10,11,12,13,14] have achieved strong predictive performance under diverse operating conditions [15,16,17]. More recently, ensemble-based and explainable-AI methods such as random forest (RF), Adaboost, gradient boosting machine (GBM), and XGBoost have been introduced, often in combination with SHAP-based post hoc interpretation frameworks to enhance model transparency [18,19,20,21]. Despite their advantages, these models require substantial parameter tuning and computational resources and still operate largely as “black boxes,” limiting operator trust and reducing their applicability in full-scale DWTP operation [17]. Deep-learning models trained on large-scale operational datasets have also been explored for coagulant dose optimization; however, these approaches remain computationally intensive and lack the transparency required for routine use in full-scale DWTP operations [22].

A recent systematic review also summarized the rapid expansion of AI-based optimization methods for coagulation processes, highlighting persistent challenges related to model complexity, interpretability, and real-world deployability in DWTPs [23].

These challenges highlight the need for an approach that simultaneously balances predictive accuracy, scientific and operational interpretability, and simplicity suitable for real-time deployment. Motivated by this gap, the present study develops a scientifically interpretable yet practically deployable framework based on polynomial multiple linear regression (PMLR) with regularization. Polynomial expansion captures nonlinear interactions among key water-quality parameters, while Ridge and Lasso penalties constrain model complexity to enhance generalization [19,20,21]. This formulation quantifies each variable’s contribution to coagulant demand, revealing mechanistic dependencies among turbidity, pH, and EC and providing coefficient-level transparency rarely achieved in ML-based control frameworks. The model’s simplicity enables seamless integration with existing PLC–SCADA systems and allows operators to validate or adjust dosing decisions using familiar process-control concepts.

Compared with black-box models such as ANN or XGBoost—which require complex hyperparameter tuning and post hoc interpretation—the proposed PMLR + Lasso framework offers explicit coefficient-based interpretability while maintaining comparable predictive accuracy [19]. Previous research has primarily emphasized performance optimization using complex ML architectures, often at the expense of interpretability and operational usability. However, no study has systematically examined how an interpretable regression model behaves under high-degree polynomial expansion when applied to long-term full-scale DWTP data. This distinction is critical, because DWTPs require models that remain stable as raw-water conditions fluctuate seasonally and during turbidity shocks, without demanding frequent retuning or specialized ML expertise. In this study, we show that Lasso-regularized PMLR uniquely maintains generalization even as the polynomial degree increases—a behavior not observed with unregularized PMLR or Ridge—thereby reducing the tuning burden and enabling robust real-time deployment. This proportional stability under increasing polynomial degrees constitutes a key practical advantage for DWTP automation, where model maintainability is as important as predictive accuracy.

To the best of our knowledge, no previous study has systematically evaluated an interpretable and SCADA-ready regression framework for coagulant dosing using one year of full-scale DWTP data, particularly under extreme turbidity events and seasonal variability. Accordingly, the objectives of this study are threefold: (1) to develop a scientifically interpretable yet operationally simple regression-based framework for PACS coagulant dosing; (2) to evaluate its predictive accuracy and stability using one year of full-scale operational data; and (3) to demonstrate its applicability as a transparent and field-ready decision-support tool for DWTP operators.

2. Methodology

2.1. Data Collection

Operational data were obtained from a full-scale drinking water treatment plant (DWTP) in A City, Republic of Korea, with a treatment capacity of approximately 200,000 m³/day. The plant treats surface water using a conventional process train consisting of coagulation, flocculation, sedimentation, sand filtration, and disinfection. Online instruments measuring turbidity, pH, electrical conductivity (EC), temperature, and color are installed immediately upstream of the coagulation stage and continuously record raw-water conditions that guide chemical dosing decisions.

All measurements were acquired through the plant’s PLC (Programmable Logic Controller)–HMI (Human–Machine Interface) system in 2020. Instruments included a turbidity analyzer (1720E, Hach Company, Loveland, CO, USA), pH and electrical conductivity (EC) sensors (TP 44,900 series, Endress+Hauser, Reinach, Switzerland), and temperature and color sensors integrated into the SC200 controller platform (Hach Company, Loveland, CO, USA). These sensors comply with national water-quality monitoring standards defined by the Korea Water and Wastewater Works Association (KWWA) and Korean Industrial Standards (KS), and were calibrated as part of the plant’s routine quality-management program to ensure accurate and reliable operation.

Hourly measurements were automatically logged in the PLC–HMI database and screened to remove missing or erroneous values arising from sensor maintenance, cleaning, or communication faults. Quality-control rules were applied consistently across all parameters: records containing any missing fields were removed, and physically implausible values—such as turbidity < 0 NTU, pH < 4 or >10, EC < 0 µS/cm, or temperature < 0 °C or >40 °C—were excluded based on established operational ranges. Short-duration spikes caused by maintenance or flushing events were identified by cross-checking with plant logs and discarded. After these steps, a total of 8303 complete hourly observations remained for model development.

The monthly distribution of influent water quality—including turbidity, pH, EC, temperature, and color—is summarized in

Table 1. Monthly influent water quality at the DWTP in A city, Republic of Korea.

Sampling Point	Raw Water
Month	JAN	FEB	MAR	APR	MAY	JUN	JUL	AUG	SEP	OCT	NOV	DEC
Temperature (°C)	6.4 a	7.0	9.6	13.2	17.8	23.2	23.5	22.5	21.7	18.1	13.7	7.4
	(5.7–7.6) b	(5.8–8.2)	(7.8–11.9)	(11.9–15.0)	(15.1–20.7)	(20.4–25.0)	(22.1–24.7)	(21.3–24.1)	(20.7–24.1)	(15.8–20.7)	(11.4–16.6)	(4.4–12.0)
Turbidity (NTU)	5.8	3.8	3.3	4.3	3.9	4.4	6.6	32.2	14.6	12.0	5.6	2.2
	(1.7–13.4)	(1.5–11.2)	(1.2–12.1)	(2.1–8.5)	(1.6–9.0)	(1.6–11.8)	(1.1–83.9)	(2.3–100.0)	(2.5–39.3)	(0.1–100.0)	(1.2–69.2)	(0.3–8.4)
pH (-)	7.5	7.9	7.6	7.8	7.0	6.5	6.4	6.1	6.2	6.6	6.6	7.2
	(7.1–8.0)	(7.2–8.6)	(6.9–8.7)	(6.7–8.7)	(6.4–7.9)	(6.0–7.4)	(6.0–7.2)	(5.6–6.5)	(5.8–7.4)	(5.9–7.5)	(6.0–7.1)	(6.6–7.8)
E.C. (µS/cm)	145.7	146.6	140.6	147.9	145.5	157.0	164.8	112.5	111.2	133.2	141.6	193.6
	(110–192)	(115–199)	(112–182)	(124–179)	(108–176)	(108–194)	(104–204)	(101–144)	(101–123)	(101–162)	(113–181)	(175–213)
Color (°)	1.2	1.0	1.1	1.0	1.0	1.0	3.7	31.8	5.4	2.6	1.7	1.0
	(1.0–2.0)	(1.0–2.0)	(1.0–2.0)	(1.0–2.0)	(1.0–2.0)	(1.0–2.0)	(1.0–42.0)	(3.0–321)	(2.0–21.0)	(2.0–7.0)	(1.0–4.0)	(1.0–2.0)
Previous-day PACS dosing rate((mg/L)·h)	0.8	0.7	0.9	0.9	1.0	1.1	1.4	2.3	1.6	1.3	1.4	1.0
	(0.7–1.4)	(0.5–1.2)	(0.5–1.5)	(0.7–1.3)	(0.6–1.7)	(0.8–1.6)	(0.9–2.7)	(1.1–4.1)	(1.0–2.2)	(0.9–1.9)	(1.1–2.0)	(0.9–1.6)
Current PACS dosing rate ((mg/L)·h)	0.8	0.7	0.9	0.9	1.0	1.1	1.5	2.2	1.6	1.3	1.4	1.0
	(0.7–1.4)	(0.5–1.2)	(0.5–1.5)	(0.7–1.3)	(0.6–1.7)	(0.8–1.6)	(0.9–4.0)	(1.1–4.1)	(1.0–2.2)	(0.9–1.9)	(1.1–2.0)	(0.9–1.6)

^a Average data, ^b Range of data.

, illustrating the seasonal variability captured in the dataset and the range of raw-water conditions under which the model was evaluated.

The monitoring system provides raw-water measurements at minute-level resolution; however, practical coagulation control in full-scale DWTPs typically operates at 30–60 min update intervals. Minute-level turbidity or pH signals exhibit substantial short-term fluctuations due to hydraulic instability and sensor noise, whereas chemical dosing pumps respond on the scale of tens of minutes rather than seconds. Therefore, aligning all parameters to an hourly interval offers a stable and operationally meaningful basis for model training and evaluation. The proposed framework is not restricted to 60-min data; if utilities deploy higher-frequency measurements (e.g., 10–15 min), the model can generate predictions at any desired control interval.

2.2. Model Fitting

Six input variables—temperature, turbidity, pH, electrical conductivity (EC), color, and the previous-day PACS dosing rate—were used as predictors, while the current PACS dosing rate served as the target variable. The previous-day dosing term (t–1 d) was included to capture slow-response and carry-over effects commonly observed in full-scale coagulation systems. It was defined as the mean PACS dosage applied during the preceding 24 h and aligned to the subsequent day at hourly resolution.

A total of 8303 observations were divided chronologically into two subsets: 75% for model development and 25% for validation. All predictors were standardized (zero mean, unit variance) to prevent scale imbalance and ensure numerical stability during the regression optimization. After model training, the learned coefficients were inversely transformed to their original units to allow direct physical interpretation of each parameter’s influence on coagulant demand.

Because the dataset consists of sequential operational records from a continuously operating DWTP, random k-fold cross-validation was not used, as it would break temporal structure and introduce information leakage. Instead, a chronological train–test split was adopted to preserve temporal dependence, and the final model used for coefficient interpretation was refitted on the full dataset after validation to obtain the most stable coefficient estimates.

To avoid leakage, data preprocessing steps—including StandardScaler fitting, PolynomialFeatures expansion, and the construction of all interaction terms—were performed after the train_test_split. All transformations were fitted exclusively on the training subset and subsequently applied to the validation subset.

Finally, polynomial expansion was applied to capture nonlinear interactions among predictors. The purpose of the degree exploration in this study was not to identify a single “optimal” polynomial degree, but to evaluate how regularization behaves under increasingly complex feature spaces. Therefore, polynomial degrees from 1 to 10 were examined to assess stability, generalization, and the scalability of regularization methods under high-dimensional expansion. A detailed explanation of the regularization strategies is provided in Section 2.7.

2.3. Implementation

All model development and analyses were performed in Python 3.8 using the Jupyter Notebook environment (Anaconda distribution). Data handling and preprocessing were conducted with the pandas and NumPy libraries. Input variables were standardized using scikit-learn’s StandardScaler, and the dataset was divided into training and testing subsets using the train_test_split function in accordance with the chronological framework described in Section 2.2.

Polynomial expansion and model fitting were implemented using scikit-learn’s PolynomialFeatures, LinearRegression, Ridge, and Lasso classes. Model evaluation employed standard statistical metrics—R², RMSE, and MAPE—as defined in Section 2.4, computed with scikit-learn functions and cross-verified using custom Python scripts to ensure numerical consistency.

All visualizations, including prediction performance and residual analyses, were generated using matplotlib. This open-source configuration enables full reproducibility of the modeling workflow, facilitates transparent examination of regression coefficients, and supports straightforward integration of the trained model into SCADA or decision-support environments.

2.4. Performance Metrics

Model performance was evaluated using four standard statistical metrics: the Pearson correlation coefficient (r), root mean squared error (RMSE), mean absolute percentage error (MAPE), and the coefficient of determination (R²). The correlation coefficient (r) quantifies the linear agreement between observed and predicted dosing rates, while RMSE and MAPE assess absolute and relative prediction errors, respectively. Together, these indices provide a comprehensive evaluation of model accuracy.

The Pearson correlation coefficient (r) quantifies the linear association between the input and output variables (Equation (1)):

$$r={\displaystyle \frac{n\left(\sum xy\right)-\left(\sum x\right)\left(\sum y\right)}{[n\sum x^2-{\left(\sum x\right)}^2] [n\sum y^2-{\left(\sum y\right)}^2]}}$$

(1)

where n is the number of data points, x represents input variable values, and y represents output variable values.

The root-mean-square error (RMSE) measures the deviation between predicted and observed values (Equation (2)):

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(O_p\left(i\right)-O_a\left(i\right)\right)}^2}$$

(2)

where O_p(i) is the predicted dosing rate, O_a(i) is the observed dosing rate, and n is the number of data points.

The mean absolute percentage error (MAPE) expresses relative prediction error as a percentage (Equation (3)):

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{100}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{O_p\left(i\right)-O_a\left(i\right)}{O_a\left(i\right)}}\right|$$

(3)

The coefficient of determination (R²) evaluates the proportion of variance in the observed data explained by the model (Equation (4)):

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^n{\left(O_p\left(i\right)-O_a\left(i\right)\right)}^2}{\sum _{i=1}^n{\left(O_a\left(i\right)-O_{mean}\left(i\right)\right)}^2}}$$

(4)

where O_mean is the mean of the observed dosing rate values.

2.5. Multiple Linear Regression

The general form of the MLR model is expressed in Equation (5):

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots + {\beta }_n{X}_n+\epsilon$$

(5)

where Y is the predicted dosing rate ((mg/L)·h), X₁–X_n are the input parameters, β are the regression coefficients, n is the number of predictors, and ε is the error term.

2.6. Polynomial Multiple Linear Regression

Because the coagulation process in DWTPs is inherently nonlinear, PMLR was employed by expanding predictors into higher-order and interaction terms. This allows the model to reflect physical and chemical interactions, such as the combined effects of turbidity and pH on dosing requirements.

Polynomial degrees ranging from 1 to 10 were examined not to identify a single “optimal” polynomial order, but to evaluate how model stability and generalization change as feature-space complexity increases. This design allows the study to systematically assess the scalability of PMLR under high-dimensional expansion and the role of regularization (Ridge and Lasso) in maintaining numerical stability—a critical requirement for deployable real-time control in DWTPs.

The general polynomial form is expressed in Equation (6):

$$Y={\beta }_0+{\beta }_{1}X+{\beta }_2{X}^2+\cdots + {\beta }_n{X}^n+\epsilon$$

(6)

where Y is the predicted dosing rate, X is an input variable, n is the polynomial degree, and ε is the error term.

When the polynomial degree is 1, the PMLR reduces to a standard MLR model with six predictors (Equation (7)):

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+ {\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6$$

(7)

When the degree is increased to 2, squared terms and pairwise interaction terms are added, resulting in 27 predictors (Equation (8)):

$$\begin{array}{ll}Y=& {\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+ {\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+\\ & {\beta }_7{X_1}^2+{\beta }_8{X}_1{X}_2+{\beta }_9{X}_1{X}_3+{\beta }_{10}{X}_1{X}_4+{\beta }_{11}{X}_1{X}_5+{\beta }_{12}{X}_1{X}_6+\\ & {\beta }_{13}{X_2}^2+{\beta }_{14}{X}_2{X}_3+{\beta }_{15}{X}_2{X}_4+{\beta }_{16}{X}_2{X}_5+{\beta }_{17}{X}_2{X}_6+\\ & {\beta }_{18}{X_3}^2+{\beta }_{19}{X}_3{X}_4+{\beta }_{20}{X}_3{X}_5+{\beta }_{21}{X}_3{X}_6+\\ & {\beta }_{22}{X_4}^2+{\beta }_{23}{X}_4{X}_5+{\beta }_{24}{X}_4{X}_6+\\ & {\beta }_{25}{X_5}^2+{\beta }_{26}{X}_5{X}_6+\\ & {\beta }_{27}{X_6}^2\end{array}$$

(8)

This explicit expansion illustrates how the number of predictors grows rapidly with polynomial degree. Beyond degree 2, the number of higher-order and interaction terms becomes very large; therefore, only the degree-2 expansion is shown here, while higher-degree expansions follow the same principle. Polynomial degrees from 1 to 10 were examined to investigate the scalability and stability of PMLR under increasingly complex feature spaces, rather than to determine a single optimal degree. Among these, degree 4 yielded the lowest validation RMSE for the unregularized PMLR model, and this selection criterion has been explicitly applied in the baseline evaluation.

2.7. Lasso and Ridge Regularization

Polynomial expansion significantly increases the number of predictors, which can lead to overfitting when the model complexity becomes comparable to or exceeds the available sample size. To address this issue, two regularization techniques—Ridge and Lasso—were applied.

• Ridge regression penalizes the squared magnitude of coefficients, effectively reducing variance and improving numerical stability in the presence of multicollinearity. However, Ridge does not eliminate redundant variables, as all coefficients remain nonzero.
• Lasso regression, in contrast, imposes an absolute (L₁) penalty that can shrink less influential coefficients exactly to zero, thereby simplifying the model and enabling embedded variable selection. This sparsity provides interpretability by identifying only the most physically meaningful contributors to coagulant demand and reducing the dimensionality of the expanded polynomial space.

Both methods were systematically tested to identify the balance between predictive.

Although the six raw input variables exhibited limited multicollinearity, the high-degree polynomial expansion introduced substantial collinearity among interaction terms. Under this high-dimensional setting, regularization is essential to prevent overfitting and to maintain numerical stability.

Both methods were systematically tested to evaluate the balance between predictive accuracy and model simplicity. In this study, Ridge regression slightly improved model stability but retained weakly influential predictors. In contrast, the Lasso-regularized PMLR model demonstrated superior generalization and provided the most consistent predictive performance across polynomial degrees, achieving the best trade-off between accuracy and parsimony. This behavior aligns with the study’s objective to develop a transparent, operator-oriented framework, as the reduced set of active predictors can be interpreted directly in terms of measurable physicochemical parameters.

Model performance was evaluated using R², RMSE, and MAPE, confirming that Lasso regularization produced the most robust and physically interpretable coefficients. For the Lasso model, the regularization parameter was set to α = 1.0, which yielded stable performance without degrading predictive accuracy.

3. Results and Discussion

3.1. Multiple Linear Regression

Multiple linear regression (MLR) was first developed using six input variables—temperature, turbidity, pH, electrical conductivity (EC), color, and the previous-day PACS dosing rate—to predict the current PACS dosage. The Pearson correlation coefficients for these variables are summarized in

Table 2. Pearson correlation coefficients among input and output variables.

Parameters	Temperature (°C)	Turbidity (NTU)	pH (-)	E.C. (µS/cm)	Color (°)	Precious-Day PACS Dosing Rate ((mg/L)·h)	Current PACS Dosing Rate (mg/L)·h
Temperature (°C)	1.000	0.296	−0.739	−0.309	0.201	0.510	0.516
Turbidity (NTU)		1.000	−0.297	−0.387	0.349	0.590	0.573
pH (-)			1.000	0.287	−0.268	−0.608	−0.601
E.C. (µS/cm)				1.000	−0.237	−0.418	−0.416
Color (°)					1.000	0.668	0.660
Previous-day PACS dosing rate ((mg/L)·h)						1.000	0.944
Current PACS dosing rate (mg/L)·h)							1.000

. Turbidity and the previous-day dosing rate exhibited relatively strong positive correlations with the output variable, whereas pH and EC showed negative correlations, consistent with their known physicochemical influence on coagulation effectiveness.

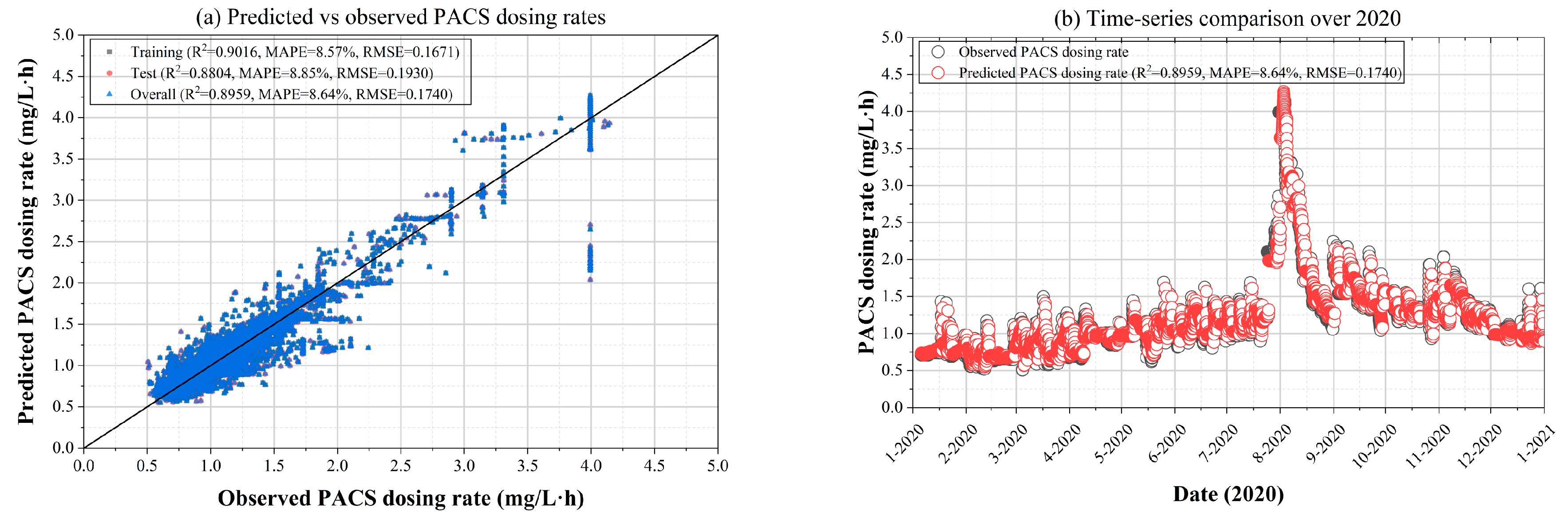
The predictive performance of the MLR model is shown in Figure 1, with R² values of 0.902 (training), 0.880 (testing), and 0.896 (overall). Corresponding MAPE values were 8.57%, 8.85%, and 8.64%, and RMSE values were 0.167, 0.193, and 0.174, respectively. These metrics indicate that MLR achieved moderately high predictive accuracy. However, residuals were not uniformly distributed across operating conditions. Errors increased markedly during high-turbidity events (>30 NTU) and low-temperature conditions (<10 °C), reflecting the inability of linear models to capture the nonlinear interactions that dominate coagulation behavior under extreme influent variability. From an operational standpoint, this suggests that relying solely on MLR could lead to under- or overestimation of coagulant demand during challenging water-quality episodes, with potential risks to treated water quality.

The regression coefficients for the six predictors were 2.994 × 10⁻³ (temperature), 9.452 × 10⁻⁴ (turbidity), –2.584 × 10⁻² (pH), –4.186 × 10⁻⁴ (EC), 2.213 × 10⁻³ (color), and 8.279 × 10⁻¹ (previous-day dosing), with an intercept of 0.380. These coefficients align with the correlation structure, confirming that turbidity and historical dosing exert the strongest influence on current dosing requirements.

This strong influence is mechanistically reasonable. Turbidity directly reflects the concentration of colloidal particles requiring charge neutralization and is therefore the primary determinant of coagulant demand. The previous-day dosing rate captures a residual carry-over effect: hydrolyzed aluminum species (e.g., Al(OH)²⁺, Al(OH)₂⁺, and polymeric Al₁₃ clusters) persist for several hours in full-scale DWTPs and influence particle stability in subsequent periods. This persistence explains why historical dosing remains a dominant predictor. In addition, dosing adjustments in full-scale DWTPs are typically made on a daily basis through jar-test-based decision-making combined with flow-paced control, creating day-to-day continuity in operator-driven dosing patterns. The previous-day dosing rate therefore reflects both physicochemical carry-over and operational behavior, explaining its consistently high importance in the model.

3.2. Polynomial Multiple Linear Regression

To better capture nonlinear interactions among influent water-quality parameters, polynomial multiple linear regression (PMLR) was applied. By introducing higher-order and interaction terms, PMLR can represent complex physicochemical relationships—for example, the combined effects of turbidity and pH on coagulant demand.

Polynomial expansion increased the number of predictors from 6 (degree = 1) to 8007 (degree = 10). This exponential growth highlights the risk of overfitting as model complexity approaches or exceeds the number of available samples. With 8007 predictors and 8303 samples, the model operates in a near p ≈ n regime (p/n ≈ 0.96). Under such high-dimensional conditions, the design matrix becomes nearly rank-deficient because of strong multicollinearity among polynomial interaction terms. This inflates coefficient variance, destabilizes ordinary least squares (OLS) estimation, and ultimately leads to severe overfitting. These dimensionality constraints justify the need for regularization to ensure generalization and numerical stability.

Predictive performance for polynomial degrees 1–4 is shown in Figure 2. As the polynomial degree increased, model accuracy improved: R² increased from 0.896 (degree = 1, equivalent to baseline MLR) to 0.958 (degree = 4), while MAPE decreased from 8.64% to 6.68%. These results demonstrate the benefit of polynomial expansion in capturing nonlinear dynamics of the coagulation process.

However, when the degree increased further (degrees 5–10), overfitting became pronounced (Figure 3). Training R² values exceeded 0.97, yet test-set performance deteriorated sharply, with error values exceeding MAPE > 100% at degrees ≥ 7. Predictions diverged unrealistically from observed values, indicating numerical instability. From an operational standpoint, such instability would result in erratic or unsafe dosing recommendations that cannot be used in real-time DWTP operation.

Overall, these findings indicate that moderate polynomial expansion (degrees 2–4) improves predictive accuracy by capturing essential nonlinear effects, whereas higher-degree expansions introduce excessive model complexity and poor generalization. This trade-off underscores the necessity of robust regularization techniques to balance accuracy and stability when employing polynomial features—motivating the application of Ridge and Lasso methods examined in Section 3.3.

3.3. Polynomial Multiple Linear Regression with Lasso and Ridge Regularizations

Polynomial expansion substantially increased the expressive capacity of the regression model, but also amplified the risk of overfitting. As shown in Figure 4, unregularized PMLR exhibited steadily increasing training R² (exceeding 0.97 at degree 10), while test errors diverged sharply beyond degree 4. This divergence reflects a fundamental limitation of ordinary least squares under high-dimensional expansion: increased model complexity enhances in-sample fit but undermines predictive reliability under unseen conditions. Such instability is unacceptable for real-time coagulant dosing in DWTPs. Therefore, model performance was evaluated using the chronological 75:25 train–test split described in Section 2.2 to prevent temporal information leakage.

To mitigate overfitting, Ridge and Lasso regularizations were applied (Figure 5 and Figure 6). Ridge regression reduced variance relative to unregularized PMLR; however, residual overfitting persisted at higher degrees, as test errors failed to converge and correlated coefficients grew in magnitude. In contrast, Lasso regularization demonstrated consistent generalization, with training and testing metrics converging smoothly across polynomial degrees. R² values increased gradually, while both RMSE and MAPE decreased for the training, testing, and overall datasets.

The superior performance of Lasso arises from its ability to shrink less influential coefficients exactly to zero, performing embedded variable selection. For example, variables such as color, which exhibited weak correlation with coagulant demand, were effectively excluded, whereas turbidity and pH retained strong influence. This sparsity reduces unnecessary polynomial terms, enhances interpretability, and prevents coefficient inflation within the expanded feature space.

Ridge and Lasso were further compared in terms of their stability as the polynomial degree (D) increased. Ridge regression provided initial variance reduction but showed progressive overfitting at higher degrees, particularly when multicollinearity intensified among interaction terms. In contrast, Lasso maintained stable generalization by suppressing redundant predictors and preserving only the most physically meaningful contributors. This indicates that the L₁ penalty is more robust than the L₂ penalty for managing the severe collinearity present in high-degree polynomial expansions. Consequently, the Lasso-regularized PMLR was selected as the most suitable configuration, achieving the best balance between predictive accuracy, numerical stability, and scientific transparency.

The robustness of the Lasso-regularized PMLR is further illustrated in Figure 7, which presents observed versus predicted dosing for the degree-10 model. Unlike the unregularized degree-10 model, which exhibited unstable divergence, the Lasso-regularized degree-10 model achieved highly stable predictions (R² = 0.951, RMSE = 0.120, MAPE = 7.02%). This confirms that even with thousands of predictors, Lasso can accommodate complex nonlinearities while maintaining generalization. For DWTP operation, this stability translates into reliable and interpretable dosing recommendations across diverse water quality conditions, including atypical turbidity events.

Although both Ridge and Lasso were examined, Elastic Net regularization—which blends L₁ and L₂ penalties—was not applied in this study. The six original influent variables exhibited limited multicollinearity, and the high-dimensional polynomial terms were sufficiently stabilized by the L₁ penalty alone. Therefore, Lasso provided the necessary sparsity and interpretability without the added complexity of Elastic Net. In comparison with ANN or tree-based ensemble models (e.g., GBM, XGBoost), which require post hoc techniques such as SHAP to interpret variable importance, the Lasso-regularized PMLR offers direct coefficient-based interpretability with minimal computational overhead—a key advantage for real-time SCADA integration.

Temporal dependence in DWTP operation was addressed through the previous-day dosing feature. More complex sequential models (e.g., ARIMA, LSTM) were not adopted because they provide limited interpretability and are not easily transferable to full-scale PLC–SCADA systems. Future work will extend the framework to include Elastic Net and ensemble models to quantitatively compare interpretability, numerical stability, and operational applicability across regularization strategies.

4. Conclusions

Accurate determination of coagulant dosing is essential for maintaining stable and efficient operation of drinking water treatment plants (DWTPs). This study developed a scientifically interpretable and operationally transferable regression framework for predicting coagulant demand using routinely monitored water-quality data. By combining polynomial multiple linear regression (PMLR) with Lasso regularization, the proposed approach provides both high predictive accuracy and coefficient-level transparency, enabling operators to understand, validate, and adjust dosing behavior without specialized machine learning expertise.

Among the evaluated models, the Lasso-regularized PMLR achieved the most balanced and robust performance (R² ≈ 0.95, RMSE = 0.12, MAPE = 7.0%). Its ability to maintain stable generalization across increasing polynomial degrees demonstrates that the L₁ penalty effectively controls the severe multicollinearity generated by high-degree expansions—an important requirement for real-time deployment in DWTPs. The resulting sparse coefficient structure offers mechanistic interpretability, revealing how turbidity, pH, and conductivity jointly influence coagulant demand and linking data-driven predictions to well-established physicochemical coagulation mechanisms.

Importantly, the one-year operational dataset included high-turbidity periods (>30 NTU) and winter low-temperature conditions (<10 °C), conditions under which many ML models struggle to generalize. The Lasso-regularized PMLR maintained stable performance across these challenging conditions, indicating that its predictive structure is resilient to seasonal and episodic fluctuations in raw-water quality.

From a practical standpoint, the proposed framework can be seamlessly integrated into existing PLC–SCADA architectures, providing transparent and real-time dosing recommendations without the tuning burden associated with complex black-box models. This transparency enhances operator trust and supports mechanism-aware decision-making, which is essential for sustainable and resilient DWTP operation.

Future research should validate the model across multiple treatment plants, coagulant types, and seasonal regimes to assess its transferability. Extending the framework to include Elastic Net or hybrid explainable ensemble approaches may further strengthen its robustness across diverse influent conditions. Additionally, incorporating treated-water quality indicators (e.g., settled turbidity, filtered turbidity, and residual aluminum) would enable direct assessment of how prediction errors translate into downstream water-quality outcomes, thereby enhancing the operational reliability and real-time applicability of the framework.