Convective Drying of Pirul (Schinus molle) Leaves: Kinetic Modeling of Water Vapor and Bioactive Compound Retention

Abstract

Schinus molle L. is a tree commonly found in agricultural fields, deserts, and semi-arid areas of central Mexico. Its distinctive aroma makes it a source of essential oil, extracted mainly from the bark and fruits. The leaves contain phenolic compounds, and their extracts have demonstrated antimicrobial activity. Obtaining these extracts requires a prior drying process. This study aimed to evaluate the effect of convective drying on phenolic compounds in pirul leaves and determine the thermodynamic properties of the process, including the effective diffusivity of water vapor (D) and activation energy (Ea). Drying kinetics were conducted at different air-drying temperatures (30, 40, and 50 °C) at a constant rate of 1 ms⁻¹, and the results were fitted to the second Fick’s law and semi-empirical models. After drying, a decrease in total flavonoid content was observed as the drying temperature increased, with losses of 37%, 49%, and 62% at 30, 40, and 50 °C, respectively. The final values ranged from 37.96 to 21.02 mg QE/100 g of dry leaf. The D varied between 1.32 × 10⁻¹² and 6.71 × 10⁻¹² m² s⁻¹, with an Ea of 66.06 kJ mol⁻¹. The fitting criteria (R², RMSE, AIC/BIC) indicated that the Logarithmic model best described the kinetics at 30–40 °C, while Page was adequate at 50 °C. These findings suggest an inverse relationship between drying temperature and flavonoid content, while higher temperatures accelerate water vapor diffusivity, reducing the processing time, as observed in plant matrices.

1. Introduction

Schinus molle, commonly known in Mexico as the Pirul tree, is a species of flowering plant in the cashew family, Anacardiaceae. It is an evergreen tree native to the semi-arid regions of Peru and Bolivia in South America. It is known for its aromatic leaves and pinkish-red berries, which are often used as a spice. It has been introduced globally for ornamental and forestry purposes due to its adaptability to dry climates and rapid growth [1]. Additionally, S. molle has been utilized to produce mildly alcoholic beverages from its fruit and medicinal purposes from its leaf extracts and sap [2]. Mature berries are also used as a pepper substitute in culinary applications and for the production of essential oils in perfumery [3]. The essential oils from S. molle leaves and fruits have been studied for their chemical composition and potential uses in food flavors and fragrances. These oils are characterized by a high content of hydrocarbon monoterpenes and are responsible for their spicy aromatic odor [3,4].

Extracts from S. molle leaves exhibit antioxidant and antimicrobial properties, due to essential oils and other bioactive compounds (such as phenolic compounds) contribute to their antimicrobial, insecticidal, and antioxidant activities. Also, it exhibits significant antimicrobial properties against a range of microorganisms, including Escherichia coli, Staphylococcus aureus, and Candida albicans. These properties are attributed to phenolic acids (gallic, caffeic, ferulic, chlorogenic) and flavonoids such as apigenin and quercetin [5,6,7]. These compounds can disrupt microbial membranes and inhibit protein and nucleic acid synthesis, thereby impairing microbial growth [8]. Phytochemical analyses have further identified catechin, derivatives of quercetin (quercetin-3-O-hexosyl-pentoside and quercetin-3-O-galloyl-glucose) and apigenin (apigenin-7-O-methyl ether), as well as biflavonoids like masazinoflavanone, predominantly localized in epidermal and mesophyll cells [9,10,11,12]. Collectively, these bioactives support the potential of S. molle leaves as a source of natural antimicrobial and antioxidant agents [6,13,14,15].

Drying is one of the most traditional methods for food preservation and is also used as a pretreatment for plant materials prior to extraction. However, it is well known that during hot air drying, the material undergoes structural, chemical, and nutritional physical changes that can affect quality properties such as texture, color, odor, flavor, and nutritional value [16,17]. Drying involves the simultaneous transfer of heat and mass. Heat transfer properties in food are well understood; therefore, process design requires the estimation of mass transfer properties [18]. Analysis of water diffusivity during drying is a necessary parameter for designing, optimizing, and reducing operating costs in drying processes [19]. Although there are reports on the drying of leaves in other Schinus species, such as S. terebinthifolius (known as aroeira) [20,21,22], to our knowledge, the drying of S. molle leaves has not yet been studied. Most available research has focused on essential oils obtained after drying, overlooking the drying process itself and the preservation of thermolabile, non-volatile bioactive compounds such as phenolics and flavonoids. Moreover, it is important to evaluate the effect of the drying process on the content of bioactive compounds in the leaves, such as total flavonoids compounds.

The objective of this project was to study the effect of convective drying on the leaves of Schinus molle on the stability of their flavonoid compounds. Furthermore, theoretical and semi-empirical drying models were used to simulate drying kinetics and determine the thermodynamic properties, effective water vapor diffusivity, and activation energy.

2. Materials and Methods

2.1. Chemicals

Ethanol (analytical grade), deionized water, and aluminum chloride (AlCl₃) were obtained from Golden Bell Reagents (Guadalajara, Jalisco, Mexico). Quercetin (≥95%) was purchased from Sigma-Aldrich Chemical Co. (St. Louis, MO, USA).

2.2. Plant Material

Fresh mature leaves of 10-year-old S. molle trees were collected from gardens at the Technological University of Tecamachalco (Tecamachalco, Puebla, Mexico, 18°51′51″ N, 97°43′15″ W). The trees grow in sandy loam soil, and they are irrigated every seven days. The leaves were selected for homogeneous color and free from injuries/disease-insect pest infestation, and the apex was removed. They were washed with deionized water to eliminate foreign matter, and excess moisture was removed at room temperature. The leaves (~50 g) were placed in trays in a single layer and introduced into the dryer at the operating temperature. The initial moisture of the samples was determined by the AOAC gravimetric method no. 905.10 [23]. Briefly, 2 g of sample was placed in an aluminum tray at constant weight in a vacuum oven (Prendo, model HS-30, Puebla, Mexico) at 60 °C and 60 kPa until a constant weight was achieved. Leaf thickness (2$l$) was measured using a digital micrometer (Mitutoyo Corporation, Tokyo, Japan) and was determined as 480 ± 46 µm.

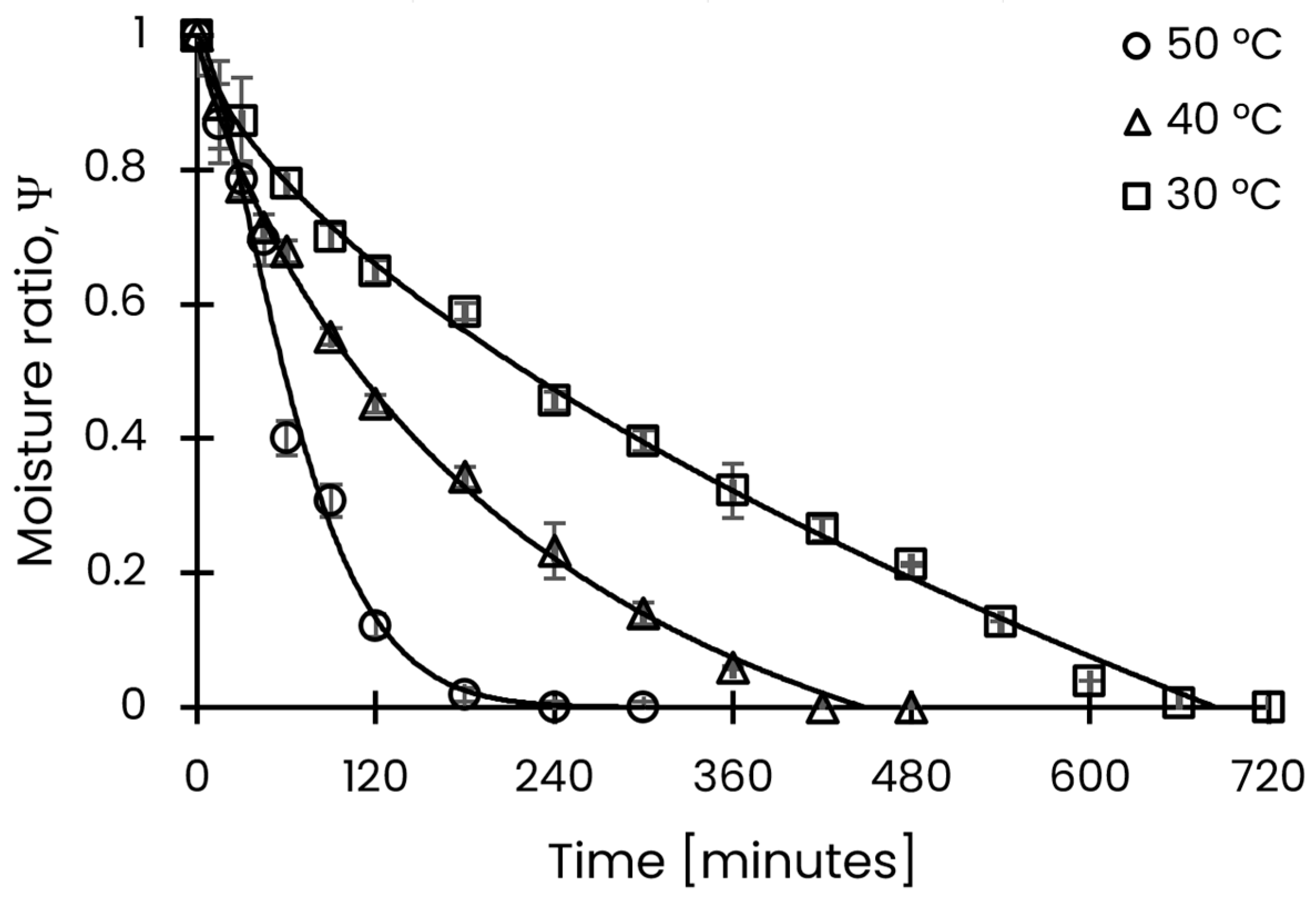
2.3. Drying Kinetics

A tray dryer (Hidrosam, model Didactic, Puebla, Mexico) was used to conduct the drying kinetics. The air velocity was set at 1 ms⁻¹ and measured with a digital anemometer with turbine (UNI-T, model UT363S, Hong Kong, China). The drying temperatures evaluated were 50, 40, and 30 °C, which are representative of the ranges reported for drying medicinal leaves [16,21,22]. Representative samples were taken at different drying times (every 15 min during drying). Drying curves were obtained by periodically determining the weight using an analytical balance (Velab, model VE-204, CDMX, Mexico). The drying process was considered complete when the weight difference was less than 0.005 g. The moisture content of the dried product was determined using the AOAC gravimetric method no. 905.10 [23]. Each drying kinetic experiment was performed in triplicate.

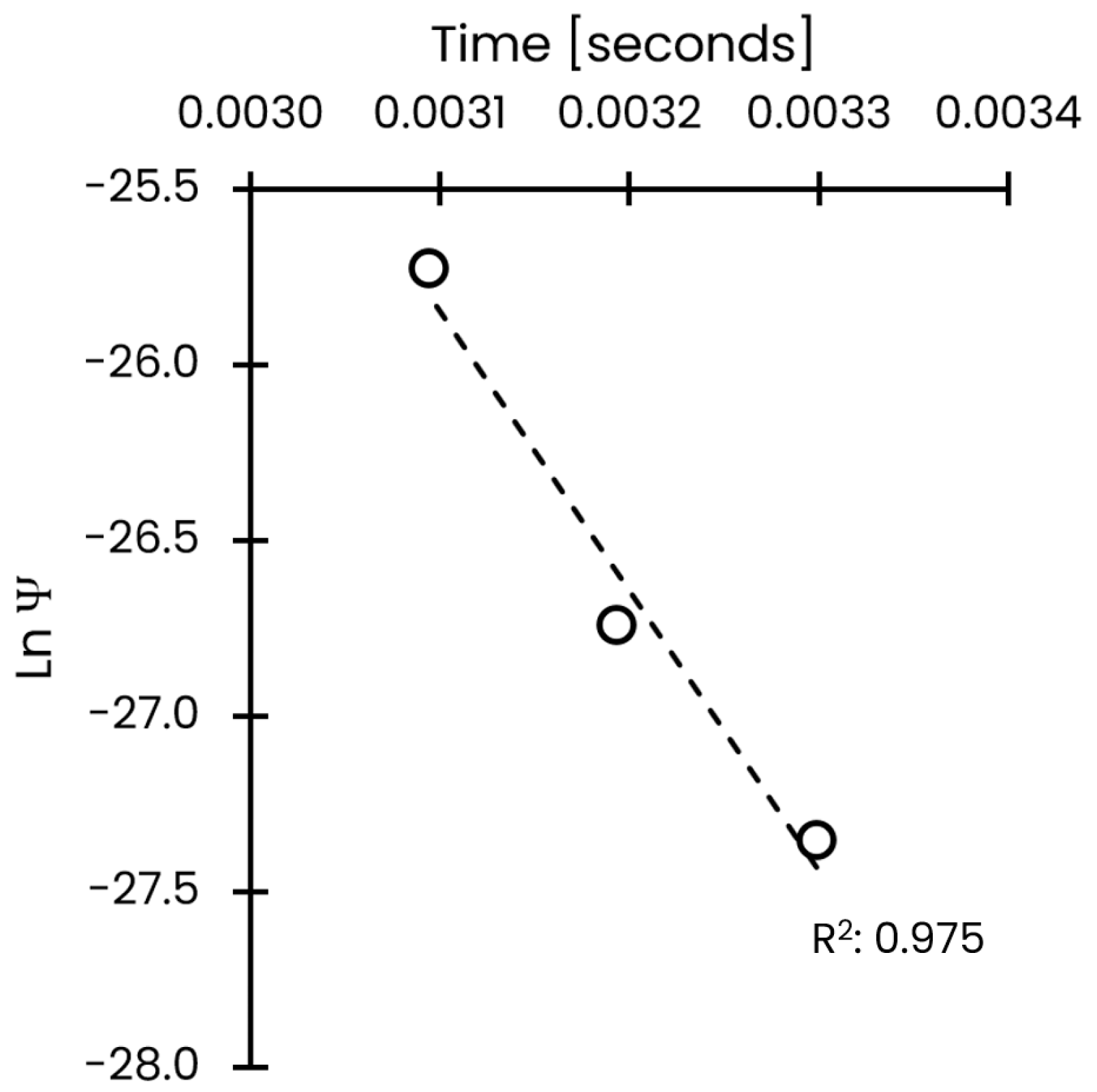
2.4. Estimation of Effective Diffusivity Coefficients

To estimate the effective diffusivity coefficient, the mathematical solution of Fick’s second law (Equation (1)) was applied. For sufficiently long drying times, only the first term of the series expansion was used (Equation (2)) [24]. The following assumptions were considered: internal mass transfer is the controlling mechanism, pirul leaves are modeled as a flat-plate geometry with $l$ equal to half thickness of the leaf due drying occurs from both sides, and mass transport occurs in one dimension.

$$\Psi ={\displaystyle \frac{X-X_e}{X_0-X_e}}={\displaystyle \frac{8^2}{{\pi }^4}}{\sum }_{n=1}^{\infty }{\displaystyle \frac{1}{{\left(2n-1\right)}^2}}\mathit{exp}\left(-{\displaystyle \frac{{\left(2n-1\right)}^2{\pi }^{2}Dt}{4l^2}}\right)$$

(1)

$$\Psi ={\displaystyle \frac{8}{{\pi }^2}}\mathit{exp}\left(-{\displaystyle \frac{{\pi }^{2}Dt}{4l^2}}\right)$$

(2)

$\Psi$ is the dimensionless moisture content, $X$ is the moisture content (kg of water/kg of dry solids), $X_e$ is the moisture content at equilibrium, and $X_0$ is the moisture content at the beginning of the drying process.

Following the approach proposed by Páramo et al. [25], the effective moisture diffusivity ($D$) was estimated by fitting the linear portion of the semilogarithmic plot of dimensionless moisture ratio ($\Psi$) against drying time to the analytical solution of Fick’s second law for a flat plate geometry. This ensures that the diffusivity is determined within the diffusion-controlled falling-rate period, thereby providing a physically consistent parameter.

In the semilogarithmic plot of Ψ versus time (Equation (3)), the slope in the linear region corresponds to $m$, while a represents the intercept, as described in Equation (4) [19].

$$\mathit{ln}\Psi =\mathit{ln}{\displaystyle \frac{8}{{\pi }^2}}-{\displaystyle \frac{{\pi }^{2}Dt}{4l^2}}$$

(3)

$$\mathit{ln}\Psi =a+mt$$

(4)

where:

$$m={\displaystyle \frac{{\pi }^{2}D}{4l^2}}$$

(5)

The 95% confidence interval for the diffusivities (the slopes, $m$) was calculated using:

$$m_0=m\pm t_{0.975\left(\nu \right)}\sqrt{s_m^2}$$

(6)

where $m_0$ represents the 95% confidence interval for slope calculated from the linear regression ($m$), $s_m^2$ is the estimated variance of the linear parameter ($m$), $t_{0.975\left(\nu \right)}$ is the value from the cumulative distribution of the t-student function for a 0.975 probability, $\nu$ represents the degrees of freedom $(v=n-2)$ and $n$ is the number of experimental drying kinetics points.

The activation energy ($Ea$) was determined using the relationship between the effective diffusivity ($D$) and the drying air temperature (Equation (7)).

$$\mathit{ln}D=\mathit{ln}{D}_0-{\displaystyle \frac{Ea}{R}}{\displaystyle \frac{1}{T}}$$

(7)

For estimation of the effective diffusivity coefficients, plotting, and numerical fitting were performed using Microsoft Excel 365 software.

2.5. Semi-Empirical Drying Modeling

The dimensionless moisture content (Ψ) calculated according to Equation (1) were fitted to different thin-layer drying models commonly used in the literature [16,26]: Lewis (8), Page (9), Henderson and Pabis (10), Logarithmic (11), Midilli (12), and Two-term (13). Nonlinear regression was carried out using MATLAB (version 2025b, MathWorks, Natick, MA, USA) with the lsqcurvefit function.

$$\Psi =e^{(-kt)}$$

(8)

$$\Psi =e^{(-k{t}^n)}$$

(9)

$$\Psi =a e^{(-k{t}^n)}$$

(10)

$$\Psi =a e^{(-k{t}^n)}+b$$

(11)

$$\Psi =a e^{(-k{t}^n)}+bt$$

(12)

$$\Psi =a e^{(-k_{0}t)}+b e^{(-k_{1}t)}$$

(13)

where $k$, $n$, $a$, $b$, $k_0$ and $k_1$ are empirical constants in models The quality of fit was assessed using the coefficient of determination ($R^2$), the root mean square error (RMSE), and the reduced chi-square (${\chi }^2$), defined, respectively, as:

$$RMSE=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^N{\left(M{R}_{i,p}-M{R}_{i,e}\right)}^2}{N}}}$$

(14)

$${\chi }^2={\displaystyle \frac{{\sum }_{i=1}^N{\left(M{R}_{i,p}-M{R}_{i,e}\right)}^2}{N-n}}$$

(15)

where $M{R}_{i,p}$ and $M{R}_{i,e}$ represent the predicted and experimental values of moisture ratio, respectively, $N$ is the number of observations, and $n$ the number of model parameters.

Additionally, two information criteria were employed to compare models while penalizing parameter complexity: the Akaike Information Criterion ($AIC$) and the Bayesian Information Criterion ($BIC$) [27,28]. These criteria were calculated using:

$$AIC=-2loglike+2p$$

(16)

$$BIC=2loglike+p \mathrm{l}\mathrm{n}\left(n\right)$$

(17)

where $p$ is the number of parameters, $loglike$ is the logarithm of the likelihood function considering the estimates of the parameters and $n$ number of observations. The best-fitting model for each drying temperature was selected based on the combination of high R², low RMSE and χ², and the lowest AIC and BIC values. This approach ensured a robust and unbiased selection of the most suitable model to represent the drying behavior of S. molle leaves. The models were fitted to the mean moisture ratio at each time point. All drying kinetics represent the mean of three independent replicates (n = 3).

2.6. Total Flavonoid Analysis

For the analysis of total flavonoids in fresh and dried S. molle leaves, an ultrasound-assisted maceration method was employed. A total of 0.25 g of ground leaf solids were placed in 25 mL of 80% ethanol. The flavonoid content was determined using the AlCl₃ method. Specifically, 1 mL of extract was mixed with 3 mL of 80% ethanol and vortexed for 10 s. Then, 1 mL of a 2% AlCl₃ solution was added, and the mixture was vortexed again. The solution was incubated in darkness for 10 min at 25 ± 1 °C, and the absorbance was measured at 420 nm in a spectrophotometer UV-Vis (Dynamica, model HALO XB-10, MK, UK). A quercetin calibration curve was used, and the results are expressed as quercetin equivalents per 100 g of dry leaf (mg QE·100 g⁻¹ dry weight). Each analysis was performed in triplicate.

The total flavonoids retention during the drying process was determined by the relation between total flavonoids in a drying time (${TF}_x$) and total flavonoids in fresh leaves (${TF}_0$) using the following equation (Equation (18)).

$$Total flavonoid retention [\%]={\displaystyle \frac{{TF}_x}{{TF}_0}}\ast 100$$

(18)

2.7. Statistical Analysis

All the analyses were carried out in triplicate. Experimental results were presented as means with standard deviations and statistical analyses were performed using one-way ANOVA followed by Tukey’s pairwise comparison test, with a significance level set at p < 0.05. Analyses were conducted using Minitab software (version 16, State College, PA, USA).

3. Results

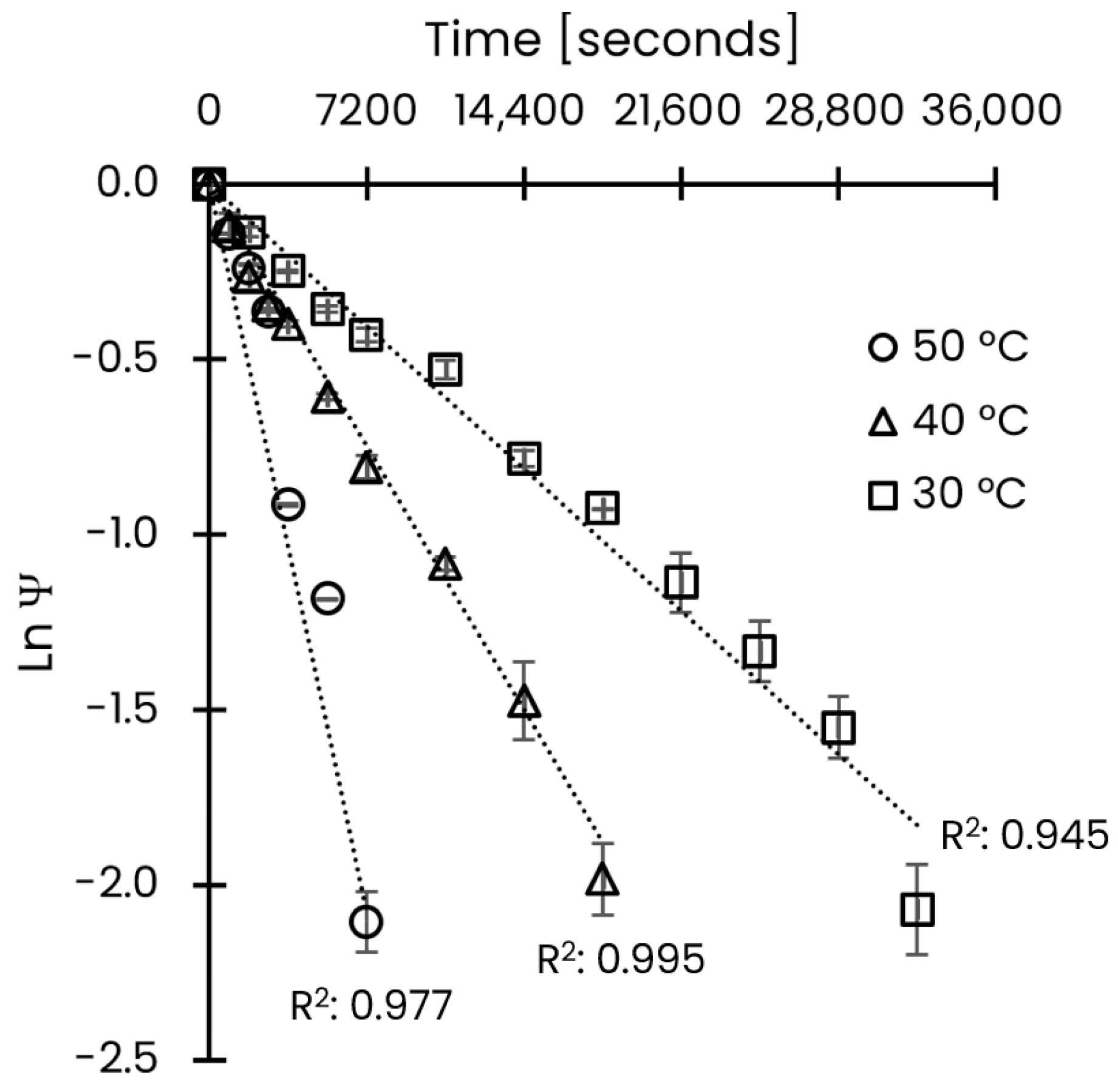
3.1. Drying Kinetics of Schinus molle Leaves

The leaves of pirul (S. molle) have been studied for various biological activities, including antifungal and insecticidal properties. Drying leaves is a crucial process for preserving their nutritional and biological properties, reducing moisture content to prevent spoilage, and enhancing shelf life. The moisture content of S. molle fresh leaves in present study was 66.5 ± 2.6%, it is consistent with those reported by another authors for S. terebinthifolius: 58–65% [21], 64.5 ± 0.2% [9] and 66 ± 2% [20].

In Figure 1, the drying kinetics are presented. As expected, an increase in air temperature reduced the time required to reach moisture equilibrium. The drying times were 240, 420, and 660 min at 50, 40, and 30 °C, respectively. These results are consistent with those reported by Berbert et al. [22], who observed drying times of 250 ± 17, 450 ± 30, and 610 ± 62 min at 45, 40, and 35 °C, respectively. Similarly, Silva and Ferreira [20] reported drying times ranging from 80 to 600 min for S. terebinthifolius leaves using a rotating drum dryer at 50, 60, and 70 °C. Similar results for the drying process of leaves have been reported, for example, for jambu leaves (Acmella oleracea) [29] at temperatures ranging from 35 to 60 °C and for purple basil (Ocimum basilicum L.) leaves [30] dried at 40–70 °C.

The term $\Psi$ is a dimensionless normalized variable used to describe the relative moisture within the leaves during the drying process (Equation (1)). Figure 2 shows the evolution of $\Psi$ during the convective drying of S. molle leaves at different air temperatures.

Higher drying temperatures reduce the drying time significantly and increase the drying rates. This approach not only reduces drying time but also affects the quality and content of bioactive compounds. In the following sections, thermodynamic properties, semi-empirical drying modeling and total flavonoid compounds of S. molle leaves during drying process will be discussed.

3.2. Effective Diffusion and Activation Energy Coefficients

Optimizing these parameters is essential for preserving the nutritional and medicinal properties of leaves while ensuring efficient and sustainable drying processes.

Fick’s second law describes how moisture content varies as a function of time and distance within the material during the drying process (Equation (2)). It utilizes the moisture concentration gradient to describe the rate at which moisture diffuses within the material. The effective diffusivity of water vapor is a measure of how easily water vapor moves through a porous medium during the drying process. The effective water vapor diffusivity (Equation (3)) during the drying of S. molle leaves was determined based on the relationship between the natural logarithm of moisture content and drying time at different drying temperatures presented in Figure 3.

Table 1. Effective moisture diffusivity ($D$) of Schinus molle leaves at different drying temperatures. Values are reported as estimate ± 95% confidence interval (CI).

Temperature [°C]	Effective Diffusivity [m2/s]	95% CI [m2/s]
30	1.32 × 10−12	(1.31–1.33) × 10−12
40	2.43 × 10−12	(2.42–2.44) × 10−12
50	6.71 × 10−12	(6.58–6.83) × 10−12

presents effective water vapor diffusivity at different drying air temperatures. Confidence intervals correspond to the 95% level computed from the slope SE of the linear fit to Ln Ψ vs. time in the falling-rate region (Figure 3). As expected, diffusivity increases with temperature. This increase in effective diffusivity indicates that water vapor moves more easily through the porous material, typically resulting in faster drying. Porous materials, such as leaves, have an internal structure that influences the ease with which water vapor can diffuse through them.

Goneli et al. [21] and Berbert et al. [22] reported effective diffusivity values for the convective drying of Brazilian pepper tree leaves (S. terebinthifolius), ranging from 0.15 to 1.58 × 10⁻¹¹ m² s⁻¹ at drying temperatures of 40 to 70 °C [21] and 3.18 to 8.06 × 10⁻¹¹ m² s⁻¹ at 35 to 45 °C [22]. During drying, moisture migrates from the leaf interior to the surface and is subsequently transferred to the surrounding air. This movement occurs mainly by diffusion of liquid water and vapor through the porous leaf structure, driven by temperature and humidity gradients between the material and the air. Elevated temperatures enhance the kinetic energy of water molecules, which increases effective moisture diffusivity and accelerates their migration to the surface, thereby reducing the overall drying time [16,31]. In this context, activation energy ($Ea$) is the minimum energy required for water molecules to detach from the material’s surface and evaporate. For the tray convective drying of S. molle leaves, the $Ea$ was determined to be 66.06 kJ mol⁻¹ (Figure 4). The $D$ and $Ea$ values obtained in this study fall within the range of magnitudes reported for most agricultural and food products [16]. Additionally, activation energy values of 74.96 kJ mol⁻¹ [21] and 78.05 kJ mol⁻¹ [22] have been reported.

These discrepancies in the determination of thermodynamic properties are primarily attributed to leaf geometry and structural characteristics within the genus, specifically S. terebinthifolius and S. molle, from this study. Additionally, Berbert et al. [22] reported that the Lewis model better predicted thin-layer drying behavior than the theoretical diffusion model based on Fick’s second law. This limitation of the diffusion model was attributed to the simplifying assumptions it adopts, such as constant leaf thickness, uniform initial moisture distribution, and the absence of significant temperature gradients. In the following section, different semi-empirical drying models were evaluated.

3.3. Semi-Empirical Kinetic Drying Modeling

Table 2. Empirical constants and statistical parameters for models analyzed, during the drying of Schinus molle leaves under different conditions of temperature.

Model	Empirical Constants						Statistical Parameters
	50 °C
	$\mathit{k}$	$\mathit{n}$	$\mathit{a}$	$\mathit{b}$	${\mathit{k}}_0$	${\mathit{k}}_1$	${\mathit{R}}^2$	RMSE	${\mathit{\chi }}^2$	$\mathit{A}\mathit{I}\mathit{C}$	BIC
Lewis	0.0129	--	--	--	--	--	0.961	0.073	0.005	−155.367	−153.966
Page	0.0017	1.4844	--	--	--	--	0.988	0.040	0.002	−188.589	−185.787
Henderson and Pabis	0.0014	1.5255	0.9857	--	--	--	0.988	0.040	0.002	−187.068	−182.865
Logarithmic	0.0014	1.5255	0.9857	8.83 × 10−8	--	--	0.988	0.040	0.003	−185.068	−179.463
Midilli	0.0014	1.5255	0.9857	9.0 × 10−8	--	--	0.988	0.040	0.002	−185.068	−179.463
Two-term	--	--	0.4956	0.5768	0.0140	0.0140	0.968	0.066	0.005	−155.006	−149.401
40 °C
Lewis	0.0067	--	--	--	--	--	0.992	0.030	0.0010	−263.272	−261.608
Page	0.0069	0.9940	--	--	--	--	0.992	0.030	0.0011	−261.579	−258.252
Henderson and Pabis	0.0054	1.0360	0.9762	--	--	--	0.992	0.029	0.0011	−261.897	−256.906
Logarithmic	0.0115	0.8132	1.2394	−0.2370	--	--	0.998	0.015	0.0003	−298.729	−292.075
Midilli	0.0128	0.8356	1.0012	−0.0003	--	--	0.998	0.015	0.0003	−297.628	−290.974
Two-term	--	--	0.5846	0.4019	0.0066	0.0066	0.992	0.029	0.0012	−259.770	−253.115
30 °C
Lewis	0.00351	--	--	--	--	--	0.977	0.048	0.0025	−268.549	−266.743
Page	0.00250	1.05921	--	--	--	--	0.978	0.047	0.0026	−268.480	−264.867
Henderson and Pabis	0.00106	1.19406	0.9404	--	--	--	0.980	0.044	0.0024	−272.374	−266.954
Logarithmic	0.00249	0.64912	6.3133	−5.3115	--	--	0.997	0.018	0.0004	−340.132	−332.906
Midilli	0.01415	0.65590	1.0009	−0.0005	--	--	0.997	0.018	0.0004	−339.887	−332.661
Two-term	--	--	0.5959	0.3959	0.00348	0.00348	0.977	0.048	0.0035	−262.762	−255.536

presents the empirical parameters obtained from the fitting of different models describing the drying kinetics of S. molle leaves. Low values of root mean square error (RMSE) indicate a satisfactory fit, while high coefficients of determination (R² > 0.90) and reduced chi-square (${\chi }^2$) values further confirm the adequacy of the models. To select the best predictive model, the Akaike Information Criterion (AIC) and Schwarz’s Bayesian Information Criterion (BIC) were also considered, as lower values of these criteria reflect superior agreement between the model and experimental data. According to Wolfinger [32], the lowest values for these criteria indicate the best fit of the model to the experimental data of drying kinetics. According to this approach, the Page model provided the best fit at 50 °C (Figure 2), while at 40 and 30 °C the Logarithmic and Midilli models offered the most accurate description of the drying curves, with the Logarithmic model yielding the lowest AIC and BIC values.

Drying at higher temperature (50 °C) moisture removal was faster but more variable, reducing model robustness. Similar behavior was reported by Goneli et al. [21] for S. terebinthifolius leaves, where elevated temperatures accelerated drying but increased the dispersion of diffusivity values due to structural heterogeneity. At 40 °C simpler models such as Lewis and Page provided acceptable fits (R² ≈ 0.992), more flexible models like Logarithmic and Midilli taken the nonlinear moisture profiles with higher accuracy (R² ≈ 0.998). These findings are consistent with Berbert et al. [22] for aroeira-vermelha (S. terebinthifolius) leaves, report that empirical models with additional parameters outperform simpler exponential models when describing the transition between constant and falling rate periods. At the lowest temperature (30 °C), drying was predominantly governed by internal diffusion mechanisms, leading to longer drying times and more pronounced curvature in moisture ratio curves. Under these conditions, the Logarithmic and Midilli models achieved the best performance (R² ≈ 0.997, AIC: −266.95 to −332.906), confirming their suitability to represent slow moisture transport in porous leaf matrices.

The physical interpretation of these results can be related to the drying mechanisms and the leaf microstructure of S. molle. Drying occurs in two main stages: an initial rapid phase dominated by evaporation of free water on the surface and transpiration through stomata and intercellular spaces, followed by a slower phase governed by internal diffusion through cell walls and porous tissues. This two-stage behavior produces the characteristic curvature in the moisture ratio profiles [13,22]. Empirical models that incorporate additional parameters or combined terms (Page, Logarithmic, Midilli, Two-term) are therefore more suitable to capture this superposition of mechanisms. The Page model, by introducing the exponent n, accounts for deviations from pure exponential decay due to structural heterogeneity or anomalous transport. The Midilli model, which combines an exponential and a linear term, describes both the rapid initial water loss (exponential term) and the slower release of strongly bound water or tissue collapse effects (linear term). Similarly, the Logarithmic model introduces a residual term that may be interpreted as equilibrium moisture or strongly retained water fractions. In contrast, simpler models such as Lewis or the idealized solution of Fick’s law fail to accurately represent the process when multiple transport mechanisms occur simultaneously or when structural heterogeneity is significant. This adaptability makes the Midilli model one of the most widely applied to medicinal and aromatic plants, as it effectively describes the rapid initial water loss often observed in these matrices [16].

3.4. Bioactive Compounds During Drying Kinetics

Flavonoids have been shown to exhibit antioxidant properties, which help combat oxidative stress and protect cells from damage caused by free radicals. Additionally, they demonstrate antimicrobial activity against pathogens of interest in the agri-food industry [33]. Understanding the kinetics of flavonoid changes during drying helps optimize both nutritional quality and processing efficiency.

Figure 5 presents the total flavonoid retention kinetics during convective drying. As can be seen, the drying temperature increases, and the flavonoid content tends to decrease due to thermal degradation. Similar results have been reported for Moringa oleifera [34] and Rebaudiana bertoni [35]. The most pronounced total flavonoid decrease occurs during the first 100 to 200 min, especially at 50 °C. This fact suggests a rapid degradation phase during the period of free moisture loss. Drying at lower temperatures generally results in higher flavonoid retention in leaves, such as Ocimum basilicum L. [30] and Allium sativum L. [36]. The pirul leaves dried at 30 °C showed less degradation of flavonoid compounds but the drying process was too slow for practical purposes.

Table 3. Total flavonoid content in Schinus molle leaves dehydrated at different drying air temperatures.

Temperature [°C]	Total Flavonoids Content [mg QE/100 g Dry Leaf] (Mean ± SD)
Fresh leaves	57.53 ± 1.54 a
30	36.27 ± 1.57 b
40	29.31 ± 0.73 c
50	21.76 ± 0.7 d

Values that do not share the same letter are statistically different (n = 3, p < 0.05).

presents the total flavonoid content in pirul leaves after drying at different drying air temperatures. A decrease in total flavonoid content was observed, at higher drying temperatures, with values ranging from 37.96 to 21.02 mg QE/100 g of leaf. As observed, higher drying temperatures result in lower flavonoid recovery in the leaves 37, 49, and 62% at 30, 40, and 50 °C, respectively. The thermosensitivity of these compounds can explain this. Similar results were reported by Silva et al. [20] for the drying of S. terebinthifolius leaves from Brazil using a rotary drum.

High drying temperatures may disrupt the chemical bonds of bioactive compounds, leading to their inactivation or transformation into other molecules. In addition, the presence of oxygen in the drying air promotes both enzymatic and non-enzymatic oxidation, further contributing to the degradation of antioxidants. Flavonoids, together with other phenolic compounds and glycosides, possess a molecular structure characterized by a benzene ring and hydroxyl (-OH) groups with high reducing capacity [37].

Under convective drying at elevated temperatures, these hydroxyl groups readily react with oxygen, triggering oxidation reactions that represent the primary mechanism of flavonoid degradation. As temperature increases, the rate of oxidation intensifies, resulting in a more pronounced loss of flavonoids and consequently lower retention in the dried product [20]. From an application perspective, maintaining the integrity of flavonoids is crucial, as these compounds are directly related to the antioxidant and antimicrobial properties of S. molle extracts. The results obtained suggest that drying at moderate temperatures (≤40 °C) offers a better balance between process efficiency and retention of bioactive compounds.

4. Conclusions

The effect of drying air temperature (30, 40, and 50 °C) on total flavonoid retention and water transport during the drying of pirul (Schinus molle) leaves was investigated. The results confirm that drying temperature is inversely proportional to the flavonoid content of the dried leaves. As expected, higher temperatures enhance effective water vapor diffusivity, thereby reducing processing time. Among the tested models, the Logarithmic equations provided the best description of the drying kinetics at 30–40 °C, whereas the Page model was more adequate at 50 °C. These findings highlight the importance of selecting flexible models to capture the nonlinear behavior of moisture removal in leaves. These thermodynamic properties, together with the influence of temperature on the retention of bioactive compounds, provide crucial information for optimizing the production process of functional extracts, which is of particular interest to the food and pharmaceutical industries due to the antimicrobial properties of flavonoids. Future research should include the analysis of leaf microstructure and the evaluation of the stability of other bioactive compounds during drying, as well as their scaling up under industrial conditions, should be a priority.