Flexible Job Shop Scheduling Optimization with Multiple Criteria Using a Hybrid Metaheuristic Framework
Abstract
1. Introduction
2. Problem Description
2.1. Extension of the Dataset
2.1.1. Due Dates
2.1.2. Sequence-Dependent Setup Times
2.2. Scheduling Problem Introduction
- Machine assignment constraint: Ensure that each operation k of job j is assigned to exactly one machine out of the available machine among available machines. This ensures that no operation is processed by multiple machines simultaneously.
- Completion time constraint: The completion time of operation k of job j on machine i is the sum of its start time, processing time, and setup time.
- Precedence constraint: For each job j, the start time of operation (k + 1) must occur after the finish of operation k. Each job consists of multiple operations that must be performed sequentially.
2.3. Multi-Purpose Machine Environment
2.4. Single-Purpose Machine Environment
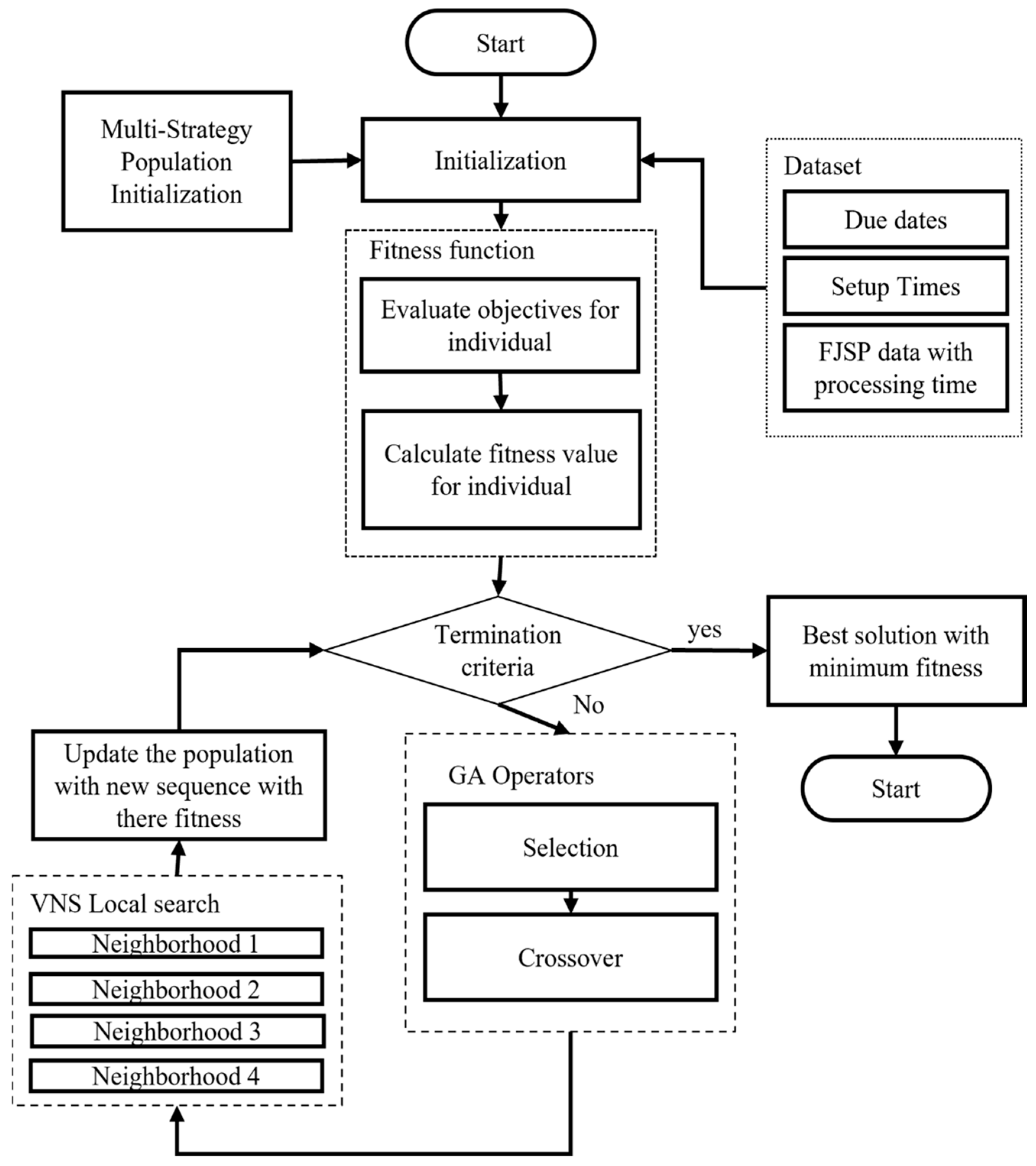
3. Proposed Method for Scheduling
3.1. Multi-Strategy Population
3.2. Fitness Function
3.3. GA Operators
3.3.1. Selection
3.3.2. Crossover
3.4. Local Search
- N1 (swap): randomly select two operations from the sequence and swap their positions.
- N2 (reversion): randomly selects two positions from the sequence and reverses all operations between those positions.
- N3 (insertion): two operations are chosen randomly, and the second operation is placed in front of the first.
- N4 (rearrangement): four positions are randomly chosen from the sequence and shuffled in their order.
| Algorithm 1 Local search |
|
|
|
|
|
|
|
Set |
|
|
3.5. Termination Criteria
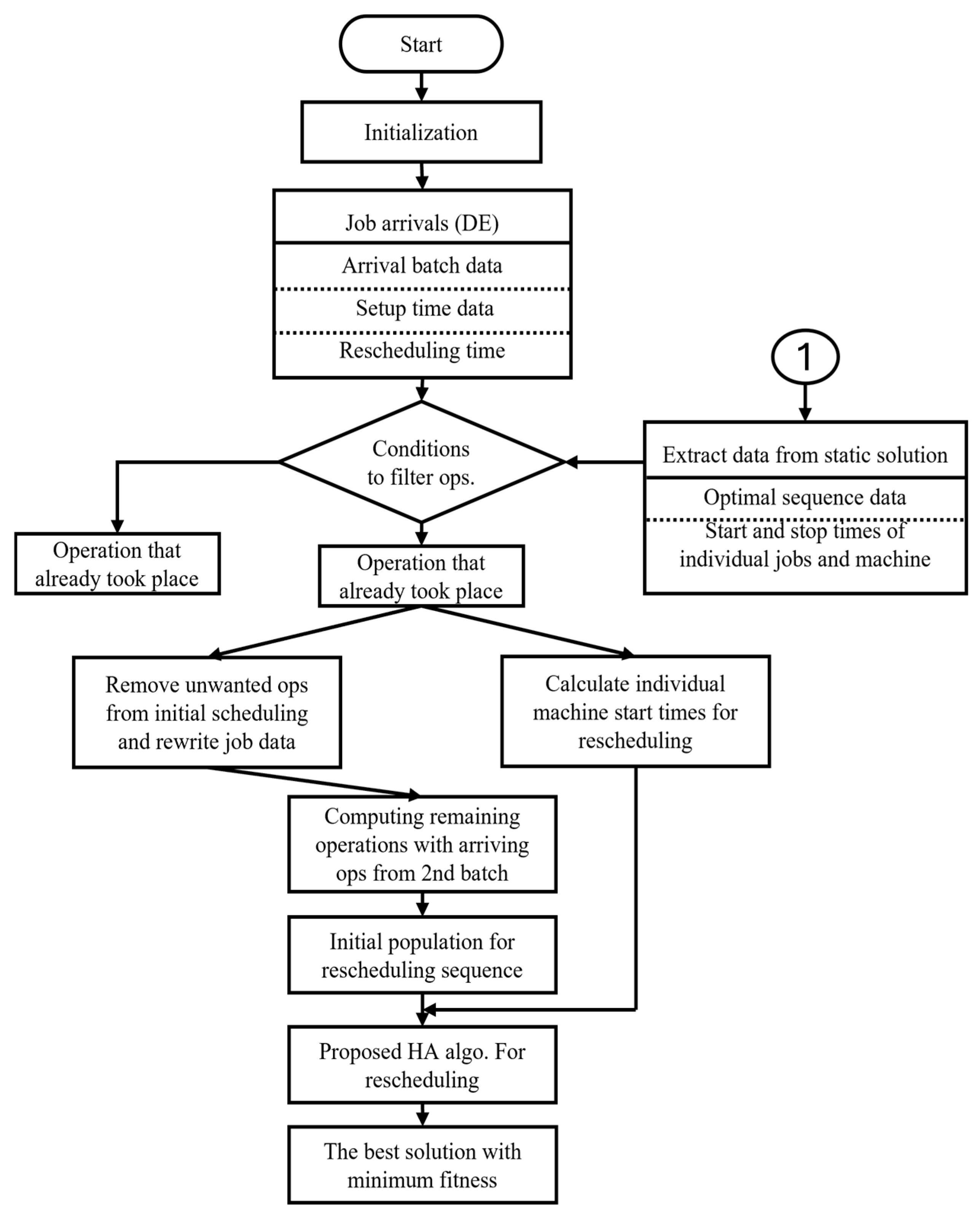
4. Proposed Rescheduling Methods for Dynamic Events
4.1. Rescheduling for Job Arrival
- Operations Oi,j that started before the rescheduling time—that is, the start time Si,j of the operation is earlier than the rescheduling time Tresch—will be excluded from the rescheduling process.
- 2.
- Operations that did not start before the rescheduling time—that is, the start time Si,j of the operation is later than the rescheduling time Tresch—will be included in the rescheduling process.
4.2. Rescheduling for Machine Breakdown
- Operations affected by machine breakdown (operations to reschedule):
- 1.
- Operations that extend beyond the breakdown time, that is, when the completion time Ci,j of the operation Oi,j is greater than or equal to the breakdown time Tb, will be included in the rescheduling strategy (Ci,j ≥ Tb).
- 2.
- Operations that started after the breakdown time, that is, when the start time Si,j of the operation Oi,j is greater than the breakdown time Tb, will be included in the rescheduling strategy (Si,j ≥ Tb).
- Operations not affected by machine breakdown (operations not to be rescheduled):
- 3.
- Operations that are finished successfully before the breakdown occurs, that is, when the completion time Ci,j of the operation Oi,j is less than the breakdown time Tb, will not be considered in the rescheduling strategy (Ci,j < Tb).
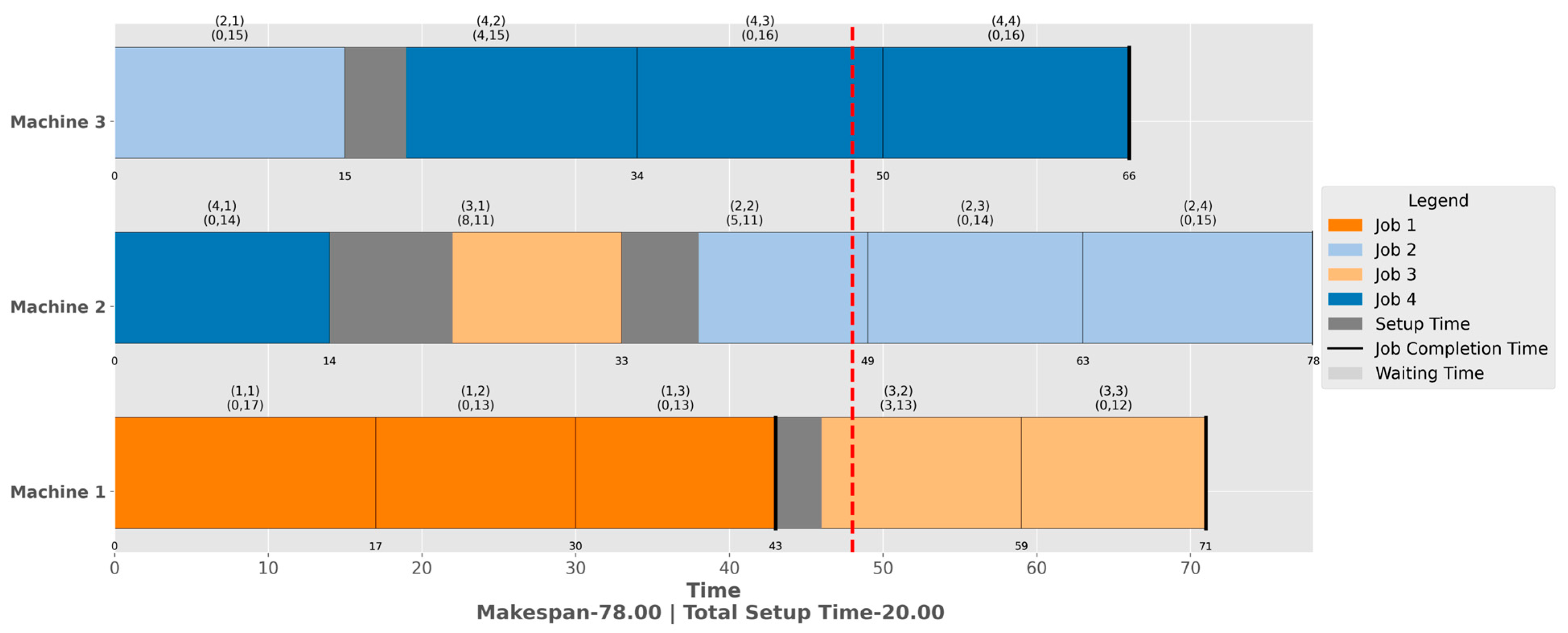
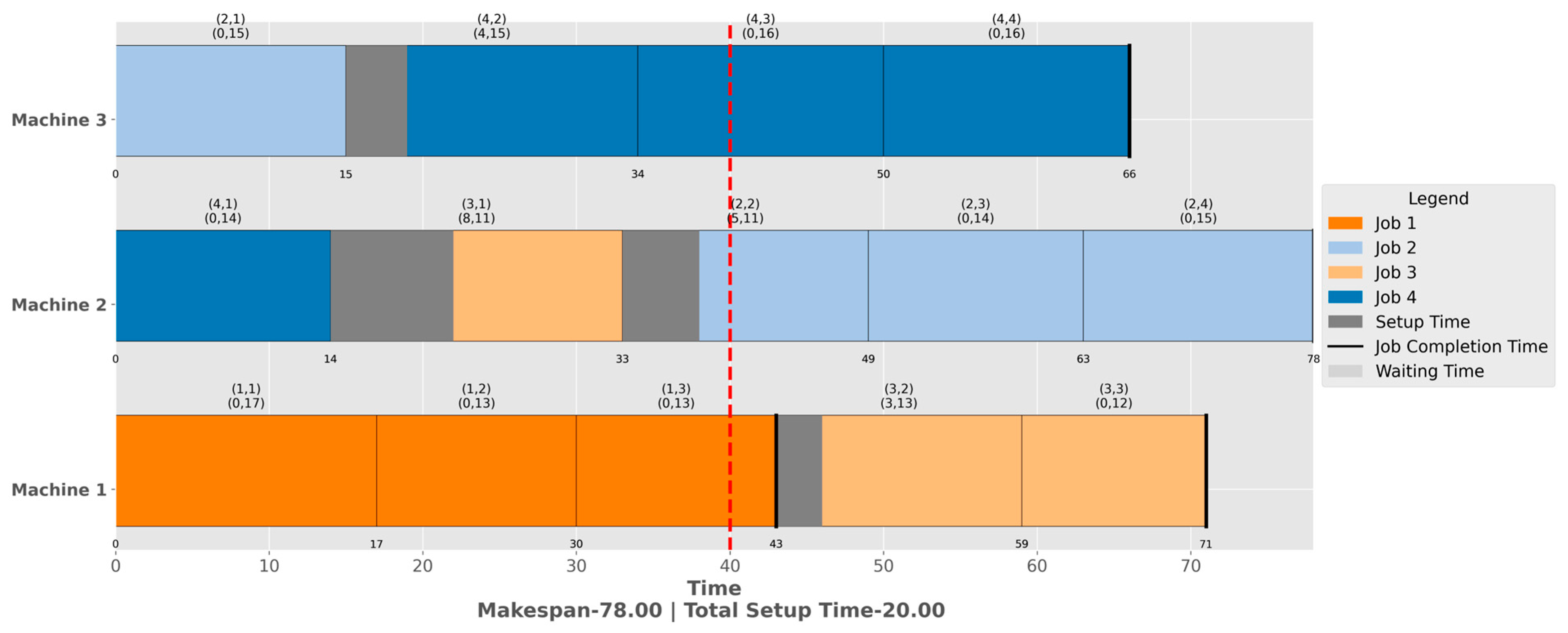
5. Results and Discussion
5.1. Static Flexible Job Shop Scheduling
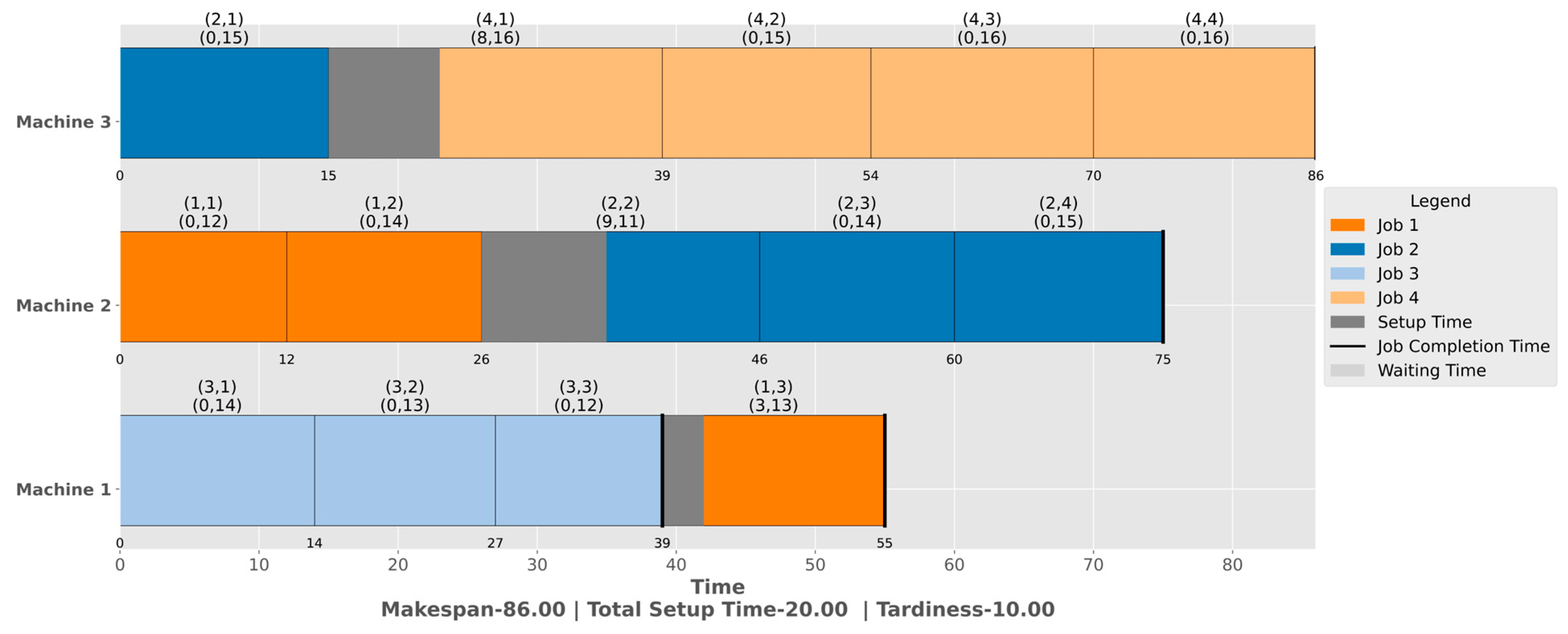
5.1.1. For a Single-Purpose Machine
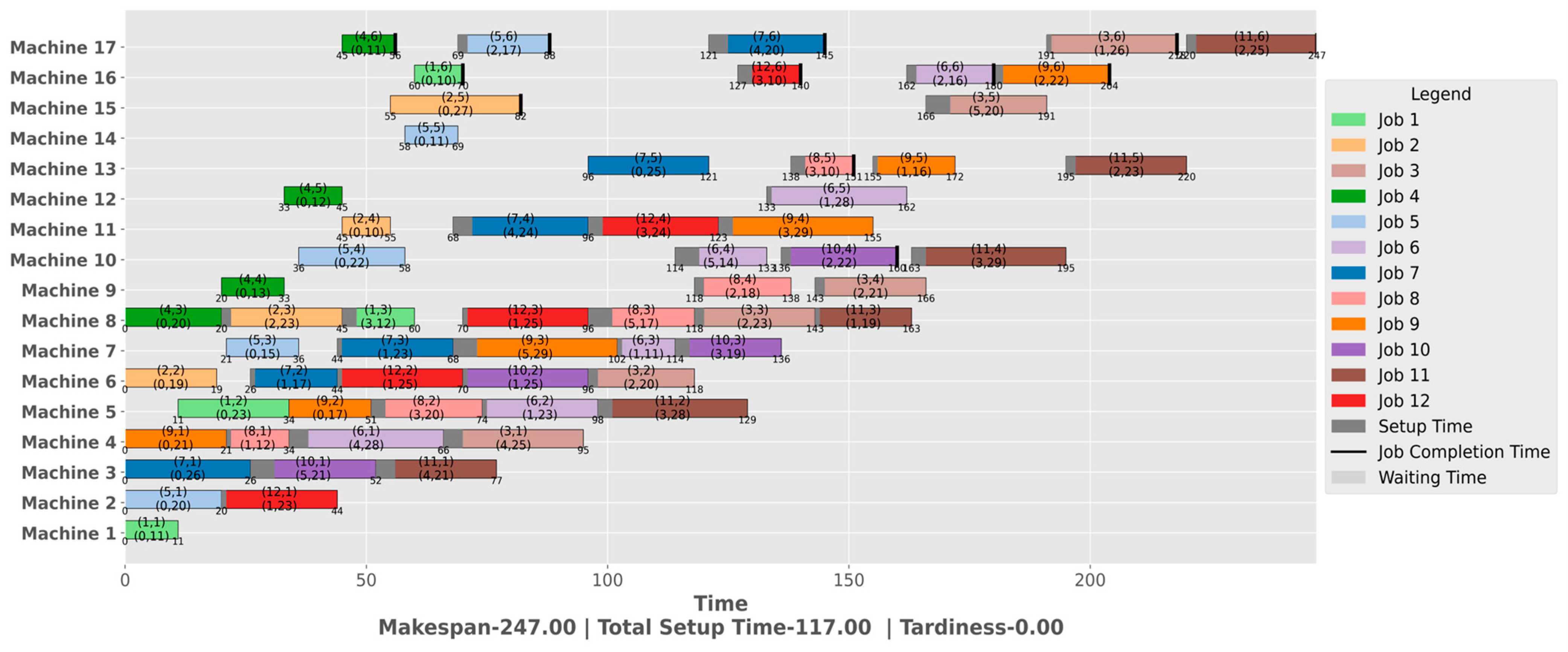
5.1.2. For a Multi-Purpose Machine
5.2. Dynamic Flexible Job Shop Scheduling
5.2.1. Job Arrival
5.2.2. Machine Breakdown
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fattahi, P.; Fallahi, A. Dynamic Scheduling in Flexible Job Shop Systems by Considering Simultaneously Efficiency and Stability. CIRP J. Manuf. Sci. Technol. 2010, 2, 114–123. [Google Scholar] [CrossRef]
- Türkyılmaz, A.; Şenvar, Ö.; Ünal, İ.; Bulkan, S. A Research Survey: Heuristic Approaches for Solving Multi Objective Flexible Job Shop Problems. J. Intell. Manuf. 2020, 31, 1949–1983. [Google Scholar] [CrossRef]
- Baykasoǧlu, A. Linguistic-Based Meta-Heuristic Optimization Model for Flexible Job Shop Scheduling. Int. J. Prod. Res. 2002, 40, 4523–4543. [Google Scholar] [CrossRef]
- Xie, J.; Gao, L.; Peng, K.; Li, X.; Li, H. Review on Flexible Job Shop Scheduling. IET Collab. Intell. Manuf. 2019, 1, 67–77. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, S. Flexible Assembly Job-Shop Scheduling with Sequence-Dependent Setup Times and Part Sharing in a Dynamic Environment: Constraint Programming Model, Mixed-Integer Programming Model, and Dispatching Rules. IEEE Trans. Eng. Manag. 2018, 65, 487–504. [Google Scholar] [CrossRef]
- Blackstone, J.H.; Phillips, D.T.; Hogg, G.L. A State-of-the-Art Survey of Dispatching Rules for Manufacturing Job Shop Operations. Int. J. Prod. Res. 1982, 20, 27–45. [Google Scholar] [CrossRef]
- Holthaus, O.; Rajendranb, C. Efficient Dispatching Rules for Scheduling in a Job Shop. Int. J. Prod. Econ. 1997, 48, 87–105. [Google Scholar] [CrossRef]
- Shi, X.; Long, W.; Li, Y.; Deng, D. Multi-Population Genetic Algorithm with ER Network for Solving Flexible Job Shop Scheduling Problems. PLoS ONE 2020, 15, e0233759. [Google Scholar] [CrossRef]
- Shady, S.; Kaihara, T.; Fujii, N.; Kokuryo, D. Evolving Dispatching Rules Using Genetic Programming for Multi-Objective Dynamic Job Shop Scheduling with Machine Breakdowns. Procedia CIRP 2021, 104, 411–416. [Google Scholar] [CrossRef]
- Ozturk, G.; Bahadir, O.; Teymourifar, A. Extracting Priority Rules for Dynamic Multi-Objective Flexible Job Shop Scheduling Problems Using Gene Expression Programming. Int. J. Prod. Res. 2019, 57, 3121–3137. [Google Scholar] [CrossRef]
- Cheung, W.; Zhou, H. Using Genetic Algorithms and Heuristics for Job Shop Scheduling with Sequence-Dependent Setup Times. Ann. Oper. Res. 2001, 107, 65–81. [Google Scholar] [CrossRef]
- Özgüven, C.; Yavuz, Y.; Özbakir, L. Mixed Integer Goal Programming Models for the Flexible Job-Shop Scheduling Problems with Separable and Non-Separable Sequence Dependent Setup Times. Appl. Math. Model. 2012, 36, 846–858. [Google Scholar] [CrossRef]
- dos Santos, F.; Costa, L.; Varela, L. Multi-Objective Optimization of the Job Shop Scheduling Problem on Unrelated Parallel Machines with Sequence-Dependent Setup Times; Springer Nature: Cham, Switzerland, 2023; Volume 14105, LNCS; ISBN 9783031371073. [Google Scholar]
- Ortíz-Barrios, M.; Petrillo, A.; De Felice, F.; Jaramillo-Rueda, N.; Jiménez-Delgado, G.; Borrero-López, L. A Dispatching-Fuzzy Ahp-Topsis Model for Scheduling Flexible Job-Shop Systems in Industry 4.0 Context. Appl. Sci. 2021, 11, 5107. [Google Scholar] [CrossRef]
- Thenarasu, M.; Rameshkumar, K.; Di Mascolo, M.; Anbuudayasankar, S.P. Multi-Criteria Scheduling of Realistic Flexible Job Shop: A Novel Approach for Integrating Simulation Modelling and Multi-Criteria Decision Making. Int. J. Prod. Res. 2024, 62, 336–358. [Google Scholar] [CrossRef]
- Liu, N.; Qin, K. Research on Improved Genetic Algorithm Based on Multi-Objective Optimization for Flexible Shop Scheduling Problem. In Proceedings of the 2025 5th International Conference on Sensors and Information Technology (ICSI 2025), Nanjing, China, 21–23 March 2025; pp. 719–722. [Google Scholar] [CrossRef]
- He, A.; Liu, X.; Gong, G.; Yuan, Z.; Huang, H.; Zhou, Y.; Li, J. Multi-Objective Optimization for Distributed Flexible Job Shop Scheduling Problem with Job Priority. Swarm Evol. Comput. 2025, 98, 102075. [Google Scholar] [CrossRef]
- Sels, V.; Gheysen, N.; Vanhoucke, M. A Comparison of Priority Rules for the Job Shop Scheduling Problem under Different Flow Time- and Tardiness-Related Objective Functions. Int. J. Prod. Res. 2012, 50, 4255–4270. [Google Scholar] [CrossRef]
- Rahmati, S.H.A.; Zandieh, M.; Yazdani, M. Developing Two Multi-Objective Evolutionary Algorithms for the Multi-Objective Flexible Job Shop Scheduling Problem. Int. J. Adv. Manuf. Technol. 2013, 64, 915–932. [Google Scholar] [CrossRef]
- Draz, U.; Ali, T.; Yasin, S.; Chaudary, M.H.; Ayaz, M.; Aggoune, E.H.M.; Yasin, I. Hybridization and Optimization of Bio and Nature-Inspired Metaheuristic Techniques of Beacon Nodes Scheduling for Localization in Underwater IoT Networks. Mathematics 2024, 12, 3447. [Google Scholar] [CrossRef]
- Tay, J.C.; Ho, N.B. Evolving Dispatching Rules Using Genetic Programming for Solving Multi-Objective Flexible Job-Shop Problems. Comput. Ind. Eng. 2008, 54, 453–473. [Google Scholar] [CrossRef]
- Lunardi, W.T.; Birgin, E.G.; Ronconi, D.P.; Voos, H. Metaheuristics for the Online Printing Shop Scheduling Problem. Eur. J. Oper. Res. 2021, 293, 419–441. [Google Scholar] [CrossRef]
- Fuladi, S.K.; Kim, C.S. Dynamic Events in the Flexible Job-Shop Scheduling Problem: Rescheduling with a Hybrid Metaheuristic Algorithm. Algorithms 2024, 17, 142. [Google Scholar] [CrossRef]
- Ben Ali, K.; Bechikh, S.; Louati, A.; Louati, H.; Kariri, E. Dynamic Job Shop Scheduling Problem with New Job Arrivals Using Hybrid Genetic Algorithm. IEEE Access 2024, 12, 85338–85354. [Google Scholar] [CrossRef]
- Tariq, A.; Khan, S.A.; But, W.H.; Javaid, A.; Shehryar, T. An IoT-Enabled Real-Time Dynamic Scheduler for Flexible Job Shop Scheduling (FJSS) in an Industry 4.0-Based Manufacturing Execution System (MES 4.0). IEEE Access 2024, 12, 49653–49666. [Google Scholar] [CrossRef]
- Ben Ali, K.; Telmoudi, A.J.; Gattoufi, S. An Improved Genetic Algorithm with Local Search for Solving the DJSSP with New Dynamic Events. In Proceedings of the IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA), Torino, Italy, 4–7 September 2018; pp. 1137–1144. [Google Scholar] [CrossRef]
- Thi, L.M.; Mai Anh, T.T.; Van Hop, N. An Improved Hybrid Metaheuristics and Rule-Based Approach for Flexible Job-Shop Scheduling Subject to Machine Breakdowns. Eng. Optim. 2023, 55, 1535–1555. [Google Scholar] [CrossRef]
- Ding, L.; Guan, Z.; Luo, D.; Rauf, M.; Fang, W. An Adaptive Search Algorithm for Multiplicity Dynamic Flexible Job Shop Scheduling with New Order Arrivals. Symmetry 2024, 16, 641. [Google Scholar] [CrossRef]
- Pezzella, F.; Morganti, G.; Ciaschetti, G. A Genetic Algorithm for the Flexible Job-Shop Scheduling Problem. Comput. Oper. Res. 2008, 35, 3202–3212. [Google Scholar] [CrossRef]
- Azzouz, A.; Ennigrou, M.; Ben Said, L. Flexible Job-Shop Scheduling Problem with Sequence-Dependent Setup Times Using Genetic Algorithm. In Proceedings of the ICEIS 2016—18th International Conference on Enterprise Information Systems, Rome, Italy, 25–28 April 2016; Volume 2, pp. 47–53. [Google Scholar] [CrossRef][Green Version]
- Huang, X.; Yang, L. A Hybrid Genetic Algorithm for Multi-Objective Flexible Job Shop Scheduling Problem Considering Transportation Time. Int. J. Intell. Comput. Cybern. 2019, 12, 154–174. [Google Scholar] [CrossRef]
- Türkylmaz, A.; Bulkan, S. A Hybrid Algorithm for Total Tardiness Minimisation in Flexible Job Shop: Genetic Algorithm with Parallel VNS Execution. Int. J. Prod. Res. 2015, 53, 1832–1848. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Q. A Hybrid Genetic Algorithm for Flexible Job Shop Scheduling Problem with Sequence-Dependent Setup Times and Job Lag Times. IEEE Access 2021, 9, 104864–104873. [Google Scholar] [CrossRef]
- Sun, K.; Zheng, D.; Song, H.; Cheng, Z.; Lang, X.; Yuan, W.; Wang, J. Hybrid Genetic Algorithm with Variable Neighborhood Search for Flexible Job Shop Scheduling Problem in a Machining System. Expert Syst. Appl. 2023, 215, 119359. [Google Scholar] [CrossRef]
- Ojstersek, R.; Tang, M.; Buchmeister, B. Due Date Optimization in Multi-Objective Scheduling of Flexible Job Shop Production. Adv. Prod. Eng. Manag. 2020, 15, 481–492. [Google Scholar] [CrossRef]
- Ho, N.B.; Tay, J.C. Evolving Dispatching Rules for Solving the Flexible Job-Shop Problem. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation (IEEE CEC 2005), Edinburgh, Scotland, 2–5 September 2005; Volume 3, pp. 2848–2855. [Google Scholar] [CrossRef]
- Ojstersek, R.; Palcic, I.; Buchmeister, B. Production Scheduling Using Twk and Slk Methods. Ann. DAAAM Proc. 2021, 32, 228–234. [Google Scholar] [CrossRef]
- Rahman, H.F.; Janardhanan, M.N.; Poon Chuen, L.; Ponnambalam, S.G. Flowshop Scheduling with Sequence Dependent Setup Times and Batch Delivery in Supply Chain. Comput. Ind. Eng. 2021, 158, 107378. [Google Scholar] [CrossRef]
- Madhav, S.; Ahamad, A.; Singh, P.; Mishra, P.K. A Review of Textile Industry: Wet Processing, Environmental Impacts, and Effluent Treatment Methods. Environ. Qual. Manag. 2018, 27, 31–41. [Google Scholar] [CrossRef]
- Meng, L.; Cheng, W.; Zhang, B.; Zou, W.; Duan, P. A Novel Hybrid Algorithm of Genetic Algorithm, Variable Neighborhood Search and Constraint Programming for Distributed Flexible Job Shop Scheduling Problem. Int. J. Ind. Eng. Comput. 2024, 15, 813–832. [Google Scholar] [CrossRef]
- Jayamohan, M.S.; Rajendran, C. New Dispatching Rules for Shop Scheduling: A Step Forward. Int. J. Prod. Res. 2000, 38, 563–586. [Google Scholar] [CrossRef]
- Chiang, T.C.; Fu, L.C. Using a Family of Critical Ratio-Based Approaches to Minimize the Number of Tardy Jobs in the Job Shop with Sequence Dependent Setup Times. Eur. J. Oper. Res. 2009, 196, 78–92. [Google Scholar] [CrossRef]





| Jobs | Operations | Processing Ti. | ||
|---|---|---|---|---|
| M1 | M2 | M3 | ||
| Job1 | O11 | 17 | 12 | 13 |
| O12 | 13 | 14 | 15 | |
| O13 | 13 | - | 16 | |
| Job2 | O21 | 12 | - | 15 |
| O22 | 14 | 11 | - | |
| O23 | - | 14 | 17 | |
| O24 | 11 | 15 | 12 | |
| Job3 | O31 | 14 | 11 | 16 |
| O32 | 13 | - | - | |
| O33 | 12 | 18 | 15 | |
| Job4 | O41 | 18 | 14 | 16 |
| O42 | 12 | - | 15 | |
| O43 | 15 | 11 | 16 | |
| O44 | 18 | 19 | 16 | |
| Machine 1 | Machine 2 | Machine 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J1 | J2 | J3 | J4 | J1 | J2 | J3 | J4 | J1 | J2 | J3 | J4 | |
| J′1 | 0 | 5 | 7 | 6 | 0 | 6 | 6 | 4 | 0 | 6 | 3 | 3 |
| J′2 | 9 | 0 | 7 | 8 | 7 | 0 | 5 | 9 | 9 | 0 | 4 | 9 |
| J′3 | 3 | 3 | 0 | 9 | 6 | 5 | 0 | 3 | 5 | 8 | 0 | 3 |
| J′4 | 6 | 8 | 8 | 0 | 5 | 7 | 8 | 0 | 4 | 3 | 4 | 0 |
| Job | J1 | J2 | J3 | J4 |
|---|---|---|---|---|
| Due Dates | 57 | 72 | 54 | 79 |
| Task | OP1 | OP2 | OP3 | OP4 | OP5 | OP6 |
|---|---|---|---|---|---|---|
| Job/Resources | MG1 (M1/M2/M3/M4) | MG2 (M5/M6) | MG3 (M7/M8) | MG4 (M9/M10/M11) | MG5 (M12/M13/M14/M15) | MG6 (M16/M17) |
| Job 1 | 11/14/16/12 | 23/14 | 17/12 | - | - | 10/12 |
| Job 2 | - | 25/19 | 21/23 | 17/19/10 | 29/24/21/27 | - |
| Job 3 | 28/20/17/25 | 10/20 | 25/23 | 21/20/27 | 21/18/15/20 | 29/26 |
| Job 4 | - | - | 16/20 | 13/16/14 | 12/19/21/25 | 15/11 |
| Job 5 | 24/20/21/23 | - | 15/14 | 10/22/20 | 14/15/11/17 | 15/17 |
| Job 6 | 27/26/20/28 | 23/20 | 11/16 | 13/14/25 | 28/27/21/26 | 16/19 |
| Job 7 | 22/23/26/24 | 16/17 | 23/26 | 14/22/24 | 29/25/24/22 | 22/20 |
| Job 8 | 14/15/13/12 | 20/25 | 24/17 | 18/26/21 | 19/10/17/18 | - |
| Job 9 | 27/22/25/21 | 17/18 | 29/22 | 20/23/29 | 17/16/13/15 | 22/23 |
| Job 10 | 23/25/21/26 | 24/25 | 19/27 | 26/22/24 | - | - |
| Job 11 | 22/24/21/25 | 28/22 | 20/19 | 26/29/25 | 20/23/24/25 | 20/25 |
| Job 12 | 19/23/29/27 | 17/25 | 20/25 | 21/19/24 | - | 10/12 |
| Job | J1 | J2 | J3 | J4 | J5 | J6 |
| Due Dates | 94 | 142 | 222 | 104 | 140 | 202 |
| Job | J7 | J8 | J9 | J10 | J11 | J12 |
| Due Dates | 234 | 154 | 230 | 172 | 254 | 170 |
| Population (P) | Machine Selection | Operation Sequencing |
|---|---|---|
| P1 | Random | Random |
| P2 | SPT | Random |
| P3 | Random | LWKR + FDD |
| P4 | Random | CR |
| Extended Dataset | Iteration Size | GA [26] | Proposed | Improve in % with GA |
|---|---|---|---|---|
| SPM_FJSP_5jx7mg | 500 | 79 | 78 | 1.27% |
| SPM_FJSP_6jx6mg | 500 | 72 | 73 | −1.99% |
| SPM_FJSP_6jx7mg | 500 | 85 | 83 | 2.25% |
| SPM_FJSP_6jx10mg | 600 | 127 | 124 | 2.36% |
| SPM_FJSP_7jx4mg | 600 | 60 | 57 | 5.00% |
| SPM_FJSP_8jx6mg | 600 | 103 | 99 | 3.88% |
| SPM_FJSP_8jx7mg | 600 | 120 | 120 | 0% |
| SPM_FJSP_8jx8mg | 700 | 125 | 118 | 5.60% |
| SPM_FJSP_10jx7mg | 700 | 169 | 165 | 2.37% |
| SPM_FJSP_10jx8mg | 800 | 184 | 179 | 2.72% |
| SPM_FJSP_11jx4mg | 800 | 93 | 89 | 4.30% |
| Extended Dataset (Job × Machine) | Iteration Size | A1 | A2 | A3 | GA [26] | Proposed | MK/TST/TT | Improve in % with GA |
|---|---|---|---|---|---|---|---|---|
| MK01 (10 × 6) | 500 | 196 | 226 | 134 | 131 | 125 | 102/216/61 | 4.5% |
| MK02 (10 × 6) | 500 | 62 | 79 | 81 | 53 | 47 | 58/84/0 | 11.32% |
| MK03 (15 × 8) | 600 | 250 | 250 | 239 | 184 | 187 | 267/299/1 | −1.7% |
| MK04 (15 × 8) | 600 | 140 | 147 | 130 | 101 | 99 | 103/183/14 | 1.9% |
| MK05 (15 × 4) | 600 | 420 | 423 | 430 | 444 | 420 | 261/216/796 | 5.4% |
| MK06 (10 × 15) | 700 | 187 | 194 | 187 | 151 | 147 | 155/290/0 | 2.6% |
| MK07 (20 × 5) | 700 | 372 | 365 | 540 | 206 | 192 | 234/210/138 | 6.8% |
| MK08 (20 × 10) | 700 | 1024 | 837 | 781 | 698 | 698 | 635/594/886 | 0.0% |
| MK09 (20 × 10) | 700 | 627 | 581 | 504 | 421 | 320 | 430/540/0 | 23.9% |
| MK10 (20 × 15) | 800 | 470 | 502 | 394 | 340 | 306 | 393/534/0 | 10.0% |
| 6.51% overall |
| Jobs | Operations | Processing Time | ||
|---|---|---|---|---|
| M1 | M2 | M3 | ||
| Job5 | O51 | 17 | 14 | 16 |
| O52 | 11 | 15 | 12 | |
| O53 | 19 | - | 11 | |
| Job6 | O61 | 13 | 17 | 12 |
| O62 | 11 | 15 | 17 | |
| O63 | 15 | - | 18 | |
| O64 | 14 | 11 | 16 | |
| Job7 | O71 | 18 | 19 | 16 |
| O72 | 17 | 12 | 15 | |
| O73 | 13 | - | 16 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuladi, S.K.; Kim, C.S. Flexible Job Shop Scheduling Optimization with Multiple Criteria Using a Hybrid Metaheuristic Framework. Processes 2025, 13, 3260. https://doi.org/10.3390/pr13103260
Fuladi SK, Kim CS. Flexible Job Shop Scheduling Optimization with Multiple Criteria Using a Hybrid Metaheuristic Framework. Processes. 2025; 13(10):3260. https://doi.org/10.3390/pr13103260
Chicago/Turabian StyleFuladi, Shubhendu Kshitij, and Chang Soo Kim. 2025. "Flexible Job Shop Scheduling Optimization with Multiple Criteria Using a Hybrid Metaheuristic Framework" Processes 13, no. 10: 3260. https://doi.org/10.3390/pr13103260
APA StyleFuladi, S. K., & Kim, C. S. (2025). Flexible Job Shop Scheduling Optimization with Multiple Criteria Using a Hybrid Metaheuristic Framework. Processes, 13(10), 3260. https://doi.org/10.3390/pr13103260






