The Impact of Solar Radiation at Different Colombian Thermal Floors on an Adsorption Refrigeration Cycle

Abstract

The process of energy transition in Colombia has sparked an exploration into appropriate geographical areas for the utilization of solar energy. The country’s rugged terrain and significant climate variability pose challenges for implementing standardized technologies uniformly across all regions. Consequently, this study aims to develop and apply a mathematical model to characterize the performance of a solar adsorption cooling system under the environmental conditions found in six distinct Colombian cities, taking into account different thermal profiles and extreme weather periods such as the El Niño and La Niña phenomena. The selected mathematical model was simulated in these cities, considering ambient temperature and solar radiation variables over a twelve-month period during these extreme weather phenomena and an additional twelve-month period representative of a typical year with minimal influence from these phenomena. The results indicated that despite a lower coefficient of performance (COP) compared to the other cities, Riohacha demonstrated a greater number of ice production days owing to its high levels of solar radiation.

1. Introduction

Similar to other forms of renewable energy, solar energy exhibits intermittent behavior, resulting in an unpredictable energy flow. Consequently, any solar radiation harnessing design must consider the variable atmospheric conditions prevailing at the chosen sites [1,2,3]. The utilization of renewable energy sources largely depends on the local climatic conditions of the study areas. Understanding these conditions is essential in identifying suitable locations for power generation using solar, wind, biomass, and other energy sources. In some cases, it may be necessary to employ hybrid systems to optimize efficiency in harnessing renewable sources. For photovoltaic and solar thermal technologies, it is critical to consider the specific location or region of interest for system implementation. A comprehensive set of meteorological data or atmospheric conditions, including wind variables, cloudiness, and solar irradiation variations, should be taken into account. Understanding these variables is crucial for developing equipment with efficiencies tailored to the local atmospheric conditions [4,5].

Typically, investigations into climate variability rely on a representative year to demonstrate the energy potential with seasonal fluctuations over an extended duration, aiming to reduce uncertainty in the findings. Nevertheless, certain researchers contend that for evaluating the potentials of photovoltaic and thermal solar energy, a broader contextual framework is imperative, surpassing the limitations inherent in a conventional annual representation [6,7].

The effects of global warming are currently linked to the emission of greenhouse gases from fossil fuels, particularly due to the production of CO${}_2$. The present concentration of CO${}_2$ in the atmosphere is approximately $417 \mathrm{p}\mathrm{p}\mathrm{m}$ by volume and is increasing at an approximate rate of $2.07 \mathrm{p}\mathrm{p}\mathrm{m}$ per year. Renewable energy resources, such as solar energy, present a viable solution to help mitigate the effects of climate change [8,9]. However, the phenomena associated with climate change, specifically extended periods of excessive drought known as “El Niño” and periods of intense rainfall known as “La Niña”, can significantly impact the harnessing of solar resources. Consequently, it is crucial to take these phenomena into account when evaluating energy potentials.

Similarly, in countries with diverse topography, it is crucial to take into account the thermal floors that exhibit distinct climatic characteristics due to the effects of altitude. Specifically, the impact of altitude on the evaluation of solar energy potential has not been extensively studied.

The work presented by Ospino [10] conducts a study on the solar energy potential in the Colombian Caribbean. It emphasizes that the geographical position and savanna conditions augment the feasibility of harnessing this type of energy. However, it does not discuss additional climatic aspects that could further enhance the potential in the area. La Guajira is located at the northernmost tip of South America in the northeastern region of Colombia, bordering the Caribbean Sea and Venezuela. It is important to note that insolation in La Guajira is higher than in other regions of Colombia, and it is also higher than in some countries in Europe and Central America [11].

La Guajira is currently recognized as an epicenter for solar generation in Colombia, prompting numerous studies on this territory to characterize solar radiation, generally via meteorological stations [11], or through satellite projections presented by organizations such as the National Aeronautics and Space Administration (NASA) [12] and the Colombian Institute of Hydrology, Meteorology, and Environmental Studies (IDEAM) [13]. While the data indicate exceptional potential for solar radiation and thus significant energy potential in the region, it remains crucial to analyze additional aspects, such as climate and temperature variability, to establish minimum radiation potentials for solar equipment design.

Typically, the analysis of solar radiation energy potential relies on information from meteorological or satellite stations. These data are then utilized to construct maps that guide decision making. This work seeks to make a complementary contribution specifically by applying solar adsorption cooling technology [14,15,16,17,18]. The coefficient of performance (COP) of this technology is modeled based on the ambient temperature and solar radiation conditions in six cities located at different altitudes: Riohacha, Medellin, Cali, Bucaramanga, Bogota, and Tunja. Importantly, this work also considers periods influenced by the El Niño/La Niña interannual climate variability phenomena as well as periods not influenced by these phenomena (referred to in this work as a typical period/year).

The goal of this study is to evaluate the COP of an intermittent ice-making solar adsorption system, considering the input conditions—ambient temperature and solar radiation—in six cities of varying altitudes and affected by the El Niño and La Niña interannual climate variability phenomena. This study aims to quantify the number of ice production days throughout the year.

2. Methodology

The methodological approach of this research is divided into three parts. The first part involves developing a theoretical model of a solar adsorption ice-maker, in which the operating variables are contingent upon the site’s ambient temperature and solar radiation. The second part entails an analysis of the radiation potential in various Colombian cities located at different altitudes, taking into account climate variations due to the El Niño and La Niña phenomena. The third part involves a numerical solution where parameters of interest such as the Coefficient of Performance (COP), the minimum solar radiation required for ice production (I${}_{G,min})$, and the cooling capacity (i.e., the energy transfer in the evaporator) (SCE) are determined. Further details on these methodological components are provided in the sections below [19,20].

2.1. Development of the Theoretical Model of a Solar Thermal System That Operates through an Adsorption Refrigeration Cycle

The proposed system is an adsorption intermittent ice-maker featuring four theoretical stages. The adsorbent–adsorbate system comprises activated carbon solid (CA) and methanol vapor $(m_r,g)$. For a three-component absorption ice-maker, the configuration is depicted in Figure 1a, while the thermal process diagram is shown in Figure 1b.

The first stage occurs in the collector, where an initial maxima concentration of the $x_i=m_{r,g}/CA$ is observed before sunrise (point A). As the sun intensifies, the system temperature increases at a constant concentration until the pressure reaches saturation (point B).

The second stage takes place at a constant pressure. Here, increased radiation encourages desorption until a minimum concentration is reached in the collector (point D), which is followed by a heat exchange process in which the collector has a net heat gain and the desorbed methanol transitions to the condenser.

The third stage begins at sunset with a minimum concentration of the $x_f=m_{r,g}/CA$ constant. As the environment cools, the pressure reaches saturation (point F).

The fourth stage occurs as the temperature continues to drop at constant pressure during an adsorption process (point A). This stage is accompanied by an imminent heat exchange in the evaporator, where heat is extracted from the medium, and the methanol transitions to the collector [21,22].

Figure 1. Solar adsorption cooling system. (a) Equipment configuration, (b) Thermal process diagram [19,23,24].

Figure 1. Solar adsorption cooling system. (a) Equipment configuration, (b) Thermal process diagram [19,23,24].

Upon defining the process and thermal equipment for evaluating solar potential, a mathematical model is developed. This model governs the behavior of the variables involved in the mass and energy balances [25].

The ratio of methanol (working fluid) to activated carbon (the adsorbent) is derived from the difference between the maximum and minimum concentrations of methanol occurring in the collector. This balance leads to Equation (1).

$$m_{r,g}/m_a=\left(x_i-x_f\right)$$

(1)

In the equation, $m_{(r,g)}$ represents the mass of the generated refrigerant, $m_a$ denotes the mass of the absorbent, $x_i$ is the initial concentration, and $x_f$ is the final concentration.

Taking into account the heat transfer between the system and its surroundings, we obtain the total heat balance equations for one operational day (one cycle), as shown in Equations (2)–(8) [25,26].

$$Q_T+Q_e-Q_A-Q_c=0$$

(2)

$$Q_T=Q_{ISOS}+Q_{DES}$$

(3)

$$\frac{Q_{ISOS}}{m_a}=\left(C{p}_a+C{p}_r·x_i\right)\left(T_{g1}-T_i\right)$$

(4)

$$\frac{Q_{DES}}{m_a}=\left[C{p}_a+C{p}_r\frac{\left(x_i+x_f\right)}{2}\right]\left(T_f-T_{g1}\right)+\left(x_i-x_f\right)H_{ads}$$

(5)

$$\frac{Q_e}{m_a}=SCE=\left[L-C{p}_r\left(T_i-T_e\right)\right]\left(x_i-x_f\right)$$

(6)

$$COP=\frac{\left(Q_e/m_a\right)}{\left(Q_T/m_a\right)}$$

(7)

$$I_{G,min}=\frac{\left(Q_T/m_a\right)}{{\eta }_C}\left(\frac{m_a}{A_C}\right)$$

(8)

In these equations, $Q_T$ is the heat gained in the collector–generator, $Q_e$ refers to the heat gained in the evaporator, $Q_A$ is the heat given up in the collector–generator, and $Q_c$ is the heat given up in the condenser. $Q_{ISOS}$ denotes the heat in the isosteric heating stage, and $Q_{DES}$ is the heat in the desorption stage. $Q_{ISOS}/m_a$ is the heat gain needed to execute the isochoric process per unit mass of $CA$, while $Q_{DES}/m_a$ is the heat gain required to conduct the isobaric desorption process per unit mass of $CA$. $Q_e/m_a$ represents the balance in the evaporator per unit mass of CA. COP is the coefficient of performance, and $I_{G,min}$ is the minimum incident solar energy needed for one cycle during an operational day. $C{p}_a$ is the specific heat of the adsorbent, and $C{p}_r$ stands for the specific heat of the refrigerant. $T_{g1}$ is the unknown temperature at the beginning of desorption. $T_i$ is the initial temperature, $T_f$ is the final temperature, $T_E$ is the evaporator temperature related to $P_E$, and $T_C$ is related to $P_C$. $H_{ads}$ is the constant heat adsorption for the methanol–$CA$ working pair ($H_{ads}$ = $1400 \mathrm{k}\mathrm{J}\mathrm{/}\mathrm{k}\mathrm{g}$). L is the latent heat of vaporization of methanol. ${\eta }_c$ is the collector efficiency, and $A_C$ is the collector area.

This research starts with a fixed evaporator temperature $(T_e$ = $-5{ }^{\mathrm{\circ }}\mathrm{C})$. The model then calculates the uptake temperature $T_{g1}$, which signifies the minimum temperature required for desorption to initiate and to ensure the refrigeration cycle. This calculation employs an implicit iterative method with a minimum error-stopping criterion, as shown in Equation (9), utilizing MATLAB. This equation is nonlinear and hinges on the bivariate Dubinin–Astakhov equilibrium concentration of an adsorbent–adsorbate working pair and methanol saturation state equation [25,27]. However, as the $T_f$ temperatures decrease, the implicit method may fail to derive logical results. Consequently, an explicit method, outlined in Equation (10), is applied. Although this method provides a good approximation to the real values, its error is typically larger than that obtained using the implicit method.

$$x_i\left(T_i,P_E\left(T_E\right)\right)-x\left(T_{g1},P_c\left(T_c\right)\right)=0$$

(9)

$$T_{g1}\left(x,P\right)=\left({\left[ln\left(x_0/x\right)/D\right]}^{1/n}+B\right)/\left(A-lnP-lnk\right)$$

(10)

An additional challenge presented by the proposed model involves determining the minimum solar radiation intensity required for ice production through mass and energy balances. In addressing this challenge, the results derived from Equation (8) are contrasted with the daily, real-time radiation data at each reference location. This approach enables the establishment of the climatic conditions necessary for ice production over extended periods of analysis.

2.2. Atmospheric Conditions as a Function of El Niño and La Niña Events at Different Altitudes

This analysis is fundamental to feed the mathematical model, for which six Colombian cities located at different altitudes (masl) were selected: (1) Riohacha (11.53${}^{\circ }$ N, 72.92${}^{\circ }$ W, 3 masl); (2) Bucaramanga (7.12${}^{\circ }$ N, 73.18${}^{\circ }$ W, 959 masl); (3) Cali (3.38${}^{\circ }$ N, 76.53${}^{\circ }$ W, 1018 masl); (4) Medellín (6.22${}^{\circ }$ N, 75.59${}^{\circ }$ W, 1495 masl); (5) Bogotá (4.79${}^{\circ }$ N, 74.05${}^{\circ }$ W, 2625 masl) and (6) Tunja (5.68${}^{\circ }$ N, 72.97${}^{\circ }$ W, 2782 masl), which are identified in Figure 2.

In each city, satellite georeferencing was employed to estimate the average daily solar radiation data for a year, including the respective maximum, minimum, and average ambient temperatures. The dataset consists of continuous records spanning a year dominated by the El Niño effect, another year dominated by La Niña, and a third year with minimal influence from both El Niño and La Niña. This comprehensive analysis incorporates over 20,000 data points, ensuring a robust evaluation of the solar energy potential in each location.

To assess the predominance of these phenomena, we considered the Oceanic Niño Index (ONI), which evaluates the interplay between the atmosphere and the ocean within the El Niño-Southern Oscillation (ENSO) system. The ONI is provided by the National Oceanic and Atmospheric Administration (NOAA) [28], and their portal serves as a key resource for understanding the interannual relations of extreme climate variability, such as heavy rainfall, droughts, and storms. The ONI index indicates the intensity and type of climatic variability. Negative values below $-0.5$ correspond to the La Niña phenomenon, indicating cold periods, while positive values above $0.5$ indicate the presence of El Niño, signifying warm periods. Values between $-0.5$ and $0.5$ are considered to have no significant influence from either phenomenon and are considered typical values.

According to the ONI criteria, twelve consecutive months were identified based on the highest frequency of negative values below $0.5$, indicating the presence of the La Niña phenomenon. Additionally, twelve months were selected based on the highest frequency of positive values exceeding $0.5$, representing the occurrence of El Niño. The chosen periods, comprising twelve consecutive months each for El Niño, La Niña, and a typical year, are presented in

Table 1. Years chosen by the ONI index to collect data on solar radiation in Niño, Niña phenomena, and year without Niño/Niña influence [28].

Año	DJF	JFM	FMA	MAM	AMJ	MJJ	JJA	JAS	ASO	SON	OND	NDJ
2010						−0.6	−1.0	−1.4	−1.6	−1.7	−1.7	−1.6
2011	−1.4	−1.1	−0.8	−0.6	−0.5
2015					1.0	1.2	1.5	1.8	2.1	2.4	2.5	2.6
2016	2.5	2.2	1.7	1.0
2017	−0.3	−0.1	0.1	0.3	0.4	0.4	0.2	−0.1	−0.4	−0.7	−0.9	−1.0

. This approach ensures a comprehensive analysis of the respective climatic phenomena and establishes a solid foundation for the study.

The data presented in Table 1 for each month are formed by an average that includes the value of the previous month, reference month, and month after the reference data. For example, $JFM$ is the average data for February, which is obtained from the values of January, February, and March.

Table 1 displays the specific months selected for each phenomenon. For the La Niña phenomenon, the chosen months are from June to December 2010 and from January to May 2011. Regarding the El Niño phenomenon, the selected months are from May to December 2015 and from January to April 2016. For the year unaffected by these phenomena, all months of 2017 were considered. Meteorological data, including ambient temperature and solar radiation, were obtained from the IDEAM databases. In addition, NASA data were used to supplement the periods corresponding to each specific year of interest, as indicated by the geographical coordinates.

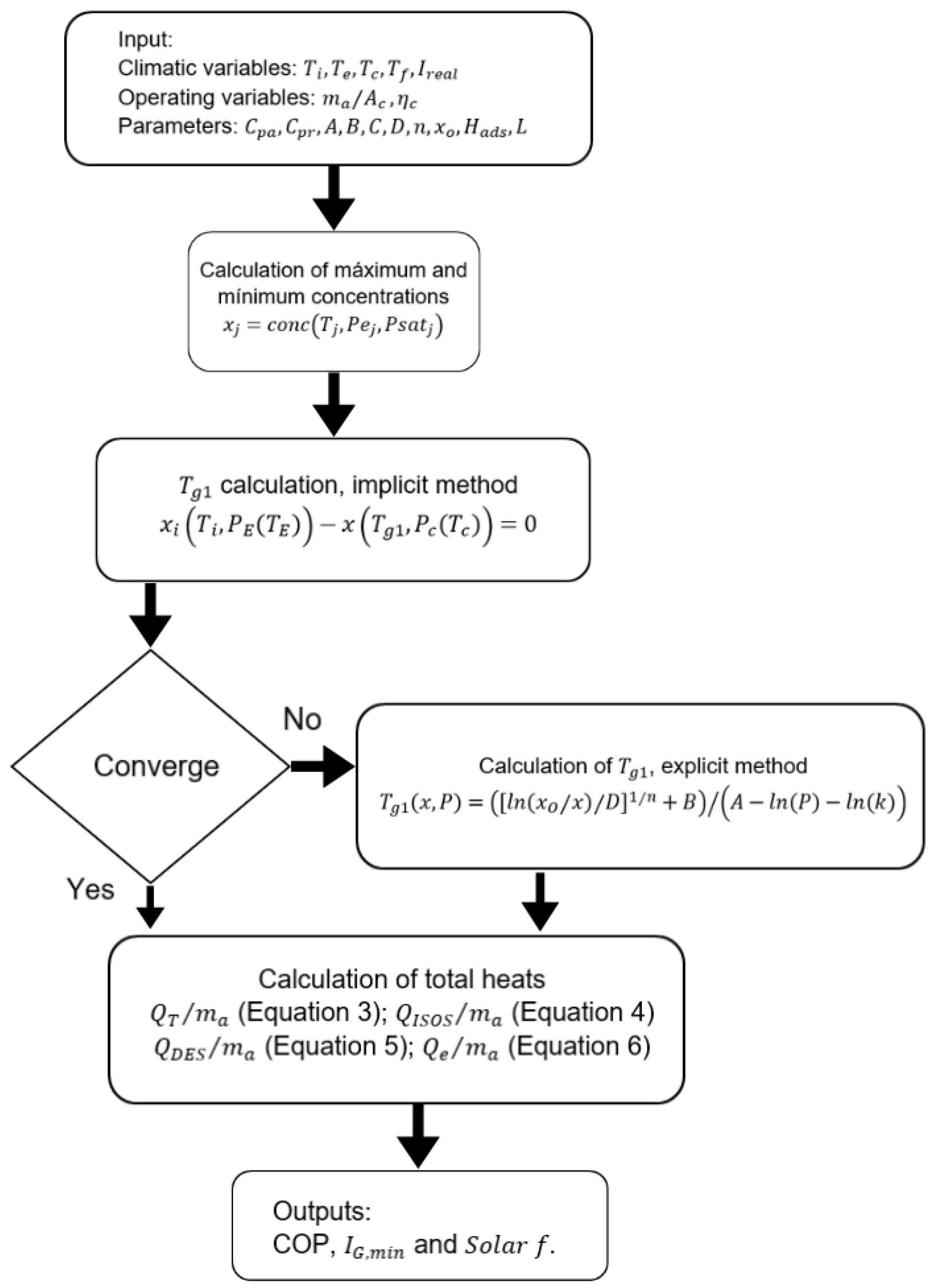
2.3. Numerical Solution

The information from the mathematical model and the climatic variables of analysis (ambient temperature and solar radiation) are integrated into the process shown in the diagram in Figure 3, following reference [25].

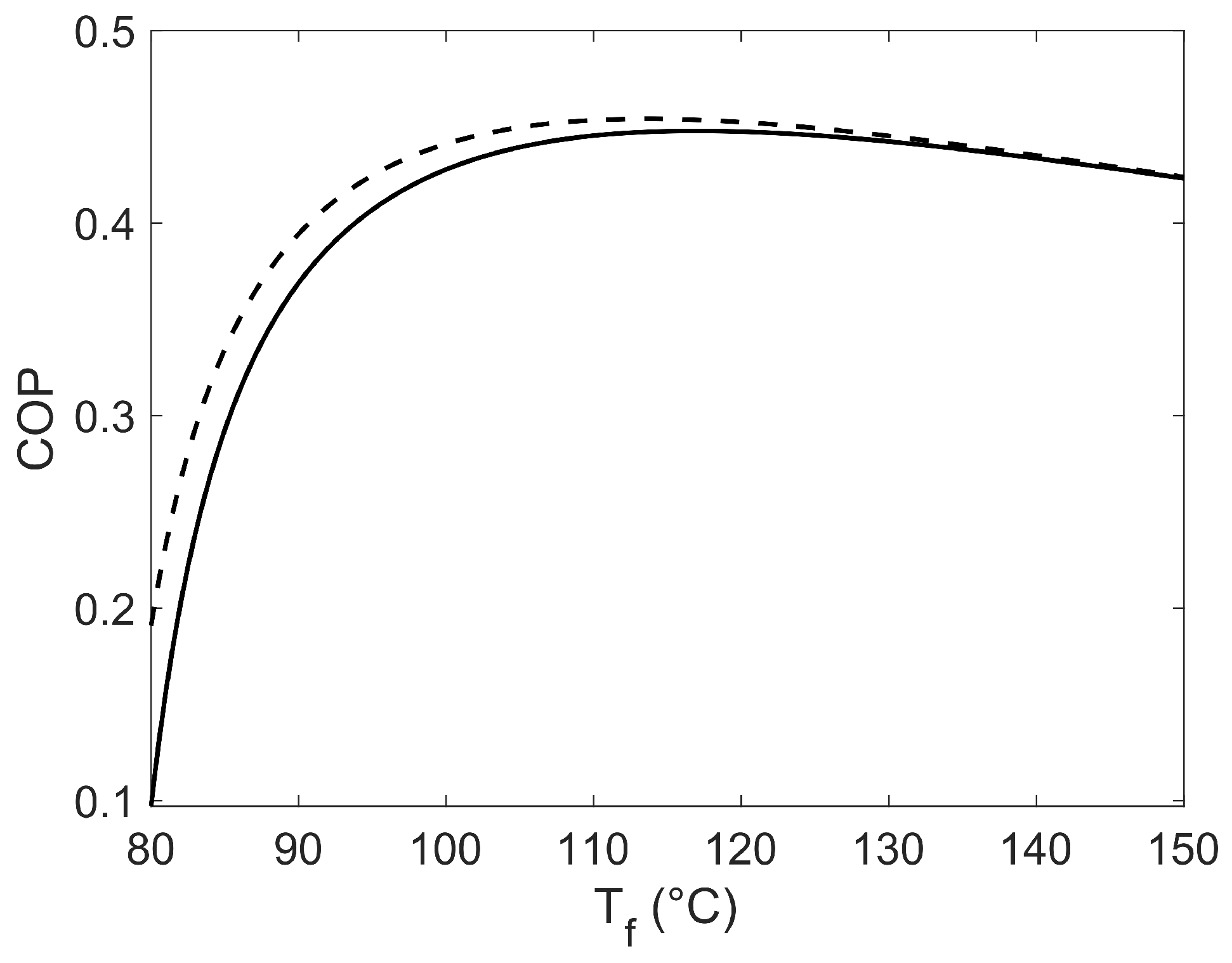
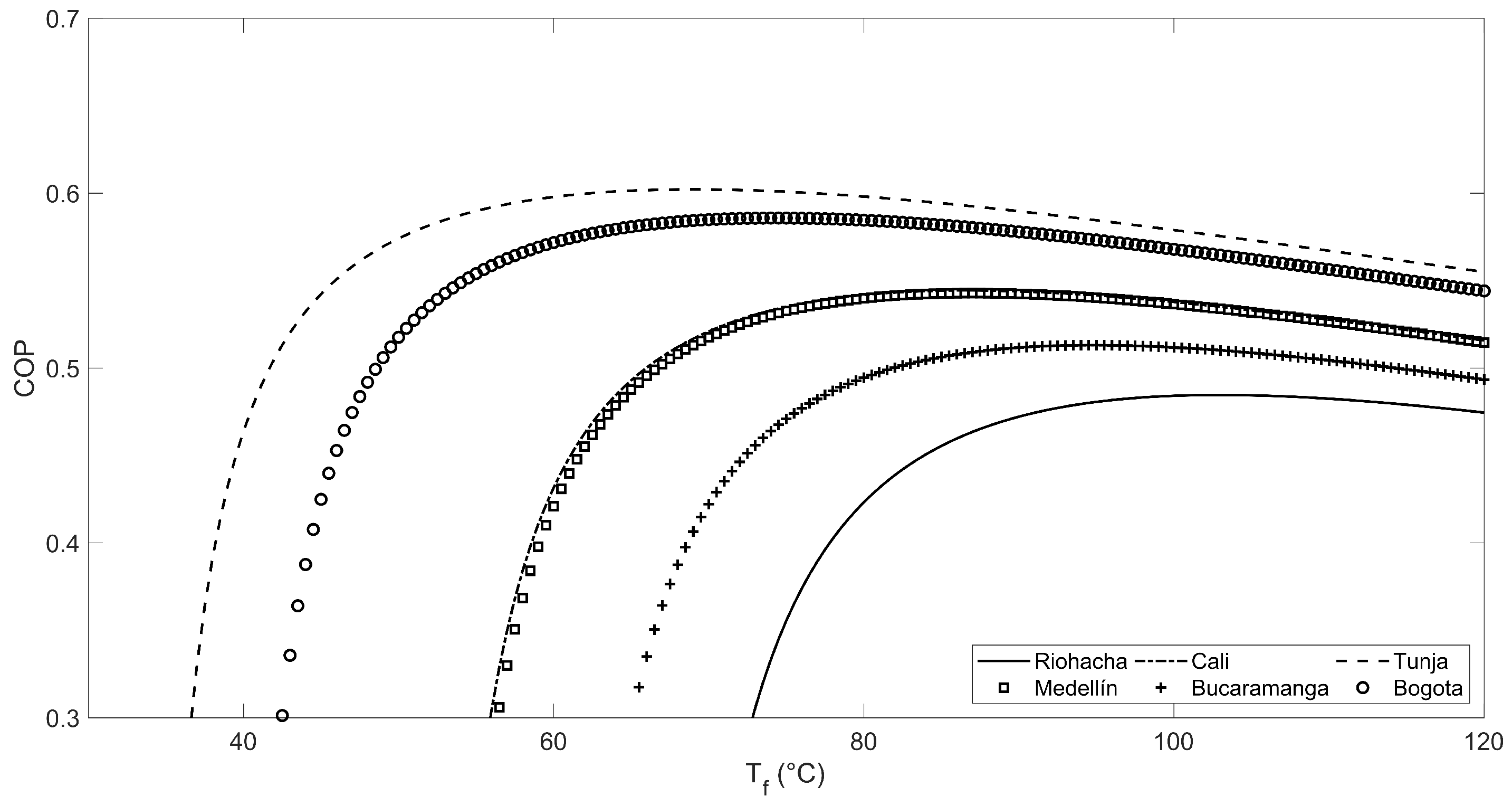
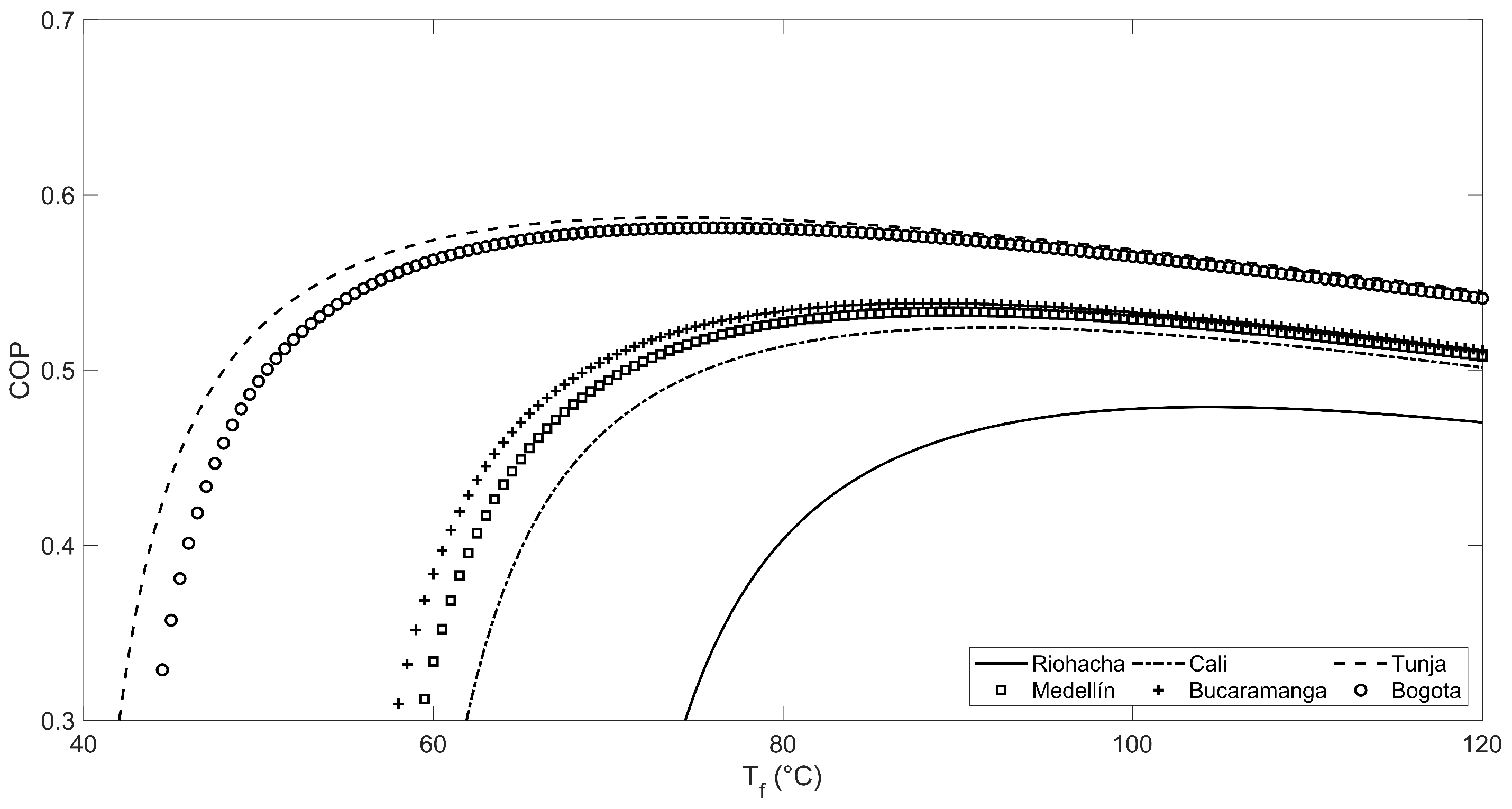
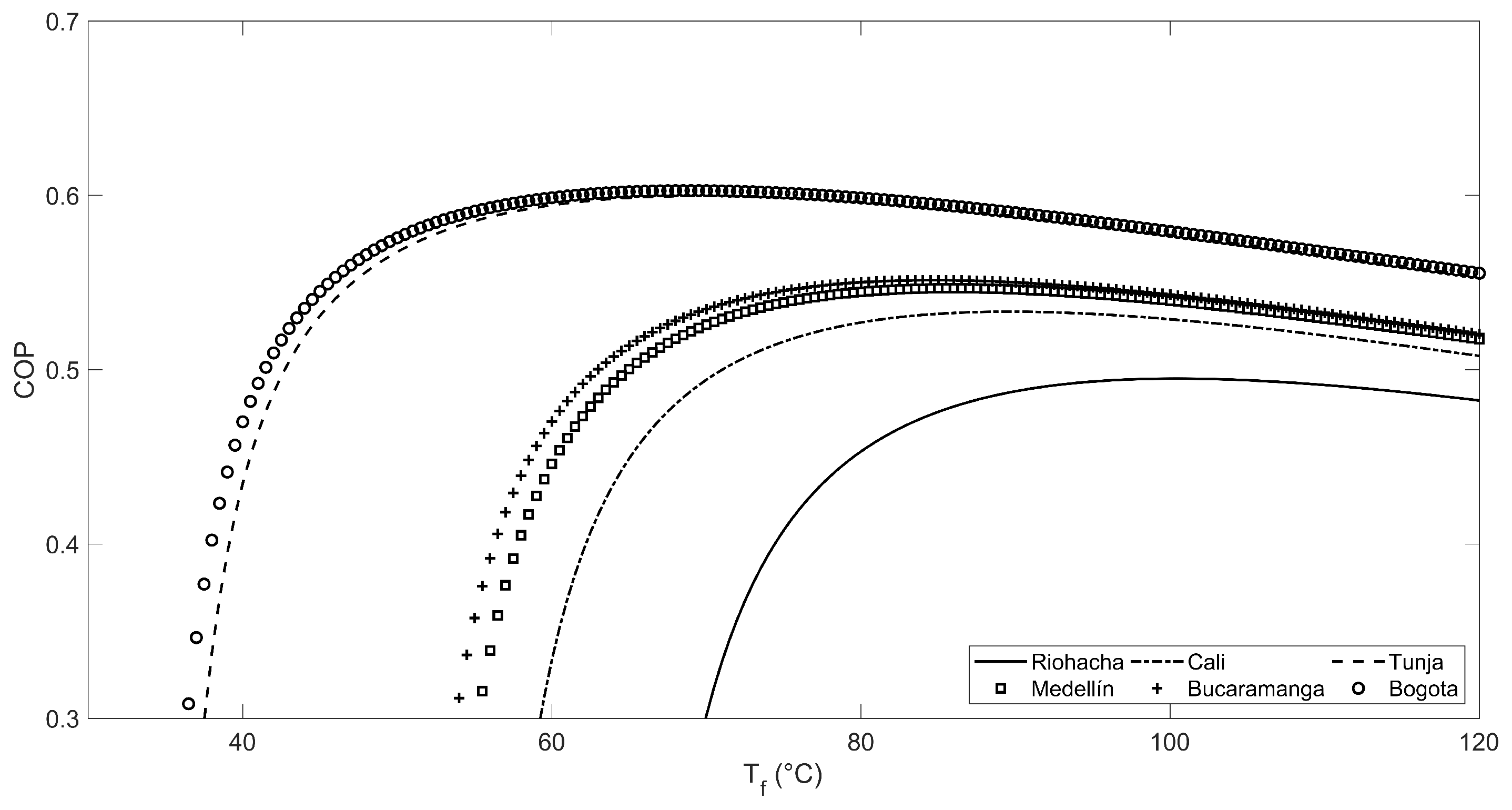
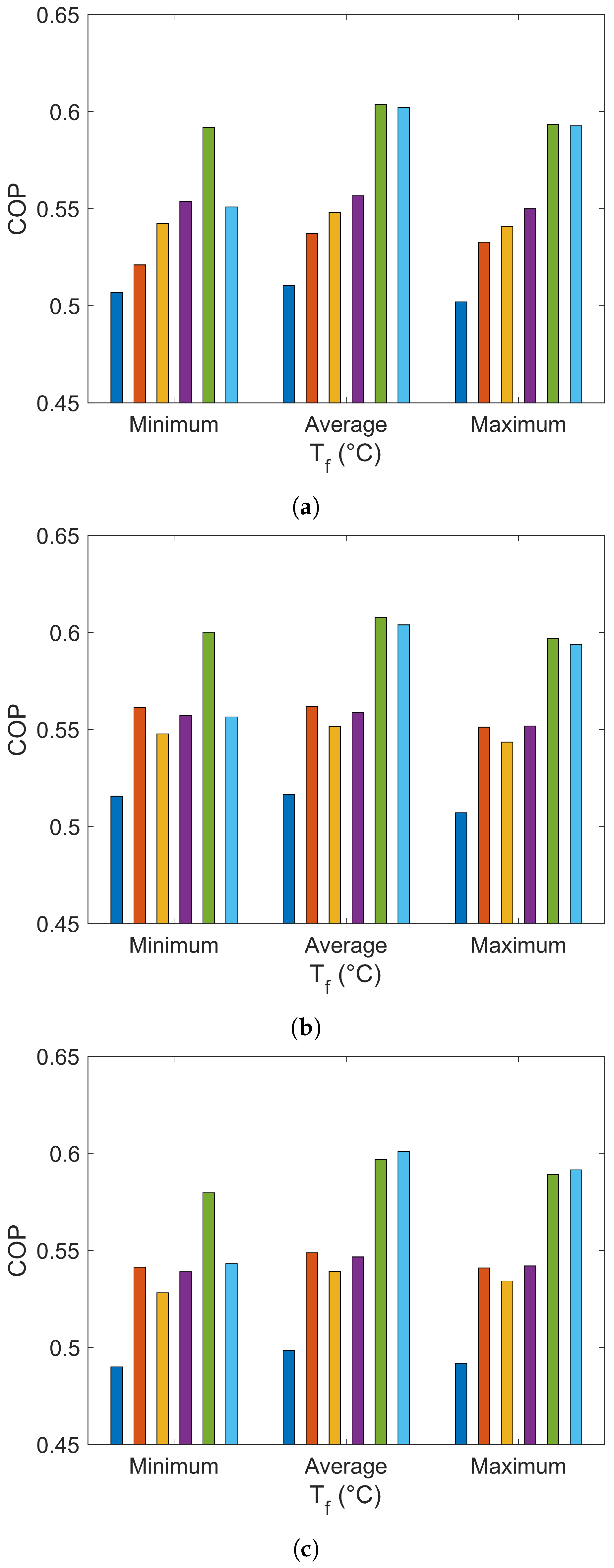
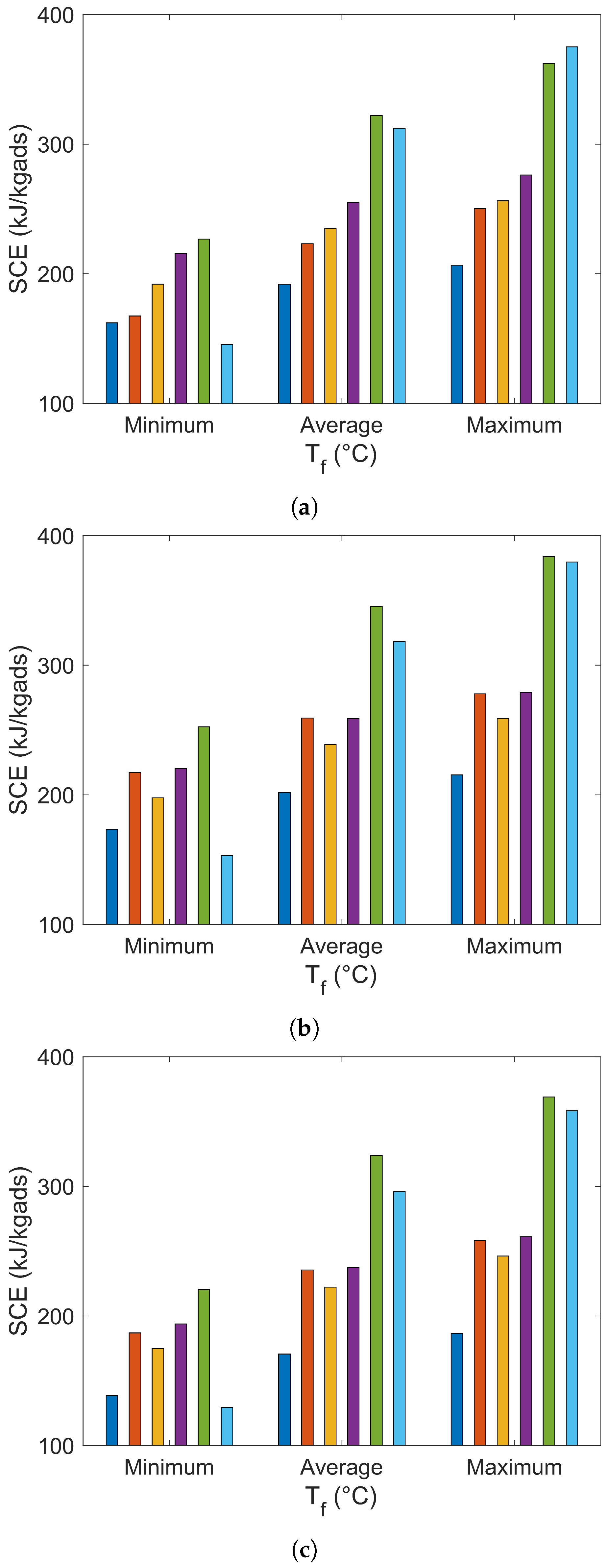
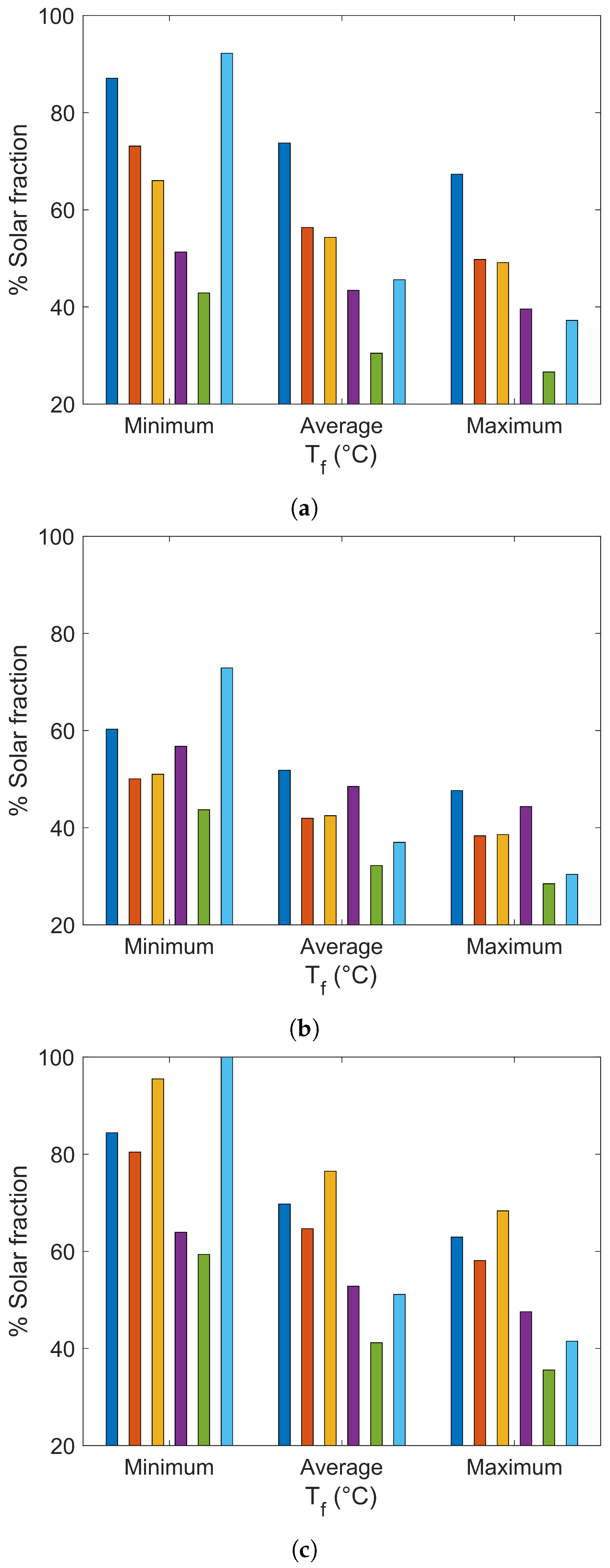
3. Results and Discussion

Coefficients of performance (COPs) were obtained by applying both the explicit and implicit convergent methods for a typical year in the city of Riohacha. When comparing these COPs, it was noted that for the lower temperatures, there is a 5% variation which decreases as temperature rises, as shown in Figure 4. This indicates that both methods can be used.

The initial temperature ($T_i$) and the condenser temperature ($T_C$) were taken from the atmospheric data and with values of $28.9{ }^{\mathrm{\circ }}\mathrm{C}$ and $38{ }^{\mathrm{\circ }}\mathrm{C}$, respectively. In addition, the evaporator temperature ($T_E$) was set at $-5{ }^{\mathrm{\circ }}\mathrm{C}$, resulting in an efficiency of the equipment of 30% and a mass ratio of the activated carbon of $20 \mathrm{k}\mathrm{g}\mathrm{/}{\mathrm{m}}^{\mathrm{2}}$. It is observed that the maximum COP can be achieved at a temperature $T_f$ of $95{ }^{\mathrm{\circ }}\mathrm{C}$, thereby transferring heat to the medium.

The approach to work with the set of almost 20,000 data points for the analysis consists of aggregating the variables reported for each phenomenon studied by calculating the monthly mean values. This organization is presented in

Table A1. Summary of the average data taken from IDEAM for each phenomenon studied.

Month/City	Phenomenon	Riohacha (3 masl)		Bucaramanga (959 masl)		Cali (1018 masl)		Medellin (1495 masl)		Bogotá (2625 masl)		Tunja (2782 masl)
		${\mathit{T}}_{\mathbf{ave}}$ ${}^{\mathrm{\circ }}$C	${\mathit{T}}_{\mathbf{ave}}$ kWh/m2/Day	${\mathit{T}}_{\mathbf{ave}}$ ${}^{\circ }$C	${\mathit{T}}_{\mathbf{ave}}$ kWh/m2/Day	${\mathit{T}}_{\mathbf{ave}}$ ${}^{\circ }$C	${\mathit{T}}_{\mathbf{ave}}$ kWh/m2/Day	${\mathit{T}}_{\mathbf{ave}}$ ${}^{\circ }$C	${\mathit{T}}_{\mathbf{ave}}$ kWh/m2/Day	${\mathit{T}}_{\mathbf{ave}}$ ${}^{\circ }$C	${\mathit{T}}_{\mathbf{ave}}$ kWh/m2/Day	${\mathit{T}}_{\mathbf{ave}}$ ${}^{\circ }$C	${\mathit{T}}_{\mathbf{ave}}$ kWh/m2/Day
January	Niño	26.9	5.0	21.8	3.5	24.4	4.5	22.5	4.9	13.1	5.9	13.5	5.1
	Niña	27.4	5.0	23.4	5.4	24.6	5.3	24.0	4.6	17.9	5.4	17.5	5.5
	Typical	26.9	4.5	26.6	4.8	23.7	4.4	22.4	4.3	14.5	4.1	14.0	4.7
February	Niño	26.8	5.4	21.9	5.0	24.2	4.0	22.8	4.8	13.7	3.5	14.1	4.4
	Niña	28.5	5.0	24.0	5.3	26.8	5.1	24.7	4.5	18.4	4.4	17.7	5.1
	Typical	27.6	5.5	26.9	5.5	24.5	4.9	23.6	5.1	14.6	4.9	13.7	5.6
March	Niño	26.8	5.5	21.5	5.2	23.8	4.2	22.3	4.9	13.6	3.8	14.4	4.0
	Niña	29.0	5.6	24.0	5.4	22.2	4.8	24.9	4.4	18.8	4.1	18.5	5.3
	Typical	27.7	5.1	26.6	4.3	24.1	4.3	22.1	3.7	14.7	3.0	15.4	4.4
April	Niño	28.0	5.6	21.8	5.2	24.0	4.0	21.9	4.4	14.5	3.4	15.6	3.8
	Niña	29.1	5.3	23.0	4.3	22.0	4.5	23.8	3.9	17.3	3.3	17.3	4.0
	Typical	29.8	5.5	26.5	5.0	24.7	4.8	22.9	4.0	15.5	3.8	14.4	4.8
May	Niño	28.5	5.2	22.1	4.8	24.6	4.2	22.7	4.4	18.2	3.7	15.6	3.5
	Niña	30.6	5.4	22.9	5.6	25.3	4.4	23.8	5.2	16.6	3.9	17.7	4.6
	Typical	30.0	5.8	26.4	4.1	24.2	4.2	22.8	4.2	15.8	3.6	14.7	4.3
June	Niño	29.4	5.5	22.3	3.0	24.2	4.1	22.7	4.9	14.0	4.0	14.9	3.9
	Niña	32.0	6.4	23.2	5.2	25.5	4.4	23.9	5.3	18.8	4.0	16.3	4.1
	Typical	30.1	6.1	24.3	4.2	24.2	4.4	23.0	4.4	18.4	3.6	14.6	3.9
July	Niño	29.1	5.6	21.6	3.2	23.8	4.1	22.2	4.6	13.7	3.9	14.9	4.0
	Niña	31.4	6.0	23.2	5.6	25.6	4.3	24.0	5.0	19.1	4.2	15.8	4.3
	Typical	30.3	6.1	25.6	4.2	24.9	5.0	23.7	4.8	18.2	4.1	14.1	3.4
August	Niño	28.4	5.4	22.1	3.1	24.5	4.4	22.9	5.0	13.2	3.6	13.8	4.5
	Niña	29.5	6.4	23.4	5.5	26.2	4.6	23.9	4.9	16.6	4.2	15.9	4.1
	Typical	29.7	6.1	27.4	4.4	24.5	5.2	23.5	4.8	18.7	4.2	13.8	4.4
September	Niño	27.6	5.1	21.6	3.1	24.0	4.1	21.8	4.6	13.7	3.9	14.4	4.1
	Niña	30.0	6.0	23.5	5.5	26.7	4.6	24.3	5.0	16.5	4.1	15.5	4.4
	Typical	29.4	5.5	27.0	4.7	17.9	5.3	23.0	4.2	19.1	4.2	13.5	4.6
October	Niño	28.1	5.0	21.7	3.8	23.9	4.2	22.4	4.7	14.0	4.0	14.8	4.3
	Niña	29.1	4.8	23.4	5.1	25.6	4.3	23.3	4.0	16.8	4.1	16.0	4.4
	Typical	28.9	5.0	26.3	4.7	24.0	4.2	22.4	3.9	17.3	3.8	14.0	4.5
November	Niño	26.8	3.8	21.2	3.6	23.2	3.4	21.6	4.2	14.1	3.4	15.1	3.6
	Niña	28.5	4.3	22.5	4.6	24.8	4.7	23.0	3.9	16.5	3.8	15.8	4.1
	Typical	28.2	4.4	27.0	4.6	17.4	4.4	22.4	3.9	17.3	3.5	14.5	4.6
December	Niño	26.7	4.1	21.0	3.0	23.4	3.6	21.9	4.2	13.4	4.1	14.4	4.2
	Niña	28.8	4.4	23.9	5.1	25.8	5.8	24.0	4.2	16.7	4.1	15.4	4.7
	Typical	28.0	4.7	26.8	5.1	17.6	4.3	22.4	4.3	16.9	3.9	13.6	5.1

, which provides an overview of the data for each city. Additionally, graphical representations can be generated for each phenomenon, considering the minimum, average, and maximum condenser temperatures $\left(T_c\right)$, and accounting for the specific environmental conditions in each city. Figure 5, Figure 6 and Figure 7 present the relationship between the coefficient of performance (COP) and the final temperatures $\left(T_f\right)$ for the average condenser temperatures associated with each phenomenon.

In the figures, it is evidenced that the maximum COP follows a pattern based on the altitude of the cities, regardless of the phenomenon being studied. In this regard, Tunja, being the highest city, exhibits the highest maximum COP, which is followed by Bogotá, Medellín, Bucaramanga, Cali, and Riohacha. In Figure 5, during a typical year, the maximum COP for Tunja is 0.55 at a final temperature ($T_f$) of $45{ }^{\mathrm{\circ }}\mathrm{C}$ with a condenser temperature ($T_C$) of $14.2{ }^{\mathrm{\circ }}\mathrm{C}$ (room temperature). For the El Niño phenomenon (Figure 6), these values are 0.50, $50{ }^{\mathrm{\circ }}\mathrm{C}$, and $6{ }^{\mathrm{\circ }}\mathrm{C}$, respectively. Similarly, for the La Niña phenomenon (Figure 7), these values are 0.55, $47{ }^{\mathrm{\circ }}\mathrm{C}$, and $14.6{ }^{\mathrm{\circ }}\mathrm{C}$, respectively. A significant reduction in COP is observed when comparing these values with those obtained for the city of Riohacha, along with a considerable increase in $T_f$ at an ambient or condenser temperature of approximately $29{ }^{\mathrm{\circ }}\mathrm{C}$.

In Figure 6 (El Niño) and Figure 7 (La Niña), it is observed that the COP does not correspond to the altitude of each city. For instance, during El Niño, the COP of Bucaramanga is higher than that of Medellin and Cali, even though Bucaramanga is at a lower altitude. Similar observations can be made for the COP during the La Niña phenomenon. These analyses were conducted using the explicit method, which presented a 5% deviation of the data initially, which was possibly due to the effects of El Niño and La Niña phenomena.

In general, the figures demonstrate that as altitude increases, the performance of an adsorption cooling system can be more effectively utilized due to lower ambient temperatures interacting with the condenser despite the decrease in radiation. However, in cities with high radiation at sea level, such as Riohacha, high tropical temperatures pose challenges for efficient heat exchange in cooling. Therefore, it is essential to consider adapting the environment to improve yields or exploring alternative approaches. However, relying solely on global monthly averages for each annual phenomenon is insufficient to define the detailed behavior of solar potential in solar adsorption cooling. Consequently, the maximum, average, and minimum temperatures of monthly atmospheric conditions are considered for the selected cities, and the COP, solar fraction, and cooling capacity are determined for each scenario.

Figure 8 presents a comparison of different environmental temperatures (minimum, average, and maximum) under extreme conditions, including the month of March in a typical year, the month of November during a La Niña year, and the month of December during an El Niño year. Once again, the lower performance in Riohacha is consistently observed, despite higher radiation, due to cooling challenges resulting from the reasons mentioned above.

In Figure 8, Figure 9 and Figure 10, the dark blue bar represents Riohacha, the orange bar represents Bucaramanga, the yellow bar represents Cali, the purple bar represents Medellin, the green bar represents Bogota and the light blue bar represents Tunja.

On the other hand, the COP during the La Niña phenomenon is higher, particularly for average or minimum temperatures. This is due to the rainy climate during these seasons, resulting in lower environmental temperatures. However, this effect is not noticeable in the cities of Tunja and Bogotá, as they already experience low temperatures regardless of the phenomenon.

The Specific Cooling Energy (SCE) exhibits a similar behavior to COP with higher values during the La Niña phenomenon. However, within a specific phenomenon, SCE is higher for higher final temperatures ($T_f$), which is contrary to the behavior of COP, as shown in Figure 9. There is a partially direct relationship between COP and SCE. Therefore, the ambient temperature, as well as the frequency of drought or rain, are not the sole determinants of SCE values. Radiation also plays a crucial role, making it an important indicator, but it is not sufficient to determine if temperatures close to $-5{ }^{\mathrm{\circ }}$ in the evaporator for ice production can be achieved. Hence, an additional complementary criterion called the Percentage of Solar Fraction (PFS) is needed. PFS can be defined as the relationship between the “real” radiation reported by IDEAM and NASA in each analyzed city and the theoretical radiation obtained from the model $(I_{\mathrm{real}}/I_{\min })$.

Figure 10 presents the PFS for the studied phenomena at minimum, average, and maximum temperatures. It demonstrates that Riohacha has the highest PFS values, but high PFS values persist at low temperatures for all cities regardless of the presence of rainy or drought phenomena. During the El Niño phenomenon, the PFS values are high for Riohacha, Cali, and Tunja at low temperatures, indicating that solar radiation can be more effectively utilized during periods of drought in cool environments. This is why the PFS value in Riohacha is lower than in the other two cities mentioned for this particular case.

To complement the analysis and discussion,

Table 2. Summary of the output data for each variable studied.

City	Final Temperatures ${\mathit{T}}_{\mathit{f}}$ (${}^{\circ }$C)	La Niña Phenomenon				El Niño Phenomenon				Typical Year
		COP	SCE (kJ/kgads)	Solar f.	Ice Days	COP	SCE (kJ/kgads)	Solar f.	Ice Days	COP	SCE (kJ/kgads)	Solar f.	Ice Days
Riohacha (3 masl)	$T_{min}$ = 89.34	0.51	167.09	0.86	91	0.49	140.34	1.03	174	0.49	147.52	1.00	165
	$T_{ave}$ = 102.11	0.51	197.13	0.73	19	0.50	173.53	0.84	97	0.50	179.59	0.82	85
	$T_{max}$ = 114.88	0.50	211.87	0.67	0	0.46	201.50	0.67	0	0.46	206.28	0.65	0
Bucaramanga (959 masl)	$T_{min}$ = 75.32	0.56	211.96	0.55	0	0.54	182.44	0.83	65	0.52	173.11	0.77	35
	$T_{ave}$ = 89.06	0.56	254.92	0.46	0	0.55	231.85	0.67	0	0.54	228.33	0.59	0
	$T_{max}$ = 102.79	0.55	274.25	0.42	0	0.54	256.11	0.59	0	0.53	255.22	0.53	0
Cali (1018 masl)	$T_{min}$ = 76.73	0.53	180.88	0.65	3	0.53	172.77	0.79	55	0.55	215.94	0.66	10
	$T_{ave}$ = 89.44	0.54	226.09	0.53	1	0.54	220.57	0.63	2	0.56	256.09	0.55	0
	$T_{max}$ = 102.16	0.54	249.64	0.47	0	0.53	245.91	0.56	0	0.55	275.60	0.50	0
Medellín (1495 masl)	$T_{min}$ = 76.52	0.55	211.70	0.66	4	0.54	191.70	0.70	9	0.55	207.42	0.62	0
	$T_{ave}$ = 88.44	0.56	251.57	0.55	0	0.55	235.19	0.58	1	0.55	248.47	0.52	0
	$T_{max}$ = 100.37	0.55	272.87	0.50	0	0.54	258.96	0.52	0	0.55	270.57	0.47	0
Bogotá (2625 masl)	$T_{min}$ = 54.26	0.60	253.79	0.51	3	0.57	191.62	0.68	25	0.57	184.54	0.67	26
	$T_{ave}$ = 71.39	0.61	346.64	0.37	0	0.59	298.44	0.45	0	0.59	288.38	0.43	0
	$T_{max}$ = 88.51	0.60	385.05	0.33	0	0.58	346.05	0.38	0	0.59	333.99	0.37	0
Tunja (2782 masl)	$T_{min}$= 44.43	0.56	170.11	0.76	55	0.52	117.63	1.14	214	0.57	187.85	0.78	59
	$T_{ave}$ = 66.54	0.61	332.75	0.41	0	0.60	290.24	0.50	0	0.61	348.23	0.43	0
	$T_{max}$ = 88.66	0.60	392.68	0.34	0	0.59	357.69	0.40	0	0.60	406.64	0.36	0

summarizes the output data for each studied variable, including the number of days when temperatures below $0{ }^{\mathrm{\circ }}\mathrm{C}$ are reached (ice production days). The table shows that based on the conditions of the adsorption–cooling model, Riohacha can produce ice independently of the presented phenomena despite the high ambient temperatures and the relatively low COP values obtained. Similarly, Tunja can also produce ice independently of the phenomena, even though it has lower radiation values compared to Riohacha. The favorable factors in Tunja include its low ambient temperatures and periods of drought.

4. Conclusions

The mathematical model utilized for simulating the adsorption solar cooling system effectively evaluated the system’s performance in terms of the COP, the minimum solar radiation required for ice production, and the cooling capacity. Nevertheless, it is important to note that the COP alone is not the primary factor determining ice production. For example, in cities such as Riohacha, where the maximum system temperatures remain below $89.34{ }^{\mathrm{\circ }}\mathrm{C}$, the system can produce ice for 91 days, whereas cities such as Tunja, despite having a higher COP, can produce ice for 55 days at temperatures below $44.43{ }^{\mathrm{\circ }}\mathrm{C}$. Furthermore, the results indicate that the system is well-suited for ice production in cities located at sea level. However, in cities with altitudes higher than 900 masl, the system can be utilized as a heat pump for heating purposes. Lastly, in intermediate altitude cities such as Bucaramanga, Medellin, and Cali, the influence of El Niño and La Niña phenomena on the COP is notable.