Study on Mushy Zone Coefficient in Solidification Heat Transfer Mathematical Model of Thin Slab with High Casting Speed

Abstract

When the casting speed of the thin slab continuous caster is increased, the ratios of the solid and liquid phases in the solidification front of the molten steel in the mold change, which affects the thickness of the solidified shell. In order to accurately calculate the thickness of the solidified shell and determine the value range of the mushy zone coefficient suitable for the mathematical model of solidification heat transfer at high casting speed, this paper established the solidification heat transfer mathematical model in thin slab funnel mold, and the influence of different mushy zone coefficients on the accuracy of solidification heat transfer mathematical model was analyzed and compared with the actual solidified shell thickness. The results showed that, when the casting speed was increased to 4~6 m/min and the coefficient of the mush zone coefficient was 3 × 10⁸~9 × 10⁸ kg/(m³⋅s), the thickness of solidified shell calculated by the solidification heat transfer model was in good agreement with that measured in practice. The research in this paper provides an important reference for the establishment of the solidification heat transfer mathematical model at high casting speed in the future.

1. Introduction

In the process of continuous casting, the flow condition of molten steel in the mold, the temperature distribution and the growth of the initial solidification shell all have great influence on the quality of the slab. With the improvement of the computer computing performance and the development of commercial software, numerical simulation has become an important means to study the transmission behavior of the continuous casting process, in which finite volume software Fluent is widely used in the numerical simulation of physical phenomena related to molten steel flow in the continuous casting process.

The solidification process of molten steel is carried out in a temperature range (liquidus temperature to solidus temperature), which is macroscopically manifested as a solid–liquid two-phase zone—that is, a mushy zone [1,2]. The forming slab generally has a surface chill layer, a central equiaxed crystal region and a middle columnar crystal region. It can be seen that, in the solidification process, the mushy region consists of columnar crystals or (and) equiaxed crystals and a liquid phase group. Among them, some columnar crystals are interrupted by the flowing molten steel and move with the molten steel; the rest of the columnar crystals move with the solidified shell and grow forward, and the equiaxed crystals are deposited with the flow of the liquid steel or downward. Columnar crystals and equiaxed crystals can hinder the flow of molten steel in the mushy zone and then affect the heat transfer and solidification process of molten steel. Two methods are generally used to deal with the flow of molten steel in the mushy zone, namely the variable viscosity method and the Darcy source term method. Because the viscosity data of the mushy zone are not easy to obtain when using the variable viscosity method, the Darcy source term method is widely used. The dendrites in the mushy zone are regarded as porous media that move along the solidification front and are filled with the liquid phase and a fraction of the solid phase changes continuously by the Darcy source term method [3,4,5,6,7]. Among them, permeability is an important parameter to reflect the transmission performance of porous media, which can reflect the flow characteristics of the liquid phase with a certain momentum in porous media, mainly affected by the structural characteristics and physical properties of porous media [8,9]. Pfeiler et al. [10,11] calculated the permeability using the Blake–Kozeny law and considered that the permeability was a function of the primary dendrite spacing. The expression given by Beckermann et al. [12,13] also believed that the permeability is related to the primary dendrite spacing. However, most scholars [14,15,16] use the Carman–Kozeny equation to deal with permeability and regard permeability as a function of secondary dendrite spacing. The mushy zone coefficient (A_mush) is a physical quantity related to permeability. For general fluid software such as Fluent, Open FOAM, COMSOL, etc., in the process of establishing the solidification heat transfer model, the A_mush introduces a damping term into the porous medium model. The A_mush has a great influence on the numerical calculation of the flow and solidification behavior of molten steel, but the correct expression of the A_mush is rarely given in the literature. Most scholars ignore the effect of the mushy zone coefficient on the solidification heat transfer model and usually use the default value of 1 × 10⁵ kg/(m³⋅s) as the A_mush, resulting in the calculation results being inconsistent with reality [17,18]. Some scholars, Refs. [19,20,21], use a smaller A_mush, resulting in the calculation results of overheating dissipation too fast, the liquid surface is too cold and so on. Trindade et al. [22,23] adopted the default value of Fluent 1 × 10⁵ kg/(m³⋅s) as the A_mush, resulting in the liquid phase ratio of the steel at the center of the mold outlet being lower than 1. Hietanen et al. [24,25] studied the effect of A_mush at 1 × 10³~1 × 10⁷ kg/(m³⋅s) on the solidification of molten steel, and the results showed that, when the A_mush value was low, the temperature of molten steel dropped too fast, which was inconsistent with reality. When the A_mush was 1 × 10⁷ kg/(m³⋅s), the calculated results were more realistic. However, when the A_mush is increased to 1.5 × 10⁷ kg/(m³⋅s), the calculation is difficult to converge. Wang Qiangqiang [26] pointed out that, when the A_mush was 1 × 10⁵ kg/(m³⋅s), the molten steel temperature in the mold was mostly lower than the liquidus temperature, and there was almost no formed solidified shell near the impact zone of the narrow surface flow. It can be seen that it is very important to select the appropriate A_mush for the understanding and grasp of the flow and solidification phenomenon of molten steel in the mold.

At present, with the increasing of the casting speed of the thin slab continuous casting caster, the range of A_mush values satisfying the mathematical model of solidification heat transfer at high casting speed is worth discussing. Therefore, this study only considers the scope of application of A_mush in the solidification process of thin slab continuous casting with high casting speed and focuses on studying the temperature field of molten steel in the mold and the law of solidified shell growth. Moreover, the thickness of the solidified shell is compared with that calculated by numerical simulation through actual measurement. The value range of A_mush in the heat transfer solidification model with high casting speed is determined, which provides a theoretical basis and reference for industrial production.

2. Experiment and Simulation

2.1. Basic Assumptions

Based on the complex metallurgical physical phenomenon in the thin slab continuous casting mold, combined with the characteristics of the thin slab continuous casting process, the following basic assumptions are made about the flow of molten steel and solidification heat transfer in the funnel mold to simplify the calculation process [27,28]:

(1)

The flow process of molten steel is a viscous incompressible fluid, and the effects of the phase change, vibration, protective slag and solidification shrinkage are not considered.

(2)

The effects of the fluctuation of the mold meniscus, taper, phase transformation of Fe-C alloy, solidified shell shrinkage and vibration on solidification heat transfer are ignored.

(3)

The continuous casting process is regarded as a steady state, and the turbulent effect of molten steel is simulated by the low Reynolds number standard k-ε model.

(4)

The mushy zone is regarded as a porous medium, and the flow in the mushy zone obeys Darcy’s law.

(5)

The movement speed of the solidified shell is consistent with the casting speed.

2.2. Governing Equation

In this part, the enthalpy–porous medium method is used to deal with the flow, heat transfer and solidification of molten steel in a funnel mold. The differential equation for heat transfer control is shown in (1).

$$\rho C_P\frac{dT}{dt}+\nabla ·\left(\rho \overrightarrow{v}H\right)=\nabla ·\left(\lambda \nabla T\right)+S_h$$

(1)

Among them,

$$H=h_{ref}+{\int }_{T_{ref}}^T{C}_{p}dT+\beta L_N$$

(2)

Porosity is equal to the liquid phase volume fraction β, as shown in (3).

$$\beta =\left\{\begin{array}{c}0(T<T_s)\\ \frac{T-T_s}{T_l-T_s}(T<T_s)\\ 1(T>T_l)\end{array}\right.$$

(3)

Formula: $T_l$ is the liquidus temperature, K; $T_s$ is the solidus temperature, K; $S_h$ is the heat source term, J/(m³⋅s); $C_p$ is the specific heat capacity, J/(kg$·$K); $L_N$ is the latent heat of the solidification, J/kg; the reference enthalpy is h_ref with respect to the T_ref; H is the total enthalpy of the system, J; $\beta$ is the liquid phase volume fraction.

The liquidus temperature T_L and solidus temperature T_S of molten steel are calculated by the empirical Formulas (4) and (5).

T_L = 1539 − 70w[%C] + 8w[%Si] + 5w[%Mn] + 30w[%P] − 25w[%S] + 4w[%Ni] − 1.5w[%Gr]

(4)

T_s = 1536 − 415.3w[%C] − 12.3w[%Si] − 6.8w[%Mn] − 124.5w[%P] − 183.9w[%S] − 4.3w[%Ni] − 1.4w[%Gr] − 4.1w[%Al]

(5)

Formula: w is the mass fraction, %.

The basic principle of the enthalpy–porous medium method is to regard the metal solid–liquid two-phase region as a porous medium and to characterize the proportion of the liquid phase in the unit by calculating the temperature of each unit. The sum of the proportion of the liquid phase in the two phases is between 0 and 1, and the porosity is different in each cell, so the fluid resistance settings are different [29].

The momentum and turbulent kinetic energy lost during the solidification of the fluid will be added to the momentum and turbulence equations in the form of source terms.

The source term to be added to the momentum equation is shown in Equation (6).

$$S_m=-\frac{{\left(1-\beta \right)}^2}{\left({\beta }^3+\epsilon \right)}{\mathrm{A}}_{\mathrm{m}\mathrm{u}\mathrm{s}\mathrm{h}}(\overrightarrow{u}-\overrightarrow{u_p})$$

(6)

The source term to be added in the turbulence equation is shown in Equation (7).

$${\mathrm{S}}_{\mathrm{q}}=-\frac{{\left(1-\beta \right)}^2}{\left({\beta }^3+\mathsf{\epsilon }\right)}{\mathrm{A}}_{\mathrm{m}\mathrm{u}\mathrm{s}\mathrm{h}}(\overrightarrow{u}-\overrightarrow{u_p})$$

(7)

Formula: $\overrightarrow{u_p}$ is the casting speed, m/s; ${\mathrm{A}}_{\mathrm{m}\mathrm{u}\mathrm{s}\mathrm{h}}$is the mushy zone coefficient, kg/(m³⋅s).

The size of the A_mush will affect the flow in the two-phase region. To prevent the divisor from being 0, set the ε to 0.001.

2.3. Boundary Conditions and Physical Parameters

This section studies the solidification heat transfer process of molten steel in the mold. The main process parameters are as follows: grade of the steel is SS400, its main component is 0.18% ≤ C ≤ 0.20%, S ≤ 0.005% and P ≤ 0.018%, with a section (width × thickness) of 1520 × 90 mm². Other assumptions are as follows:

(1)

The superheat of molten steel is 20 K, and the inlet temperature of molten steel is 1823 K, and it is kept constant.

(2)

Due to the good heat preservation effect of the liquid surface mold slag, the free liquid surface is set as the adiabatic condition, and the submerged entry nozzle (SEN) wall is also set as the adiabatic wall.

(3)

The temperature gradient perpendicular to the symmetric plane is zero.

(4)

The moving speed of a narrow face and wide face is consistent with the casting speed, which is given by Patch. The boundary heat flux of the mold area is given according to the real-time monitoring data of the actual production computer; that is, the boundary condition of the mold is defined by the second type of boundary condition of heat transfer.

The heat transfer and solidification of molten steel are simulated by the commercial software Fluent. The initial inlet velocity of the model was calculated according to the inner diameter of the SEN (80 mm), the casting speed and the size of the funnel mold. The numerical calculation method is used with the standard K-ε turbulence model, opening the energy equation and calculating in combination with the solidification and melting model. The superheat and specific heat of molten steel are added through the operation interface settings, and the heat flow is applied through the user-defined function. The hydrothermal physical properties of molten steel used in the simulation are shown in

Table 1. Related parameters for the solidification heat transfer model.

Thermophysical Property Parameters	Value
Molten steel density	7020 (kg/m3)
Molten steel viscosity	0.0064 (Pa⋅s)
Casting speed	(4, 5, 6) m/min
Initial value of velocity (casting speed: (4, 5, 6) m/min)	(1.82, 2.27, 2.72) m/s
Turbulent kinetic energy (casting speed: (4, 5, 6) m/min)	(6.32, 9.31, 1.28) m2/s2
Turbulent dissipation rate (casting speed: (4, 5, 6) m/min)	1.48, 2.63, 4.24
Superheat of molten steel	20 K
Solidus temperature (TS)	1763 K
Liquidus temperature (TL)	1803 K
Specific Heat Capacity (Cp)	680 J/(kg$·$K)
Latent heat of solidification (LN)	270,000 J/kg
Wide surface heat flux (${\overline{q}}_w:$4 m/min, 5 m/min, 6 m/min)	(2.0, 2.1, 2.2) × 106 W/m2
Narrow surface heat flux (${\overline{q}}_n$: 4 m/min, 5 m/min, 6 m/min)	(1.8, 1.9, 2.0) × 106 W/m2
Specific heat capacity (CW)	4.2 × 10³ J/(kg$·$K)

[30]. It should be noted that, since the two-phase region is approximately treated as a porous medium, the heat transfer in the two-phase region can be approximately treated as the heat transfer in a porous medium.

2.4. Grid and Computing Domain

The three-dimensional (3D) geometric model of two-phase flow 1/2 combined with a funnel mold and the SEN is shown in Figure 1. The fluid domain is molten steel.

The MESH module in ANSYS software is used to mesh the 3D geometric model of SEN and the funnel mold. Due to the complexity of the structure of the SEN and the funnel mold, the model adopts hexahedral nonstructural mesh division. In order to consider the accuracy of the calculation results and the stability of the calculation process, the mesh encryption process was carried out at the molten steel surface of the fluid domain in the mold, and the total number of the mesh was about 1.4 million. The reflux at the outlet of the mold seriously affects the calculation accuracy and convergence. After repeated trial and error, the length of the calculation domain of the mold was determined to be 2200 mm. The local grid division is shown in Figure 2.

2.5. Numerical Methods

Considering that there are many coupling models, the residual curve is prone to oscillations and difficult to converge, so the Couple algorithm is used for transient calculation, where the time step gradually increases from 0.001 s to 0.005 s. The momentum equation adopts the second-order upwind discrete scheme. Convergence is considered when the convergence standard is set as ≤1.0 × 10⁻⁵, and the ratio between the difference of inlet and outlet flow and the value of inlet flow is ≤1%.

2.6. Test Scheme

The expression of A_mush is shown in Equation (8).

$$A_{mush}=\frac{u_l}{K}$$

(8)

Formula: K is the permeability; $u_l$ is the laminar viscosity, Pa·s.

In the solidification process of molten steel, many scholars and experts have obtained different permeability expressions through experiments. The expression given by Beckermann shows that the permeability is related to the primary dendrite spacing, as shown in Equation (9).

$$K=6\times {10}^{-4}{\lambda }_1^2\frac{{\beta }^3}{{(1-\beta )}^2}$$

(9)

Formula: λ₁ is the primary dendrite spacing size, m.

Figure 3 shows the measured relationship between the primary dendrite spacing of a continuous casting slab and the thickness of the slab. When β = 0.3, the variation rule of A_mush with the thickness of the slab can be obtained. From the surface of the slab to the thickness center, A_mush gradually decreases from 3.1 × 10⁸ kg/(m³⋅s) to 1.7 × 10⁸ kg/(m³⋅s).

Previous studies have found that permeability is closely related to the secondary dendrite spacing and solidification state of a continuous casting slab, as shown in Equation (10).

$$K=\frac{{\lambda }_2^2{u}_l{\beta }^3}{180{\left(1-\beta \right)}^2}$$

(10)

Formula: λ₂ is the secondary dendrite spacing, m.

Due to the selective crystallization in the solidification process, some components are enriched in the liquid phase, which affects the liquidus temperature. Therefore, temperature and solute redistribution need to be considered in order to accurately predict the solidification process, and permeability is an important parameter for accurately predicting tissue properties [31]. In order to make the calculation results of the solidification heat transfer model of thin slabs with high casting speed more accurate, based on previous studies, this paper set six groups of parameters for the A_mush value in the solidification heat transfer model of thin slabs with high casting speed, as shown in

Table 2. A_mush value ranges.

Number	Amush (kg/(${\mathbf{m}}^3·$s))
A	1 × 105
B	1 × 107
C	1 × 108
D	3 × 108
E	6 × 108
F	9 × 108

. The influence of the A_mush value on the solidification heat transfer model was quantitatively studied. The paper provides a reference for the coefficient A_mush of the mushy zone to establish the solidification heat transfer model of thin slabs with high casting speed in the future.

3. Results and Discussion

3.1. Description of the Effect of A_mush on Heat Transfer and Solidification of Molten Steel

As can be seen from

Table 3. Picture of the solid- and liquid-phase distribution in the middle surface of the funnel mold thickness. Unit: kg/(m³⋅s).

${\mathrm{A}}_{\mathrm{m}\mathrm{u}\mathrm{s}\mathrm{h}}$	A: 1 × 105	B: 1 × 107	C: 1 × 108
Picture of solid- and liquid-phase distribution
${\mathrm{A}}_{\mathrm{m}\mathrm{u}\mathrm{s}\mathrm{h}}$	D: 3 × 108	E: 6 × 108	F: 9 × 108
Picture of solid and liquid phase distribution

, when the A_mush is set to a smaller value of 1 × 10⁵ kg/(m³⋅s), the liquid-phase fraction of the molten steel near the liquid level at the SEN outlet is about 0.8, and between the solidification front of the narrow surface of the mold and the molten steel, blue bars are obviously visible from the mold liquid level to the SEN outlet, indicating that the mushy zone is large and there is almost no formed solidified shell on the narrow face.

When the A_mush is 1 × 10⁷ kg/(m³⋅s), a large part of the region with a low liquid fraction near the liquid surface of the mold and SEN outlet still exists, but the solidified shell thickness gradually increases from below the meniscus, and the solidified shell also begins to solidify on the impact path of the flow stream, but the mushy zone is still obvious. When the A_mush is 1 × 10⁸ kg/(m³⋅s), the simulation results are similar to those when A_mush is 1 × 10⁷ kg/(m³⋅s), but the mushy zone is still clearly visible in the lower part. When the A_mush is ≥3 × 10⁸ kg/(m³⋅s), the lower liquid fraction region disappears, but when the A_mush is 3 × 10⁸ kg/(m³⋅s), the solidified shell thickness is not obvious in the upper part of the mold, and the solidified shell formation is thin, but the mushy zone is significantly reduced. When the A_mush is 9 × 10⁸ kg/(m³⋅s), the thickness of the solidified shell starts from the liquid side down, and the thickness increases obviously. In order to further determine the numerical range of the A_mush, the numerical simulation results were compared with the actual measurement of solidified shell thickness, and the value of the A_mush was determined.

3.2. A_mush Parameter Determination and Heat Transfer Solidification Model

3.2.1. Election of A_mush Parameters

At present, there are three methods to determine the thickness of a solidified shell: namely, the empirical method, the heat balance method and the test method. Due to the restriction conditions of the empirical method and heat balance method, such as open casting, protective casting, molten steel composition, liquidus temperature and solid-phase temperature, they have great influence on the thickness of a solidified shell. At present, the test determination method should be widely used, such as “punching and draining liquid method”, “nail method”, “trace method” and other methods, but these methods are difficult to measure, and the measurement accuracy is relatively low. In recent years, the method of measuring solidified shell thickness using the test method has developed rapidly, and the method is simple and has high precision. Therefore, this part uses the test method to measure the thickness of the solidified shell—that is, using the solidified shell that is leaked in the production process, cutting the solidified shell along different heights and then measuring the average thickness of each position.

In this part, a continuous casting slab with a cross-section (width × thickness) of 1520 × 90 mm², SEN immerse depth of 160 mm and casting speed of 5 m/min was cut and measured. The measuring positions were at one-fourth of the width of the solidified shell and at the middle of the narrow surface along the thickness, respectively. The distance from the liquid surface of the mold was 0.3 m, 0.7 m and 0.9 m. Then, the thickness of the solidified shell was measured at the symmetric position of the outer arc side and inner arc side, each position was measured three times and the average value of the thickness data was taken. The measurement process is shown in Figure 4.

The thickness of the solidified shell at the three measuring points on the narrow surface was about 4.2 mm, 6.9 mm and 10.2 mm from the liquid side down. The thickness of the wide solidified shell was about 4.0 mm, 8.2 mm and 10.6 mm in turn. As can be seen in Figure 4, no matter the narrow face or the wide face, the position of the measuring point from the liquid level down to the first measuring point and the third measuring point were wrapped by three solidified shell thickness curves calculated by numerical simulation with A_mush values of D, E and F, followed by C, and A and B being the worst. The second measurement point was in poor agreement with the numerical simulation calculation of the solidified shell thickness, because the measurement point was located at the impact position of the main jet and the turbulent flow area near the main jet, and the formation of the solidified shell thickness had great instability. In summary, when the value of A_mush ranges from 3 × 10⁸ to 9 × 10⁸ kg/(m³⋅s), the solidified shell thickness calculated by the mathematical model is more accurate. Therefore, when calculating the solidification mathematical model in this section, the value of the A_mush was 6 × 10⁸ kg/(m³⋅s).

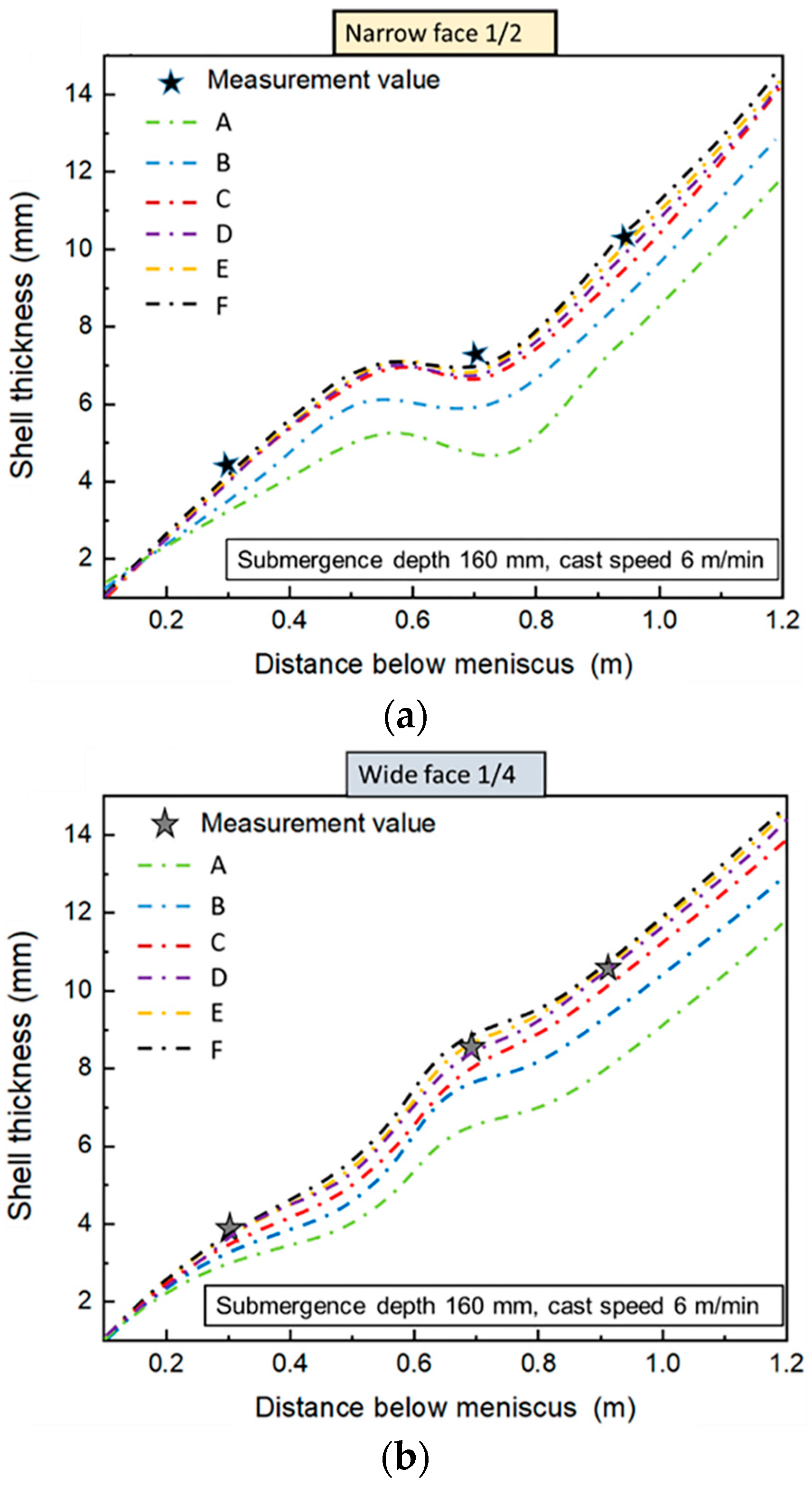
3.2.2. Verification of the Heat Transfer Solidification Model

According to the curve of the solidified shell thickness calculated when the value of A_mush is 6 × 10⁸ kg/(m³⋅s), it can be seen that the solidified shell thickness shows a gradual increasing trend along the mold height direction, which can be said to be linear growth, and the solidified shell thickness reaches about 14 mm at the outlet position. However, as can be seen from the narrow face comparison diagram in Figure 5a, the growth rate of the solidified shell thickness decreased significantly at a distance of 600~800 mm from the meniscus of the mold, and a turning point appeared. The thickness of the solidified shell was only about 5.2 mm at the thinnest point, and then, the solidified shell thickness began to increase. Both the measured values and the simulated values indicated that the high-speed jet in the mold impaction on the narrow surface and the probability of steel leakage and slag inclusion was greater there. The reason is that there is a large temperature gradient and intense heat exchange at and near the impact point of the high-speed molten steel flow, and the strong scour effect of the high-speed molten steel flow makes heat replenishment there in time and the temperature is high, resulting in a growth lag of the solidified shell. The width face comparison diagram of the mold shows that the thickness of the solidified shell fluctuates greatly in the area of about 400~900 mm, but the overall growth is relatively stable. The reason is that the molten steel flowing out of the SEN outlet at high speed is very active in the flow path area, and because of the wide and thin section of the mold, the heat replenishment of the wide surface solidified shell is timely, resulting in slow solidification of the molten steel and a thin solidified shell. The flow of the molten steel in the center of the vortex is poor, and the temperature is low, which leads to the thickness of the solidified shell. The measurement results at 0.7 m away from the meniscus are not in good agreement with the mathematical simulation results, because the molten steel flow here is disordered, and there is no obvious rule. On the whole, the simulated calculation of the solidified shell thickness in this study is basically consistent with the actual measurement of the solidified shell thickness, which indicates that the solidification mathematical model established in this study has high reliability.

4. Conclusions

By developing a 3D solidification heat transfer mathematical model of a thin slab continuous casting mold, the effects of the mushy zone coefficient A_mush on the flow, heat transfer and solidification process of molten steel in the two-phase zone at high casting speed were analyzed, and the thickness of the solidified shell was compared with that of an actual thin slab. We came to the following conclusions:

• The smaller the mushy zone coefficient is, the higher the liquid–solid-phase ratio of steel near the liquid level, which is inconsistent with the actual situation. The larger the mushy zone between the solid and liquid in the front of the solidified shell, the thinner the solidified shell. The larger the mushy zone coefficient is, the lower the solid-phase ratio near the liquid surface, and the smaller the mushy zone area is, the thicker the solidified shell.
• The mushy zone coefficient of 3 × 10⁸~9 × 10⁸ kg/(m³⋅s) can reliably reveal the actual solidification phenomenon in the mold of thin slab continuous casting at high casting speed.