Optimal Design of Motor–Pump Parameters for Direct Load-Sensitive EHA Based on Multi-Objective Optimization Algorithm

Abstract

The electro-hydrostatic actuator (EHA) is a highly integrated and reliable actuation system which has been widely used in aerospace and construction machinery. In addition, the direct load sensitive EHA (DLS–EHA) has been investigated by introducing load-sensitive techniques which can well match the system output and external loads. More importantly, the matching design of motor–pump parameters is an important stage in the pre-design phase of DLS–EHA. For this reason, a multi-objective optimization design method for DLS–EHA motor–pump parameters is proposed in this paper. Firstly, the motor–pump mass and energy loss models are constructed based on similarity criteria. Secondly, the multi-objective particle swarm optimization algorithm (MOPSO) is used to optimize the design of the motor-pump parameters, and the Pareto frontier solutions of the optimized parameters are obtained. Further, the optimal design parameters are selected on the basis of meeting the actual requirements. Finally, the DLS–EHA prototype is designed based on the optimized design parameters and experimental verification is completed. The results of the study show that the optimized design parameters can meet the design requirements. The design method proposed in this paper provides an important theoretical basis for the optimized design of DLS–EHA.

1. Introduction

The electro-hydrostatic actuator (EHA) is a new type of actuator system with high reliability and integration [1,2,3], which usually consists of a motor, a pump, an actuator, a controller and other accessories. The EHA is now widely used in many fields such as aerospace and construction machinery [4,5,6]. The EHA can be categorized into a variety of configurations depending on the form of motor speed and pump displacement change, including the fixed displacement pump and variable speed motor–EHA (FPVM–EHA), variable displacement pump and fixed speed motor–EHA (VPFM–EHA), variable displacement pump and variable speed motor–EHA (VPVM–EHA) [5,7,8]. Among them, the direct load-sensitive EHA (DLS–EHA) is realized by introducing load-sensitive technology on the basis of VPVM–EHA. The high-pressure oil of the system is introduced into the variable mechanism, which in turn realizes the matching of the system output with the external load, as shown in the schematic diagram in Figure 1.

The comprehensive and optimized design process of DLS–EHA is necessary to ensure high performance and reliability. Specifically, the design of DLS–EHA is a multi-parameter and multi-field coupling design process, which involves a number of disciplines such as mechanical engineering, electrical engineering, and fluid transmission. Most importantly, the matching of motor and pump parameters is an important aspect of the optimal design of the DLS–EHA. In the early stages of the motor-pump design, only a few design parameters are available, but a large number of design parameters must be determined and multiple characteristics should be considered at the same time, which are usually in conflict with each other and difficult to balance. The selection of the optimal combination of design parameters with the same design specifications is important [9,10].

There is some research on the optimal design of EHA parameters. An optimized design approach for EHA for aircraft ailerons is explored in [11]. This research involves combining non-causal modeling and multi-tip simulation meta-modeling approaches to construct an EHA mass model using a surface response model, which enables a fast and optimal design of EHA mass and geometric integration. A design methodology for finding and evaluating optimal architectures for aircraft actuators with EHA safety and reliability as design goals is presented in [12]. Efficient and fast trade-offs between different actuator technologies are realized by this method, which provides an important theoretical basis for actuator pre-design. A preliminary optimization design method for aircraft actuators based on scaling laws is presented in [13]. The method presents guidelines for categorizing numerous design parameters in the pre-design phase of an actuator. The challenge of not easily determining the design parameters faced during the pre-design phase of an actuator is addressed by allowing the development of component models from a limited number of input parameters. In order to refine the design methodology of EHA under various transient operating conditions, a methodology for the optimal design of EHA under multiple constraints is proposed in [14]. A MATLAB/Simulink-based EHA sizing and simulation optimization tool was also developed with EHA quality as the optimization objective, and the parameter optimization design of EHA was completed with the flight rudder surface of Boeing 737-800 as the research object [15]. A multi-objective optimization design method for EHA under multiple constraints is proposed in [16]. The optimal design of the parameters of the motor, pump, and actuator cylinder was completed. In reference [17] the design of the pump displacement and other parameters was completed using a multi-objective optimization algorithm with mass, stiffness, and efficiency as the optimization objectives. A multi-objective optimization design method for EHA based on AMESim and Python is proposed in [18]. The dynamics model of the EHA was constructed using AMESim, and the Python script completed the optimal design of the design parameters by using an intelligent search method and transferring it to the AMESim model. This method helps in determining the design parameters of the actuator during the design phase.

However, the above studies have some limitations. Firstly, all the above studies on EHA mainly focus on FPVM–EHA, and there is no content on the optimized design of the motor–pump parameters of DLS–EHA. For DLS–EHA the pump displacement varies with the system working pressure, which makes the determination of the rated torque of the motor a difficult problem. In addition, for the calculation of system energy consumption, especially the motor energy consumption, a completed calculation process is not given in all the references. Hence, they do not accurately provide guidance for the pre-design of the DLS–EHA.

Therefore, in order to improve the process of the pre-design stage of DLS–EHA, this paper proposes a motor–pump parameter-matching optimization method based on a multi-objective particle swarm optimization algorithm. Combined with the design index of EHA and working condition demands, an accurate motor–pump mass and energy consumption model are established, and the design parameters are determined. Furthermore, the optimal design of the motor–pump parameters was accomplished using the multi-objective particle swarm optimization algorithm, and the Pareto frontier solution was obtained. On this basis, the parameter relationship matrix (PRM) is constructed using quality function development (QFD) theory to choose the design parameters of the motor–pump that can be best used in practice.

2. Multi-Objective Optimization Model

2.1. Mass Model of the Motor–Pump

The mass model of the motor–pump can be expressed as:

$$m_{\mathrm{pm}}=m_{\mathrm{pump}}+m_{\mathrm{motor}},$$

(1)

where $m_{\mathrm{pm}}$ indicates the sum mass of pump and motor, and $m_{\mathrm{pump}}$ and $m_{\mathrm{motor}}$ represent the mass of pump and motor, respectively.

A straightforward way to obtain the mass model is to use a data package similar to that used in some commercial software, in which the volume of the object is known and then calculated by defining the corresponding material. However, this approach cannot be implemented in the early stages of EHA design, since it is not possible to know the exact volume of the component. In order to obtain an accurate mass model in the early stage, the similarity criterion is adopted in this paper.

2.1.1. The Parameter Estimation Based on Similarity Criterion

The similarity criterion is an effective method to study the impact of parameter variations on system performance, which has the advantage of accomplishing estimates over a range of product quality with only one or a relatively small number of parameters [19,20]. The parameter estimation process based on similarity criterion is shown in Figure 2.

The similarity ratio for a given parameter can be defined as follows:

$$x^{*}=\frac{x^{\prime }}{x_{\mathrm{ref}}},$$

(2)

where $x^{*}$ is the similarity ratio for a given parameter to be estimated, $x^{\prime }$ is the parameter to be estimated, and $x_{\mathrm{ref}}$ is the parameter used as the reference.

For instance, the schematic of geometric shafts with geometric similarity is shown in Figure 3. The similarity ratio of dimensional parameters and the mass can be expressed as follows under all geometrical parameters in identical variations.

$$r^{*}=\frac{r}{r_{\mathrm{ref}}},l^{*}=\frac{l}{l_{\mathrm{ref}}},$$

(3)

$$r^{*}=l^{*},$$

(4)

$$V^{*}=\frac{V^{\prime }}{V_{\mathrm{ref}}}=\frac{\pi r^{2}l}{\pi r_{\mathrm{ref}}^2{l}_{\mathrm{ref}}}=r^{*2}{l}^{*}=l^{*3},$$

(5)

$$m={\displaystyle \int \rho dV\Rightarrow m^{*}=l^{*3}},$$

(6)

where $V$, $r$, $l$, $\rho$ and $m$ represent the volume, radius, length, density and mass, respectively. Therefore, all definition parameters can be related to a dimensional parameter similarity ratio for geometrically similar parts.

2.1.2. Mass Model of the Pump

Generally, there is a relationship between the mass and the displacement of the pump. Therefore, in the estimation process of pump mass, the displacement $D_{\mathrm{p}}$ can be selected as the definition parameter, by assuming the materials and maximum working pressure of the pump are the same. Accordingly, the similarity ratio of the relational parameters can be expressed as follows:

$${\rho }^{*}=E^{*}=p_{\max }^{*}=1,$$

(7)

where ${\rho }^{\ast }$ is the similarity ratio of the material density, $E^{*}$ is the similarity ratio of Young’s modulus, and $p_{\max }^{*}$ is the similarity ratio of maximum pump pressure.

The pump displacement is the geometrical volume of the cavity in one rotation of the pump. Due to the geometrically similar characteristics of the pumps, all dimensional parameters have the same similarity ratio. The similarity ratio of displacement and mass can be linked to the dimensional similarity ratio which can be expressed as follows:

$$D_{\mathrm{p}}^{*}=l_{\mathrm{p}}^{*3},$$

(8)

$$m_{\mathrm{pump}}^{*}=l_{\mathrm{p}}^{*3},$$

(9)

where $D_{\mathrm{p}}^{*}$ is the similarity ratio of the pump displacement, $m_{\mathrm{pump}}^{*}$ is the similarity ratio of the pump mass, and $l_{\mathrm{p}}^{*}$ is the similarity ratio dimensional parameter of the pump.

Combining Equations (8) and (9), the mass similarity ratio of the pump can be expressed as:

$$m_{\mathrm{pump}}^{*}=D_{\mathrm{p}}^{*},$$

(10)

As shown in Equation (10), the mass of the pump is positively related to the pump displacement. In order to obtain the mass model of the pump, the mass data of the Paker pumps at the same pressure level are collected and the fitted data can be obtained as shown in Figure 4. Eventually, the pump mass model can be obtained as follows:

$$m_{\mathrm{pump}}=0.21D_{\mathrm{p}}+2.15,$$

(11)

where $m_{\mathrm{pump}}$ denotes the mass of pump.

2.1.3. Mass Model of the Motor

Likewise, the motor rated torque $T_{\mathrm{nom}}$ can be selected as the definition parameter, while the dimensional parameter is defined as $l_{\mathrm{m}}$. In order to avoid the magnetic saturation of the motor, the magnetic density of the motor cannot exceed the maximum given value of the material. During the estimation process of the motor, it is assumed that the electromagnetic components have the same maximum magnetic flux density, which can be expressed as follow.

$$B^{*}=1,$$

(12)

The electromagnetic working torque of motor can be obtained as follows according to the Laplace Equation [13].

$$T={\displaystyle \int J_{\mathrm{cd}}Brdv},$$

(13)

$$T^{*}=J_{\mathrm{cd}}^{*}{B}^{*}{l}_{\mathrm{m}}^{*}{}^4=J_{\mathrm{cd}}^{*}{l}_{\mathrm{m}}^{*4},$$

(14)

where $T$ and $T^{*}$ are the working torque and the similarity ratio of $T$, respectively, $J_{\mathrm{cd}}$ and $J_{\mathrm{cd}}^{*}$ are the current density and its similarity ratio, respectively, $l_{\mathrm{m}}$ is the dimensional parameter of the motor, and $l_{\mathrm{m}}^{*}$ is the similarity ratio of $l_{\mathrm{m}}$. The square of the current density is inversely proportional to the winding length for the same maximum temperature limitation [20]; hence, the current density similarity ratio can be expressed as:

$$J_{\mathrm{cd}}^{*}=l_{\mathrm{m}}^{*-1/2},$$

(15)

In addition, the similarity ratios of the rated torque and working torque are the same, namely $T_{\mathrm{nom}}^{*}=T^{*}$. The relationship between the similarity ratio of the rated torque and the similarity ratio of the dimensional parameter can be obtained as:

$$T_{\mathrm{nom}}^{*}=l_{\mathrm{m}}^{*3.5},$$

(16)

Therefore, the similarity ratio of the motor mass can be obtained as Equation (17) according to Equations (6) and (16).

$$m_{\mathrm{motor}}^{*}=T_{\mathrm{nom}}^{*3/3.5},$$

(17)

It can be seen that the motor mass is positively correlated with the (3/3.5) power of the motor rated torque. By collecting the mass data of the motor, the mass model of the motor can be obtained as follows [16]:

$$m_{\mathrm{motor}}=0.628T_{\mathrm{nom}}^{3/3.5}+0.783,$$

(18)

2.2. Energy Loss Model of the Motor–Pump

The energy loss model for the motor–pump can be expressed as:

$$E_{\mathrm{pm}}={\displaystyle \underset{0}{\overset{t}{\int }}\left(P_{\mathrm{motor}}+P_{\mathrm{pump}}\right)}dt,$$

(19)

where $E_{\mathrm{pm}}$ represents the sum of the energy loss of the motor and pump at a certain time, $P_{\mathrm{pump}}$ is the power loss of the pump, and $P_{\mathrm{motor}}$ is the power loss of the motor.

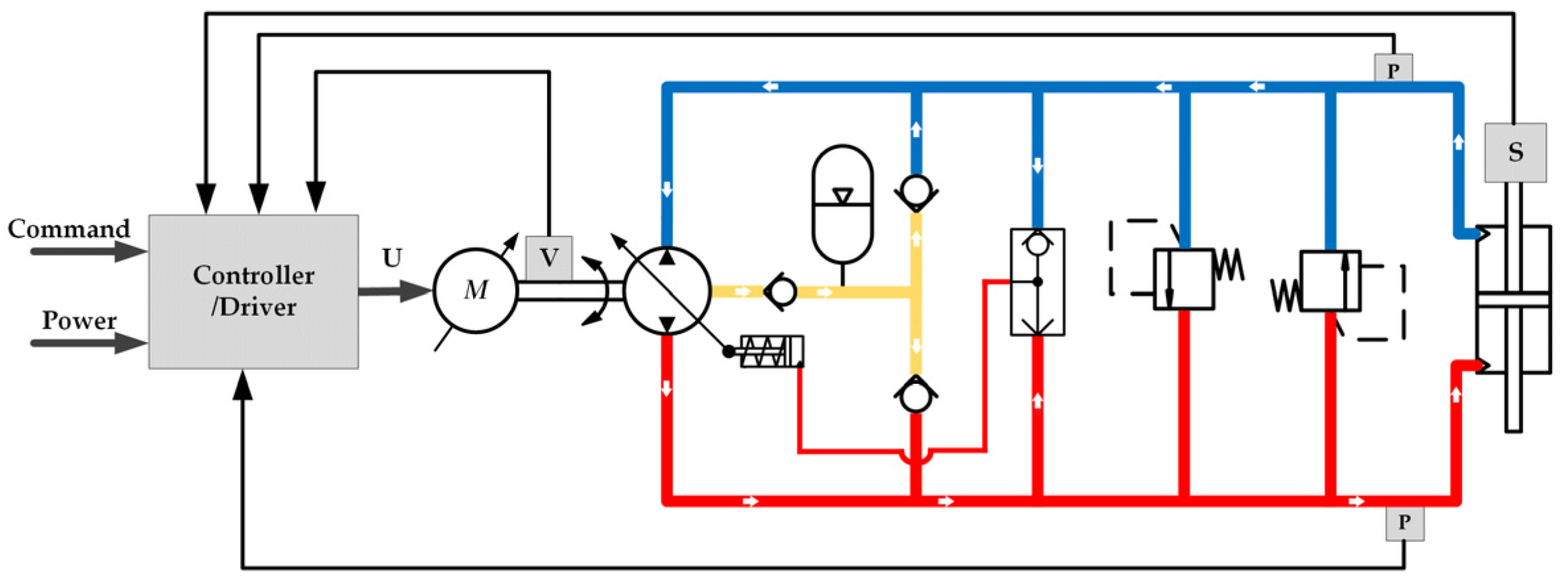
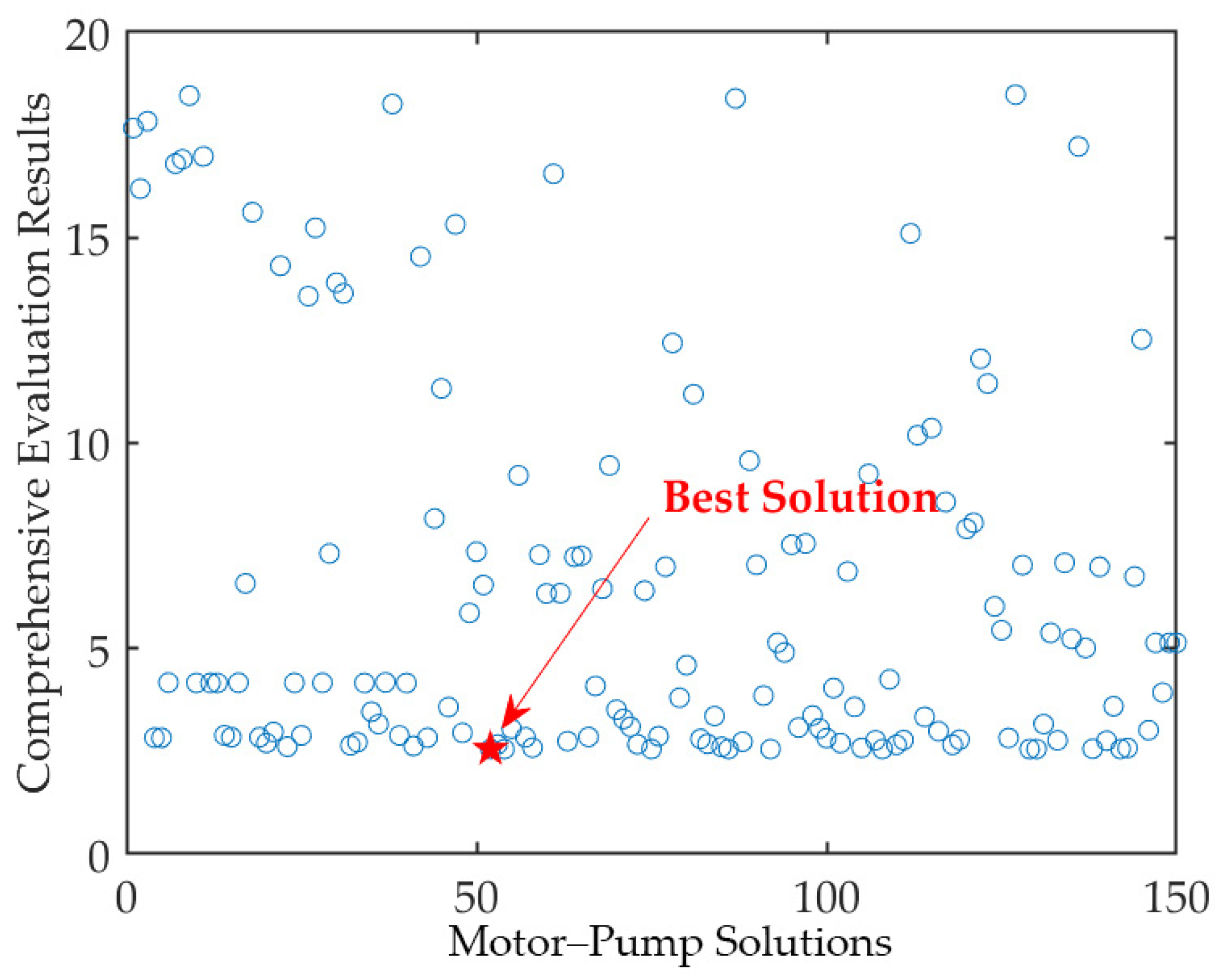
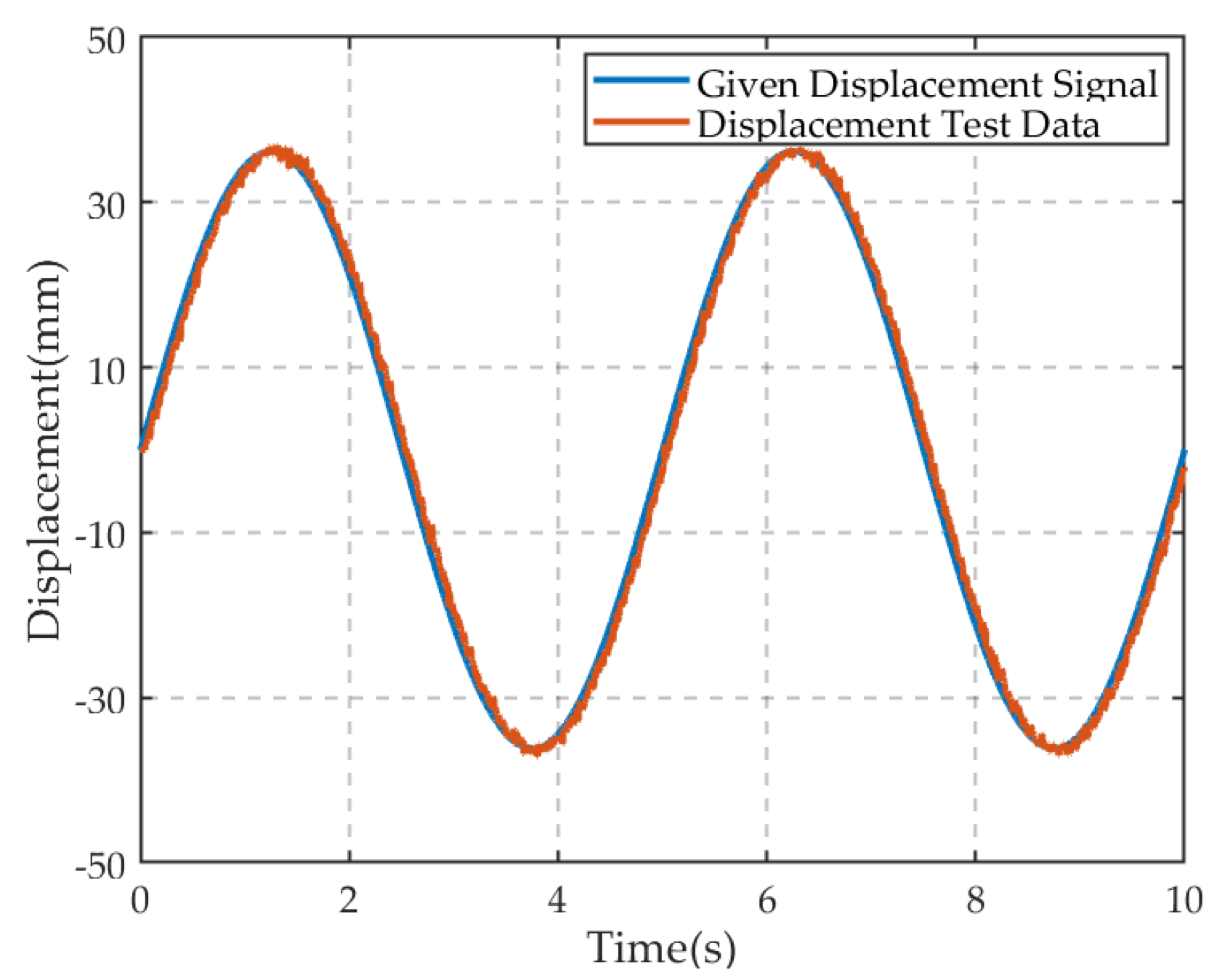
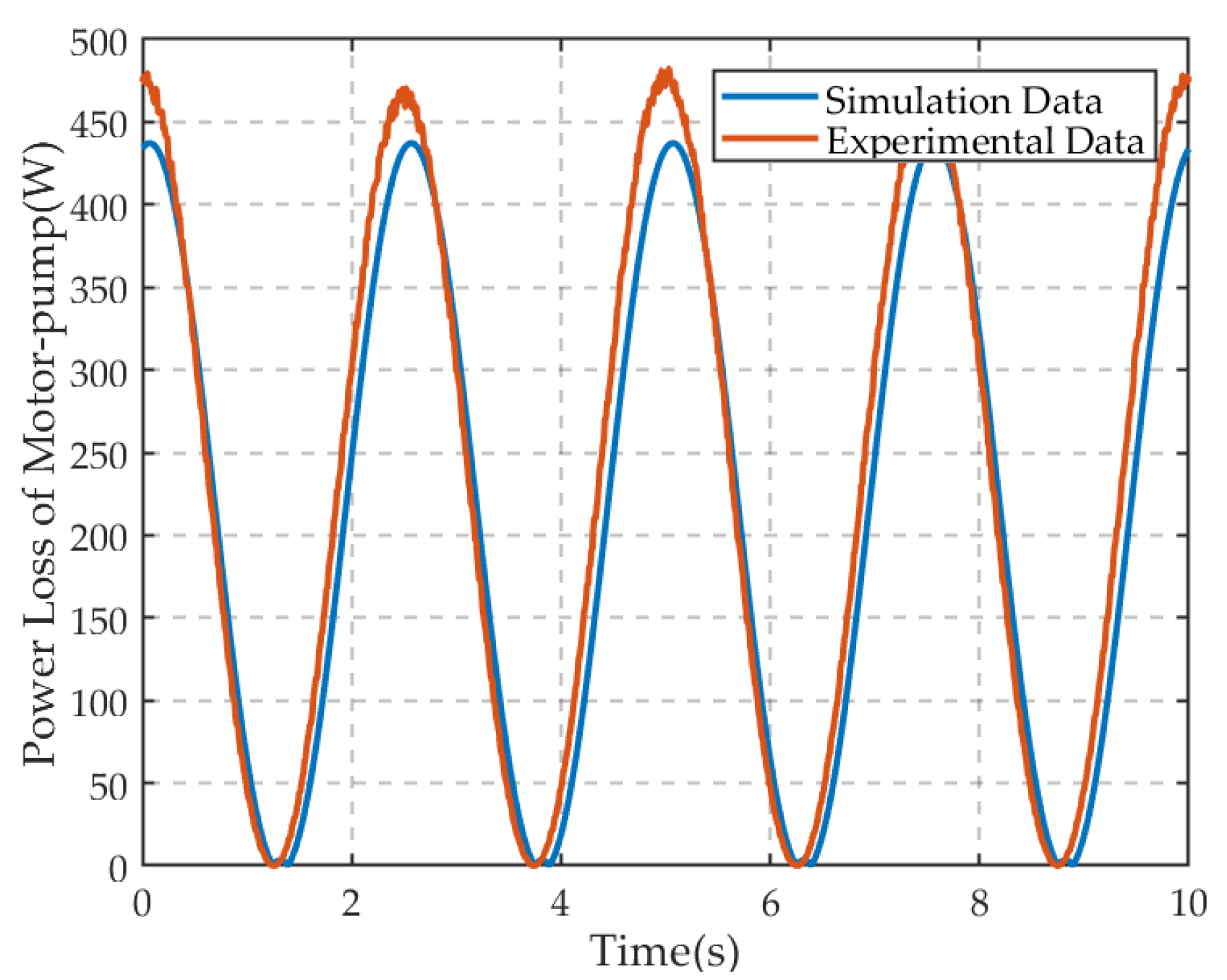
2.2.1. Power Loss of the Pump

The power loss of the pump is composed of mechanical and volumetric power loss, which can be expressed as:

$$P_{\mathrm{pump}}=P_{\mathrm{p},\mathrm{m}}+P_{\mathrm{p},\mathrm{v}},$$

(20)

where $P_{\mathrm{p},\mathrm{m}}$ and $P_{\mathrm{p},\mathrm{v}}$ represent the mechanical power loss and volumetric power loss, respectively.

In addition, the mechanical power loss $P_{\mathrm{p},\mathrm{m}}$ can be expressed as Equation (21).

$$P_{\mathrm{p},\mathrm{m}}=\Delta T_{\mathrm{p}}\omega =\left(\Delta T_{\mathrm{s}}+\Delta T_{\mathrm{v}}+\Delta T_{\mathrm{t}}\right)\omega ,$$

(21)

where $\Delta T_{\mathrm{p}}$ is the torque loss of the pump, $\Delta T_{\mathrm{s}}$ represents the pump torque loss generated by the friction pair, $\Delta T_{\mathrm{v}}$ is the pump torque loss generated by oil viscosity, $\Delta T_{\mathrm{t}}$ is the pump torque loss generated by fluid churn, and $\omega$ is the angular velocity of the pump.$\Delta T_{\mathrm{s}}$, $\Delta T_{\mathrm{v}}$ and $\Delta T_{\mathrm{t}}$ can be expressed as Equations (22)–(24), respectively.

$$\Delta T_{\mathrm{s}}={\displaystyle \sum A_{\mathrm{p}}pfr}=(\frac{{\displaystyle \sum A_{\mathrm{p}}fr}}{D_{\mathrm{p}}})p{D}_{\mathrm{p}}=C_{\mathrm{s}}p{D}_{\mathrm{p}},$$

(22)

$$\Delta T_{\mathrm{v}}={\displaystyle \sum A_{\mathrm{R}}\tau r}={\displaystyle \sum A_{\mathrm{R}}(\mu \frac{\omega r}{s})r}=C_{\mathrm{v}}\mu n{D}_{\mathrm{p}},$$

(23)

$$\Delta T_{\mathrm{t}}=\frac{{\displaystyle \sum {(2\pi )}^{2/3}{A}_{\mathrm{t}}{r}^3}}{2D_{\mathrm{p}}^{5/3}}=C_{\mathrm{t}}{\rho }_{\mathrm{oil}}{n}^2{D}_{\mathrm{p}}^{5/3},$$

(24)

where $A_{\mathrm{p}}$ is the pressure area, $f$ is the frictional coefficient of the friction pair, $r$ is the distance from the friction to the center of the rotation axis, $C_{\mathrm{s}}$ is the mechanical loss coefficient, $A_{\mathrm{R}}$ is the projected area of the friction area, $\tau$ is the oil shear stress on unit area, $C_{\mathrm{v}}$ is the viscous friction coefficient, $A_{\mathrm{t}}$ is the projected area of the turbulent follow channel, ${\rho }_{\mathrm{oil}}$ is the density of the oil, $n$ is the rotational speed of the pump, $C_{\mathrm{t}}$ is the churning loss coefficient, $p$ is the working pressure of the pump, and $\mu$ is the dynamic viscosity of the fluid.

Combining Equations (21)–(24), the expression for the mechanical power loss of the pump can be obtained as:

$$P_{\mathrm{p},\mathrm{m}}={C^{\prime }}_{\mathrm{s}}pn{D}_{\mathrm{p}}+{C^{\prime }}_{\mathrm{v}}\mu n^2{D}_{\mathrm{p}}+{C^{\prime }}_{\mathrm{t}}{\rho }_{\mathrm{oil}}{n}^3{D}_{\mathrm{p}}^{5/3},$$

(25)

where ${C^{\prime }}_{\mathrm{s}}=2\pi C_{\mathrm{s}}/60$, ${C^{\prime }}_{\mathrm{v}}=2\pi C_{\mathrm{v}}/60$, and ${C^{\prime }}_{\mathrm{t}}=2\pi C_{\mathrm{t}}/60$.

In addition, the volumetric power loss of the pump is generated by the leakage of the sealing surface. The volumetric power loss and the leakage equation can be expressed as follows:

$$P_{\mathrm{p},\mathrm{v}}=\Delta Q_{\mathrm{p}}p=\left(\Delta Q_{\mathrm{s}}+\Delta Q_{\mathrm{t}}\right)p,$$

(26)

where $\Delta Q_{\mathrm{p}}$ is the leakage of the pump, and $\Delta Q_{\mathrm{s}}$ and $\Delta Q_{\mathrm{t}}$ denote the leakage in laminar and turbulent, respectively, which can be expressed as follows.

$$\Delta Q_{\mathrm{s}}={\displaystyle \sum \frac{p{s}^{3}b}{12\mu l_{\mathrm{a}}}}=C_{\mathrm{sv}}\frac{D_{\mathrm{p}}}{2\pi \mu }p,$$

(27)

$$\Delta Q_{\mathrm{t}}=u{\displaystyle \sum j}=\sqrt{\frac{2p}{{\rho }_{\mathrm{oil}}}}{\displaystyle \sum j}=C_{st}\sqrt{\frac{2p}{{\rho }_{\mathrm{oil}}}}{D}_{\mathrm{p}}^{2/3},$$

(28)

where $s$ is the height of the leakage gap, $b$ is the length of the leakage boundary, $l_{\mathrm{a}}$ is the length of the leakage channel, $C_{\mathrm{sv}}$ is the laminar leakage coefficient, and $C_{\mathrm{st}}$ is the turbulent leakage coefficient. Therefore, the volumetric power loss of the pump can be obtained as:

$$P_{\mathrm{p},\mathrm{v}}=C_{\mathrm{sv}}\frac{D_{\mathrm{p}}}{2\pi \mu }{p}^2+C_{st}p\sqrt{\frac{2p}{{\rho }_{\mathrm{oil}}}}{D}_{\mathrm{p}}^{2/3},$$

(29)

According to Equations (20), (25) and (29), the power loss of the pump can be expressed as follows:

$$P_{\mathrm{pump}}={C^{\prime }}_{\mathrm{s}}pn{D}_{\mathrm{p}}+{C^{\prime }}_{\mathrm{v}}\mu n^2{D}_{\mathrm{p}}+{C^{\prime }}_{\mathrm{t}}{\rho }_{\mathrm{oil}}{n}^3{D}_{\mathrm{p}}^{5/3}+C_{\mathrm{sv}}\frac{D_{\mathrm{p}}}{2\pi \mu }{p}^2+C_{\mathrm{st}}p\sqrt{\frac{2p}{{\rho }_{\mathrm{oil}}}}{D}_{\mathrm{p}}^{2/3},$$

(30)

According to Equation (30), it can be found that the power loss of the pump is a function of the system pressure and the displacement of the pump.

2.2.2. Power Loss of the Motor

Generally, the motor power loss is mainly composed of electrical loss which consists of copper and iron losses. The expression of the motor loss can be presented as follows:

$$P_{\mathrm{motor}}=\Delta P_{\mathrm{e}}=\Delta P_{\mathrm{Cu}}+\Delta P_{\mathrm{Fe}},$$

(31)

where $\Delta P_{\mathrm{e}}$ is the electrical power loss, and $\Delta P_{\mathrm{Cu}}$ and $\Delta P_{\mathrm{Fe}}$ indicate the copper and iron losses, respectively, which can be expressed as follows:

$$\Delta P_{\mathrm{Cu}}=N{I}^{2}R,$$

(32)

$$\Delta P_{\mathrm{Fe}}=k_{\mathrm{h}}{f}_{\mathrm{m}}{B}^{\alpha }+k_{\mathrm{c}}{(B{f}_{\mathrm{m}})}^2+k_{\mathrm{e}}{(B{f}_{\mathrm{m}})}^{1.5},$$

(33)

where $N$ is the number of phases of the motor winding, $I$ is the RMS value of the winding phase current, $R$ is the phase resistance, $k_{\mathrm{h}}$ is the hysteresis loss coefficient, $f_{\mathrm{m}}$ is the frequency of alternating magnetic field, $\alpha$ is the Steinmetz coefficient, and $k_{\mathrm{c}}$ is the additional loss coefficient.

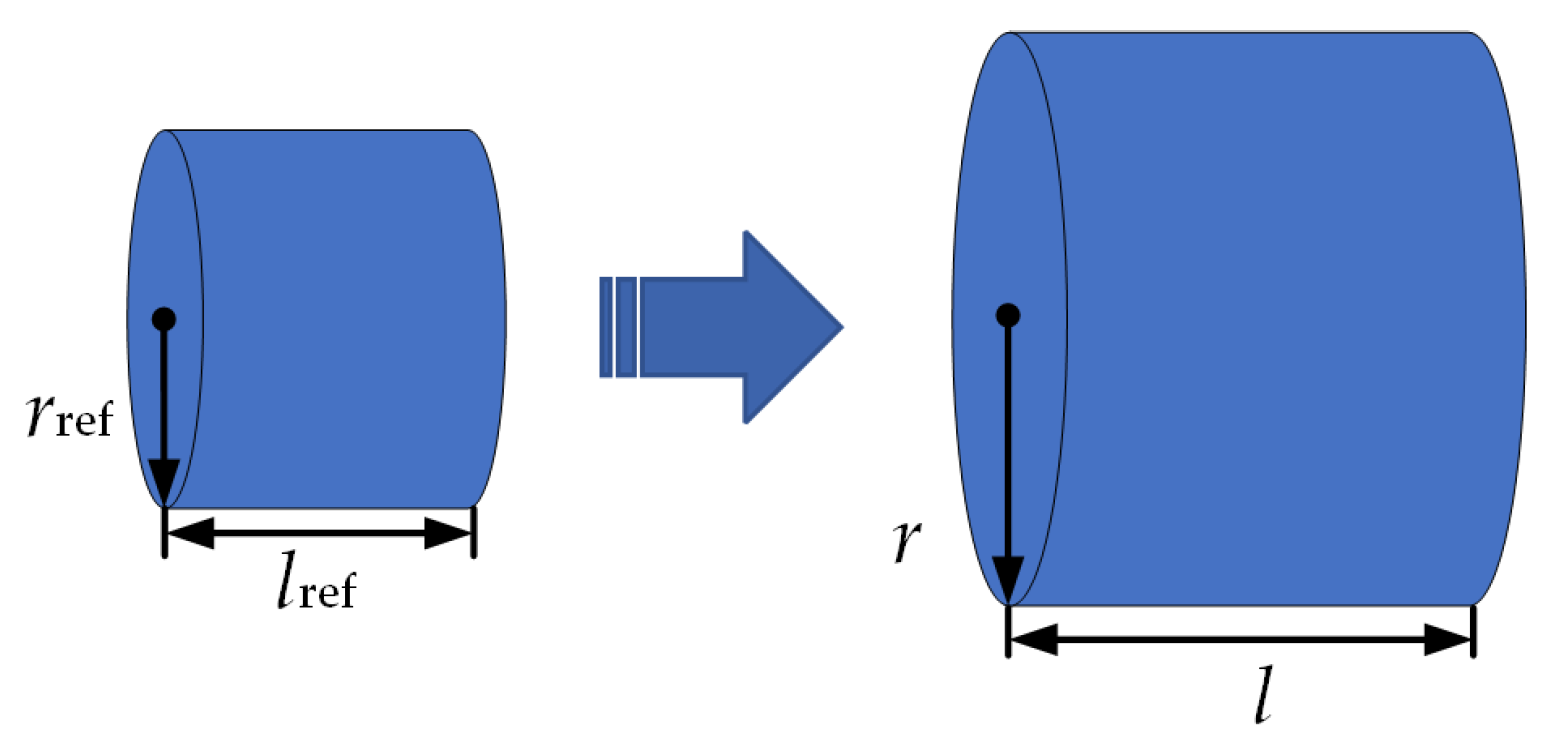
The copper and iron losses of the motor depend greatly on the design structure and the material of the motor according to Equations (32) and (33). However, it is difficult to determine the specific parameters of the motor at the beginning of EHA design. The loss model of the motor can also be obtained by using similarity criterion. Similarly, the motor rated torque $T_{\mathrm{nom}}$ is selected as the definition parameter, while the dimensional parameter is defined as $l_{\mathrm{m}}$.

(1)

Copper Loss Calculation

The relationship between motor output torque and current can be expressed as:

$$T_{\mathrm{m}}=k_{\mathrm{t}}I,$$

(34)

where $T_{\mathrm{m}}$ is the output torque of the motor, and $k_{\mathrm{t}}$ is the torque coefficient of the motor.

Combining Equations (32) and (34), the relationship of the copper loss and the output torque can be expressed as:

$$\Delta P_{\mathrm{Cu}}=\frac{NR}{k_{\mathrm{t}}^2}{T}_{\mathrm{m}}^2={\alpha }_{\mathrm{t}}{T}_{\mathrm{m}}^2,$$

(35)

where ${\alpha }_{\mathrm{t}}$ can be defined as the coefficient between copper loss and the output torque. Meanwhile, the similarity ratio of the ${\alpha }_{\mathrm{t}}$ can be expressed as:

$${\alpha }_{\mathrm{t}}^{*}=\frac{R^{*}}{k_t^{*}},$$

(36)

The value of the motor torque coefficient and back EMF coefficient can be considered equal for the permanent magnet synchronous motor. Thus, the similar ratio for the torque coefficient can be expressed as follows based on the formula for back EMF.

$$k_{\mathrm{t}}^{*}=\frac{U^{*}}{{\omega }^{*}},$$

(37)

where $U^{*}$ is the similarity ratio of back EMF, and ${\omega }^{*}$ is the similarity ratio of the rotational speed.

In the high-speed operation process, the motor rotor contains a large centrifugal force. The maximum rotational speed of the motor is generally limited by the mechanical constraints caused by the centrifugal force for safety. Assuming that the motor possesses the same scale factor in all dimensions, the similarity ratio of the concentrated stress of the shaft can be expressed as Equation (38) according to the centrifugal force calculation method.

$${\sigma }^{*}={\omega }^{*2}{l}_{\mathrm{m}}^{*2},$$

(38)

where ${\sigma }^{*}$ is the similarity ratio of the concentrated stress of the shaft.

Furthermore, assuming that the motors are produced from the same material that contains the same stress limits, ${\sigma }^{*}={\rho }^{*}=E^{*}=1$. Therefore, the similarity ratio of rotational speed, the shaft shear force and torque can be obtained as follows, respectively:

$${\omega }^{*}=l_{\mathrm{m}}^{*-1},$$

(39)

$$F_{\mathrm{m}}{}^{*}=l_{\mathrm{m}}^{*2},$$

(40)

$$T_{\mathrm{m}}{}^{*}=l_{\mathrm{m}}^{*3},$$

(41)

Combining Equations (37) and (39), the similarity ratio for the torque coefficient can be obtained as:

$$k_{\mathrm{t}}^{*}=U^{*}{l}_{\mathrm{m}}^{*},$$

(42)

The similarity ratio of the winding resistance can be obtained as Equation (43) according to the calculation method of the motor winding resistance.

$$R^{*}=N_{}^{*}{l}_{\mathrm{m}}^{*-1},$$

(43)

where $N_{}^{*}$ is the similarity ratio of the winding number, which can be expressed as:

$$N_{}^{*}=\frac{U^{*}}{l_{\mathrm{m}}^{*2}{B}^{*}{\omega }^{*}}=U^{*}{l}_{\mathrm{m}}^{*-1},$$

(44)

Combining Equations (43) and (44), the final representation of the winding resistance similarity ratio can be expressed as:

$$R^{*}=U^{*2}{l}_{\mathrm{m}}^{*-3},$$

(45)

Furthermore, for a given motor shaft material, the ratio between the fatigue stress and the maximum stress is fixed. Therefore, the ratio between the rated torque of the motor and its maximum torque is also fixed, which can be expressed as:

$$T_{\max }^{*}=T_{\mathrm{nom}}^{*}=T_{\mathrm{m}}{}^{*},$$

(46)

where $T_{\max }^{*}$ and $T_{\mathrm{nom}}^{*}$ represent the similarity ratio of the maximum and the rated torque, respectively.

Moreover, the relationship between the similarity ratio of ${\alpha }_{\mathrm{t}}$ and the rated torque can be obtained as Equation (47) according to Equations (16), (36), (42) and (45).

$${\alpha }_{\mathrm{t}}^{*}=\frac{U^{*2}{l}_{\mathrm{m}}^{*-3}}{U^{*2}{l}_{\mathrm{m}}^{*2}}=l_{\mathrm{m}}^{*-5}=T_{\mathrm{nom}}^{*-5/3.5},$$

(47)

(2)

Iron Loss Calculation

The flux density of the motor in engineering is generally $1\mathrm{T}<\mathrm{B}<1.8\mathrm{T}$; therefore, the iron loss of the motor can be simplified as:

$$\Delta P_{\mathrm{Fe}}=k_{\mathrm{Fe}}{f}^{1.3}{B}^2{m}_{\mathrm{s}},$$

(48)

where $k_{\mathrm{Fe}}$ is the loss coefficient of stator material, and $m_{\mathrm{s}}$ is the mass of the stator. Substituting the motor rotational speed versus frequency, the expression for iron loss of the motor can be regained as follows:

$$\Delta P_{\mathrm{Fe}}={\beta }_{\mathrm{t}}{\omega }^{1.3},$$

(49)

where ${\beta }_{\mathrm{t}}=k_{\mathrm{Fe}}{B}^2{m}_{\mathrm{s}}{(\frac{p_{\mathrm{m}}}{2\pi })}^{1.3}$ is the coefficient representing the relationship between iron loss and rotational speed, and the similarity ratio of ${\beta }_{\mathrm{t}}$ can be expressed as follows:

$${\beta }_{\mathrm{t}}^{*}=m_{\mathrm{s}}^{*}=l_{\mathrm{m}}^{*3}=T_{\mathrm{nom}}^{*3/3.5},$$

(50)

(3)

Calculation Method of ${\alpha }_{\mathrm{t}}$ and ${\beta }_{\mathrm{t}}$

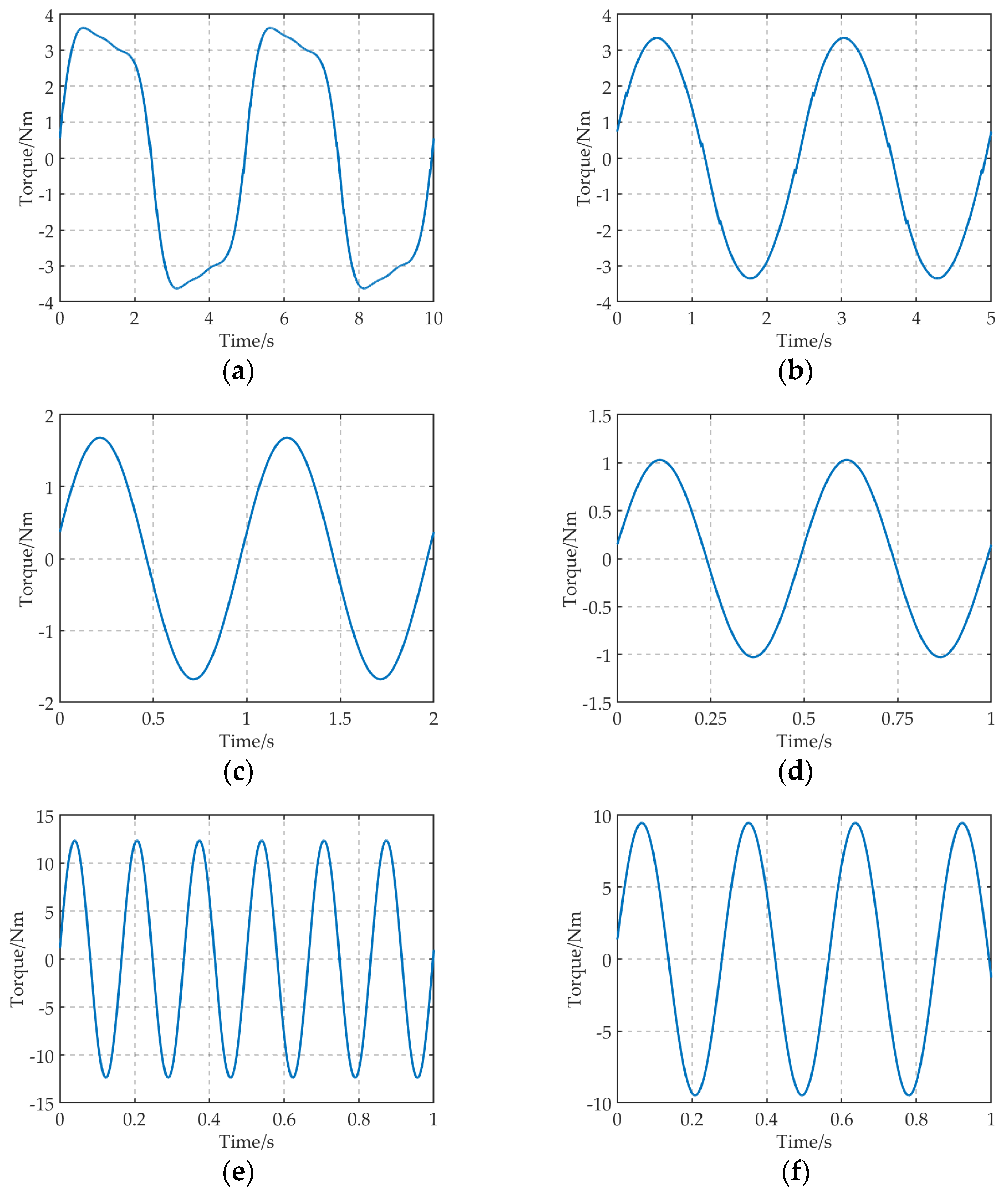
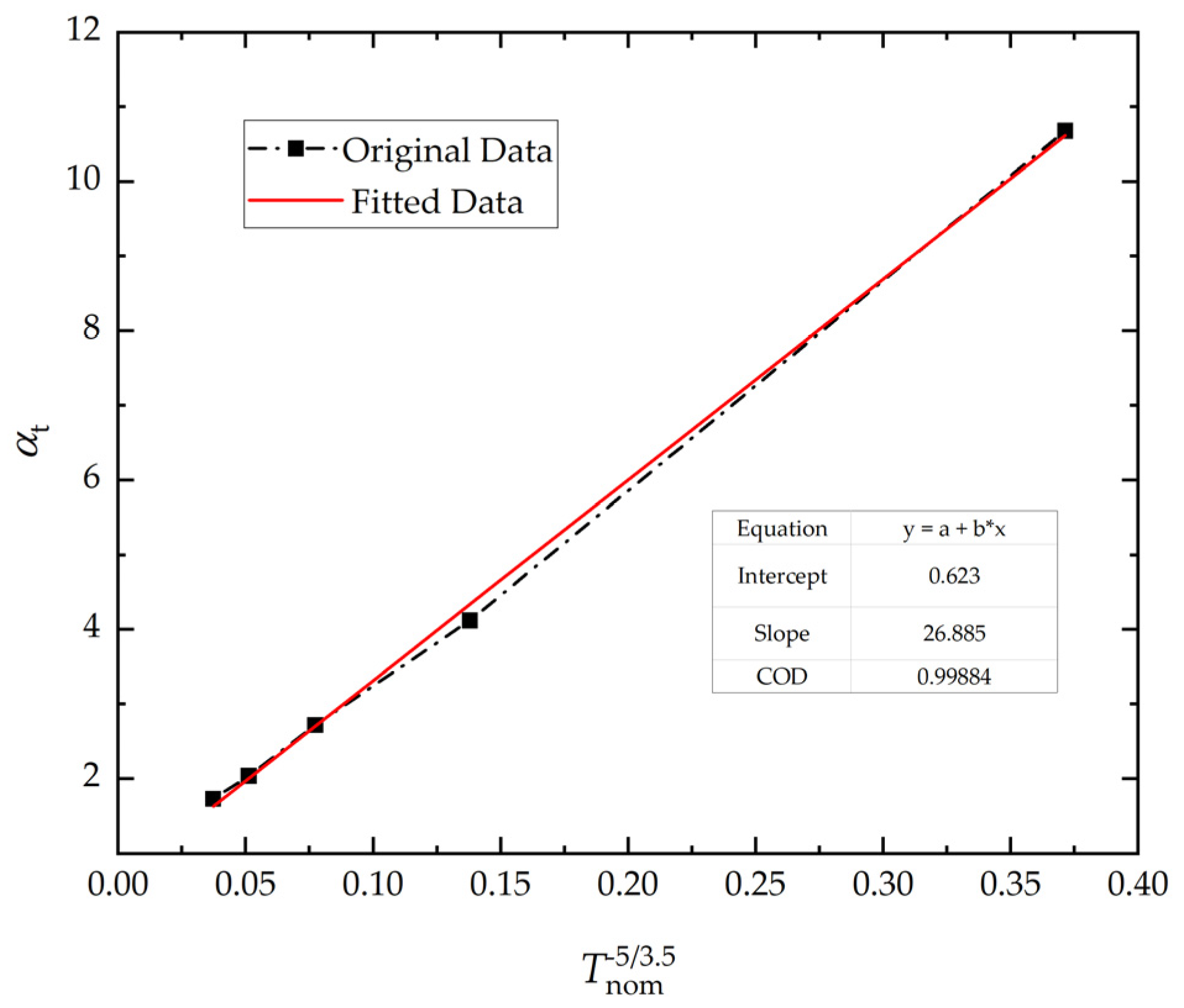
In order to obtain the specific expression of ${\alpha }_{\mathrm{t}}$ and ${\beta }_{\mathrm{t}}$, the motor simulation models are established as shown in Figure 5. The simulation results of power loss at different rated operating conditions are shown in

Table 1. Simulation results of motor power loss.

Number	Rated Torque	Copper Loss (W)	Iron Loss (W)
1	2	42.69	288.17
2	4	65.85	150.00
3	6	97.83	100.36
4	8	130.3	76.00
5	10	172.9	65.00

. Further, the loss coefficients versus rated torque graphic can be obtained by combining Equations (47) and (50), as shown in Figure 6 and Figure 7, respectively. Ultimately, the expressions for ${\alpha }_{\mathrm{t}}$ and ${\beta }_{\mathrm{t}}$ can be denoted as Equations (51) and (52), respectively.

$${\alpha }_{\mathrm{t}}=26.885T_{\mathrm{nom}}^{-5/3.5}+0.623,$$

(51)

$${\beta }_{\mathrm{t}}=0.0017T_{\mathrm{nom}}^{3/3.5}+0.0082,$$

(52)

Finally, the motor loss calculation model can be expressed as follows by combining Equations (35), (49), (51) and (52).

$$P_{\mathrm{motor}}=P_{Cu}+P_{\mathrm{Fe}}=\left(26.885T_{\mathrm{nom}}^{-5/3.5}+0.623\right)T_{\mathrm{m}}^2+\left(0.0017T_{\mathrm{nom}}^{3/3.5}+0.0082\right){\omega }^{1.3},$$

(53)

According to Equation (53), it can be found that the power loss of the motor is a function of the motor output torque and rotational speed, which is related to the motor working conditions.

3. Determination of Multi-Objective Optimization Parameters

According to the above calculations, it can be found that the mass of EHA is directly related to the pump displacement and the rated torque of the motor, and the energy loss is related to the pump output pressure, speed and rated torque of the motor. These parameters are directly related to the actual working conditions and design specifications of the EHA. Therefore, the multi-objective optimization parameter domains need to be determined in combination with the design indicators and the working conditions. The design objectives and working condition requirements of a certain EHA are shown in

Table 2. The design objectives of EHA.

Items	Symbols	Number	Unit
Maximum output force	$F_{\max }$	120	kN
Maximum stroke	$S_{\max }$	±50	mm
Maximum linear speed	$v_{\max }$	110 × 10−3	m/s
Maximum system pressure	$p_{\max }$	28	MPa
Maximum rotational speed	$n_{\max }$	20,000	r/min

and

Table 3. The working conditions.

Steps	System Flow Rate (L/min)	System Pressure (MPa)	Working Time (min)
1	$15\cos \left(2\pi \times 0.2\times t\right)$	$26\sin \left(2\pi \times 0.2\times t\right)$	4.2
2	$20\cos \left(2\pi \times 0.4\times t\right)$	$15\sin \left(2\pi \times 0.4\times t\right)$	13
3	$10\cos \left(2\pi \times 1\times t\right)$	$3\sin \left(2\pi \times 1\times t\right)$	10
4	$4\cos \left(2\pi \times 2\times t\right)$	$1.5\sin \left(2\pi \times 2\times t\right)$	33.3
5	$30\cos \left(2\pi \times 6\times t\right)$	$1.5\sin \left(2\pi \times 6\times t\right)$	0.2
6	$36.5\cos \left(2\pi \times 3.5\times t\right)$	$3\sin \left(2\pi \times 3.5\times t\right)$	0.2

, respectively.

In addition, there is a direct relationship between the displacement of the load-sensing variable displacement pump and the system working pressure. The variable rules for the direct load-sensing variable pump are shown in Figure 8. The variable pump works at the maximum displacement when the system working pressure is less than the variable initial pressure due to the existence of a certain preload in the variable mechanism of the variable pump. Furthermore, the load-sensitive pump displacement is linearly related to the system operating pressure when the system operating pressure exceeds the variable initial pressure.

Therefore, the variable rule for direct load-sensitive pumps can be expressed as:

$$D_{\mathrm{p}}=\left\{\begin{array}{cc}{D}_{\mathrm{p},\max }\hfill & ,p\le p_{\mathrm{c}}\\ -\frac{D_{\mathrm{p},\max }-D_{\mathrm{p},\min }}{p_{\max }-p_c}\cdot p+\frac{D_{\mathrm{p},\max }-D_{\mathrm{p},\min }}{p_{\max }-p_{\mathrm{c}}}\cdot p_{\max }+D_{\mathrm{p},\min }\hfill & ,p>p_{\mathrm{c}}\end{array}\right.,$$

(54)

where $D_{\mathrm{p}}$, $D_{\mathrm{p},\max }$ and $D_{\mathrm{p},\min }$ are the working displacement, maximum displacement and the minimum displacement of the direct load-sensing variable pump, respectively; $p_{\max }$ is the maximum pressure of the system; and $p_{\mathrm{c}}$ is the initial pressure at which the pump begins to change variables. In addition, the maximum displacement of the pump needs to meet the maximum flow demand of the system, which can be obtained as:

$$D_{\mathrm{p},\max }\ge \frac{Q_{\max }}{n_{\max }{\eta }_{\mathrm{v}}},$$

(55)

where $Q_{\max }$ is the maximum flow rate as shown in Table 3; $n_{\max }$ is the maximum rotational speed as shown in Table 2; and ${\eta }_{\mathrm{v}}$ is the volumetric efficiency of the pump.

In addition, due to the direct connection between the motor and the pump via splines in the EHA, the output torque of the motor is the same as the input torque of the pump, which can be expressed as:

$$T_{\mathrm{m}}=T_{\mathrm{p}}+\Delta T_{\mathrm{p}},$$

(56)

where $T_{\mathrm{p}}$ is the output torque of the pump; $\Delta T_{\mathrm{p}}$ is the torque loss of the pump which can be obtained from Equation (21) to (24). Thus, the output torque of the motor can be finally expressed as:

$$T_{\mathrm{m}}=\left\{\begin{array}{cc}{C}_{\mathrm{p}}p{D}_{\mathrm{p},\max }+C_{\mathrm{v}}\mu n{D}_{\mathrm{p},\max }+C_{\mathrm{t}}{\rho }_{\mathrm{oil}}{n}^2{D}_{\mathrm{p},\max }^{5/3}+J_{\mathrm{pm}}{\alpha }_{\mathrm{p}}\hfill & ,p\le p_{\mathrm{c}}\\ \begin{array}{l}\left(C_{\mathrm{p}}p+C_{\mathrm{v}}\mu n\right)\left(-m\cdot p+m{p}_{\max }+D_{\mathrm{p},\min }\right)\\ +C_{\mathrm{t}}{\rho }_{\mathrm{oil}}{n}^2{\left(-m\cdot p+m{p}_{\max }+D_{\mathrm{p},\min }\right)}^{5/3}+J_{\mathrm{pm}}{\alpha }_{\mathrm{p}}\end{array}\hfill & ,p>p_{\mathrm{c}}\hfill \end{array}\right.,$$

(57)

where $C_{\mathrm{p}}$ is the coefficient which can be expressed as $C_{\mathrm{p}}=C_{\mathrm{s}}+\frac{1}{2\pi }$; $J_{\mathrm{pm}}$ is the sum of the rotational inertia of the motor and pump; and $m$ is an intermediate parameter which can be expressed as $m=\frac{D_{\mathrm{p},\max }-D_{\mathrm{p},\min }}{p_{\max }-p_c}$.

In addition, according to Equations (18) and (51), it can be found that motor mass and energy loss are directly related to rated torque. Therefore, it is critical to determine the rated torque of the motor in the early stages of EHA optimization design. In this study, the motor torque variation law under multiple sets of parameters was analyzed and the same simulation trend obtained according to the EHA working conditions shown in Table 3, combined with the motor torque calculation in Equation (57). The simulation results under one set of parameter conditions are shown in Figure 9.

According to the working conditions shown in Table 3, the working conditions from 1 to 4 require the motor to work continuously for a long time, and the rated torque of the motor needs to meet the maximum torque demand of these working conditions. As for working conditions 5 and 6, the motor working time is short and can be defined as transient working conditions. The maximum torque of the motor can be satisfied by the short time overload of the motor. Furthermore, according to the simulation results of Figure 9, the required maximum torque for working condition 1 can be defined as the rated torque of the motor.

Ultimately, $D_{\mathrm{p},\max }$, $D_{\mathrm{p},\min }$, $p_{\mathrm{c}}$ and $J_{\mathrm{pm}}$ can be chosen as the initial EHA design parameters combining the objective functions of motor–pump mass and energy loss, and the parameter ranges are defined in

Table 4. Multi-objective optimization parameters.

Design Variables	Symbols	Parameter Ranges	Units
Maximum displacement of the variable pump	$D_{\mathrm{p},\max }$	[2, 5]	mL/r
Initial pressure	$p_{\mathrm{c}}$	[1, 5]	MPa
Minimum displacement of the variable pump	$D_{\mathrm{p},\min }$	[0.1, 0.5]	mL/r
Rotational inertia of the motor and pump	$J_{\mathrm{pm}}$	[1 × 10−4, 3 × 10−4]	kg/m2

.

4. Multi-Objective Optimization Design

In order to obtain the optimal design parameters in the case of comprehensive optimal motor–pump mass and energy loss, the multi-objective particle swarm optimization (MOPSO) algorithm was adopted in this paper. The calculation process of the MOPSO algorithm is shown in Figure 10, while the velocity and position of the particle update functions can be defined as follows:

$$v_i\left(t+1\right)={\omega }_{\mathrm{p}}{v}_i\left(t\right)+c_1{r}_1\left(x{p}_i\left(t\right)-x_i\left(t\right)\right)+c_2{r}_2\left(xg\left(t\right)-x_i\left(t\right)\right),$$

(58)

$$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t+1\right),$$

(59)

where $x_i$ is the position of the i-th particle; $v_i$ is the velocity of the i-th particle; $x{p}_i$ denotes the best position of the i-th particle; $xg$ is the best position found in particle swarm; ${\omega }_{\mathrm{p}}$ is a weight for one particle, which can be defined as 0.7298; $c_1$ and $c_2$ are the acceleration coefficients of the particles; and $r_1$ and $r_2$ are random numbers that follow a normal distribution.

According to the motor–pump mass and energy loss models, the optimization objectives are selected as $f_1=\min \left(m_{\mathrm{pm}}\right)$ and $f_2=\min \left(E_{\mathrm{pm}}\right)$, respectively. Meanwhile, the mass model $m_{\mathrm{pm}}$ and the energy loss model $E_{\mathrm{pm}}$ are obtained in Section 2. The particle population size is set to 300, the size of the external reserve set is 120, and the number of iterations is set to 200 during the optimal simulation. The Pareto front solution of optimization results are obtained in Figure 11.

It should be noted that the Pareto front is a set of optimized solutions, and how to select optimal design parameters from the Pareto front requires further analysis. Therefore, in order to obtain an optimal set of design parameters in Pareto front solutions, a parameter relationship matrix (PRM) for EHA is constructed based on the Quality Function Development (QFD) method. The PRM of the EHA can be established as

Table 5. The PRM of EHA.

Design Variables	Weights
Mass	5
Energy Loss	3
Maintainability	-

. The greater the weight of the characteristic parameters in the table, the greater the importance of the feature parameter to the system. The weight Y indicates the requirement that the system must have maintainability. For aviation EHA, mass is the decisive factor for whether it can be applied to the aircraft, so a high value of quality weight is given in the PRM.

Furthermore, the comprehensive evaluation function of the EHA can be constructed as follows according to the PRM.

$$\begin{array}{cc}\hfill F& =\min f\left(f_{\mathrm{m}},f_{\mathrm{E}}\right)\hfill \\ & =\min \left[{\left(\frac{f_{\mathrm{m}}}{f_{\mathrm{m}0}}\right)}^{{\gamma }_{\mathrm{m}}}+{\left(\frac{f_{\mathrm{E}}}{f_{\mathrm{E}0}}\right)}^{{\gamma }_{\mathrm{E}}}\right]\hfill \end{array},$$

(60)

where $F$ is the coefficient of comprehensive evaluation function; $f_{\mathrm{m}}$ is mass function of the system which can be expressed as $f_{\mathrm{m}}=m_{\mathrm{motor}}+m_{\mathrm{pump}}$; $f_{\mathrm{E}}$ is energy loss function of the system which can be expressed as $f_{\mathrm{E}}=E_{\mathrm{motor}}+E_{\mathrm{pump}}$; and $f_{\mathrm{m}0}$ and $f_{\mathrm{E}0}$ are acceptable initial values for system mass and energy loss, respectively. ${\gamma }_{\mathrm{m}}$ and ${\gamma }_{\mathrm{E}}$ are the coefficients related to the weight in the PRM which can be obtained as follows:

$${\gamma }_{\mathrm{m}}=1+\frac{{\delta }_{\mathrm{m}}+1}{2}=1+\frac{5+1}{2}=4,$$

(61)

$${\gamma }_{\mathrm{E}}=1+\frac{{\delta }_{\mathrm{E}}+1}{2}=1+\frac{3+1}{2}=3,$$

(62)

Finally, the comprehensive evaluation results of each design solution in Pareto front set are obtained in Figure 12. The smallest evaluation result in the figure can be regarded as the optimal design solution which is listed in

Table 6. Multi-objective optimization design results for EHA.

Design Variables	Symbols	Data	Units
Maximum displacement of the variable pump	$D_{\mathrm{p},\max }$	3.2	mL/r
Initial pressure	$p_{\mathrm{c}}$	5	MPa
Minimum displacement of the variable pump	$D_{\mathrm{p},\min }$	0.4	mL/r
Rotational inertia of the motor and pump	$J_{\mathrm{pm}}$	2.5 × 10−4	kg/m2
Rated torque of the motor	$T_{\mathrm{nom}}$	4.8	Nm
Mass of the pump	$m_{\mathrm{pump}}$	3.8	kg
Mass of the motor	$m_{\mathrm{motor}}$	3.2	kg
Energy loss in one period	$E_{\mathrm{EHA}}$	9787	J

.

5. Experimental Validation

In order to verify the validity of the optimization results, a prototype of the EHA was designed and the test rig was constructed as shown in Figure 13. Moreover, the design parameters of the motor–pump were determined from Table 6. The test rig was composed of the DC power source, EHA prototype, motor driver and controller and the host computer.

Working condition 1 in Table 3 was chosen as the system input during the experiment. Meanwhile, the system load in condition 1 was ignored due to the experimental conditions without loading device. It should be further clarified that because EHA’s position is a closed-loop control, the system flow rate given in Table 3 could not be directly used as the system input. Rather, it needed to be converted according to the parameters of the actuator cylinder to obtain the displacement change rule of the actuator cylinder, which was used as the given target of the EHA position control. The displacement response and the power loss of the EHA are shown in Figure 14 and Figure 15, respectively.

As can be seen in Figure 14, the displacement response of the EHA designed according to the optimized parameters can follow the position command satisfactorily, which suggests the system performance is good.

Since the external load effect is neglected, the power loss of the motor–pump can be approximated by the input power of the EHA. From Figure 15, it can be seen that the simulation and experimental data of the motor–pump loss have the same trend, and the difference is not significant, which illustrates the effectiveness of the optimized design parameters. The motor–pump losses obtained from the experiments were slightly larger than the simulation data, mainly due to the fact that only the motor–pump losses were taken into account in the simulation process while the actuator losses were neglected.

6. Conclusions

This paper proposes a parameter-matching optimization design method of a motor–pump based on MOPSO for EHA. The mass and energy consumption models of the motor–pump are first constructed using similarity criteria based on a detailed analysis of the motor and pump design conditions. In addition, the design indicators and working conditions of the EHA are defined and the parameter determination, such as the motor rated torque, is clarified. The motor–pump design parameters have been optimized using MOPSO with the objective of minimizing the mass and energy losses. Furthermore, a comprehensive evaluation function constructed based on PRM and the optimized design parameters for the motor–pump were obtained. Finally, in order to verify the validity of the design parameters, an EHA prototype was designed and the test rig constructed. The experimental results show that the optimized EHA system had better displacement tracking performance, and the motor–pump energy consumption matches well with the theoretical calculation results. The research presented in this paper provides an effective method for optimizing motor–pump parameters of EHA, which can lead to significant savings in EHA pre-design costs and provide a theoretical basis for an EHA optimal design.