Reliability Modelling through the Three-Parametric Weibull Model Based on Microsoft Excel Facilities
Abstract
:1. Introduction
- Estimating the function of distribution of failure times using the BETA.INV function;
- Identification of the bi-parametric Weibull model by the known method of linear regression;
- Identification of the optimal location parameter—for which the resulting three-parametric Weibull model has the maximum coefficient of determination R;
- Argumentation the efficiency of the proposed method, based exclusively on the facilities of the Microsoft Excel program, by the superior likelihood of the three-parametric Weibull model that are obtained compared to the bi-parametric model.
2. Methods and Results
2.1. The Three-Parametric Weibull Model Parameters
- -
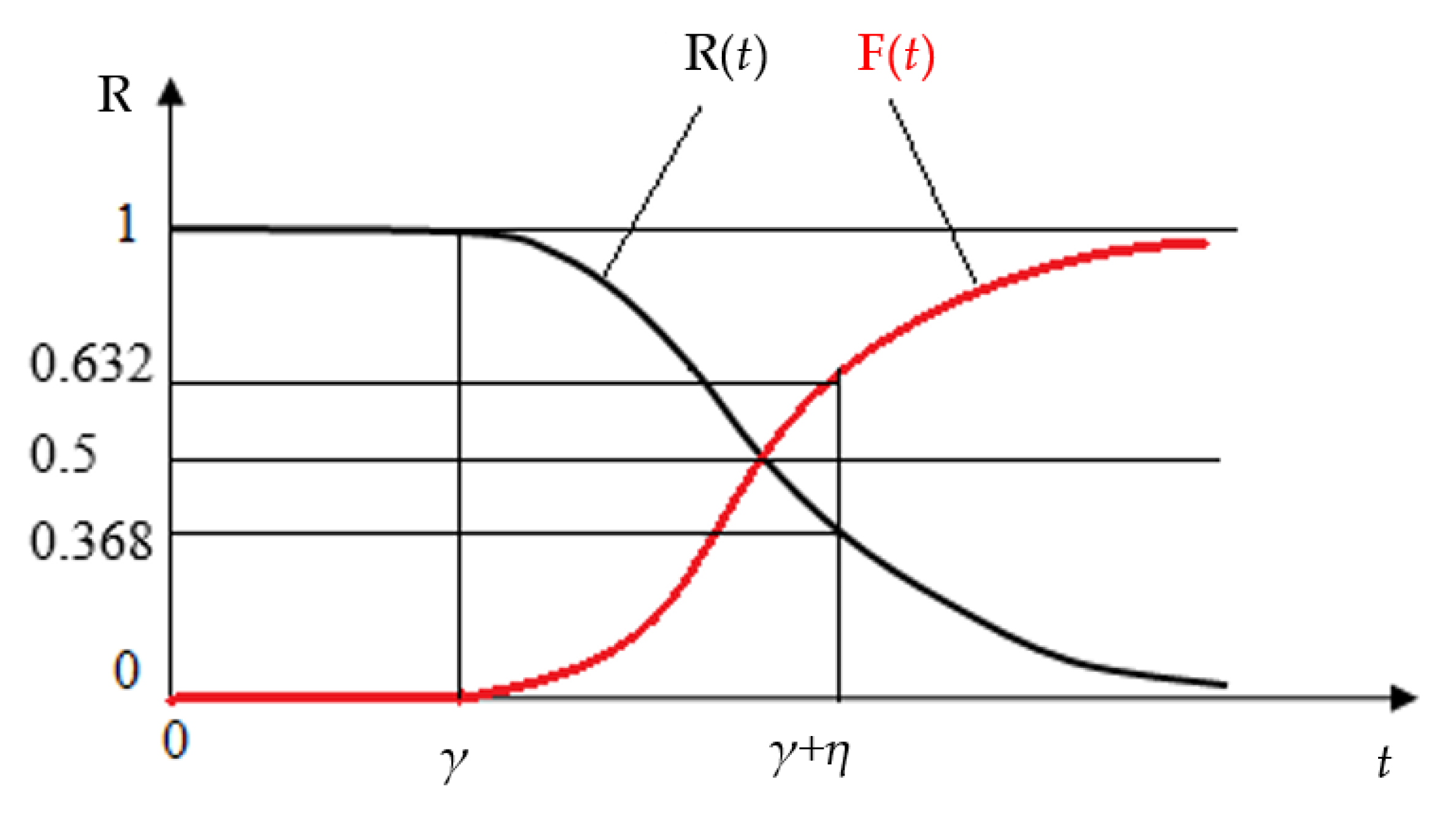
- γ—location parameter or position parameter, this being a constant value that defines when the variation of the survival function R(t) starts.
- -
- η—scale parameter, which characterizes the extent of the distribution on the time axis. So, in the particular case when (t − γ) is equal to η, this parameter can be highlighted; because R(t) calculated with the relation (1) will be:
- -
- β—shape parameter, is dimensionless and is the parameter that determines the variation of the variation curves for the reliability indicators.
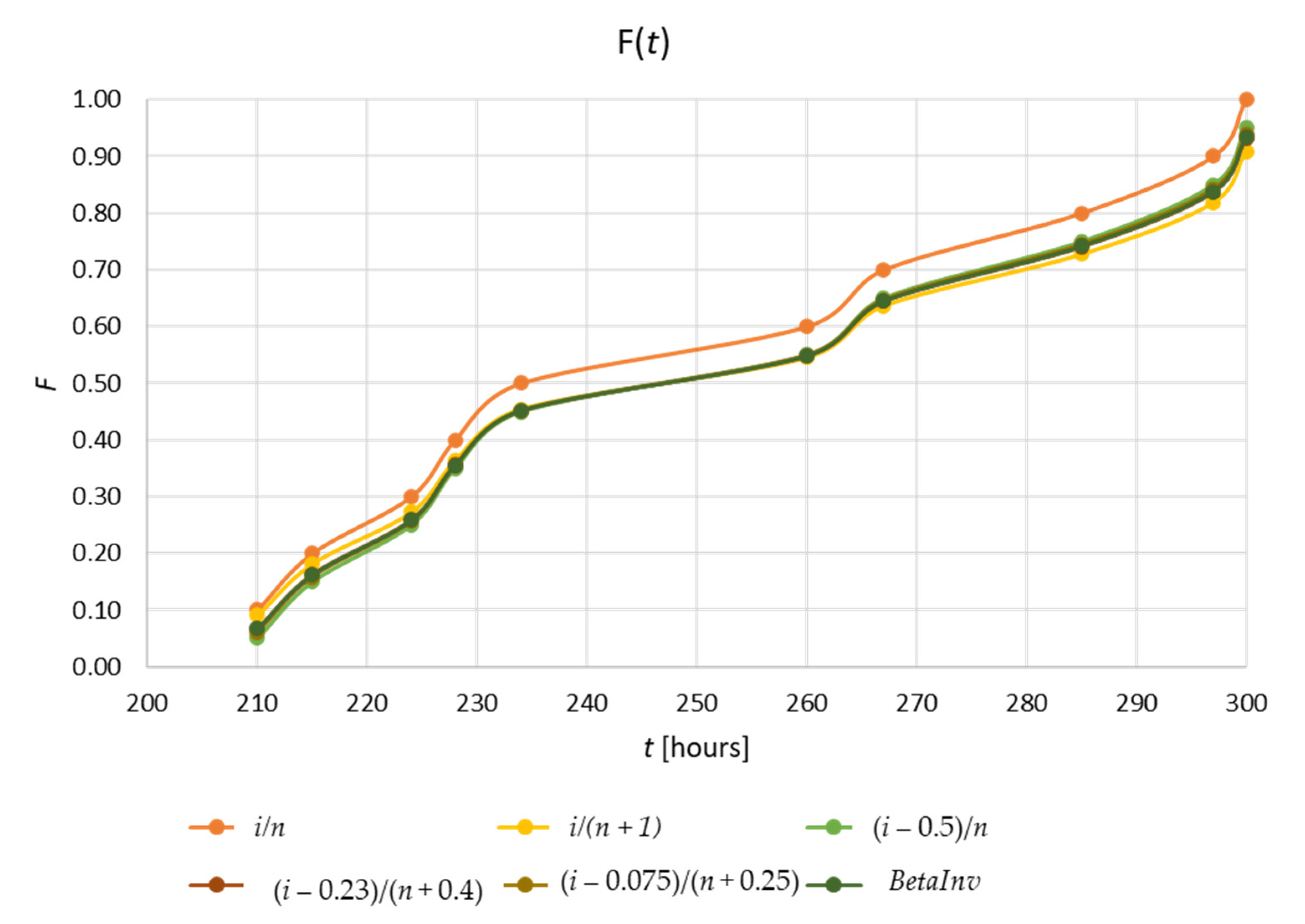
2.2. Choosing the Optimal Estimator for the Distribution Function F(t)
- -
- the Herd–Johnson estimator, used in 1960–1964, but also proposed by Weibull in 1939 [4]:
- -
- the Hazen estimator (2014):
- -
- the Benard estimator (1953):
- -
- the Blom estimator (1958) [20]:
2.3. Determining the Parameters of the Three-Parametric Weibull Model
- -
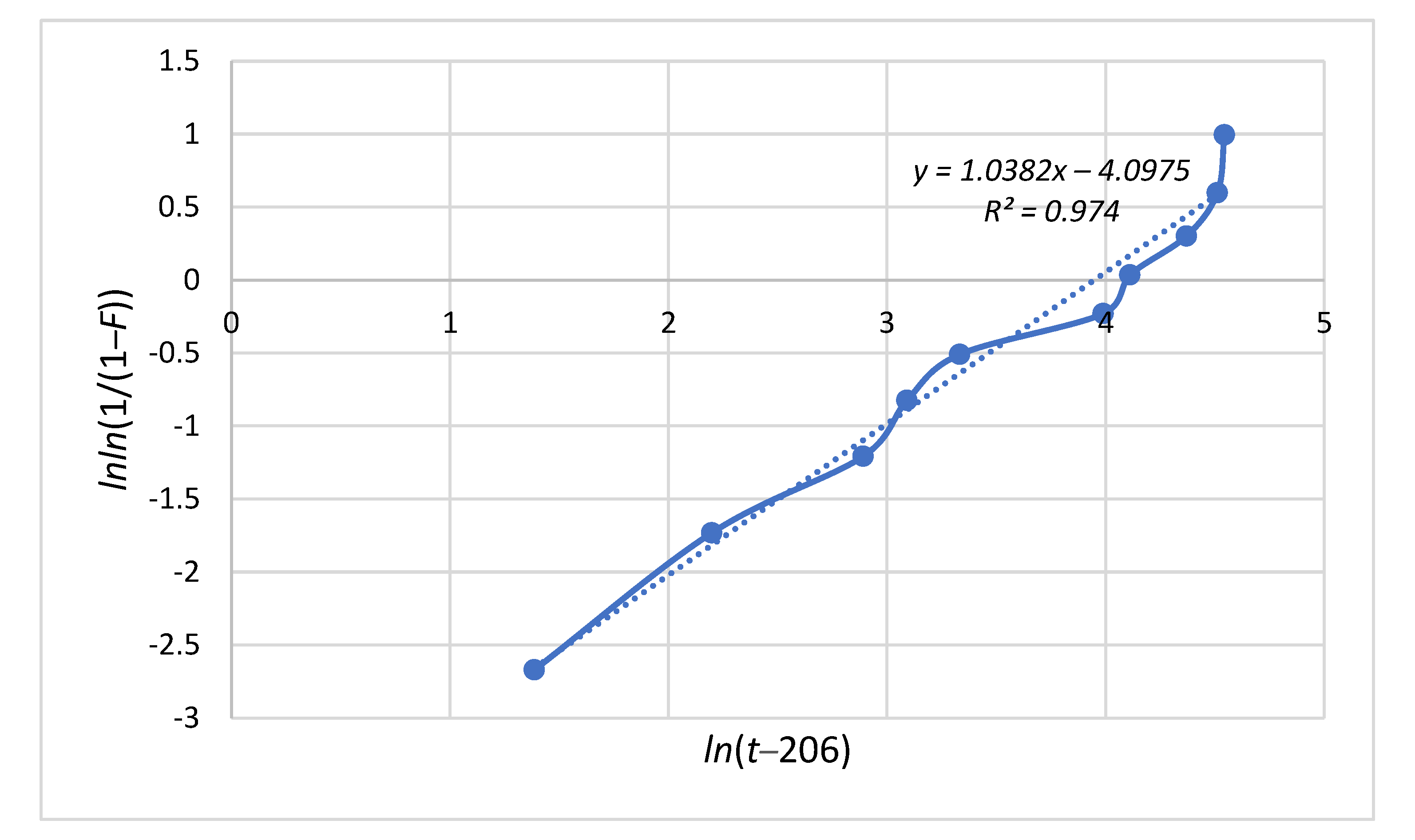
- shape parameter: β = 1.0382.
- -
- the scale parameter: .
3. Discussion
- In many works MR is approximated with various algebraic estimators (i.e., Benard, Hazen etc.), more or less adequate, but now the MR values can be accurately identified, using the BETA.INV function that is available in the Microsoft Excel calculator.
- The use of the location parameter is mandatory in some cases, such as for the product operability, where the location parameter shows the guaranteed operating time of the object.
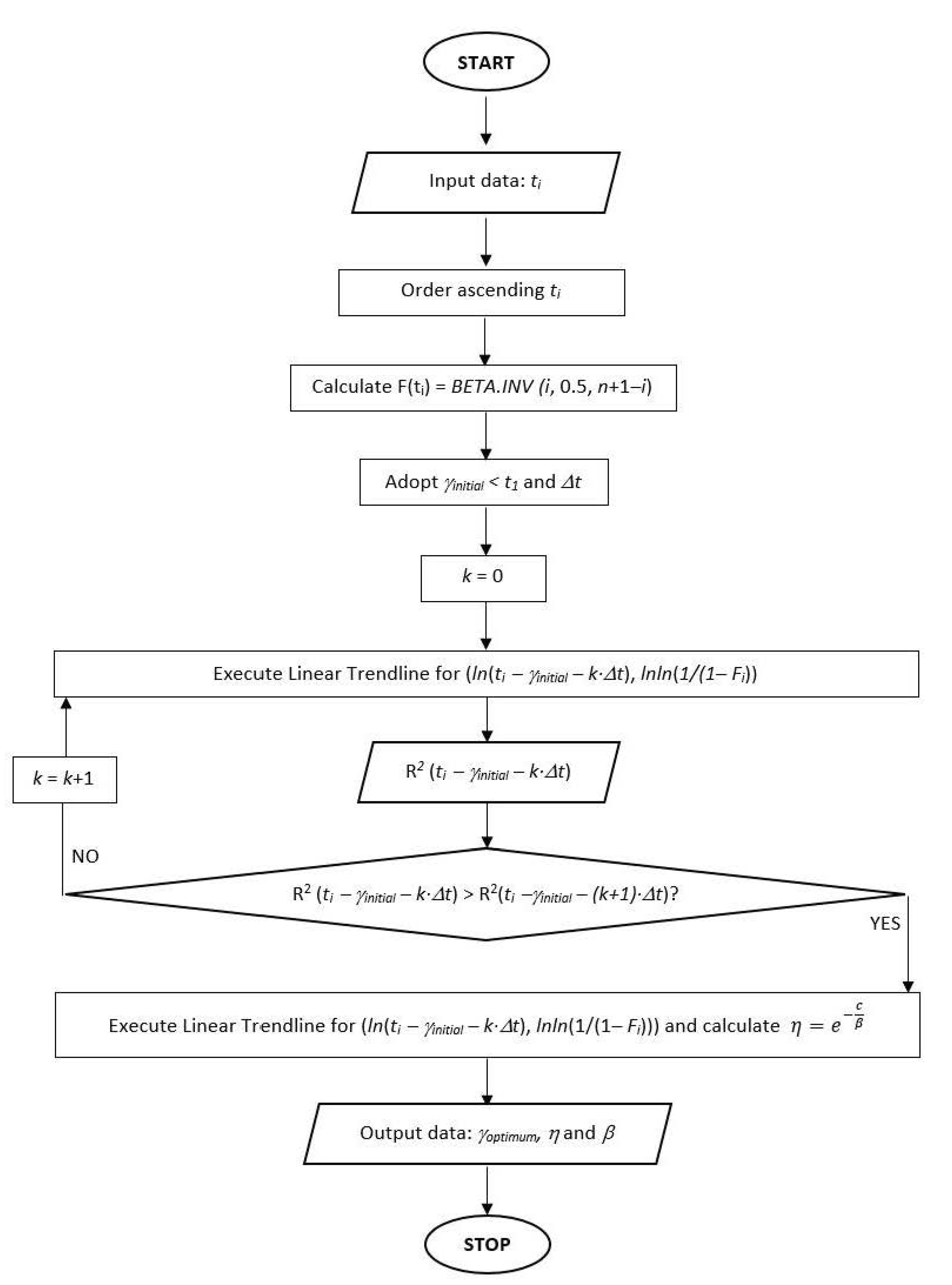
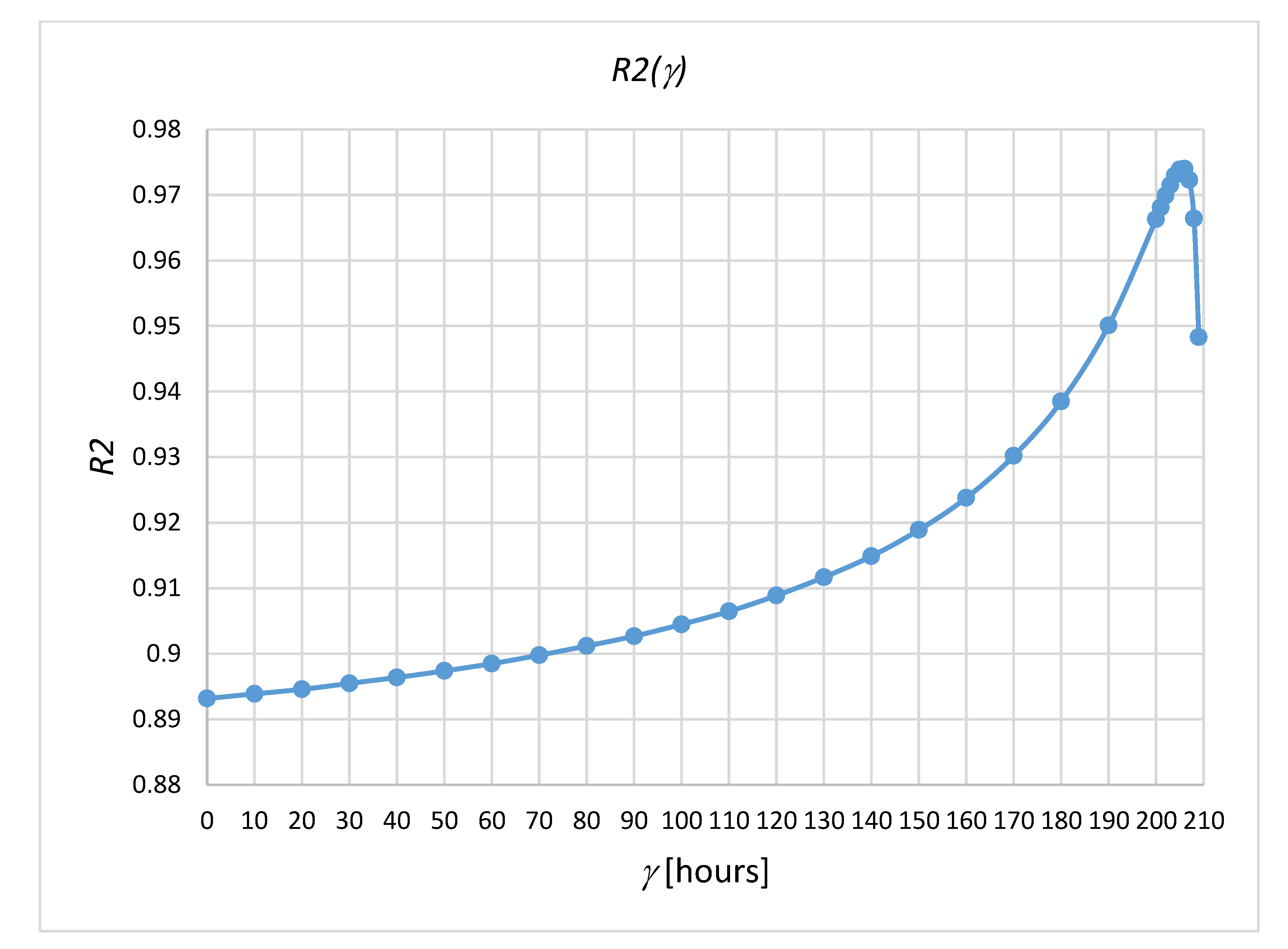
- By representing in logarithmic coordinates, we determined three-parametric Weibull models for different values that were initially adopted for the location parameter.
- Using as a criterion the coefficient of determination that was obtained using the trendline function for the linear model, it was possible to identify, by successive tests, the optimal value of the location parameter.
- The accuracy with which the optimal parameter γoptimum is identified is equal to the value of the adopted step t by the user, which can be more or less fine, depending on the desired level of detail.
- The proposed methodology can be easily translated into a calculation program, as can be seen in the flowchart that was made.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basumatary, H.; Sreevalsan, E.; Sasi, K.K. Weibull parameter estimation—A comparison of different methods. Wind Eng. 2005, 29, 309–315. [Google Scholar] [CrossRef]
- IEC 61649:2008; Weibull Analysis. IEC: Geneva, Switzerland, 2008.
- Elmahdy, E.E. A new approach for Weibull modeling for reliability life data analysis. Appl. Math. Comput. 2015, 250, 708–720. [Google Scholar] [CrossRef]
- Elsayed, A.E. Reliability Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Evans, J.W.; Kretschmann, D.E.; Green, D.W. Procedures for Estimation of Weibull Parameters; USDA Forest Service, Forest Products Laboratory: Madison, WI, USA, 2019. [Google Scholar] [CrossRef]
- Fernandez, A.; Vazquez, M. Improved Estimation of Weibull Parameters Considering Unreliability Uncertainties. IEEE Trans. Reliab. 2011, 61, 32–40. [Google Scholar] [CrossRef]
- Lei, Y. Evaluation of three methods for estimating the Weibull distribution parameters of Chinese pine (Pinus tabulaeformis). J. For. Sci. 2008, 54, 566–571. [Google Scholar] [CrossRef]
- McCool, J.I. Inference on the Weibull Location Parameter. J. Qual. Technol. 1998, 30, 119–126. [Google Scholar] [CrossRef]
- Morariu, C.O.; Şimon, A.E. Estimation of the Weibull Location Parameter through the Correlation Coefficient Method. Bull. Transilv. Univ. Brașov 2004, 11, 187–190. [Google Scholar]
- Palisson, F. Détermination des paramètres du modèle de Weibull à partir de la méthode de l’actuariat, Revue de statistique appliquée. Tome 1989, 37, 5–39. Available online: http://www.numdam.org/article/RSA_1989__37_4_5_0.pdf (accessed on 20 January 2022).
- Pobočíková, I.; Sedliačková, Z. Comparison of four methods for estimating the Weibull distribution parameters. Appl. Math. Sci. 2014, 8, 4137–4149. [Google Scholar] [CrossRef]
- Westfall, P.; Henning, K. Understanding Advanced Statistical Methods; CRC Press: Boca Raton, FL, USA, 2013; ISBN 9781466512108. [Google Scholar]
- Liu, S.; Wu, H.; Meeker, W.Q. Understanding and Addressing the Unbounded “Likelihood” Problem. Am. Stat. 2015, 69, 191–200. [Google Scholar] [CrossRef]
- Zaiontz, C. Fitting a Weibull Distribution via Regression. 2021. Available online: https://www.real-statistics.com/distribution-fitting/fitting-weibull-regression/ (accessed on 20 January 2022).
- Zhao, J. Robust Parameter Estimation in the Weibull and the Birnbaum-Saunders Distribution. Master’s Thesis, Clemson University, Clemson, SC, USA, 2012. [Google Scholar]
- Assis, R.; Marques, P.C. A Dynamic Methodology for Setting Up Inspection Time Intervals in Conditional Preventive Maintenance. Appl. Sci. 2021, 11, 8715. [Google Scholar] [CrossRef]
- Rantini, D.; Iriawan, N. Irhamah On the Reversible Jump Markov Chain Monte Carlo (RJMCMC) Algorithm for Extreme Value Mixture Distribution as a Location-Scale Transformation of the Weibull Distribution. Appl. Sci. 2021, 11, 7343. [Google Scholar] [CrossRef]
- Villa-Covarrubias, B.; Piña-Monarrez, M.R.; Barraza-Contreras, J.M.; Baro-Tijerina, M. Stress-Based Weibull Method to Select a Ball Bearing and Determine Its Actual Reliability. Appl. Sci. 2020, 10, 8100. [Google Scholar] [CrossRef]
- Sourri, P.; Argyri, A.A.; Panagou, E.Z.; Nychas, G.-J.E.; Tassou, C.C. Alicyclobacillus acidoterrestris Strain Variability in the Inactivation Kinetics of Spores in Orange Juice by Temperature-Assisted High Hydrostatic Pressure. Appl. Sci. 2020, 10, 7542. [Google Scholar] [CrossRef]
- Park, C. A Note on the Existence of the Location Parameter Estimate of the Three-Parameter Weibull Model Using the Weibull Plot. Math. Probl. Eng. 2018, 2018, 6056975. [Google Scholar] [CrossRef]
- Barraza-Contreras, J.M.; Piña-Monarrez, M.R.; Molina, A. Fatigue-Life Prediction of Mechanical Element by Using the Weibull Distribution. Appl. Sci. 2020, 10, 6384. [Google Scholar] [CrossRef]
- Molina, A.; Piña-Monarrez, M.R.; Barraza-Contreras, J.M. Weibull S-N Fatigue Strength Curve Analysis for A572 Gr. 50 Steel, Based on the True Stress—True Strain Approach. Appl. Sci. 2020, 10, 5725. [Google Scholar] [CrossRef]
- Zhao, Q.; Jia, X.; Cheng, Z.; Guo, B. Bayesian Estimation of Residual Life for Weibull-Distributed Components of On-Orbit Satellites Based on Multi-Source Information Fusion. Appl. Sci. 2019, 9, 3017. [Google Scholar] [CrossRef]
- Ono, K. A Simple Estimation Method of Weibull Modulus and Verification with Strength Data. Appl. Sci. 2019, 9, 1575. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Villanueva, D. Wind Turbine Power Curves Based on the Weibull Cumulative Distribution Function. Appl. Sci. 2018, 8, 1757. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. A Software Reliability Model with a Weibull Fault Detection Rate Function Subject to Operating Environments. Appl. Sci. 2017, 7, 983. [Google Scholar] [CrossRef]
- Dubey, S.D. Hyper-efficient estimator of the location parameter of the weibull laws. Nav. Res. Logist. Q. 1966, 13, 253–264. [Google Scholar] [CrossRef]
- Dubey, S.D. On some statistical inferences for weibull laws. Nav. Res. Logist. Q. 1966, 13, 227–251. [Google Scholar] [CrossRef]

| i | ti [Hours] | i/n | i/(n + 1) | (i − 0.5)/n | (i − 0.3)/(n + 0.4) | (i − 0.375)/(n + 0.25) | BETA.INV (0.5; i; n + 1 − i) |
|---|---|---|---|---|---|---|---|
| 1 | 210 | 0.100 | 0.091 | 0.050 | 0.067 | 0.061 | 0.067 |
| 2 | 215 | 0.200 | 0.182 | 0.150 | 0.163 | 0.159 | 0.162 |
| 3 | 224 | 0.300 | 0.273 | 0.250 | 0.260 | 0.256 | 0.259 |
| 4 | 228 | 0.400 | 0.364 | 0.350 | 0.356 | 0.354 | 0.355 |
| 5 | 234 | 0.500 | 0.455 | 0.450 | 0.452 | 0.451 | 0.452 |
| 6 | 260 | 0.600 | 0.545 | 0.550 | 0.548 | 0.549 | 0.548 |
| 7 | 267 | 0.700 | 0.636 | 0.650 | 0.644 | 0.646 | 0.645 |
| 8 | 285 | 0.800 | 0.727 | 0.750 | 0.740 | 0.744 | 0.741 |
| 9 | 297 | 0.900 | 0.818 | 0.850 | 0.837 | 0.841 | 0.838 |
| 10 | 300 | 1.000 | 0.909 | 0.950 | 0.933 | 0.939 | 0.933 |
| i | ti [Hours] | ln(ti) | F = BETA.INV (0.5; i; n + 1 − i) | lnln [1/(1 − F)] |
|---|---|---|---|---|
| 1 | 210 | 5.3471 | 0.0670 | −2.6691 |
| 2 | 215 | 5.3706 | 0.1623 | −1.7313 |
| 3 | 224 | 5.4116 | 0.2586 | −1.2067 |
| 4 | 228 | 5.4293 | 0.3551 | −0.8240 |
| 5 | 234 | 5.4553 | 0.4517 | −0.5093 |
| 6 | 260 | 5.5607 | 0.5483 | −0.2297 |
| 7 | 267 | 5.5872 | 0.6449 | 0.0347 |
| 8 | 285 | 5.6525 | 0.7414 | 0.3020 |
| 9 | 297 | 5.6937 | 0.8377 | 0.5980 |
| 10 | 300 | 5.7038 | 0.9330 | 0.9946 |
| i | t [Hours] | Int | F = BETA.INV (0.5; i; n + 1 − i) | lnln [1/(1 − F)] |
|---|---|---|---|---|
| 1 | 4 | 1.3863 | 0.0670 | −2.6691 |
| 2 | 9 | 2.1972 | 0.1623 | −1.7313 |
| 3 | 18 | 2.8904 | 0.2586 | −1.2067 |
| 4 | 22 | 3.0910 | 0.3551 | −0.8240 |
| 5 | 28 | 3.3322 | 0.4517 | −0.5093 |
| 6 | 54 | 3.9890 | 0.5483 | −0.2297 |
| 7 | 61 | 4.1109 | 0.6449 | 0.0347 |
| 8 | 79 | 4.3694 | 0.7414 | 0.3020 |
| 9 | 91 | 4.5109 | 0.8377 | 0.5980 |
| 10 | 94 | 4.5433 | 0.9330 | 0.9946 |
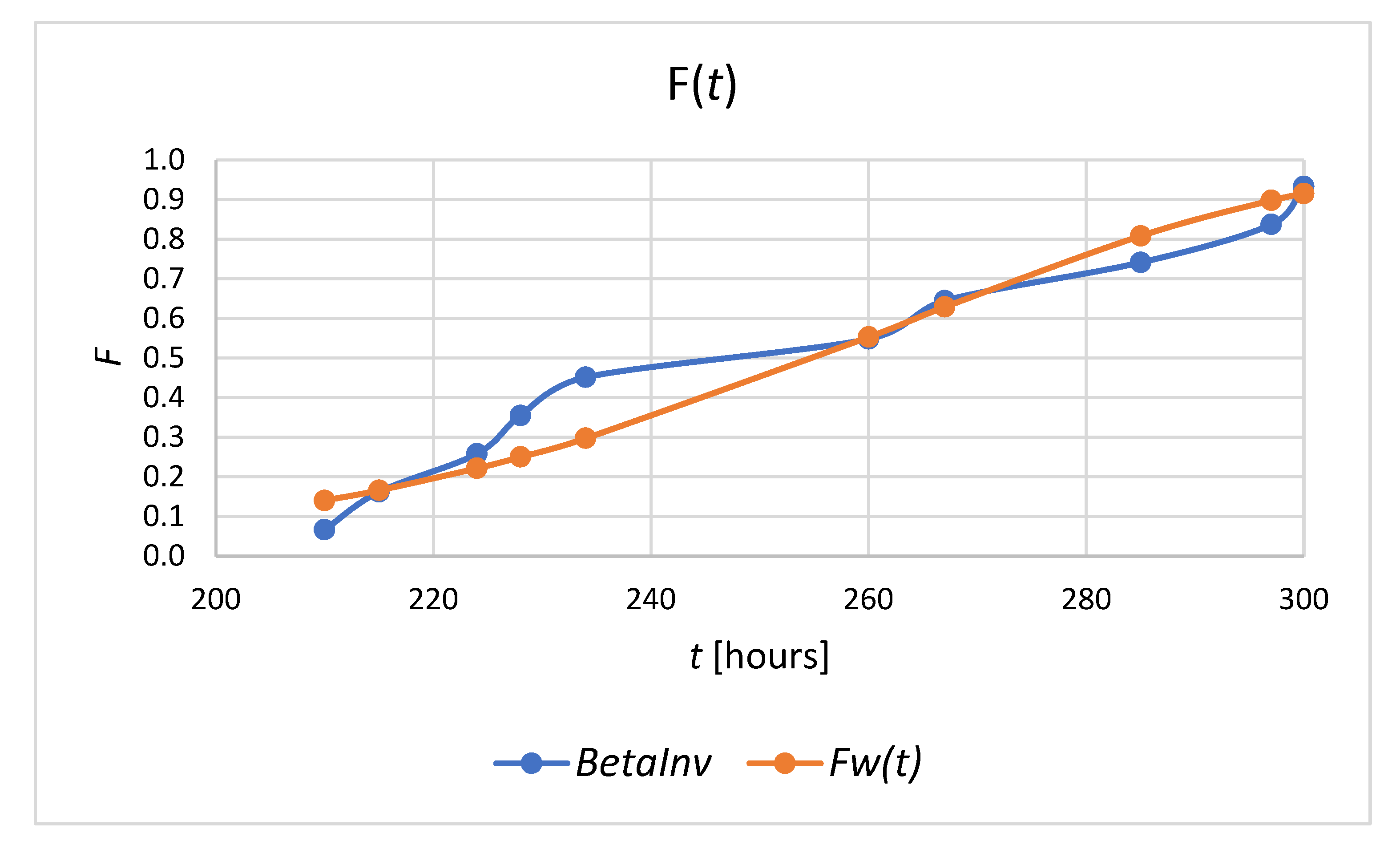
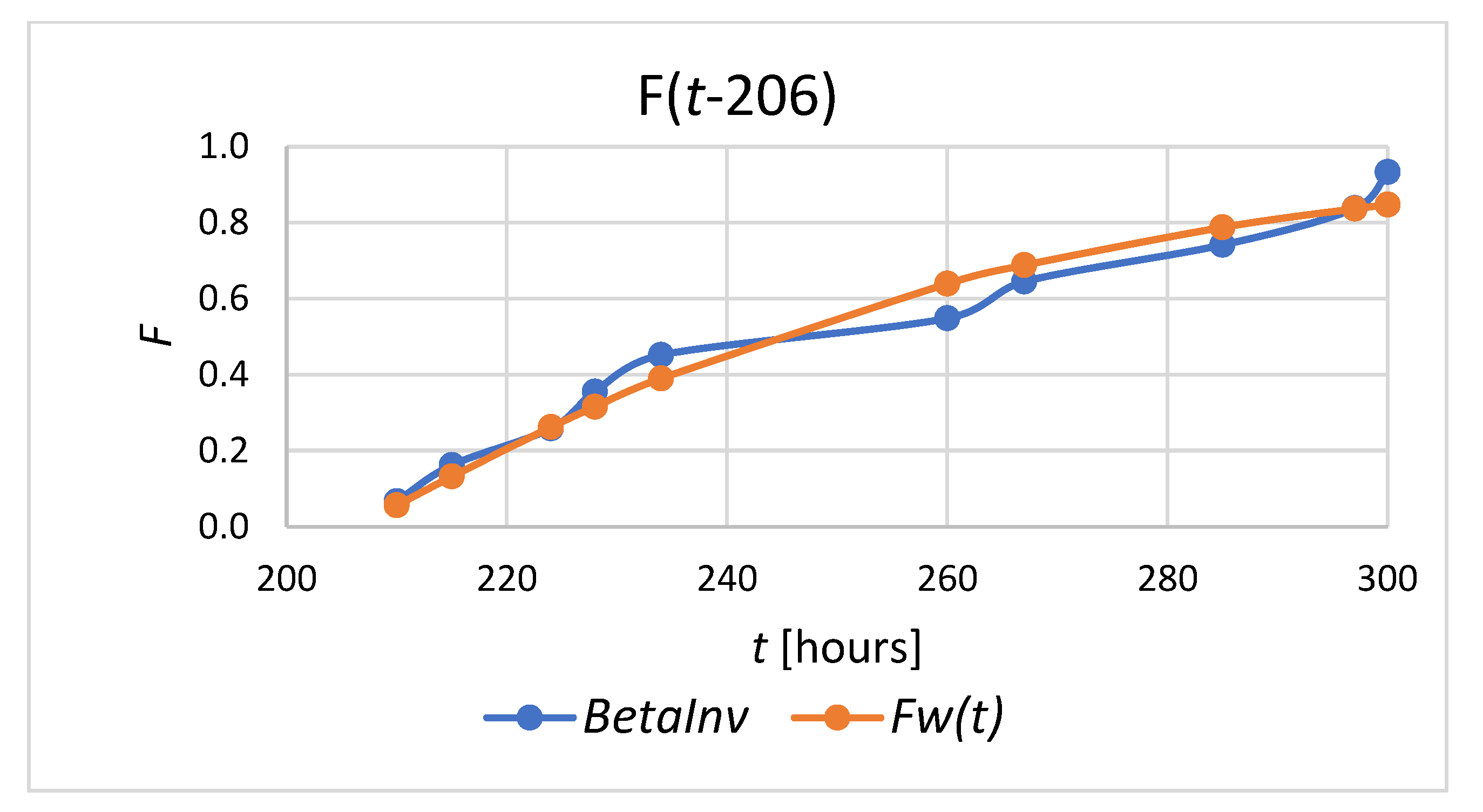
| T [Hours] | BETA.INV | F(t) | |
|---|---|---|---|
| WEIBULL.DIST (t; beta; eta; TRUE) | WEIBULL.DIST (t-206; beta; eta; TRUE) | ||
| 210 | 0.0670 | 0.1404 | 0.0564 |
| 215 | 0.1623 | 0.1663 | 0.1322 |
| 224 | 0.2586 | 0.2218 | 0.2623 |
| 228 | 0.3551 | 0.2503 | 0.3157 |
| 234 | 0.4517 | 0.2975 | 0.3903 |
| 260 | 0.5483 | 0.5532 | 0.6392 |
| 267 | 0.6449 | 0.6292 | 0.6884 |
| 285 | 0.7414 | 0.8086 | 0.7877 |
| 297 | 0.8377 | 0.8981 | 0.8365 |
| 300 | 0.9330 | 0.9155 | 0.8469 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Titu, A.M.; Boroiu, A.A.; Boroiu, A.; Dragomir, M.; Pop, A.B.; Titu, S. Reliability Modelling through the Three-Parametric Weibull Model Based on Microsoft Excel Facilities. Processes 2022, 10, 1585. https://doi.org/10.3390/pr10081585
Titu AM, Boroiu AA, Boroiu A, Dragomir M, Pop AB, Titu S. Reliability Modelling through the Three-Parametric Weibull Model Based on Microsoft Excel Facilities. Processes. 2022; 10(8):1585. https://doi.org/10.3390/pr10081585
Chicago/Turabian StyleTitu, Aurel Mihail, Andrei Alexandru Boroiu, Alexandru Boroiu, Mihai Dragomir, Alina Bianca Pop, and Stefan Titu. 2022. "Reliability Modelling through the Three-Parametric Weibull Model Based on Microsoft Excel Facilities" Processes 10, no. 8: 1585. https://doi.org/10.3390/pr10081585
APA StyleTitu, A. M., Boroiu, A. A., Boroiu, A., Dragomir, M., Pop, A. B., & Titu, S. (2022). Reliability Modelling through the Three-Parametric Weibull Model Based on Microsoft Excel Facilities. Processes, 10(8), 1585. https://doi.org/10.3390/pr10081585











