Automated Intracranial Hematoma Classification in Traumatic Brain Injury (TBI) Patients Using Meta-Heuristic Optimization Techniques

Abstract

Traumatic Brain Injury (TBI) is a devastating and life-threatening medical condition that can result in long-term physical and mental disabilities and even death. Early and accurate detection of Intracranial Hemorrhage (ICH) in TBI is crucial for analysis and treatment, as the condition can deteriorate significantly with time. Hence, a rapid, reliable, and cost-effective computer-aided approach that can initially capture the hematoma features is highly relevant for real-time clinical diagnostics. In this study, the Gray Level Occurrence Matrix (GLCM), the Gray Level Run Length Matrix (GLRLM), and Hu moments are used to generate the texture features. The best set of discriminating features are obtained using various meta-heuristic algorithms, and these optimal features are subjected to different classifiers. The synthetic samples are generated using ADASYN to compensate for the data imbalance. The proposed CAD system attained 95.74% accuracy, 96.93% sensitivity, and 94.67% specificity using statistical and GLRLM features along with KNN classifier. Thus, the developed automated system can enhance the accuracy of hematoma detection, aid clinicians in the fast interpretation of CT images, and streamline triage workflow.

1. Introduction

Traumatic Brain Injury (TBI) is a neurological disorder with high rates of disability and mortality worldwide. TBI includes both primary and secondary injuries, which can progressively deteriorate brain function. Hence, most TBI survivors suffer from physical and mental disabilities that require long-term support and medical attention [1,2,3]. TBI can cause accumulation of blood (hemorrhage) inside the cranium leading to increased intracranial pressure. The global annual frequency of TBI occurrence and mortality are predicted to be 369 and 20, respectively, among 100,000 subjects. Approximately, 5–10% of mortality is due to injuries, and 40% of the mortality can be attributed to TBI. There was an 8.4% increase in the age-standardized prevalence of TBI between 1990 and 2016 [4]. Therefore, early identification and diagnosis of hemorrhage is crucial for TBI severity detection and patient management.

Computed Tomography (CT) is the gold-standard used for hematoma detection due to its high speed, wide availability, low cost, and high sensitivity [5,6]. However, rapid and accurate manual diagnosis of Intracranial Hemorrhage (ICH) is a tedious and laborious task due to the inherent limitations present in CT grayscale images including noise, artefacts, uneven boundaries, variations in pixel-wise intensities, and poor tissue contrast. Existing research studies shows that the occurrence of significant misinterpretations and discrepancies is a major problem in the detection of hematoma, especially by resident doctors without input from expert radiologists [7,8]. Manual quantification of hematoma is also subjected to observer variabilities and may introduce estimation errors, particularly for large, irregular, and acute hematoma cases [9,10]. Manual inspection and estimation is a hectic and daunting process that may generate inadvertent delays and errors in the detection process, particularly in a large clinical set-up environment [11,12]. Therefore, automated techniques for fast, reliable, and accurate detection of ICH using Computer Aided Diagnosis (CAD) systems can facilitate better clinical care and patient outcome.

2. Related Work

CAD systems offer more reliable, reproducible, and accurate clinical features, which can aid clinicians in appropriate treatment, planning, and strategic decision-making [13,14]. Computer-assisted techniques can significantly reduce human error and enable quick and cost-effective detection and evaluation of hematoma.

Several CAD systems proposed for brain related classification work are given below. The Probabilistic Neural Network (PNN) classifier combined with entropy features has obtained a classification accuracy of 97.37% [15]. The SVM with wavelets, GLCM, and statistical features yielded an accuracy of 80% [16]. The hierarchical classification approach with handcrafted features have been used for multiclass labelling [17]. An automated model using shape-based features and a logistic classifier yielded an accuracy of 92% [18]. A hematoma classification technique employed the C4.5 algorithm to a set of features extracted based on the axes of the major hyperdense areas in CT slices [19]. The SVM-based pathological slice detection algorithm compared the texture and histogram features extracted from both the brain hemispheres and yielded an accuracy of 90% [20]. The subarachnoid hematoma (SAH) detection model applied a Bayesian classifier with distance features obtained from different anatomical landmarks and yielded a sensitivity of 100% [21]. An automated model extracted features pertaining to position, shape, and size for classification on segmented blood clusters. The authors have reported a sensitivity of 98% [22]. A bleed area detection approach that used information about the location and intensity features in CT slices reported a sensitivity of 82.5% [23]. The random classifier with handcrafted intensity features was able to predict the voxel level ICH probability with a DSI of 0.899 [24]. A symmetry-based detection approach was able to diagnose acute ICH in three-dimensional CT images with an accuracy of 80.6% [25]. A hematoma detection technique involving adaptive thresholding, case-based reasoning, and a genetic algorithm was proposed in [26].

From the above literature, it is evident that the existing CAD systems have utilized various features and machine learning algorithms for hematoma classification. However, only a handful of studies include the removal of noisy and redundant features, which is an important step for significantly improving classification performance, especially for large and challenging heterogeneous datasets. The majority of the reported systems involve complex engineering techniques such as image registration and skull stripping in the initial phases of automation. These methods require specific rules and selection or adjustment of control parameters to obtain maximum performance. Some of these methods are time consuming, expensive, and require manual involvement at various levels. Hence, there is a need for a fast, accurate, efficient, and fully automated CAD system for hematoma detection that will lead to improved patient outcome and quality of care. The main objective of this research study is to develop a simple, rapid, and efficient CAD system for identification of hematoma with significant and discerning sets of textural features.

3. Materials

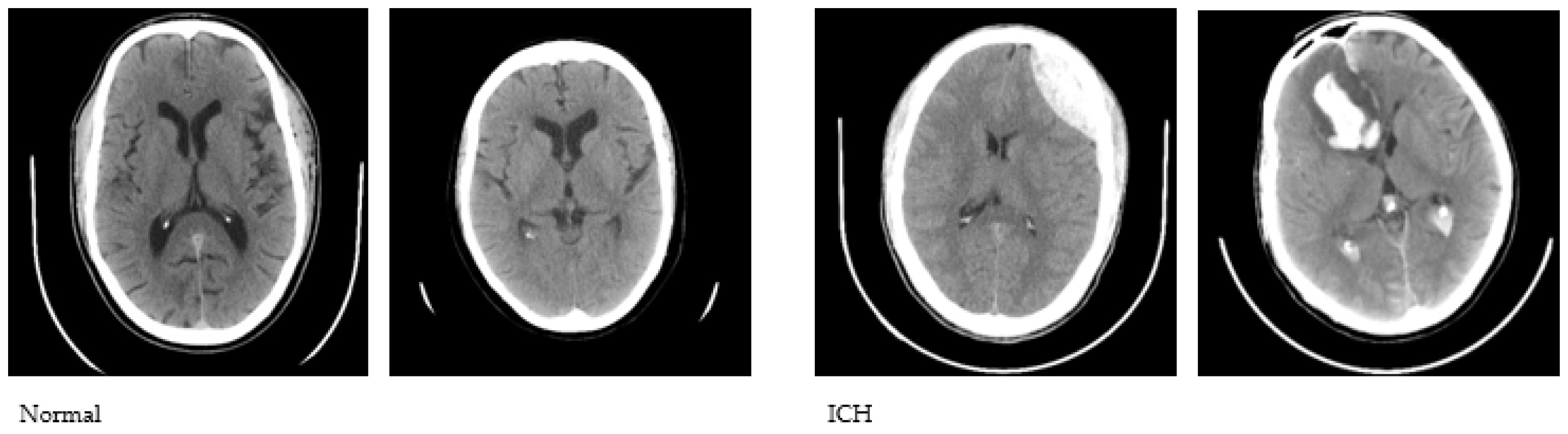
We used the publicly available CQ500 database to conduct this study. The CQ500 dataset [27] includes CT scans of 491 subjects that were employed to construct a Convolutional Neural Network (CNN)-based model for the classification of hematoma subtypes, calvarial fractures, and midline shift in a fully automated fashion. We used a total of 1831 CT images, of which 1000 are healthy and 831 are with hematoma. The CT images were initially converted to JPG format with a 512 × 512 dimension. A sample set of normal and abnormal axial CT images is shown in Figure 1.

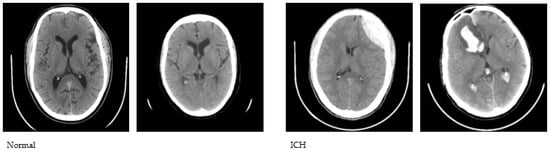
Figure 1. Sample CT images used to conduct the study.

4. Proposed Research Framework

Our novel approach can automatically classify normal and ICH images with a minimal set of powerful features and supervised classifiers. The proposed automated classification technique consists of four major steps. Initially, pre-processing is carried out to remove noise and artefact present in the CT images and to extract the brain region in the image for further processing. Secondly, various textural features are extracted from the pre-processed images using several methods, which are detailed in Section 4.2. Thereafter, the essential and powerful discriminating features are selected using different meta-heuristic algorithms. Finally, the set of refined features are presented to various classifiers to predict normal versus hematoma imagery. The outline of the proposed technique is illustrated in Figure 2.

Figure 2. Outline of the proposed technique.

4.1. Preprocessing

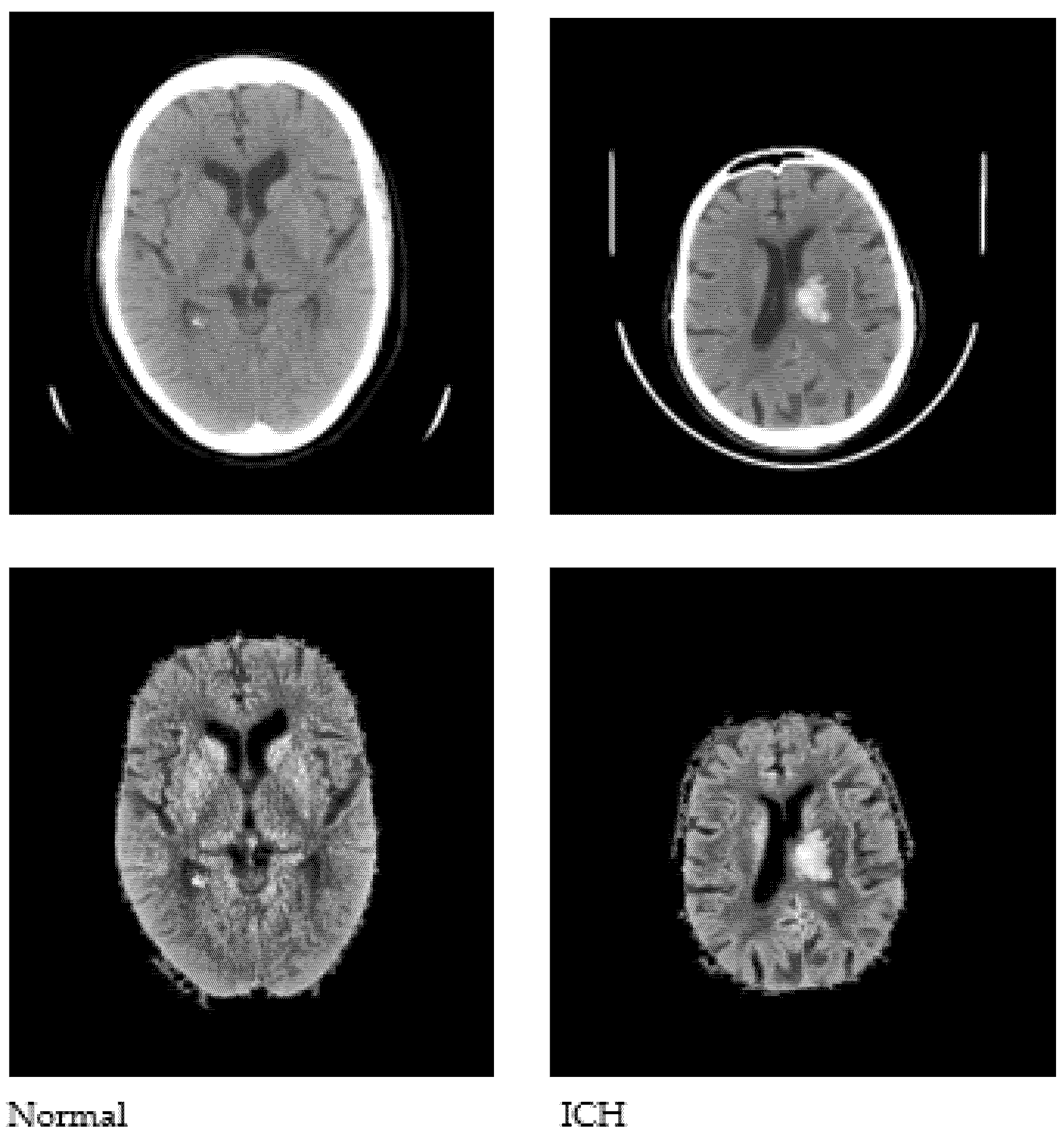
Pre-processing is performed as a fundamental step to enhance the quality of the input images, which aids in the subsequent stages of image analysis. Pre-processing facilitates the removal of noise, unwanted areas in the input images (such as the skull and scalp), and the extraction of the intracranial region of the brain in the image. Contrast Limited Adaptive Histogram Equalization (CLAHE) [28] is used, followed by Otsu’s thresholding [29], in order to obtain binarized image data. The largest connected component is selected as the skull mask, and the region of interest (ROI) is extracted by masking the enhanced images. Sample images after pre-processing are shown in Figure 3.

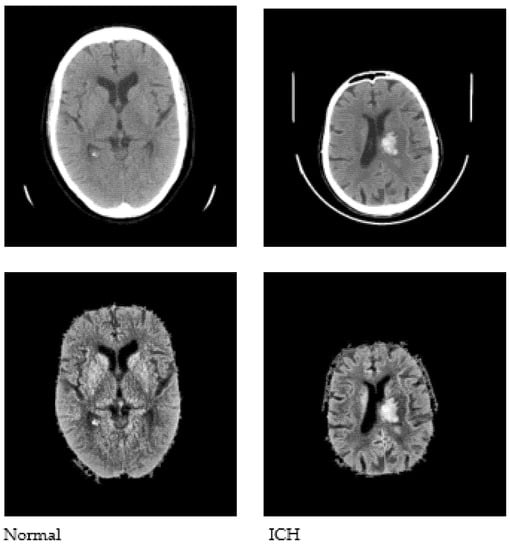
Figure 3. Sample CT images after pre-processing.

4.2. Feature Extraction

Features are unique characteristics that can help differentiate various input patterns. Hence, the identification of discriminant features is very important in order to identify normal versus abnormal CT imagery. In the proposed technique, various features that will help describe the texture and intensity variations are used. The texture features in each image are extracted using several techniques, namely, the Gray Level Co-occurrence Matrix (GLCM) and the Gray Level Run Length Matrix (GLRLM). Features related to first-order statistics such as kurtosis, skewness, and variance are also extracted to obtain the pixel-level details present in the input imagery. Seven Hu’s invariant moments are also utilized for the extraction of features.

4.2.1. Gray Level Co-Occurrence Matrix (GLCM)

The Gray Level Co-occurrence Matrix considers the spatial relationships among pairs of pixels using co-occurrence matrices. An entry P (i, j |d, θ) in the GLCM matrix indicates the number of occurrences of pixel intensity pairs [i, j] in the image at a distance d in the direction θ [30,31]. Haralick et al. [30] proposed various second-order statistical features using GLCM to characterize the texture present in an image. The computed set of GLCM features include homogeneity, entropy, contrast, correlation, energy, angular second-order moments, inverse difference moments, and their variants [30,31,32].

4.2.2. Gray Level Run Length Matrix (GLRLM)

The Gray Level Run Length Matrix characterizes textural features using the run length of the intensity values present in the image. Run length indicates the number of occurrences of successive pixels with the identical intensity value in a definite course of direction. Hence, each entry P (i, j | θ) in GLRLM denotes the frequency of which the intensity value i appears in the image with run length j [33]. The various texture features that are computed based on GLRLM include run percentage, gray-level non-uniformity, short-run emphasis, run length non-uniformity, long-run emphasis, and different variants [33,34].

4.2.3. Hu’s Invariant Moments

Hu proposed seven invariant moments that remain insensitive to parallel projection and image geometrical transformation, namely, translation, scaling, and rotation [35,36]. The moment of (p + q) order for a two-dimensional function f (x, y) is given as

$$m_{pq}={{\displaystyle \int }}_{-\infty }^{+\infty }{{\displaystyle \int }}_{-\infty }^{+\infty }{x}^p{y}^{q}f\left(x,y\right)dxdy$$

(1)

where p = 0, 1, 2, … and q = 0, 1, 2…

The central moments can be defined as [35,36]

$${\mu }_{pq}={{\displaystyle \int }}_{-\infty }^{+\infty }{{\displaystyle \int }}_{-\infty }^{+\infty } {\left(x-\overline{x}\right)}^p{\left(y-\overline{y}\right)}^{q}f\left(x,y\right)dxdy$$

(2)

where $\overline{x}$ and $\overline{y}$ are the centroids of the image that can be computed as

$$\overline{x}=\frac{m_{10}}{m_{00}},\overline{y}=\frac{m_{01}}{m_{00}}$$

The central moments are further normalized to make them insensitive to scale, which can be defined as

$${\eta }_{pq=\frac{{\mu }_{pq}}{{\mu }_{00}^{\left(1+\frac{p+q}{2}\right)}}}$$

(3)

4.3. Synthetic Sample Generation

Learning from imbalanced data adversely affects the performance of the classification model. Synthetic data generation techniques can be used to balance the normal and abnormal classes in the dataset. In this work, we used Adaptive Synthetic Sampling (ADASYN) to generate the artificial samples of the abnormal hematoma class. ADASYN utilizes a weighted distribution to decide the amount of artificial samples that need to be generated, which are also difficult to learn [37]. The quantity of majority and minority class samples is utilized to estimate the number of synthetic samples that should be generated for each minority sample [37]. The current study included 831 hematoma images and 1000 normal images. ADASYN was applied to generate synthetic samples for different subsets of extracted features as shown in Table 1.

Table 1. Amount of samples before and after applying ADASYN.

Feature Extraction Scheme	No. of Samples before ADASYN	No. of Samples after ADASYN
GLRLM + statistical features	831	946
GLCM	831	831
Hu’s invariant moments	831	831
GLRLM+ statistical features + GLCM	831	831
GLRLM + statistical features + Hu’s invariant moments	831	831
GLCM + Hu’s invariant moments	831	831
GLRLM + statistical features + GLCM + Hu’s invariant moments	831	831

4.4. Feature Optimization

Feature optimization is the process of generating feature subsets from high-dimensional datasets, which are less redundant and possess great discriminative power, thereby leading to high classification accuracy. Traditional optimization techniques are less efficient, particularly in the case of high-dimensional datasets, as they generate one local optimal solution as the final subset [38,39,40]. Meta-heuristic algorithms are applied to obtain efficient and effective solutions while preserving the accuracy of classification [38,39]. Numerous nature-inspired meta-heuristic algorithms are popular as they use the knowledge of previous iterations from the population to deliver near-optimal solutions [39,40]. In this paper, the Bat Algorithm (BA), Grey Wolf Optimization (GWO), and Whale Optimization Algorithm (WOA) were selected to generate the best set of features.

The Bat Algorithm uses the echolocation behavior of microbats to find the obstacles, the type of prey, their distance, and also to hunt in complete darkness [41]. The algorithm is simple to implement and generates near-optimal solutions rapidly. The swarm intelligence combined with echolocation makes its more powerful and effective as compared to other optimization algorithms [42]. The Grey Wolf Optimization (GWO) algorithm imitates the four-level hierarchy and hunting features of grey wolves [43,44]. The optimal solution is based on the solutions offered by alpha, beta, and delta wolves instead of one solution. Hence, GWO significantly reduces the chance of generating sub-optimal solutions with superior precision and speed [44]. The Whale Optimization Algorithm (WOA) mimics the bubble-net hunting behavior of humpback whales [45,46]. The most powerful characteristic of WOA is its ability to balance the exploration and exploitation phases in the search process. The algorithm requires less operators for its implementation and provides high flexibility, simplicity, and convergence speed [45,46]. A brief explanation of the three meta-heuristic algorithms is included in the subsections below.

4.4.1. Bat Algorithm

The Bat Algorithm uses the behavior of microbats based on echolocation to detect prey [41]. The entire group of bats is assigned with a constant frequency f_min, loudness A₀, and wavelength λ. Each bat in the population is initialized with a position x_i and velocity v_i, and the bats can modify the pulse emission rate in the range of [0, 1] based on their proximity to the target. The frequency is adjusted to generate a new solution, and the position and velocity of each bat is updated in each iteration. The solutions proposed by all the bats in each iteration are compared to obtain the global solution [41,47]. Each bat also generates a local solution based on the current global solution by random flying. The pulse emission rate and the loudness are updated in every iteration, and as each bat is nearing its target, it will reduce its loudness and increase the rate of emitting pulses. Once the bat is successful in detecting its prey, the loudness is reduced to zero [41,47].

4.4.2. Grey Wolf Optimization

The grey wolf optimization algorithm models the leadership and hunting characteristics of grey wolves [43]. A four-level hierarchy is followed, which includes alpha, beta, delta, and omega wolves, respectively. The alpha wolf may be a male or female and plays the leading role in the pack, i.e., the decision maker for hunting, discipline, sleep, and wake-up time. The beta wolf is the best candidate for the alpha wolf and supports the alpha wolf in making decisions and various other activities [37,40]. The delta wolves are superior to omega wolves, which include the elderly, caretakers, sentinels, and scouts. The omega wolves are responsible for maintaining the hierarchical structure. The algorithm begins with a random number of wolves in the search space, and the position of the wolf can be updated with respect to the prey by adjusting the parameters a and C [37,40]. The parameter a, which is initialized with 2, will be reduced to 0 at the end of all iterations so that the wolf will be near to its prey. It is assumed that the alpha, beta, and delta wolves have a superior assessment of the location of the prey, and the rest of the wolves have to update their positions accordingly. The location of the alpha wolf is considered as the best optimal solution at the end of all iterations [40,43].

4.4.3. Whale Optimization

The Whale Optimization Algorithm models the unique hunting strategy of humpback whales, called the bubble-net feeding technique [45]. The algorithm begins with a set of n whales, which are distributed randomly in the d-dimensional search space, and the best solution is decided. Then, the rest of the whales update their positions based on the current best solution. Further, each whale encircles the prey with a spiral-shaped network of bubbles and follows a movement along a spiral trajectory to attack the prey [45,48]. There exists a 50% probability of choosing the encircling mechanism or following a spiral path in each iteration [45]. Moreover, each whale can update its position with respect to a random one, thus facilitating a global search. The best solution is obtained once all of the iterations are completed and the termination criteria are satisfied.

4.5. Classification

Classification is the final task of categorizing input images based on extracted features and assigning class labels to them. Supervised classifiers are initially trained on a labelled set of data and then used to predict the class of the unknown data. In this work, we used fine, weighted, and ensemble subspace k-Nearest Neighbor (KNN) [49]; wide and medium Neural Network (NN) [50]; and Cubic Support Vector Machine (SVM) [50]. Various performance metrics such as accuracy, sensitivity, and specificity were calculated based on a 5-, 7-, and 10-fold cross-validation framework to evaluate the proposed research work.

5. Results

The non-contrast axial CT images are initially pre-processed to remove the unwanted regions and to extract the brain tissue for further analysis. Each image is subdivided into blocks of 128 × 28, and the features are obtained from each sub block using the various feature extraction schemes described earlier. The different feature extraction schemes and the total number of extracted features are given in Table 2.

Table 2. Number of features extracted using various feature extraction schemes.

Feature Extraction Scheme	No. of Extracted Features
GLRLM + statistical features	224
GLCM	368
Hu’s invariant moments	112
GLRLM+ statistical features + GLCM	592
GLRLM + statistical features + Hu’s invariant moments	336
GLCM + Hu’s invariant moments	480
GLRLM + statistical features + GLCM + Hu invariant moments	704

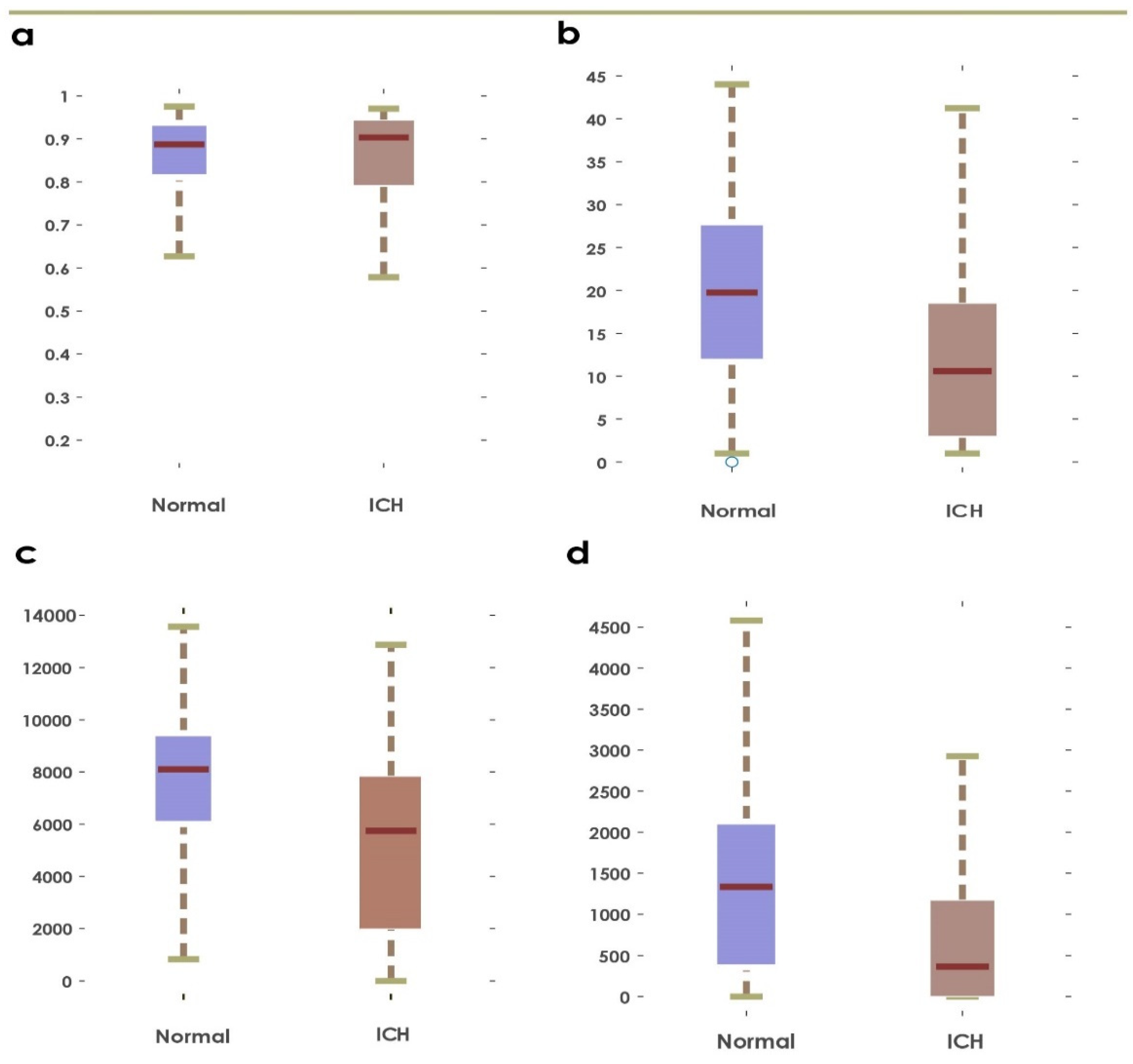
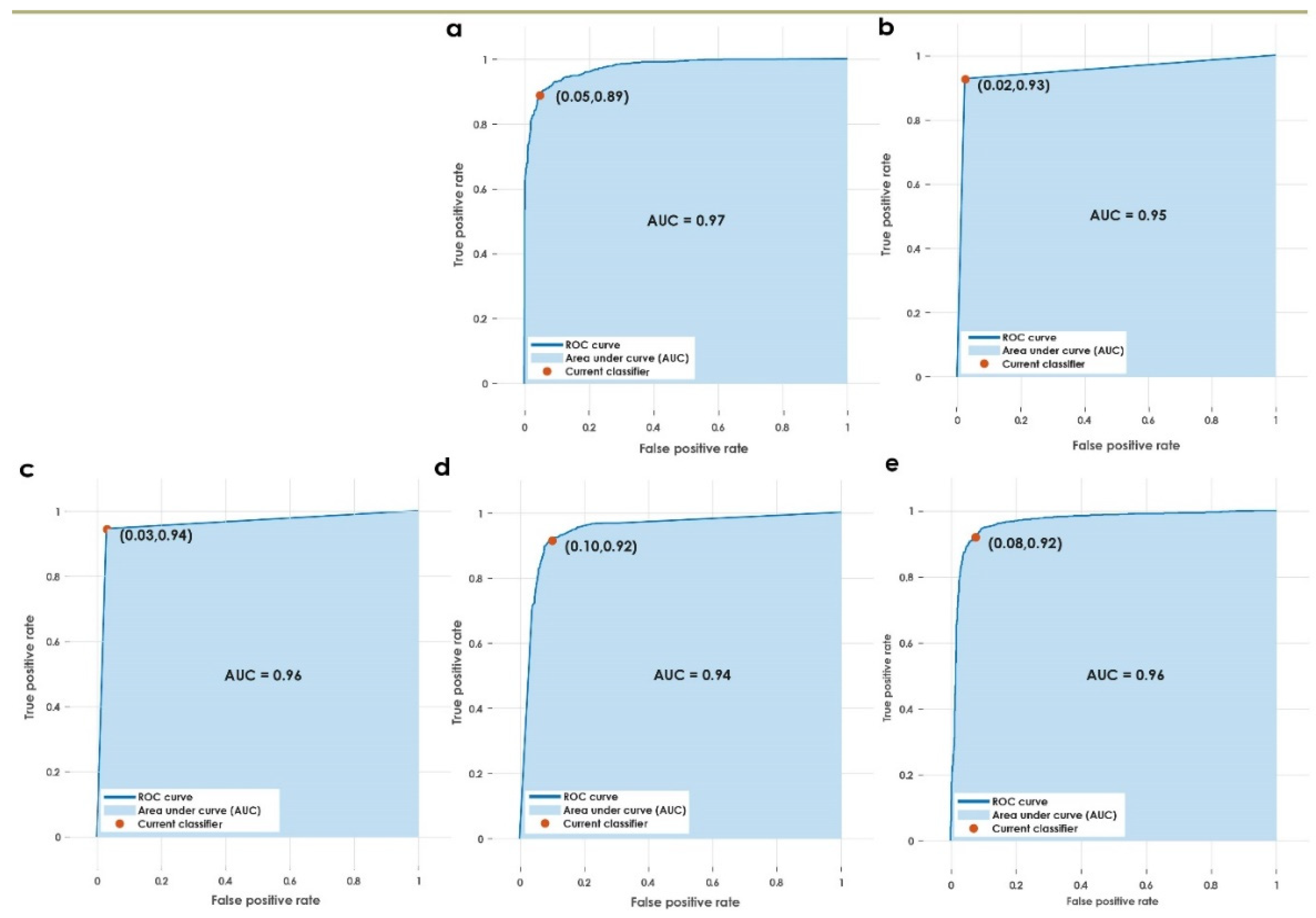
The synthetic samples for the features obtained using each of the feature extraction schemes are generated using ADASYN as shown in Table 1. The subsets of features are then subjected to different meta-heuristic algorithms for the selection of optimal feature sets. Finally, different classifiers are used to test the efficiency of optimal subset of features. Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 present the best performances obtained by using 5-, 7-, and 10-fold cross-validation schemes. The proposed technique achieved an optimum performance of 95.74% accuracy, a sensitivity of 96.93%, and a specificity of 94.67% using a combination of GLRLM and statistical features along with the Grey Wolf Optimization technique. Table 10 shows the best performance of each classifier in the proposed model. Figure 4 shows the boxplots that were obtained before and after applying Grey Wolf Optimization for GLCM and Hu moments, as well as GLRLM and statistical features, respectively. The ROC curve for various classifiers used in the approach is shown in Figure 5. The entire proposed technique was executed and tested in MATLAB environment with a system configuration of Core i5 7200U (2.50 GHz) with 4GB RAM.

Table 3. Performance of various classifiers using GLRLM and statistical features.

Classifiers	Optimization Technique	Fold	Results				Confusion Matrix Parameters
			Accuracy	Error Rate	Sensitivity	Specificity	tn	fp	fn	tp
Wide NN	Grey Wolf Version 1	10	90.60%	9.40%	90.80%	90.40%	904	96	87	859
Fine KNN	Grey Wolf Version 1	10	95.07%	4.93%	97.57%	92.70%	927	73	23	923
Weighted KNN	Grey Wolf Version 1	10	92.14%	7.86%	95.77%	88.70%	887	113	40	906
Optimizable KNN	Grey Wolf Version 1	7	95.74%	4.26%	96.93%	94.67%	994	56	29	917
Cubic SVM	Grey Wolf Version 1	10	92.29%	7.71%	92.49%	92.10%	921	79	71	875

Table 4. Performance of various classifiers using GLCM features.

Classifiers	Optimization Technique	Fold	Results				Confusion Matrix Parameters
			Accuracy	Error Rate	Sensitivity	Specificity	tn	fp	fn	tp
Wide NN	Bat	10	90.11%	9.89%	89.17%	90.90%	909	91	90	741
Fine KNN	Whale	10	92.30%	7.70%	91.34%	93.10%	931	69	72	759
Weighted KNN	Grey Wolf Version 2	10	88.97%	11.03%	84.96%	92.30%	923	77	125	706
Optimizable KNN	Whale	10	92.57%	7.43%	91.34%	93.60%	936	64	72	759
Cubic SVM	Bat	10	90.88%	9.12%	88.57%	92.80%	928	72	95	736

Table 5. Performance of various classifiers using Hu’s invariant moments.

Classifiers	Optimization Technique	Fold	Results				Confusion Matrix Parameters
			Accuracy	Error Rate	Sensitivity	Specificity	tn	fp	fn	tp
Wide NN	Grey Wolf Version 1	10	83.23%	16.77%	80.99%	85.10%	851	149	158	673
Fine KNN	Whale	10	85.69%	14.31%	83.15%	87.80%	878	122	140	691
Weighted KNN	Whale	5	80.23%	19.77%	71.00%	87.90%	879	121	241	590
Optimizable KNN	Whale	10	89.13%	10.87%	87.36%	90.60%	906	94	105	726
Cubic SVM	Whale	10	76.84%	23.16%	59.69%	91.10%	911	89	335	496

Table 6. Performance of various classifiers using GLRLM, statistical features, and Hu’s invariant moments.

Classifiers	Optimization Technique	Fold	Results				Confusion Matrix Parameters
			Accuracy	Error Rate	Sensitivity	Specificity	tn	fp	fn	tp
Wide NN	Bat	10	89.46%	10.54%	87.97%	90.70%	907	93	100	731
Fine KNN	Grey Wolf Version 2	10	93.06%	6.94%	91.22%	94.60%	946	54	73	758
Weighted KNN	Whale	10	87.55%	12.45%	84.24%	91.00%	728	72	131	700
Optimizable KNN	Grey Wolf Version 1	7	93.77%	6.23%	92.18%	95.10%	951	49	65	766
Cubic SVM	Grey Wolf Version 1	7	91.26%	8.74%	88.93%	93.20%	932	68	92	739

Table 7. Performance of various classifiers using GLRLM, statistical features, and GLCM features.

Classifiers	Optimization Technique	Fold	Results				Confusion Matrix Parameters
			Accuracy	Error Rate	Sensitivity	Specificity	tn	fp	fn	tp
Wide NN	Grey Wolf Version 1	10	90.61%	9.39%	89.65%	91.40%	914	86	86	745
Fine KNN	Whale	10	93.23%	6.77%	91.94%	94.30%	943	57	67	764
Weighted KNN	Grey Wolf Version 1	10	90.39%	9.61%	85.68%	94.30%	943	57	119	712
Optimizable KNN	Whale	10	93.66%	6.34%	91.46%	95.50%	955	45	71	760
Cubic SVM	Grey Wolf Version 1	10	91.75%	8.25%	89.41%	93.70%	937	63	88	743

Table 8. Performance of various classifiers using GLCM and Hu’s invariant moments.

Classifiers	Optimization Technique	Fold	Results				Confusion Matrix Parameters
			Accuracy	Error Rate	Sensitivity	Specificity	tn	fp	fn	tp
Wide NN	Grey Wolf Version 1	10	90.82%	9.18%	90.01%	91.50%	915	85	83	748
Fine KNN	Bat	7	91.26%	8.74%	89.17%	93.00%	930	70	90	741
Weighted KNN	Bat	10	89.68%	10.32%	84.48%	94.00%	940	60	129	702
Optimizable KNN	Grey Wolf Version 1	7	92.63%	7.37%	91.10%	93.90%	939	61	74	757
Cubic SVM	Bat	10	90.72%	9.28%	88.09%	92.90%	929	71	99	732

Table 9. Performance of various classifiers using GLRM, statistical features, GLCM, and Hu’s invariant moments.

Classifiers.	Optimization Technique	Fold	Results				Confusion Matrix Parameters
			Accuracy	Error Rate	Sensitivity	Specificity	tn	fp	fn	tp
Wide NN	Grey Wolf Version 2	10	90.55%	9.45%	88.81%	92.00%	920	80	93	738
Fine KNN	Bat	10	92.95%	7.05%	90.97%	94.60%	946	54	75	756
Weighted KNN	Whale	10	90.01%	9.99%	85.56%	93.70%	937	63	120	711
Optimizable KNN	Bat	10	93.56%	6.44%	91.82%	95.00%	950	50	68	763
Cubic SVM	Whale	10	91.48%	8.52%	89.53%	93.10%	931	69	87	744

Table 10. The maximum performance of each classifier in our approach.

Classifiers	Feature Extraction Scheme	Optimization Technique	Fold	Results				Confusion Matrix Parameters
				Accuracy	Error Rate	Sensitivity	Specificity	tn	fp	fn	tp
Wide NN	GLCM + Hu’s invariant moments	Grey Wolf Version 1	10	90.82%	9.18%	90.01%	91.50%	915	85	83	748
Fine KNN	GLRLM+ Statistical features	Grey Wolf Version 1	10	95.07%	4.93%	97.57%	92.70%	927	73	23	923
Weighted KNN	GLRLM+ Statistical features	Grey Wolf Version 1	10	92.14%	7.86%	95.77%	88.70%	887	113	40	906
Optimizable KNN	GLRLM+ Statistical features	Grey Wolf Version 1	7	95.74%	4.26%	96.93%	94.67%	994	56	29	917
Cubic SVM	GLRLM+ Statistical features	Grey Wolf Version 1	10	92.29%	7.71%	92.49%	92.10%	921	79	71	875

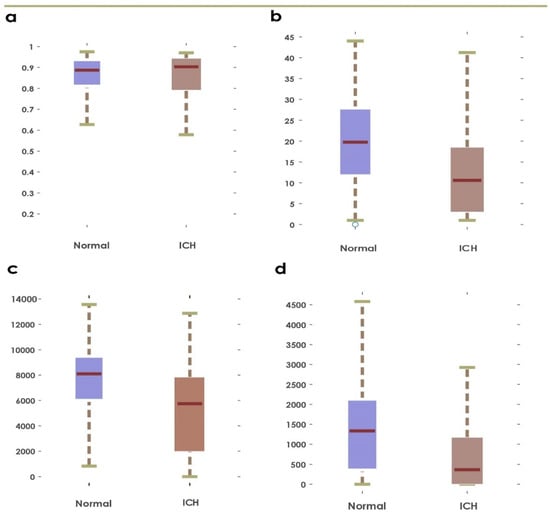
Figure 4. Boxplots obtained using first ranked feature before and after applying Grey Wolf Optimization: (a,b): GLCM and Hu’s invariant moments, (c,d): GLRLM and statistical features.

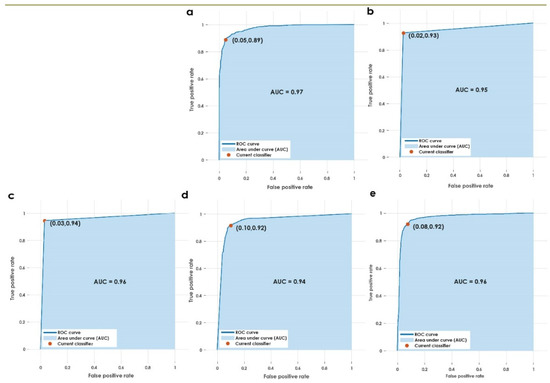
Figure 5. AUC for the various classifiers used in the proposed approach. (a) Weighted KNN, (b) fine KNN, (c) optimizable KNN, (d) wide NN, (e) cubic SVM.

6. Discussion

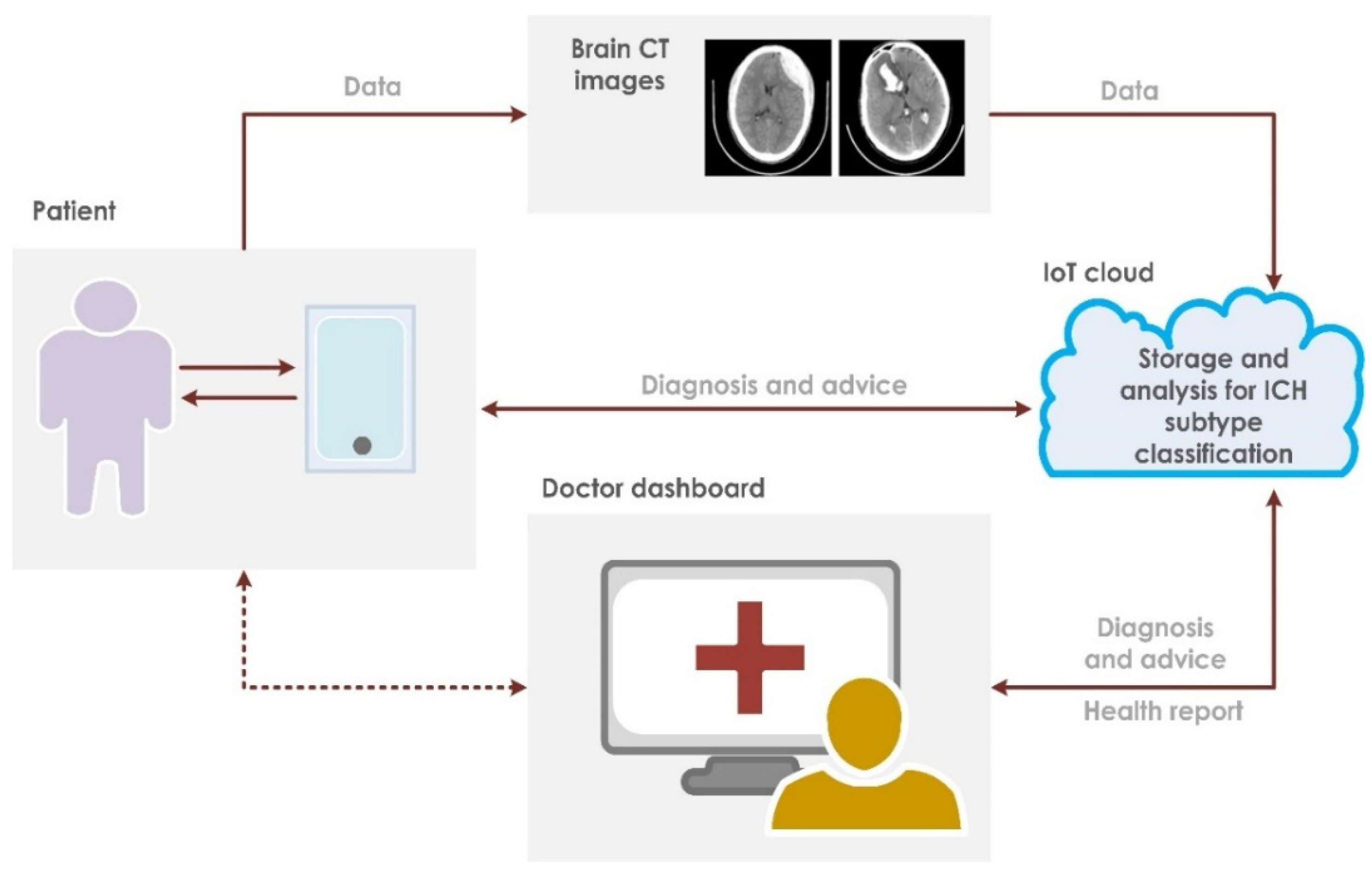
This paper presents a fully automated technique for the diagnosis of hematoma in non-contrast CT images. The proposed research technique can clearly categorize normal and hematoma classes with an accuracy of 95.74% using an optimizable KNN classifier. It is observed that the combination of GLRLM and statistical features are powerful in capturing the structural variations in the CT imagery. The proposed research model is an initial attempt in hematoma classification using various meta-heuristic algorithms for optimal feature selection. It is observed from Table 10 that the optimal classification performance is achieved by using the Grey Wolf Optimization technique. Table 11 shows the quantitative comparison of various CAD schemes for the classification of normal and hematoma subjects using CT images. It is noted that the proposed approach handled a larger number of images effectively using the optimized set of GLRLM and statistical features. It is observed from Figure 4 that both sets of feature extraction schemes clearly distinguish normal versus hematoma images using the first ranked feature. From Figure 5, the area under the ROC curve ranges from 0.94 to 0.97, which shows that the classifiers are highly adept in distinguishing healthy versus hematoma subjects. Another significant characteristic of the proposed model is the use of multiple cross-validation schemes. It is evident that the seven-fold cross-validation scheme achieved the optimal performance. The optimizable KNN is able to distinguish normal versus pathological images with a specificity of 94.67%. The proposed model also achieved a sensitivity of 96.93% in discerning the hematoma subjects. Hence, the developed fully automated model can assist attending physicians in interpreting CT scans swiftly and accurately for effective decision making and treatment. This, in turn, can help improve patient outcome. Figure 6 presents the architecture for a futuristic ICH diagnosis model based on the Internet of Things (IoT) cloud platform, wherein the remote diagnostic feedback and advice will reach the patient swiftly through the doctor and facilitate quality patient care.

Table 11. Performance comparison of different techniques.

Approaches	CT Dataset	Method	Classifier	Performance
Raghavendra et al. [15]	1603	Entropy-based non-linear features	PNN	Acc: 97.37%
Shahangian and Pourghassem [17]	627	Modified Distance Regularized Level Set Evolution (MDRLSE), texture and shape features	Hierarchical structure	Acc: 94.13%
Al-Ayyoub et al. [18]	76	Region growing	Logistic	Acc: 92%
Xiao et al. [19]	48	Multi-resolution thresholding+ region growing + primary and derived features based on long and short axes	C4.5	Acc: 0.975
Tong et al. [20]	450	LBP texture features and histogram features	SVM	Acc: 90%
Li et al. [21]	129	Distance features based on landmark	Bayesian	Sen: 100
Yuh et al. [22]	273	thresholding, spatial filtering, and cluster analysis and classification based on location, size, and shape of clusters	-	Sen: 98
Zaki et al. [23]	720	FCM + multi-level thresholding + location and intensity features	-	Sen: 82.5%
Muschelli et al. [24]	112	Intensity-based predictors	Random forest classifier	DSI: 0.899
Foo et al. [25]	108	Multiple thresholding and symmetry detection	-	Accuracy: 80.6
Zhang et al. [26]	426	Adaptive thresholding and case-based reasoning	Genetic algorithm	Detection rate: 94.9%
Our approach	1831	GLRLM and statistical features	Optimizable KNN	Accuracy: 95.74% Sensitivity:96.93% Specificity:94.67%

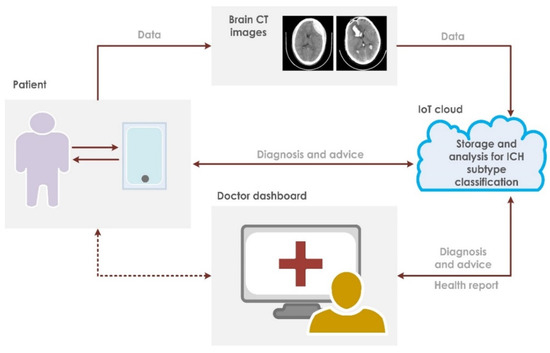
Figure 6. Proposed IoT-based architecture for ICH classification.

The prominent characteristics of the proposed CAD model are as follows:

• Achieved a classification accuracy of 95.74% in categorizing normal versus hematoma patients.
• The features are selected using meta-heuristic algorithms, which will generate globally optimal features to improve overall performance.
• The system is highly robust, as the method is evaluated using 5-, 7-, and 10-fold cross-validation schemes.
• A relatively large dataset is used, which consists of 1831 non-axial CT images.

7. Conclusions

In this research study, a fully automated CAD system used to discern normal and hematoma images is developed. With the aid of a fine KNN classifier, the proposed method achieved a maximum accuracy of 95.74%, a sensitivity of 96.93%, and a specificity of 94.67% using a combination of GLRLM and statistical features. The obtained results show that the proposed technique is more accurate and robust, and may assist doctors in strategic decision-making and treatment planning, particularly during critical and emergency scenarios. The performance of the proposed technique should be validated using larger and more diverse datasets for real-time applicability. Hence, our future work aims to include more subjects and to perform classification of various types of hematoma. Additionally, we would like to incorporate more features and deep CNN architectures to design fast and powerful CAD schemes for hematoma diagnosis.