1. Introduction
As an essential preprocessing stage for machine learning, feature selection endeavors to identify significant predictors from a feature-rich dataset with high dimensionality. The primary objective is to enhance prediction accuracy by selecting the most representative features. This study presents an innovative strategy that integrates binary decision trees and genetic algorithms to effectively handle extensive datasets and support informed decision making. The purpose of this algorithm is to use a GA as classifier system to find an optimized tree structure along with an optimal terminal set of a BDT, and to promote and select the elitist as a solution, which will enable the classification of datasets by undergoing a training, validation, and testing phase, along with an ensemble method that combines multiple BDT structures to improve classification performance.
This approach utilizes binary decision trees (BDTs) for classification purposes and genetic algorithms (GAs) for selecting the most optimal attributes, thus minimizing the likelihood of overfitting. The experimental application of this methodology to wine chemical analysis yields promising outcomes. The combination of binary decision trees and genetic algorithms offers a novel solution for managing significant subsets of wine data with assigned weights using a machine learning model through a multi-disciplinary approach, testing it on real-world chemical substance data, and refining it. It also offers valuable insights for future work with a human-centric perspective. To achieve this, machine learning classification utilizing an optimization method is employed to gather valid information from this specific field of interest. The identification of wine types necessitates an understanding of how respondents’ answers correspond to three distinct classes: 1, 2, and 3. The outcomes reveal subsets of attributes that effectively replace the initial attribute set, achieving high accuracy/fitness levels (above 80%) with varying numbers of attributes based on the class. It is important to clarify that this study encompasses two distinct decision-making processes. The first relates to the chemical substances which identify the wine’s origin, while the second pertains to the core analysis conducted using machine learning to generate results minimizing the risk of decision.
AI-supervised learning is employed to analyze wine data and predict the factors influencing a wine’s type. The data is extracted from the Institute of Pharmaceutical and Food Analysis and Technologies in Italy. The primary objective of this study is to examine, process, classify, and evaluate datasets to generate reliable insights regarding the chemical substances which are responsible for determining a wine’s origin. Thirteen continuous variables—Alcohol, Malic Acid, Ash, Alkalinity of Ash, Magnesium, Total Phenols, Flavonoids, Nonflavonoid Phenols, Proanthocyanins, Color Intensity, Hue, OD280/OD315 of Diluted Wines, and Proline—refer to the chemical substances that classify a wine’s type [
1].
This study addresses the challenge of hybrid data classification by introducing an optimization population-based metaheuristic method that combines two distinct methods and a programming technique into a unified entity. The BDT algorithm is used for data classification, while the GA algorithm is used for optimization, and the wrapping technique facilitates communication and data exchange between the two methods. This model uses BDTs to efficiently handle, categorize, and extract insights from raw data, resulting in precise subsets of data instead of using the entire set of features. It is tested in different conditions, including various numbers and types of features, record numbers, and industry contexts. The goal is to generate optimal feature subsets that reduce processing time and improve prediction accuracy. The algorithm’s logic is explained, and the best attribute subsets are presented using graphs and histograms.
While the proposed machine learning model integrating a GA wrapper with BDTs demonstrates promising results in classifying the wine substances that affect the wine’s origin, it is important to acknowledge certain limitations and consider further avenues for exploration. The current study focused on a specific dataset from the wine industry, limiting the generalizability of the findings to other domains. Future research could expand the scope by incorporating diverse datasets from various industries to assess the model’s applicability and performance in different contexts. Following, the wine industry is known for its dynamic nature, characterized by evolving production techniques and regional variations. To enhance the practicality and relevance of the model, it would be valuable to explore its adaptability to these dynamic factors. Investigating how the model can effectively capture and adapt to changes in winemaking practices, as well as variations in regional characteristics, could provide deeper insights into its robustness and generalizability. In addition to improving the model’s practical application, the study could further investigate the interpretability and explainability of the model’s decision-making process. While the accuracy and performance of the model are crucial, understanding the underlying factors and features that contribute to its predictions is equally important. By incorporating interpretability techniques, researchers and domain experts can gain insights into which wine substances play a dominant role in determining the wine’s origin, facilitating the validation and acceptance of the model in real-world scenarios.
2. Related Work
The current research attempt discusses the use of hybrid machine learning in wine data. Thus, the field of study combines the machine learning model implementation stages and its contribution to the wine industry. The literature review part refers to both machine learning and wine decision making.
Referring to the cases where machine learning was introduced in a wine field of study, there are a series of publications that verify its use. To begin with, research was conducted aiming to use a large generic wine dataset to classify and highlight the differences in wines around the world. A world wine dataset, the X-Wines dataset, was created, including data from user reviews and ratings for recommendation systems, machine learning and data mining, and general purposes, opening the way to researchers and students to use it freely. Using evaluation metrics, this project involved data collection, dataset description, training, verification, and validation, and results measurement [
2].
Another significant approach [
3] referred to a machine learning application in wine quality prediction. The excellence of New Zealand Pinot noir wine led a team of researchers to use machine learning algorithms to predict wine quality by using synthetic and available experimental data collected from different regions of New Zealand. An Adaptive Boosting (AdaBoost) classifier showed 100% accuracy when trained and evaluated without feature selection, with feature selection (XGB), and with essential variables (features found important in at least three feature selection methods) [
3].
Another study [
4] examined the performance of different machine learning models, namely Ridge Regression (RR), Support Vector Machine (SVM), Gradient Boosting Regressor (GBR), and multi-layer Artificial Neural Network (ANN), was compared for the prediction of wine quality. An analysis of multiple parameters that determine wine quality was conducted. It was observed that the performance of GBR surpassed that of all other models, with mean squared error (MSE), correlation coefficient (R), and mean absolute percentage error (MAPE) values of 0.3741, 0.6057, and 0.0873, respectively. This work demonstrates how statistical analysis can be utilized to identify the key components that primarily influence wine quality prior to production. This information can be valuable for wine manufacturers in controlling quality before the wine production process [
4].
Regarding the application of machine learning methods to the wine industry, there is a series of significant research attempts which verifies that the proper use of advanced statistics can mitigate the decision error and provide valid information on wine products. Previous research [
5,
6] has shown that GAs and BDTs have been utilized together in various optimization and classification tasks in recent decades, as evidenced by the existing literature. The GA wrapper, also used for user authentication through keystroke dynamics, involves analyzing a person’s typing pattern to determine whether to grant or deny access. This was achieved by creating a timing vector that consists of keystroke duration and interval times. However, deciding which features to use in a classifier was a common feature selection issue. One potential solution was a genetic-algorithm-based wrapper approach, which not only resolves the problem but also generates a pool of effective classifiers that can be used as an ensemble. The preliminary experiments demonstrate that this approach outperforms both the two-phase ensemble selection approach and the prediction-based diversity term approach [
5,
6] (pp. 654–660).
Another study [
7] focused on the development of an automated algorithm for feature subset selection in unlabeled data, where two key issues were identified: the identification of the appropriate number of clusters in conjunction with feature selection, and the normalization of feature selection criteria bias with respect to dimensionality. Thus, the Feature Subset Selection using Expectation-Maximization (EM) clustering (FSSEM) approach and the evaluation of candidate feature subsets using scatter separability and maximum likelihood criteria were developed. Proofs were provided on the biases of these feature criteria concerning dimensionality, and a cross-projection normalization scheme to mitigate these biases was proposed. The results show the necessity of feature selection and the importance of addressing these issues, as well as the efficacy of this proposed solution [
7].
Another study [
8] introduced a novel wrapper feature selection algorithm, referred to as the hybrid genetic algorithm (GA) and extreme learning machine (ELM)-based feature selection algorithm (HGEFS) for classification problems. This approach employed GA to wrap ELM and search for optimal subsets in the extensive feature space. The selected subsets were then utilized for ensemble construction to enhance the final prediction accuracy. To prevent GA from being stuck in local optima, an efficient and innovative mechanism was proposed specifically designed for feature selection issues to maintain the GA’s diversity. To evaluate the quality of each subset fairly and efficiently, a modified ELM known as the error-minimized extreme learning machine (EM-ELM) was adopted, which automatically determines the appropriate network architecture for each feature subset. Moreover, EM-ELM exhibits excellent generalization capability and extreme learning speed, enabling the execution of wrapper feature selection procedures affordably. In other words, the feature subset and classifier parameters were optimized simultaneously. After concluding the GA’s search process, a subset of EM-ELMs from the obtained population based on a specific ranking and selection strategy was selected to improve the prediction accuracy and achieve a stable outcome. To evaluate HGEFS’s performance, empirical comparisons were carried out on various feature selection methods and HGEFS using benchmark data sets. The outcomes demonstrate that HGEFS was a valuable approach for feature selection problems and consistently outperformed other algorithms in comparison [
8].
The approach of using multiple classifiers to solve a problem, known as an ensemble, has been found to be highly effective for classification tasks. One of the fundamental requirements for creating an effective ensemble was to ensure both diversity and accuracy. In this study, a new ensemble creation technique that utilized GA wrapper feature selection was introduced. These experimental results on real-world datasets demonstrated that the proposed method was promising when the training data size was restricted [
9] (pp. 111–116).
A different study [
9] employed a GA hybrid to pinpoint a subset of attributes that were most relevant to the classification task. The optimization process was composed of two stages. During the outer optimization stage, a wrapper method was employed to conduct a global search for the most optimal subset of features. In this stage, the GA employs the mutual information between the predictive labels of a trained classifier and the true classes as the fitness function. The inner optimization stage involves a filter approach to perform local search. In this stage, an enhanced estimation of the conditional mutual information was utilized as an independent measure for feature ranking, taking into account not only the relevance of the candidate features to the output classes but also their redundancy with the already-selected features. The inner and outer optimization stages work together to achieve high global predictive accuracy as well as high local search efficiency. The experimental results demonstrate that the method achieves parsimonious feature selection and excellent classification accuracy across various benchmark data sets [
10] (pp. 1825–1844).
The concept of feature set partitioning expands on the task of feature selection by breaking down the feature set into groups of features that were collectively valuable, rather than pinpointing one individual set of features that was valuable. One research paper introduced a fresh approach to feature set partitioning that relied on a GA. Additionally, a new encoding schema was suggested, and its characteristics were explored. The study investigated the effectiveness of utilizing a Vapnik-Chervonenkis dimension bound to assess the fitness function of multiple tree classifiers that were oblivious. To evaluate the new algorithm, it was applied to various datasets, and the outcomes indicate that the proposed algorithm outperforms other methods [
11] (pp. 1676–1700).
“Comparison of Naive Bayes and Decision Tree on Feature Selection Using Genetic Algorithm for Classification Problem” stands out as the most significant work in demonstrating the effectiveness of combining DTs and GAs. That study specifically addressed the challenge of identifying optimal attribute classifications through the utilization of a GA and wrapping technique. The focus was on handling large datasets and determining the attributes that have an impact on result quality by considering factors such as irrelevance, correlation, and overlap. The study employed a combination of a DT and Naïve Bayes theorem as the most suitable models for the task. Initially, the DT was integrated with the GA wrapper, resulting in the GADT, which provided classification results. Subsequently, the Naïve Bayes model was also combined with the GA wrapper, leading to GANB for classification optimization. The research team thoroughly discussed how both NB and DT models address the classification problem by leveraging the GA’s ability to identify the best attribute subsets. The performance of each model was comparable, although the comparative analysis revealed that GADT slightly outperformed GANB in terms of accuracy [
12].
During the financial crisis of 2007, an alternative method for selecting features was employed in credit scoring modeling. Credit scoring modeling aims to accurately assess the credit risk of applicants using customer data from banks. This particular method was utilized to identify credit risks within the banking sector, eliminating irrelevant credit risk features and enhancing the accuracy of the classifier. The approach involved a two-stage process, combining a hybrid feature selection filter approach with multiple population genetic algorithms (MPGA). In the first stage, three filter wrapper approaches were employed to gather information for the MPGA. The second stage utilized the characteristics of MPGA to identify the optimal subset of features. A comparison was conducted among the hybrid approach based on the filter approach and MPGA (referred to as HMPGA), MPGA alone, and standard GA. The results demonstrated that HMPGA, MPGA, and GA outperformed the three filter approaches. Furthermore, it was established that HMPGA yielded superior results compared to both MPGA and GA [
13].
In various industries, including medicine and healthcare, two predominant machine learning approaches have emerged: supervised learning and transfer learning. These methodologies heavily rely on vast manually labeled datasets to train increasingly sophisticated models. However, this reliance on labeled data leads to an abundance of un-labeled data that remains untapped in both public and private data repositories. Addressing this issue, self-supervised learning (SSL) emerged as a promising field within machine learning, capable of harnessing the potential of unlabeled data. Unlike other machine learning paradigms, SSL algorithms generate artificial supervisory signals from unlabeled data and employ these signals for pretraining algorithms. One study dealt with two primary objectives. Firstly, it aimed to provide a comprehensive definition of SSL, categorizing SSL algorithms into four distinct subsets and conducting an in-depth analysis of the latest advancements published within each subset from 2014 to 2020. Secondly, the review focused on surveying recent SSL algorithms specifically in the healthcare domain. This endeavor aimed to equip medical professionals with a clearer understanding of how SSL could be integrated into their research efforts, with the ultimate goal of leveraging the untapped potential of unlabeled data [
14].
This article [
15] presents a multicriteria programming model aimed at optimizing the completion time of homework assignments by school students in both in-class and online teaching modes. The study defined twelve criteria that influence the effectiveness of school exercises, five of which pertain to the exercises themselves and the remaining seven to the conditions under which the exercises are completed. The proposed solution involves designing a neural network that outputs influence on the target function and employs three optimization techniques—backtracking search optimization algorithm (BSA), particle swarm optimization algorithm (PSO), and genetic algorithm (GA)—to search for optimal values. The article suggests representing the optimal completion time of homework as a Pareto set [
15].
The problem of feature subset selection involves selecting a relevant subset of features for a learning algorithm to focus on, while disregarding the others. To achieve the best performance possible with a specific learning algorithm on a given training set, it is important for a feature subset selection method to consider how the algorithm and training set interact. Another study examined the relationship between optimal feature subset selection and relevance. The proposed wrapper method searched for an optimal feature subset tailored to a specific algorithm and domain. The strengths and weaknesses of the wrapper approach were analyzed, and several improved designs were presented. The wrapper approach was compared to induction without feature subset selection and to Relief, which is a filter-based approach to feature subset selection [
16].
In many real-world applications of classification learning, irrelevant features are often present, posing a challenge for machine learning algorithms. Nearest-neighbor classification algorithms have shown high predictive accuracy in many cases but are not immune to the negative effects of irrelevant features. A new classification algorithm, called VFI5, has been proposed to address this issue. In this study, the authors compared the performance of the nearest-neighbor classifier and the VFI5 algorithm in the presence of irrelevant features. The comparison was conducted on both artificially generated and real-world data sets obtained from the UCI repository. The results show that the VFI5 algorithm achieves comparable accuracy to the nearest-neighbor classifier while being more robust to irrelevant features [
17].
Author Contributions
Conceptualization, D.C.G.; Formal analysis, D.C.G. and M.C.G.; Investigation, D.C.G.; Methodology, D.C.G.; Software, D.C.G. and T.T.; Supervision, D.C.G., T.T. and P.K.T.; Validation, D.C.G. and M.C.G.; Data curation, D.C.G. and M.C.G.; Writing—original draft, D.C.G.; Writing—review and editing, D.C.G., T.T., P.K.T. and M.C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available in a publicly accessible repository. The data presented in this study are openly available in [UCI repository]
https://doi.org/10.24432/C5PC7J, accessed on 12 April 2023.
Acknowledgments
Special thanks go to Paul D. Scott, from School of Computer Science and Electronic Engineering at University of Essex in UK, for conceptualizing and contributing the most to the design and the implementation of the initial GA wrapper model.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | Artificial Neural Network |
| BDTs | Binary Decision Trees |
| BSA | Backtracking Search Optimization Algorithm |
| DT | Decision Trees |
| ELM | Extreme Learning Machine |
| EM-ELM | Error-Minimized Extreme Learning Machine |
| GA | Genetic Algorithm |
| GADT | Genetic Algorithm Decision Trees |
| GANB | Genetic Algorithm Naïve Bayes |
| GBR | Gradient Boosting Regressor |
| HGEFS | Extreme Learning Machine-Based Feature Selection Algorithm |
| HMPGA | Hybrid Multiple Population Genetic Algorithms |
| MAPE | Mean Absolute Percentage Error |
| MPGA | Multiple Population Genetic Algorithms |
| MSE | Mean Squared Error |
| NN | Neural Network |
| PSO | Particle Swarm Optimization Algorithm |
| R | Correlation Coefficient |
| RO | Research Objective |
| RR | Ridge Regression |
| SSL | Self-Supervised Learning |
| SVM | Support Vector Machine |
| UCI | University of California, Irvine |
References
- Forina, M.; Leardi, R.; Armanino, C.; Lanteri, S. PARVUS: An Extendable Package of Programs for Data Exploration, Classification and Correlation, Version 3.0; Institute of Pharmaceutical and Food Analysis and Technologies: Genoa, Italy, 1988. [Google Scholar] [CrossRef]
- de Azambuja, R.X.; Morais, A.J.; Filipe, V. X-Wines: A Wine Dataset for Recommender Systems and Machine Learning. Big Data Cogn. Comput. 2023, 7, 20. [Google Scholar] [CrossRef]
- Bhardwaj, P.; Tiwari, P.; Olejar, K.; Parr, W.; Kulasiri, D. A machine learning application in wine quality prediction. Mach. Learn. Appl. 2022, 8, 100261. [Google Scholar] [CrossRef]
- Dahal, K.; Dahal, J.; Banjade, H.; Gaire, S. Prediction of Wine Quality Using Machine Learning Algorithms. Open J. Stat. 2021, 11, 278–289. [Google Scholar] [CrossRef]
- Jingxian, A.; Kilmartin, P.A.; Young, B.R.; Deed, R.C.; Yu, W. Decision trees as feature selection methods to characterize the novice panel’s perception of Pinot noir wines. Res. Sq. 2023. [CrossRef]
- De Caigny, A.; Coussement, K.; De Bock, K.W. A New Hybrid Classification Algorithm for Customer Churn Prediction Based on Logistic Regression and Decision Trees. Eur. J. Oper. Res. 2018, 269, 760–772. [Google Scholar] [CrossRef]
- Dy, J.G.; Brodley, C. Feature Selection for Unsupervised Learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Xue, X.; Yao, M.; Wu, Z. A Novel Ensemble-Based Wrapper Method for Feature Selection Using Extreme Learning Machine and Genetic Algorithm. Knowl. Inf. Syst. 2018, 57, 389–412. [Google Scholar] [CrossRef]
- Yu, E.; Cho, S. Ensemble based on GA wrapper feature selection. Comput. Ind. Eng. 2006, 51, 111–116. [Google Scholar] [CrossRef]
- Huang, J.; Cai, Y.; Xu, X. A hybrid GA for feature selection wrapper based on mutual information. Pattern Recognit. Lett. 2007, 28, 1825–1844. [Google Scholar] [CrossRef]
- Rokach, L. Genetic algorithm-based feature set partitioning for classification problems. Pattern Recognit. 2008, 41, 1676–1700. [Google Scholar] [CrossRef]
- Rahmadani, S.; Dongoran, A.; Zarlis, M.; Zakarias. Comparison of Naive Bayes and Decision Tree on Feature Selection UsingGenetic Algorithm for Classification Problem. J. Phys. Conf. Ser. 2018, 978, 012087. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Z.; Bai, R.; Mao, Y. A Hybrid System with Filter Approach and Multiple Population Genetic Algorithm forFeature Selection in Credit scoring. J. Comput. Appl. Math. 2018, 329, 307–321. [Google Scholar] [CrossRef]
- Chowdhury, A.; Rosenthal, J.; Waring, J.; Umeton, R. Applying Self-Supervised Learning to Medicine: Review of the State of the Art and Medical Implementations. Informatics 2021, 8, 59. [Google Scholar] [CrossRef]
- Dogadina, E.P.; Smirnov, M.V.; Osipov, A.V.; Suvorov, S.V. Evaluation of the Forms of Education of High School Students Using a Hybrid Model Based on Various Optimization Methods and a Neural Network. Informatics 2021, 8, 46. [Google Scholar] [CrossRef]
- Russel, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Güvenir, H.A. A classification learning algorithm robust to irrelevant features. In Artificial Intelligence: Methodology, Systems, and Applications, Proceedings of the 8th International Conference, AIMSA’98, Sozopol, Bulgaria, 21–23 September 1998; Giunchiglia, F., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1480. [Google Scholar] [CrossRef]
- Kohavi, R. Wrappers for Performance Enhancement and Oblivious Decision Graphs. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1996. Available online: http://robotics.stanford.edu/users/ronnyk/teza.pdf (accessed on 1 May 2023).
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Witten, I.; Frank, E.; Hall, M. Data Mining; Morgan Kaufmann Publishers: Burlington, MA, USA, 2011. [Google Scholar]
- Quinlan, J. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Quinlan, J. Simplifying decision trees. Int. J. Man Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Blockeel, H.; De Raedt, L. Top-down induction of first-order logical decision trees. Artif. Intell. 1998, 101, 285–297. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; The MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Whitley, D. A Genetic Algorithm Tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Hsu, W.H. Genetic wrappers for feature selection in decision trees induction and variable ordering in Bayesian network structure learning. Inf. Sci. 2004, 163, 103–122. [Google Scholar] [CrossRef]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991; p. 115. [Google Scholar]
- Vlahavas, P.; Kefalas, N.; Vassiliades, F.; Kokkoras, I.; Sakellariou, E. Artificial Intelligence, 3rd ed.; Gartaganis Publications: Thessaloniki, Greece, 2002; ISBN 960-7013-28-X. [Google Scholar]
- Scott, P.D. Lecture Notes in Decision Trees Induction. Machine Learning and Data Mining; Computer Science and Electronic Engineering; University of Essex: Colchester, UK, 1999. [Google Scholar]
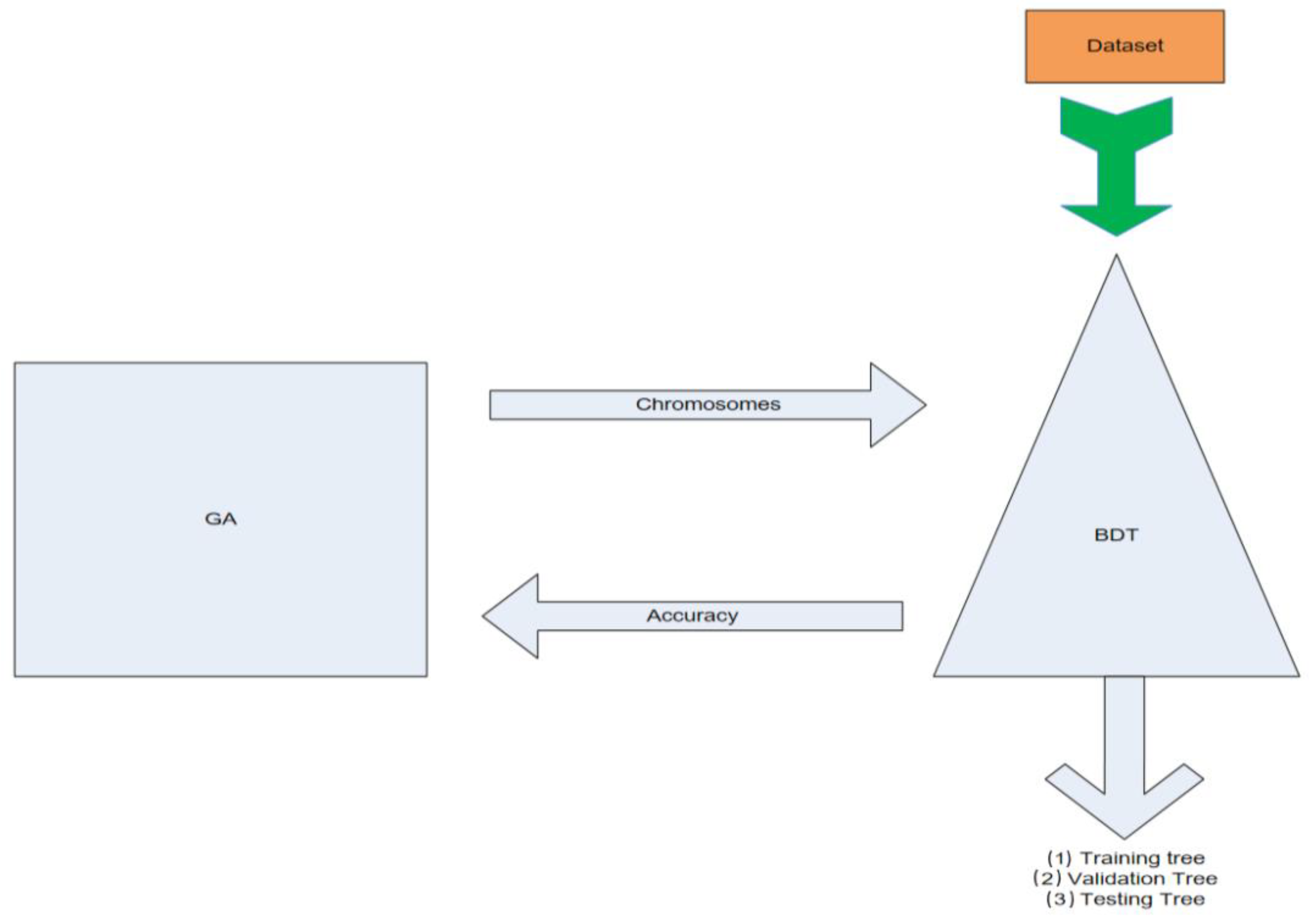
Figure 1.
GA wrapper model. This figure demonstrates the overall wrapping classification and data exchange procedure of the binary decision trees and the genetic algorithm.
Figure 2.
Flowchart for the genetic algorithm wrapper.
Figure 3.
Sequence diagram for binary decision tree and genetic algorithm communication.
Figure 4.
Dataflow diagram for the GA Wrapper generic procedures.
Figure 5.
Optimal feature/chromosome representation. The gene positions are indicated with black color and the gene class numbers are indicated with red color.
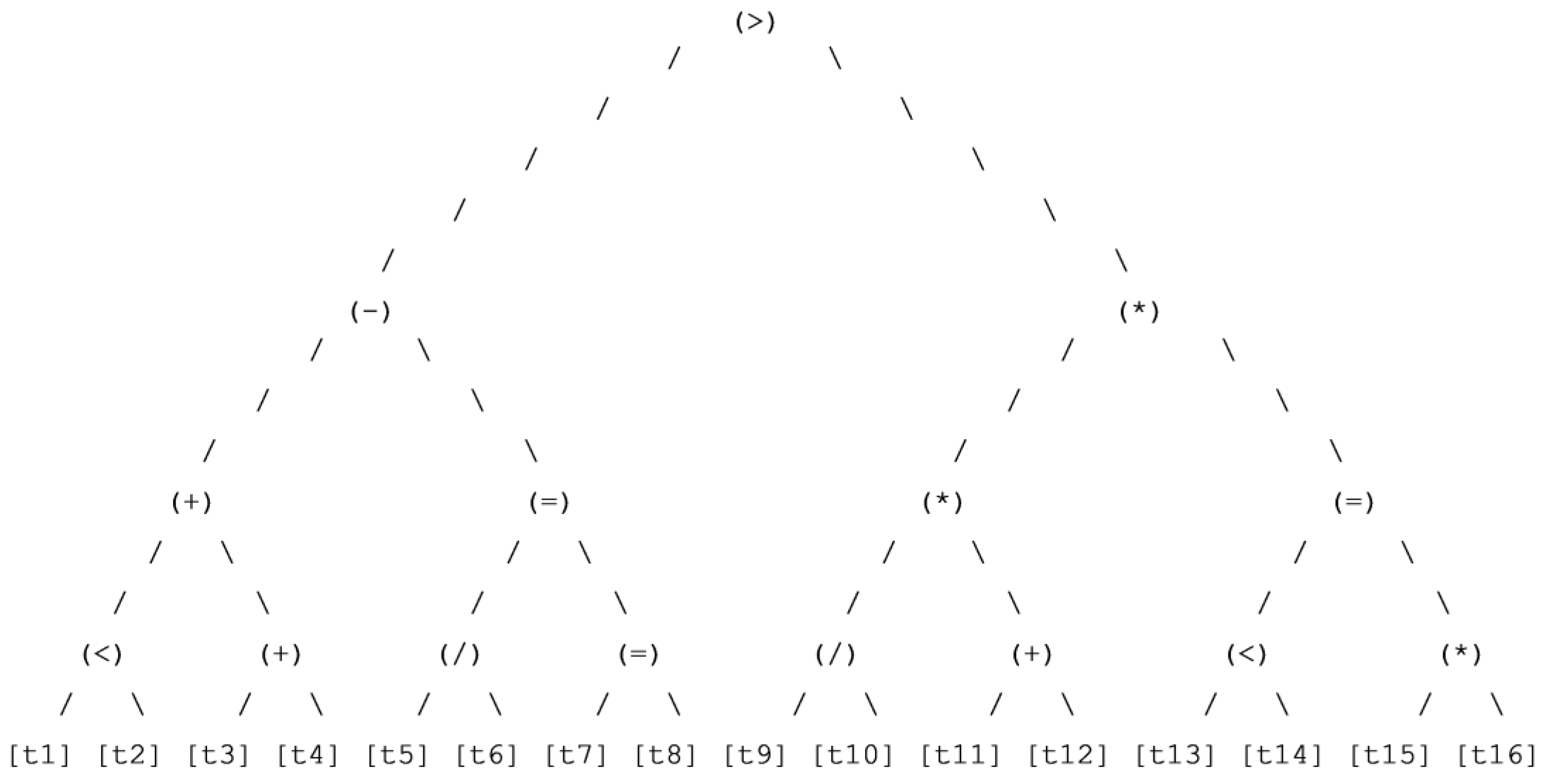
Figure 6.
Best chromosome classification (7th run).
Figure 7.
Dominant training BDT for wine classification.
Figure 8.
Dominant validation BDT for wine classification.
Figure 9.
Dominant testing BDT for wine classification.
Figure 10.
Best chromosome testing BDT for wine.
Figure 11.
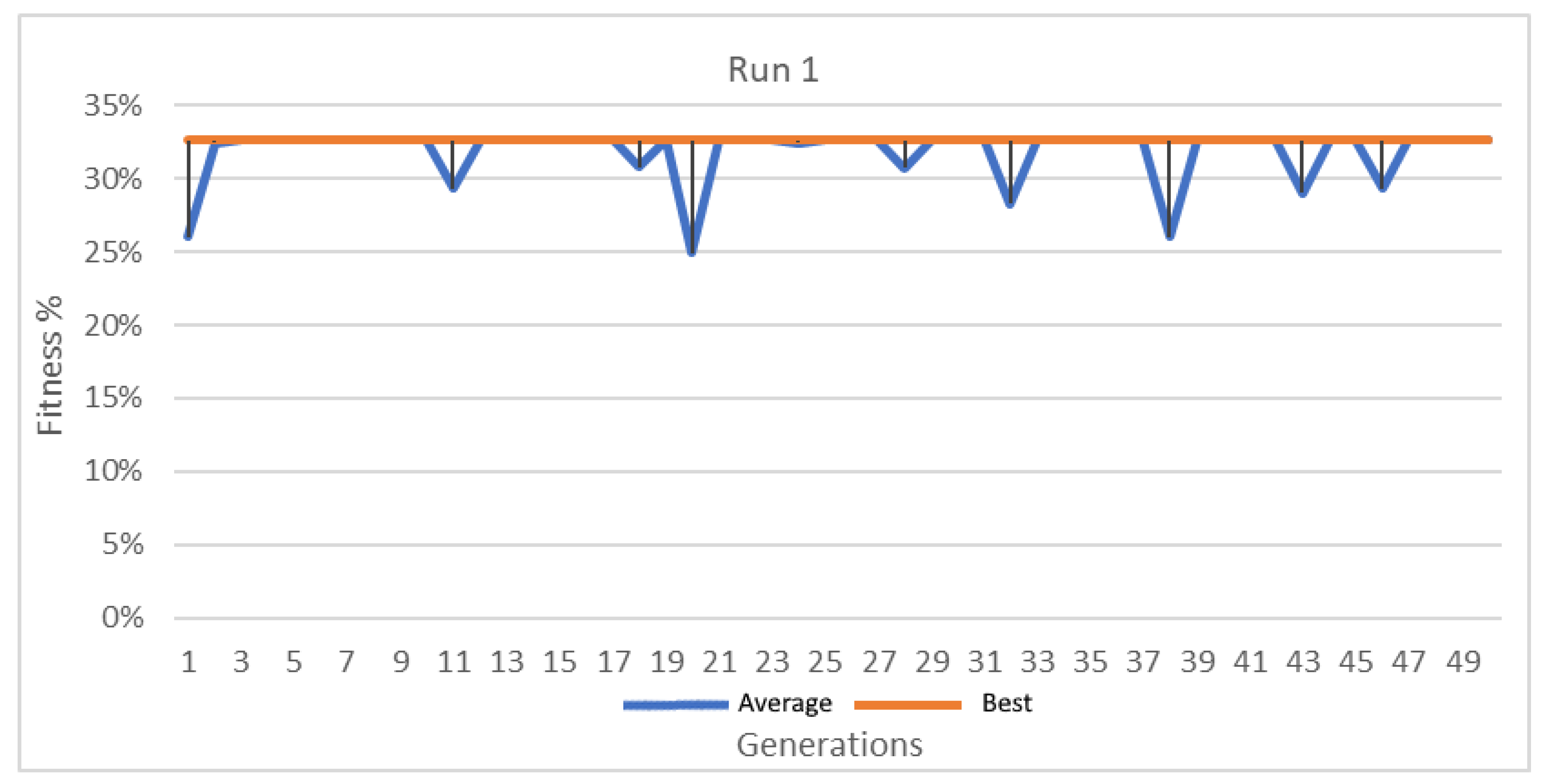
Best and average GA wrapper fitness run 1.
Figure 12.
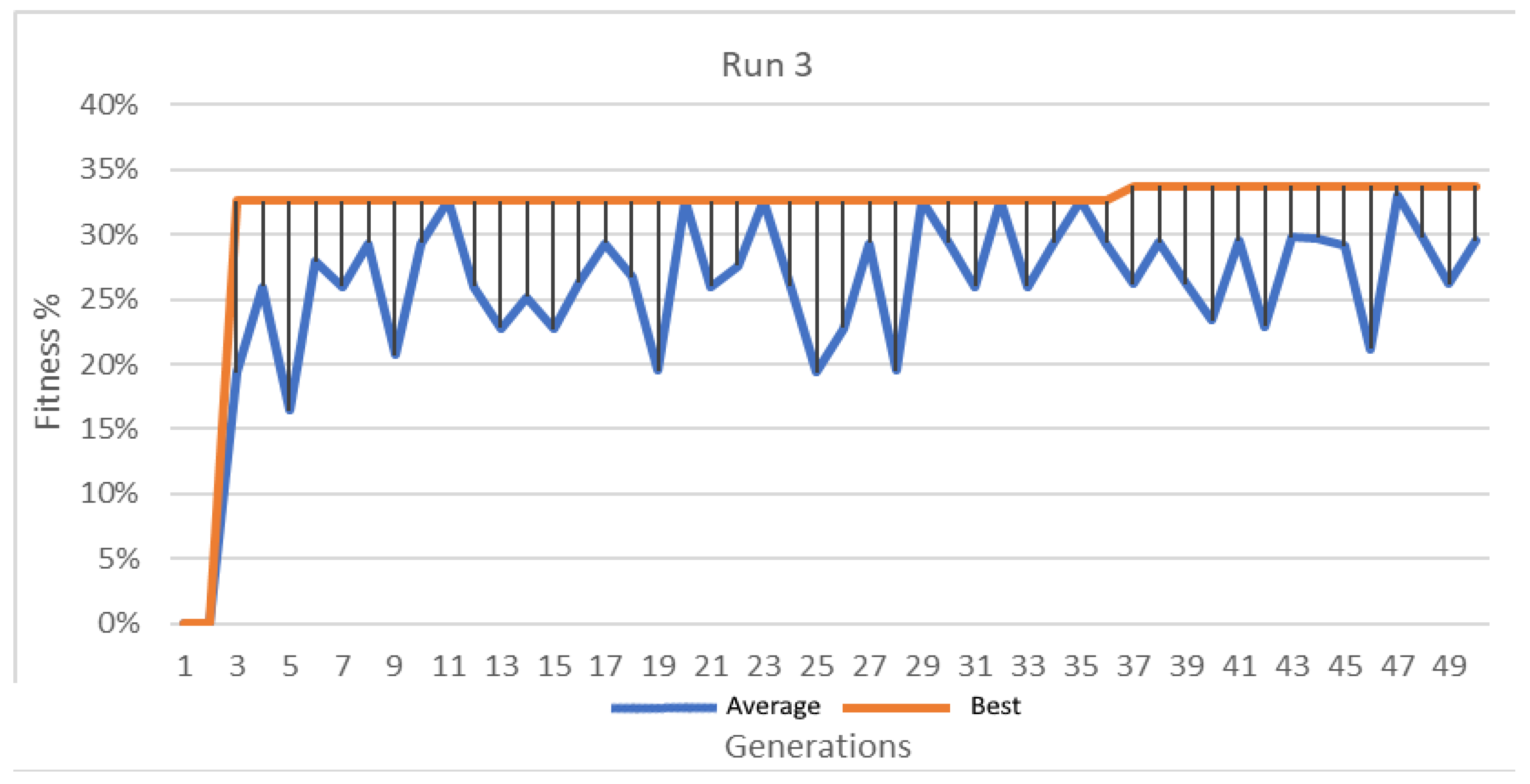
Best and average GA wrapper fitness run 3.
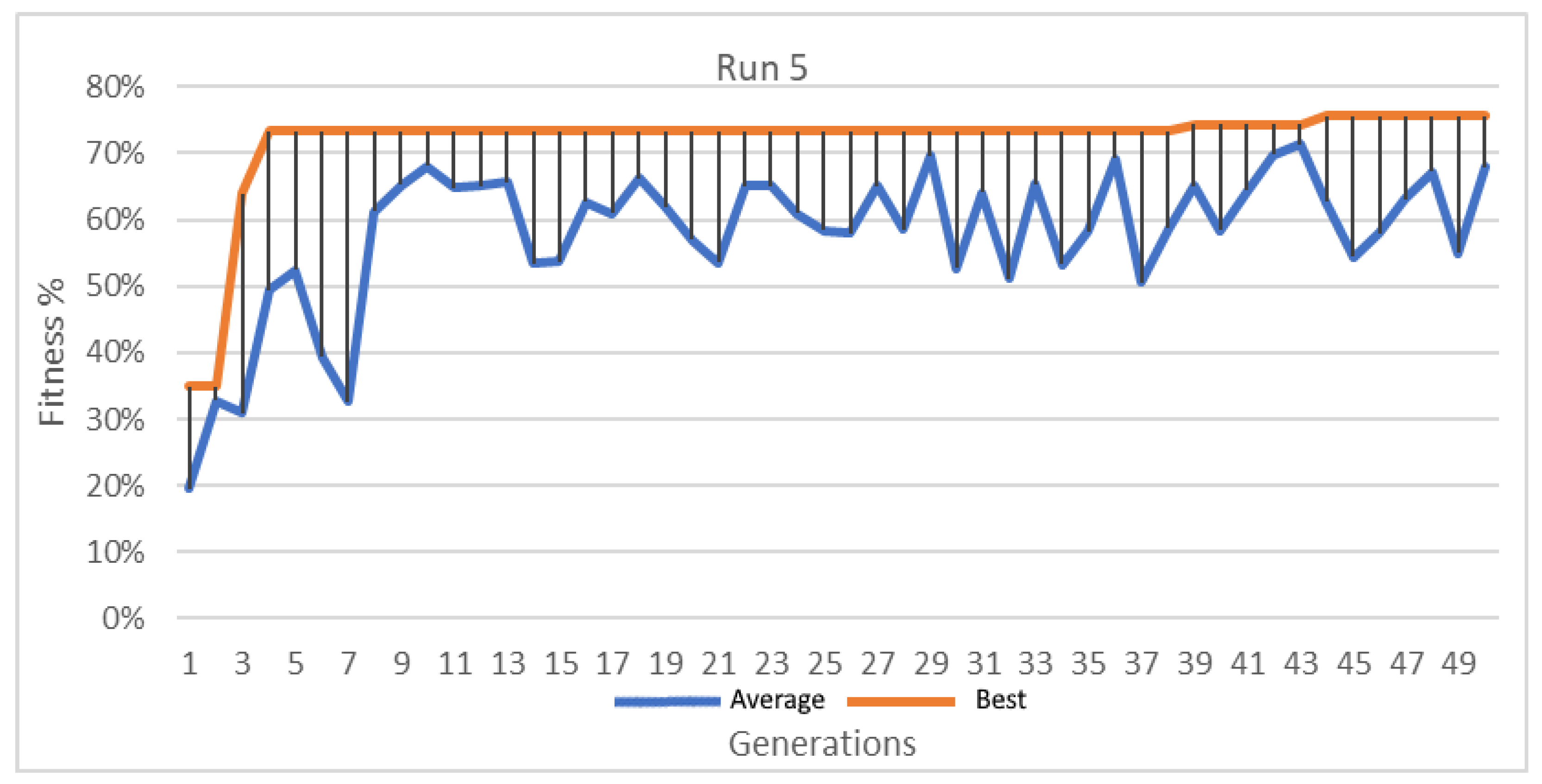
Figure 13.
Best and average GA wrapper fitness run 5.
Figure 14.
Best and average GA wrapper fitness run 7.
Figure 15.
Best and average GA wrapper ritness run 9.
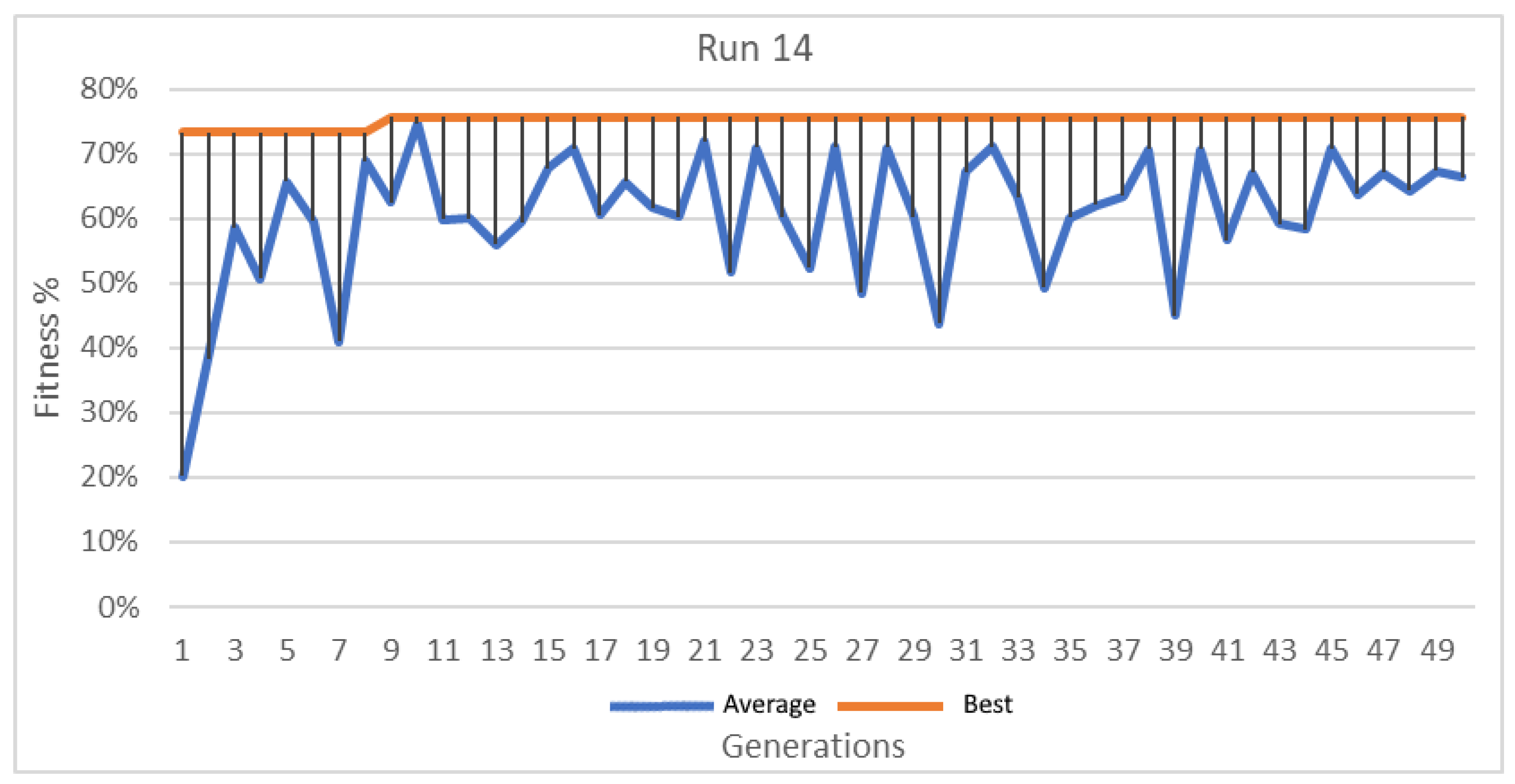
Figure 16.
Best and average GA wrapper ritness run 14.
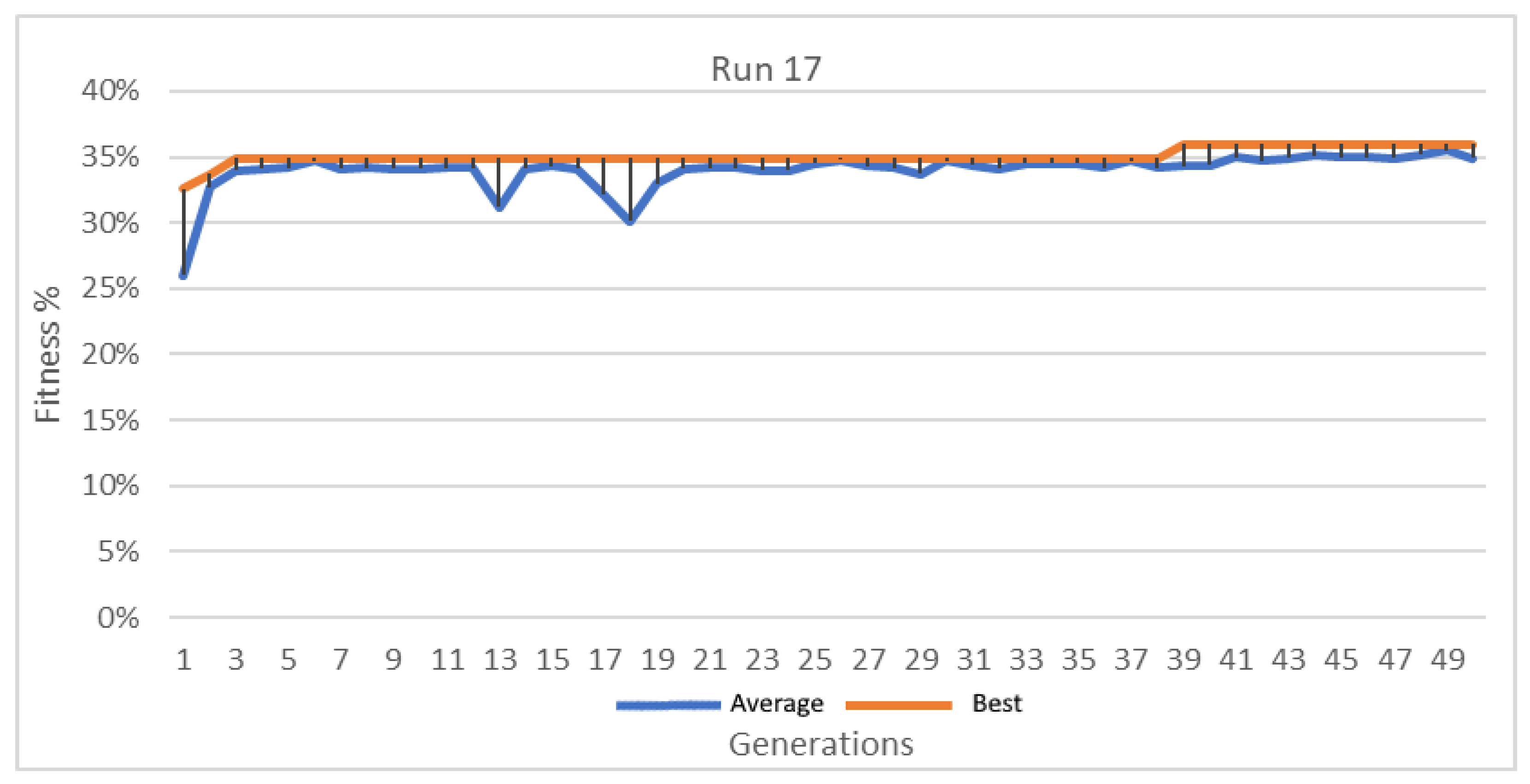
Figure 17.
Best and average GA wrapper fitness run 17.
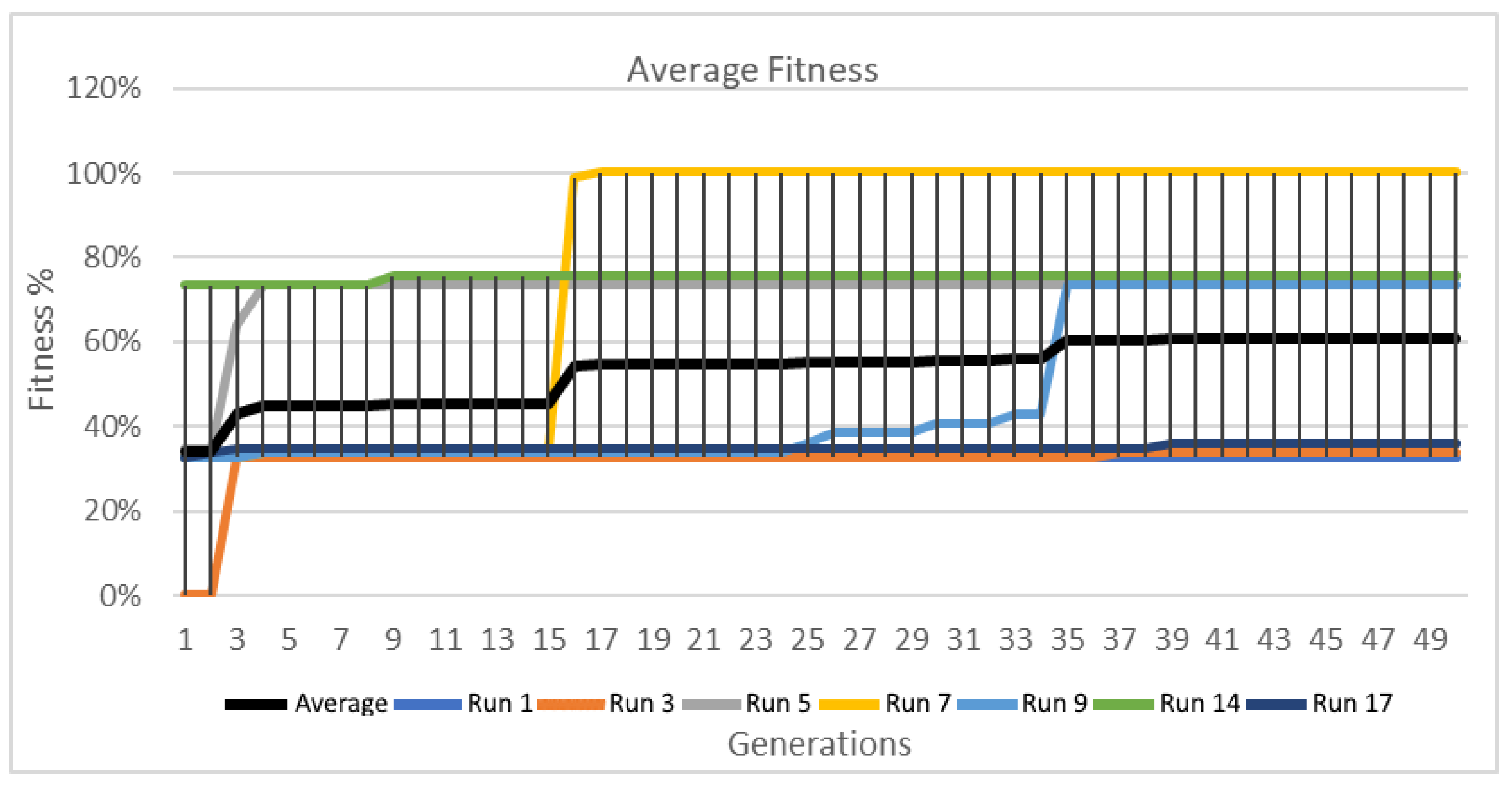
Figure 18.
GA wrapper average fitness.
Figure 19.
GA wrapper performance on wine data.
Table 1.
GA Wrapper Development Research Objectives.
| No | Research Objective (RO) | Sub-Objectives |
|---|
| 1 | GA Wrapper Model Design | |
- 2.
Define The GA Wrapper Design
|
| 2 | GA Wrapper Model
Implementation | |
- 2.
Genetic Algorithm Training
|
- 3.
Genetic Algorithm Validation
|
- 4.
Genetic Algorithm Testing
|
- 5.
Genetic Algorithm Representation
|
| 3 | GA Wrapper Model
Performance | |
- 2.
Calculate Class Errors
|
- 3.
Calculate Generations Fitness
|
- 4.
Calculate Best Fitness
|
- 5.
Calculate Optimal BDTs
|
- 6.
Visualize Dominant BDTs
|
- 7.
Calculate Best Chromosome’s Gene Sequence
|
- 8.
Represent Generations’ Fitness Graphical
|
- 9.
Calculate and Represent Average Chromosome’s Gene Frequencies
|
- 10.
Generate Rules for Wine Cultivars
|
Table 2.
Binary Decision Tree Pseudocode.
Function Decision_Tree(Atts,default,examples); Atts ⟵ Attributes; Default ⟵ default_typical_class; Examples ⟵ Examples; best_att ⟵ 0; AttsValue[i] ⟵ Atts[1…N]; Subset[i] ⟵ 0; subTree ⟵ 0; Create Node StartNode; If Examples have the same classification thendo return classification; If Examples is empty thendo return Default classification;
best_Att ⟵ Find_best_Att(Atts,examples) StartNode ⟵ best_att; For any AttsV(i) of Atts do Examples(i) ⟵ Best AttsValue[i] from Examples; If subTree is not empty do then new_atts ⟵ atts-best_att; subTree ⟵ create_Decision_Tree(subTree,new_atts); attach subtree as child of StartNode;
else
return StartNode;
|
Table 3.
GA wrapper pseudocode.
//Cross-over probability ⟵ 40%
//Mutation Probability ⟵ 60%
//Tournament Selection ⟵ 4
//Gene Probability ⟵ 0.3
Init GA()
G ⟵ 100//Generations
P ⟵ 500//Population size
OP ⟵ 0.4//Operator probability
Init elitist[], parent[], offspring[], newPop[], pop[]
for g = 0 to G
elitist = getTrainingElitist(pop)
for b = 0 to P//Breeding loop
for s = 0 to 2
parent[s] ⟵ copy(select(pop))
offspring ⟵ (getRandDouble() < OP)? crossOver(parent):mutate(parent)
newPop[b] ⟵ (getTrainingFitness(offspring[0]) > getTrainingFitness(offspring[1]))? offspring[0]: offspring[1]
pop[getRandInt(P)] ⟵ elitist;
pop ⟵ newPop; |
Table 4.
Wine dataset features.
| Features | Description |
|---|
| Title of Database | Wine recognition data |
| Updated | 21 September 1998 by C. Blake |
| Attribute | 13 |
| Attributes Values | Continuous |
| Missing Attribute Values | None |
| Class 1 | 59 |
| Class 2 | 71 |
| Class 3 | 48 |
Table 5.
Wine dataset.
| Cultivars | Genes |
|---|
| Alcohol | 1st |
| Malic Acid | 2nd |
| Ash | 3rd |
| Alkalinity of Ash | 4th |
| Magnesium | 5th |
| Total Phenols | 6th |
| Flavonoids | 7th |
| Nonflavonoid Phenols | 8th |
| Proanthocyanins | 9th |
| Color Intensity | 10th |
| Hue | 11th |
| OD280/OD315 of Diluted Wines | 12th |
| Proline | 13th |
Table 6.
Best chromosome classification for the 7th run.
| Gene | Gene Occurrence | Class |
|---|
| 0 | 1 | Class[0] = 0.32558139534883723
Class[1] = 0.0
Class[2] = 0.0 |
| 3 | 2 |
|
| 4 | 1 |
|
| 6 | 1 |
|
| 8 | 1 |
|
| 9 | 1 |
|
| 10 | 1 |
|
| 11 | 1 |
|
| 12 | 1 |
|
| 13 | 1 |
|
| 14 | 3 |
|
| 15 | 1 |
|
Table 7.
Optimal decision trees for wine classification.
| Training Votes | Validation Votes | Testing Votes |
|---|
| Tree[0] = 10,449 | Tree[0] = 3 | Tree[0] = 0 |
| Tree[1] = 0 | Tree[1] = 0 | Tree[1] = 0 |
| Tree[2] = 263,411 | Tree[2] = 225 | Tree[2] = 33 ⟵ max. no |
| Tree[3] = 1578 | Tree[3] = 0 | Tree[3] = 0 |
| Tree[4] = 15,488 | Tree[4] = 0 | Tree[4] = 0 |
| Tree[5] = 15,288 | Tree[5] = 0 | Tree[5] = 0 |
| Tree[6] = 102,215 | Tree[6] = 184 | Tree[6] = 0 |
| Tree[7] = 123,836 | Tree[7] = 38 | Tree[7] = 0 |
| Tree[8] = 10,051 | Tree[8] = 0 | Tree[8] = 0 |
| Tree[9] = 452,790 ⟵ max. no. | Tree[9] = 264 ⟵ max. no. | Tree[9] = 21 |
Table 8.
Best chromosome gene frequency for class gender.
| Gene Position | Gene Name (Feature/Attribute) | Gene Variables | Occurrences |
|---|
| 0 | Class 1, Class 2, Class 3 | - | 1 |
| 1 | Alcohol | Real | 0 |
| 2 | Malic Acid | Real | 2 |
| 3 | Ash | Real | 1 |
| 4 | Alkalinity of Ash | Real | 1 |
| 5 | Magnesium | Real | 0 |
| 6 | Total Phenols | Real | 1 |
| 7 | Flavonoids | Real | 0 |
| 8 | Nonflavonoid Phenols | Real | 1 |
| 9 | Proanthocyanins | Real | 1 |
| 10 | Color Intensity | Real | 1 |
| 11 | Hue | Real | 1 |
| 12 | OD280/OD315 of Diluted Wines | Real | 3 |
| 13 | Proline | Integer | 1 |
| 14 | Additional Classes {1,2,3} | - | 1 |
Table 9.
Average genes frequency from 7 runs for the wine origin dataset.
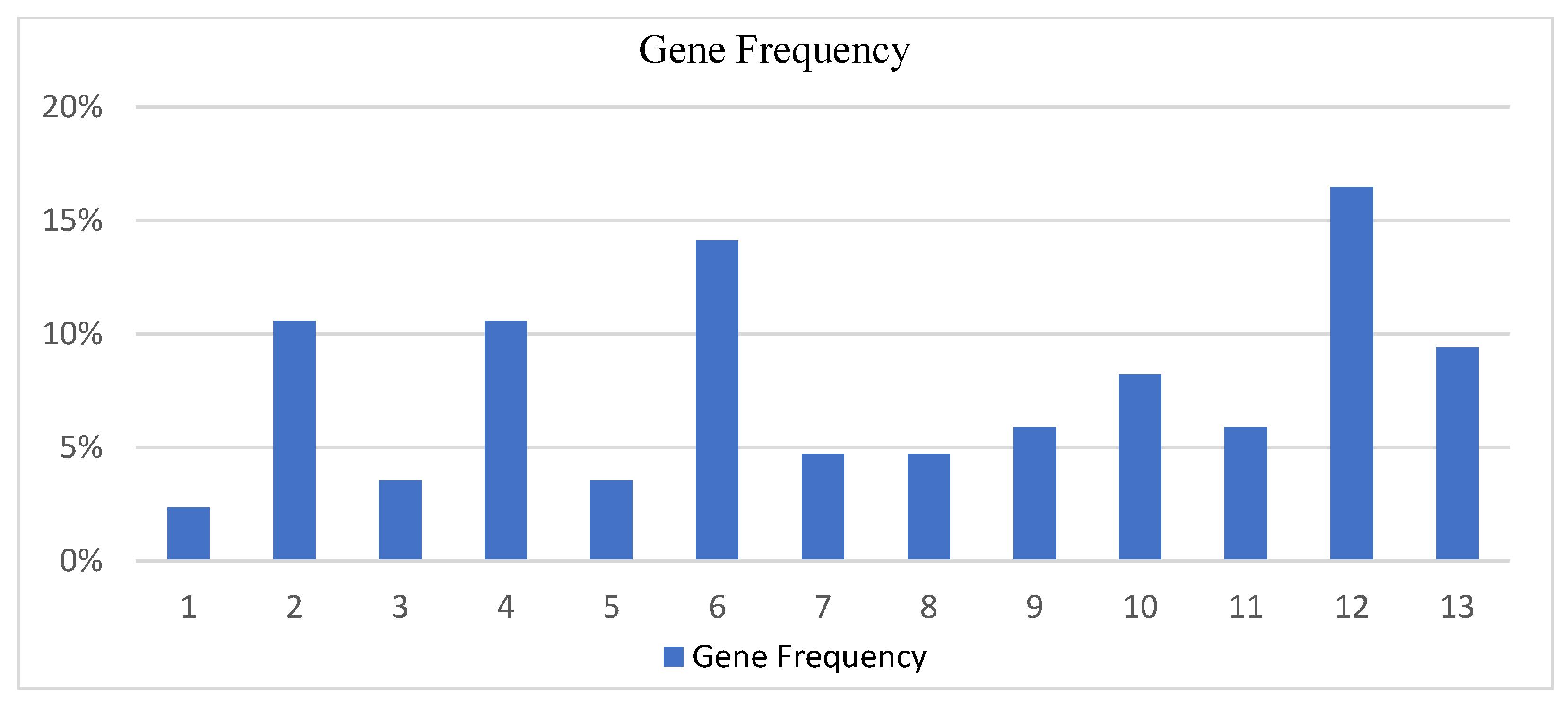
| | Runs | Genes Average Frequency of Occurrence |
|---|
| Gene | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | Avg. Occurrence | Avg. Occurrence % |
|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0.285714 | 2.35% |
| 2 | 2 | 1 | 1 | 0 | 3 | 0 | 2 | 1.285714 | 10.58% |
| 3 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0.428571 | 3.52% |
| 4 | 0 | 0 | 1 | 2 | 1 | 4 | 1 | 1.285714 | 10.58% |
| 5 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0.428571 | 3.52% |
| 6 | 2 | 2 | 4 | 0 | 1 | 2 | 1 | 1.714286 | 14.11% |
| 7 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0.571429 | 4.70% |
| 8 | 2 | 1 | 0 | 0 | 0 | 0 | 1 | 0.571429 | 4.70% |
| 9 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0.714286 | 5.88% |
| 10 | 1 | 1 | 2 | 1 | 0 | 1 | 1 | 1 | 8.23% |
| 11 | 0 | 2 | 2 | 0 | 0 | 0 | 1 | 0.714286 | 5.88% |
| 12 | 1 | 2 | 0 | 4 | 4 | 0 | 3 | 2 | 16.47% |
| 13 | 1 | 0 | 2 | 2 | 2 | 0 | 1 | 1.142857 | 9.41% |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).