1. Introduction
The economic crisis of 2008, triggered by subprime mortgages that were given the “No Income, No Job, No Assets” (NINJA) label (
Foglia et al. 2020), has demonstrated the fragility of the banking system, which is characterized by the scarce quality of the capital level and the limited liquidity (
Tajani et al. 2019;
Morano et al. 2020). Indeed, the crisis has highlighted that banks’ skills for the self-assessment of the internal capital have been overestimated and that their risk measurement methods are inadequate to capture rare but impactful events (
Dell’Atti et al. 2013). This situation caused the credit crunch, severely penalizing the global economy, especially the real estate and the construction market, which has been always linked to the liquidity generated by mortgages and loans. With the purpose of overcoming the limitations of the banking system, the Basel Committee has introduced different developments (the so-called Basel III) that are aimed at improving the capital requirements of banks and determining an adequate regulatory capital, overcoming the limits of the previous regulatory frameworks (Basel I and II) (
BCBS 2017). The regulatory scheme of Basel III stands on three pillars (
BCBS 2019):
Mandatory minimum capital requirements, concerning the introduction of new rules for a more precise quantitative assessment of corporate risks and of the assets to be allocated and moreover tending to use—for prudential purposes—corporate risk management mechanisms;
Prudential checks on capital adequacy, inherent both the supervision of the banks’ capital and the evaluation of the budget to be internally carried out by each individual intermediary;
Market discipline, regarding the effective use of the disciplining power that is performed by the market, thanks to adequate disclosure transparency, in order to encourage safe and solid banking management practices.
These pillars find practical application into two methodologies designed to a careful assessment of the credit risk, called the Standard and the Internal Ratings-Based (IRB) methods. By analyzing in detail the mortgage-backed loans on the properties, the first method defines a weighting coefficient of 35% for the residential properties, and that rises to 100% for the Income Producing Real Estate (IPRE), unless in well-developed markets. This different coefficient, necessary to establish the adequate amount of the regulatory capital, derives from the observation that the defaults linked to the loans with underlying IPRE were among the main causes of assets quality’s deterioration in the banking sector. As an alternative to the Standard method, the IRB can be used to determine the capital requirement that can be applicable to a given exposure. The IRB is based on the following risk measurement parameters: (i) probability of default (PD); (ii) loss in case of default (LGD); (iii) exposure at the time of default (EAD); and (iv) effective deadline (M).
The IRB can be articulated through two alternative approaches: (
i) the basic method, which requires banks to provide their own assessments exclusively of the PD and form on regulatory valuations for other risk components; (
ii) the advanced method, which also allows banks to assess other parameters. Both methods (Standard and IRB) are often difficult to be applied, especially for the smaller credit institutions where there is an absence of a suitable capital management function. For example, the exposure classes as coded within Basel II, although substantially in line with the consolidated banking practice, can be classified in different ways by the smaller banks, which therefore find it difficult to adapt their structure to these definitions. These limits are also found in the Basel III agreements, characterized by an excessive complexity of the methods for determining the weightings of risky activities and by high compliance charges (
Intonti 2012).
In order to overcome these weaknesses, the present research aims at proposing a multi-criteria derivation index, applied to the credit risk analysis of the debt relief operations. In fact, the mortgage down payments very often become too heavy for the borrowers and banks have to evaluate different alternative scenarios, i.e., re-discuss the original mortgage conditions (interest rate, duration of the repayment plan, down payment amount, etc.). The absence of a dynamic real estate market and the length of bureaucracy and administrative justice have led over the years to the increase in debt relief operations, relegating more aggressive practices to borderline situations.
The paper is organized as follows. In the second Section, an overview of the MultiCriteria Decision Analysis (MCDA) is provided. In the third Section the main credit risk assessment models are described. In the fourth Section the aim of the work and the principal features of the methodology are defined. The fifth Section refers to the development of the proposed index and in particular to the determination of the criteria and the related weights considered, whereas in the sixth Section the normalization of the scores that are assigned to the criteria and the aggregation of the results are described. In the seventh Section, the proposed index is applied to a real case study that occurs for a medium entrepreneur operating in the construction and the hospitality sector in the city of Rome (Italy). Finally, the conclusions are drawn by highlighting the advantages and limitations along with future developments.
2. Overview on the MCDA
The increase in the complexity of decision-making processes due to the several actors involved, each with specific interests, has made it necessary to create tools to support choices in scenarios of uncertainty, a need to which the MultiCriteria Decision Analysis (MCDA) has answered. The need, therefore, to synthesize the different expertise participating in the decision-making process through shared platforms, has encouraged the spread and application of MCDA in various disciplines, attracting attention from the scientific community. The MCDA, due to their flexibility, find application in many different complex decision problems, such as the regeneration of the urban peripheries (
Locurcio et al. 2019), the cultural heritage enhancement (
Morano et al. 2016), the analysis of the urban renewal projects (
Morano et al. 2015), and the management of the credit risk under strict uncertainty (
Pla-Santamaria et al. 2020).
Nowadays, there are so much MCDA—due to the progress of the research—which is difficult to provide an exhaustive classification and an accurate census of them.
Ishizaka and Nemery (
2013) provided guidelines on how to choose the best MCDA according to the category and the characteristics of decision problems by proposing a classification of the major MCDA into three groups:
Full aggregation approach (or American school);
Outranking approach (or French school);
Goal, aspiration or reference level approach.
Taking up the classification of the DECERNS (Decision Evaluation in ComplEx Risk Network Systems) software, it is possible to divide the MCDAs into:
Basic MCDA methods;
Advanced MCDA methods;
Fuzzy MCDA methods.
Larichev (
2000) proposed a classification of MCDA with respect to the type of starting input, distinguishing methods based on:
Quantitative measurements;
Qualitative initial measurements;
Pairwise comparison of alternatives;
Qualitative measurements not converted to quantitative variables.
For the specific features of the problem analyzed in this work and with respect to the different decision-making steps, the following three MCDA were combined in order to exploit the logical-operational potential of each one and at the same time compensate for the limits of each one thanks to the integration of the three:
Analytic Hierarchy Process (AHP);
Preference Ranking Organization METHod for Enrichment of Evaluations (PROMETHEE);
Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS).
The choice of these MCDA, pertaining to the “basic MCDA methods” category, depended on the level of definition of the inputs of the problem considered and on the desire to avoid an excessive computational complication that could have excluded less expert subjects from the possibility of replicating and use the proposed methodology. Specifically, it was decided to apply the AHP for the identification of the weights of each criterion because (
i) this method allows us to consider subjective contributions deriving from the judgment of experts; (
ii) the problem under analysis has a limited number of criteria (less than 10); and (
iii) the presence of a consistency measure that allows to verify the consistency of the pairwise comparisons by decreasing the arbitrariness of the judgments in the assignment of weights. This last reason makes the AHP method more robust than others such as the Stepwise Weight Assessment Ratio Analysis (SWARA) method or the PIvot Pairwise RElative Criteria Importance Assessment (PIPRECIA) method, which, while considering the opinions of experts, do not present the possibility of guaranteeing a consistency check through a Consistent Index (
Alinezhad and Khalili 2019). Although other methods, such as the Multi-Objective Optimization Ratio Analysis (MOORA) and the COmplex PRoportional ASsessment (COPRAS) method, have been shown to be the most stable results in the case of input data oscillating compared to AHP (
Kraujaliene 2019), they do not allow us to highlight the essential contribution, albeit of a subjective nature, deriving from experts in the field with experience and deep knowledge of the dynamics that raise up in the analyzed process. The AHP is the most widespread method in decision-making processes focused on the role of experts: based on the analysis of
Linkov and Moberg (
2011), 48% of intervention types focused on stakeholder participation use AHP. Furthermore, the AHP, together with TOPSIS, appear to be consolidated methods in the context of the analysis of this work, so much so that they are also explained in important regulatory references of the Italian territorial context such as the Italian National Anti-Corruption Authority Guidelines No. 2. The TOPSIS, instead, was preferred over conceptually similar methods, such as the VlseKriterijuska Optimizacija I Komoromisno Resenje (VIKOR), since, unlike the latter, it allows to obtain different rankings depending on the approach used for normalization of the values associated to each alternative; therefore, it is poorly applied in risk and financial management problems (
Mardani et al. 2016).
According to the indications of the Decision Maker (DM), it was possible to identify the preference functions associated with some criteria, and thus it was considered appropriate to take this information into account through the PROMETHEE. This method not only allows criteria in which the optimal value is unknown to be considered, as happens with the Additive Ratio ASsessment (ARAS) method (
Zavadskas and Turskis 2010), or in which there are conflicting objectives (minimization/maximization) associated with different criteria, as occurs with the Weighted Aggregated Sum Product Assessment (WASPAS) method (
Chakraborty et al. 2015), but also allows the possibility of the preference function to be graphed, making it clear even to non-expert users. Furthermore, PROMETHEE has shown itself to be particularly used in applications in financial decisions such as credit risk assessment and portfolio selection (
Spronk et al. 2005).
Among different MCDA, the ones applied in the present research—AHP, PROMETHEE, and TOPSIS—have been employed in numerous scientific works for analyzing or assessing the credit risk exposure for banks or firms, some of that listed in
Table 1. Ranging from the implementation of traditional-based procedure to the development of hybrid or novel model (
Froelich and Hajek 2020;
Yang et al. 2019), the issues addressed remain mostly the same: to provide decision-support tools for aiding stakeholders that are involved in credit risk analysis and evaluation by considering a multitude of criteria, data and functional relationships.
As can be noticed, a unique methodology to assess the credit risk issues does not exist, especially in the field of the MCDA where their flexibility is able to create numerous hybrid models in order to avoid singularly weaknesses of each technique or address a specific issue of some problems. In particular, the construction of a methodology that, with a proper structure, combines the objectivity of the financial variables related to the debt restructuring operations, and with a deep knowledge of the experts operating the real estate finance sector can be an innovative contribution in the reference literature.
3. The Credit Risk Management and Assessment Models
Credit risk management is a constantly evolving research sector and the methods adopted by financial institutions (FI) are widely diversified. Depending on the type of the counterparties (i.e., the individual entrepreneurs or the sovereign governments), the customs of the debt covenants (i.e., the auto loans or the complex derivatives transactions), and the size of the credit institution, the different valuation models and techniques are implemented. Generally, the main goal of a credit risk assessment model is to evaluate the probability distribution of each future loss in a bank’s portfolio, by analyzing the counterparty’s ability to satisfy the debt obligations.
The first step in the assessment model creation process is to define the type of the loss to be analyzed (
Hirtle et al. 2001). According to
Fatemi and Fooladi (
2006), the counterparty default risk is the type of the credit risk with higher interest to the FI, which is then followed—in terms of the importance—by the counterparty migration risk, the default risk, and the migration risk at the portfolio level. The academic literature has focused on the counterparty risk’s price effects, especially after the changing regulatory framework related to the post economic crisis period (
Zhu and Pykhtin 2007;
Assefa et al. 2009;
Du et al. 2019).
The types of the credit risk assessment approaches, according to
Doumpos et al. (
2019), can be divided into three main groups: the judgmental approaches, the data-driven empirical models, and the financial models.
The judgmental or qualitative approach is the traditional method that is firstly used for the assessment of the credit risk exposures. The most important counterparty’s factor analyzed is their willingness to repay (
Hempel 1994), which is followed by profitability, liquidity, cash flows, leverage, capitals structure, stock market performance, and financial projections. Hence, several disadvantages can be identified for the judgmental method: first of all, the subjectivity related to the interpretation of the information data (
Libby 1975); secondly, the several factors considered can be contradicted by other similar ones, compromising the analysis; finally, most FI that implement this method usually employ few analysts, and this can result in non-in-depth assessments that lack credibility of outcomes, by exacerbating the judgmental bias that already exists (
Kalapodas and Thomson 2006).
The data-driven approaches employ the historical data about the loans accepted, rejected, paid as agreed and the cases in default. They are applicable to both the corporate and the consumer loans, in accordance with the available data. The United States Federal Reserve made the first effort to promote the uniformity in the credit evaluation field by proposing the Fair Isaac COrporation (FICO) model (
Ignatius et al. 2018). After this attempt, important works have been addressed to exploit a variety of analytical tools (
Tsai and Wu 2008;
Wang et al. 2011;
Trustorff et al. 2011;
Caruso et al. 2018), in order to shape data-driven solutions for both the bankruptcy and the credit risk settlement. From the analysis of the existing literature, a wide variety of soft computing methods (
Lahsasna et al. 2010;
Capotorti and Barbanera 2012), as Support Vector Machines (
Bellotti and Crook 2009;
Danenas and Garsva 2015), nearest neighbor approach (
Marinakis et al. 2008), machine learning techniques (
Aithal and Jathanna 2019), rough set theory (
Wang and Chen 2006;
Yeh et al. 2012), decision tree (
Bastos 2008;
Zhang et al. 2010), multi-criteria and operations research techniques (
Li et al. 2011;
Zhang et al. 2014,
2019;
Ferreira et al. 2014;
Krohling and Pacheco 2015), and statistical regressions (
Bensic et al. 2005;
Blanco et al. 2013) are available for those that are well-known as the scoring and the rating models.
The credit scoring problem is the most broadly approached in the reference literature. The logistic regression and Artificial Neural Networks are applied to improve the predictive accuracy of the credit risk management concerning the mortgage accounts (
Chi and Hsu 2012;
Munkhdalai et al. 2020;
Teles et al. 2020).
Angelini et al. (
2008) develop two neural network systems tested on a real-world data concerning Italian small businesses for assessing the credit risk. A credit scoring solution can be built also by using the Fuzzy logic due to its ability to deal with imprecise, partial, and vague data (
Akkoç 2012;
Sanchez-Roger et al. 2019).
In contrast to the empirical above reported methods, the financial models are mostly built on a theory and a regulatory approach, which is focused on the corporate debt. Two main types for the credit risk modeling can be identified: the structural models and the reduced form models. The former type of models assumes that default credit risk is related to a firm’s structural characteristics, such as the value of its assets and the debt. The reduced form models, instead, adopt a different approach assuming the default as a random event that may happen at any time. Such models use market data on bonds and credit derivatives as the main source of information about a firm’s credit risk structure (
Ericsson and Reneby 2004;
Arora et al. 2005). Among the financial models, another one market-to-market based also exists that is created to provide the portfolio risk management by making credit risk analysis more systematic: the Credit Metrics (CM) model. According to
Resti (
2000), the CM model is the most applied worldwide, but it requires a huge amount of data, usually not available for European banks: the work shows three possible research paths for reducing this “greed for data”.
Diaz and Gemmill (
2002) compare instead the CM with the Credit Risk
+ model.
Although the mentioned typologies of methods provide a large number of credit rating models, there are still some drawbacks that need to be addressed for the adoption of these models by the Small Credit Institutions (SCI). Firstly, the existing credit rating systems mainly depend on the financial data that are mostly unavailable. Secondly, most credit rating models assume that rating indicators should obey a specific distribution. Furthermore, the most important drawback is that the existing credit rating systems for the SCI were constructed by selecting a single indicator based on its information content or its discriminatory power.
In order to attempt this lack for the SCI, some Authors have carried out specific credit rating indicator systems.
Chai et al. (
2019) establish a credit rating indicator system composed of 17 indicators by using the partial correlation analysis and the Probit regression together with the TOPSIS fuzzy C-means technique, in order to score the credit ratings of 687 small enterprises in China. Actually, more text-based non-financial information are available rather than the quantitative financial data for the SCI. Consequently, the scholars often use the AHP or the Delphi method (
Liang et al. 2007;
Shi et al. 2018). With regard to the construction of an indicator system, a credit scoring indicator system was pioneered by
Altman (
1968). The model identifies the financial criteria that are significant in differentiating the “bad firms” from the “good firms” by building the Z-score and, consequently, the ZETA credit scoring models on the basis of the indicators, such as the return on the assets and the earnings before the interest and the tax to predict the possibility of the borrower’s default risk.
Gu et al. (
2017), instead, combine the AHP with the data envelopment analysis (DEA), using the indicators that are given from the financial status, the creditworthiness, the enterprise development, and the internet financial status to predict the default risks.
The effectiveness of a credit risk evaluation model depends on the lending FI’s flexibility in interpreting the counterparty’s information considered. The credit evaluation fronts a classical problem of the decision-making under uncertainty, where an individual’s worth is based on the assessments of the potential future incomes (
Gu et al. 2017).
4. Aim of the Work
The main methodologies that are used by the credit institutions to assess real estate credit risk suffer from the following limits: (
i) the complexity of calculating the indexes; (
ii) the difficult explanation and representation of the final results to the clients or non-expert subjects; and (
iii) the lack of a summary of the criteria and the respective quality scores that are assigned. These weaknesses translate into the difficult practical application of the relative instruments, with the consequent hurdle of real estate credit risk analysis, mainly for the banks and SME without a dedicated and structured office. In order to overcome these limits, especially in the case of the negotiations that are aimed at restructuring the debt deriving from IPRE investment properties, the work aims at identifying a synthetic risk index, called IPRE Index (
). This output is obtained by analyzing the credit risk with reference to the possible scenarios of a real intervention relating to a debt relief operation. The proposed index combines the objective values of financial variables with the subjective judgement of experts about the significance each of them (
García et al. 2013). The
IIPRE,risk is defined through the reconstruction of the decision-making process carried out by the credit manager. In particular, these needs are simultaneously considered: (
i) the creation of a platform that can be shared by the various subjects involved in the real estate financing; (
ii) the definition of a model that is suitable for different cases, such as the granting of a new credit line, the debt restructuring, the management of the Unlikely To Pay (UTP) and the Non-Performing Loans (NPLs); (
iii) the opportunity to avoid the formation of “black boxes” that are difficult to rebuild; (
iv) the clear and transparent representation of the results that are achieved; (
v) the simplification of the procedure, by avoiding the length of the bureaucracy and of the administrative justice; (
vi) the advantage of the financial exposure of the credit institution; and (
vii) the identification of a sustainable mortgage down payment for the debtor.
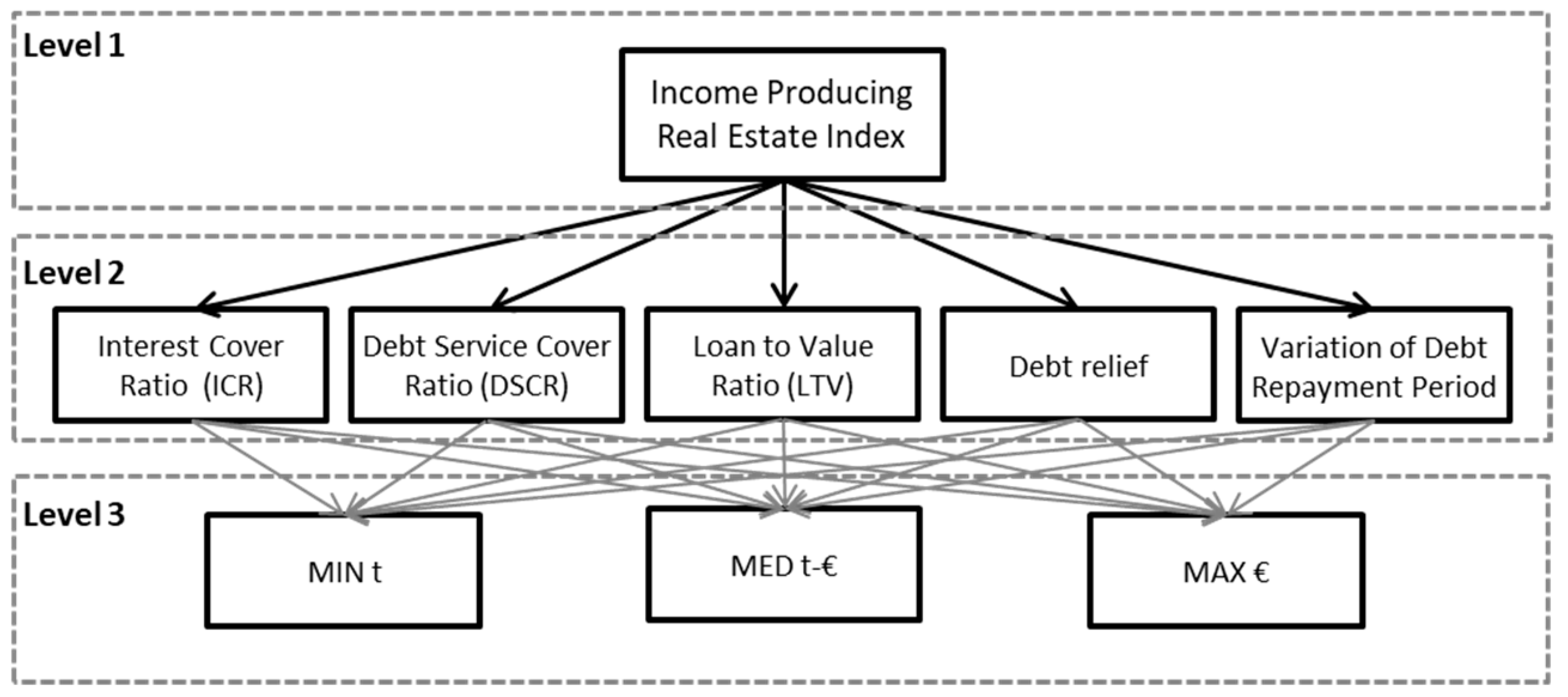
The developed methodology consists of the use of different types of MCDA, distinguished for each step of the decision-making procedure according to the approach that is carried out by the credit manager and the problem being analyzed.
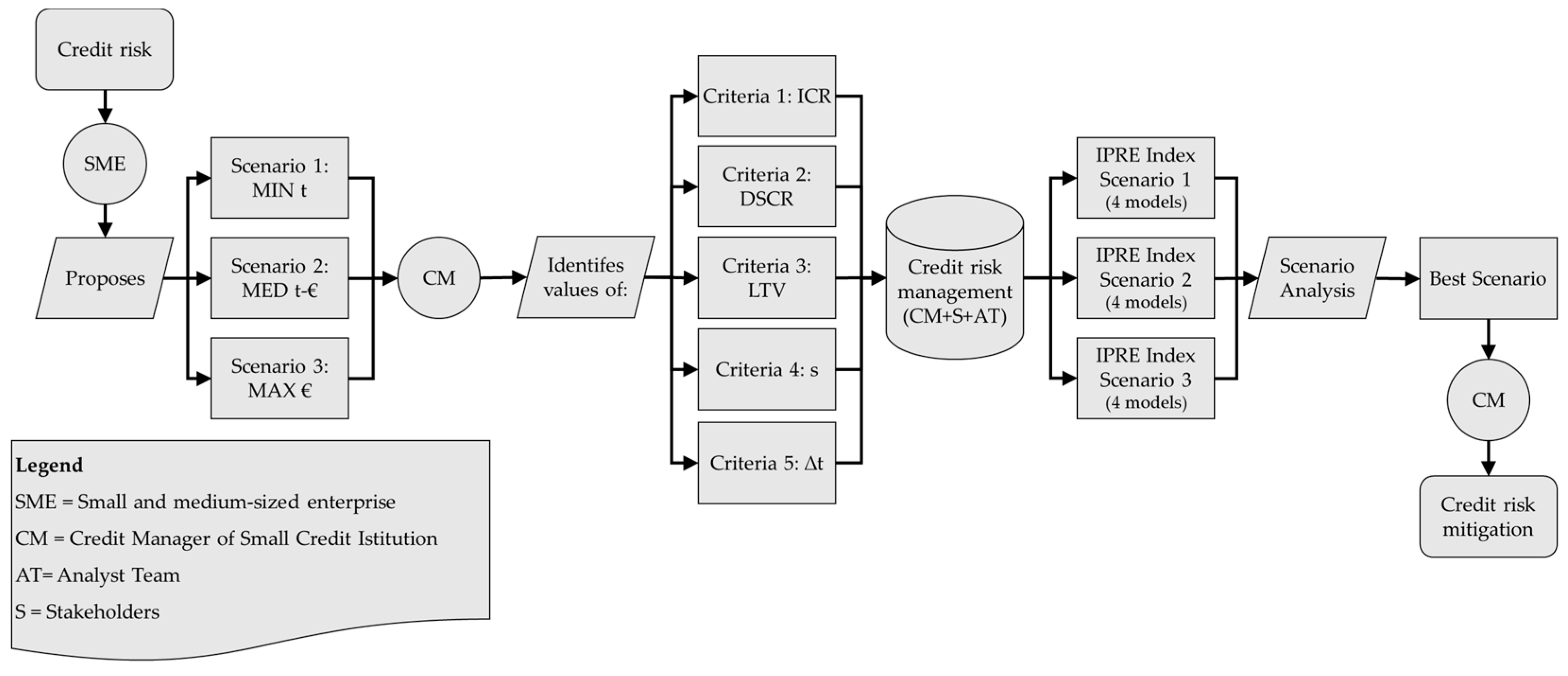
Starting from the credit risk mitigation process that is followed by the credit manager, in
Table 2 the phases leading to the definition of the IPRE Index are labeled, whereas the subject involved are below described:
The Decision Maker (DM), i.e., the credit manager who directly operates in the debt relief procedures;
The Analyst Team, which applies the skills acquired on the MCDA and the consultancy for the Investment Management and the Advisory, Valuation, and Real Estate Services companies, support the DM in the decision-making process;
The Stakeholders, i.e., the group of experts working in the real estate finance sector and faulty credit with underlying property, whose role is to determine the adequate importance of each criterion. In the present research, the panel of experts identified by the analyst team is composed of three subjects that know in depth the connection between property and credit: (a) the Head of mortgage and consumer credit issues in the Credit Department of the Italian Banking Association (ABI); (b) the CEO of a leading company specialized in the management, enhancement and disposal of NPLs with underlying real estate; and (c) the CFO of an important Investment Management Company that manages real estate funds for an Asset Under Management over 2 billion euros (SGR).
As summarized in
Table 2, the analyst team supports the DM in establishing the goal (first phase) and identifies the most suitable criteria (second phase). Subsequently, the analyst team selects a panel of experts (stakeholders) who deals with the definition of the significance of each criterion (third phase) through the application of the AHP. Approving the observations of the panel of experts, the fourth phase consists of the normalization of the scores that are assigned to criteria for which is possible to reconstruct the preference function, thanks to the PROMETHEE. After all, the results are collected and then the
is obtained, representative of the best alternative (fifth and sixth phases) by implementing the TOPSIS.
5. Criteria and Weights
In the phase of identifying the most representative criteria and sub-criteria of the credit risk relating to the financing, refinancing and debt restructuring operations for the investment properties, the analyst team proceeds through a first analysis of the respective parameters that are already established in the context of Basel II for the IPRE and the High-Volatility Commercial Real Estate (HVCRE). In particular, the following ones are analyzed:
The financial strength, including market conditions, financial indicators, stress analysis, and predictability of cash flows;
The activity’s features, concerning the location, design, and conditions of the properties under construction;
The solidity of the sponsor or the promoter, relating to the financial capacity and the willingness to promote the property, the reputation and the previous experience with similar properties and the relationships with relevant experts in the sector;
The guarantees package, regarding the nature of the privilege, the assignment of lease contracts, and the quality of insurance coverage.
Downstream of the simplification of the aforementioned parameters through various brainstorming sessions, the analyst team identifies the five most representative criteria useful for the credit risk management. By this way, the timing of the procedure is reduced, thus allowing the smaller credit institutions to carry out these assessments using lower investigation costs. The five criteria thus identified which therefore constitute the
(see
Table 3) are: the main debt covenants—according to
Duke and Hunt (
1988)—also considered in the context of Basel II (criteria 1, 2, and 3); further two criteria, namely the debt relief (criterion 4) and the variation of debt repayment period (criterion 5), which are designed for the goal of the present work. These two last criteria take into account the frequent contingence that the credit managers have to deal with when it is necessary to discuss again the debt of defaulting entrepreneurs: in these cases, the definition of new conditions (further debt, longer repayment period, etc.) for minimizing possible losses for the bank and taking into account the actual financial availability of the debtor is required.
Table 3 shows a brief description of each criterion considered and the related formulas where
EBIT is the Earnings Before Interest and Taxes;
is the Mortgage Amount;
is the Appraised Property Value, i.e., the mortgage lending value;
is the Further Debt Repayment Period; and
is the Initial Debt Repayment Period.
The definition of the importance, i.e., the weight,
, of each criterion occurs by implementing the AHP multi-criteria technique, which provides the assumption that the decision-maker, during its choice, applies, more or less consciously, a hierarchy of all the several elements that are included in the decisional procedure (
Saaty 1988). The use of such type of ordered structures through its division into progressively smaller “units” allows a detailed knowledge of the complex phenomena to be achieved. The procedure requires that the weights are defined firstly by submitting the following question to the panel of experts:
“With the aim of financing, refinancing and restructuring the debt that is derived from the investment properties, between the criterion a and the criterion b which of them is the most important?”
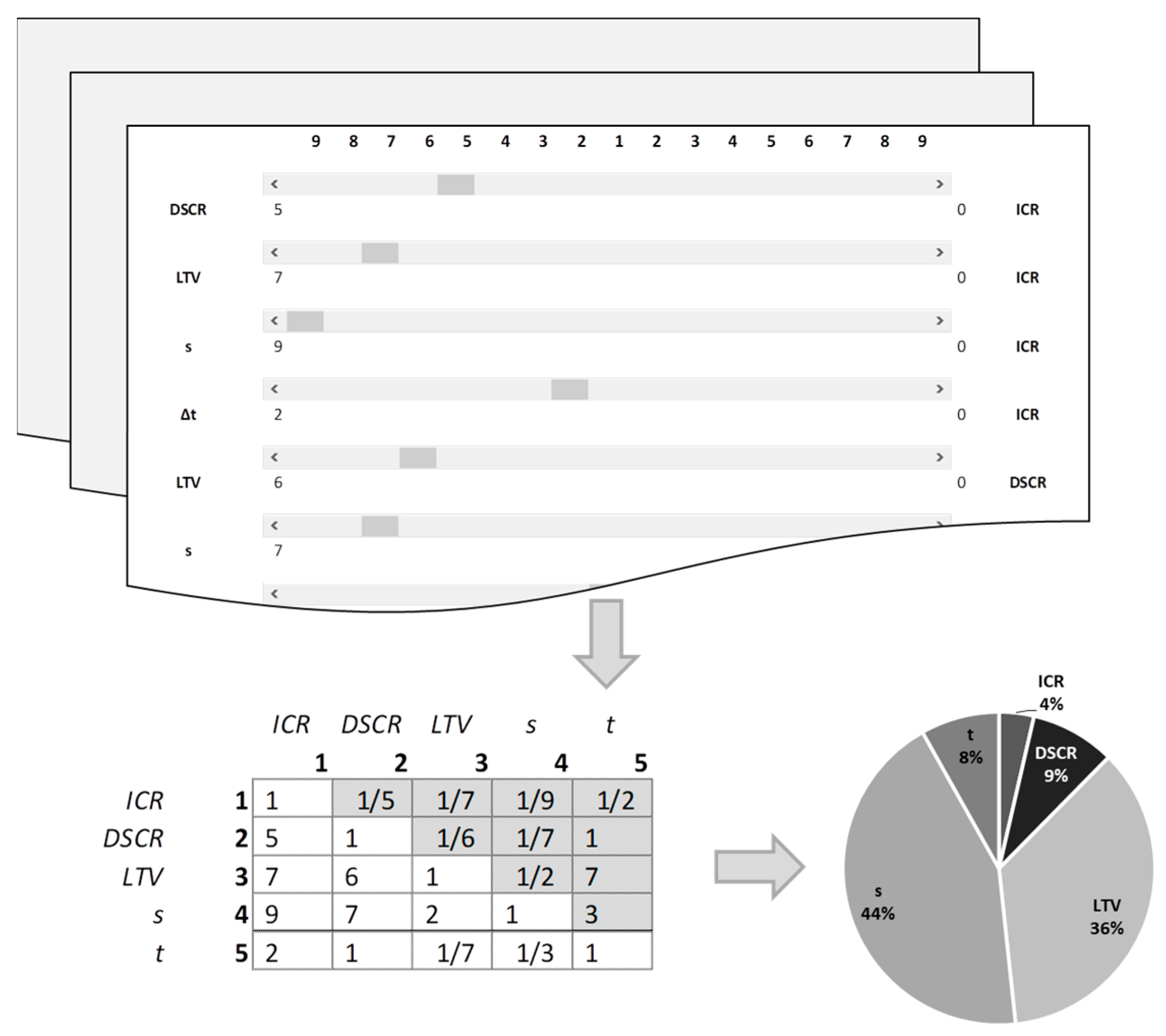
where a, b = 1, 2, 3, 4, 5 are the five criteria studied. Then, in order to translate the verbal expressions used in the pairwise comparisons between the criteria made by the group of experts into mathematical language, the well-known Saaty scale is adopted (
Saaty 2008). In order to facilitate the pairwise comparison in the input phase, an easy-to-read model is set up, consisting of bars and cursors whose scrolling is associated with a certain value; in this way, the comparisons allow to build the matrix of the criteria, which is capable of determining the weights of each criterion represented by a pie chart (see
Figure 1).
Through the Consistency Ratio (CR), it is possible to verify that all the stakeholders respect the property of transitivity in the pairwise comparisons, i.e., in all the cases there is a CR ≤ 10%; this check ensures the reliability of the internal consistency of the responses, and thus the actual representativeness of the weight of each criterion with respect to the preferences expressed by the experts. From the examination of the last row of the
Table 4, it can be observed that the CR associated to each answer given by the stakeholders interviewed is similar, especially in the cases of the ABI and the SGR. At the end of this phase, based on the pairwise comparisons made by each stakeholder, the final weight that is associated to each criterion is determined by calculating the average of the weights assigned to them by each member of the group of expert (see last column of
Table 4) following the approach also used in the ARCAS technique (
Stanujkic et al. 2017).
The different weight that corresponds to each criterion reflects the point of view of the subjects involved: the NPLs and the SGR consider that it is important to contain the debt relief (), whereas unexpectedly this criterion is not among the most significant for the ABI, who prefers to avoid cash strains, and therefore to contain the , which is also a relevant criterion for the SGR; for the NPLs, unlike other experts, among the important criteria there is also the containment of the loan to value. Contrary to what was initially assumed by the analyst team, the variation of debt repayment period () is a minor criterion for all the stakeholders interviewed; similarly, the also appears to be an irrelevant criterion for all the respondents, probably because the relationship between the and the financing is detected more effectively by the .
Ultimately, the stakeholders that represent the banking sector (ABI) and the investment management companies (SGR) have a long-term vision and are more interested in the stability of the cash flows in support of the debt; on the other hand, the stakeholders that manage the NPLs with underlying property assets aim at containing the leverage, probably to prevent the default debt. In order to check the reliability of the questions set, at this point it was asked if each of the criteria that have been identified effectively describes the goal, or if it is necessary to change/add other ones; all the respondents replied that the chosen criteria are adequate to describe the issue and that is not necessary to introduce new ones.
6. Normalization and Determination of the Best Alternative
To determine the best alternative solution, the judgements assigned to each alternative in relation to each criterion can be normalized to avoid a condition where higher numeric satisfaction values dominate the smaller ones (
Shih et al. 2007). According to
Vafaei et al. (
2016), the normalization techniques allow the aggregation of criteria for ordering in a suitable way the final results in multi-criteria decision making processes. Several studies on the effects of different normalization techniques on the ranking of alternatives in MCDA problems have shown that certain approaches are more suitable for specific problems than others (
Chakraborty and Yeh 2009).
For each criterion, the analyst team firstly defines the goal of the DM, summarized by the operator of column 4 of the
Table 5. Subsequently, the analyst team performs the reconstruction of the mathematical model on the basis of the logic of the preferences, with the likely presence of a range of values that can assume the criteria and of the thresholds of absolute preference/indifference or unacceptability. The absolute preference—or respectively indifference—threshold represents a constraint to each criterion, beyond which the preference is highest (or respectively lowest); the unacceptability threshold represents a constraint value beyond which the alternative is automatically excluded from the comparison. In this way, the principle of non-comparability is imposed, and thus, in the presence of certain conditions, the compensatory effect among the criteria ceases. In
Table 5, there are the range and limits of the criteria which allow to reconstruct the system of the decision-making approach carried out by the DM: in the “operator” column there is “MAX”—or respectively “MIN”—if the optimization consists in maximizing—or respectively minimizing—the value that is associated to the criterion; in the “range” column the reference intervals for each criterion or the acronym NA are reported, which stands for not available, if it is impossible to define an interval; and similarly, in the last two columns the preference and the veto thresholds are listed.
The threshold values of criteria 4 and 5—
e
—are set according to the ones generally practiced in similar transactions by the stakeholders, whereas the veto thresholds of criteria 2 and 3—
e
—comply with the provisions on the subject drawn up by the
Bank of Italy (
2006). As for the
—criterion 1—must be higher than 100% to ensure firms’ capacity to pay cost of debt (
Bonazzi and Iotti 2014); therefore, in the present work, it is higher than 170% as recommended on real estate financing transactions (
Morri and Mazza 2014).
The standard limits that are specified for the and the represent the veto thresholds of these indicators, below which the credit institutes actuate the safeguard measures; alongside these, the stakeholders, based on specific experiences, identify a maximum debt relief equal to 40%. In this case, if the veto thresholds are exceeded, the default of the debt is decreed; therefore, the relative alternative is considered unacceptable. The best practice requires that the and the must be assessed year by year during the entire duration of the repayment plan; however, a simplification has been assumed, so the two criteria have been considered by adding the amounts that occur during the overall duration of the repayment plan.
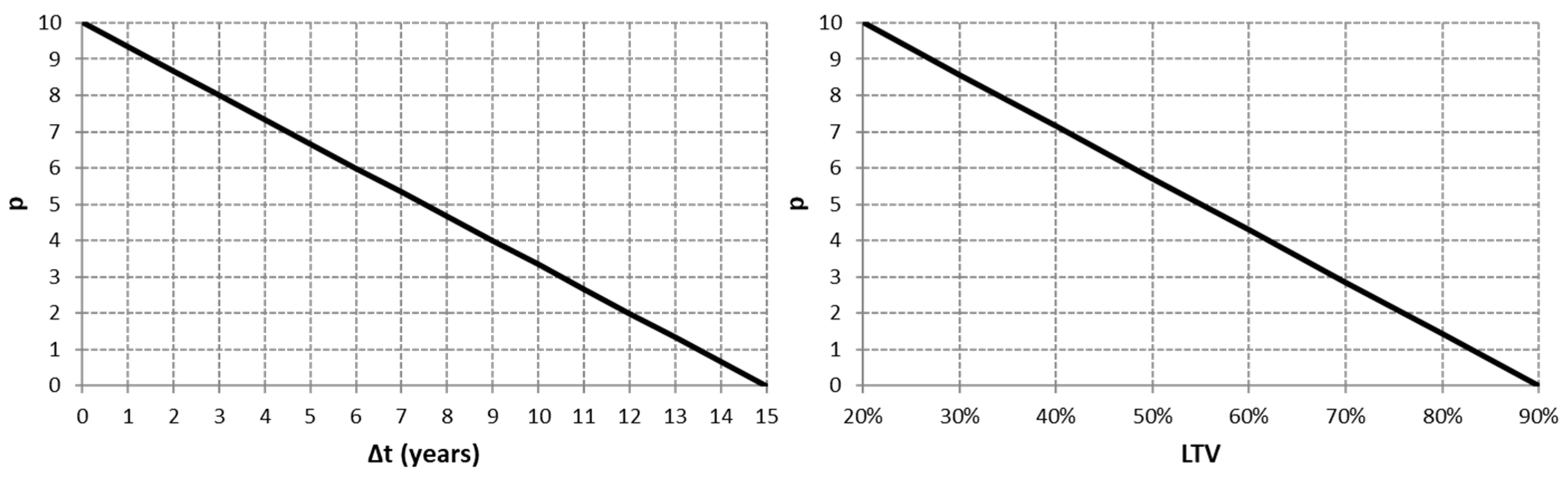
For the
and
criteria, the stakeholders identify a specific range within which a linear preference function is well-defined (see
Figure 2), with the application of the multi-criteria technique PROMETHEE; in this way, it is possible to assign a preference degree (
) on the basis of the analysis of the DM.
The two preference functions are the follow ones, respectively:
Taking into account the described assumptions for the preference and the veto limit, it should be noted that if or , the alternative will be automatically rejected, whereas if therefore .
Therefore, in order to make the final result independent by the normalization and the worst and the best comparison alternatives, the TOPSIS technique is used. The fundamental idea of the TOPSIS is that the best solution is characterized by the minimum distance to the ideal solution and the furthest distance from the anti-ideal solution. The values associated to each alternative are normalized according to two approaches:
- -
distributive normalization
- -
ideal normalization
where the denominator in the ratio corresponds to the mathematical operator present in the column 4 of the
Table 5. The values of the
related to the
,
and s criteria are directly calculated from the specific characteristics of the alternative under assessment; for the
and
criteria it is necessary to translate the input values into preferences by using the previously described formulas.
Successively, the weighted normalized decision matrix is calculated:
Later the positive ideal solution (
A+) and the negative ideal solution (
A−) are determined, by collecting the best and the worst performances on each criterion and by assuming an absolute ideal and anti-ideal point. The identification of the positive ideal solution (
A+) and the negative ideal solution (
A−) collecting the best and the worst performances on each criterion leads to get:
where
, therefore,
,
and the term operator recalls the respective different typologies reported in the column 4 of the
Table 5.
In the case of determining the positive ideal solution (
) and the negative ideal solution (
) assuming an absolute ideal and anti-ideal point, the following results are obtained:
where
with
is the weight of each criterion.
Afterwards, the Euclidean distances from the positive (
) and the negative (
) ideal solution (
Krohling and Pacheco 2015) are calculated:
Lastly, the relative closeness
for each alternative related to the positive ideal solution is determined, as given by the following formula:
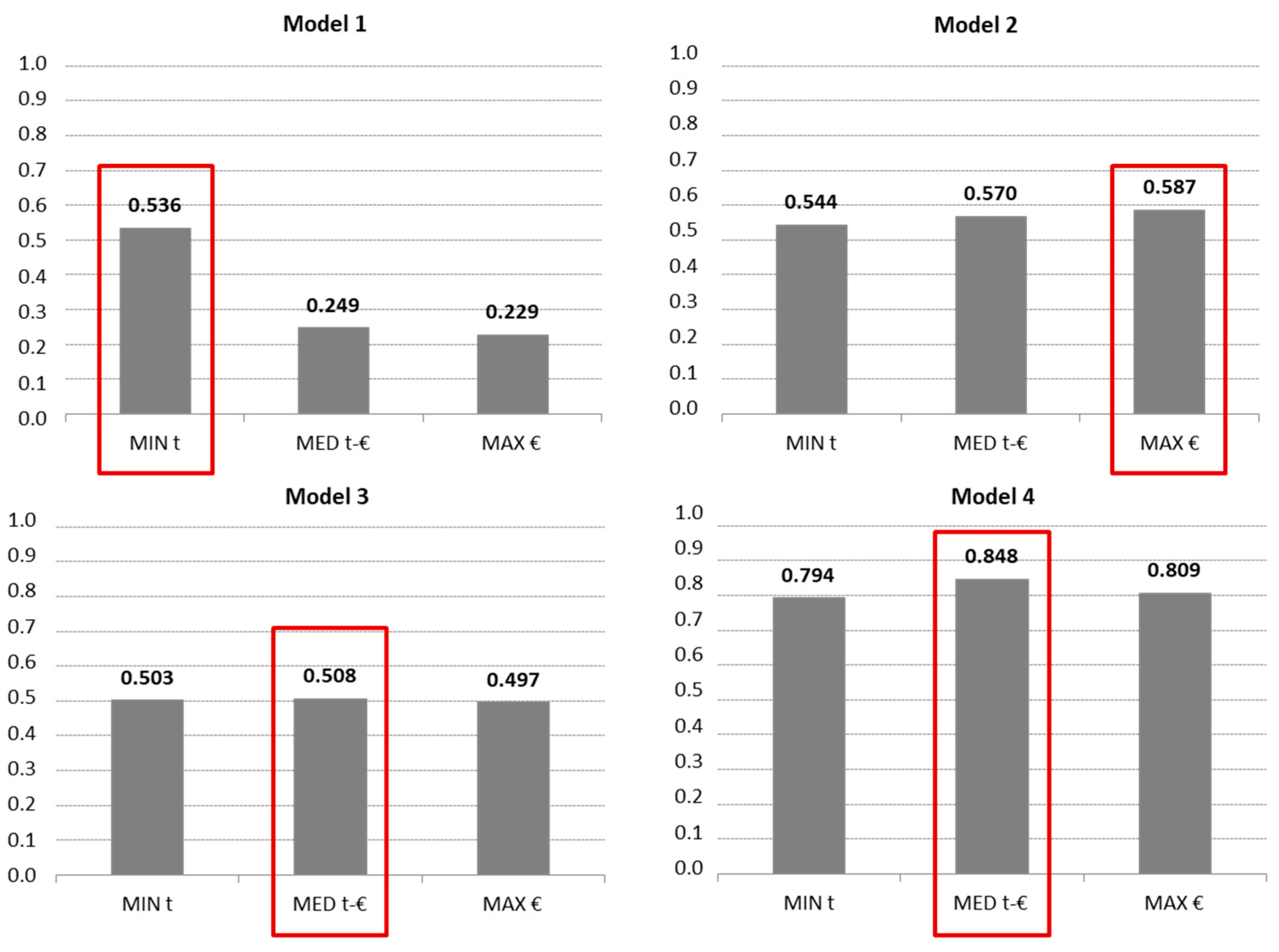
Finally, for each alternative, there are four possible
associated to four models with features that depend by the chosen standardization and the approach used to identify the positive (
) and the negative (
) ideal solution in order to make the comparison (
Table 6).
The TOPSIS application allows to obtain 4 possible arrangements of the alternatives (models 1, 2, 3, and 4), that are differentiated according to the specific normalization used (distributive or ideal) and the type of ideal solutions chosen (see
Table 6).
In order to verify the robustness of the index all the four possible arrangements of the alternatives have been compared in the present work: the more the models will agree in the identification of the optimal solution, the more the output will be correct and vice versa.
7. Case Study
The IPRE Index (
) has been applied to a real case. This involves a minor credit institution and the respective credit manager, who is entrusted with the task of renegotiating the debt position of a customer—a medium entrepreneur operating in the construction and hospitality sector—with a debt of approximately EUR 8.5 million (initial debt). This debt is guaranteed by two properties: a hotel with the restaurant activity and a commercial-office building both located in the city of Rome (Italy). The properties as guarantees of the credit exposure generate a total gross rent of approximately EUR 1.0 million per year: this amount, net of the management costs, is not sufficient to cover the debt according to the initial modalities agreed (
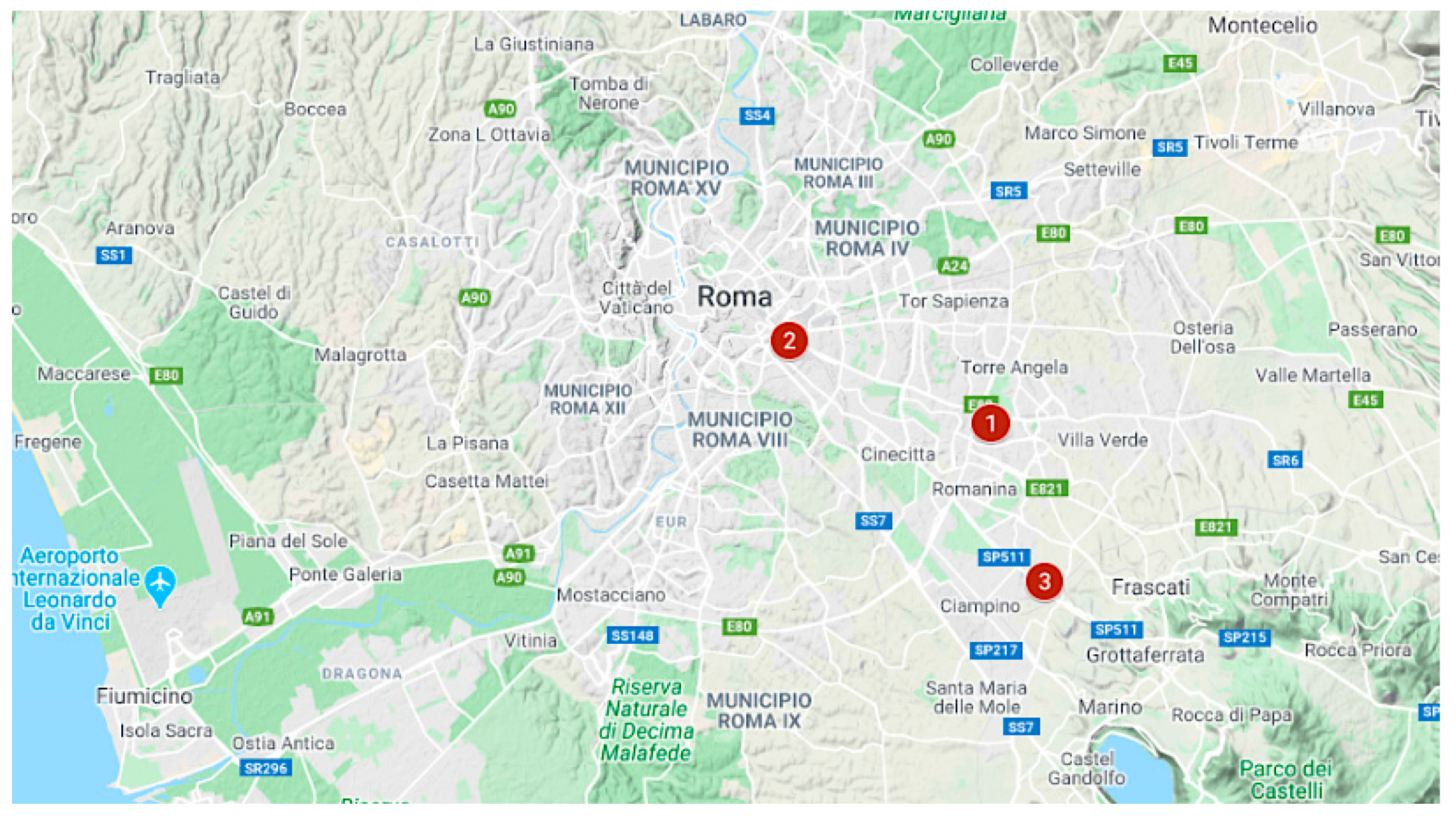
). In order to heal his debt position, the entrepreneur has requested a new credit line, for an amount of about EUR 3.5 million, aimed at the construction of a residential building. In this way, the entrepreneur sets the objective of repaying both the debt that has accumulated over the years and the new one, through the rents and the sale of the dwellings built. The repayment and the recovery forecasts are affected by the financial flows connected with the lease and by the cash flows that are generated by the real estate development operation. Since the amount of debt examined is below the threshold of EUR 20 million, which is typical of small entrepreneur with a limited number of properties—three in this case—the proposed methodology well fits with the specific goal. Otherwise, if the debt had been higher than EUR 20 million and the property portfolio properties had been larger, the adoption of the methodologies provided by the Basel accords would have been inevitable. In
Figure 3 the position of the three properties is illustrated, the data of which are summarized in the
Table 7.
The property n.1 is a hotel of six floors, located in a semi-peripheral area of the city of Rome, characterized by a restaurant on the ground floor. Built in the 1980s, the structure consists of several reinforced concrete volumes; it has a marble base and it is in a good state of maintenance; inside the finishes of the rooms are made of stoneware, parquet, or marble flooring and the walls are plastered.
The property n.2 is situated in a semi-central area of the city of Rome and has several commercial activities on the ground floor (11 total windows), and there are offices on the first floor. The construction dates back to the 1960s and includes a single reinforced concrete volume; the finishes are of medium quality level because the floors are in stoneware and parquet; the fixtures are in wood with double-glazing and the exterior is made up of exposed brickwork alternating with plastered portions. The overall state of maintenance is good, both from a construction and plant engineering point of view, also thanks to the recent refurbishment works.
The property n. 3 is located in the south-east suburbs of the center and it is a buildable area. The low coverage ratio, the positioning on a slight hill and the construction of the apartments with an energy class A, guarantee a good overall level of housing quality for the future occupiers. The building will develop on four levels, one of which is a basement that is used as a garage and the remaining three above-ground; there are 36 total apartments of different sizes (two-room and three-room apartments) divided into four staircases.
The entrepreneur involved in the debt renegotiation operation proposes different scenario alternatives, each of them characterized as follows:
First Scenario (Scenario n.1 of
Table 8): is summarized by the wording “MIN t”—which stands for
MINimization of
Time—and consists in the most practicable reduction Variation of Debt Repayment Period.
Second Scenario (Scenario n.2 of
Table 8): is summarized by the wording “MED t-€”—which stands for
MEDium
Time and further debt in euros (EUR)—and is a compromise scenario between the one that is aimed at the minimization of Variation of Debt Repayment Period and the one that is aimed at the maximization of the Further Debt.
Third Scenario (Scenario n.3 of
Table 8): is summarized by the wording “MAX €”—which stands for
MAXimization of the further debt in euros (EUR)—and represents the maximum possible Further Debt.
The credit manager, on the basis of the cash flows serving the debt, modulates the loan assuming two lines of credit: the first one with a constant payment—so-called “French”—related to the further debt that has to be restructured; the second one, needed to allow the development of the buildable area, carried out according to the mechanism called the “Allocated Loan Amount”, with a release price equal to 120%. After carrying out the appropriate analyzes, the credit manager determines, for each scenario, the financial covenants previously mentioned and described, i.e., the DSCR, the ICR, and the LTV (
Table 8).
On the basis of the input data indicated in the
Table 8 it is possible to set out the three scenarios (
Figure 4) and to rank the alternatives, according to the relative closeness coefficients that are obtained for the four different models, summarized in
Table 6.
In the following flowchart (
Figure 5) is represented the credit risk mitigation process applied to the present case study.
By examining the outputs for each of the four models (
Figure 6), it is interesting to note that the values of the
IIPRE,risk index obtained are: in the “MED t-€” scenario the highest for two models out of four (see models 3 and 4), for the remaining perform better respectively the “MIN-t” scenario (Model 1) and the “MAX-€” (Model 2). For these reasons appears preferable the “MED t-€” scenario which is recommended by the DM as the best compromise solution. Therefore the “MED t-€” alternative represents a compromise solution between the “MAX €” scenario, which is characterized by the containment of the debt relief at the expense of the variation of the debt repayment and the financial covenants, and the “MIN t” one, which is characterized by the reduction of the variation of the debt repayment, but by a high debt relief with the improvements in the financial covenants compared to the other scenarios. The result obtained does not depend on the positive and the negative ideal solution that is used for the comparison with the alternatives; therefore, this guarantees the reliability of the
proposed.
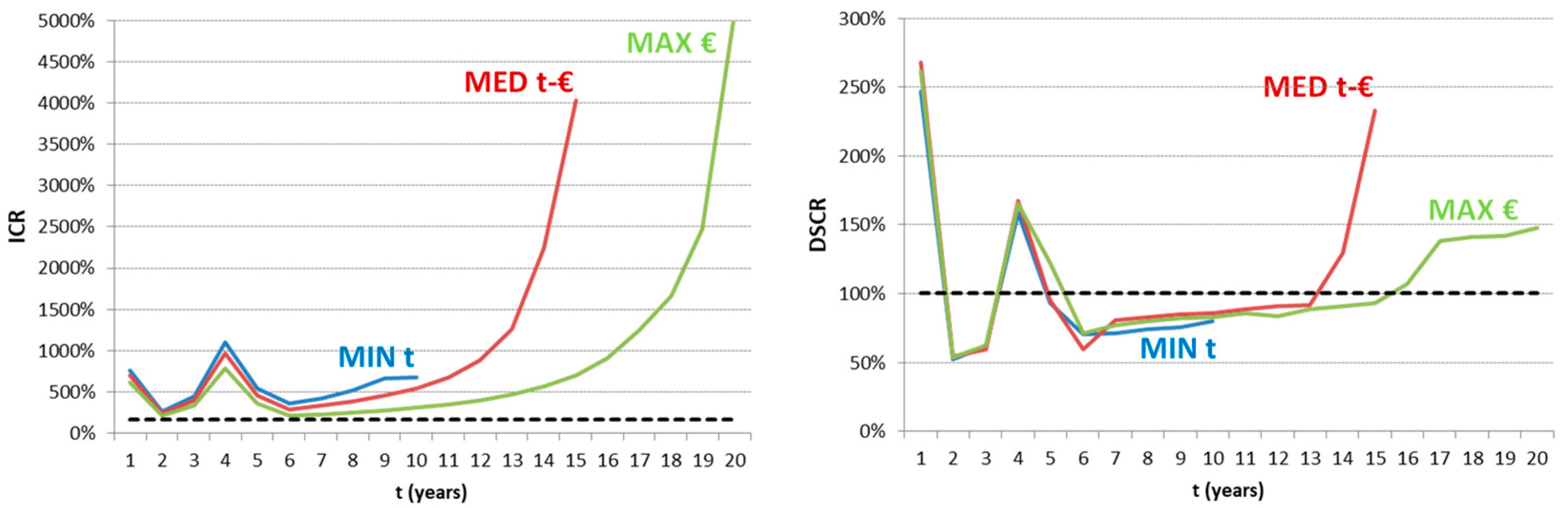
It should be highlighted that the proposed methodology does not consider the temporal evolution of the considered criteria. In fact, if the trend of the
and the
is observed, considering only the net cash flows and not the accumulated one (
Figure 7), it is evident that, while for the criterion
all the scenarios respect the limit indicated in
Table 5, for the
criterion, there are several periods below the threshold, especially for the “MIN-t” scenario for which, even in the last year, the imposed limit is not respected.
However, this limit represents an acceptable approximation given the need for simplification of the analyzed problem and immediate application of the index.
8. Conclusions
The financial crisis of 2008 has highlighted the need to define a high level of quality of credit institutions’ assets in order to reduce the opacity of the banking assets (
Guarini et al. 2017;
Morano et al. 2019). With the Basel agreements introduction, the need to strengthen the solidity of the international banking organization has been translated into rigid weighting coefficients structures that, especially for the smaller credit institutions, are complex to apply (
Birindelli and Intonti 2018). Italian credit institutions have implemented numerous strategies aimed at improving the quality of credit in the portfolio, obtaining a 60% reduction in NPLs in the period 2015–2019, even if the smaller credit institutions performed worse than the bigger one (
KPMG 2020).
Starting from these premises, in this paper, a credit real estate risk indicator was developed. The aim was to provide for a support of the minor credit institutions in defining a first indication of the reliability of the financial plan that is proposed for the restructuring and debt reduction processes of the IPRE. The was developed by the analyst team starting from the reasoning of the DM and identifying, for each phase of the decision-making processes, the type of MCDA that best fits the needs outlined. The involvement of a qualified panel of experts—characterized by the same goal but by complementary and specific skills for the operations to be examined—has helped to create a shared platform that has permitted to support the process of legitimizing the final decision represented by the best compromise alternative among those considered.
The innovative contributions of the work are: (i) the enhancement of the several and significative skills operating the real estate finance sector through the application of interviews; (ii) the management of credit risk, which is performed through a tool of simple implementation and shared by the different subjects involved in the decision making process; (iii) the reduction of the complexity of structuring the operations of the credit manager for minor credit institutions—which often do not have the appropriate skills for applying the methodologies set out in Basel III accords—and small and medium-sized enterprises (SME), which are interested into simple and easily applicable procedures; and (iv) obtaining a synthetic risk index capable of summarizing in a single numerical value the contribution that of the financial variables that affect the debt restructuring steps. The adoption of a methodology specifically created to fit the needs of DM of minor credit institutions through the hybridization of different MCDA techniques (AHP, PROMETHEE, and TOPSIS) allows the reduction of the weaknesses in each phase of debt restructuring process, from the identification of the initial goal to the determination of the best scenario. This is a significant contribution to the research, taking into account that several studies in the reference literature related to credit risk operations apply multi-criteria methodologies that are not immediately replicable by final users. The results obtained from the application to a real case study have demonstrated the effectiveness of the proposed methodology, highlighting that the absence of an appropriate risk indicator could lead the DM to choose a financially profitable but potentially unfeasible alternative (“MAX €” scenario) or a not so financially advantageous but more stable one (“MIN t” scenario). The usefulness lies in simultaneously considering several factors that intervene in the debt restructuring process, and objectifying the choices made by the credit manager; this approach has the goal of proposing a corporate policy within the banks, which is able to implement the principles set out in Basel agreements.
Future insights of this approach could be (
i) large-scale experimentation, in order to grasp some aspects not adequately integrated in the model, such as the creditworthiness and the analysis of the trend over the years of the debt covenants; (
ii) verification of the robustness of the index by introducing further check-parameters such as the Criteria Importance Through Intercriteria Correlation (CRITIC) method for determining the objective weights of criteria, and (
iii) integration of the index into a Geographic Information System (GIS) to map the geographical concentration of risk through appropriate spatial analysis methods (
Balena et al. 2013) and identify intra-sectoral interdependencies among real estate market participants (
Foglia and Angelini 2020).