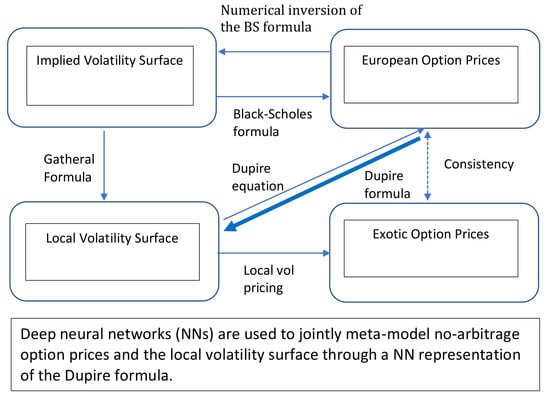
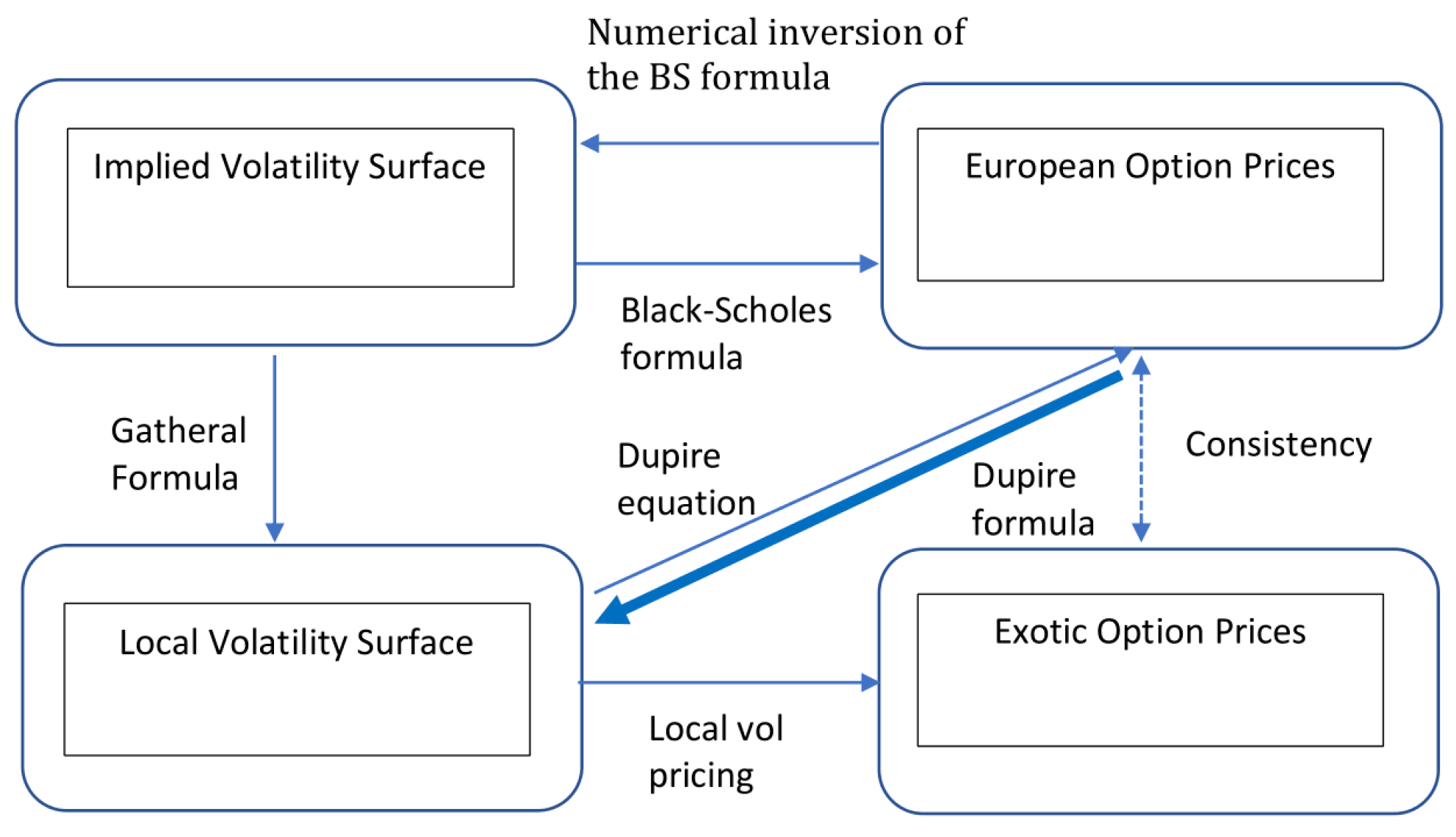
Deep Local Volatility †
Abstract
1. Introduction
2. Problem Statement
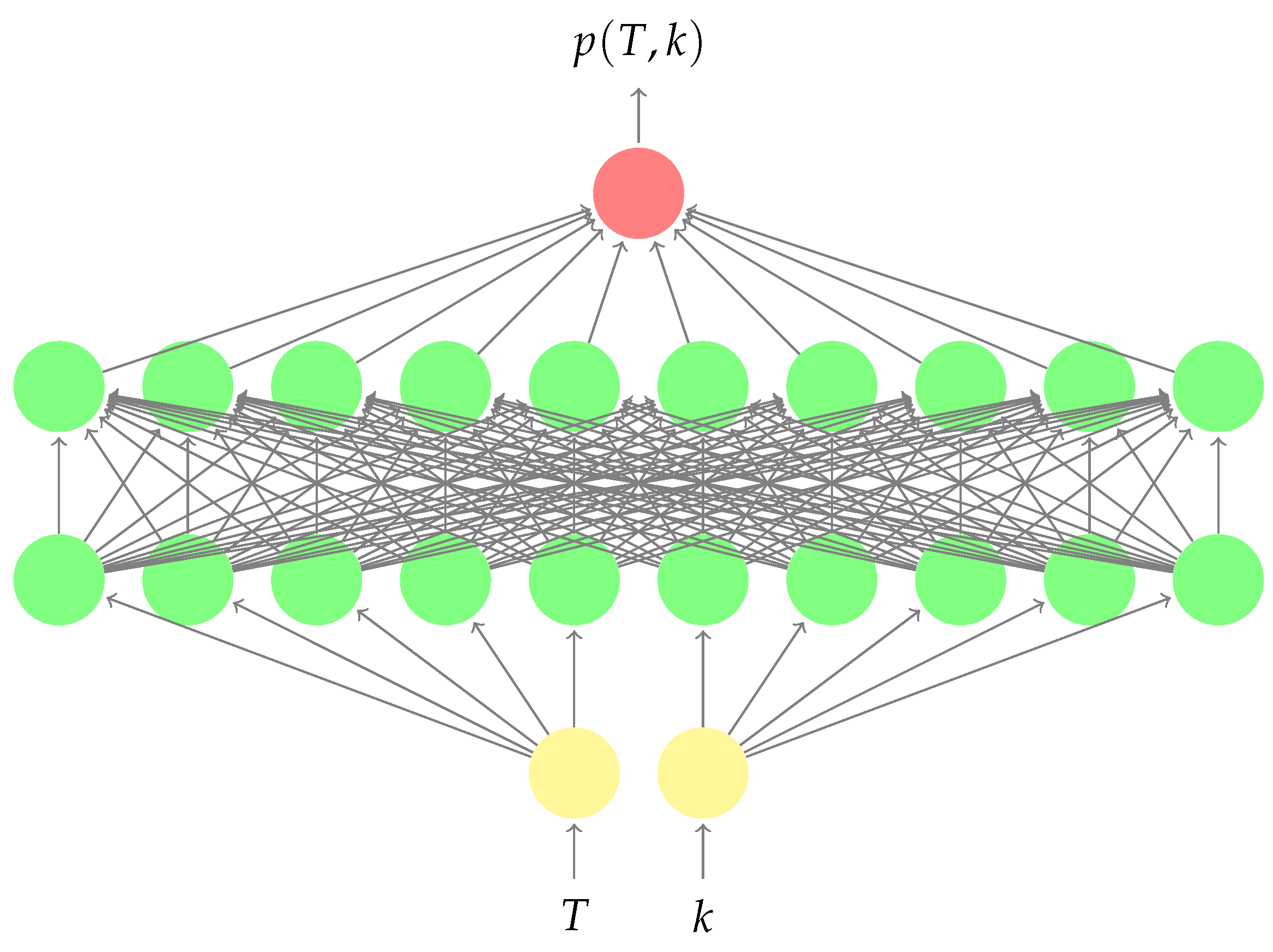
3. Shape Preserving Neural Networks
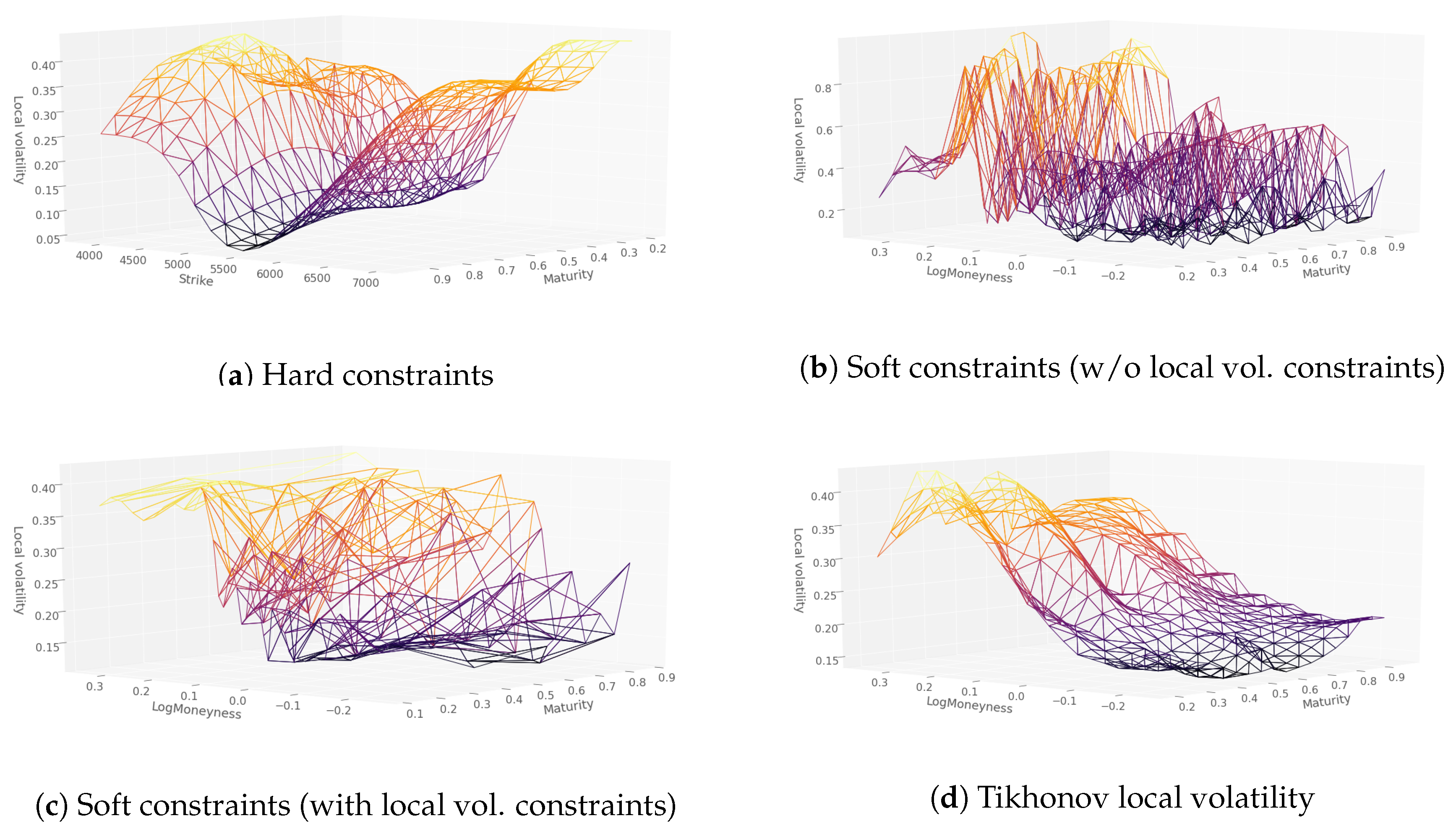
3.1. Hard Constraints Approach
3.2. Soft Constraints Approach
4. Numerical Methodology
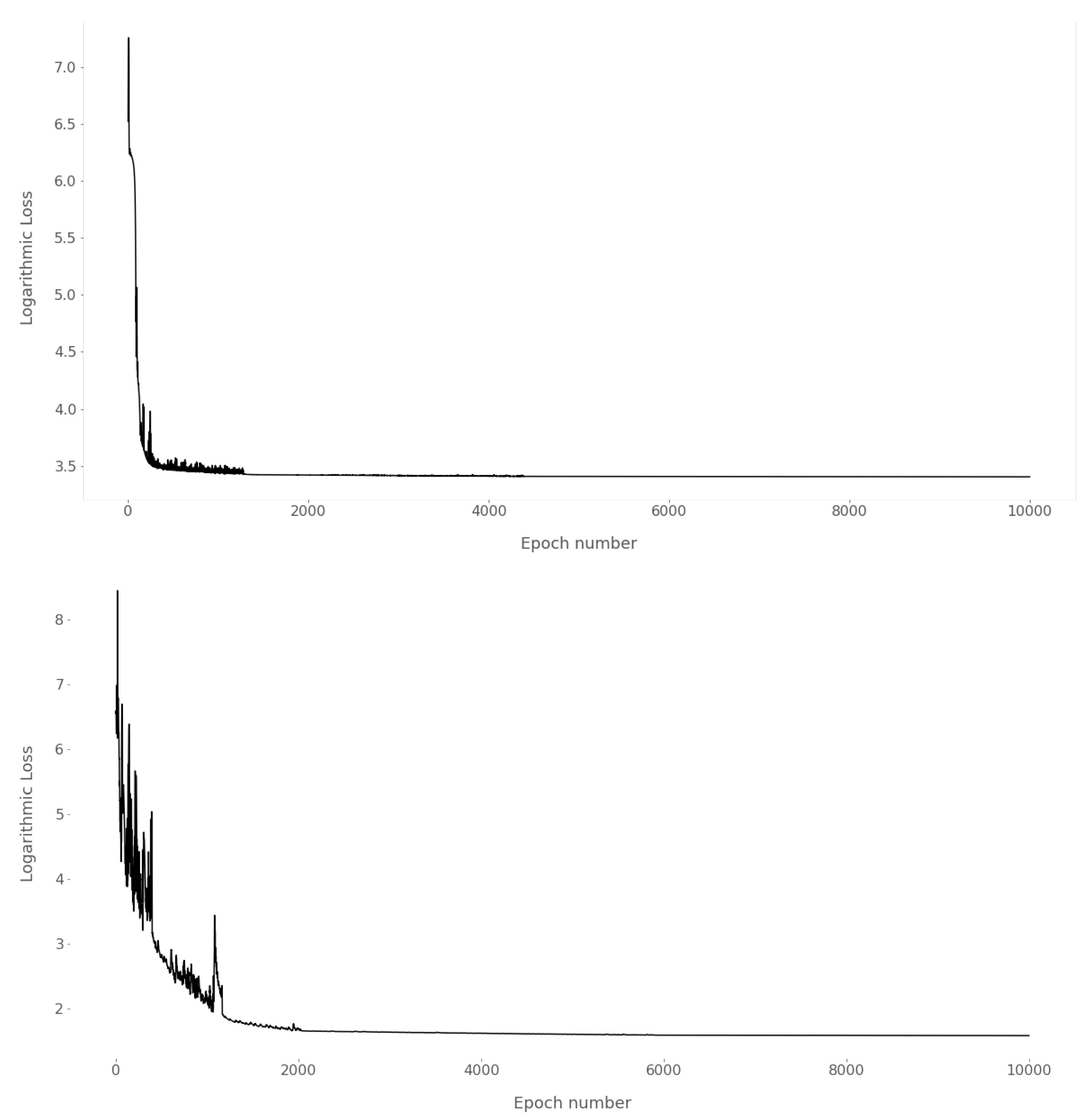
4.1. Training
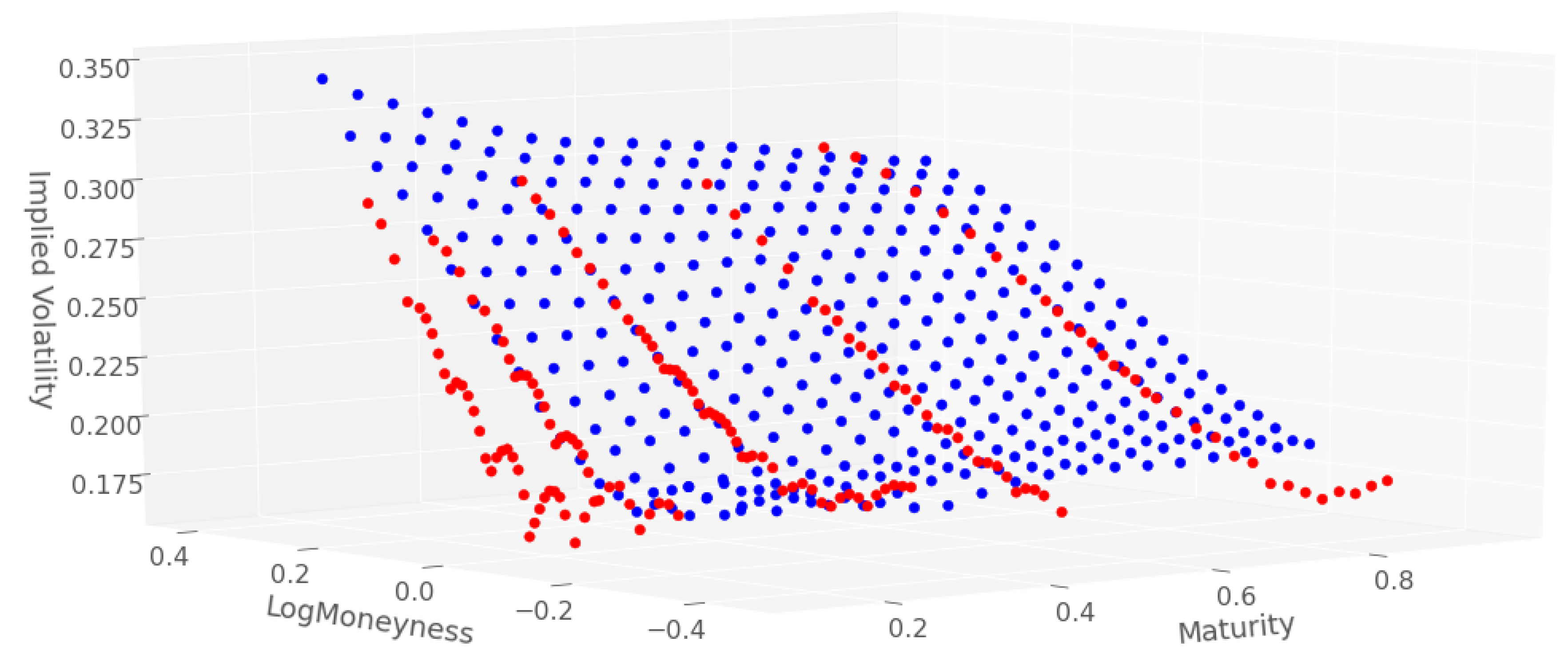
4.2. Experimental Design
- sparse network but soft constraints, i.e., ignoring the non-negative weight restriction in Section 3.1, but using in (3) and (4),
5. Numerical Results without Dupire Penalization
6. Numerical Results with Dupire Penalization
7. Robustness
7.1. Numerical Stability through Recalibration
7.2. Monte Carlo Backtesting Repricing Error
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Change of Variables in the Dupire Equation
Appendix B. Network Sparsity and Approximation Error Bound

References
- Ackerer, Damien, Natasa Tagasovska, and Thibault Vatter. 2019. Deep Smoothing of the Implied Volatility Surface. Available online: https://ssrn.com/abstract=3402942 (accessed on 29 July 2020).
- Aubin-Frankowski, Pierre-Cyril, and Zoltan Szabo. 2020. Hard shape-constrained kernel machines. arXiv arXiv:2005.12636. [Google Scholar]
- Crépey, Stéphane. 2002. Calibration of the local volatility in a trinomial tree using Tikhonov regularization. Inverse Problems 19: 91. [Google Scholar] [CrossRef][Green Version]
- Crépey, Stéphane. 2003. Calibration of the local volatility in a generalized Black–Scholes model using Tikhonov regularization. SIAM Journal on Mathematical Analysis 34: 1183–206. [Google Scholar] [CrossRef]
- Crépey, Stéphane. 2004. Delta-hedging vega risk? Quantitative Finance 4: 559–79. [Google Scholar] [CrossRef]
- Crépey, Stéphane. 2013. Financial Modeling: A Backward Stochastic Differential Equations Perspective. Springer Finance Textbooks. Berlin: Springer. [Google Scholar]
- Dugas, Charles, Yoshua Bengio, François Bélisle, Claude Nadeau, and René Garcia. 2009. Incorporating functional knowledge in neural networks. Journal of Machine Learning Research 10: 1239–62. [Google Scholar]
- Dupire, Bruno. 1994. Pricing with a smile. Risk 7: 18–20. [Google Scholar]
- Garcia, René, and Ramazan Gençay. 2000. Pricing and hedging derivative securities with neural networks and a homogeneity hint. Journal of Econometrics 94: 93–115. [Google Scholar] [CrossRef]
- Gatheral, Jim. 2011. The Volatility Surface: A Practitioner’s Guide. Hoboken: Wiley. [Google Scholar]
- Gençay, Ramazan, and Min Qi. 2001. Pricing and hedging derivative securities with neural networks: Bayesian regularization, early stopping, and bagging. IEEE Transactions on Neural Networks 12: 726–34. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. 2016. Deep Learning. Cambridge: MIT Press. [Google Scholar]
- Hutchinson, James M., Andrew W. Lo, and Tomaso Poggio. 1994. A nonparametric approach to pricing and hedging derivative securities via learning networks. The Journal of Finance 49: 851–89. [Google Scholar] [CrossRef]
- Itkin, A. 2019. Deep learning calibration of option pricing models: Some pitfalls and solutions. arXiv arXiv:1906.03507. [Google Scholar]
- Márquez-Neila, Pablo, Mathieu Salzmann, and Pascal Fua. 2017. Imposing hard constraints on deep networks: Promises and limitations. arXiv arXiv:1706.02025. [Google Scholar]
- Ohn, Ilsang, and Yongdai Kim. 2019. Smooth Function Approximation by Deep Neural Networks with General Activation Functions. Entropy 21: 627. [Google Scholar] [CrossRef]
- Roper, Michael. 2010. Arbitrage Free Implied Volatility Surfaces. Available online: https://talus.maths.usyd.edu.au/u/pubs/publist/preprints/2010/roper-9.pdf (accessed on 29 July 2020).
| 1 | The call and put prices must also be decreasing and increasing by strike respectively. |
| 2 | A function is locally quadratic if ∃ an open interval over which is three times continuously differentiable with bounded derivatives and s.t. and . |
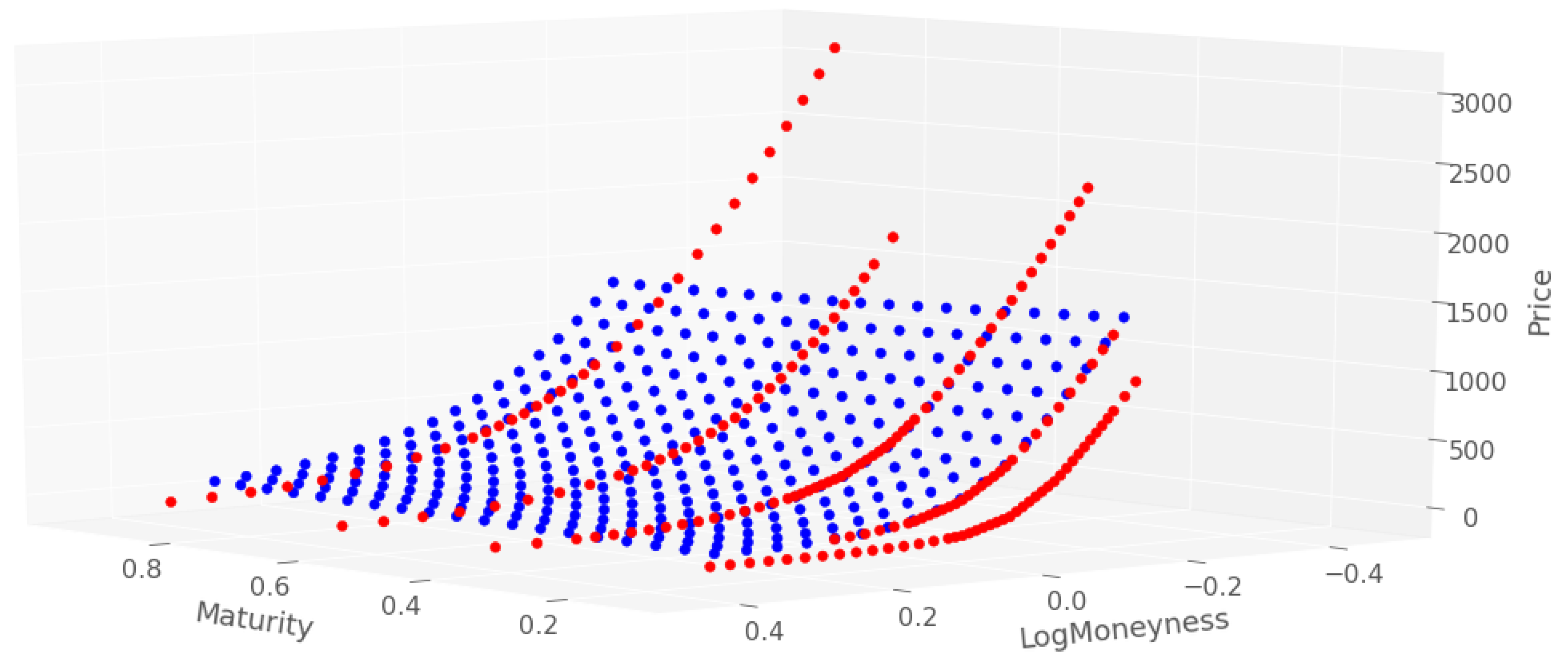
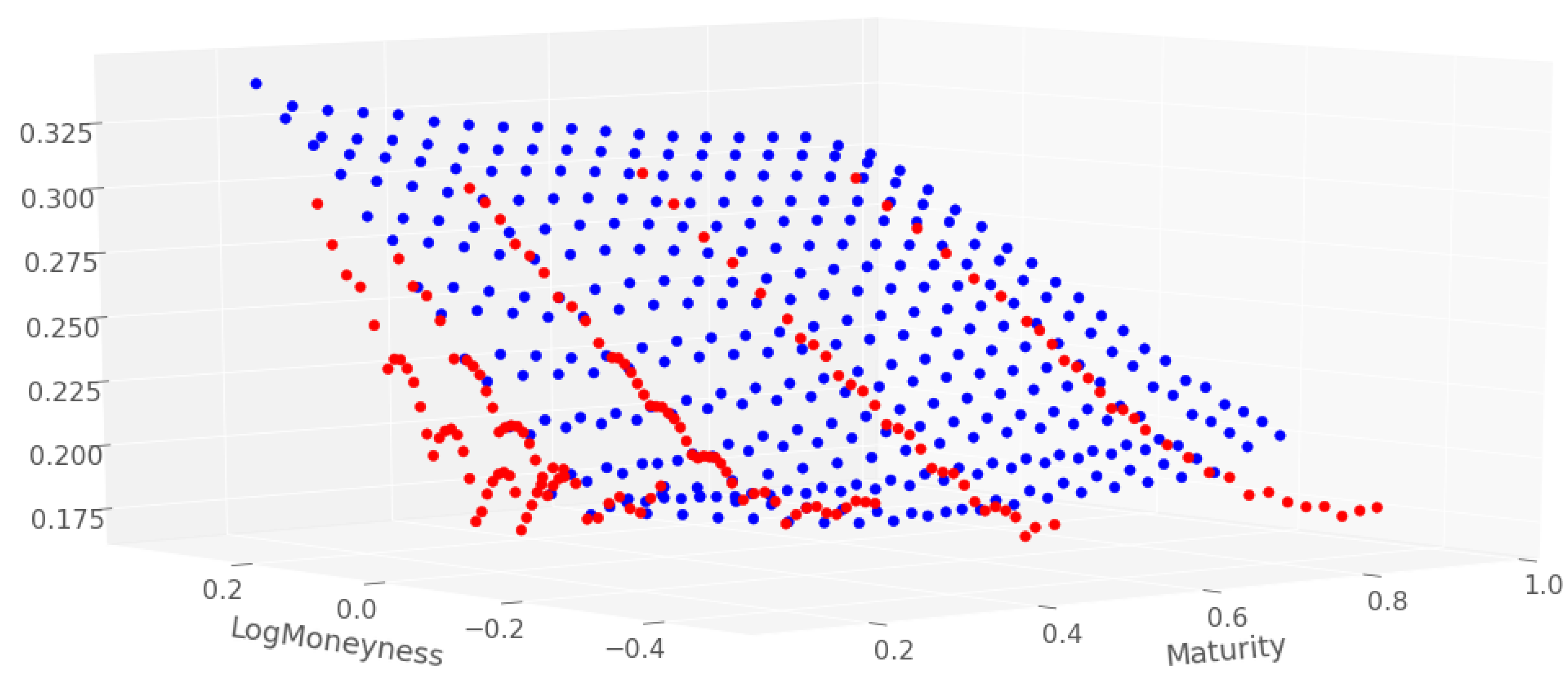
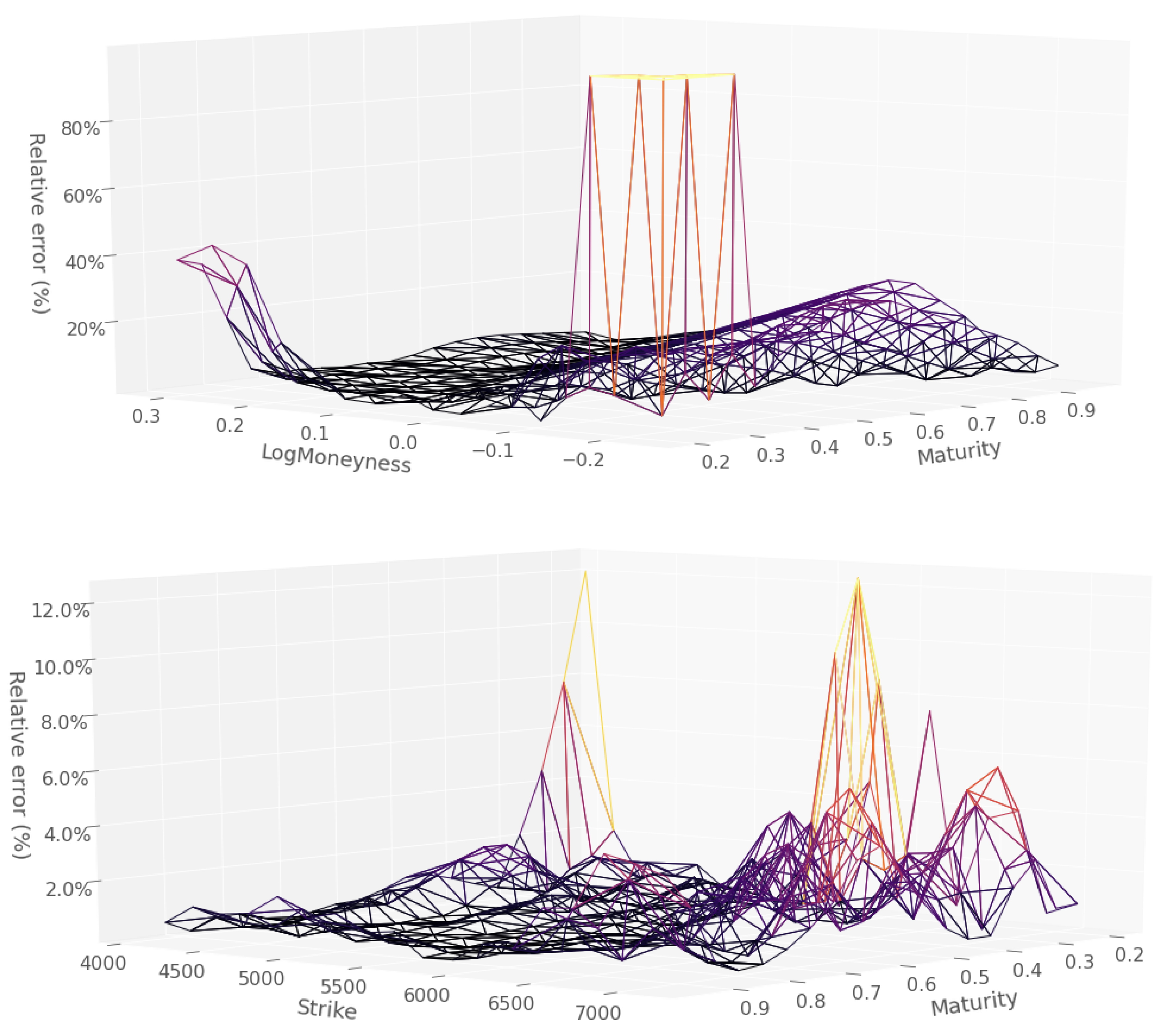

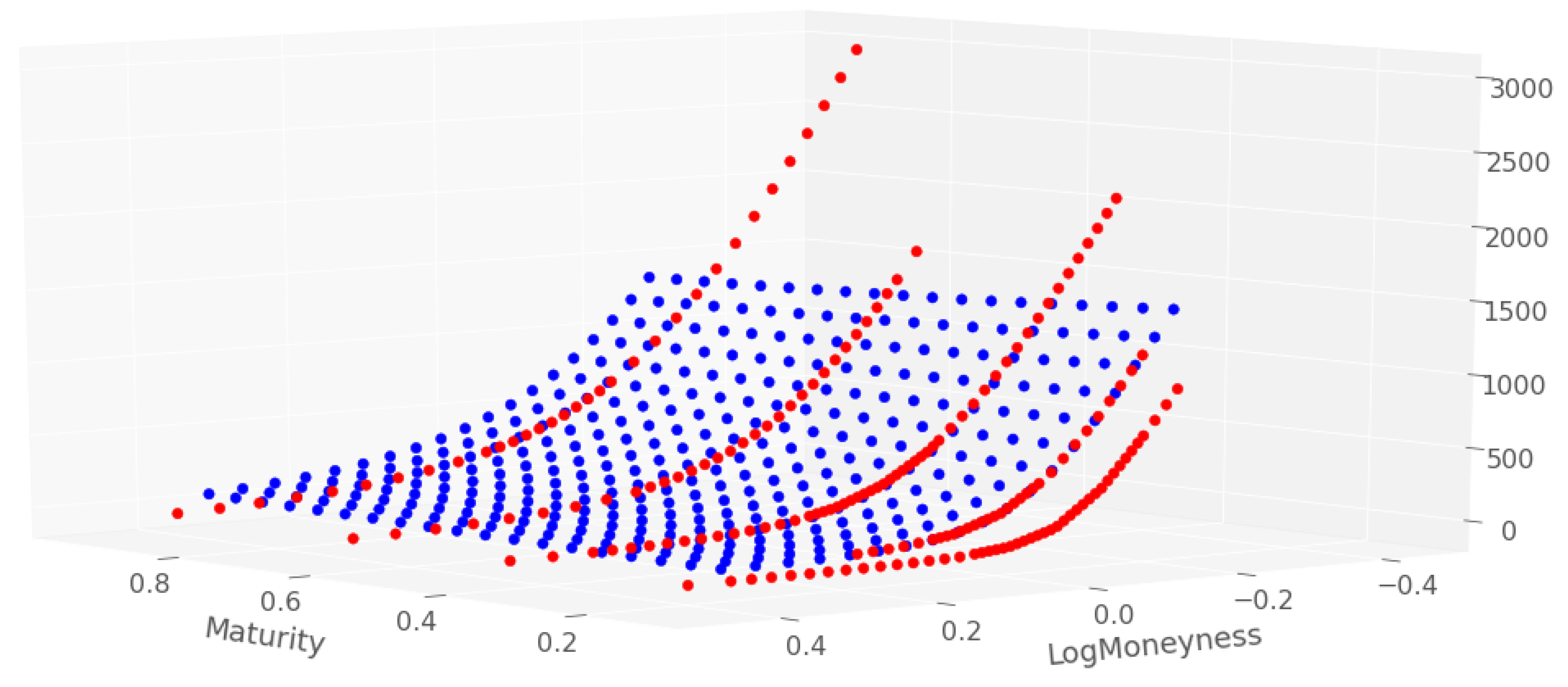


| Sparse Network | Dense Network | |||
|---|---|---|---|---|
| Hard Constraints | Soft Constraints | Soft Constraints | No Constraints | |
| Training dataset | 28.13 | 6.87 | 2.28 | 2.56 |
| Testing dataset | 28.91 | 4.09 | 3.53 | 3.77 |
| Indicative training times | 200 s | 400 s | 200 s | 120 s |
| Sparse Network | Dense Network | |||
|---|---|---|---|---|
| Hard Constraints | Soft Constraints | Soft Constraints | No Constraints | |
| Training dataset | 0 | 1/254 | 0 | 63/254 |
| Testing dataset | 0 | 2/360 | 0 | 44/360 |
| Sparse Network | Dense Network | |||
|---|---|---|---|---|
| Hard Constraints | Soft Constraints | Soft Constraints | No Constraints | |
| Training dataset | 28.04 | 3.44 | 2.48 | 3.48 |
| Testing dataset | 27.07 | 3.33 | 3.36 | 4.31 |
| Indicative training times | 400 s | 600 s | 300 s | 250 s |
| Sparse Network | Dense Network | |||
|---|---|---|---|---|
| Hard Constraints | Soft Constraints | Soft Constraints | No Constraints | |
| Training dataset | 0 | 0 | 0 | 30/254 |
| Testing dataset | 0 | 2/360 | 0 | 5/360 |
| # Hidden Units | Surface | RMSE | |
|---|---|---|---|
| Training | Testing | ||
| 50 | Price | 3.01 | 3.60 |
| Impl. Vol. | 0.0173 | 0.0046 | |
| 100 | Price | 3.14 | 3.66 |
| Impl. Vol. | 0.0304 | 0.0049 | |
| 200 | Price | 2.73 | 3.55 |
| Impl. Vol. | 0.0181 | 0.0036 | |
| 300 | Price | 2.84 | 3.88 |
| Impl. Vol. | 0.0180 | 0.0050 | |
| 400 | Price | 2.88 | 3.56 |
| Impl. Vol. | 0.0660 | 0.0798 | |
| Train RMSE | Test RMSE | |
|---|---|---|
| ADAM | 2.48 | 3.36 |
| Nesterov accelerated gradient | 5.67 | 6.92 |
| RMSProp | 2.76 | 3.66 |
| Tikhonov Monte Carlo | Dense Network with Soft Constraints and Dup. penal. | Dense Network with Soft Constraints | Hard Constraint with Dup. Penal. | Hard Constraint w/o Dup. Pen. | |
|---|---|---|---|---|---|
| 7 August 2001 | 5.42 | 10.18 | 68.48 | 48.57 | 50.44 |
| 8 August 2001 | 5.55 | 7.44 | 50.82 | 56.63 | 56.98 |
| 9 August 2001 | 4.60 | 8.18 | 59.39 | 66.23 | 65.50 |
| Tikhonov Trin. Tree | NN Pred. (Dense Network with Soft Constraints and Dup. Penal). | |
|---|---|---|
| 7 August 2001 | 2.42 | 2.66 |
| 8 August 2001 | 2.67 | 2.48 |
| 9 August 2001 | 2.45 | 2.34 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chataigner, M.; Crépey, S.; Dixon, M. Deep Local Volatility. Risks 2020, 8, 82. https://doi.org/10.3390/risks8030082
Chataigner M, Crépey S, Dixon M. Deep Local Volatility. Risks. 2020; 8(3):82. https://doi.org/10.3390/risks8030082
Chicago/Turabian StyleChataigner, Marc, Stéphane Crépey, and Matthew Dixon. 2020. "Deep Local Volatility" Risks 8, no. 3: 82. https://doi.org/10.3390/risks8030082
APA StyleChataigner, M., Crépey, S., & Dixon, M. (2020). Deep Local Volatility. Risks, 8(3), 82. https://doi.org/10.3390/risks8030082