Joshi’s Split Tree for Option Pricing

Abstract

In a thorough study of binomial trees, Joshi introduced the split tree as a two-phase binomial tree designed to minimize oscillations, and demonstrated empirically its outstanding performance when applied to pricing American put options. Here we introduce a “flexible” version of Joshi’s tree, and develop the corresponding convergence theory in the European case: we find a closed form formula for the coefficients of $1/n$ and $1/n^{3/2}$ in the expansion of the error. Then we define several optimized versions of the tree, and find closed form formulae for the parameters of these optimal variants. In a numerical study, we found that in the American case, an optimized variant of the tree significantly improved the performance of Joshi’s original split tree.

1. Motivation and Outline

There is a vast collection of literature describing numerical methods for evaluating options. Among the most popular ones is the binomial tree method which is broadly used because of its simplicity and flexibility. In most binomial models, the price $C^n$ of a call/put option is connected to the price $C^{BS}$ of the same call/put option in the Black–Scholes model via an equation of the form

$$C^n=C^{BS}+\frac{c_n}{n}+O\left(n^{-3/2}\right),$$

(1)

where $c_n$ is bounded but usually not constant, as it depends on n. When $c_n$ is constant, one can use Richardson extrapolation to achieve convergence at a speed of order $n^{-3/2}$. For European options, models have been found Joshi (2009b); Leduc (2016a) for which the error has the form

$$C^n=C^{BS}+O\left(n^{-i_0/2}\right),$$

for an arbitrary value of $i_0$. Obviously, there is a well-known closed form formula for the price of European put/call options in the Black–Scholes model. However, this is not the case for the American put. Yet techniques developed for path-independent European options proved to extend to the study of path-dependent options—for instance, in Bock and Korn (2016); Carbone (2004); Grosse-Erdmann and Heuwelyckx (2016); Heuwelyckx (2014); Leduc and Palmer (2019); Lin and Palmer (2013). Note that the behavior of American options is also connected to the behavior of European options: the American put can be expressed as the sum of a European put and an integral of digital options Carr, Jarrow and Myneni (1992).

Many binomial trees have been suggested in the literature for computing option prices—among others, Chance (2008); Chang and Palmer (2007); Chriss (1996); Cox, Ross and Rubinstein (1979); Diener and Diener (2004); Jarrow and Rudd (1983); Jarrow and Turnbull (2000); Joshi (2009a, 2010); Korn and Müller (2013); Lamberton (1998); Leduc (2016b); Leisen and Reimer (1996); Tian (1993, 1999); Trigeorgis (1991); Van Den Berg and Koudjeti (2000); Walsh (2003); Wilmott (1998). In addition to the intellectual curiosity of understanding how tree models converge to their limits (which is part of the important study of random sums of random variables), the interest in tree methods for pricing security derivatives is motivated by those cases where no simple closed form formula exists. This is the case for American options, for which explicit values for the coefficients $c_i\left(n\right)$ in the expansion of the error

$$C^n=C^{BS}+\frac{c_1\left(n\right)}{n}+\frac{c_2\left(n\right)}{n^{3/2}}+\cdots +O\left(n^{-(i_0+1)/2}\right),$$

(2)

are unknown, and finding them is a challenging and interesting problem. Even the speed of convergence of binomial trees to its Black–Scholes limit remains a long lasting and difficult problem Lamberton (1998, 2002, 2018). Thus far, only convergence has been established Amin and Khanna (1994); Jiang and Dai (2004); Lamberton (1993). However, Joshi (2009b) pointed out that trading houses need to efficiently price thousands of American options, and that understanding which tree is the best at doing so is an important problem. Because of the lack of theoretical results, such questions and a lot of the insight about the behavior of the convergence of tree methods for American put options have been assessed through empirical studies, such as Broadie and Detemple (1996); Chan et al. (2009); Chen and Joshi (2012); Hull and White (1988); Joshi (2009b, 2012); Staunton (2005); Tian (1999). Joshi (2009b) studied a broad collection of trees for pricing American options, and found that the most effective ones are the one from Tian (1993) and the split tree which was specifically designed by Joshi to minimize the oscillations of the error. However, the convergence theory for the split tree has never been done. The goal of this paper is to describe and generalize the split tree, analyze and optimize its convergence in the European case, and numerically verify that variants of the split tree introduced in this paper significantly improve the convergence of Joshi’s original split tree in the American case.

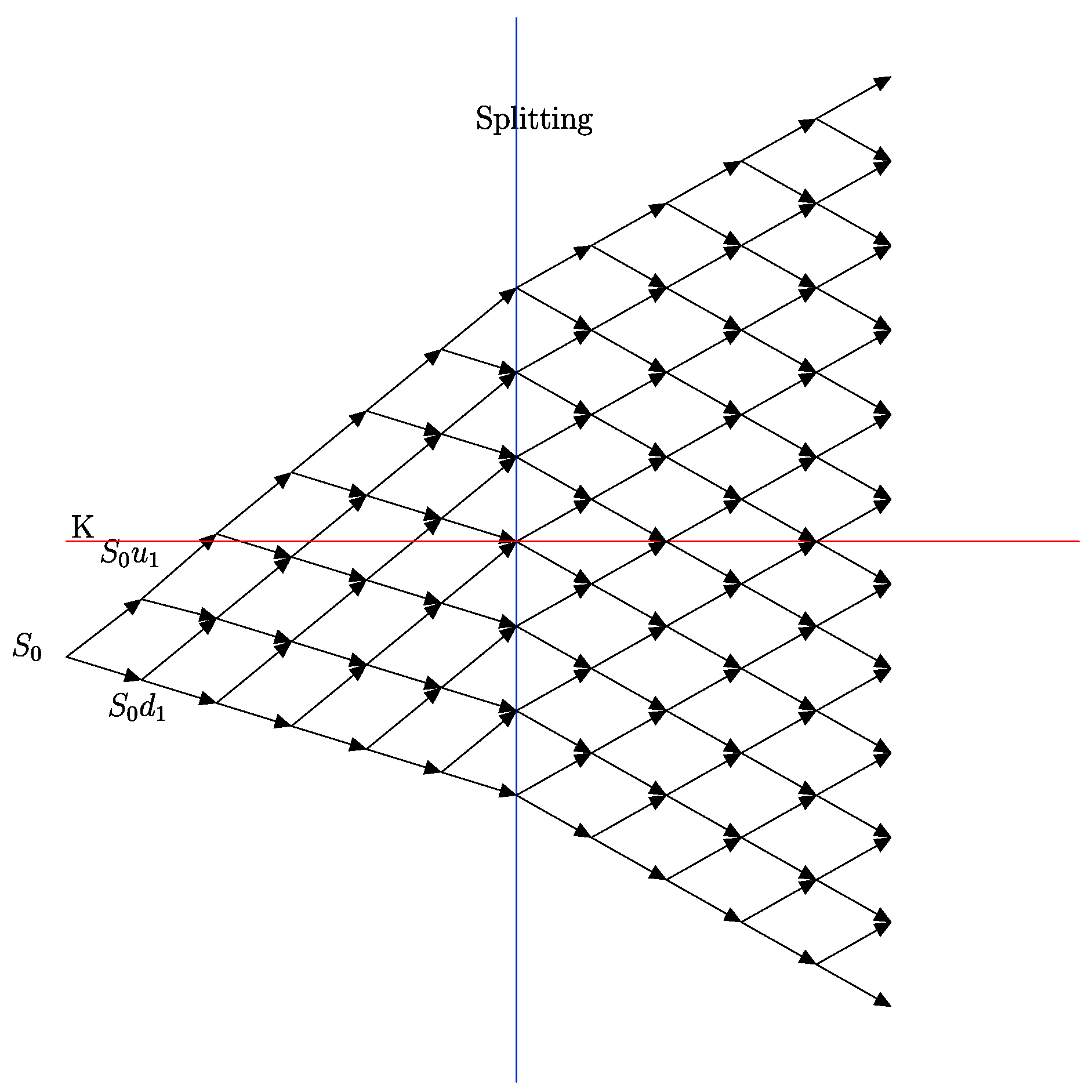
First we introduce a “flexible” version of Joshi’s original split tree. In Joshi’s original split tree, a drift parameter $\lambda$ is used in the binomial model up to a split time $\tau$, after which the tree becomes a Cox Ross Rubinstein (CRR) tree. Moreover, Joshi sets the split time to be the first time step $\tau$ greater than or equal to half of the maturity, and he sets the drift parameter $\lambda$ in such a way that after the split, half the nodes of the tree are located on each side of the strike K. We relax these constraints on $\lambda$ and $\tau$ for the flexible split tree, and we only require that the strike be exactly halfway between two nodes in the log-space, in order to maintain smoothness of the convergence. Joshi’s original split tree is illustrated in Figure 1 where, for simplicity, the log-transformed values of the tree are displayed.

Next we analyze the convergence of the split tree in the European case. For self-similar binomial trees (those for which the up and down mechanism is identical at every time step) the coefficients $c_n$ in the expansion of the error (1) can be calculated with great generality using Diener and Diener (2004) or Chang and Palmer (2007). However, the split tree is not self-similar because it is the mixture of two trees: a flexible binomial tree as in Chang and Palmer (2007), and the Cox Ross Rubinstein (CRR) tree. Hence Diener and Diener (2004) or Chang and Palmer (2007) cannot be used to calculate $c_n$. The calculation of $c_n$ is the first result of this paper. To the best of our knowledge, it is the first time that an explicit error formula has been found for non-self-similar trees.

Then we define optimal versions of the split tree. When fixing all the parameters of a split tree except its split time $\tau$, we say that a split time ${\tau }^{\ast }$ is the optimal split time if the magnitude of the coefficient $c_n$ in (1) is minimized when the split time is ${\tau }^{\ast }$. When $\tau$ is the optimal split time, we say that the tree is an optimal split tree. First we prove a general result which provides a close form formula for the optimal split time ${\tau }^{\ast }$. However, there are many optimal split trees, even when the parameters $S_0$, K, r, $\sigma$, and T are fixed. We consider optimal split trees under three natural constraints. The first constraint is to have all the nodes in the final layer of the tree centered around the strike K, as in Joshi’s original split tree. Joshi’s arbitrarily fast converging tree for European vanilla options Joshi (2010) is also centered around the strike. This motivates studying the optimal split tree under this natural constraint, and we call it the optimal centered split tree. However, the “centered” constraint sometimes prevents us from getting $c_n=0$. This is our motivation for the maximal range optimal split tree, which is the optimal split tree under the constraint that the range of values of the spot $S_0$ for which $c_n=0$ at the optimal split time ${\tau }^{\ast }$ is maximized. Now, the maximal range optimal split tree may result in a very small optimal split time ${\tau }^{\ast }$ and a large drift ${\lambda }^{\ast }$. If ${\tau }^{\ast }$ is very small and the number of time steps n is not large, there can be very few time steps prior to the split time, which may result in increased oscillations of the error. This is the motivation for our last optimal split tree. In the optimal split tree near $\tau$, we seek to choose the drift $\lambda$ in such a way that $c_n=0$ occurs at a split time which is as close as possible to some target $\tau$.

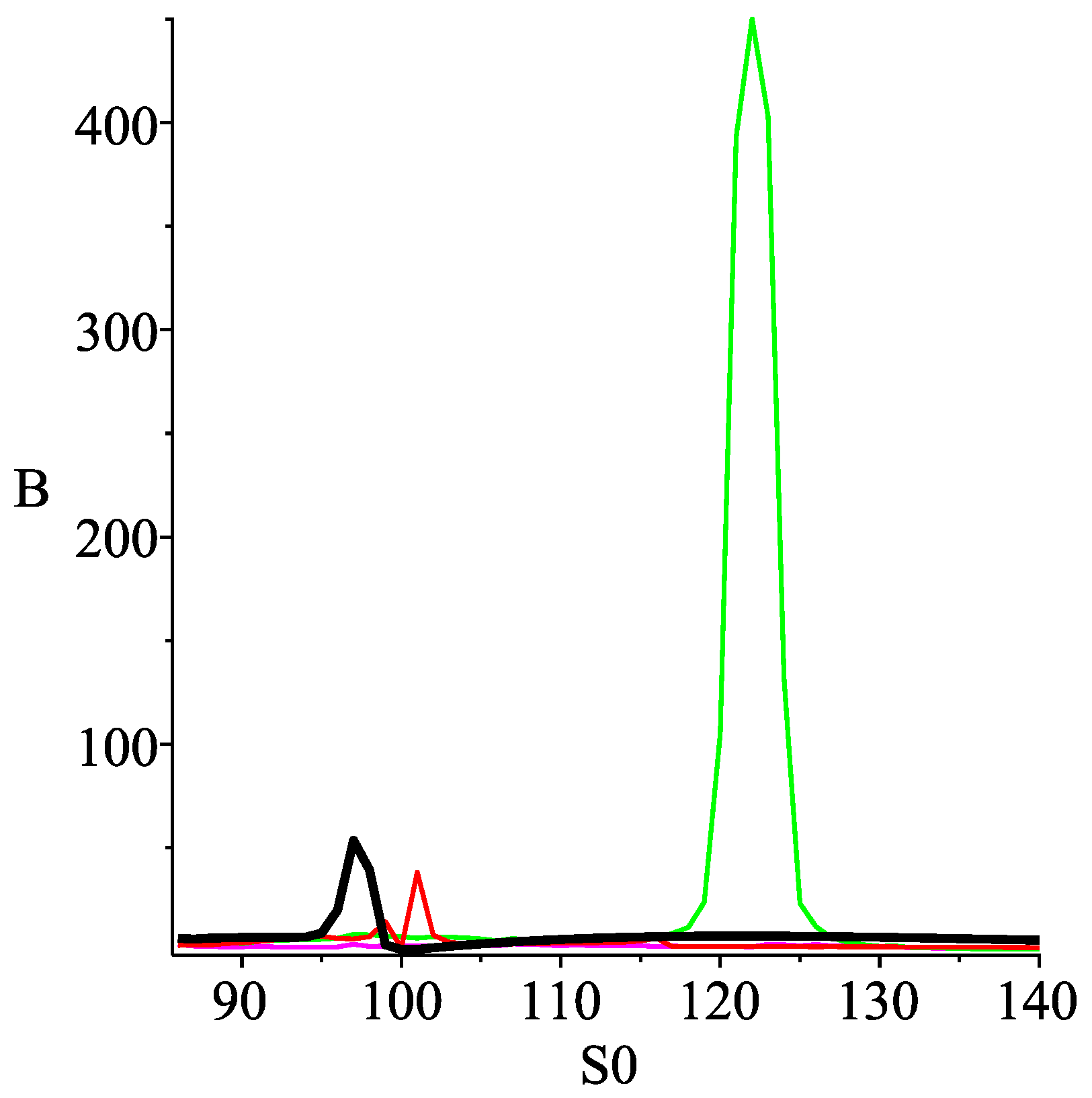
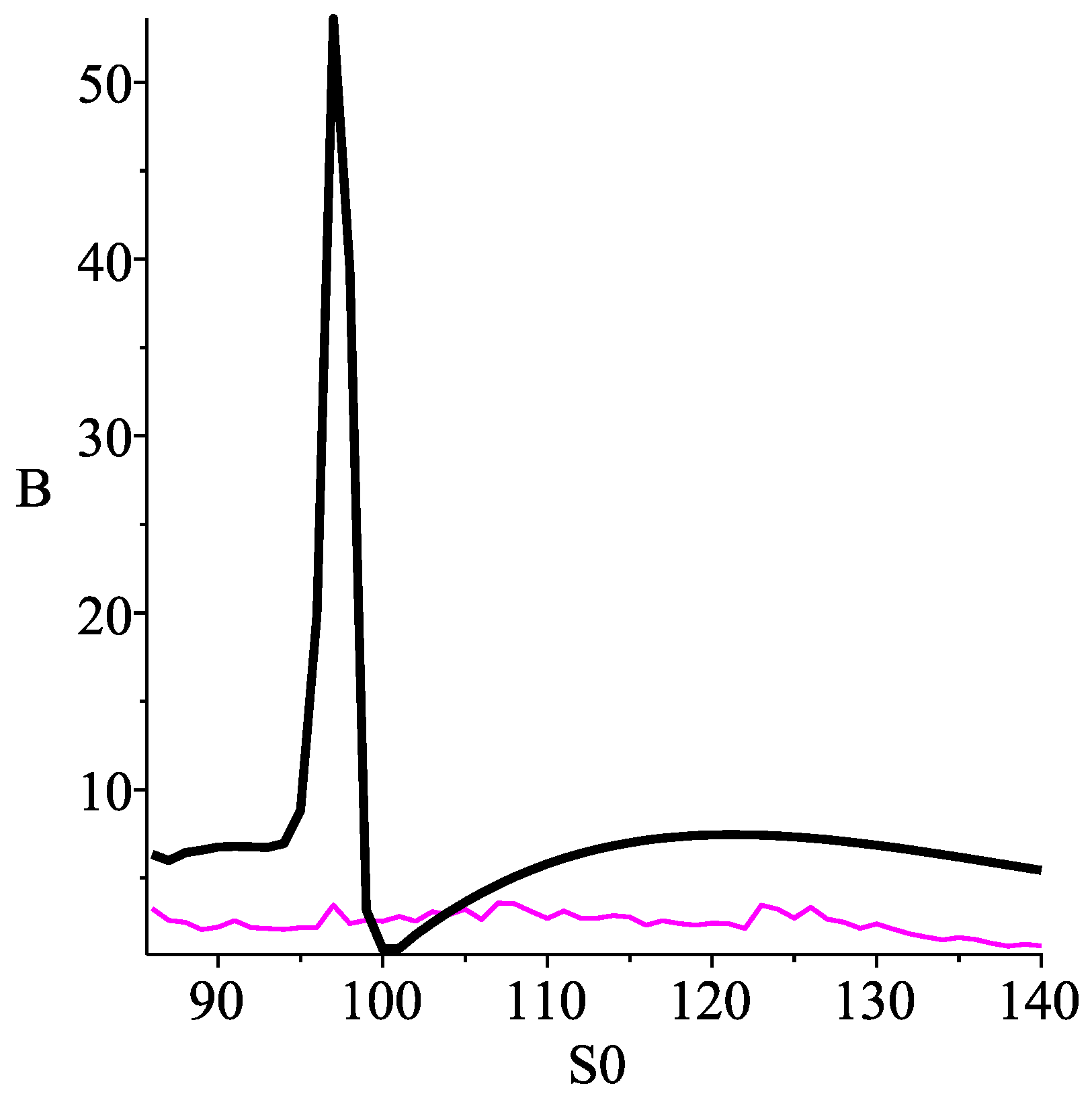
Finally, we test our split trees in the American case. Our numerical results suggest that one of our optimal split trees is capable of significantly improving the accuracy of the convergence of Joshi’s original split tree for the American put. We explain how this increased accuracy translates in a measure of increased speed. In this measure, our numerical result suggests that one of our optimal split trees could be significantly faster than Joshi’s original tree.

2. The Split Tree

In the setting of put or call options in the Black–Scholes model with spot price $S_0$, strike K, risk free rate r, volatility $\sigma$, and maturity T, the binomial tree method with n time steps, is equivalent to replacing the Black–Scholes geometric Brownian motion with a process $S_t^n$ such that at every positive time t which is a multiple $T/n$, the process jumps from its current position $S_{t-}^n$ to $S_{t-}^{n}u$ with probability p, and jumps to $S_{t-}^{n}d$ with probability $1-p$. Such trees are called self-similar because the jumping mechanism is identical at every time step.

Binomial trees typically exhibit an oscillatory convergence, and numerous choices of $u,d,$ and p have been proposed to smooth and accelerate this convergence. In the Cox Ross Rubinstein (CRR) model Cox, Ross and Rubinstein (1979), the choices are

$$u=e^{\sigma \sqrt{T/n}},d=1/u,p=\left(e^{rT/n}-d\right)/\left(u-d\right).$$

(3)

In the flexible binomial trees, Chang and Palmer (2007); Tian (1999), the values of u, d, and p are given by

$$u=e^{\lambda {\sigma }^{2}T/n+\sigma \sqrt{T/n}},d=e^{\lambda {\sigma }^{2}T/n-\sigma \sqrt{T/n}},p=\left(e^{rT/n}-d\right)/\left(u-d\right),$$

(4)

where the additional drift parameter $\lambda$ may depend on n but must remain bounded.

Let $t_k:=kT/n$. In the split tree with split time $0<\tau \le T$ and drift parameter $\lambda$, the process $S_t^n$ follows a flexible binomial tree with parameter $\lambda$ on the interval $0\le t_k\le \tau$, and it follows the CRR model thereafter. This means that the values of $u,$ d and p used to calculate

$$S_{t_k}^n=\left\{\begin{array}{cc}{S}_{t_{k-1}}^{n}u\hfill & \mathrm{with}\mathrm{probability}p\hfill \\ S_{t_{k-1}}^{n}d\hfill & \mathrm{with}\mathrm{probability}1-p\hfill \end{array}\right.$$

at time $t_k$ are constant for $0<t_k\le \tau$ and $\tau <t_k\le T$. In fact, the split tree uses u, d, and p from (4) for $0<t_k\le \tau$, and it uses (3) for $\tau <t_k\le T$. Seeking good convergence properties, the split tree requires that $\log K$ falls exactly halfway between two nodes in the log-space. Here $\tau :=\tau \left(n\right)$ is any number in the interval $(0,T]$. However, given a split time $0<\tau <T$, the actual time at which the values of u and d switch from (4) to (3) can only be a multiple of $T/n$. When $\tau$ is not a multiple of $T/n$, we round it to the nearest multiple of $T/n$. In this manner, we can assume that $\tau$ is a multiple of $T/n$. Note that the cases where $\tau =T$ and $\tau =0$ correspond to no splitting, which is treated in Chang and Palmer (2007). Thus, in order to simplify the exposition, when calculating the coefficient of the error $c_n$ in

$$C^n=C^{BS}+\frac{c_n}{n}+O\left(n^{-3/2}\right),$$

(5)

we make the assumption that

$$0<{\underline{\lim }}_{n\to \infty }\tau \le {\overline{\lim }}_{n\to \infty }\tau <T.$$

(6)

As for $\lambda$, we can express it in the form

$$\lambda =\frac{\ln \left(\widehat{K}/S_0\right)}{\tau {\sigma }^2}$$

(7)

where, for some integer $\ell =0,\pm 1,\pm 2,\dots$ depending on n,

$$\widehat{K}=\left\{\begin{array}{cc}K\exp \left(2\ell \sigma \sqrt{T/n}\right)\exp \left(\sigma \sqrt{T/n}\right)\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}\hfill \\ K\exp \left(2\ell \sigma \sqrt{T/n}\right)\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd}\hfill \end{array}\right.$$

(8)

or equivalently

$$\widehat{K}=K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)\exp \left(\left(2\ell \right)\sigma \sqrt{T/n}\right).$$

The parameter $\widehat{K}$ is actually a practical way of determining $\lambda$ because one of the defining properties of the split tree is that $\log K$ falls exactly halfway between two nodes in the log-space and this is guaranteed by (7) and (8). To see this, consider first the special case where n is even, and where $\tau =mT/n$ with m even. Then an even number of time steps, $n-m$, is left until maturity T. At time $\tau$, the tree is centered around

$$S_0{e}^{\lambda {\sigma }^{2}mT/n}=\widehat{K}=K\exp \left(2\ell \sigma \sqrt{T/n}\right)\exp \left(\sigma \sqrt{T/n}\right).$$

This means that, if at time $\tau$ the total number of up movements is equal to the total number of down movements in the tree, then the value of $S_{\tau }$ is $\widehat{K}$. As an even number of time steps is left until maturity, it follows that in the CRR model (and therefore in the split tree) $\widehat{K}$ is a terminal node. Hence, in the log space, the terminal nodes of the tree have the form

$$\log K+\left(2\ell +2j+1\right)\sigma \sqrt{T/n},\mathrm{for}j=0,\pm 1,\pm 2,\cdots .$$

The cases $j=-\ell$ and $j=-\ell -1$ give the two neighbors of $\log K$. Thus, $\log K$ falls exactly halfway between two nodes in the log-space, as claimed. The other cases (n even and m odd, n odd and m odd, and n odd and m even) can be treated in a similar manner. Throughout this paper we make the assumption that $\lambda :=\lambda \left(n\right)$ satisfies

$${\overline{\lim }}_{n\to \infty }\left|\lambda \right|<\infty ,$$

(9)

or equivalently

$$0<{\underline{\lim }}_{n\to \infty }\widehat{K}\le {\overline{\lim }}_{n\to \infty }\widehat{K}<\infty .$$

(10)

The simplest way to specify a split tree is via the split time $\tau$ and the implicit parameter ℓ. Here is a formal definition.

Definition 1

(Split tree with parameters $\tau$ and ℓ). Consider a spot price $S_0$, a strike K, a risk free rate r, a volatility σ, a maturity T, and a number of time steps $n\ge 2$. Given a split time $0<\tau \in \left(T/n\right)\mathbb{N}$, and some integer ℓ, define $\widehat{K}$ by (8), and define λ by (7). Define also $u\left(t\right)$, $d\left(t\right)$, and $p\left(t\right)$ by

$$\begin{array}{cc}\hfill u\left(t\right)& =e^{\lambda {\sigma }^{2}T/n+\sigma \sqrt{T/n}}if0<t\le \tau ,u\left(t\right)=e^{\sigma \sqrt{T/n}}ift>\tau ,\hfill \\ \hfill d\left(t\right)& =e^{\lambda {\sigma }^{2}T/n-\sigma \sqrt{T/n}}if0<t\le \tau ,d\left(t\right)=e^{-\sigma \sqrt{T/n}}ift>\tau \hfill \\ \hfill p\left(t\right)& =\left(e^{rT/n}-d\left(t\right)\right)/\left(u\left(t\right)-d\left(t\right)\right).\hfill \end{array}$$

Finally, define the time steps $t_k$, for $k=0,1,\dots$, by $t_k=kT/n$. The split tree $S_t^n$ with parameter τ and ℓ is the stochastic process which is constant on each interval $[t_k,t_{k+1})$, such that $S_0^n=S_0$, and which at every time step $0<t\in \left(T/n\right)\mathbb{N}$, jumps from its current position $S_{t-}^n$ to $S_{t-}^{n}u\left(t\right)$ with probability $p\left(t\right)$, and jumps to $S_{t-}^{n}d\left(t\right)$ with probability $1-p\left(t\right)$.

Definition 2.

We say that a split tree is centered if $\ell =0$.

Definition 3.

Joshi’s original split tree is the special case where $\ell =0$, and τ is the smallest time step greater than or equal to $T/2$.

3. Rate of Convergence of the Split Tree

In this section, we provide two expressions for the coefficient of $1/n$ in the expansion in powers of $1/\sqrt{n}$ of the error for the split tree value of a call option $C^n$, against the Black–Scholes price $C^{BS}$. We also show that the coefficient of $1/n^{1.5}$ is null. Given splitting parameters $\tau$ and $\lambda$, we find an explicit formula for the value of $c:=c\left(\lambda ,\tau \right)$ in $C^n=C^{BS}+c/n+O\left(n^{-2}\right)$. Here c is a smooth function of $\lambda$ and $\tau$. In Section 3.1 we provide a generic expression for c, and in Section 3.2 we transform this generic expression into an explicit closed-form formula.

3.1. Generic Expressions for the Coefficients of $1/n$ in the Error

We use the semigroup notation introduced by Leduc in Leduc (2013). Consider any Markov process, for instance, a discrete Markov process $S_t$, $t=0,$ $\Delta t,$ $2\Delta t,\dots$ with $S_t=S_0{e}^{W_t}$ for some process $W_t$ with independent increments. Consider now $E_x$, the conditional expectation given that $S_0=x$. Then for any non-negative measurable function f, any $0\le t\le T$, and any $x>0$, the Markov property gives that

$$E_x\left(f\left(S_T\right)\right)=E_x\left(E_{S_t}\left(f\left(S_{T-t}\right)\right)\right).$$

Obviously, with

$${\mathcal{E}}_{t}f\left(x\right):=e^{-rt}{E}_x\left(f\left(S_t\right)\right)$$

we obtain the discounted expectation semigroup operator. It satisfies

$${\mathcal{E}}_{t+s}f\left(x\right)={\mathcal{E}}_t{\mathcal{E}}_{s}f\left(x\right)=e^{-rt}{E}_x\left({\mathcal{E}}_{s}f\left(S_t\right)\right).$$

In other words, ${\mathcal{E}}_{t}f\left(x\right)$ is the price of an option with maturity t and payoff function f, when $S_0=x$.

As always, the strike K, spot price $S_0$, maturity T, risk free rate r, and volatility $\sigma$ are fixed. We denote by $S_t^{\lambda ,n}$ the flexible binomial model of Chang and Palmer (2007) with parameter $\lambda$ and n time-steps until maturity. Hence $S_t^{\lambda ,n}$ is the stochastic process associated with $u,d,$ and p given by (4). We denote by ${\mathcal{E}}_t^{\lambda ,n}$ its semigroup operator. Note that the CRR model corresponds to a flexible binomial model where $\lambda =0$. Given a split time $\tau \in \left(T/n\right)\mathbb{N}$ and drift parameter $\lambda$, we denote by $S_t^n$ and ${\mathcal{E}}_t^n$ the stochastic process and semigroup operator associated with the corresponding split tree. Finally, ${\mathcal{E}}_t$ denotes the semigroup operator associated with the geometric Brownian motion.

To shorten expressions we set

$$g\left(x\right)=\max \left(x-K,0\right).$$

Then

$${\mathcal{E}}_t^n=\left\{\begin{array}{cc}{\mathcal{E}}_t^{\lambda ,n}\hfill & \mathrm{for}0\le t\le \tau \hfill \\ {\mathcal{E}}_{\tau }^{\lambda ,n}{\mathcal{E}}_{t-\tau }^{0,n}\hfill & \mathrm{for}\tau \le t,\hfill \end{array}\right.$$

(11)

and the price $C_T^n\left(S_0\right)$ of a call option with maturity T in the split tree model can be written as

$$C_T^n\left(S_0\right)={\mathcal{E}}_T^{n}g\left(S_0\right)={\mathcal{E}}_{\tau }^{\lambda ,n}{\mathcal{E}}_{T-\tau }^{0,n}g\left(S_0\right)=e^{-r\tau }{E}_{S_0}\left({\mathcal{E}}_{T-\tau }^{0,n}g\left(S_{\tau }^n\right)\right).$$

Motivated by our extension of the results in Leduc (2013), Theorem A2 in Appendix C, we introduce another abbreviation: given a non negative measurable bounded function h, we write:

$${\mathrm{Flex}}_{\tau }^{\lambda }h\left(S_0\right):=-{\displaystyle {\sum }_{k=2}^4}\frac{{\Delta }_k\left(\tau ,\lambda \right)}{k!}{x}^k\frac{{\partial }^k}{\partial x^k}{\mathcal{E}}_{\tau }h\left(S_0\right),$$

(12)

where

$$\begin{array}{cc}\hfill {\Delta }_2\left(\tau ,\lambda \right)& :={\tau }^2\left({\sigma }^4{\lambda }^2+(-{\sigma }^4-2r{\sigma }^2)\lambda +(r^2+r{\sigma }^2+\frac{5}{12}{\sigma }^4)\right),\hfill \\ \hfill {\Delta }_3\left(\tau ,\lambda \right)& :=2{\tau }^2{\sigma }^2\left({\sigma }^2+r-{\sigma }^2\lambda \right),\hfill \\ \hfill {\Delta }_4\left(\tau ,\lambda \right)& :=2{\tau }^2{\sigma }^4.\hfill \end{array}$$

If h is smooth enough then Theorem A2 says that ${\mathrm{Flex}}_{\tau }^{\lambda }h\left(x\right)$ is the coefficient of $1/n$ in the expansion of the error for an option with payoff h evaluated in the flexible model with parameter $\lambda$ when $S_0=x$.

Moreover, for every $0\le t\le T$ and $x>0$, we also use the notation

$${\mathrm{CRR}}_t\left(x\right):=e^{-\frac{1}{2}{d}_{1,t}^2\left(x\right)}{A}_t^0\left(x\right),$$

(13)

where $d_{1,t}\left(x\right)$ and $A_t^{\lambda }\left(x\right)$ are as in Chang and Palmer’s Theorem A1 given in Appendix B; that is,

$$\begin{array}{cc}\hfill A_t^{\lambda }\left(x\right)& =-{\sigma }^{2}t\left(6+d_{1,t}^2\left(x\right)+d_{2,t}^2\left(x\right)\right)+4t\left(d_{1,t}^2\left(x\right)-d_{2,t}^2\left(x\right)\right)\left(r-\lambda {\sigma }^2\right)\hfill \\ \hfill & -12t^2{\left(r-\lambda {\sigma }^2\right)}^2+12t{\sigma }^2,\hfill \\ \hfill d_{1,t}\left(x\right)& =\frac{\ln \left(\frac{x}{\mathsf{K}}\right)+\left(r+\frac{1}{2}{\sigma }^2\right)t}{\sigma \sqrt{t}},d_{2,t}\left(x\right)=d_{1,t}\left(x\right)-\sigma \sqrt{t}.\hfill \end{array}$$

Note that ${\mathrm{CRR}}_t\left(x\right)$ is the coefficient of $1/n$ in the expansion of the error of a call option in the CRR model when $S_0=x$.

Let $C_t^{BS}\left(x\right)$ be the price of a call option in the Black–Scholes model of the option, when the maturity is t, the strike is K, the risk free rate is r, the volatility is $\sigma$, and the spot price is x. The next proposition provides a generic expression that connects the option’s price $C_T^n\left(S_0\right)$ in the split model to the price $C_T^{BS}\left(S_0\right)$ in the Black–Scholes model.

Proposition 1.

Consider a European call option with strike K, spot price $S_0$, maturity T, risk free rate r, and volatility σ. Let the split time $\tau :=\tau \left(n\right)$, $0<\tau <T$, be bounded away from 0 and T. Moreover, let the drift $\lambda :=\lambda \left(n\right)$ be bounded and of the form $\lambda =\ln \left(\widehat{K}/S_0\right)/\left(\tau {\sigma }^2\right)$ for some $\widehat{K}:=\widehat{K}\left(n\right)$ of the form (8). Then the price $C_T^{BS}\left(S_0\right)$ in the Black–Scholes model is related to the price $C_T^n\left(S_0\right)$ in the split tree model by the equation

$$C_T^n\left(S_0\right)=C_T^{BS}\left(S_0\right)+{\mathrm{Split}}_{\tau }\left(S_0\right)\frac{1}{n}+O\left(n^{-2}\right),$$

(14)

where

$${\mathrm{Split}}_{\tau }\left(S_0\right):=\left(\frac{T}{\tau }\right){\mathrm{Flex}}_{\tau }^{\lambda }{C}_{T-\tau }^{BS}\left(S_0\right)+\left(\frac{T}{T-\tau }\right){\mathcal{E}}_{\tau }{\mathrm{CRR}}_{T-\tau }\left(S_0\right).$$

(15)

3.2. Explicit Expressions for the Coefficients of $1/n$ in the Error

In this section we give an explicit closed form formula for ${\mathrm{Split}}_{\tau }\left(S_0\right)$ of (15). First note that

$$C_{T-\tau }^{BS}\left(x\right)={\mathcal{E}}_{T-\tau }g\left(x\right)\mathrm{with}g\left(x\right)=\max \left(x-K,0\right).$$

and

$${\mathcal{E}}_{\tau }{\mathcal{E}}_{T-\tau }g\left(S_0\right)={\mathcal{E}}_{T}g\left(S_0\right)=C_T^{BS}\left(S_0\right).$$

It follows from (12) that

$${\mathrm{Flex}}_{\tau }^{\lambda }{C}_{T-\tau }^{BS}\left(S_0\right)=-{\displaystyle {\sum }_{k=2}^4}\frac{1}{k!}{\Delta }_k\left(\tau ,\lambda \right)S_0^k\frac{{\partial }^k}{\partial x^k}{C}_T^{BS}\left(S_0\right).$$

(16)

The derivatives with respect to the spot price $S_0$ of a call option in the Black–Scholes model are well known, and from there we see that for $0\le \tau <T$,

$$\begin{array}{cc}\hfill {\mathrm{Flex}}_{\tau }^{\lambda }{C}_{T-\tau }^{BS}\left(S_0\right)& =\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{\sqrt{2\pi }}\left(-\frac{{\Delta }_2\left(\tau ,\lambda \right)}{2}\frac{1}{\sigma \sqrt{T}}+\frac{{\Delta }_3\left(\tau ,\lambda \right)}{6}\frac{d_1+\sqrt{T}\sigma }{T{\sigma }^2}\right.\hfill \\ \hfill & \left.-\frac{{\Delta }_4\left(\tau ,\lambda \right)}{24}\frac{2T{\sigma }^2+d_1^2+3d_1\sqrt{T}\sigma -1}{T^{\frac{3}{2}}{\sigma }^3}\right),\hfill \end{array}$$

(17)

where ${\Delta }_k:={\Delta }_k\left(\tau ,\lambda \right)$ is as in Section 3.1, and

$$d_1:=d_{1,T}\left(S_0\right)={\displaystyle \frac{\ln \left(\frac{S_0}{K}\right)+\left(r+\frac{1}{2}{\sigma }^2\right)T}{\sigma \sqrt{T}}},d_2:=d_1-\sigma \sqrt{T}.$$

With simple algebraic manipulation we re-write (17) as

$${\mathrm{Flex}}_{\tau }^{\lambda }{C}_{T-\tau }^{BS}\left(S_0\right)=\frac{{\tau }^2}{T^2}\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24{\sigma }^{3}T\sqrt{2\pi T}}\Delta +\frac{{\tau }^2}{T^2}\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24\sigma \sqrt{2\pi T}}\mathcal{P}\left(\lambda \right)$$

(18)

where

$$\mathcal{P}\left(\lambda \right):=4T^{\frac{3}{2}}{\sigma }^2\left(\sqrt{T}{\sigma }^2+6\sqrt{T}r-2\sigma d_1\right)\lambda -12T^2{\sigma }^4{\lambda }^2,$$

(19)

and

$$\begin{array}{cc}\hfill \Delta & :=-12T{\sigma }^2{\Delta }_2+4\sqrt{T}\sigma \left(d_1+\sqrt{T}\sigma \right){\Delta }_3+\left(1-2T{\sigma }^2-3\sqrt{T}\sigma d_1-d_1^2\right){\Delta }_4,\hfill \\ \hfill {\Delta }_k& :={\Delta }_k\left(T,0\right).\hfill \end{array}$$

(20)

The following theorem, proved in Appendix A, provides an explicit closed form formula for the coefficient ${\mathrm{Split}}_{\tau }\left(S_0\right)$ of $1/n$ in the expansion of the error of a call option evaluated with the split tree.

Theorem 1.

Consider a European call option with strike K, spot price $S_0$, maturity T, risk free rate r, and volatility σ. Let the split time $\tau :=\tau \left(n\right)$, $0<\tau <T$, be bounded away from 0 and T. Moreover, let the drift $\lambda :=\lambda \left(n\right)$ be bounded and of the form $\lambda =\ln \left(\widehat{K}/S_0\right)/\left(\tau {\sigma }^2\right)$ for some $\widehat{K}:=\widehat{K}\left(n\right)$ of the form (8). Then the price $C_T^{BS}\left(S_0\right)$ in the Black–Scholes model is related to the price $C_T^n\left(S_0\right)$ in the split tree model by the equation

$$C_T^n\left(S_0\right)=C_T^{BS}\left(S_0\right)+{\mathrm{Split}}_{\tau }\left(S_0\right)\frac{1}{n}+O\left(n^{-2}\right),$$

(21)

where

$${\mathrm{Split}}_{\tau }\left(S_0\right)=\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24{\sigma }^{3}T\sqrt{2\pi T}}\Delta +\frac{\tau }{T}\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24\sigma \sqrt{2\pi T}}\mathcal{P}\left(\lambda \right)+\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24\sigma \sqrt{2\pi T}}\left(4T{\sigma }^2\right),$$

(22)

with

$$\begin{array}{cc}\hfill \mathcal{P}\left(\lambda \right)& :=4T^{\frac{3}{2}}{\sigma }^2\left(\sqrt{T}{\sigma }^2+6\sqrt{T}r-2\sigma d_1\right)\lambda -12T^2{\sigma }^4{\lambda }^2,\hfill \\ \hfill d_1& :=\frac{\ln \left(\frac{S_0}{K}\right)+\left(r+\frac{1}{2}{\sigma }^2\right)T}{\sigma \sqrt{T}}.\hfill \end{array}$$

Note that when $S_0=K$ and n is odd, $\lambda =0$, and regardless of the value of $\tau$, there is no splitting since the process is CRR throughout. Our error formula therefore coincides with the formula in Chang and Palmer (2007); that is,

$${\mathrm{Split}}_T\left(S_0\right)=\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24{\sigma }^{3}T\sqrt{2\pi T}}\Delta +\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24\sigma \sqrt{2\pi T}}\left(4T{\sigma }^2\right)=\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24\sigma \sqrt{2\pi T}}{A}_T^0\left(S_0\right).$$

(23)

Note also that the case $\tau =T$ does not fall under the assumption of Theorem 1 above. However, when $\tau =T$ there is actually no splitting and because K is exactly halfway between two nodes; the oscillating term ${\Delta }_n$ in the formula of Chang and Palmer (2007) vanishes. Simple algebraic manipulations show again that our formula coincides with the formula in Chang and Palmer (2007) (see Theorem A1 in Appendix B); that is

$$\begin{array}{cc}\hfill {\mathrm{Split}}_T\left(S_0\right)& =\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24{\sigma }^{3}T\sqrt{2\pi T}}\Delta +\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24\sigma \sqrt{2\pi T}}\mathcal{P}\left(\lambda \right)+\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24\sigma \sqrt{2\pi T}}\left(4T{\sigma }^2\right)\hfill \\ \hfill & =\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24\sigma \sqrt{2\pi T}}{A}_T^{\lambda }\left(S_0\right).\hfill \end{array}$$

(24)

The following provides another expression for ${\mathrm{Split}}_{\tau }\left(S_0\right)$ which we will use for defining optimal split trees.

Lemma 1.

For $0<\tau \le T$, the term ${\mathrm{Split}}_{\tau }\left(S_0\right)$ can be rewritten as

$${\mathrm{Split}}_{\tau }\left(S_0\right)=\mathrm{F}\left(a-b/\tau \right).$$

(25)

where

$$\begin{array}{cc}\hfill \mathrm{F}& =\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24{\sigma }^{3}T\sqrt{2\pi T}}\hfill \\ \hfill a& :=\left(\Delta +4T^2{\sigma }^4\right)+\ln \left(\widehat{K}/S_0\right)\left(T\left({\sigma }^2+6r\right)-2\sigma \sqrt{T}{d}_1\right)4T{\sigma }^2,\hfill \\ \hfill b& :=12T^2{\sigma }^2{\ln }^2\left(\widehat{K}/S_0\right).\hfill \end{array}$$

(26)

Proof. 

This follows from minor algebraic manipulation of (22) after replacing $\lambda$ by $\ln \left(\widehat{K}/S_0\right)/\left(\tau {\sigma }^2\right)$. ☐

4. Optimal Split Trees

It is natural to optimize the splitting parameters $\tau$ and $\lambda$ (or equivalently $\tau$ and ℓ) for performance: we want to minimize the value of $\left|{\mathrm{Split}}_{\tau }\left(S_0\right)\right|$ in

$$C^n=C^{BS}+{\mathrm{Split}}_{\tau }\left(S_0\right)/n+O\left(n^{-2}\right).$$

(27)

In fact, we will show in this section that unless $S_0$ is deeply in or out of the money, the splitting parameters can always be chosen in such a way that ${\mathrm{Split}}_{\tau }\left(S_0\right)=0$.

All parameters being fixed except the split time $\tau$, we say that a split time ${\tau }^{\ast }$ is the optimal split time if the magnitude of ${\mathrm{Split}}_{\tau }\left(S_0\right)$ is minimized when $\tau$ is equal to ${\tau }^{\ast }$. When the split time is equal to the optimal split time, we say that the tree is an optimal split tree.

In this section we study optimal split trees under three constraints, and under these constraints we find closed form formulae for the optimal split time ${\tau }^{\ast }$ and the optimal drift parameter ${\lambda }^{\ast }$.

• For centered trees, where $\ell =0$, we find the optimal split time ${\tau }^{\ast }$, which minimizes $\left|{\mathrm{Split}}_{\tau }\left(S_0\right)\right|$.
• We find ${\tau }^{\ast }$ and ${\lambda }^{\ast }$, which maximize the range of values of $S_0$ for which ${\mathrm{Split}}_{\tau }\left(S_0\right)=0$.
• We find ${\tau }^{\ast }$ and ${\lambda }^{\ast }$, which minimize the magnitude of ${\mathrm{Split}}_{\tau }\left(S_0\right)$ under the constraint that ${\tau }^{\ast }$ is as close as possible to some specific value $\tau$.

4.1. The Optimal Split Time ${\tau }^{\ast }$ Given ℓ

Before defining our optimal split trees, we a need a general result which is the topic of this section. Recall that

$$\widehat{K}=K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)\exp \left(\left(2\ell \right)\sigma \sqrt{T/n}\right),$$

and that, given a split time $\tau$,

$$\lambda =\ln \left(\widehat{K}/S_0\right)/\left(\tau {\sigma }^2\right).$$

Proposition 2

(Minimum of $\left|{\mathrm{Split}}_{\tau }\left(S_0\right)\right|$ given ℓ). Consider a European call option with strike K, spot price $S_0$, maturity T, risk free rate r, and volatility σ. Let

$$\begin{array}{cc}\hfill a& :=\left(\Delta +4T^2{\sigma }^4\right)+\ln \left(\widehat{K}/S_0\right)\left(T\left({\sigma }^2+6r\right)-2\sigma \sqrt{T}{d}_1\right)4T{\sigma }^2,\hfill \\ \hfill b& :=12T^2{\sigma }^2{\ln }^2\left(\widehat{K}/S_0\right).\hfill \end{array}$$

Assume that $n\ge 2$, and consider integers $\ell :=\ell \left(n\right)$ such that $\widehat{K}$ is bounded and bounded away from 0. Then the magnitude of the function $\tau \mapsto {\mathrm{Split}}_{\tau }\left(S_0\right)$ defined by (25) is minimized when τ takes the value $\widehat{\tau }:=\widehat{\tau }\left(n\right)$ given by

$$\widehat{\tau }=\left\{\begin{array}{cc}\frac{b}{a}\hfill & if{\mathrm{Split}}_T\left(S_0\right)>0and\widehat{K}\ne S_0\hfill \\ T\hfill & if{\mathrm{Split}}_T\left(S_0\right)\le 0or\widehat{K}=S_0\hfill \end{array}\right.$$

(28)

Proof. 

We use Lemma 1 to write

$${\mathrm{Split}}_{\tau }\left(S_0\right)=\mathrm{F}\left(a-b/\tau \right).$$

If $b=0$ (or equivalently $\widehat{K}=S_0$) then the value of ${\mathrm{Split}}_{\tau }\left(S_0\right)$ does not depend on $\tau$. Hence $\tau =T$ minimizes $\left|{\mathrm{Split}}_{\tau }\left(S_0\right)\right|$. Note that $b\ge 0$. Hence it is clear that ${\mathrm{Split}}_{\tau }\left(S_0\right)\le {\mathrm{Split}}_T\left(S_0\right)$ for every $0<\tau \le T$. Thus, if ${\mathrm{Split}}_T\left(S_0\right)\le 0$, then the magnitude of ${\mathrm{Split}}_{\tau }\left(S_0\right)$ is minimized when $\tau =T$. It remains to consider the case where $b\ne 0$ and ${\mathrm{Split}}_T\left(S_0\right)>0$. Then $a>0$ because ${\mathrm{Split}}_T\left(S_0\right)=a-b/T>0$ and $b>0$. Moreover, ${\mathrm{Split}}_{\tau }\left(S_0\right)=0$ when $\tau$ takes the value $b/a$. Since $a>0$ and $b>0$, it is clear that $b/a$ is always strictly positive. It remains to show that $b/a\le T$. In fact, $b/a<T$ because ${\mathrm{Split}}_{\tau }\left(S_0\right)$ is a strictly increasing function of $\tau$, ${\mathrm{Split}}_{b/a}\left(S_0\right)=0$, and ${\mathrm{Split}}_T\left(S_0\right)>0$. ☐

Theorem 2

(Optimal splitting time ${\tau }^{\ast }$ given ℓ). Consider a European call option with strike K, spot price $S_0$, maturity T, risk free rate r, and volatility σ. Let $a_n$, $b_n$, $c_n$ be defined by

$$\begin{array}{cc}\hfill a_n& :=\left(\Delta +4T^2{\sigma }^4\right)+\ln \left(\widehat{K}/S_0\right)\left(T\left({\sigma }^2+6r\right)-2\sigma \sqrt{T}{d}_1\right)4T{\sigma }^2,\hfill \\ \hfill b_n& :=12T^2{\sigma }^2{\ln }^2\left(\widehat{K}/S_0\right),c_n:={\mathrm{Split}}_T\left(S_0\right)=a_n-b_n/T.\hfill \end{array}$$

Assume that $n\ge 2$, and consider integers $\ell :=\ell \left(n\right)$ such that $\widehat{K}$ is bounded, bounded away from 0, and $\widehat{K}:=\widehat{K}\left(n\right)$ converges to ${\widehat{K}}_{\infty }$ as $n\to \infty$. Let $a_{\infty }$, $b_{\infty }$, and $c_{\infty }$ be the limits of respectively $a_n$, $b_n$, and $c_n$. When $c_{\infty }>0$, assume additionally that n is large enough so that $a_n,b_n,c_n>0$. Let $\widehat{\tau }:=\widehat{\tau }\left(n\right)$ given by

$$\widehat{\tau }=\left\{\begin{array}{cc}\frac{b_n}{a_n}\hfill & if{c}_{\infty }>0and{b}_{\infty }>0\hfill \\ T\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

(29)

Round $\widehat{\tau }$ into ${\tau }^{\ast }:={\tau }^{\ast }\left(n\right)$, the nearest multiple of $T/n$ in the interval $(0,T]$, and consider the value $C^n$ of a call option evaluated in the split tree with parameters ℓ and ${\tau }^{\ast }$. If $c_{\infty }>0$ and $b_{\infty }>0$, then $C^n$ converges to its Black–Scholes limit $C^{BS}$ at a speed of order $1/n^2$. Otherwise, the convergence occurs at a speed of order $1/n$.

Proof. 

When $\widehat{\tau }=T$, the tree is not a split tree but rather a flexible binomial tree with parameter $\lambda =\ln \left(\widehat{K}/S_0\right)/\left(T{\sigma }^2\right)$ and the rate of convergence is $1/n$, as shown in Chang and Palmer (2007).

We just need to consider the case where $c_{\infty }>0$ and $b_{\infty }>0$. In this case we assume that n is big enough so that $b_n>0$ is bounded away from 0, and $a_n>0$. Note that $a_n$ is bounded. Thus $\widehat{\tau }=b_n/a_n$ is bounded away from 0. It follows that ${\tau }^{\ast }$ is also bounded away from 0. From Lemma 1

$$c_n={\mathrm{Split}}_T\left(S_0\right)=a_n-b_n/T>0\mathrm{and}{\mathrm{Split}}_{\tau }\left(S_0\right)=a_n-b_n/\tau .$$

Because ${\mathrm{Split}}_{\widehat{\tau }}\left(S_0\right)=0$ we see that $\widehat{\tau }<T$. Note, furthermore, that it is not possible that $\widehat{\tau }\to T$ when $n\to \infty$, because otherwise

$$0=\underset{n\to \infty }{\lim }\left(a_n-\frac{b_n}{\widehat{\tau }}\right)=a_{\infty }-\frac{b_{\infty }}{T}=c_{\infty }>0.$$

Thus ${\tau }^{\ast }$ is also bounded away from T. We have shown that ${\tau }^{\ast }$ is bounded away from 0 and from T.

Finally, the rounding of $\widehat{\tau }$ into its nearest strictly positive time step, ${\tau }^{\ast }$, affects the value of

$${\mathrm{Split}}_{\widehat{\tau }}\left(S_0\right)=\mathrm{F}\left(a_n-b_n/\widehat{\tau }\right)=0$$

by an amount of order $1/n$, since $\tau \to {\mathrm{Split}}_{\tau }\left(S_0\right)$ is continuously differentiable for $\tau >0$ and its first derivative, $b_n/{\tau }^2$, is bounded. Thus

$${\mathrm{Split}}_{\widehat{\tau }}\left(S_0\right)=0\mathrm{implies}\mathrm{that}{\mathrm{Split}}_{{\tau }^{\ast }}\left(S_0\right)=\mathcal{O}\left(1/n\right).$$

Theorem 1 then yields that

$$\begin{array}{cc}\hfill C^n& =C_T^{BS}\left(S_0\right)+{\mathrm{Split}}_{{\tau }^{\ast }}\left(S_0\right)\frac{1}{n}+O\left(n^{-2}\right)\hfill \\ \hfill & =C_T^{BS}\left(S_0\right)+O\left(n^{-2}\right),\hfill \end{array}$$

as wanted. ☐

Remark 1.

When considering optimal split tree with maturity T, the case where $\tau =T$ can be seen as a degenerate case of the split tree. Trees of this family, introduced by Chang and Palmer (2007), are called flexible trees. We set $\tau =T$ when the magnitude of the coefficient $a_n$ of $1/n$ in the expansion of the error (5) is not minimized by any split tree but is rather minimized by a flexible tree.

4.2. The Optimal Centered Split Tree

Joshi’s original split tree is a centered split tree because $\ell =0$. However, in general, Joshi’s tree is not the optimal centered split tree because it does not minimize the magnitude of the coefficient of $1/n$ in the expansion of the error. This is because $\tau =0.5$ is not, in general, the optimal split time. The optimal split time is given by Theorem 2. Note that, obviously, when $\ell =0$,

$$\underset{n\to \infty }{\lim }\widehat{K}=\underset{n\to \infty }{\lim }K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)=K.$$

When noting that $a_n$, $b_n$, and $c_n$ converge to $a_{\infty },b_{\infty },c_{\infty }$ where

$$\begin{array}{cc}\hfill a_n& :=\left(\Delta +4T^2{\sigma }^4\right)+\ln \left(\widehat{K}/S_0\right)\left(T\left({\sigma }^2+6r\right)-2\sigma \sqrt{T}{d}_1\right)4T{\sigma }^2,\hfill \\ \hfill b_n& :=12T^2{\sigma }^2{\ln }^2\left(\widehat{K}/S_0\right),c_n:=a_n-b_n/T,\hfill \\ \hfill a_{\infty }& :=\left(\Delta +4T^2{\sigma }^4\right)+\ln \left(K/S_0\right)\left(T\left({\sigma }^2+6r\right)-2\sigma \sqrt{T}{d}_1\right)4T{\sigma }^2,\hfill \\ \hfill b_{\infty }& :=12T^2{\sigma }^2{\ln }^2\left(K/S_0\right),c_{\infty }:=a_{\infty }-b_{\infty }/T,\hfill \end{array}$$

it is easy to apply Theorem 2 in order to find the optimal split time.

Definition 4

(Optimal centered split tree). Consider a European call option with strike K, spot price $S_0$, maturity T, risk free rate r, and volatility σ. Let $n\ge 2$, assume that $\ell =0$ for every n, and let ${\tau }^{\ast }$ be as in Theorem 2. The optimal centered split tree is defined to be the split tree with parameters ℓ and ${\tau }^{\ast }$.

4.3. The Maximal Range Optimal Split Tree

Recall that if $C_T^n\left(S_0\right)$ is the price of a call option in a split tree model, and $C_T^{BS}\left(S_0\right)$ is the corresponding Black–Scholes price, then

$$C_T^n\left(S_0\right)=C_T^{BS}\left(S_0\right)+{\mathrm{Split}}_{\tau }\left(S_0\right)\frac{1}{n}+O\left(n^{-2}\right).$$

In the optimal centered split tree, ${\mathrm{Split}}_{\tau }\left(S_0\right)=0$ unless $S_0$ is too deep in or out of money. Otherwise, the value of $|{\mathrm{Split}}_{\tau }\left(S_0\right)|$ is minimized. This occurs under the constraint that $\ell =0$. Here we want to lift that constraint in order to maximize the range of values of $S_0$ for which ${\mathrm{Split}}_{\tau }\left(S_0\right)=0$ can be achieved.

Recall that for split trees

$$\begin{array}{cc}\hfill \lambda & =\ln \left(\widehat{K}/S_0\right)/\left(\tau {\sigma }^2\right),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill \widehat{K}& =K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)e^{2\ell \sigma \sqrt{T/n}}\mathrm{for}\mathrm{some}\ell \in \mathbb{Z}.\hfill \end{array}$$

(31)

Assume that $\widehat{K}:=\widehat{K}\left(n\right)$ is bounded, bounded away from zero, and converges to ${\widehat{K}}_{\infty }$ as $n\to \infty$. Recall $a_n$ and $b_n$ from Theorem 2. Then the optimal time ${\tau }^{\ast }$ takes the form ${\tau }^{\ast }=b_n/a_n$ and ${\mathrm{Split}}_{{\tau }^{\ast }}\left(S_0\right)=0$ when

$$c_{\infty }=\underset{n\to \infty }{\lim }{c}_n=\underset{n\to \infty }{\lim }\left(a_n-\frac{b_n}{T}\right)=\underset{n\to \infty }{\lim }{\mathrm{Split}}_T\left(S_0\right)>0.$$

A glance at (25) reveals that ${\mathrm{Split}}_T\left(S_0\right)$ is a polynomial of degree 2 in $\ln \left(\widehat{K}/S_0\right)$, and the coefficient of ${\ln }^2\left(\widehat{K}/S_0\right)$ is negative. Alternatively, ${\mathrm{Split}}_T\left(S_0\right)$ can also be seen as a polynomial of degree 2 in $\lambda$,

$$\lambda =\ln \left(\widehat{K}/S_0\right)/\left(T{\sigma }^2\right),$$

and again the coefficient of ${\lambda }^2$ is negative. We want to find the value of $\ell :=\ell \left(n\right)$ (or the corresponding value of $\lambda$) which maximizes ${\mathrm{Split}}_T\left(S_0\right)$. This maximizes the range of values of $S_0$ for which $c_{\infty }>0$ and ${\mathrm{Split}}_{{\tau }^{\ast }}\left(S_0\right)=0$ are guaranteed.

As a function of $\lambda$, ${\mathrm{Split}}_T\left(S_0\right)$ achieves its maximum whenever $T\mathcal{P}\left(\lambda \right)$ reaches its maximum. Now $T\mathcal{P}\left(\lambda \right)$ is just a polynomial of degree two in $\lambda$,

$$T\mathcal{P}\left(\lambda \right)=\alpha {\lambda }^2+\beta \lambda ,\alpha =-12T^2{\sigma }^4,\beta =4T^{\frac{3}{2}}{\sigma }^2\left(\sqrt{T}{\sigma }^2+6\sqrt{T}r-2\sigma d_1\right).$$

Hence it reaches its maximum at

$$\widehat{\lambda }=-\frac{4T^{\frac{3}{2}}{\sigma }^2\left(\sqrt{T}{\sigma }^2+6\sqrt{T}r-2\sigma d_1\right)}{2\left(-12T^2{\sigma }^4\right)}=\frac{2Tr-\ln \left(S_0/K\right)}{3T{\sigma }^2}.$$

(32)

Through the formula (30) and (31), the optimal drift $\widehat{\lambda }$ translates into an optimal choice $\widehat{\ell }$ of ℓ given by

$$\widehat{\ell }=\left\{\begin{array}{cc}{\displaystyle \frac{T{\sigma }^2\widehat{\lambda }-\ln (K{e}^{\sigma \sqrt{T/n}}/S_0)}{2\sigma \sqrt{T/n}}}\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}\\ {\displaystyle \frac{T{\sigma }^2\widehat{\lambda }-\ln \left(K/S_0\right)}{2\sigma \sqrt{T/n}}}\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd},\end{array}\right.$$

or equivalently

$$\widehat{\ell }={\displaystyle \frac{T{\sigma }^2\widehat{\lambda }-\ln (K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)/S_0)}{2\sigma \sqrt{T/n}}}.$$

We can also write $\widehat{\ell }$ as

$$\widehat{\ell }={\displaystyle \frac{D}{2\sigma \sqrt{T/n}}}-\frac{1}{2}\left(\left(n+1\right)\mathrm{mod}2\right),$$

(33)

where

$$D=T{\sigma }^2\widehat{\lambda }-\ln (K/S_0).$$

However, $\widehat{\ell }$ may not be integer, so we round it to the nearest integer ${\ell }^{\ast }$. This is essential to preserve the structure of a split tree. Let us write ${\overline{\kappa }}_n:=\widehat{\ell }-{\ell }^{\ast }$. Obviously $-0.5\le {\overline{\kappa }}_n<0.5$. It is easy to verify that

$$\widehat{K}=K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)\exp \left(D-{\overline{\kappa }}_{n}2\sigma \sqrt{T/n}\right).$$

Hence

$$\underset{n\to \infty }{\lim }\widehat{K}=K{e}^D.$$

In this manner we can define the maximal range optimal split tree in a similar manner as we defined the optimal centered split tree.

Definition 5

(Maximal range optimal split tree). Consider a European call option with strike K, spot price $S_0$, maturity T, risk free rate r, and volatility σ. Let $n\ge 2$, let $\widehat{\ell }$ be as in (33), let ${\ell }^{\ast }$ be the nearest integer to $\widehat{\ell }$, and set $\ell ={\ell }^{\ast }$ for every n. Let ${\tau }^{\ast }$ be as in Theorem 2. The maximal range optimal split tree is defined to be the split tree with parameters ${\ell }^{\ast }$ and ${\tau }^{\ast }$.

4.4. The Optimal Split Tree Near $\tau$

Suppose that a constant $0<\tau <T$ is given. Recall $\Delta$ defined in (20), and note that ${\mathrm{Split}}_{\tau }\left(S_0\right)$ can be written as

$${\mathrm{Split}}_{\tau }\left(S_0\right)=\frac{S_0{e}^{-\frac{1}{2}{d}_1^2}}{24{\sigma }^{3}T\sqrt{2\pi T}}{\mathcal{P}}_{\tau }\left(\lambda \right),$$

where

$$\begin{array}{cc}\hfill {\mathcal{P}}_{\tau }\left(\lambda \right)& =a_{\tau }{\lambda }^2+b_{\tau }\lambda +c,\hfill \\ \hfill a_{\tau }& =-12T^2{\sigma }^6\tau ,b_{\tau }=4T^{\frac{3}{2}}{\sigma }^4\tau \left(\sqrt{T}{\sigma }^2+6\sqrt{T}r-2\sigma d_1\right),c=\left(4T^2{\sigma }^4+\Delta \right).\hfill \end{array}$$

Here our goal is to choose $\widehat{\tau }$ as close as possible to $\tau$ in such a way that ${\mathrm{Split}}_{\widehat{\tau }}\left(S_0\right)=0$, or if this cannot be achieved, we want to choose $\widehat{\tau }$ in a way that minimizes $|{\mathrm{Split}}_{\widehat{\tau }}\left(S_0\right)|$.

Let ${\mathcal{D}}_{\tau }:=b_{\tau }^2-4a_{\tau }c$. Then ${\mathcal{D}}_{\tau }=\alpha {\tau }^2+\beta \tau$, where

$$\begin{array}{cc}\hfill \alpha & =16T^3{\sigma }^8{\left(\sqrt{T}{\sigma }^2+6\sqrt{T}r-2\sigma d_1\right)}^2,\beta =48T^2{\sigma }^6\left(4T^2{\sigma }^4+\Delta \right).\hfill \end{array}$$

We need to consider three cases. Case (1) ${\mathcal{D}}_{\tau }\ge 0$. Then it is possible to choose a real value $\widehat{\lambda }$ of $\lambda$ such that ${\mathcal{P}}_{\tau }\left(\widehat{\lambda }\right)=0$. There are two choices for $\widehat{\lambda }$ which are given by

$$\widehat{\lambda }=\frac{-b_{\tau }\pm \sqrt{b_{\tau }^2-4a_{\tau }c}}{2a_{\tau }}.$$

Case (2) ${\mathcal{D}}_{\tau }<0$ and $\alpha >0$. This implies that $\beta <0$. Now if we replace $\tau$ by $0<\widehat{\tau }=-\beta /\alpha$ then ${\mathcal{D}}_{\widehat{\tau }}=0$. Note that

$$-\frac{\beta }{\alpha }=-\frac{12T^2{\sigma }^4+3\Delta }{4{\sigma }^2{\left(2Tr-\ln \left(S_0/K\right)\right)}^2}.$$

(34)

Note also that the roots of $x⟼{\mathcal{D}}_x$ are 0 and $\widehat{\tau }$. Since $\alpha >0$, this means that ${\mathcal{D}}_x<0$ if and only if $0<x<\widehat{\tau }$. Thus $0<\tau <\widehat{\tau }$. Now there are two possibilities: either $\tau <\widehat{\tau }<T$ or $\tau <T\le \widehat{\tau }$. In the first case the value of $\lambda$ that we want is given by

$$\widehat{\lambda }=-\frac{b_{\widehat{\tau }}}{2a_{\widehat{\tau }}}=\frac{2Tr-\ln \left(S_0/K\right)}{3T{\sigma }^2},$$

since it gives ${\mathcal{P}}_{\widehat{\tau }}\left(\widehat{\lambda }\right)=0$. In the second case, We understand that ${\mathcal{P}}_T\left(\lambda \right)<0$ for every value of $\lambda$. Hence we want to maximize ${\mathcal{P}}_T\left(\lambda \right)$. This means choosing

$$\widehat{\lambda }=-\frac{b_T}{2a_T}=\frac{2Tr-\ln \left(S_0/K\right)}{3T{\sigma }^2}.$$

Case (3) ${\mathcal{D}}_{\tau }<0$ and $\alpha =0$. This implies that $\beta <0$. In this case, ${\mathcal{D}}_x<0$ for every x, and thus ${\mathcal{P}}_{\widehat{\tau }}\left(\widehat{\lambda }\right)<0$ for every value of $\widehat{\tau }$ and $\widehat{\lambda }$. However, we know from Lemma 1 that regardless of the value of the parameter ℓ, if ${\mathrm{Split}}_{\tau }\left(S_0\right)<0$ for every $\tau$ then ${\mathrm{Split}}_{\tau }\left(S_0\right)$ is maximized when $\tau =T$. Hence we select $\widehat{\tau }=T$, and we want to maximize ${\mathcal{P}}_T\left(\widehat{\lambda }\right)$. The maximum occurs at

$$\widehat{\lambda }=-\frac{b_T}{2a_T}=\frac{2Tr-\ln \left(S_0/K\right)}{3T{\sigma }^2}.$$

The three cases can be summed up in the following definitions:

$$\widehat{\tau }=\left\{\begin{array}{cc}\tau \hfill & \mathrm{if}\mathcal{D}\ge 0\hfill \\ (-\beta /\alpha )\wedge T\hfill & \mathrm{if}\mathcal{D}<0\mathrm{and}\alpha >0\hfill \\ T\hfill & \mathrm{if}\mathcal{D}<0\mathrm{and}\alpha =0.\hfill \end{array}\right.$$

(35)

and

$$\widehat{\lambda }=\left\{\begin{array}{cc}\frac{-b_{\widehat{\tau }}\pm \sqrt{b_{\widehat{\tau }}^2-4a_{\widehat{\tau }}c}}{2a_{\widehat{\tau }}}\hfill & \mathrm{if}\widehat{\tau }=\tau \hfill \\ -\frac{b_{\widehat{\tau }}}{2a_{\widehat{\tau }}}=\frac{2Tr-\ln \left(S_0/K\right)}{3T{\sigma }^2}\hfill & \mathrm{if}\widehat{\tau }\ne \tau .\hfill \end{array}\right.$$

(36)

Using the (30) and (31), with ${\ell }^{\ast },{\tau }^{\ast },{\lambda }^{\ast }$ replaced by their approximations $\widehat{\ell },\widehat{\tau },\widehat{\lambda }$ we obtain

$$\widehat{\ell }={\displaystyle \frac{\widehat{\tau }{\sigma }^2\widehat{\lambda }-\ln (K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)/S_0)}{2\sigma \sqrt{T/n}}},$$

which can be re-written as

$$\widehat{\ell }={\displaystyle \frac{D}{2\sigma \sqrt{T/n}}}-\frac{1}{2}\left(\left(n+1\right)\mathrm{mod}2\right),$$

(37)

where

$$D=\widehat{\tau }{\sigma }^2\widehat{\lambda }-\ln (K/S_0).$$

(38)

In order to preserve the structure of a split tree, $\widehat{\ell }$ is rounded to the nearest integer ${\ell }^{\ast }$. From ${\ell }^{\ast }$, we obtain $\widehat{K}$ as

$$\widehat{K}=K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)e^{2{\ell }^{\ast }\sigma \sqrt{T/n}}.$$

We define ${\overline{\kappa }}_n:=\widehat{\ell }-{\ell }^{\ast }$. Obviously $-0.5\le {\overline{\kappa }}_n<0.5$. Then

$$\widehat{K}=K\exp \left(\left(\left(n+1\right)\mathrm{mod}2\right)\sigma \sqrt{T/n}\right)\exp \left(D-{\overline{\kappa }}_{n}2\sigma \sqrt{T/n}\right),$$

and

$$\underset{n\to \infty }{\lim }\widehat{K}=K{e}^D.$$

The rounded value of $\widehat{\tau }$ appears to be a good estimate of ${\tau }^{\ast }$, but nothing guarantees that it is accurate. We need to apply Theorem 2 in order to find ${\tau }^{\ast }$ from ${\ell }^{\ast }$. However, there can be two values of ${\ell }^{\ast }$ (corresponding to the possible two different values for $\widehat{\ell }$). It turns out that we can carefully choose $\widehat{\ell }$ in order to further smooth out the convergence. Note that the choice of $\widehat{\ell }$ exists only when ${\tau }^{\ast }<T$. In this case, Theorem 2 says that

$${\tau }^{\ast }=\frac{b_n}{a_n}=\frac{12T^2{\sigma }^2{\ln }^2\left(K\exp \left(\widehat{D}\right)/S_0\right)}{\left(\Delta +4T^2{\sigma }^4\right)+\ln \left(K\exp \left(\widehat{D}\right)/S_0\right)\left(T\left({\sigma }^2+6r\right)-2\sigma \sqrt{T}{d}_1\right)4T{\sigma }^2},$$

where

$$\widehat{D}:=D-{\overline{\kappa }}_{n}2\sigma \sqrt{T/n}.$$

Because $\widehat{D}$ has oscillations of order $\sqrt{1/n}$, so does ${\tau }^{\ast }$. The best choice of D is the one for which these oscillations are minimized. Hence we determine the value of D (and therefore the values of $\widehat{\lambda }$, $\widehat{\ell }$, ${\ell }^{\ast }$, and ${\tau }^{\ast }$) by choosing the value of D for which the magnitude of $\partial {\tau }^{\ast }/\partial D$ is minimized. Now

$$\left|\frac{\partial }{\partial D}{\tau }^{\ast }\right|=\left|\frac{\partial }{\partial D}\frac{12T^2{\sigma }^2{\ln }^2\left(K\exp \left(D\right)/S_0\right)}{\left(\Delta +4T^2{\sigma }^4\right)+\ln \left(K\exp \left(D\right)/S_0\right)\left(T\left({\sigma }^2+6r\right)-2\sigma \sqrt{T}{d}_1\right)4T{\sigma }^2}\right|.$$

By simplifying, we obtain

$$\left|\frac{\partial }{\partial D}{\tau }^{\ast }\right|=\left|\frac{12T^2{\sigma }^2\left(D+\ln \left(K/S_0\right)\right)\left(\left(\Delta +4T^2{\sigma }^4\right)+\theta \right)}{{\theta }^2}\right|,$$

(39)

where

$$\theta :=\left(\Delta +4T^2{\sigma }^4\right)+\left(D+\ln \left(K/S_0\right)\right)\left(T\left({\sigma }^2+6r\right)-2\sigma \sqrt{T}{d}_1\right)4T{\sigma }^2.$$

(Note that the case where $\theta =0$ is irrelevant since it corresponds to a situation in Theorem 2 where ${\tau }^{\ast }=T$. In this case we can arbitrarily choose the largest value of D.) The following sums up the definition of the optimal split tree near $\tau$.

Definition 6

(Optimal split tree near $\tau$). Consider a European call option with strike K, spot price $S_0$, maturity T, risk free rate r, and volatility σ. Let $n\ge 2$, Let $\widehat{\ell }$ be as in (37). In the case where (37) gives two definitions of $\widehat{\ell }$, choose the one corresponding to the smallest value of (39). Should $\theta =0$ in (39), choose the largest value of D. Next, let ${\ell }^{\ast }$ be the nearest integer to $\widehat{\ell }$, and set $\ell ={\ell }^{\ast }$ for every n. Finally, let ${\tau }^{\ast }$ be as in Theorem 2. The optimal split tree near τ is defined to be the split tree with parameters ${\ell }^{\ast }$ and ${\tau }^{\ast }$.

5. American Put

5.1. Measuring the Magnitude of the Oscillations of the Error

The split tree was invented by Joshi with the aim Joshi (2009b) of minimizing the oscillations in the convergence of the American put. If $P^n$ is the price of a put option in a tree method and $P^{BS}$ is the price in the Black–Scholes model, then we say that the convergence is smooth if

$$P^n=P^{BS}+\frac{\mathcal{A}}{n}+\mathcal{O}\left(n^{-1.5}\right),$$

(40)

for some constant $\mathcal{A}$. It has been observed—although not proven yet—that models with smooth convergence in the European case also display smooth convergence in the American case. When the convergence is smooth we can use Richardson extrapolation to obtain a value ${\tilde{P}}^n$ satisfying

$${\tilde{P}}^n=P^{BS}+\frac{{\mathcal{B}}_n}{n^{1.5}},$$

(41)

where ${\mathcal{B}}_n$ is bounded. Define

$$\mathcal{B}:=\underset{k\to \infty }{\lim }\underset{n>k}{sup}\left(n^{1.5}\left|{\tilde{P}}^n-P^{BS}\right|\right).$$

The optimal model among a collection of models to be compared is the one for which the quantity $\mathcal{B}$ is minimized. This is analogous to Korn and Muller’s optimal drift Korn and Müller (2013) which minimizes $\left|\mathcal{A}\right|$ in (40), where $\mathcal{A}$ can be written as

$$\mathcal{A}=\underset{n\to \infty }{\lim }\underset{m>n}{sup}\left(m\left|P^m-P^{BS}\right|\right),$$

and the optimal drift model is the model which minimizes the value of $\left|\mathcal{A}\right|$ among all those flexible models with smooth convergence. Here $P^{BS}$ is estimated using $P^{BS}={\tilde{P}}^{250,000}$, with ${\tilde{P}}^{250,000}$ calculated with Joshi’s original split tree. We estimate $\mathcal{B}$ using

$$\mathcal{B}\approx \underset{10,000\le 20n\le 15,000}{sup}\left({\left(20n\right)}^{1.5}\left|{\tilde{P}}^{20n}-P^{BS}\right|\right).$$

(42)

We will compare the value of $\mathcal{B}$ calculated using Joshi’s original split tree to the the value of $\mathcal{B}$ calculated with our optimal split trees.

The following lemma provides a connection between the magnitude of the oscillations, $\mathcal{B}$, and the computational effort required to estimate the price of an option. We define the computational effort needed to calculate the price of a put option in a binomial tree model with n time-steps to be equal to the number of nodes in the tree, which is $n(n+1)/2$.

Lemma 2.

For $i=1,2$, let ${\mathcal{B}}_i>0$ be the value of $\mathcal{B}$ in model 1 and model 2, respectively. Assume that ${\mathcal{B}}_1>{\mathcal{B}}_2$. Suppose also that, given $\epsilon >0$, the number of time-steps n in model i is chosen in such a way that in the worst case scenario the error is less than ε, that is, in such a way that ${\mathcal{B}}_i/n^{1.5}<\epsilon$. Then, asymptotically as $\epsilon \to 0$, the quotient of the computational effort required with model 1 over the computational effort required in model 2 is ${\left({\mathcal{B}}_1/{\mathcal{B}}_2\right)}^{4/3}$. That is, model 2 is ${\left({\mathcal{B}}_1/{\mathcal{B}}_2\right)}^{4/3}$ times as fast as model 1, or said in other words, model 2 is ${\left({\mathcal{B}}_1/{\mathcal{B}}_2\right)}^{4/3}-1$ faster than model 1.

5.2. Numerical Results

We now illustrate numerically our findings for American put options. We consider the optimal centered split tree, the maximal range optimal split tree, and the optimal split tree near $\tau =0.5T$. Calculations were perform using the classical Richardson extrapolation; that is, we calculated ${\tilde{P}}^n$ using

$${\tilde{P}}^n=\frac{n{P}^n-\left(n/2\right)P^{n/2}}{n-n/2}=2P^n-P^{n/2},$$

for n even. With $K=100$, $r=0.1$, $\sigma =0.25$, $T=1$, we calculated the values of $\mathcal{B}$, estimated by (42), for all integer values of $S_0$ such that $0.5\le P^{BS}$, that is, for $S_0=86,87,\dots ,140$, where $P^{BS}$ is the price of the option in the Black–Scholes model estimated using Joshi’s original split tree with classical Richardson extrapolation and $n=\mathrm{250,000}$ time steps. The results are shown in Figure 2 and Figure 3.

In Figure 2, we see that the value of $\mathcal{B}$ for the maximal range optimal split tree spikes at 450 when $S_0=122$. The value of $\mathcal{B}$ in Joshi’s original split tree, traced in a bold font, reaches a maximum of $53.6$ when $S_0=97$. Next, the value of $\mathcal{B}$ peeks at $38.2$ when $S_0=101$, for the optimal centered split tree. At the very bottom, the curve $S_0⟼\mathcal{B}\left(S_0\right)$ for the optimal split tree near $\tau$ is hard to spot. That makes it the best amongst all the models.

In Figure 3, we zoom in and display only the curves $S_0⟼\mathcal{B}\left(S_0\right)$ for Joshi’s original split tree (in bold) and the optimal split tree near $\tau$. We note that, except in a very small interval around the strike, the values of $\mathcal{B}$ for Joshi’s original split tree are larger than those in the optimal split tree near $\tau$. On average the value of $\mathcal{B}$ in Joshi’s original split tree is $3.3$ times the value of $\mathcal{B}$ in the optimal split tree near $\tau$. Given $S_0$, Lemma 2 can be used to translate the quotient of the values of $\mathcal{B}\left(S_0\right)$ in the two models into a measure of the relative computational effort required by both models. In this measure we obtain that, on average, over the values of $S_0=86,87,\dots ,140$, the computational effort used for Joshi’s original split tree is $5.4$ times as much as the computational effort used for the optimal split tree near $\tau$. Said another way, the optimal split tree near $\tau$ is on average $440\%$ faster than Joshi’s original tree.

More strikingly, unlike Joshi’s original tree, the optimal split tree near $\tau$ does not exhibit a huge spike in the value of $\mathcal{B}\left(S_0\right)$ for some unfavorable spot prices $S_0$. If we define

$$∥\mathcal{B}∥:=\max \left\{\mathcal{B}\left(S_0\right):S_0=86,87,\dots ,140\right\}$$

then the value of $∥\mathcal{B}∥$ in Joshi’s original split tree is $53.6$, and it is $3.59$ in the optimal split tree near $\tau$. This gives a quotient of $14.9$. Hence if for every $\epsilon$, n is chosen in such a way that $∥\mathcal{B}∥/n^{1.5}<\epsilon$, in order to guarantee that, uniformly in $S_0$, n is large enough to insure an error smaller than $\epsilon$, then Lemma 2 says that the optimal split tree near $\tau$ results in calculations which are ${\left(14.9\right)}^{4/3}-1=35.7$ times faster than in Joshi’s original split tree.

6. Conclusions

In this paper we introduced a flexible version of Joshi’s original split tree and we developed the corresponding convergence theory in the European case. Our flexible split trees are characterized by two additional parameters: the drift and the split time. This allowed us to define optimal values of these parameters under different constraints. For European options, we found an explicit formula for the coefficients of $1/n$ and $1/n^{3/2}$ in the expansion of the error, and we found closed form formulae for the parameters of our optimal split trees. Numerical results suggest that the optimal split tree near $\tau$ can significantly improve the convergence of Joshi’s original split tree.

Because stock options prices are quoted in the Black–Scholes model, binomial tree methods apply naturally to them, as a numerical method to price them when a closed form formula is not available. However, for real options requiring the modeling for several uncertainty sources, the Monte Carlo approach introduced in Longstaff and Schwartz (2001) can be the best choice (see, for instance, Lomoro et al. (2020), Pellegrino et al. (2019), or Sun et al. (2019)). The finite difference method (see, for instance, Wilmott (1998)) is another broadly used numerical tool to price options. An empirical study in the style of Joshi (2009b) that could compare, analyze, quantify, and contextualize the respective advantages of the Monte Carlo approach, the finite difference method, and the tree method, would be an broad and interesting project.