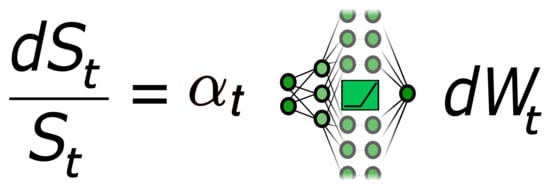
A Generative Adversarial Network Approach to Calibration of Local Stochastic Volatility Models
Abstract
1. Introduction
1.1. Local Stochastic Volatility Models as Neural SDEs
1.2. Generative Adversarial Approaches in Finance
- we have access to the unreasonable effectiveness of modeling by neural networks, due to their good generalization and regularization properties;
- the game theoretic view disentangles realistic price generation from discriminating with different loss functions, parameterized by . This reflects the fact that it is not necessarily clear which loss function one should use. Notice that (6) is not the usual form of generative adversarial network (GAN) problems, since the adversary distance is nonlinear in and , but we believe that it is worth taking this abstract point of view.
2. Variance Reduction for Pricing and Calibration Via Hedging and Deep Hedging
2.1. Black–Scholes Delta Hedge
2.2. Hedging Strategies as Neural Networks—Deep Hedging
- 1.
- Then the derivative in direction δ at satisfies
- 2.
- If additionally the derivative in direction δ at of converges ucp to as , then the directional derivative of the discretized integral, i.e.or equivalently , converges, as the discretization mesh , to
3. Calibration of LSV Models
Minimizing the Calibration Functional
4. Numerical Implementation
4.1. Implementation of the Calibration Method
4.1.1. Ground Truth Assumption
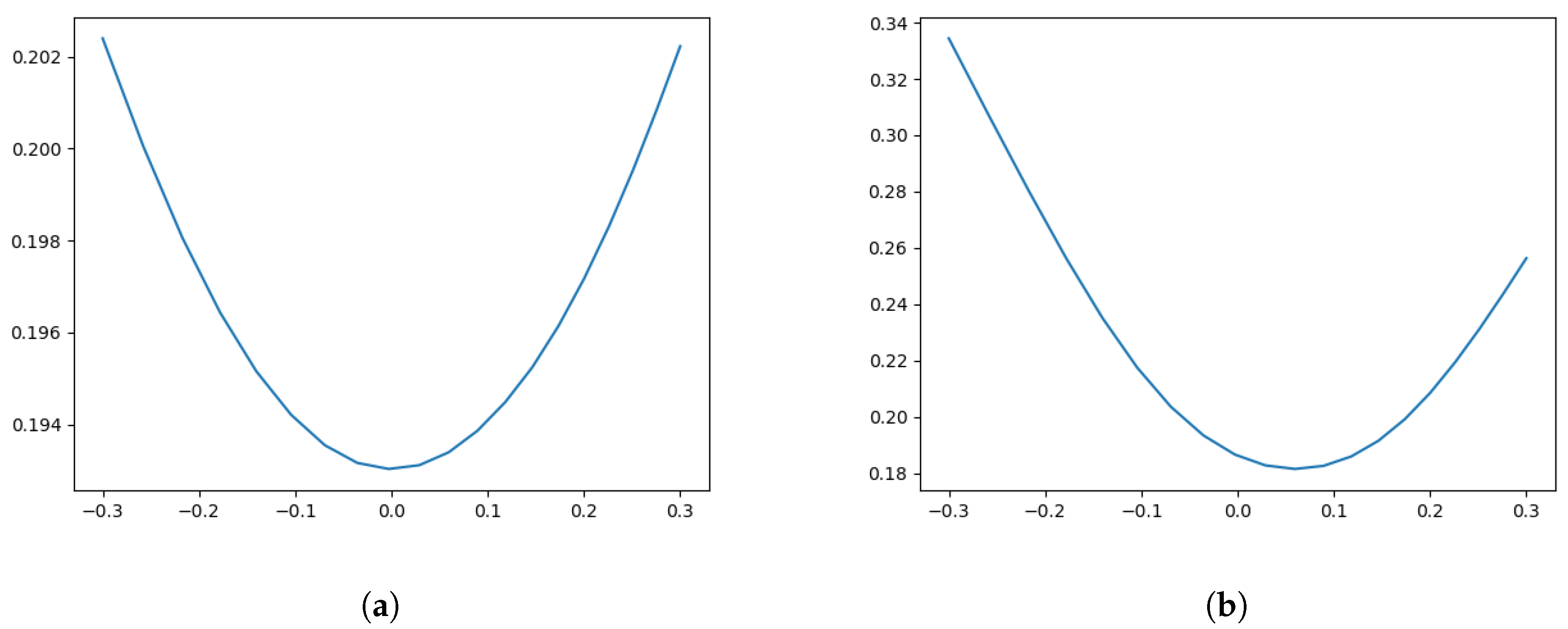
4.1.2. Performance Test
|
|
|
- For simulate parameters under the law described above.
- For each m, compute prices of European calls for maturities and strikes for and according to (27) using Brownian trajectories (for each m we use new trajectories).
- Store these prices.
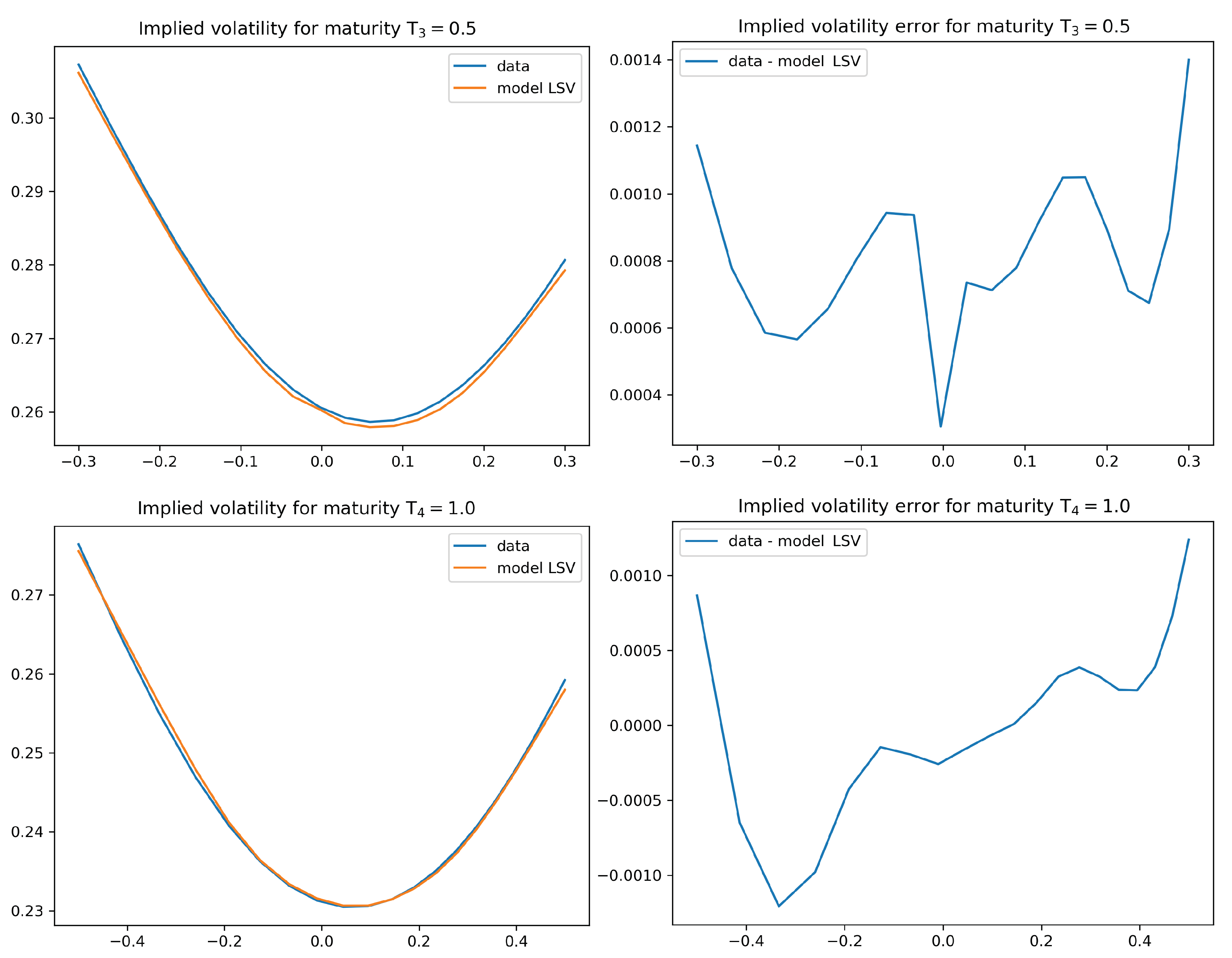
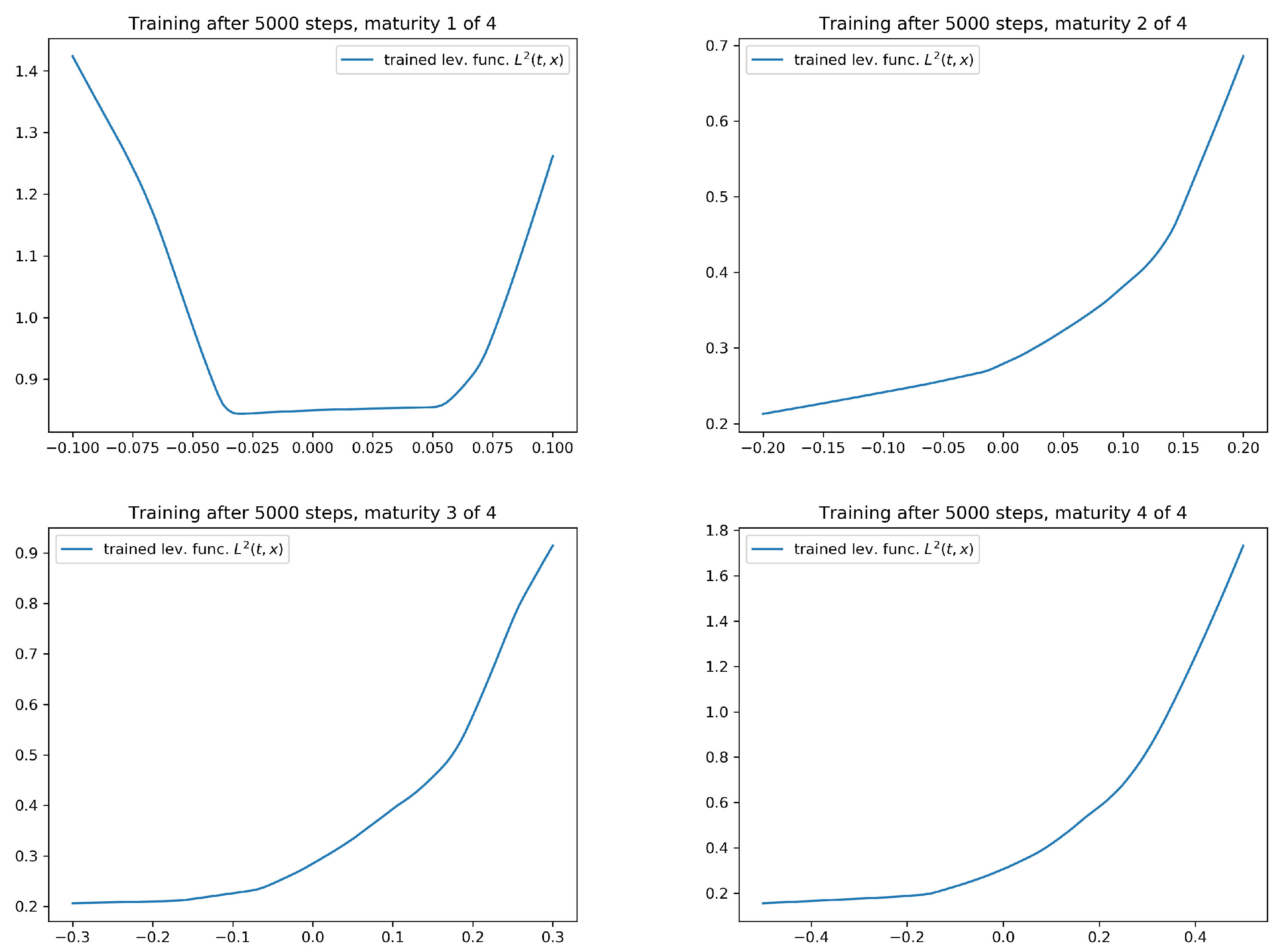
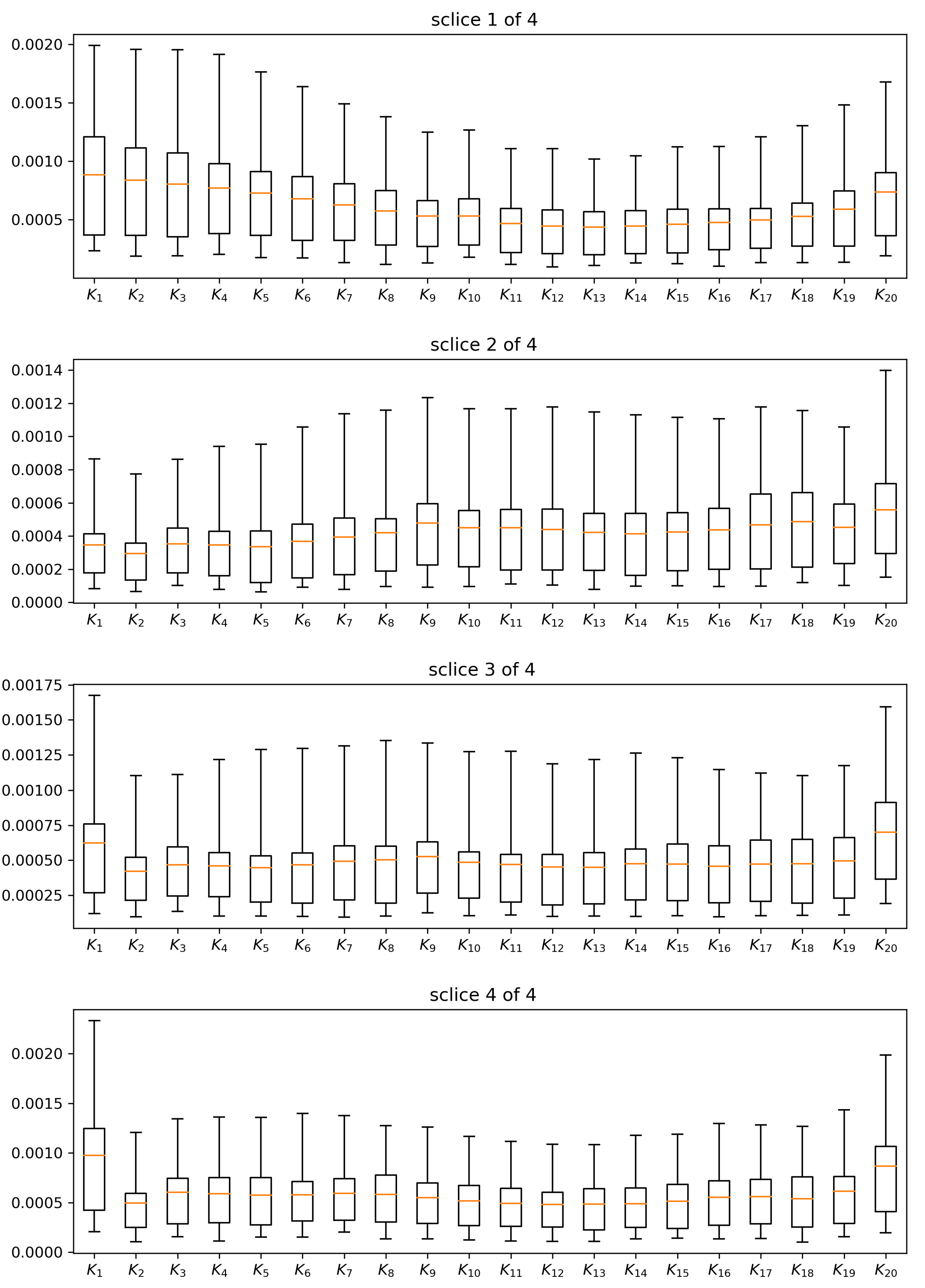
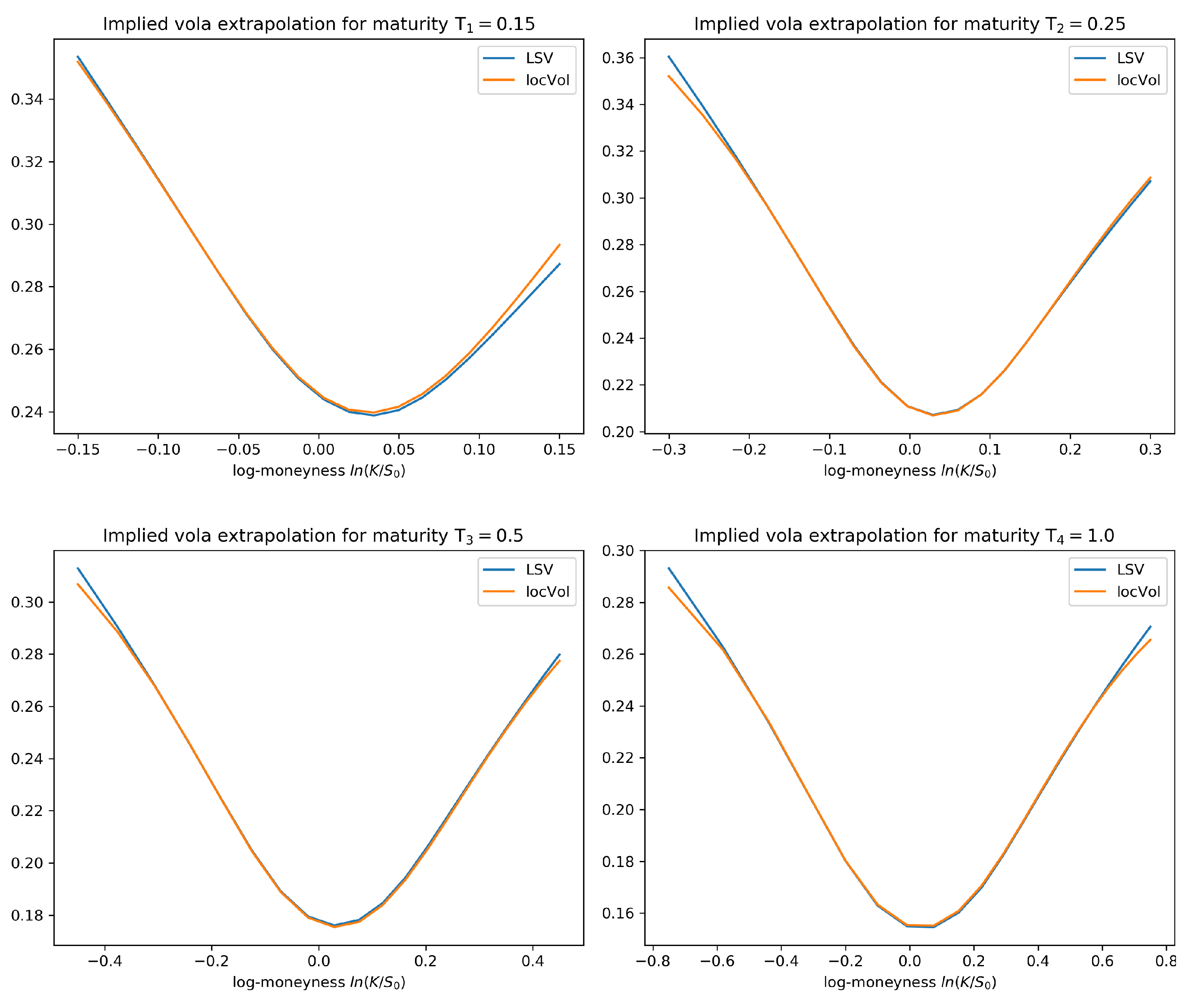
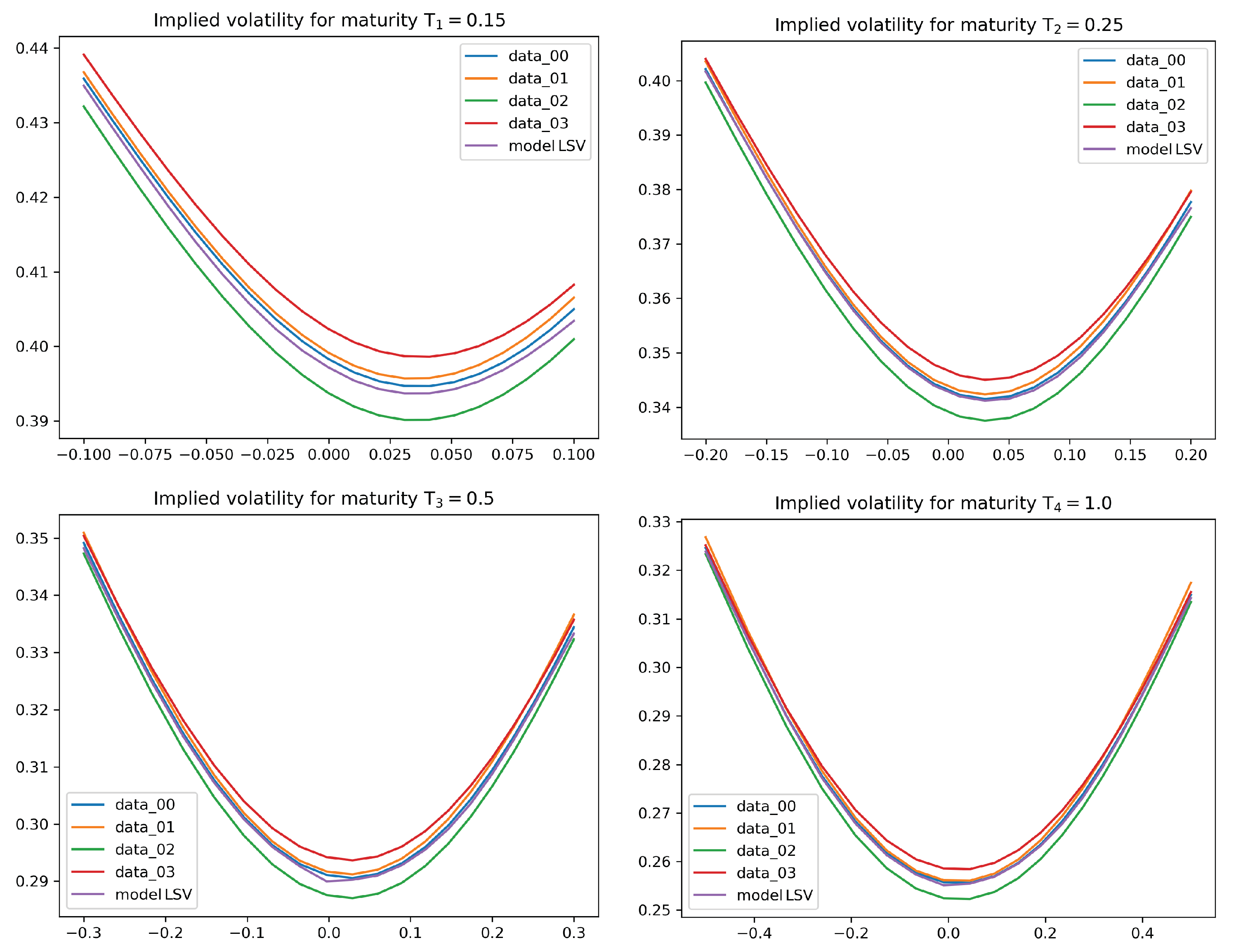
4.2. Numerical Results for the Calibration Test
4.3. Robust Calibration—An Instance of the Adversarial Approach
5. Conclusions
- The method we presented does not require any form of interpolation for the implied volatility surface since we do not calibrate via Dupire’s formula. As the interpolation is usually done ad hoc, this might be a desirable feature of our method.
- Similar to Guyon and Henry-Labordѐre (2012); Guyon and Henry-Labordѐre (2013), it is possible to “plug in” any stochastic variance process such as rough volatility processes as long as an efficient simulation of trajectories is possible.
- The multivariate extension is straight forward.
- The level of accuracy of the calibration result is of a very high degree. The average error in our statistical test is of around 5 to 10 basis points, which is an interesting feature in its own right. We also observe good extrapolation and generalization properties of the calibrated leverage function.
- The method can be significantly accelerated by applying distributed computation methods in the context of multi-GPU computational concepts.
- The presented algorithm is further able to deal with path-dependent options since all computations are done by means of Monte Carlo simulations.
- We can also consider the instantaneous variance process of the price process as short end of a forward variance process, which is assumed to follow (under appropriate assumptions) a neural SDE. This setting, as an infinite-dimensional version of the aforementioned “multivariate” setting, then qualifies for joint calibration to S&P and VIX options. This is investigated in a companion paper.
- We stress again the advantages of the generative adversarial network point of view. We believe that this is a crucial feature in the joint calibration of S&P and VIX options.
6. Plots
Author Contributions
Funding
Conflicts of Interest
Appendix A. Variations of Stochastic Differential Equations
- 1.
- the property implies for any stopping time τ,
- 2.
- there exists an increasing process such that for
Appendix B. Preliminaries on Deep Learning
Appendix B.1. Artificial Neural Networks
- 1.
- For any finite measure μ on and , the set is dense in .
- 2.
- If in addition , then is dense in for the topology of uniform convergence on compact sets.
Appendix B.2. Stochastic Gradient Descent
Appendix C. Alternative Approaches for Minimizing the Calibration Functional
Appendix C.1. Stochastic Compositional Gradient Descent
Appendix C.2. Estimators Compatible with Stochastic Gradient Descent
Appendix D. Algorithms
| Algorithm A1: In the subsequent pseudo code, the index i stands for the maturities, N for the number of samples used in the variance reduced Monte Carlo estimator as of (21) and k for the updating step in the gradient descent: |
| 1 # Initialize the network parameters 2 initialize θ1,…θ4 3 # Define initial number of trajectories and initial step 4 N, k = 400, 1 5 # The time discretization for the MC simulations and the 6 # abort criterion 7 Δt, tol = 0.01, 0.0045 8 9 for i = 1,...,4: 10 nextslice = False 11 # Compute the initial normalized vega weights for this slice: 12 wj = ῶj/ῶl with ῶj = 1/vij, where vij is the Black-Scholes 13 vega for strike Kij, the corresponding synthetic market implied 14 volatility and the maturity Ti. 15 16 while nextslice == False: 17 do: 18 Simulate N trajectories of the SABR-LSV process up 19 to time Ti, compute the payoffs. 20 do: 21 Compute the stochastic integral of the Black-Scholes 22 Delta hedge against these trajectories as of (9) 23 for maturity Ti 24 do: 25 Compute the calibration functional as of (21) 26 with ℓ(x) = x2 and weights wj with the modification that we use put 27 options instead of call options for strikes larger than the spot. 28 do: 29 Make an optimization step from to , similarly 30 as in (22) but with the more sophisticated ADAM- 31 optimizer with learning rate 10−3. 32 do: 33 Update the parameter N, the condition nextslice and 34 compute model prices according to Algorithm A2. 35 do: 36 k = k + 1 |
| Algorithm A2: We update the parameters in Algorithm A1 according to the following rules: |
| 1 if k == 500: 2 N = 2000 3 else if k == 1500: 4 N = 10000 5 else if k == 4000: 6 N = 50000 7 8 if k >= 5000 and k mod 1000 == 0: 9 do: 10 Compute model prices πmodel for slice i via MC simulation 11 using 107 trajectories. Apply the Black-Scholes Delta 12 hedge for variance reduction. 13 do: 14 Compute implied volatilities ivmodel from the model prices πmodel. 15 do: 16 Compute the maximum error of model implied volatilities 17 against synthetic market implied volatilities: 18 err_cali = ‖iv_model - iv_market‖max 19 if err_cali ≤ tol or k == 12000: 20 nextslice = True 21 else: 22 Apply the adversarial part: Adjust the weights wj 23 according to: 24 25 for j = 1,…,20: 26 wj = wj + ∣iv_modelj - iv_marketj∣ 27 This puts higher weights on the options where the fit 28 can still be improved 29 Normalize the weights: 30 for j = 1,…,20: 31 wj = wj / wℓ |
References
- Abergel, Frédéric, and Rémi Tachet. 2010. A nonlinear partial integro-differential equation from mathematical finance. Discrete and Continuous Dynamical Systems-Series A 27: 907–17. [Google Scholar] [CrossRef]
- Acciaio, Beatrice, and Tianlin Xu. 2020. Learning Dynamic GANs via Causal Optimal Transport. Working paper. [Google Scholar]
- Bayer, Christian, Blanka Horvath, Aitor Muguruza, Benjamin Stemper, and Mehdi Tomas. 2019. On deep calibration of (rough) stochastic volatility models. arXiv arXiv:1908.08806. [Google Scholar]
- Becker, Sebastian, Patrick Cheridito, and Arnulf Jentzen. 2019. Deep optimal stopping. Journal of Machine Learning Research 20: 1–25. [Google Scholar]
- Bühler, Hans, Lukas Gonon, Josef Teichmann, and Ben Wood. 2019. Deep hedging. Quantitative Finance 19: 1271–91. [Google Scholar] [CrossRef]
- Bühler, Hans, Blanka Horvath, Immanol Perez Arribaz, Terry Lyons, and Ben Wood. 2020. A Data-Driven Market Simulator for Small Data Environments. Available online: https://ssrn.com/abstract=3632431 (accessed on 22 September 2020).
- Carmona, René, and Sergey Nadtochiy. 2009. Local volatility dynamic models. Finance and Stochastics 13: 1–48. [Google Scholar] [CrossRef]
- Carmona, Rene, Ivar Ekeland, Arturo Kohatsu-Higa, Jean-Michel Lasry, Pierre-Louis Lions, Huyen Pham, and Erik Taflin. 2007. HJM: A Unified Approach to Dynamic Models for Fixed Income, Credit and Equity Markets. Berlin/Heidelberg: Springer, vol. 1919, pp. 1–50. [Google Scholar] [CrossRef]
- Cont, Rama, and Sana Ben Hamida. 2004. Recovering volatility from option prices by evolutionary optimization. Journal of Computational Finance 8: 43–76. [Google Scholar] [CrossRef][Green Version]
- Cozma, Andrei, Matthieu Mariapragassam, and Christoph Reisinger. 2019. Calibration of a hybrid local-stochastic volatility stochastic rates model with a control variate particle method. SIAM Journal on Financial Mathematics 10: 181–213. [Google Scholar] [CrossRef]
- Cuchiero, Christa, Alexia Marr, Milusi Mavuso, Nicolas Mitoulis, Aditya Singh, and Josef Teichmann. 2018. Calibration of Mixture Interest Rate Models with Neural Networks. Technical report. [Google Scholar]
- Cuchiero, Christa, Philipp Schmocker, and Teichmann Josef. 2020. Deep Stochastic Portfolio Theory. Working paper. [Google Scholar]
- Cybenko, George. 1992. Approximation by superpositions of a sigmoidal function. Mathematics Control, Signal and Systems 2: 303–14. [Google Scholar] [CrossRef]
- Dupire, Bruno. 1994. Pricing with a smile. Risk 7: 18–20. [Google Scholar]
- Dupire, Bruno. 1996. A unified theory of volatility. In Derivatives Pricing: The Classic Collection. London: Risk Books, pp. 185–96. [Google Scholar]
- Eckstein, Stephan, and Michael Kupper. 2019. Computation of optimal transport and related hedging problems via penalization and neural networks. Applied Mathematics & Optimization, 1–29. [Google Scholar] [CrossRef]
- Gao, Xiaojie, Shikui Tu, and Lei Xu. 2019. A tree search for portfolio management. arXiv arXiv:1901.01855. [Google Scholar]
- Gatheral, Jim, Thibault Jaisson, and Mathieu Rosenbaum. 2018. Volatility is rough. Quantitative Finance 18: 933–49. [Google Scholar] [CrossRef]
- Gierjatowicz, Patryk, Mark Sabate, David Siska, and Lukasz Szpruch. 2020. Robust Pricing and Hedging via Neural SDEs. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3646241 (accessed on 22 September 2020).
- Goodfellow, Ian, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. 2014. Generative adversarial nets. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 2672–80. [Google Scholar]
- Guyon, Julien, and Pierre Henry-Labordère. 2012. Being particular about calibration. Risk 25: 92–97. [Google Scholar]
- Guyon, Julien, and Pierre Henry-Labordère. 2013. Nonlinear Option Pricing. Chapman & Hall/CRC Financial Mathematics Series. [Google Scholar]
- Guyon, Julien. 2014. Local correlation families. Risk. February, pp. 52–58. Available online: https://search.proquest.com/openview/c1bb3fbf83b00ad34eaeeee071f0be52/1?pq-origsite=gscholar&cbl=32048 (accessed on 20 September 2020).
- Guyon, Julien. 2016. Cross-dependent volatility. Risk 29: 61–65. [Google Scholar] [CrossRef][Green Version]
- Han, Jiequn, Arnulf Jentzen, and Weinan E. 2017. Overcoming the curse of dimensionality: Solving high-dimensional partial differential equations using deep learning. arXiv arXiv:1707.02568. [Google Scholar]
- Hecht-Nielsen, Robert. 1989. Theory of the backpropagation neural network. Paper presented at International 1989 Joint Conference on Neural Networks, Washington, DC, USA, vol. 1, pp. 593–605. [Google Scholar] [CrossRef]
- Heiss, Jakob, Josef Teichmann, and Hanna Wutte. 2019. How implicit regularization of neural networks affects the learned function–part i. arXiv arXiv:1911.02903. [Google Scholar]
- Henry-Labordère, Pierre. 2019. Generative Models for Financial Data. Preprint. Available online: https://ssrn.com/abstract=3408007 (accessed on 22 September 2020).
- Hernandez, Andres. 2017. Model calibration with neural networks. Risk. [Google Scholar] [CrossRef]
- Hornik, Kurt. 1991. Approximation capabilities of multilayer feedforward networks. Neural Networks 4: 251–57. [Google Scholar] [CrossRef]
- Huré, Côme, Huyên Pham, Achref Bachouch, and Nicolas Langrené. 2018. Deep neural networks algorithms for stochastic control problems on finite horizon, part i: Convergence analysis. arXiv arXiv:1812.04300. [Google Scholar]
- Huré, Côme, Huyên Pham, and Xavier Warin. 2019. Some machine learning schemes for high-dimensional nonlinear PDEs. arXiv arXiv:1902.01599. [Google Scholar]
- Jex, Mark, Robert Henderson, and David Wang. 1999. Pricing Exotics under the Smile. Risk Magazine 12: 72–75. [Google Scholar]
- Jourdain, Benjamin, and Alexandre Zhou. 2016. Existence of a calibrated regime switching local volatility model and new fake brownian motions. arXiv arXiv:1607.00077. [Google Scholar]
- Kondratyev, Alexei, and Christian Schwarz. 2019. The Market Generator. Available online: https://ssrn.com/abstract=3384948 (accessed on 22 September 2020).
- Lacker, Dan, Misha Shkolnikov, and Jiacheng Zhang. 2019. Inverting the Markovian projection, with an application to local stochastic volatility models. arXiv arXiv:1905.06213. [Google Scholar]
- Lipton, Alexander. 2002. The vol smile problem. Risk Magazine 15: 61–65. [Google Scholar]
- Liu, Shuaiqiang, Anastasia Borovykh, Lech Grzelak, and Cornelis Oosterlee. 2019a. A neural network-based framework for financial model calibration. Journal of Mathematics in Industry 9: 9. [Google Scholar] [CrossRef]
- Liu, Shuaiqiang, Cornelis Oosterlee, and Sander Bohte. 2019b. Pricing options and computing implied volatilities using neural networks. Risks 7: 16. [Google Scholar] [CrossRef]
- Potters, Marc, Jean-Philippe Bouchaud, and Dragan Sestovic. 2001. Hedged Monte-Carlo: Low Variance Derivative Pricing with Objective Probabilities. Physica A: Statistical Mechanics and Its Applications 289: 517–25. [Google Scholar] [CrossRef][Green Version]
- Protter, Philip. 1990. Stochastic Integration and Differential Equations. Volume 21 of Applications of Mathematics (New York). A New Approach. Berlin: Springer. [Google Scholar]
- Ren, Yong, Dilip Madan, and Michael Qian Qian. 2007. Calibrating and pricing with embedded local volatility models. London Risk Magazine Limited 20: 138. [Google Scholar]
- Robbins, Herbert, and Sutton Monro. 1951. A stochastic approximation method. The Annals of Mathematical Statistics 22: 400–407. [Google Scholar] [CrossRef]
- Ruf, Johannes, and Weiguan Wang. Forthcoming. Neural networks for option pricing and hedging: A literature review. Journal of Computational Finance. [CrossRef]
- Samo, Yves-Laurent Kom, and Alexander Vervuurt. 2016. Stochastic portfolio theory: A machine learning perspective. arXiv arXiv:1605.02654. [Google Scholar]
- Saporito, Yuri F, Xu Yang, and Jorge Zubelli. 2019. The calibration of stochastic-local volatility models-an inverse problem perspective. Computers & Mathematics with Applications 77: 3054–67. [Google Scholar]
- Sirignano, Justin, and Rama Cont. 2019. Universal features of price formation in financial markets: Perspectives from deep learning. Quantitative Finance 19: 1449–59. [Google Scholar] [CrossRef]
- Tian, Yu, Zili Zhu, Geoffrey Lee, Fima Klebaner, and Kais Hamza. 2015. Calibrating and pricing with a stochastic-local volatility model. Journal of Derivatives 22: 21. [Google Scholar] [CrossRef]
- Vidales, Marc-Sabate, David Siska, and Lukasz Szpruch. 2018. Unbiased deep solvers for parametric pdes. arXiv arXiv:1810.05094. [Google Scholar]
- Wang, Mengdi, Ethan X Fang, and Han Liu. 2017. Stochastic compositional gradient descent: Algorithms for minimizing compositions of expected-value functions. Mathematical Programming 161: 419–49. [Google Scholar] [CrossRef]
- Wiese, Magnus, Lianjun Bai, Ben Wood, and Hans Bühler. 2019. Deep Hedging: Learning to Simulate Equity Option Markets. Available online: https://ssrn.com/abstract=3470756 (accessed on 20 September 2020).
| 1. | We here use to denote the parameters of the hedging neural networks, as shall be used for the networks of the leverage function. |
| 2. | This just means that the activation function is bounded and , with bounded and Lipschitz continuous derivatives. |
| 3. | See http://vollib.org/. |
| 4. | Recall that is the leaky-ReLu activation function with parameter if . In particular, classical ReLu is is retrieved by setting . |
| 5. | We shall often omit the dependence on . |
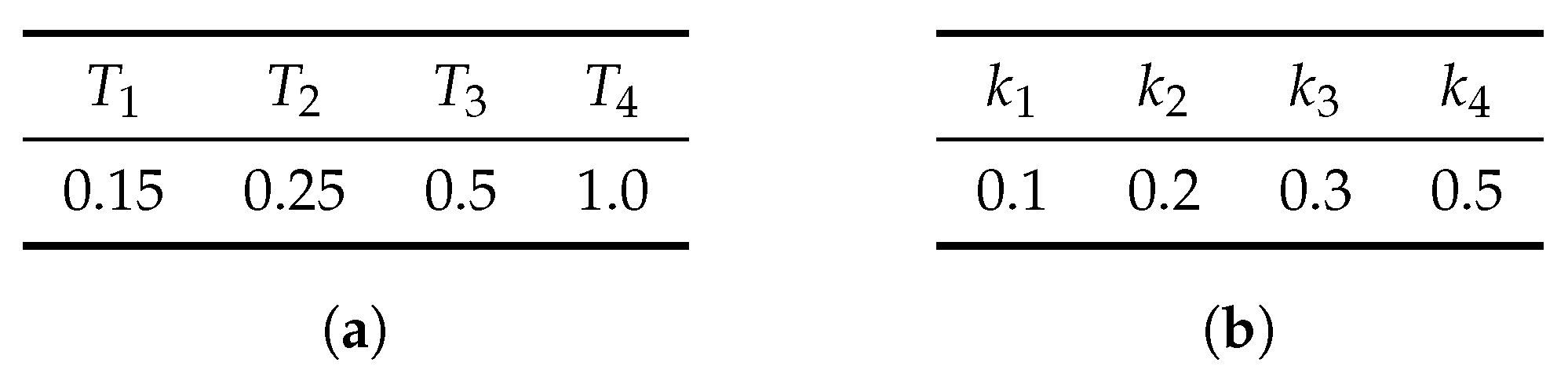

| 20 | 10 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuchiero, C.; Khosrawi, W.; Teichmann, J. A Generative Adversarial Network Approach to Calibration of Local Stochastic Volatility Models. Risks 2020, 8, 101. https://doi.org/10.3390/risks8040101
Cuchiero C, Khosrawi W, Teichmann J. A Generative Adversarial Network Approach to Calibration of Local Stochastic Volatility Models. Risks. 2020; 8(4):101. https://doi.org/10.3390/risks8040101
Chicago/Turabian StyleCuchiero, Christa, Wahid Khosrawi, and Josef Teichmann. 2020. "A Generative Adversarial Network Approach to Calibration of Local Stochastic Volatility Models" Risks 8, no. 4: 101. https://doi.org/10.3390/risks8040101
APA StyleCuchiero, C., Khosrawi, W., & Teichmann, J. (2020). A Generative Adversarial Network Approach to Calibration of Local Stochastic Volatility Models. Risks, 8(4), 101. https://doi.org/10.3390/risks8040101