Nagging Predictors
Abstract
1. Introduction
2. Feed-Forward Neural Network Regression Models
2.1. Generic Definition of Feed-Forward Neural Networks
2.2. Tweedie’s Compound Poisson Model
3. Aggregating Predictors
4. Networks and Aggregating
4.1. Empirical Generalization Losses
- (1)
- Parameter estimate is solely based on the learning data set and loss is purely evaluated on the observations of the test data set . Independence between the two data sets implies independence between parameter estimator and observations in . Thus, this provides a proper out-of-sample generalization analysis.
- (2)
- Expected generalization loss Equation (8) is based on the assumption that we can calculate the necessary moments of under its true distributional model. Since this is not possible, in practice, we replace moments by empirical moments on via Equation (12), however, the individual observations in are not necessarily i.i.d., they are only independent and have the same structure for the mean parameter , but they typically have different variances, see Equation (4).
- (3)
- Evaluation Equation (12) is based on one single estimator , only. Bootstrapping may provide an empirical mean also in parameter estimates .
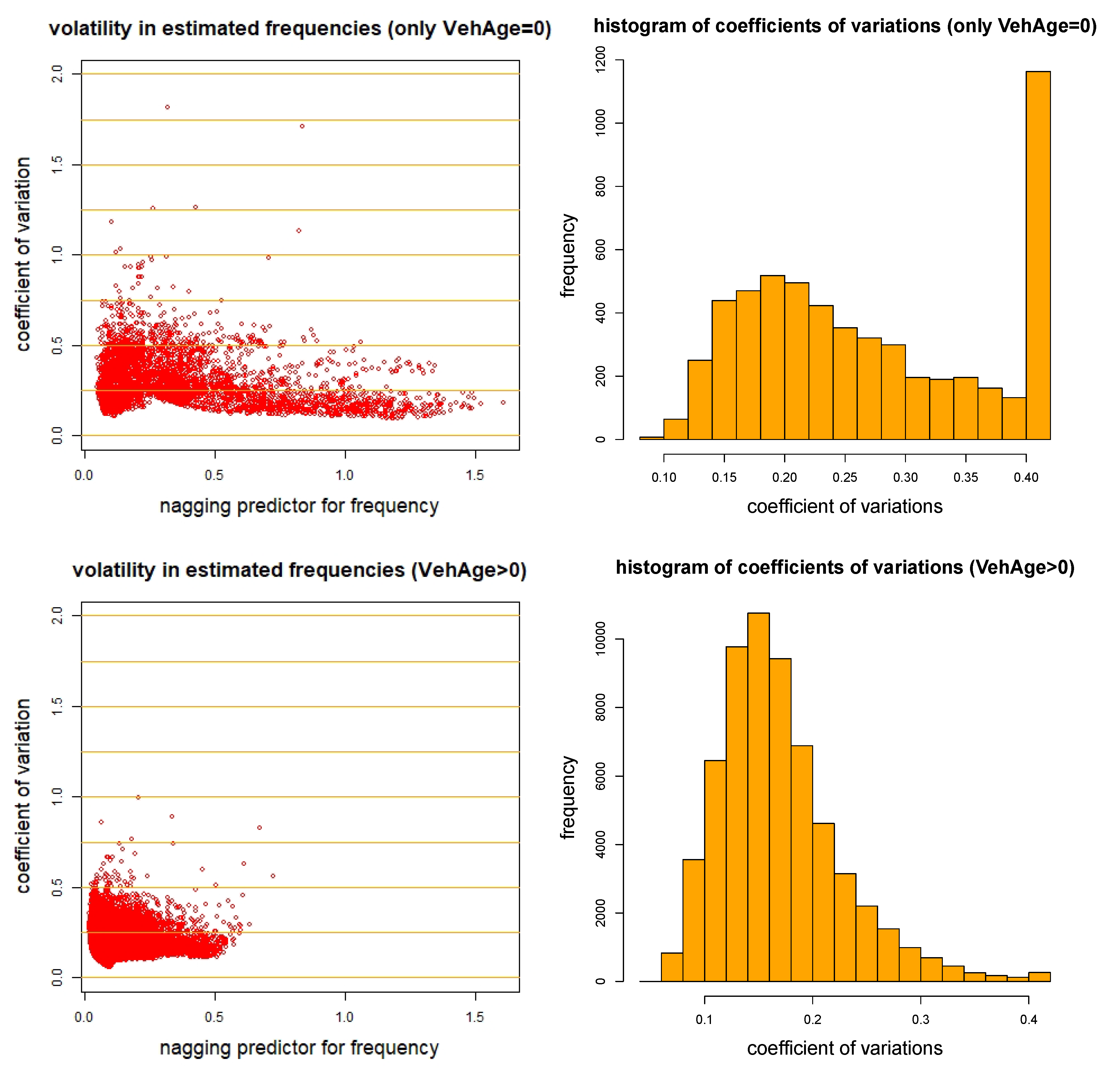
4.2. The Nagging Predictor
4.2.1. Definition of Nagging Predictors
4.2.2. Interpretation and Comparison to Bagging Predictors
Dependence on Observations
Differences between Bagging and Nagging
Unbiasedness
5. Example: French Motor Third-Party Liability Insurance
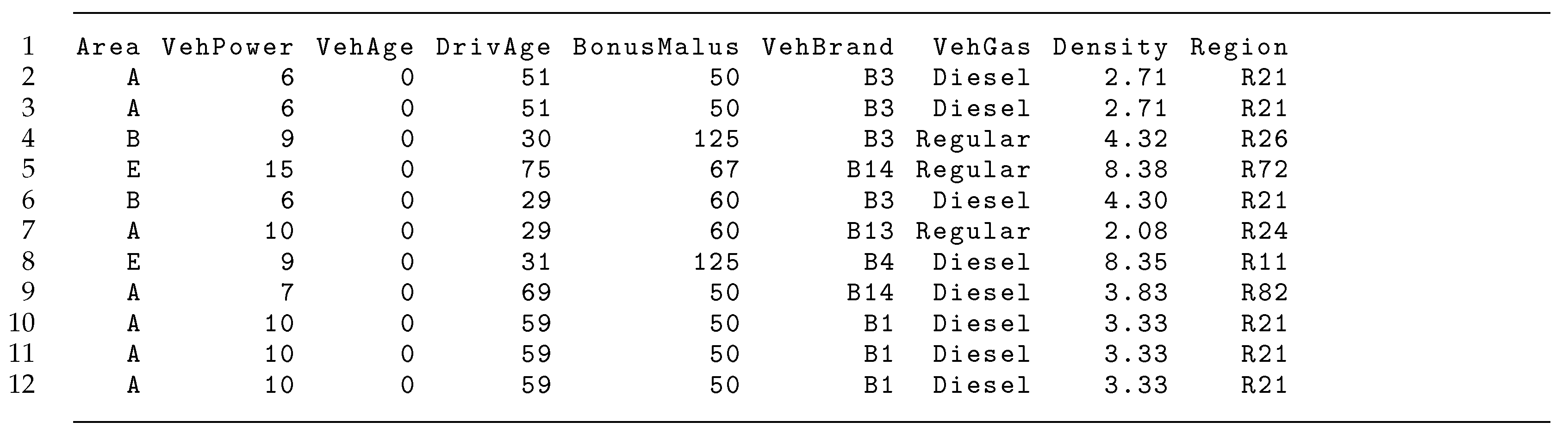
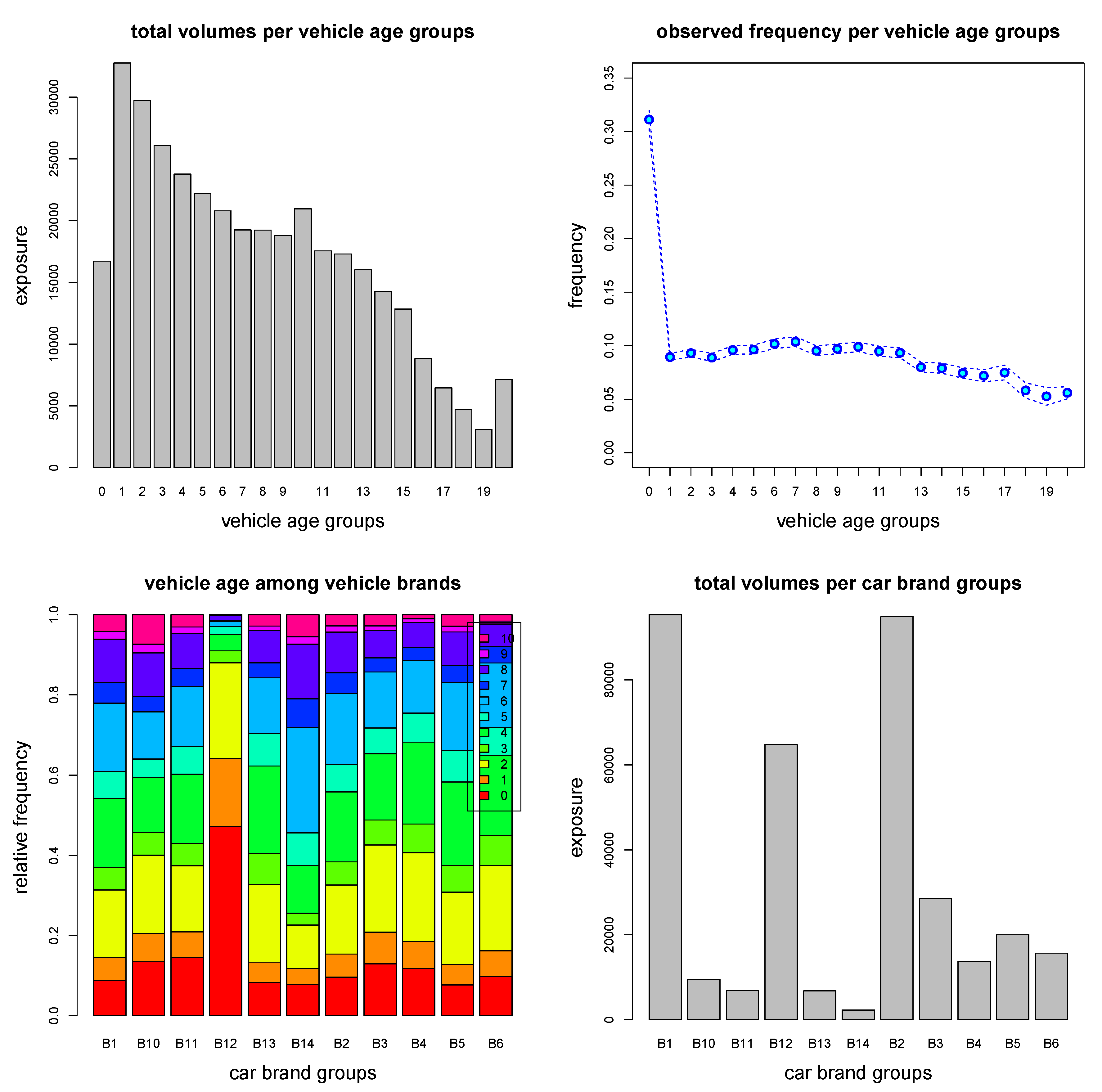
5.1. Data

5.2. Regression Design for Predictive Modeling
5.3. Selection of Learning and Test Data
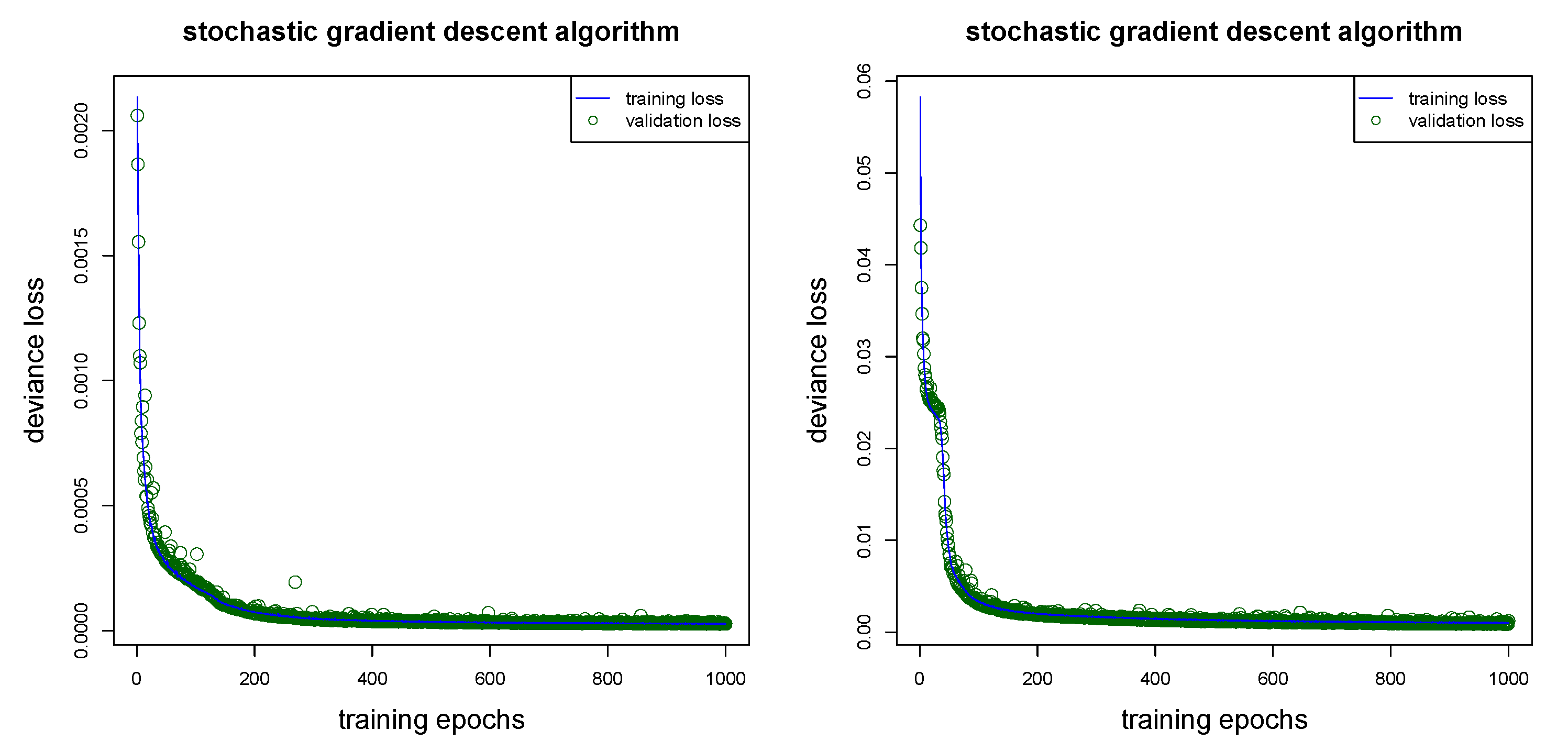
5.4. Network Architecture and Gradient Descent Fitting
- Firstly, the complexity of the network architecture should be adapted to the problem, both the sizes of the hidden layers and the depth of the network will vary with the complexity of the problem and the complexity of the regression function. In general, the bigger the network the better the approximation capacity (this follows from the universality theorems). This says that the chosen network should have a certain complexity otherwise it will be not sufficiently flexible to approximate the true (but unknown) regression function. On the other hand, for computational reasons, the chosen network should not be too large.
- Secondly, different distributions will require different choices of loss functions on line 25 of Listing A1. Some loss functions are already implemented in thekeraslibrary, others will require custom loss functions. An example of a custom loss function implementation is given in Listing 2 of Delong et al. (2020). In general, the loss function of any density that allows for an EDF representation can be implemented inkeras.
- Thirdly, we could add more specialized layers to the network architecture of Listing A1. For instance, we could add dropout layers after each hidden layer on lines 15–17 of Listing A1, for dropout layers see Srivastava et al. (2014). Dropout layers add an additional element of randomness during training, because certain network connections are switched off (at random) for certain training steps when using dropout. This switching off of connections acts as regularization during training because it prevents certain neurons from over-fitting to special tasks. In fact, under certain assumptions one can prove that dropout acts similarly to ridge regularization, see Section 18.6 in Efron and Hastie (2016). In our study we refrain from using dropout.
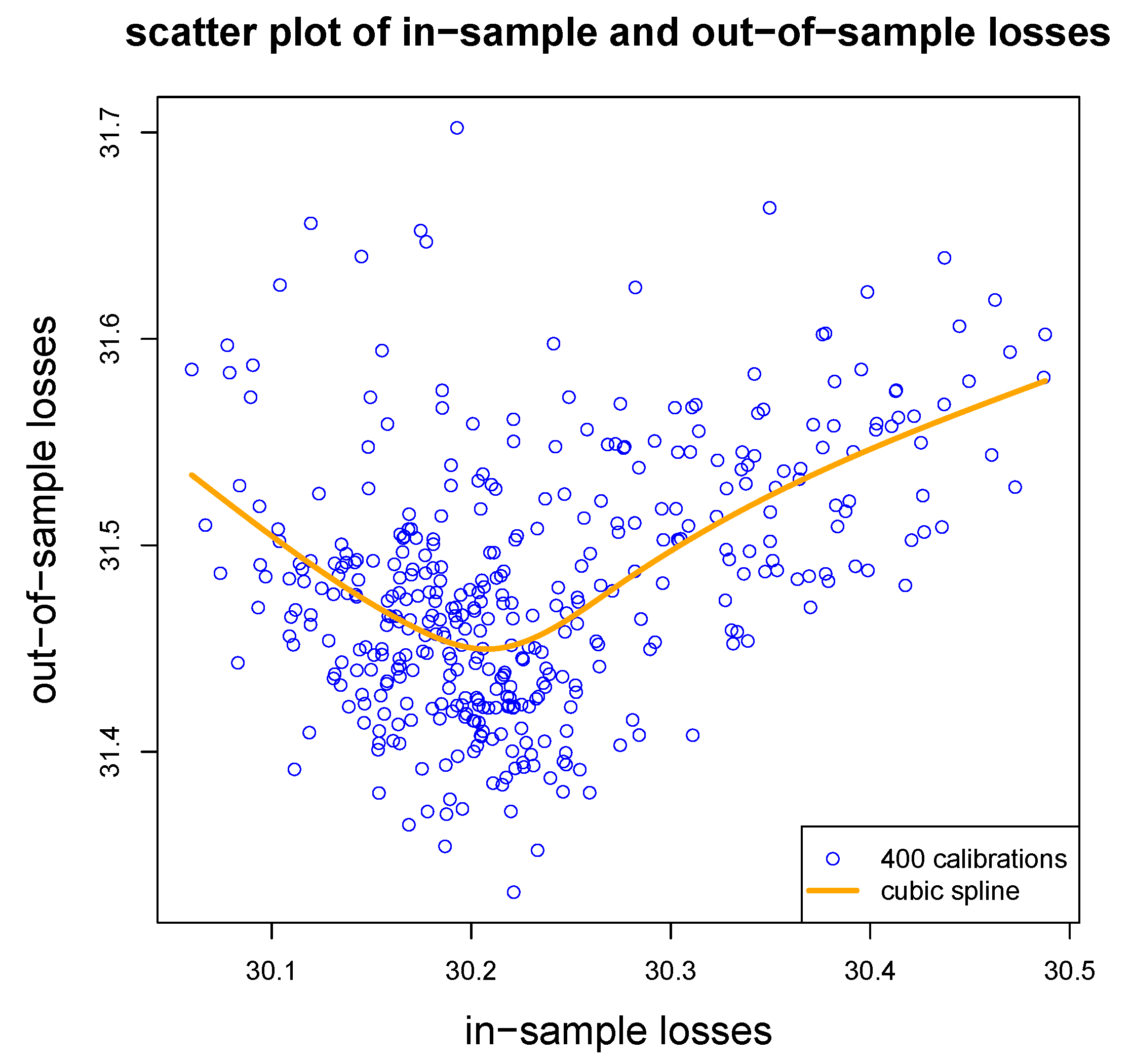
5.5. Comparison of Different Network Calibrations
- (R1)
- we randomly split learning data into training data and validation data ;
- (R2)
- we randomly split training data into mini-batches of size 5000 (to more efficiently calculate gradient descent steps); and
- (R3)
- we randomly choose the starting point of the gradient descent algorithm; the default initialization in keras is the glorot_uniform initialization which involves simulation from uniform distributions.
5.6. Nagging Predictor
5.7. Pricing of Individual Insurance Policies
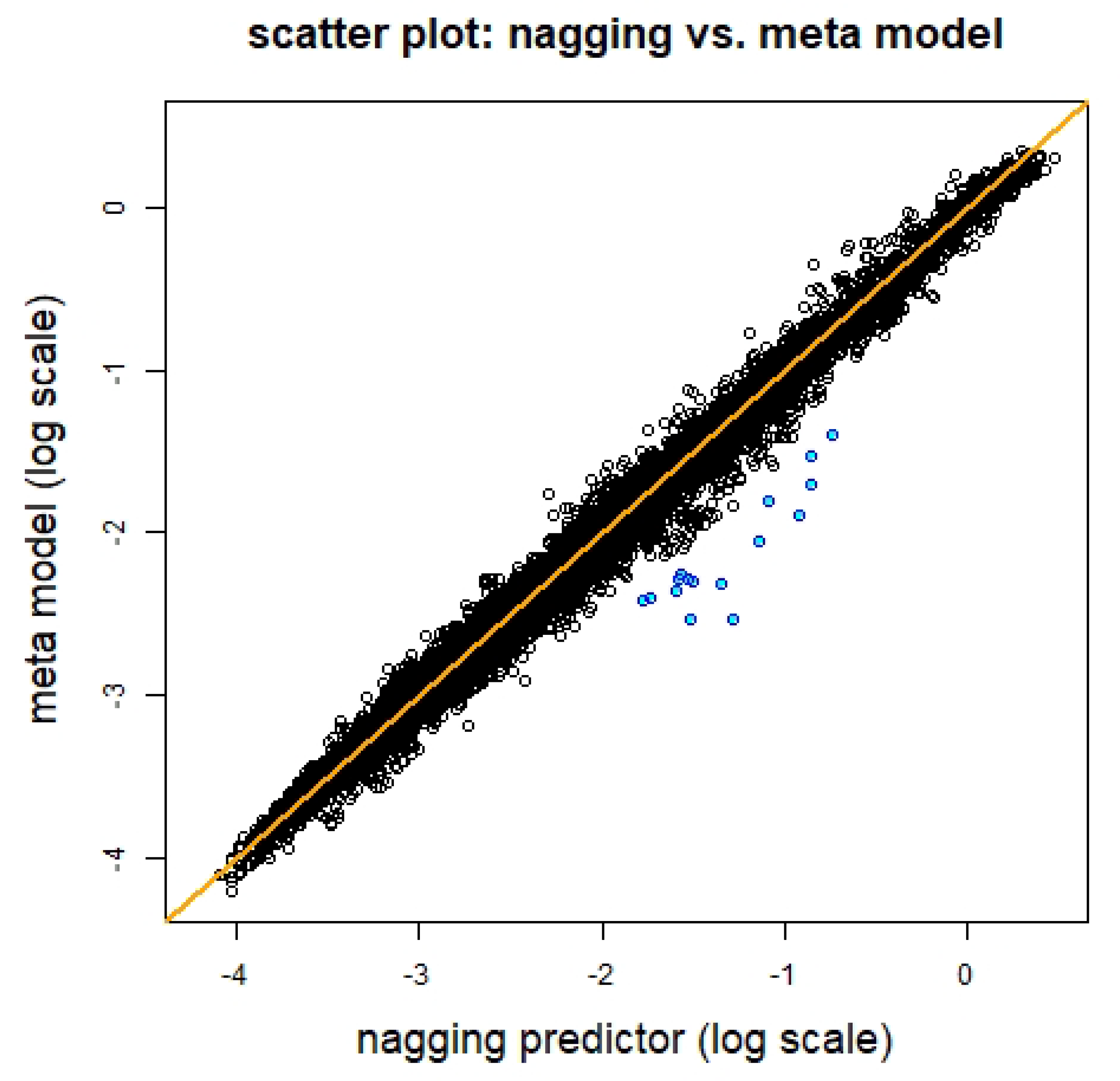
5.8. Meta Network Regression Model
6. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Appendix A. R Code

References
- Breiman, Leo. 1996. Bagging predictors. Machine Learning 24: 123–40. [Google Scholar] [CrossRef]
- Bühlmann, Peter, and Bin Yu. 2002. Analyzing bagging. The Annals of Statistics 30: 927–61. [Google Scholar] [CrossRef]
- Cybenko, George. 1989. Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals, and Systems 2: 303–14. [Google Scholar] [CrossRef]
- Delong, Łukasz, Matthias Lindholm, and Mario V. Wüthrich. 2020. Making Tweedie’s compound Poisson model more accessible. SSRN, 3622871, Version of 8 June. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3622871 (accessed on 1 July 2020). [CrossRef]
- Di Persio, Luca, and Oleksandr Honchar. 2016. Artificial neural networks architectures for stock price prediction: Comparisons and applications. International Journal of Circuits, Systems and Signal Processing 10: 403–13. [Google Scholar]
- Dietterich, Thomas G. 2000a. An experimental comparison of three methods for constructing ensembles of decision trees: Bagging, boosting, and randomization. Machine Learning 40: 139–57. [Google Scholar] [CrossRef]
- Dietterich, Thomas G. 2000b. Ensemble methods in machine learning. In Multiple Classifier Systems. Edited by Josef Kittel and Fabio Roli. Lecture Notes in Computer Science, 1857. Berlin and Heidelberg: Springer, pp. 1–15. [Google Scholar]
- Dutang, Christophe, and Arthur Charpentier. 2019. CASdatasets R Package Vignette. Reference Manual, November 13, 2019. Version 1.0-10. Available online: http://dutangc.free.fr/pub/RRepos/web/CASdatasets-index.html (accessed on 13 November 2019).
- Efron, Bradley, and Trevor Hastie. 2016. Computer Age Statistical Inference. Cambridge: Cambridge University Press. [Google Scholar]
- Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. 2016. Deep Learning. Cambridge: MIT Press. [Google Scholar]
- Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean. 2015. Distilling the knowledge in a neural network. Version 9 March. arXiv arXiv:1503.02531. [Google Scholar]
- Hornik, Kurt, Maxwell B. Stinchcombe, and Halbert White. 1989. Multilayer feedforward networks are universal approximators. Neural Networks 2: 359–66. [Google Scholar] [CrossRef]
- du Jardin, Philippe. 2016. A two-stage classification technique for bankruptcy prediction. European Journal of Operations Research 254: 236–52. [Google Scholar] [CrossRef]
- Jørgensen, Bent. 1986. Some properties of exponential dispersion models. Scandinavian Journal of Statistics 13: 187–97. [Google Scholar]
- Jørgensen, Bent. 1987. Exponential dispersion models. Journal of the Royal Statistical Society. Series B (Methodological) 49: 127–45. [Google Scholar]
- Jørgensen, Bent, and Marta C. Paes de Souza. 1994. Fitting Tweedie’s compound Poisson model to insurance claims data. Scandinavian Actuarial Journal 1994: 69–93. [Google Scholar] [CrossRef]
- König, Daniel, and Friedrich Loser. 2020. GLM, neural network and gradient boosting for insurance pricing. Kaggle. Available online: https://www.kaggle.com/floser/glm-neural-nets-and-xgboost-for-insurance-pricing (accessed on 10 July 2020).
- LeCun, Yann, Yosua Bengio, and Geoffrey Hinton. 2015. Deep learning. Nature 521: 436–44. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, Erich Leo. 1983. Theory of Point Estimation. Hoboken: John Wiley & Sons. [Google Scholar]
- Lorentzen, Christian, and Michael Mayer. 2020. Peeking into the black box: An actuarial case study for interpretable machine learning. SSRN, 3595944, Version 7 May. [Google Scholar] [CrossRef]
- Nelder, John A., and Robert W. M. Wedderburn. 1972. Generalized linear models. Journal of the Royal Statistical Society. Series A (General) 135: 370–84. [Google Scholar] [CrossRef]
- Noll, Alexander, Robert Salzmann, and Mario V. Wüthrich. 2018. Case study: French motor third-party liability claims. SSRN, 3164764, Version 5 March. [Google Scholar] [CrossRef]
- Richman, Ronald, Nicolai von Rummel, and Mario V. Wüthrich. 2019. Believe the bot-model risk in the era of deep learning. SSRN, 3444833, Version 29 August. [Google Scholar] [CrossRef]
- Smyth, Gordon K., and Bent Jørgensen. 2002. Fitting Tweedie’s compound Poisson model to insurance claims data: Dispersion modeling. ASTIN Bulletin 32: 143–57. [Google Scholar] [CrossRef]
- Srivastava, Nitish, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. 2014. Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research 15: 1929–58. [Google Scholar]
- Tweedie, Maurice C. K. 1984. An index which distinguishes between some important exponential families. In Statistics: Applications and New Directions. Proceeding of the Indian Statistical Golden Jubilee International Conference. Edited by Jayanta K. Ghosh and Jibendu S. Roy. Calcutta: Indian Statistical Institute, pp. 579–604. [Google Scholar]
- Wang, Gang, Jinxing Hao, Jian Ma, and Hongbing Jiang. 2011. A comparative assessment of ensemble learning for credit scoring. Expert Systems with Applications 38: 223–30. [Google Scholar] [CrossRef]
- Wüthrich, Mario V. 2019. From generalized linear models to neural networks, and back. SSRN, 3491790, Version of 3 April. [Google Scholar] [CrossRef]
- Zhou, Zhi-Hua. 2012. Ensemble Methods: Foundations and Algorithms. Boca Raton: Chapman & Hall/CRC. [Google Scholar]
- Zhou, Zhi-Hua, Jianxin Wu, and Wei Tang. 2002. Ensembling neural networks: Many could be better than all. Artificial Intelligence 137: 239–63. [Google Scholar] [CrossRef]





| Numbers of Observed Claims | Empirical | Size of | |||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | Frequency | Data Sets | |
| empirical probability on | 94.99% | 4.74% | 0.36% | 0.01% | 0.002% | 10.02% | |
| empirical probability on | 94.83% | 4.85% | 0.31% | 0.01% | 0.003% | 10.41% | |
| In-Sample | Out-of-Sample | |||
|---|---|---|---|---|
| Loss on | Loss on | |||
| (a) homogeneous model | 32.935 | 33.861 | ||
| (b) generalized linear model | 31.267 | 32.171 | ||
| (c) boosting regression model | 30.132 | 31.468 | ||
| (d) network regression model (seed ) | 30.184 | 31.464 | ||
| (e) average over 400 network calibrations | 30.230 | (0.089) | 31.480 | (0.061) |
| (f) nagging predictor for | 30.060 | 31.272 |
| In-Sample | Out-of-Sample | |||
|---|---|---|---|---|
| Loss on | Loss on | |||
| (d) network regression model (seed ) | 30.184 | 31.464 | ||
| (e) average over 400 network calibrations | 30.230 | (0.089) | 31.480 | (0.061) |
| (f) nagging predictor for | 30.060 | 31.272 | ||
| (g1) meta network model (un-weighted) | 30.260 | 31.342 | ||
| (g2) meta network model (weighted) | 30.257 | 31.332 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richman, R.; Wüthrich, M.V. Nagging Predictors. Risks 2020, 8, 83. https://doi.org/10.3390/risks8030083
Richman R, Wüthrich MV. Nagging Predictors. Risks. 2020; 8(3):83. https://doi.org/10.3390/risks8030083
Chicago/Turabian StyleRichman, Ronald, and Mario V. Wüthrich. 2020. "Nagging Predictors" Risks 8, no. 3: 83. https://doi.org/10.3390/risks8030083
APA StyleRichman, R., & Wüthrich, M. V. (2020). Nagging Predictors. Risks, 8(3), 83. https://doi.org/10.3390/risks8030083





