Figure 1.
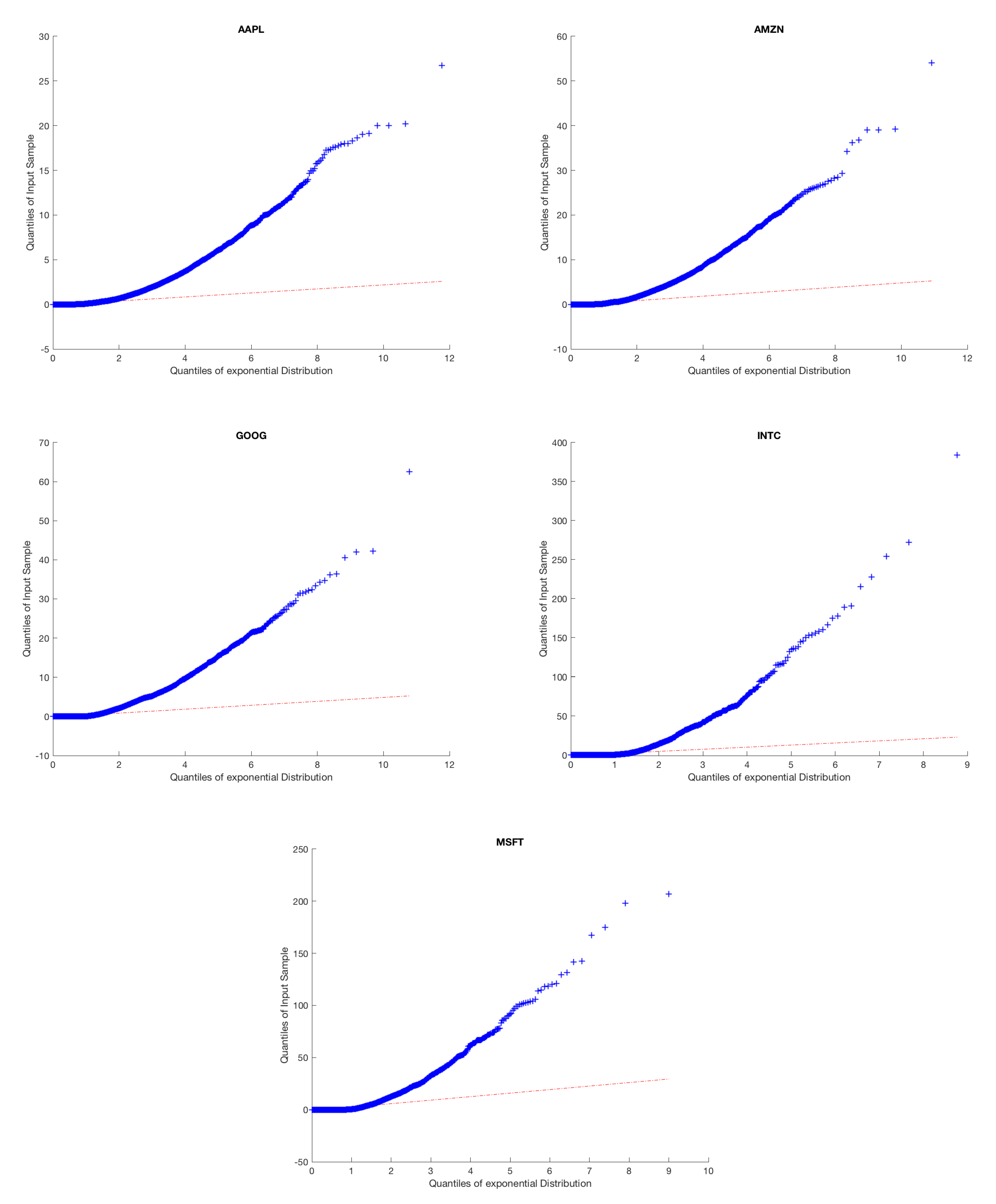
Above, we provide a quantile-quantile plot of our empirical inter-arrival times against a Poisson process for each of the five stocks. We see that the inter-arrival data does not fit the expected curve, providing evidence that the underlying arrival process is not Poisson.
Figure 1.
Above, we provide a quantile-quantile plot of our empirical inter-arrival times against a Poisson process for each of the five stocks. We see that the inter-arrival data does not fit the expected curve, providing evidence that the underlying arrival process is not Poisson.
Figure 2.
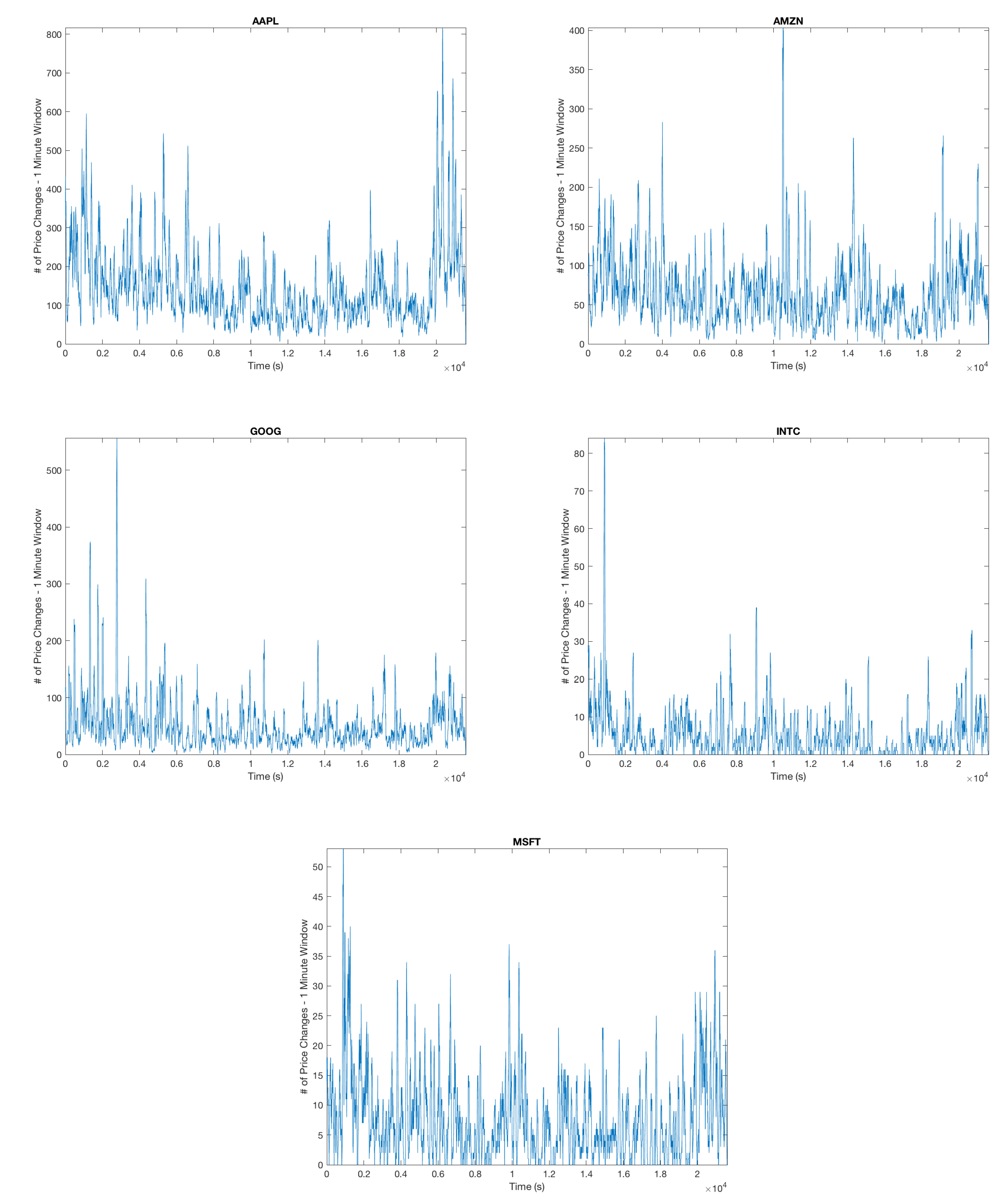
Each plot shows the number of arrivals for a moving one minute window. From this, we can conclude that there is a significant amount of clustering in the arrival of mid-price changes, motivating the Hawkes model of our arrival process.
Figure 2.
Each plot shows the number of arrivals for a moving one minute window. From this, we can conclude that there is a significant amount of clustering in the arrival of mid-price changes, motivating the Hawkes model of our arrival process.
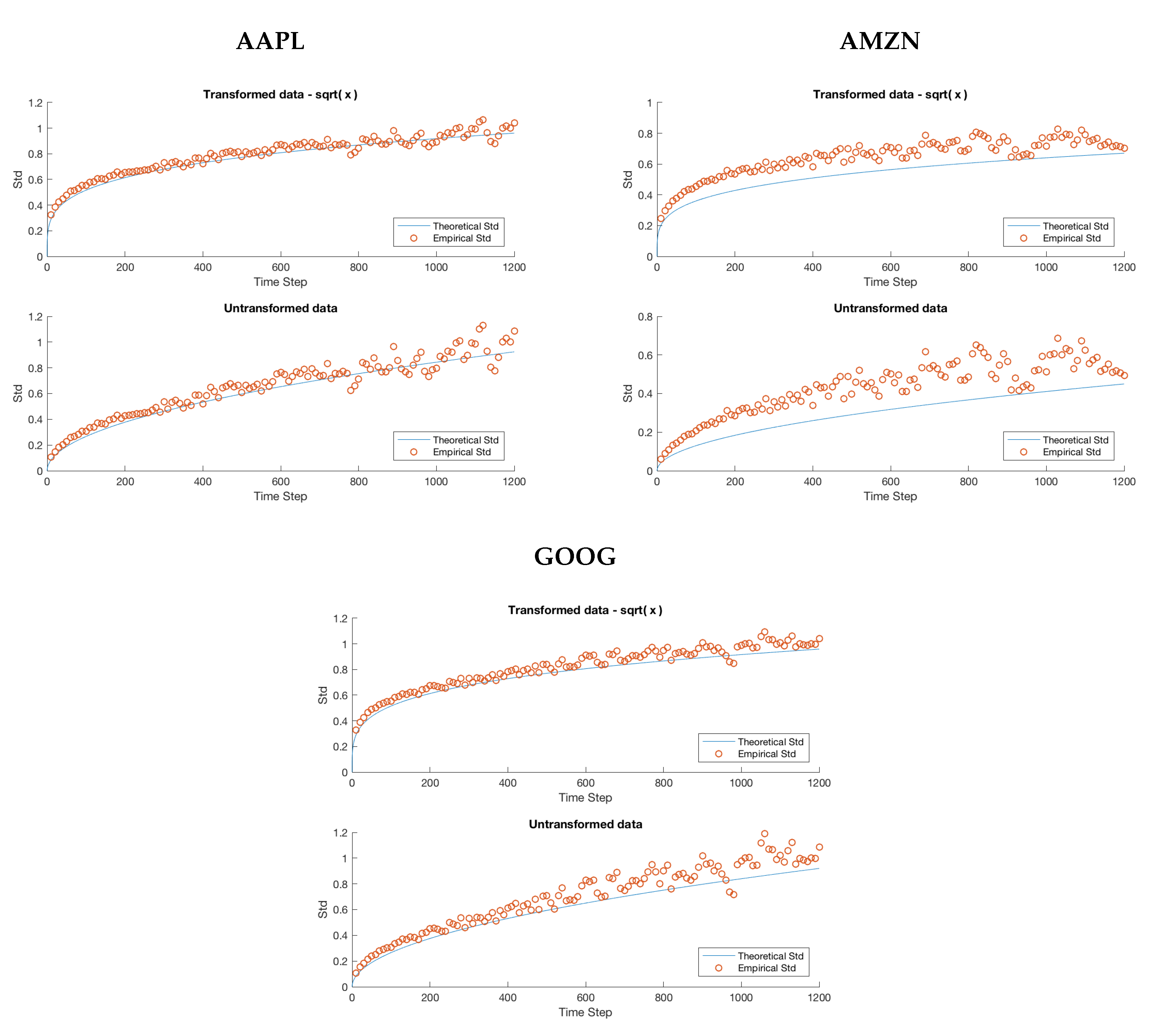
Figure 3.
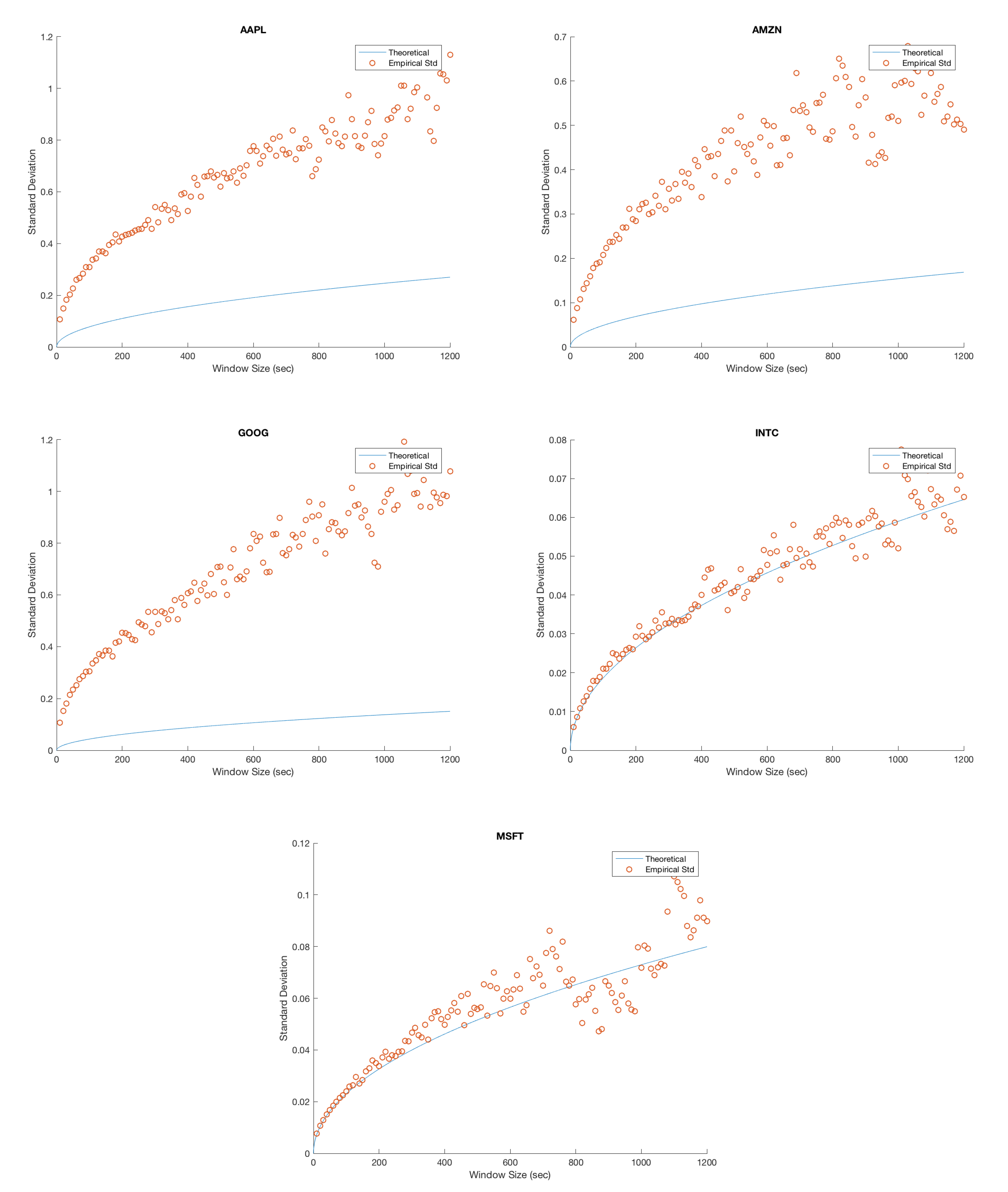
Each figure compares the empirical standard deviation for a fixed window size to the theoretical standard deviation. We have plotted an empirical standard deviation for all n from 10 s to 20 min in step sizes of 10 s. Each empirical standard deviation corresponds to a single point in the scatter plot, and the plotted curve corresponds to the predicted theoretical value.
Figure 3.
Each figure compares the empirical standard deviation for a fixed window size to the theoretical standard deviation. We have plotted an empirical standard deviation for all n from 10 s to 20 min in step sizes of 10 s. Each empirical standard deviation corresponds to a single point in the scatter plot, and the plotted curve corresponds to the predicted theoretical value.
Figure 4.
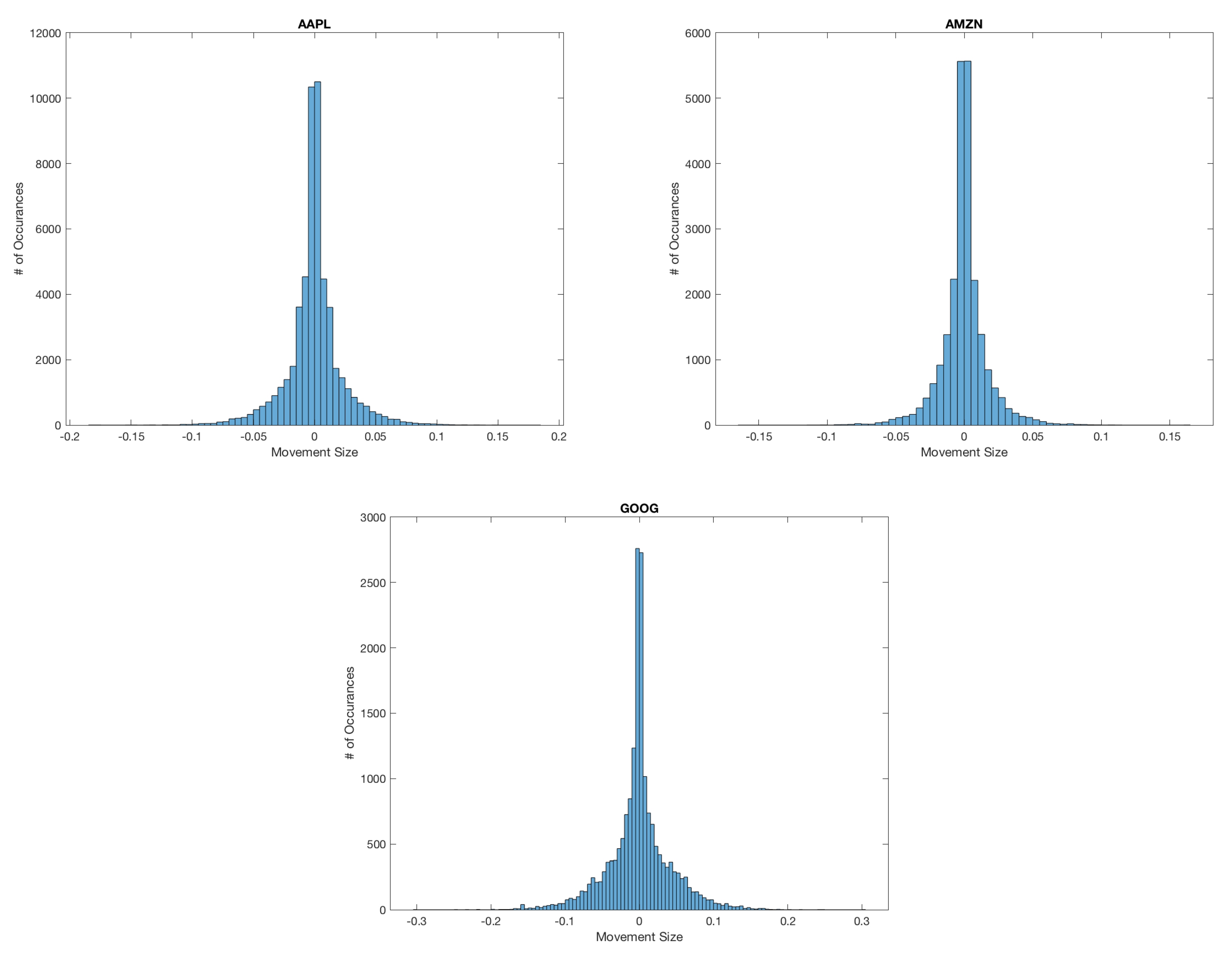
We can see clearly that the change in the mid-price is often larger than a half tick. These mid-price changes make up a significant portion of the actual data, contradicting the assumption needed for the CHPDO model that the mid-price changes occur on average at a half tick size.
Figure 4.
We can see clearly that the change in the mid-price is often larger than a half tick. These mid-price changes make up a significant portion of the actual data, contradicting the assumption needed for the CHPDO model that the mid-price changes occur on average at a half tick size.
Figure 5.
A comparison of the empirical standard deviation for a fixed window size n to the theoretical standard deviation for AAPL, AMZN and GOOG using the 2-state dependent order model. We have plotted the empirical standard deviation for all n from 10 s to 20 min in step sizes of 10 s. Each empirical standard deviation corresponds to a single point in the scatter plot and the plotted curve corresponds to the predicted theoretical value. Visually, there is a significant improvement for all stocks, although the theoretical standard deviation for AMZN is still underestimating the empirical variability.
Figure 5.
A comparison of the empirical standard deviation for a fixed window size n to the theoretical standard deviation for AAPL, AMZN and GOOG using the 2-state dependent order model. We have plotted the empirical standard deviation for all n from 10 s to 20 min in step sizes of 10 s. Each empirical standard deviation corresponds to a single point in the scatter plot and the plotted curve corresponds to the predicted theoretical value. Visually, there is a significant improvement for all stocks, although the theoretical standard deviation for AMZN is still underestimating the empirical variability.
Figure 6.
We consider the N-state model for AMZN discussed previously in the paper. While there is a slight improvement against the original fit, the model still struggles to perfectly predict the variability in the mid-price changes of our data.
Figure 6.
We consider the N-state model for AMZN discussed previously in the paper. While there is a slight improvement against the original fit, the model still struggles to perfectly predict the variability in the mid-price changes of our data.
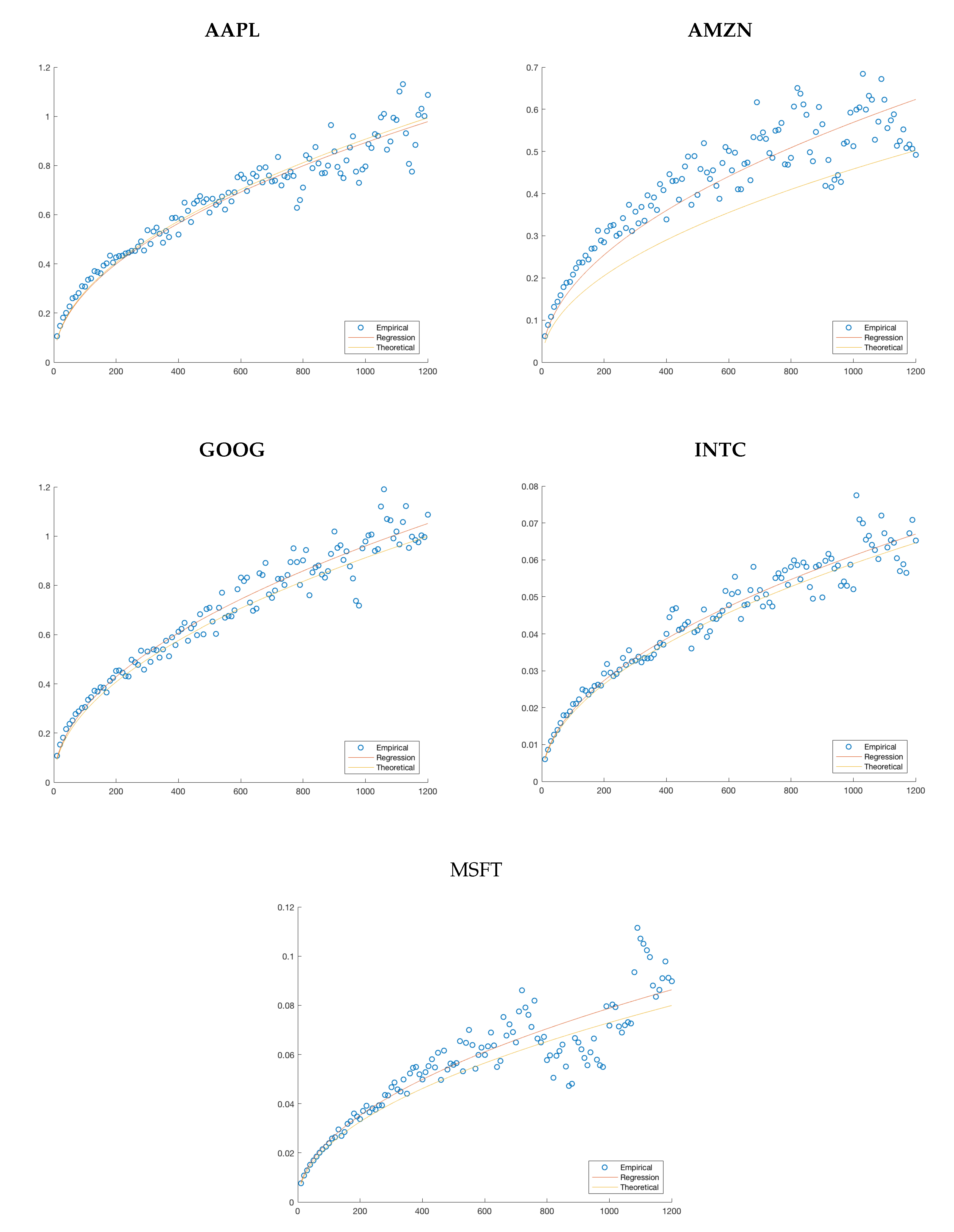
Figure 7.
A qualitative comparison of the regression to the theoretical model. For APPL, AMZN and GOOG, we have used a Markov chain generated from 16 quantiles taken on the upward movements and downward movements. For INTC and MSFT, we have taken the CHPDO coefficient since a different coefficient is not possible with the other models.
Figure 7.
A qualitative comparison of the regression to the theoretical model. For APPL, AMZN and GOOG, we have used a Markov chain generated from 16 quantiles taken on the upward movements and downward movements. For INTC and MSFT, we have taken the CHPDO coefficient since a different coefficient is not possible with the other models.
Table 1.
Stock liquidity of AAPL, AMZN, GOOG, MSFT, and INTC for 21 June 2012.
Table 1.
Stock liquidity of AAPL, AMZN, GOOG, MSFT, and INTC for 21 June 2012.
| Ticker | Avg # of Orders per 10 s | Price Changes in 1 Day |
|---|
| AAPL | 51 | 64,350 |
| AMZN | 25 | 27,557 |
| GOOG | 21 | 24,084 |
| MSFT | 173 | 3217 |
| INTC | 176 | 4060 |
Table 2.
Each parameter was estimated using a particle swarm optimization method in an attempt to globally optimize the negative log-likelihood function. The values for , and for each data set are as provided.
Table 2.
Each parameter was estimated using a particle swarm optimization method in an attempt to globally optimize the negative log-likelihood function. The values for , and for each data set are as provided.
| | | | |
|---|
| AAPL | 1.4683 | 1045.2676 | 2556.1844 |
| AMZN | 0.6443 | 653.7524 | 1556.1702 |
| GOOG | 0.4985 | 865.8553 | 1980.4409 |
| MSFT | 0.0659 | 479.3482 | 908.0032 |
| INTC | 0.0471 | 399.6389 | 760.4991 |
Table 3.
Expected number of arrivals on a unit interval using estimated parameters from an MLE method is compared against the empirical arrivals.
Table 3.
Expected number of arrivals on a unit interval using estimated parameters from an MLE method is compared against the empirical arrivals.
| | Emp. | MLE |
|---|
| AAPL | 2.4840 | 2.4841 |
| AMZN | 1.1110 | 1.1110 |
| GOOG | 0.8857 | 0.8857 |
| MSFT | 0.1395 | 0.1396 |
| INTC | 0.0991 | 0.0992 |
Table 4.
Provided above are the values for , as well as the probabilities of an upward/downward movement given an upward/downward movement for each of the five stocks in question.
Table 4.
Provided above are the values for , as well as the probabilities of an upward/downward movement given an upward/downward movement for each of the five stocks in question.
| | | | | |
|---|
| AAPL | 0.4956 | 0.4933 | 0.0049 | −1.1463 × 10 |
| AMZN | 0.4635 | 0.4576 | 0.0046 | −2.7373 × 10 |
| GOOG | 0.4769 | 0.4461 | 0.0046 | −1.4301 × 10 |
| MSFT | 0.6269 | 0.5827 | 0.0062 | −2.7956 × 10 |
| INTC | 0.6106 | 0.5588 | 0.0059 | −3.1185 × 10 |
Table 5.
is the average of the upward or downward mid-price movements. Following our previous convention, the first state will be associated with the mean of all downward mid-price movements and the second state will be associated with the mean of all upward mid-price movements.
Table 5.
is the average of the upward or downward mid-price movements. Following our previous convention, the first state will be associated with the mean of all downward mid-price movements and the second state will be associated with the mean of all upward mid-price movements.
| | | |
|---|
| AAPL | −0.0172 | 0.0170 |
| AMZN | −0.0134 | 0.0133 |
| GOOG | −0.0302 | 0.0308 |
Table 6.
Above, we have the values for , as well as the probabilities of an upwards/downwards movement, given an upwards/downwards movement for the three stocks of interest.
Table 6.
Above, we have the values for , as well as the probabilities of an upwards/downwards movement, given an upwards/downwards movement for the three stocks of interest.
| | | | | |
|---|
| AAPL | 0.4956 | 0.4933 | 0.0169 | −1.5624 × 10 |
| AMZN | 0.4635 | 0.4576 | 0.0123 | −1.0475 × 10 |
| GOOG | 0.4769 | 0.4461 | 0.0282 | −5.5095 × 10 |
Table 7.
Above, we have provided the state, associated ergodic probabilities and state values for AMZN, given a 12-state Markov chain that was obtained from choosing a 16 quantile method.
Table 7.
Above, we have provided the state, associated ergodic probabilities and state values for AMZN, given a 12-state Markov chain that was obtained from choosing a 16 quantile method.
| AMZN |
|---|
| i | | |
| 1 | 0.0275 | −0.0524 |
| 2 | 0.0281 | −0.0318 |
| 3 | 0.0264 | −0.0250 |
| 4 | 0.0382 | −0.0200 |
| 5 | 0.0576 | −0.0150 |
| 6 | 0.3249 | −0.0064 |
| 7 | 0.2321 | 0.0050 |
| 8 | 0.0923 | 0.0100 |
| 9 | 0.0578 | 0.0150 |
| 10 | 0.0353 | 0.0200 |
| 11 | 0.0412 | 0.0271 |
| 12 | 0.0387 | 0.0476 |
Table 8.
We list the mean residuals for several Markov chains with varying numbers of states. These were generated using our modified quantile approach choosing to start with 2, 8, 16 or 32 quantiles. We see that, in general, the mean residual decreases to some lower limit where we can no longer perform any better. Recall that the only observed mid-price changes for INTC and MSFT were of a half tick size, and any increase in the number of quantiles will result in the same performance.
Table 8.
We list the mean residuals for several Markov chains with varying numbers of states. These were generated using our modified quantile approach choosing to start with 2, 8, 16 or 32 quantiles. We see that, in general, the mean residual decreases to some lower limit where we can no longer perform any better. Recall that the only observed mid-price changes for INTC and MSFT were of a half tick size, and any increase in the number of quantiles will result in the same performance.
| | CHPDO | 2 | 8 | 16 | 32 |
|---|
| AAPL | 0.2679 | 0.0050 | 0.0036 | 0.0036 | 0.0036 |
| AMZN | 0.1122 | 0.0208 | 0.0131 | 0.0124 | 0.0123 |
| GOOG | 0.4036 | 0.0115 | 0.0048 | 0.0045 | 0.0047 |
| INTC | 1.7917 × 10 | 1.7917 × 10 | 1.7917 × 10 | 1.7917 × 10 | 1.7917 × 10 |
| MSFT | 1.0586 × 10 | 1.0586 × 10 | 1.0586 × 10 | 1.0586 × 10 | 1.0586 × 10 |
Table 9.
The coefficients calculated for AAPL, AMZN and GOOG are generated using a Markov chain created by 16 quantiles on the upward and downward movements, while the coefficients for INTC and MSFT are obtained from the CHPDO case.
Table 9.
The coefficients calculated for AAPL, AMZN and GOOG are generated using a Markov chain created by 16 quantiles on the upward and downward movements, while the coefficients for INTC and MSFT are obtained from the CHPDO case.
| | Theoretical Coefficient | Regression Coefficient | Percent Error |
|---|
| AAPL | 0.02868 | 0.02828 | 1.42% |
| AMZN | 0.01450 | 0.01831 | 20.8% |
| GOOG | 0.02883 | 0.03023 | 4.63% |
| INTC | 0.00186 | 0.00193 | 3.4% |
| MSFT | 0.00231 | 0.00246 | 6.4% |
Table 10.
An imagined sequence of price change events before the second thirty minute window has been removed.
Table 10.
An imagined sequence of price change events before the second thirty minute window has been removed.
| Time (s) | ⋯ | 1789 | 1795 | 1803 | ⋯ | 3193 | 3601 | 3608 | ⋯ |
| Event | ⋯ | n − 1 | n | n + 1 | ⋯ | n + k | n + k + 1 | n + k + 2 | ⋯ |
Table 11.
An imagined sequence of price change events after the second thirty minute window has been removed.
Table 11.
An imagined sequence of price change events after the second thirty minute window has been removed.
| Time (s) | ⋯ | 1789 | 1795 | 1801 | 1808 | ⋯ |
| Event | ⋯ | n − 1 | n | n + k + 1 | n + k + 2 | ⋯ |
Table 12.
A table of testing scores for various models. Computations were performed for up to the 40-quantile case for each stock, and this table represents a sample of that data. We note that the models stop obtaining appreciable performance gains at around 4–7 quantiles, fluctuating around the same scores.
Table 12.
A table of testing scores for various models. Computations were performed for up to the 40-quantile case for each stock, and this table represents a sample of that data. We note that the models stop obtaining appreciable performance gains at around 4–7 quantiles, fluctuating around the same scores.
| | AAPL | AMZN | GOOG |
|---|
| CHPDO | 0.0348 | 0.0142 | 0.0436 |
| GCHP2SDO | 0.0049 | 0.0048 | 0.0044 |
| 2-Quantiles | 0.0042 | 0.0041 | 0.0036 |
| 3-Quantiles | 0.0041 | 0.0042 | 0.0035 |
| 4-Quantiles | 0.0040 | 0.0040 | 0.0035 |
| 5-Quantiles | 4.0341 × 10 | 3.9878 × 10 | 3.4593 × 10 |
| 6-Quantiles | 4.0362 × 10 | 3.8971 × 10 | 3.4168 × 10 |
| 7-Quantiles | 4.0184 × 10 | 3.8971 × 10 | 3.3977 × 10 |
| 8-Quantiles | 4.0097 × 10 | 3.8656 × 10 | 3.3881 × 10 |
| 9-Quantiles | 4.0026 × 10 | 3.8124 × 10 | 3.3976 × 10 |
| 10-Quantiles | 3.9984 × 10 | 3.8124 × 10 | 3.425 × 10 |
| 11-Quantiles | 3.9971 × 10 | 3.81594 × 10 | 3.3867 × 10 |
| 12-Quantiles | 3.9826 × 10 | 3.81463 × 10 | 3.3906 × 10 |
| 13-Quantiles | 3.9804 × 10 | 3.81517 × 10 | 3.3562 × 10 |
| 14-Quantiles | 3.9725 × 10 | 3.81427 × 10 | 3.3549 × 10 |