Mean-Variance Optimization Is a Good Choice, But for Other Reasons than You Might Think
Abstract
1. Introduction
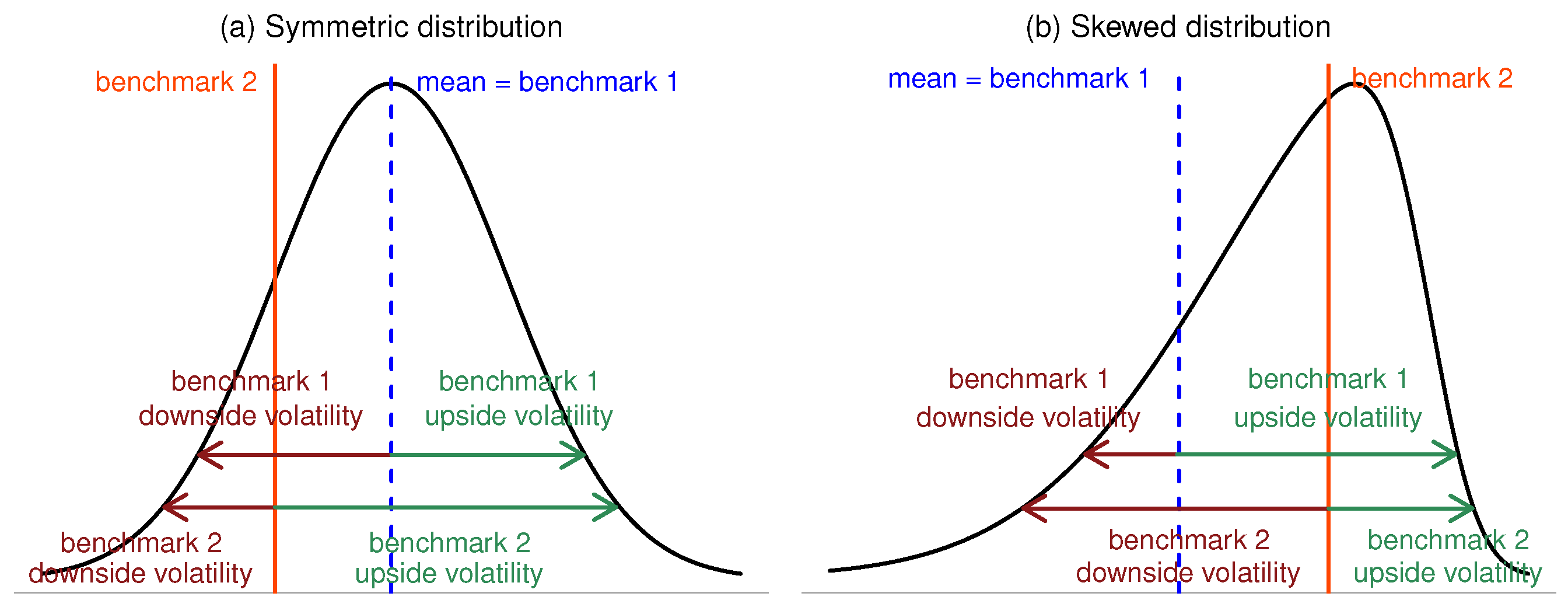
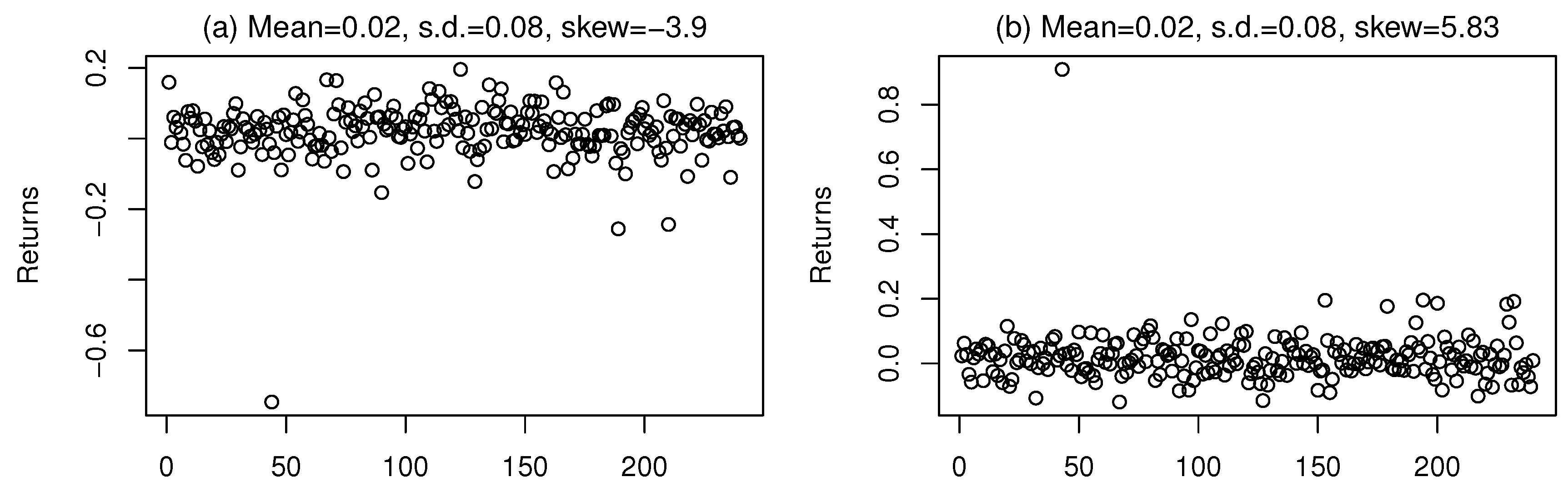
2. The Case for Downside Risk
3. The Semicovariance Matrix
3.1. Approximation of the Semicovariance Matrix
3.2. Evaluating the Impact of the Approximation Error
3.3. Parameter Uncertainty in the Covariance and Semicovariance Matrix
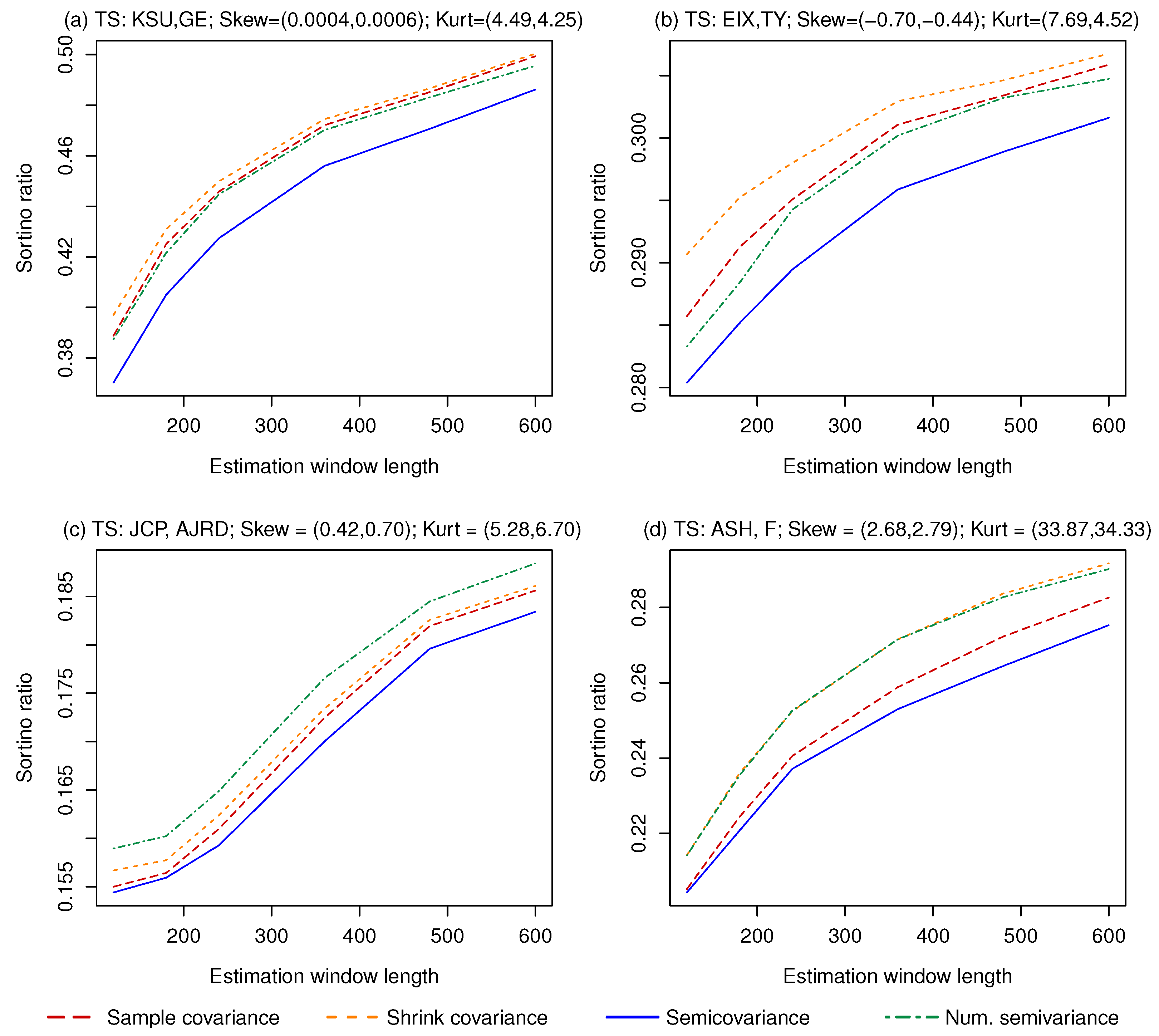
4. Performance Comparison
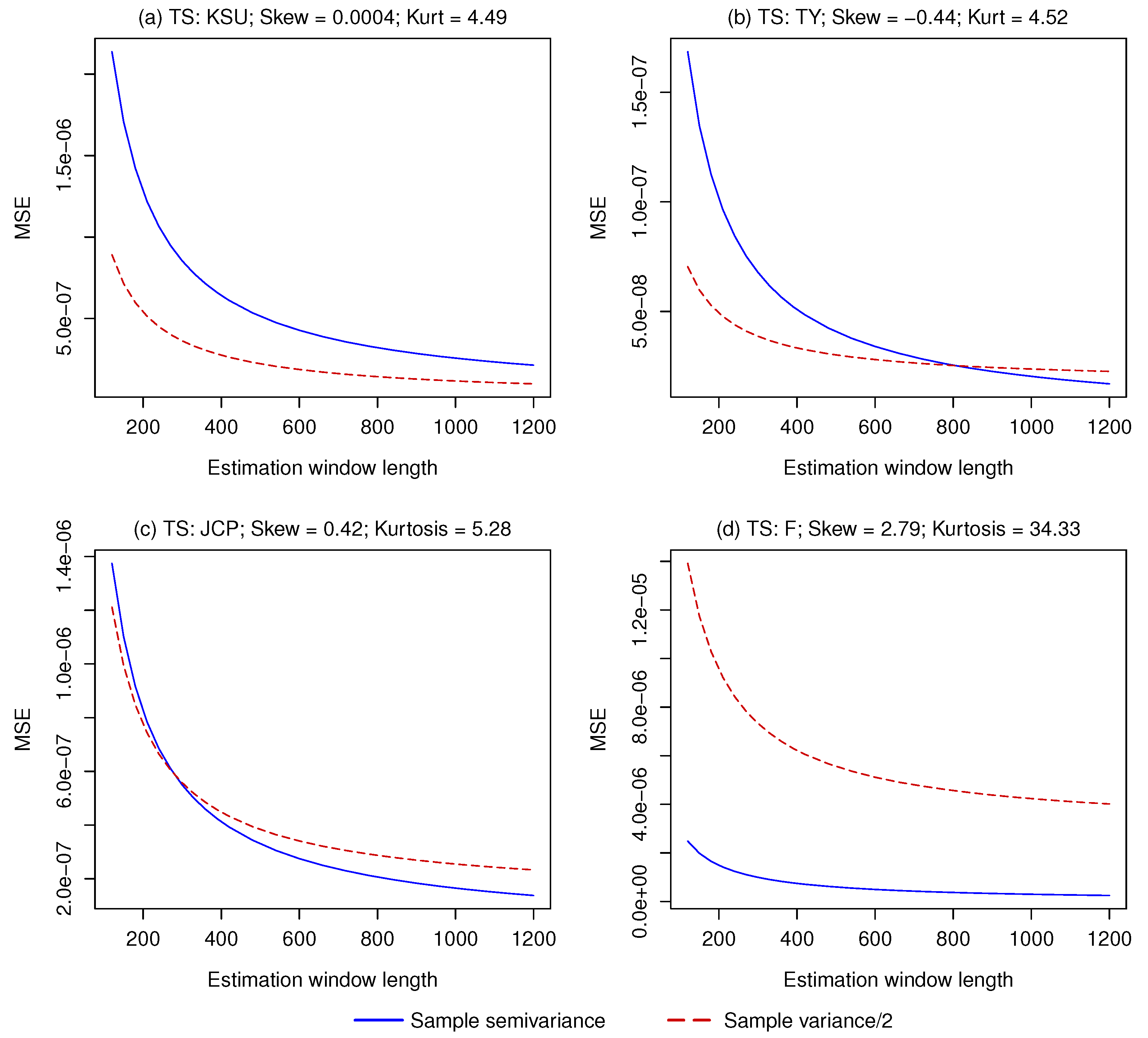
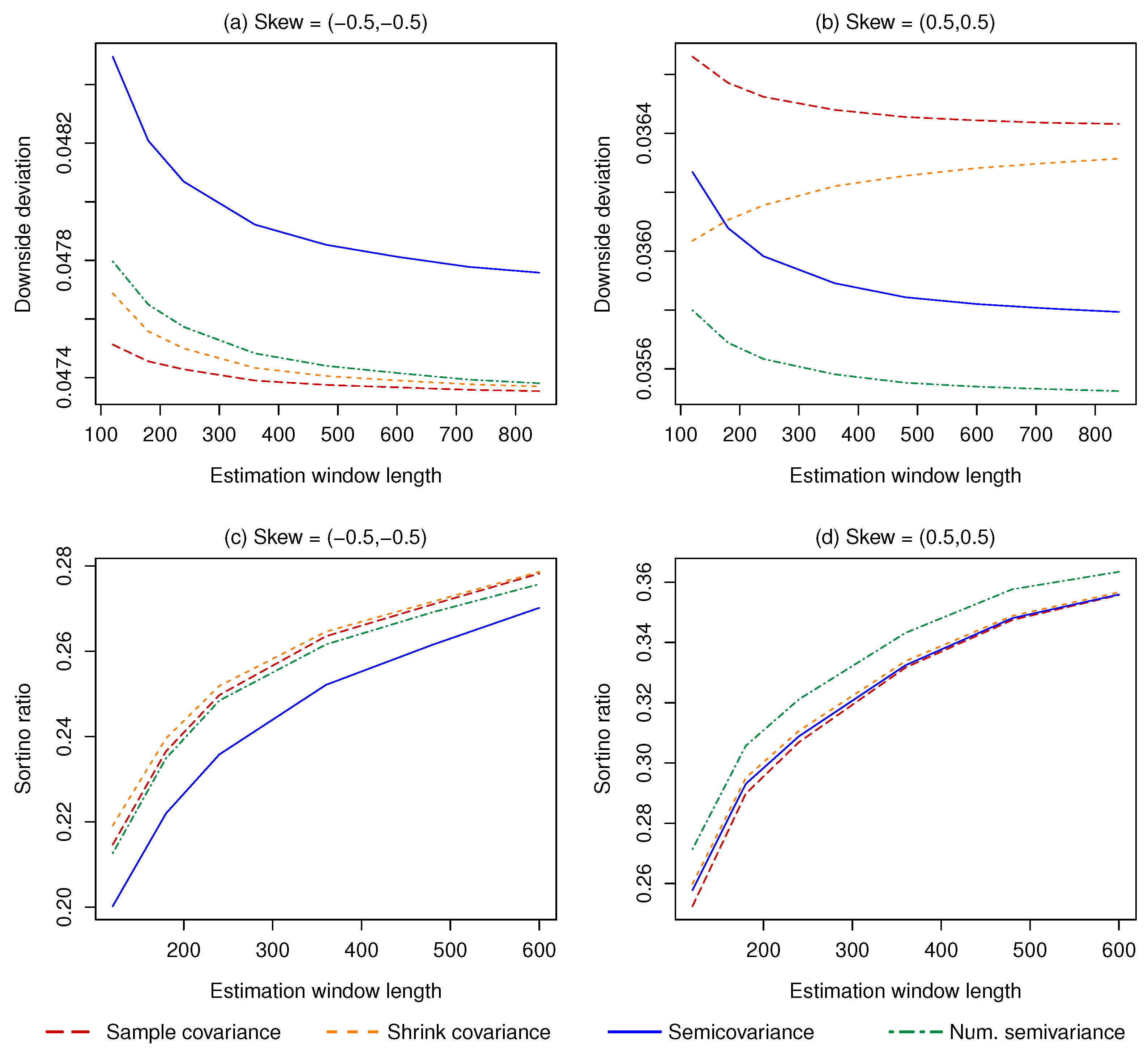
4.1. One Asset Case
- The sample semivariance, given by Equation (3). This estimator is always unbiased but has a high variance for the reasons discussed in Section 3.3.
- , where is the sample variance. This estimator is biased, even asymptotically, unless the return distribution is perfectly symmetric, but it has a lower estimation error (i.e., a lower estimator variance).
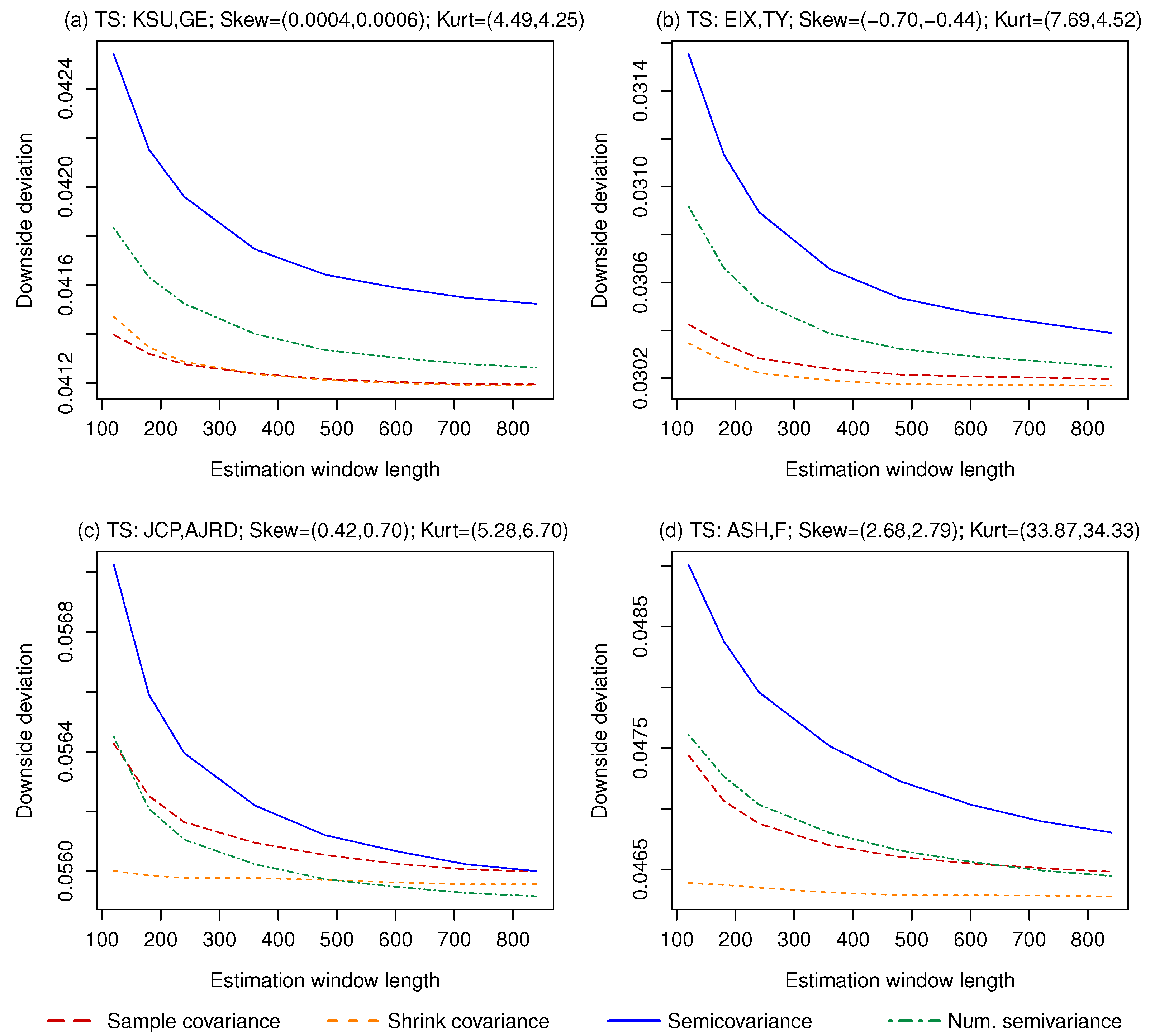
4.2. Two Risky Assets Setting
5. Empirical Test of the Minimum Semivariance and Minimum CVaR Portfolios
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Albuquerque, Rui. 2012. Skewness in stock returns: Reconciling the evidence on firm versus aggregate returns. The Review of Financial Studies 25: 1630–73. [Google Scholar] [CrossRef]
- Azzalini, Adelchi, and Alessandra Dalla Valle. 1996. The multivariate skew-normal distribution. Biometrika 83: 715–26. [Google Scholar] [CrossRef]
- Bruni, Renato, Francesco Cesarone, Andrea Scozzari, and Fabio Tardella. 2016. Real-world datasets for portfolio selection and solutions of some stochastic dominance portfolio models. Data in Brief 8: 858–62. [Google Scholar] [CrossRef] [PubMed]
- Cheremushkin, Sergei V. 2009. Why D-CAPM is a big mistake? The incorrectness of the cosemivariance statistics. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Estrada, Javier. 2008. Mean-semivariance optimization: A heuristic approach. Journal of Applied Finance 18: 57–72. [Google Scholar] [CrossRef]
- Jagannathan, Ravi, and Tongshu Ma. 2003. Risk reduction in large portfolios: Why imposing the wrong constraints helps. The Journal of Finance 58: 1651–84. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2004. A well-conditioned estimator for large-dimensional covariance matrices. Journal of Multivariate Analysis 88: 365–411. [Google Scholar] [CrossRef]
- Lim, Andrew E.B., J. George Shanthikumar, and Gah-Yi Vahn. 2011. Conditional value-at-risk in portfolio optimization: Coherent but fragile. Operations Research Letters 39: 163–71. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio selection. The Journal of Finance 7: 77–91. [Google Scholar]
- Markowitz, Harry. 1959. Portfolio Selection. New York: John Wiley and Sons. [Google Scholar]
- Rockafellar, Ralph T., and Stanislav Uryasev. 2000. Optimization of Conditional Value-at-Risk. Journal of Risk 2: 21–41. [Google Scholar] [CrossRef]
- Sarykalin, Sergey, Gaia Serraino, and Stan Uryasev. 2008. Value-at-Risk vs. Conditional Value-at-Risk in risk management and optimization. In State-of-the-Art Decision-Making Tools in the Information-Intensive Age. INFORMS Tutorials in Operations Research. Catonsville: INFORMS, pp. 270–94. [Google Scholar]
- Sortino, Frank A., and Lee N. Prince. 1994. Performance measurement in a downside risk framework. The Journal of Investing 3: 59–64. [Google Scholar] [CrossRef]
- Yamai, Yasuhiro, and Toshinao Yoshiba. 2002. On the validity of Value-at-Risk: Comparative analyses with expected shortfall. Monetary and Economic Studies 20: 57–85. [Google Scholar]
| 1. | Formally, this is the lower semicovariance matrix. The upper semicovariance matrix, which measures variability only above the benchmark, can also be computed. Since we are only interested in the former, throughout the paper we refer to it simply as a “semicovariance matrix”. |
| 2. | Notice that the semivariance is simply the square of the downside deviation, defined in Equation (1). |
| 3. | While it is possible to identify sets of weights that perfectly match the target expected return, for computational reasons, we consider the combinations with an expected portfolio return between 0.4995% and 0.5005% |
| 4. | We deem it preferable to base the risk-free rate on real data when possible, as it is when we generate series by drawing with replacement from empirical series of returns. We only use an arbitrary risk-free rate equal to 0.1% when simulating by drawing from a multivariate skew normal, as we did in Section 3.2. |
| 5. | Setting B equal to the target return is also reasonable, but if the out-of-sample portfolio return is lower than the target, this would lead to a negative Sortino ratio, which would make it difficult to interpret the results. Moreover, using the same B used when minimizing the volatility improves the comparability of the results. |
| 6. | We change the data source from the CRSP database to the dataset from Bruni et al. (2016) for reasons of data availability, as we do not have access to weekly returns from CRSP. |
| Corr. | Skew | Estrada (2008) | Numerical |
|---|---|---|---|
| −0.013 | (−0.3, −0.3) | 0.0371 | 0.0363 |
| −0.013 | (0.3, 0.3) | 0.0280 | 0.0268 |
| 0.003 | (−0.3, −0.3) | 0.0323 | 0.0311 |
| 0.003 | (0.3, 0.3) | 0.0265 | 0.0245 |
| 0.300 | (−0.3, −0.3) | 0.0328 | 0.0326 |
| 0.300 | (0.3, 0.3) | 0.0263 | 0.0261 |
| 0.743 | (−0.3, −0.3) | 0.0566 | 0.0563 |
| 0.743 | (0.3, 0.3) | 0.0508 | 0.0506 |
| Corr. | Skew | Estrada (2008) | Numerical |
|---|---|---|---|
| −0.013 | (−0.3, −0.3) | 0.1894 | 0.2114 |
| −0.013 | (0.3, 0.3) | 0.2499 | 0.2932 |
| 0.003 | (−0.3, −0.3) | 0.2779 | 0.2837 |
| 0.003 | (0.3, 0.3) | 0.3202 | 0.3371 |
| 0.300 | (−0.3, −0.3) | 0.3391 | 0.3560 |
| 0.300 | (0.3, 0.3) | 0.4221 | 0.4467 |
| 0.743 | (−0.3, −0.3) | 0.1388 | 0.1433 |
| 0.743 | (0.3, 0.3) | 0.1445 | 0.1481 |
| Strategy | St.Dev. | Dw.Dev. | Sharpe | Sortino | CVaR |
|---|---|---|---|---|---|
| 1/N | 0.0254 | 0.0172 | 0.0535 | 0.0791 | −0.0555 |
| Min Var | 0.0193 | 0.0140 | 0.0399 | 0.0552 | −0.0449 |
| Min Var Long | 0.0197 | 0.0139 | 0.0504 | 0.0713 | −0.0454 |
| Min Semivar | 0.0223 | 0.0163 | 0.0011 | 0.0014 | −0.0521 |
| Min Semivar Long | 0.0204 | 0.0144 | 0.0344 | 0.0485 | −0.0459 |
| Min CVaR | 0.0225 | 0.0168 | 0.0035 | 0.0047 | −0.0539 |
| Min CVaR Long | 0.0206 | 0.0148 | 0.0280 | 0.0389 | −0.0484 |
| Strategy | St.Dev. | Dw.Dev. | Sharpe | Sortino | CVaR |
|---|---|---|---|---|---|
| 1/N | 0.0254 | 0.0172 | 0.0535 | 0.0791 | −0.0555 |
| Min Var | 0.0196 | 0.0138 | 0.0487 | 0.0689 | −0.0454 |
| Min Var Long | 0.0205 | 0.0141 | 0.0549 | 0.0795 | −0.0465 |
| Min Semivar | 0.0210 | 0.0150 | 0.0094 | 0.0132 | −0.0483 |
| Min Semivar Long | 0.0209 | 0.0145 | 0.0374 | 0.0537 | −0.0478 |
| Min CVaR | 0.0207 | 0.0148 | 0.0055 | 0.0077 | −0.0468 |
| Min CVaR Long | 0.0205 | 0.0143 | 0.0379 | 0.0546 | −0.0470 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigamonti, A. Mean-Variance Optimization Is a Good Choice, But for Other Reasons than You Might Think. Risks 2020, 8, 29. https://doi.org/10.3390/risks8010029
Rigamonti A. Mean-Variance Optimization Is a Good Choice, But for Other Reasons than You Might Think. Risks. 2020; 8(1):29. https://doi.org/10.3390/risks8010029
Chicago/Turabian StyleRigamonti, Andrea. 2020. "Mean-Variance Optimization Is a Good Choice, But for Other Reasons than You Might Think" Risks 8, no. 1: 29. https://doi.org/10.3390/risks8010029
APA StyleRigamonti, A. (2020). Mean-Variance Optimization Is a Good Choice, But for Other Reasons than You Might Think. Risks, 8(1), 29. https://doi.org/10.3390/risks8010029




