In this Section, we tested the FCLT I of MGCPP model with the LOBSTER data and compared our results with the simulation results by MGCHP in
Guo and Swishchuk (
2020). In their paper, they applied two stocks in the LOBSTER data set, namely the mid-price of Microsoft and Intel. As for the Markov chain part, they used the two-state Markov chain (
).
In order to make our results comparable with the MGCHP, we first applied the same data set (Microsoft and Intel) and same two-state Markov chain (
) for the MGCPP model. Next, we explore more simulation examples (by Apple, Amazon, and Google data) which were mentioned in
Guo and Swishchuk (
2020). For those three stocks, we applied the MGCPP model with both two-state Markov chain and
-state Markov chain.
3.3.1. Data Description and Parameter Estimations
The level one LOBSTER data was considered in this paper. The LOBSTER data set contained the stock prices and order flows of Apple, Amazon, Google, Microsoft, and Intel on 21 June 2012. The tick size is one cent (
) and time was measured in milliseconds (0.001 s). We can find the basic data description and check the liquidity from
Table 1. Notation # is the number sign.
Next, we estimate
via the LLN assumption of
. From Assumption 1, when
n is large enough, we can derive the approximation:
Take the expectation for (
21), we have
In this way, we derived the estimated parameters
for 5 stocks in
Table 2.
In the definition of the MGCPP, we assumed Markov chains
are independent. So, we checked correlations of the price increments between 5 stocks in
Table 3. As can be seen in
Table 3, correlations are relatively weak (around 0.3). So, it is reasonable to consider Markov chains
here are independent. In the future work, we will discuss the dependent case for different data sets.
Next, we estimated parameters for the Markov chain by applying the two-state MGCPP model in Corollary 1. The transition matrix
P of two dependent state Markov chain
is denoted as
We calculated frequency in our data to estimate the
and
in
P by
where
,
,
, and
are the number of price goes up twice, goes down twice, goes up and then down, goes down and then up, respectively. The result is in
Table 4:
3.3.2. Comparison with MGCHP with Two Dependent Orders
In this Section, we compared the simulation results of MGCPP with the multivariate general compound Hawkes process (MGCHP) model to show that the simple generalized model can also reach a good accuracy as the MGCHP who has a sophisticated intensity function (see Equation (
5)). In
Guo and Swishchuk (
2020), they simulated the MGCHP with two dependent states for Microsoft and Intel’s data. So here we also conduct simulations for Microsoft and Intel’s data with the two-state MGCPP.
We tested the MGCPP model by comparing the standard deviation for the left hand side and right hand side in the FCLT:
We separated the data set into disjoint windows
. Since the time was measured in milliseconds, we set
. Then we can calculate:
and the standard deviation is in the form of
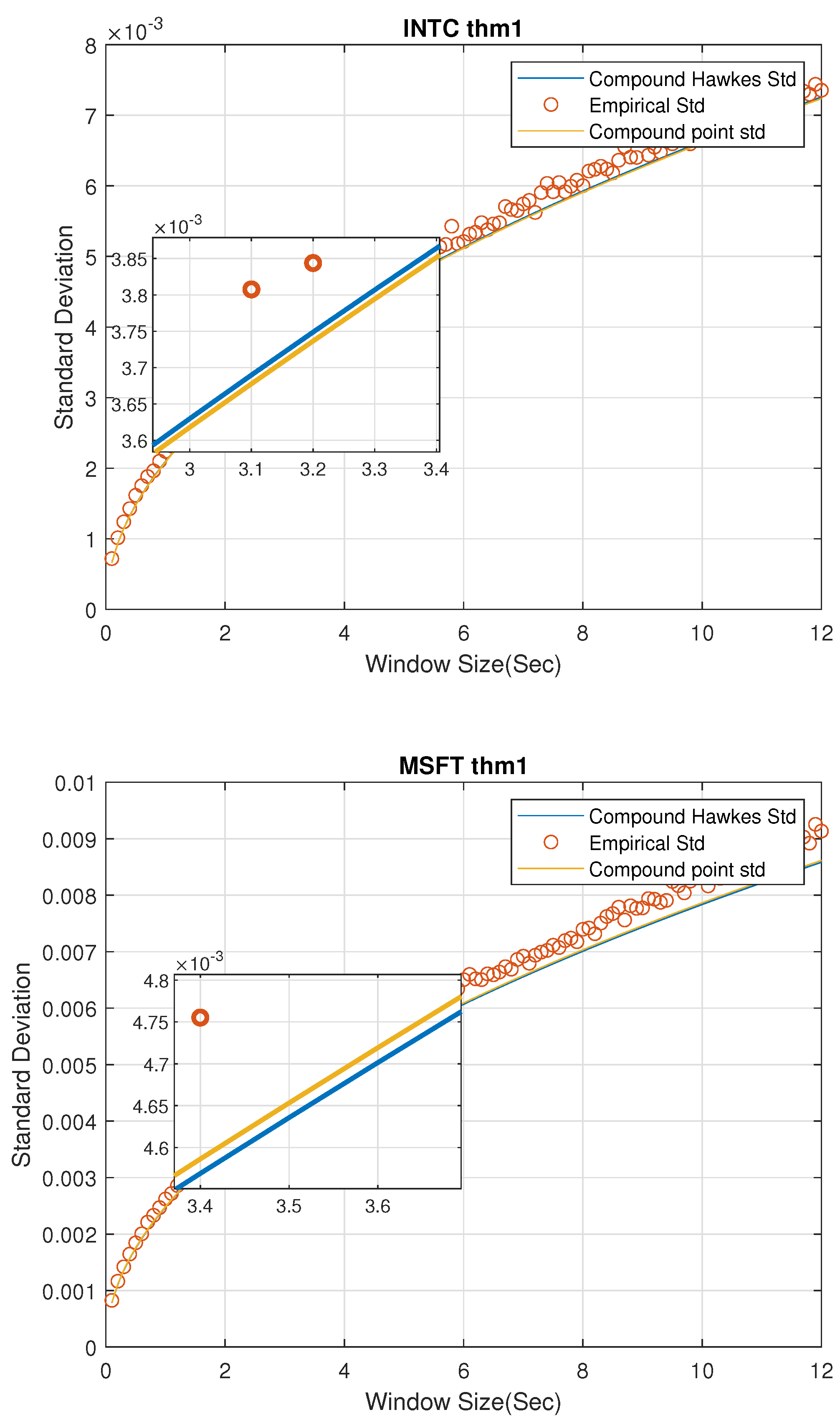
Figure 1 gives a standard deviation comparison of MGCPP, MGCHP, and the raw data for 2 stocks in different window sizes from 0.1 s to 12 s in steps of 0.1 s. First, we could find the MGCPP parameters make the standard deviation of LHS very similar to the RHS for each stocks when
n is large. So, generally speaking, we can say our MGCPP model fits the data well. Second, the MGCPP curve is very close to the MGCHP curve or we could say the simulation results via Intel and Microsoft stocks data are nearly same. It shows that even we do not have a sophisticated intensity function as the Hawkes process, we still can reach a relative good result with a simple point process model. This can help us deal with the computing efficiency problem when using the MGCHP model. We’ll give more quantitative error analysis later.
Remark 7. Since the number of windows decreases as the window size nt increases, we can find that the spread of data increases when the window size increases in Figure 1. For example, when we consider nt = 0.1 s, the number of windows is 234,000. However, a 12-s window size yields 1950 windows which will lead the standard deviation increases. Intuitively,
Figure 1 shows that the standard deviation of MGCHP and MGCPP are very close and both of them fit the real standard deviation very well. Next, we analyze MGCHP and MGCPP models quantitatively.
We computed the mean square error (MSE) of the real standard deviation and theoretical standard deviations in
Table 5. As can be seen from
Table 5, MGCHP model performs better than the MGCPP model with both Intel and Microsoft data. For Intel stock data, the MSE of MGCHP is 17% better than MGCPP and nearly 10% better than MGCPP model with the Microsoft stock data. However, when we compare the order of magnitude of the MSE (−8) with the real standard deviation (−2 and −3), we still can conclude that MGCPP is good enough for the mid-price modeling task.
Recall Equation (
23), we can find the standard deviation and the square root of time step have a linear relationship. So, we can fit the real standard deviation data with the square root curve by using the least-square regression. Then, we can set the regression curve as a benchmark and compare the benchmark coefficients with two stochastic models.
From
Table 6, we can find that the percentage error of both two stochastic models are all smaller than 5% and there is no significant difference between the MGCPP coefficient and the MGCHP coefficient.
Based on the previous analysis, we can conclude that the empirical results of MGCHP and MGCPP are very close and all of them have a very good performance in the mid-price modeling. However, as for the MGCHP, we need to estimate many parameters. As the
Guo and Swishchuk (
2020) mentioned, if we consider a two-dimensional MGCHP (two stocks), we have to estimate 5 parameters for the Hawkes process part and the number of parameters increases dramatically to 55 when we consider a 5-dimensional case (5 stocks). The parameter estimation procedure is also quite time consuming for the MGCHP because of the complicated likelihood function of multivariate Hawkes process. For example, it takes a dozen hours to estimate parameters for a 3-dimensional Hawkes process (21 parameters) with LOBSTER data set by using the maximum likelihood estimation (MLE) and the particle swarm optimization (PSO) method in
Guo and Swishchuk (
2020). On the contrary, the number of parameters for MGCPP is much smaller than the MGCHP. In the two-dimensional case, we have 2 parameters to be estimated in the simple point process part and this increases to 5 parameters in the 5-dimensional case, which is much smaller than 55. The parameter estimation procedure is also quite simple and fast (in several seconds with the same data set) because we do not have to deal with the likelihood function. In this way, from the numerical perspective, the generalized model MGCPP is better than the MGCHP because of the fast and simple estimation procedure.
Remark 8. Note that the numbers of parameters we mentioned before are all parameters of the order flow . Parameters of Markov chains for MGCHP and MGCPP are same.
In general, we showed that the results of the new generalized model are as good as the MGCHP and this kind of generalization has better numerical properties. In the following parts, we will explore the MGCPP model more.
3.3.3. MGCPP with -State Dependent Orders
We give more simulation examples by using the Google, Apple, and Amazon data with the MGCPP model with
-state dependent orders in this section. Thanks to
Swishchuk and Huffman (
2020), we can conclude that the accuracy of the general compound Hawkes process model increases when the number of states increases. For Google, Apple, and Amazon in the LOBSTER data set, the best number of states is 4 to 7. In the previous section, we also showed that simulation results of MGCPP are nearly same as the MGCHP. So, it is reasonable to consider a MGCPP model with 7-state Markov chain here.
We applied the method in
Swishchuk and Huffman (
2020) to calculate the state values
for each stock. First, we compute the changes of mid-price and separate the data into two sets by positive increments or negative increments. Next, we calculate the quantiles for both data sets and split the data set according to the quantiles. If there are identical quantiles, we merge them into one. Then, we set the state values
as the average of mid-price changes located in each quantile (or merged quantile).
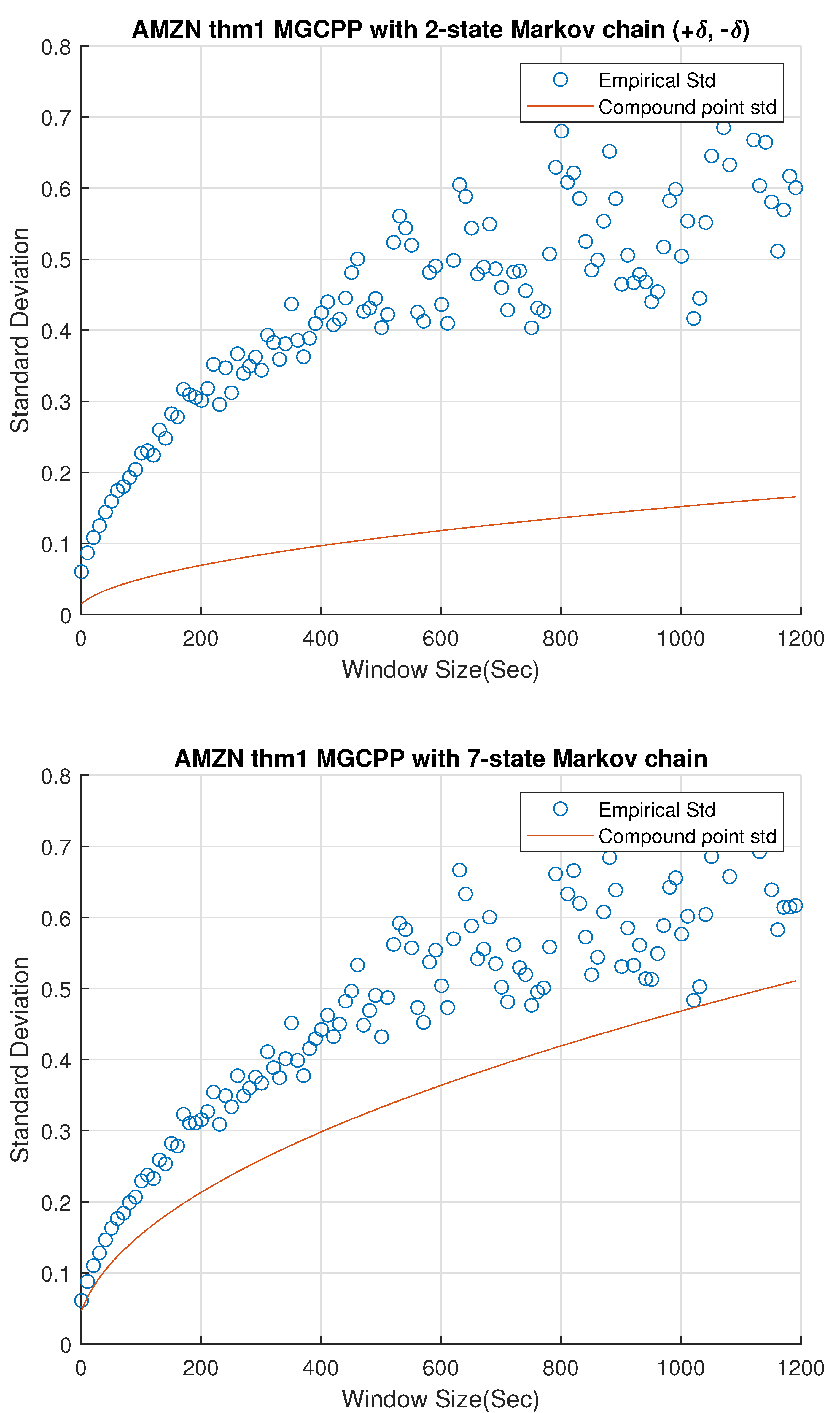
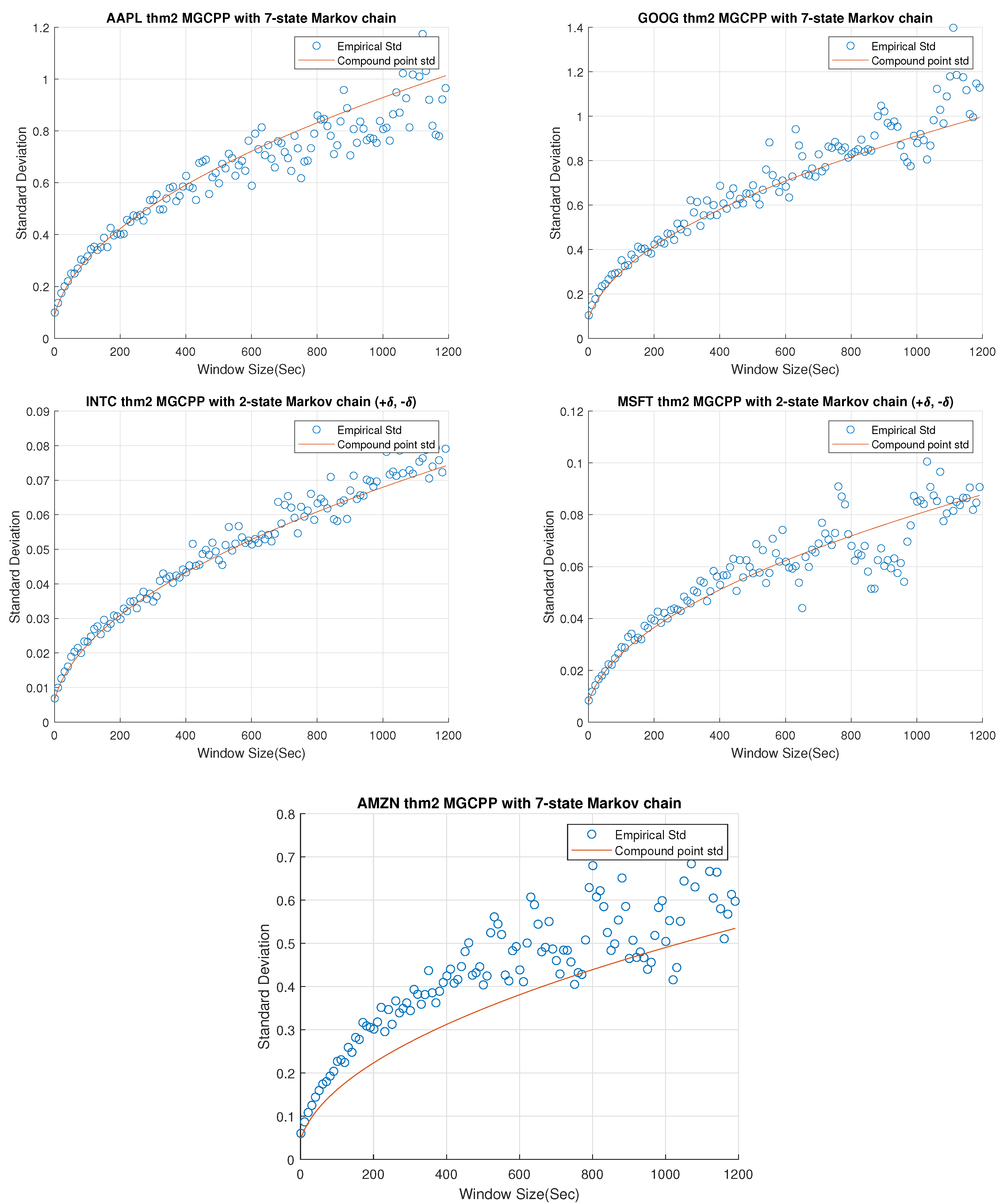
Figure 2,
Figure 3 and
Figure 4 give standard deviation comparisons for MGCPP with 2-state Markov chain and 7-state Markov chain simulated by different tickers’ data. Since the 2-state simulation results here are not as good as the results simulated by Intel’s and Microsoft’s data, we take bigger time steps and window sizes (from 10 s to 20 min with 10 s time step) to capture more dynamics. From figures we can find that the 7-state model has a significant improvement than the 2-state model. Seven-state curves for AAPL and GOOG are very close to the real standard deviation, although the theoretical curve of AMZN is underestimated even with the 7-state model.
Table 7 lists the MSE and coefficients of the 2-state and 7-state models with different tickers. We can find the improvement of 7-state model quantitatively from the table. The results of AAPL and GOOG are good enough for the mid-price modeling. As for AMZN, although we derive a remarkable improvement from 2-state model (74.60% error) to 7-state model (28.29% error), we cannot make the error smaller than 5% or 10%. This is to say, MGCPP model may not be able to capture the full dynamics for AMZN data, but it still can be a strong candidate for modeling the mid-price, which is consistent with the conclusion of compound Hawkes model in
Swishchuk and Huffman (
2020).
Remark 9. The MGCPP is not only a generalization of MGCHP, but also a generalization for all multivariate compound models whose point processes satisfy the Assumptions 1 and 2. The reason we use Hawkes process for comparison is we want to take the advantage of numerical examples in references.