On Computations in Renewal Risk Models—Analytical and Statistical Aspects
Abstract
1. Introduction
2. Model Setup
- 1.
- The function is absolutely continuous on ,
- 2.
- it holds that
3. Analytic Properties
3.1. Feynman-Kac Formulation
3.2. Regularity of Gerber-Shiu Functions
4. Numerical Procedure
4.1. Gambler’s Ruin Problem
4.2. Extended Gerber-Shiu Functional
4.3. Convergence of Numerical Scheme
5. Statistical Complement
5.1. Kernel Estimator
5.2. Uniform Consistency
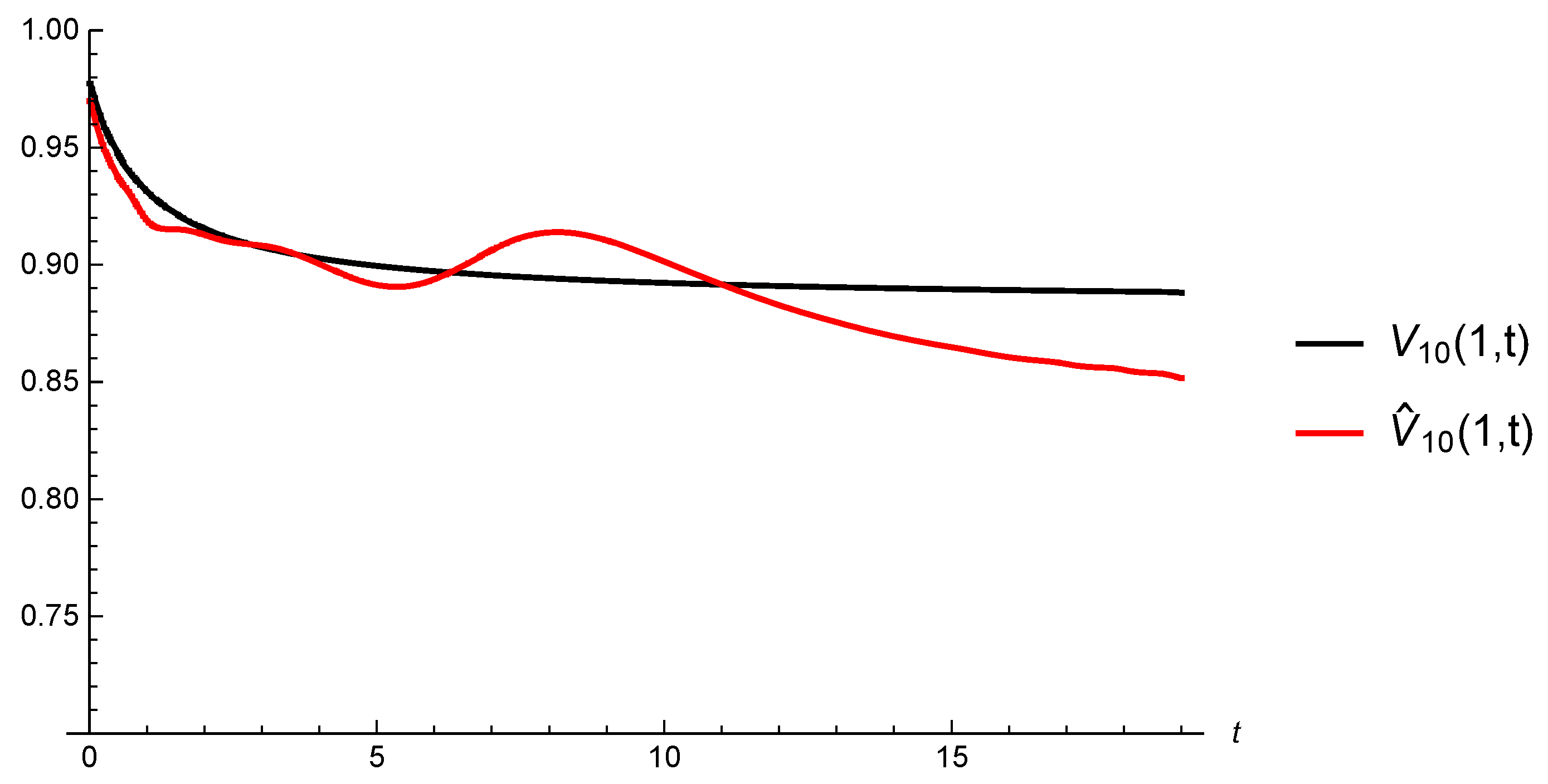
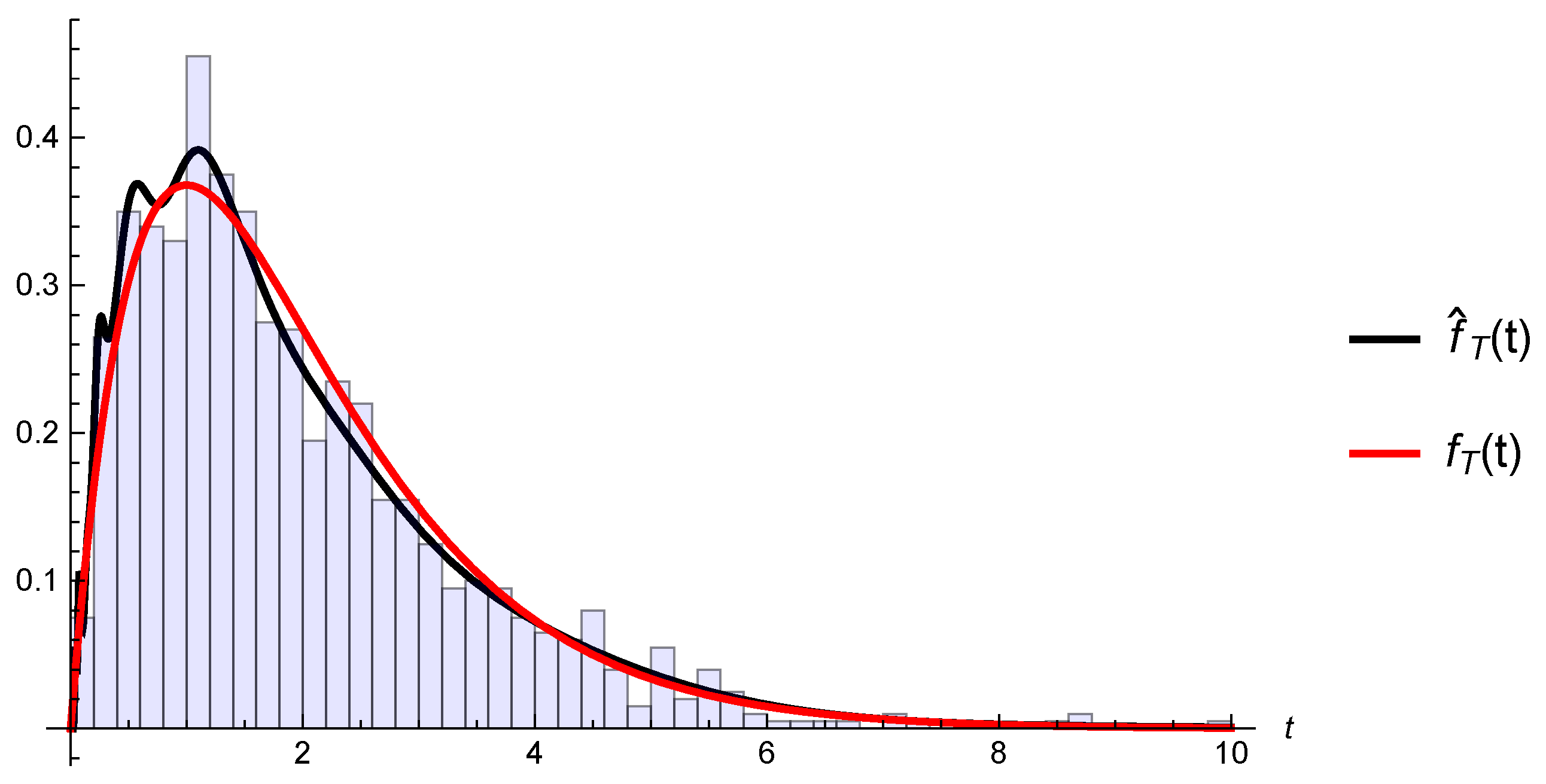
5.3. Convergence of Estimated Gerber-Shiu Functions
| → | c | uniformly, | |
| → | uniformly on compacts inand | ||
| → | uniformly |
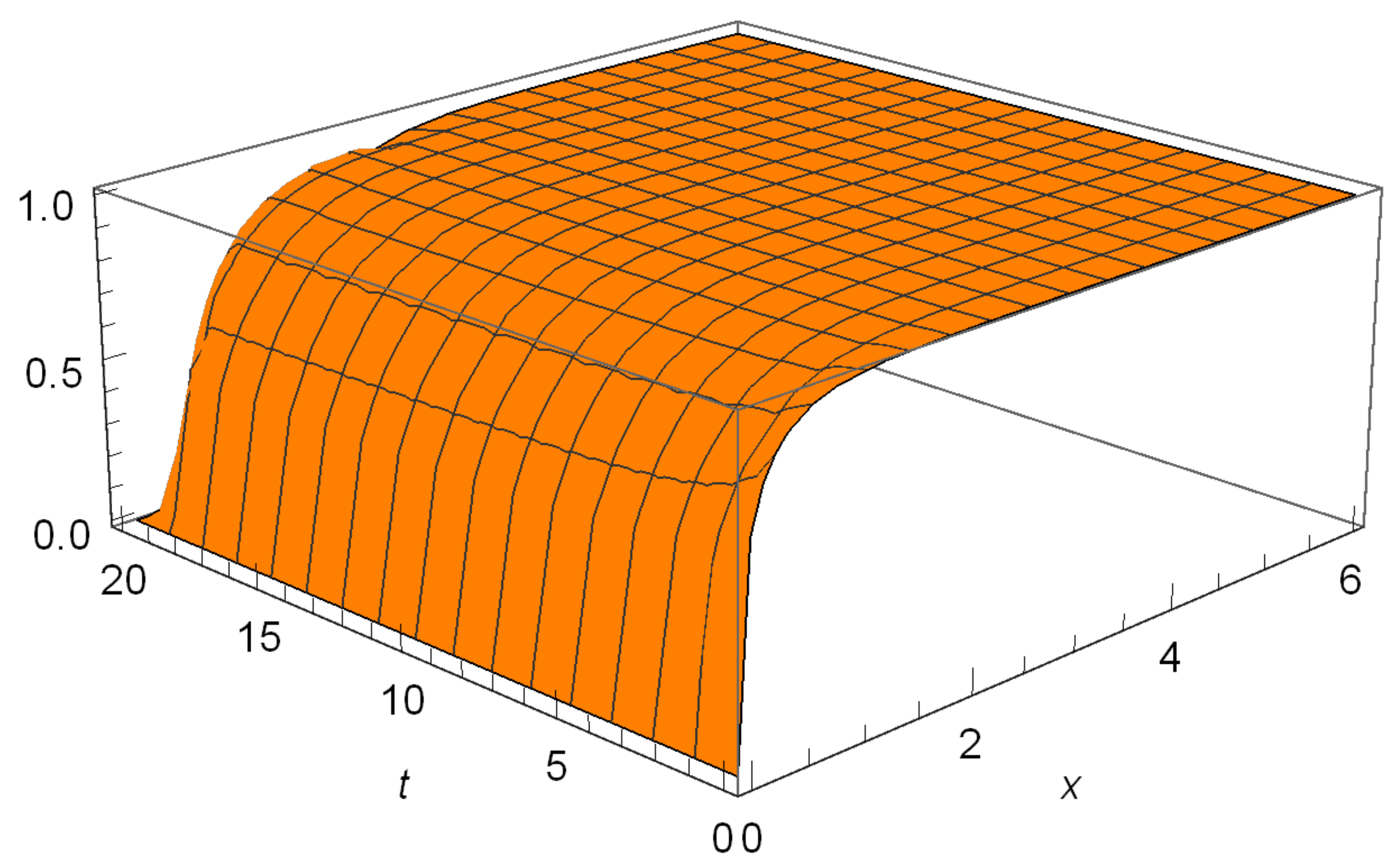
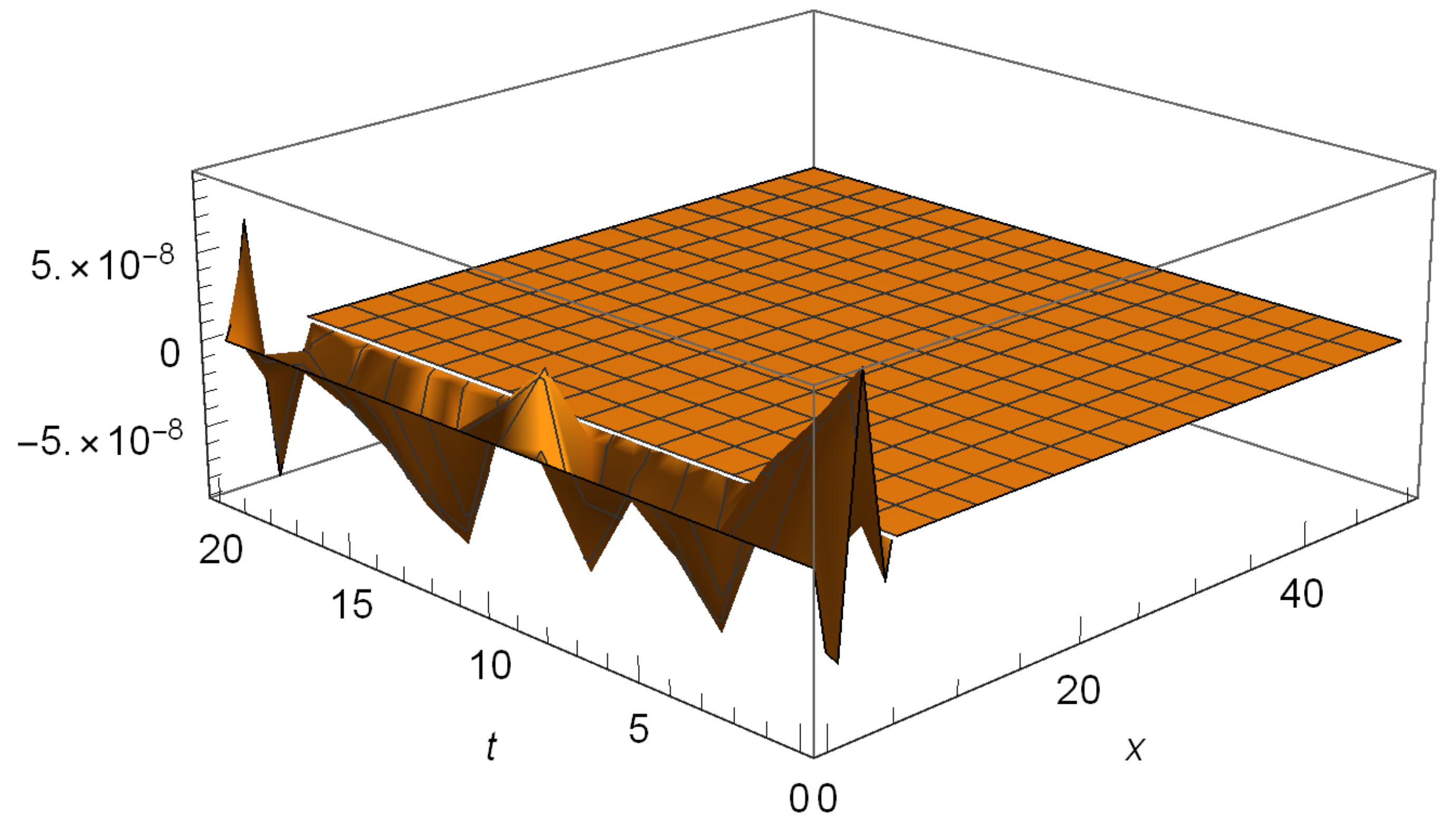
6. Numerical Illustrations
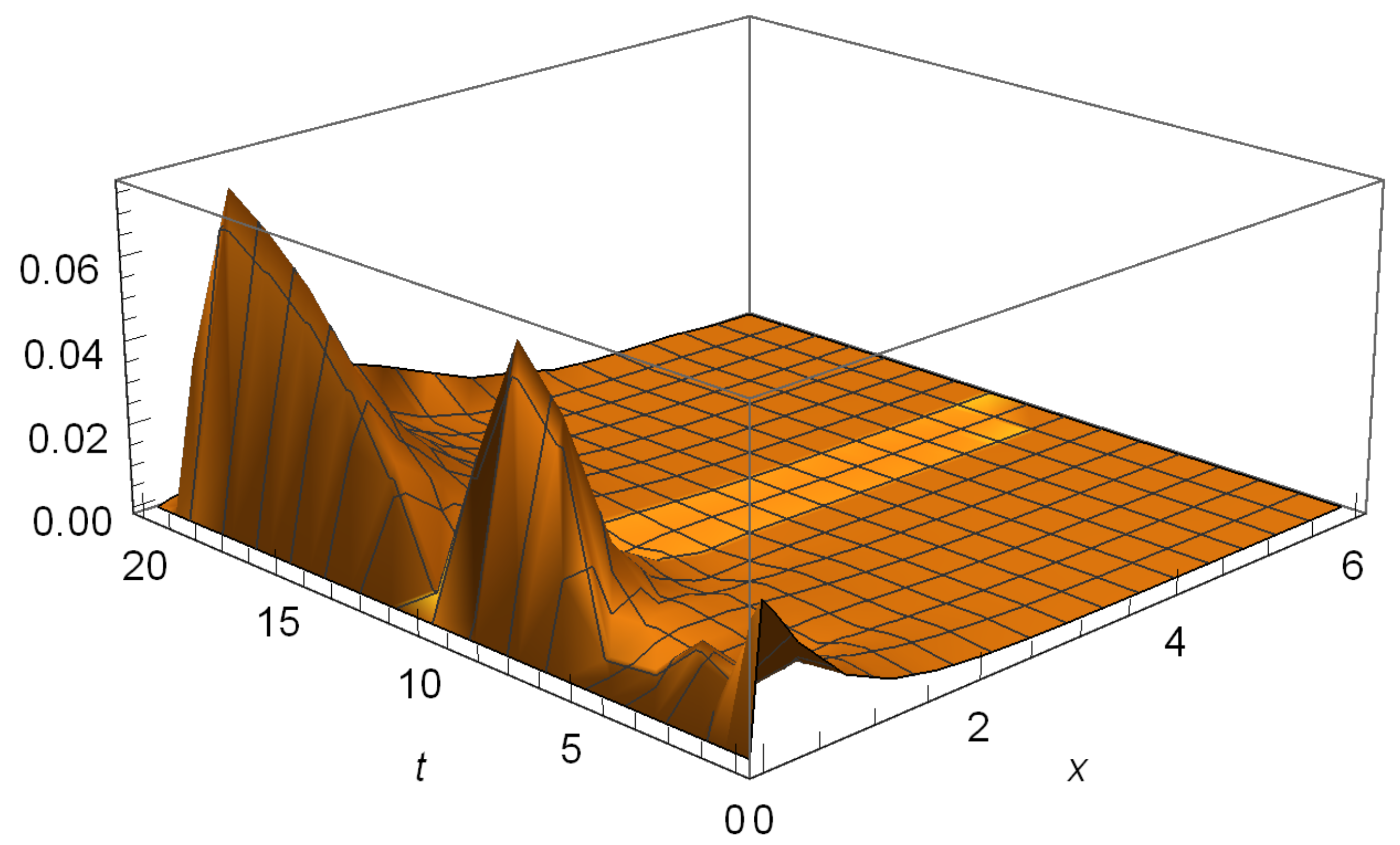
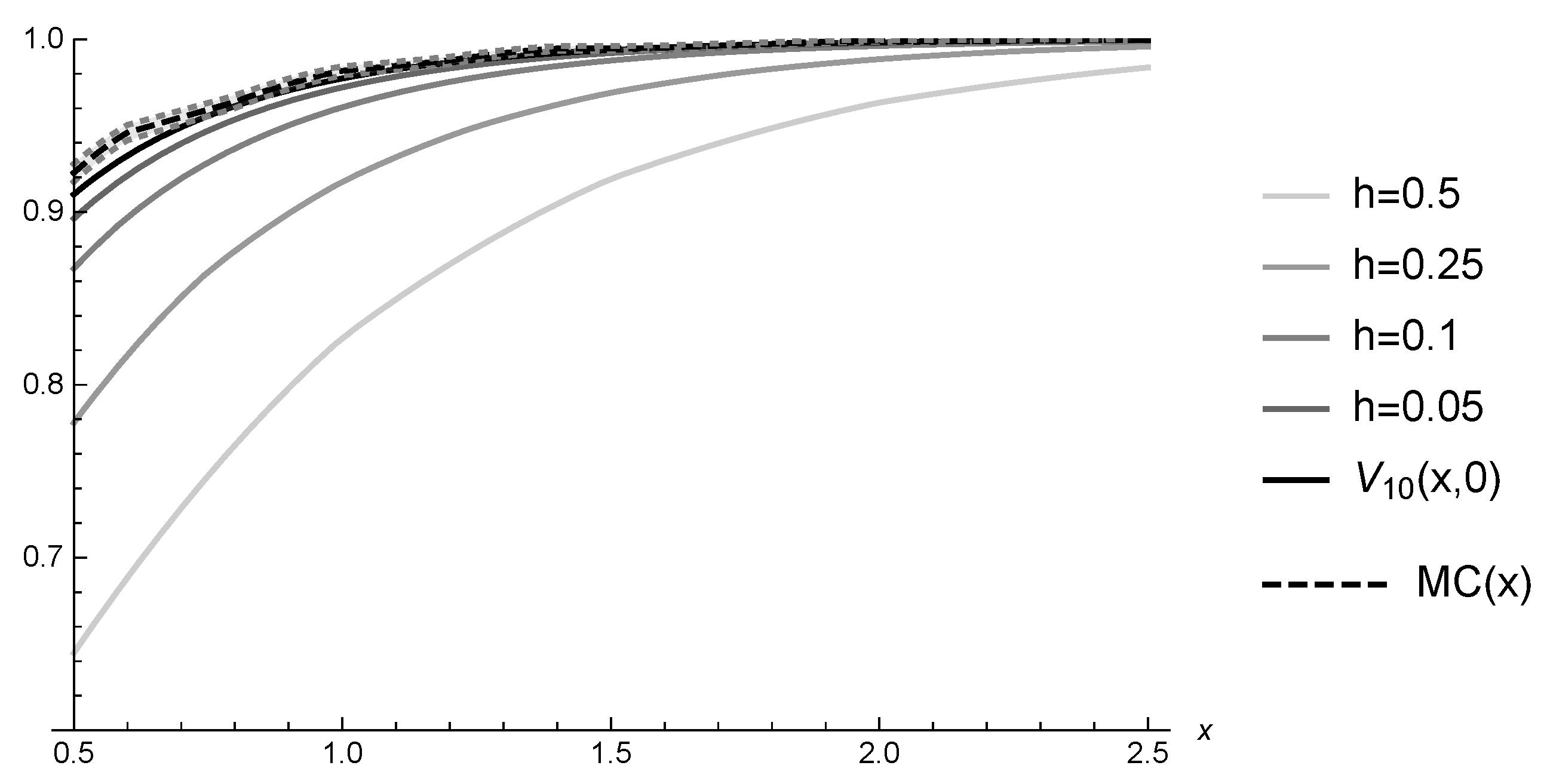
6.1. Hitting Probabilities
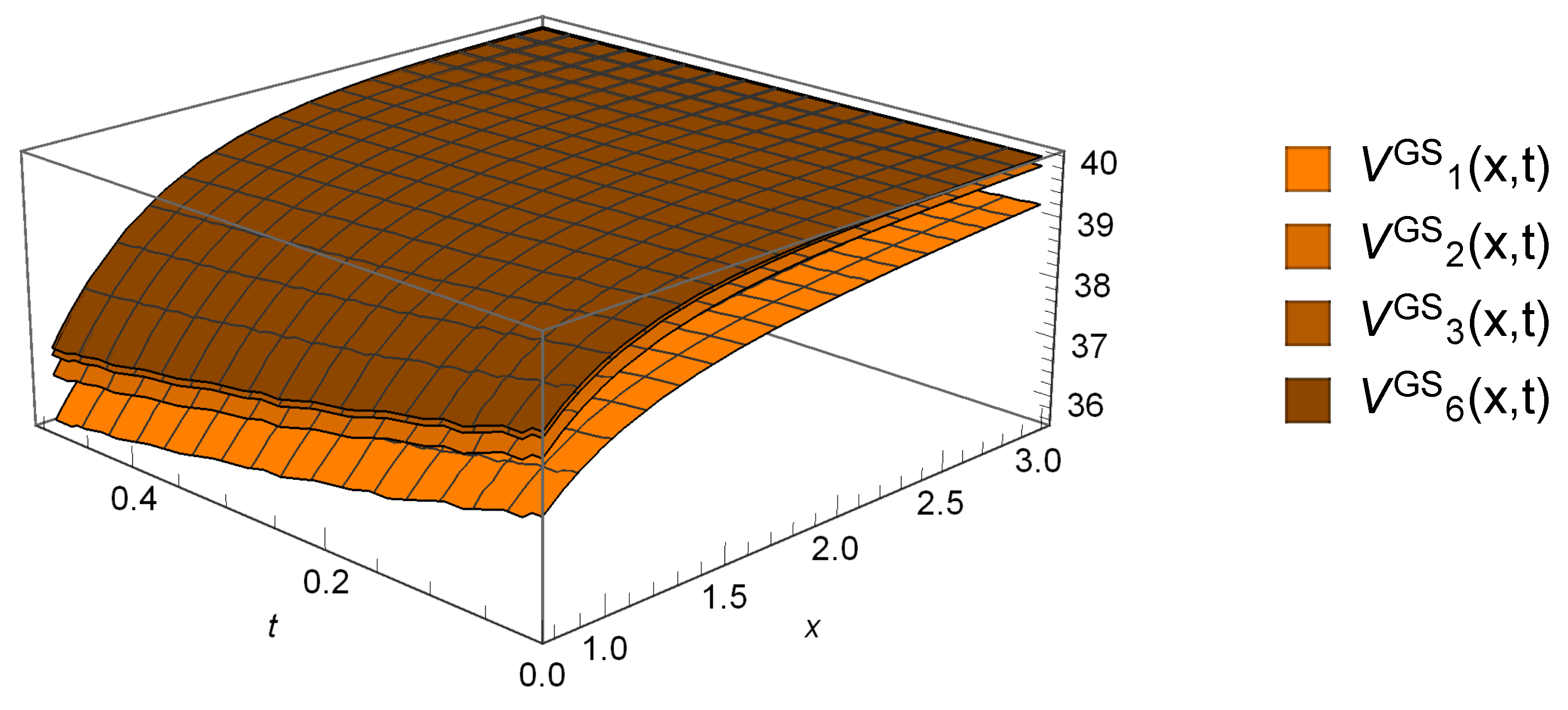
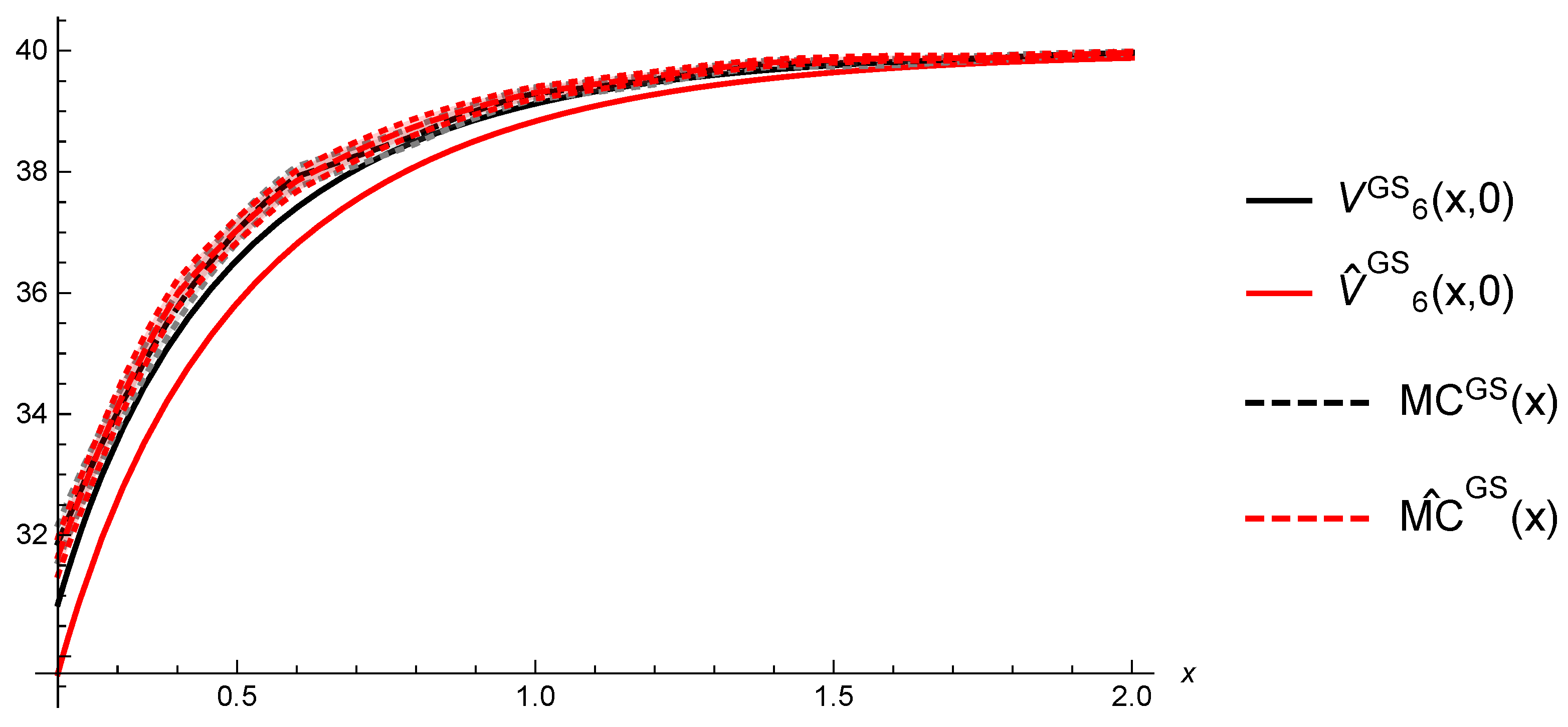
6.2. Gerber-Shiu Functions
7. Conclusions and Discussions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Albrecher, Hansjörg, and Eleni Vatamidou. 2019. Ruin Probability Approximations in Sparre Andersen Models with Completely Monotone Claims. Risks 7: 104. [Google Scholar] [CrossRef]
- Alvarez, Luis, and Larry Shepp. 1998. Optimal harvesting of stochastically fluctuating populations. Journal of Mathematical Biology 37: 155–77. [Google Scholar] [CrossRef]
- Antoniadis, Anestis, Gérard Grégoire, and Guy Nason. 1999. Density and hazard rate estimation for right-censored data by using wavelet methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 61: 63–84. [Google Scholar] [CrossRef]
- Asmussen, Søren, and Hansjörg Albrecher. 2010. Ruin Probabilities, 2nd ed. River Edge: World Scientific. [Google Scholar]
- Asmussen, Søren, Olle Nerman, and Marita Olsson. 1996. Fitting phase-type distributions via the em algorithm. Scandinavian Journal of Statistics 23: 419–41. [Google Scholar]
- Azaïs, Romain, François Dufour, and Anne Gégout-Petit. 2014. Non-parametric estimation of the conditional distribution of the interjumping times for piecewise-deterministic Markov processes. Scandinavian Journal of Statistics 41: 950–69. [Google Scholar] [CrossRef]
- Azaïs, Romain, François Dufour, and Anne Gégout-Petit. 2013. Non-parametric estimation of the jump rate for non-homogeneous marked renewal processes. Annales de l’IHP Probabilités et Statistiques 49: 1204–31. [Google Scholar] [CrossRef]
- Brémaud, Pierre. 1981. Point Processes and Queues. New York and Berlin: Springer. [Google Scholar]
- Davis, Mark. 1993. Markov Models and Optimization. London: Chapman & Hall. [Google Scholar]
- Einmahl, Uwe, and David Mason. 2005. Uniform in bandwidth consistency of kernel-type function estimators. The Annals of Statistics 33: 1380–403. [Google Scholar] [CrossRef]
- Fleming, Wendell Helms, and Halil Mete Soner. 1993. Controlled Markov Processes and Viscosity Solutions. New York: Springer. [Google Scholar]
- Gerber, Hans-Ulrich, and Elias Shiu. 1998. On the time value of ruin. North American Actuarial Journal 2: 48–78. [Google Scholar] [CrossRef]
- Gerber, Hans-Ulrich, and Elias Shiu. 2005. The time value of ruin in a Sparre Andersen model. North American Actuarial Journal 9: 49–84. [Google Scholar] [CrossRef]
- Kallenberg, Olav. 2002. Foundations of Modern Probability. (Probability and its Applications), 2nd ed. New York: Springer. [Google Scholar]
- Kritzer, Peter, Gunther Leobacher, Michaela Szölgyenyi, and Stefan Thonhauser. 2019. Approximation methods for piecewise deterministic Markov processes and their costs. Scandinavian Actuarial Journal 2019: 308–35. [Google Scholar] [CrossRef] [PubMed]
- Kushner, Harold, and Paul Dupuis. 2001. Numerical Methods for Stochastic Control Problems in Continuous Time, 2nd ed. New York: Springer. [Google Scholar]
- Liu, Regina, and John Van Ryzin. 1985. A histogram estimator of the hazard rate with censored data. The Annals of Statistics 13: 592–605. [Google Scholar] [CrossRef]
- Preischl, Michael, Stefan Thonhauser, and Robert Tichy. 2018. Integral equations, quasi-Monte Carlo methods and risk modeling. In Contemporary Computational Mathematics—A Celebration of the 80th birthday of Ian Sloan. Cham: Springer, pp. 1051–74. [Google Scholar]
- Rolski, Tomasz, Hanspeter Schmidli, Volker Schmidt, and Jozef Teugels. 1999. Stochastic Processes for Insurance and Finance. New York: John Wiley & Sons. [Google Scholar]
- Schmidli, Hanspeter. 2017. Risk Theory. Cham: Springer. [Google Scholar]
- Shimizu, Yasutaka. 2012. Non-parametric estimation of the Gerber-Shiu function for the Wiener-Poisson risk model. Scandinavian Actuarial Journal, 56–69. [Google Scholar] [CrossRef]
- Shimizu, Yasutaka, and Zhimin Zhang. 2017. Estimating Gerber-Shiu functions from discretely observed Lévy driven surplus. Insurance: Mathematics and Economics 74: 84–98. [Google Scholar] [CrossRef]
- Silverman, Bernard Walter. 1986. Density Estimation for Statistics and Data Analysis. London: Chapman & Hall, Monographs on Statistics and Applied Probability. [Google Scholar]
- Sparre Andersen, Erik. 1957. On the collective theory of risk in the case of contagion between the claims. Bulletin of the Institute of Mathematics and its Applications 2: 212–19. [Google Scholar]
- Vatamidou, Eleni, Ivo Jean Baptiste François Adan, Maria Vlasiou, and Bert Zwart. 2013. Corrected phase-type approximations of heavy-tailed risk models using perturbation analysis. Insurance: Mathematics and Economics 53: 366–78. [Google Scholar] [CrossRef][Green Version]
- Vatamidou, Eleni, Ivo Jean Baptiste François Adan, Maria Vlasiou, and Bert Zwart. 2014. On the accuracy of phase-type approximations of heavy-tailed risk models. Scandinavian Actuarial Journal 2014: 510–34. [Google Scholar] [CrossRef]
| h | a | n | Y | T | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 10 | 6 | 10 | 1000 | 20 |
| x = 0.5 | x = 1 | x = 1.5 | x = 2 | x = 2.5 | |
|---|---|---|---|---|---|
| 0.9226 | 0.9817 | 0.9946 | 0.9991 | 0.9997 | |
| 0.9228 | 0.9820 | 0.9961 | 0.9991 | 0.9998 | |
| 0.9102 | 0.9773 | 0.9938 | 0.9982 | 0.9995 | |
| 0.8917 | 0.9698 | 0.9907 | 0.9969 | 0.9989 | |
| 0.8961 | 0.9712 | 0.9917 | 0.9977 | 0.9994 | |
| 0.9001 | 0.9733 | 0.9925 | 0.9980 | 0.9995 | |
| 0.9036 | 0.9732 | 0.9915 | 0.9972 | 0.9991 | |
| 0.9159 | 0.9778 | 0.9929 | 0.9982 | 0.9997 | |
| 0.8701 | 0.9620 | 0.9884 | 0.9973 | 0.9994 |
| h | a | n | Y | T | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10 | 2 | 2 | 9 | 6 | 1000 | 20 |
| x = 0.5 | x = 1 | x = 1.5 | x = 2 | x = 2.5 | |
|---|---|---|---|---|---|
| 37.0267 | 39.2955 | 39.7925 | 39.9658 | 39.9869 | |
| 37.0351 | 39.3071 | 39.8494 | 39.9649 | 39.9903 | |
| 36.5443 | 39.1244 | 39.7592 | 39.9317 | 39.9802 | |
| 35.8309 | 38.8363 | 39.6413 | 39.8808 | 39.9577 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strini, J.A.; Thonhauser, S. On Computations in Renewal Risk Models—Analytical and Statistical Aspects. Risks 2020, 8, 24. https://doi.org/10.3390/risks8010024
Strini JA, Thonhauser S. On Computations in Renewal Risk Models—Analytical and Statistical Aspects. Risks. 2020; 8(1):24. https://doi.org/10.3390/risks8010024
Chicago/Turabian StyleStrini, Josef Anton, and Stefan Thonhauser. 2020. "On Computations in Renewal Risk Models—Analytical and Statistical Aspects" Risks 8, no. 1: 24. https://doi.org/10.3390/risks8010024
APA StyleStrini, J. A., & Thonhauser, S. (2020). On Computations in Renewal Risk Models—Analytical and Statistical Aspects. Risks, 8(1), 24. https://doi.org/10.3390/risks8010024





