Loss Reserving Estimation With Correlated Run-Off Triangles in a Quantile Longitudinal Model

Abstract

In this paper, we consider a loss reserving model for a general insurance portfolio consisting of a number of correlated run-off triangles that can be embedded within the quantile regression model for longitudinal data. The model proposes a combination of the between- and within-subportfolios (run-off triangles) estimating functions for regression parameter estimation, which take into account the correlation and variation of the run-off triangles. The proposed method is robust to the error correlation structure, improves the efficiency of parameter estimators, and is useful for the estimation of the reserve risk margin and value at risk (VaR) in actuarial and finance applications.

1. Introduction

The protection of the policyholders and the financial stability of the insurance market industry is a crucial aspect and regulatory authorities intervene to ensure it. Based on Solvency II and IFRS Phase II regulations, each insurance or reinsurance company is obliged to evaluate its insurance liabilities on a risk-adjusted basis to allow for uncertainty in cash flows that arises from the liability of the insurance contracts. Australian Prudential Regulation Authority (APRA) requires estimating a 75th percentile of the distribution of outstanding claims for recording in profit and loss statements and the risk margin should be established on a basis that is intended to secure the insurance liabilities of the insurance company at a given level of sufficiency ${\displaystyle (75\%}$).

In recent years, quantile regression has become a very popular methodology that has incorporated several new reforms in insurance and finance. The least squares estimators investigate only changes in the mean when the entire shape of the claims distribution may change dramatically. Quantile regression characterizes any particular point of a distribution and thus provides a more complete description of the distribution in comparison to linear regression. Quantile regression techniques can differentiate risk factors that lead to high level claims from those that lead to low level claims. Quantile regression estimation may be more efficient than the ordinary least squares when the distribution is not normal. Furthermore, quantile regression is more robust against outliers and does not require the specification of any error distribution. Therefore, quantile regression may be more appropriate than least squares estimation in the context of the insurance industry (see Buchinsky 1998; Koenker 2005).

In the actuarial literature, few papers deal with quantiles. Pitt (2006) used censored regression quantiles to analyze claim termination rates at different quantiles of the distribution of claim duration for income protection insurance. Chan et al. (2008) proposed a robust Bayesian analysis of loss reserves data using the generalized ${\displaystyle t}$-distribution. Dong et al. (2015) presented in detail the use of parametric and nonparametric quantile regression in non-life applications. Nevertheless, the above approaches have been used for univariate quantile regression models and are suitable for a single line of business (single run-off triangle).

In this paper, we consider a quantile regression application in a multivariate context alternative to a multivariate Chain Ladder model for a portfolio of within and between correlated run-off triangles. For a dependent line of business, it is difficult to describe and specify the underlying correlation structure, which may prevent insurance practitioners from using the quantile regression. We propose a reserving problem for a non-life insurance portfolio consisting of several run-off subportfolios corresponding to different lines of business that can be embedded within the quantile regression longitudinal model and can provide solutions to the estimation of more extreme ${\displaystyle VaRs}$ and capital margins.

The remainder of this paper is structured as follows. Section 2 presents the types of dependence (correlation) modeling in loss reserving triangles. In Section 3, we present brief introductions of quantile functions and quantile regression. Section 4 illustrates how correlated run-off triangles can be embedded in a quantile regression longitudinal model. In Section 5, we present a numerical implementation of the longitudinal quantile regression model with two run-off triangles. Section 6 provides the calculation of the risk margin (RM) based on the solvency capital requirement (SCR) estimation and according to the cost-of-capital (CoC) methodology. Finally, in Section 7, some concluding remarks are presented.

2. Dependence (Correlation) Modeling in Loss Run-Off Triangles

In this section, we highlight three types of dependence structures that may appear in loss reserving estimation. In many stochastic claims reserving models, in a single line of business, it is assumed that accident years are independent. In practice, it is evident that different accident years are not independent because of accounting year effects, claims inflation, and other exogenous factors that affect all accident years simultaneously. As pointed out by Ajne (1994) and many other researchers, when dealing with a portfolio with several lines of business, the Chain Ladder predictors for the whole portfolio differ from the sums of the Chain Ladder predictors for the different individual lines of business, because the dependence structure between the subportfolios of a portfolio is not taken into consideration. Dependence modeling was also discussed by Merz et al. (2012).

2.1. Correlation Within Claims Reserving Triangles

Barnett and Zehnwirth (2000) studied calendar year effects within probabilistic trend family models, which allowed calculating distributions of, and correlations between, future payment streams. De Jong (2012), based on time series models, investigated the correlation between accident and calendar years within triangles. In this spirit, Wuthrich (2010) presented a Bayesian inference approach that allows for the study of accounting (calendar) year effects. By restricting to the lognormal approach to chain-ladder-type models, Kuang et al. (2011) proposed a method suitable for cases where there is a sudden change in the economic environment affecting the policies for all accident years in the reserving triangle. Pešta and Okhrin (2014) proposed a generalized time series model that allows for modeling the conditional mean and variance of the claim amounts, for the claims development. They used a copula framework to incorporate modeling dependencies within the loss triangles.

2.2. Correlation Between Claims Reserving Triangles

The dependence structure between lines of business (run-off triangles) that is related to the accurate estimation of risk’s diversification is very important to the solvency capital requirement (SCR) the company should hold in order to remain healthy and avoid holding unnecessarily high levels of capital (see Avanzi et al. (2016b)).

Clark (2006), by using a times series model, estimated the correlation between future payments, due to inflation, in two or more loss reserving run-off triangles, concluding that the payments move with inflation and the variability due to inflation can be related to economic forecast models. When companies have several lines of business, it is useful to examine the presence of possible dependencies within the structure of the company and investigate the financial effect of these dependencies. Barnett and Zehnwirth (2000) proposed a model that allows dependency between all the observations that belong to the same calendar year for each line of business. According to Braun (2004), the correlation between run-off triangles can be attributed to the claims inflation affecting all or most of the run-offs of a portfolio in a similar way. Shi and Frees (2011) used copulas to model the association among multiple run-off triangles and Abdallah et al. (2015) assumed a dependence structure that links the calendar years of different lines of business. Zehnwirth and Barnett (2001) considered a more complicated situation of ${\displaystyle n}$ correlated loss triangles. Braun (2004) extended the distribution-free method of Mack (1993) to estimate the prediction error of the Chain Ladder method for a portfolio of several correlated run-off triangles. Pröhl and Schmidt (2005) proposed a multivariate Chain Ladder method that is suitable for a portfolio consisting of several subportfolios with a certain dependence structure.

By using the theory of linear mixed models, Antonio and Beirlant (2006) built a flexible loss reserving model in the framework of longitudinal data. Quarg and Mack (2004) proposed a bivariate Chain Ladder predictor for the paid and incurred aggregate claims of the same portfolio aiming to reduce the gap between the univariate Chain Ladder predictors for the paid and incurred aggregate claims of the same portfolio. Taylor and Mcguire (2005, 2007) considered the claims reserving problem in a multivariate context and generalized linear models were used to estimate loss reserves of several stochastically dependent lines of business, individually and in aggregate. Schmidt (2006) provided a review on recent multivariate models and methods of loss reserving. Merz and Wüthrich (2008a, 2008b) considered the multivariate Chain Ladder method for a portfolio of ${\displaystyle N}$ correlated run-off triangles based on multivariate age-to-age factors and derived an estimator for the mean square error of prediction for the Chain Ladder predictor of the ultimate claim of the total portfolio. Shi and Frees (2011) demonstrated the role of dependencies in the aggregation of claims from multiple run-off triangles, proposing a copula regression model for the prediction of unpaid losses for dependent lines of business. Zhang (2010) presented a general multivariate stochastic reserving model by using the seemingly unrelated regression technique. This model not only specifies contemporaneous correlation, but also allows structural connections among triangles. Hudecová and Pešta (2013) proposed the application of generalized estimating equations (GEE) for the estimation of claims reserves, where claim triangles are handled as panel data, assuming dependent claim amounts within the same accident year. De Jong (2012) developed and applied a model for loss triangles that facilitates the structuring and measurement of dependence between loss triangles. Bermudez et al. (2013), by using linear regression techniques and copulas, and assuming several dependence structures between lines of business, estimated the risk-based capital reserve for the economic capital requirements under the Standard Model and the Internal Model approach. Their sensitivity analysis on the correlation matrix assumptions between lines of business showed that modifications of the correlation and dependence assumptions have a significant impact on the solvency capital requirement (SCR) estimation, under Solvency II regulations. In insurance applications, normality assumptions may be misleading as a measure of dependency in the tails of the variables. The impact of loss triangle dependence on risk margins was also considered by Hubert et al. (2017), who proposed the FastSUR algorithm, in order to robustify the general multivariate Chain Ladder method of Zhang (2010), where the parameters were estimated using seemingly unrelated regression(SUR). Based on MM-estimators, Peremans et al. (2018) proposed a robust alternative that estimates the SUR parameters in a more outlier resistant way.

Avanzi et al. (2016a, 2016b) proposed a multivariate Tweedie approach to capture cell-wise dependence and the dependency between business segments in the non-life insurance industry, respectively, in loss reserving. In addition, Avanzi et al. (2018) constructed a broad and flexible family of models, where dependency is induced by common shock components. For an extensive analysis of loss reserving techniques, the reader may refer to the books of Taylor (2000), Wuthrich and Merz (2008) and Radtke et al. (2012).

2.3. Correlation Within and Between Claims Reserving Triangles

In actuarial applications, an insurance portfolio is subdivided into several homogeneous lines of business (subportfolios). Losses from a line of business can be viewed as a financial risk. Social and economic environment may affect several lines of business of an insurance portfolio, simultaneously. Thus, we may consider that, in addition to within correlation, insurance lines of business (run-off triangles) are related to each other due to the calendar effects. Zhang et al. (2012) proposed a Bayesian non-linear hierarchical model, where data from individual companies are treated as repeated measurements of various run-off triangles of claims, thus respecting the correlation between successive observations. Shi et al. (2012) examined calendar year effects in a multivariate loss-reserving context through a log-normal model. They used random effects to accommodate the correlation due to accounting year effects within and between run-off triangles. This specification is in line with De Jong (2012), who introduced the calendar year effects through the correlation matrix. In the spirit of Shi et al. (2012), Merz and Wüthrich (2008a) defined a multivariate log-normal model that allows modeling both dependence between different run-off triangles and dependence within run-off triangles, such as claims inflation.

2.4. Why Quantile Regression Models with Correlated Run-off Triangles?

In the insurance practice, some regulation rules indicate that some changes over time occurred across the claim distribution. Therefore, it is very important to investigate these changes at different points of the distributions. For example, Australian insurance regulations require that a risk margin should be established at 75% percentile of the discounted value less than the best estimate (see Pitt (2006)). Most studies consider only correlation as a measure of dependency, focusing on reserving at mid-range ${\displaystyle VaRs}$. Consideration of capital margins at more extreme ${\displaystyle VaRs}$ opens up the question of tail dependency, and a whole new field of exploration (see Avanzi et al. (2016b)).

Each quantile regression characterizes a particular point of a distribution, and thus provides more complete description of the distribution, taking into account the correlations in the tail of distributions. Furthermore, quantile regression is more robust against outliers and does not require specifying any error distribution (see Fu and Wang (2012)).

One implication of our model is the diversification effect of a portfolio of reserve risks and can be used as a risk measure with applications in actuarial science. Practically, our quantile approach leads to a provision of a specified probability, say 80%, sufficient to cover the run-off claims. Adding the necessary margin to the central estimate, the evaluation of the claims liability is provided and the provision is sufficient to cover the future liabilities.

3. Preliminaries on Quantile Functions and on Quantile Regression

Here, we provide some preliminaries on quantile regression that are needed below for loss reserving estimation.

3.1. Quantile Function

For a random variable ${\displaystyle Y}$ with cumulative distribution function ${\displaystyle F_Y\left(y\right)=P(Y\le y)}$, the ${\displaystyle \theta }$th quantile of ${\displaystyle Y}$ is defined as the inverse function

$$\begin{array}{c}\hfill Q_Y\left(\theta \right)=F_Y^{-1}\left(\theta \right)=inf\{y:F\left(y\right)\ge \theta \},\end{array}$$

(1)

where ${\displaystyle 0\le \theta \le 1}$. In case that ${\displaystyle F(·)}$ is a strictly increasing and continuous probability distribution function, ${\displaystyle F_Y^{-1}\left(\theta \right)}$ is the unique real number ${\displaystyle t}$ such that ${\displaystyle F\left(t\right)=\theta }$ (Gilchrist 2000).

Quantiles are connected with operations of ordering the sample observations that are used to define them. For a random sample ${\displaystyle \{y_1,\cdots ,y_n\}}$ of ${\displaystyle Y}$, the general ${\displaystyle \theta }$th sample quantile ${\displaystyle \xi \left(\theta \right)}$ may be formulated as the solution of the optimization problem

$$\underset{\xi \in \Re }{min}\sum _{i=1}^n{\rho }_{\theta }(y_i-\xi ),where{\rho }_{\theta }\left(z\right)=z(\theta -I(z<0))$$

(2)

and ${\displaystyle I(·)}$ denotes the indicator function. This loss function is an asymmetric absolute loss function because it is a weighted sum of absolute deviations, where the weight ${\displaystyle (1-\theta )}$ is assigned to the negative deviations while the weight ${\displaystyle \theta }$ is assigned to the positive deviations.

3.2. Quantile Regression Estimation

In the regression case, we assume a sample ${\displaystyle (Y_i,x_i)}$, ${\displaystyle i=1,...,n}$, where ${\displaystyle Y_i}$ is the dependent variable, ${\displaystyle x_i}$ is a ${\displaystyle k\times 1}$ vector of explanatory variables, and ${\displaystyle \mathbf{\beta }}$ is a ${\displaystyle k\times 1}$ vector of coefficients. The general linear model has the form

$$Y_i=x_i^T\mathbf{\beta }+u_i,andE\left(Y_i\right|x_i)=x_i^T\mathbf{\beta },$$

(3)

while the ${\displaystyle \theta }$th conditional quantile of ${\displaystyle Y_i}$ given ${\displaystyle x_i}$ can be written as (see Koenker and Basset 1982)

$$Q_{Y_i}\left(\theta \right|x_i)=x_i^T{\mathbf{\beta }}_{\theta }.$$

(4)

We consider the ${\displaystyle \theta }$th sample quantile ${\displaystyle {\widehat{q}}_i\left(\theta \right)}$. Mosteller proved the limiting normality of ${\displaystyle {\widehat{\xi }}_{Y_i|x_i}^{\theta }}$ that provides a realization of the least estimation of the form

$${\widehat{q}}_i^{\theta }=x_i^T{\mathbf{\beta }}_{\theta }+u_i,$$

(5)

where ${\displaystyle \mathbf{\beta }\left(\theta \right)}$ is a vector to be estimated and ${\displaystyle u_i}$ is the error term. The linear conditional quantile function, ${\displaystyle Q\left(\theta \right|X=x)=x^{\prime }\beta \left(\theta \right)}$, can be estimated by solving

$$\underset{\mathbf{\beta }}{min}\frac{1}{n}\sum _{i=1}^n{\rho }_{\theta }\left(u_i\right)=\underset{\left(\mathbf{\beta }\right)}{min}\left(\sum _{i:y_i\ge x_i^{{}^{\prime }}\mathbf{\beta }}^{}\theta |Y_i-x_i^T\mathbf{\beta }|+\sum _{i:Y_i<x_i^T\mathbf{\beta }}^{}(1-\theta )|Y_i-x_i^T\mathbf{\beta }|\right),$$

(6)

where ${\displaystyle {\rho }_{\theta }\left(t\right)}$ is already defined in Equation (2) and ${\displaystyle I(·)}$ is the indicator function for any quantile ${\displaystyle \theta \in (0,1)}$. The case ${\displaystyle \theta =1/2}$, which minimizes the sum of absolute residuals, corresponds to median regression, which is also known as ${\displaystyle L_1}$ regression. The minimization of Equation (6) was produced by Koenker and D’Orey (1994).

Under certain conditions, for independent observations, the asymptotic variances for ${\displaystyle u_i}$ can be obtained as (see Buchinsky 1998)

$$w_{\theta }=\frac{\theta (1-\theta )}{n{f}^2\left(F^{-1}\left(\theta \right)\right)}$$

(7)

and the covariance matrix of ${\displaystyle {\widehat{\mathbf{\beta }}}_{\theta }}$ is

$${\widehat{\Sigma }}_{\theta }={\left(X^T{\mathsf{\Omega }}_{\theta }^{-1}X\right)}^{-1},with{\mathsf{\Omega }}_{\theta }=w_{\theta }.I_{n\times n}.$$

(8)

With quantile regression, we can show how various financial characteristics are different at different quantiles. Thus, the quantile regression method allows the marginal effects to change for claims at different points in the conditional distribution by estimating ${\displaystyle {\mathbf{\beta }}_p}$ using several different values of ${\displaystyle p}$, ${\displaystyle p\in (0,1)}$. This means that the quantile regression allows for parameter heterogeneity across different types of claims.

4. Correlated Run-Off Triangles in a Quantile Longitudinal Model

The reserving procedure for multiple run-off triangles is an important issue of an insurance company because the connections among the triangles may show correlations which are initially unknown. The correlations of different lines of business may produce more efficient estimations for the total reserve. If for example the two run-off triangles are positively correlated, then the variability of the total reserves exceeds the sum of variabilities of the total reserve from each triangle. Ajne (1994) noted the commonly used approach in actuarial practice, which is the division of the portfolio into several subportfolios and then making calculations using each single line of business. However, this method ignores the dependencies among the subportfolios.

When the run-off triangles are linked with a known structure, such as the paid and incurred triangles, then the Munich Chain Ladder (MuCL) model by Quarg and Mack (2004) is a good method of estimation. Moreover, instead of studying the structural correlations, the correlations between the triangles is an important issue and several papers have been produced (e.g., Braun (2004); Kremer (2005); Schmidt (2006); Merz and Wüthrich (2008a, 2008b)). According to Holmberg (1994), correlations in a run-off triangle may arise among losses as they develop over time or in different accident years. Other authors have studied correlations over calendar year incorporating the trends of inflation which appear. Harrison and Hulin (1989) used generalized estimating equations (GEE) as a promised analytic tool that takes into consideration the correlation of responses within a specific subject for response variables. A more interesting characteristic of these equations is the flexibility they have to analyze not normally distributed response variables.

Suppose that ${\displaystyle N}$ run-off triangles are available and ${\displaystyle i\in \{1,2,\cdots ,N\}}$ refers to the ${\displaystyle i}$th triangle while ${\displaystyle r\in \{1,2,\cdots ,I\}}$ refers to the accident year and ${\displaystyle j\in \{1,2,\cdots ,I\}}$ refers to the development year. Denote ${\displaystyle Y_{rj}={(Y_{rj}^{\left(1\right)},\cdots ,Y_{rj}^{\left(N\right)})}^T}$ the ${\displaystyle n_N\times 1}$ vector with the incremental losses at accident year ${\displaystyle r}$ and development year ${\displaystyle j}$ for all triangles ${\displaystyle N}$.

Denote ${\displaystyle D=\{Y_{rj},r+j\le I+1,1\le r\le I,1\le j\le I\}}$ as the observed losses, ${\displaystyle D_{·,j}=\{Y_{rj},1\le r\le I,j\le k\}}$ as the losses up to development year ${\displaystyle k}$ (including it), and ${\displaystyle D_{r,j}=\{Y_{rj},k\le j\}}$ as the losses for accident year ${\displaystyle r}$ up to development year ${\displaystyle j}$ (including it). According to the data, the sets ${\displaystyle D_{·,j}}$ and ${\displaystyle D_{r,j}}$ are the observed values and should be used to estimate the adequate reserve to fund losses that have been incurred but not yet developed.

Here, we are not going to use a triangulation form to model the data. Let ${\displaystyle y_{ik}}$ be the ${\displaystyle k}$th measurement for the ${\displaystyle i}$th subject (triangle), which describes the total claims amount or the number of claims at the ${\displaystyle i}$ run-off triangle for ${\displaystyle i=1,\cdots ,N}$, ${\displaystyle k=1,\cdots ,n_i}$ where ${\displaystyle n_i}$ is the number of the observed data of the triangle ${\displaystyle i}$. We consider the case where longitudinal data analyses are based on a linear regression model such as

$$\begin{array}{c}\hfill y_{ik}=x_{ik}^T\mathbf{\beta }+{ϵ}_{ik}={\beta }_1{x}_{ik1}+{\beta }_2{x}_{ik2}+\cdots +{\beta }_p{x}_{ikp}+{ϵ}_{ik},\end{array}$$

(9)

where ${\displaystyle \mathbf{\beta }={({\beta }_1,\cdots ,{\beta }_p)}^T}$ is a p-vector of unknown regression coefficients while ${\displaystyle {ϵ}_{ik}}$ is a random variable with mean zero and represents the deviation of the response from the model prediction ${\displaystyle x_{ik}^T\mathbf{\beta }}$. Usually, ${\displaystyle x_{ik1}=1}$ for all ${\displaystyle i=1,\cdots ,N}$ and all ${\displaystyle k=1,\cdots ,n_i}$ and then the coefficient ${\displaystyle {\beta }_1}$ is the intercept term of the regression model. For the rest of the explanatory variables, ${\displaystyle x_{ikl}=1}$, for ${\displaystyle i=1,\cdots ,N}$, ${\displaystyle k=1,\cdots ,n_i}$ and ${\displaystyle l=1,\cdots p}$, if the observation ${\displaystyle y_{ik}}$ corresponds to ${\displaystyle i}$ triangle, for accident year ${\displaystyle r}$ or development year ${\displaystyle j}$ (in Table 1); otherwise, ${\displaystyle x_{ikj}=0}$. For more details, see Christofides (1990).

Table 1. Representation of ${\displaystyle N}$ run-off triangles.

Accident	Development Year j
Yearr	1	2	${\displaystyle \cdots }$	j	${\displaystyle \cdots }$	I${\displaystyle -}$1	I
1	${\displaystyle Y_{11}}$	${\displaystyle Y_{12}}$	${\displaystyle \cdots }$	${\displaystyle Y_{1j}}$	${\displaystyle \cdots }$	${\displaystyle Y_{1,I-1}}$	${\displaystyle Y_{1I}}$
2	${\displaystyle Y_{21}}$	${\displaystyle Y_{22}}$	${\displaystyle \cdots }$	${\displaystyle Y_{2j}}$	${\displaystyle \cdots }$	${\displaystyle Y_{2,I-1}}$
${\displaystyle ⋮}$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$
r	${\displaystyle Y_{r1}}$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle Y_{r,I+1-r}}$
${\displaystyle ⋮}$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$
I	${\displaystyle Y_{I1}}$

In the classical linear model, the ${\displaystyle {ϵ}_{ik}}$ would be mutually independent ${\displaystyle N(0,{\sigma }^2)}$ random variables and represent the error term of the model. Mathematically, the ${\displaystyle Cov(y_{ij},y_{ik})}$ of two different observations of the same subject, is not equal to zero. In the longitudinal structure the errors ${\displaystyle {ϵ}_{ik}}$ are expected to be correlated within subjects (see Diggle et al. 2002). The data for the ${\displaystyle N}$ run off triangles are displayed in Table 2.

Table 2. N Run-off Triangles in a Longitudinal Form.

Subject	Observation	Response	Covariates
1	1	${\displaystyle y_{11}}$	${\displaystyle x_{111}}$	${\displaystyle \cdots }$	${\displaystyle x_{11p}}$
1	2	${\displaystyle y_{12}}$	${\displaystyle x_{121}}$	${\displaystyle \cdots }$	${\displaystyle x_{12p}}$
${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$
1	${\displaystyle n_1}$	${\displaystyle y_{1n_1}}$	${\displaystyle x_{1n_{1}1}}$	${\displaystyle \cdots }$	${\displaystyle x_{1n_{1}p}}$
${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$
${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$
N	1	${\displaystyle y_{N1}}$	${\displaystyle x_{N11}}$	${\displaystyle \cdots }$	${\displaystyle x_{N1p}}$
N	2	${\displaystyle y_{N2}}$	${\displaystyle x_{N21}}$	${\displaystyle \cdots }$	${\displaystyle x_{N2p}}$
${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$	${\displaystyle \cdots }$
N	${\displaystyle n_N}$	${\displaystyle y_{N{n}_N}}$	${\displaystyle x_{N{n}_{N}1}}$	${\displaystyle \cdots }$	${\displaystyle x_{N{n}_{N}p}}$

Using matrices, the regression equation for the ${\displaystyle i}$th subject has the following form:

$$\begin{array}{c}\hfill Y_i=X_i^T\mathbf{\beta }+{\mathbf{ϵ}}_i,\end{array}$$

(10)

where ${\displaystyle X_i^T}$ is a ${\displaystyle n_i\times p}$ matrix and ${\displaystyle {\mathbf{ϵ}}_i={({ϵ}_{i1},\cdots ,{ϵ}_{i{n}_i})}^T}$.

Let ${\displaystyle X}$ be an ${\displaystyle \sum _{i=1}^N{n}_i\times p}$ matrix of explanatory variables and ${\displaystyle {\sigma }^{2}V}$ be a block-diagonal matrix with non-zero ${\displaystyle n_i\times n_i}$ blocks ${\displaystyle {\sigma }^2{V}_i}$, each representing the variance-covariance matrix for the vector of measurements on the ${\displaystyle i}$th subject. Then, ${\displaystyle y={(y_1,\cdots ,y_N)}^T}$ is a realization of a multivariate Gaussian random vector ${\displaystyle Y}$, with

$$\begin{array}{c}\hfill Y\sim N_p(X\mathbf{\beta },{\sigma }^{2}V).\end{array}$$

(11)

In case we want to analyze data generated by the model in Equation (11), the block-diagonal structure of ${\displaystyle {\sigma }^{2}V}$ is very important, because we use each subject in order to estimate ${\displaystyle {\sigma }^{2}V}$ without making any parametric assumptions about this form. The replication across the subjects is a very crucial characteristic because it affects the structure of the matrix ${\displaystyle {\sigma }^{2}V}$ (Diggle et al. 2002).

4.1. Quantile Regression with Longitudinal Data

By considering the linear quantile regression model of Chen et al. (2004), Fu and Wang (2012) proposed a combination of the between and within subject estimating functions for parameter estimation, which takes into account the correlations and variation of the repeated measurements for subjects. Their model is an extension of the univariate quantile regression proposed by Wang et al. (2009) and Pang et al. (2012). Let ${\displaystyle y_{ik}}$ be the ${\displaystyle k}$th measurement for the ${\displaystyle i}$th subject, where ${\displaystyle k=1,\cdots ,n_i}$ and ${\displaystyle i=1,\cdots ,N}$. We also suppose that ${\displaystyle x_{ik}}$ is the corresponding covariate vector and measurements from the same subject are dependent while those from different subjects are independent. We assume that the ${\displaystyle 100\theta }$th quantile of ${\displaystyle y_{ik}}$ is ${\displaystyle x_{ik}^T\mathbf{\beta }}$, where ${\displaystyle \mathbf{\beta }}$ is a ${\displaystyle p\times 1}$ unknown parameter vector. Using this notation, we consider the following model for the conditional quantile functions

$$Q_{\theta }\left(y_{ik}\right|x_{ik})=x_{ik}^T{\mathbf{\beta }}_0,$$

(12)

where ${\displaystyle {\mathbf{\beta }}_0}$ is the true value of the vector ${\displaystyle \mathbf{\beta }}$. Let the error term ${\displaystyle {ϵ}_{ik}=y_{ik}-x_{ik}^T{\mathbf{\beta }}_0}$, which satisfies the condition ${\displaystyle P({ϵ}_{ik}\le 0)=\theta }$. What is of interest is finding an efficient estimate for the unknown vector ${\displaystyle \mathbf{\beta }}$ for a particular value of ${\displaystyle \theta }$. According to Chen et al. (2004), under the independence working model assumption, the estimates ${\displaystyle {\widehat{\mathbf{\beta }}}_I}$ are obtained by minimizing the function

$$L_{\theta }\left(\mathbf{\beta }\right)=\sum _{i=1}^N\sum _{k=1}^{n_i}{\rho }_{\theta }(y_{ik}-x_{ik}^T\mathbf{\beta }).$$

(13)

We differentiate Equation (13) with respect to ${\displaystyle \mathbf{\beta }}$ and take the following estimating functions to make inferences about the unknown vector ${\displaystyle \mathbf{\beta }}$:

$$\begin{array}{c}\hfill W_{\theta }\left(\mathbf{\beta }\right)=\sum _{i=1}^N\sum _{k=1}^{n_i}{x}_{ik}{S}_{ik}\end{array}$$

where ${\displaystyle S_{ik}=\theta -I(y_{ik}-x_{ik}^T\mathbf{\beta }\le 0)}$ is a discontinuous function which takes the value ${\displaystyle \theta -1}$ when ${\displaystyle y_{ik}-x_{ik}^T\mathbf{\beta }\le 0}$ and the value ${\displaystyle \theta }$ otherwise.

4.2. The Uniform Correlation Model

In the uniform correlation model (also known as exchangeable or compound symmetry correlation model), it is assumed that there is correlation, ${\displaystyle \rho }$, between any two measurements on the same subject. In matrix notation, this corresponds to

$$\begin{array}{c}\hfill V_i=(1-\rho )I_{n_i}+\rho J_{n_i},\end{array}$$

(14)

where ${\displaystyle I_{n_i}}$ denotes the ${\displaystyle n_i\times n_i}$ identity matrix and ${\displaystyle J_{n_i}}$ the ${\displaystyle n_i\times n_i}$ matrix all of whose elements are 1 (Searle et al. 1992). To justify the uniform correlation model we should think that the observed measurements, ${\displaystyle y_{ik}}$, are realizations of random variables, ${\displaystyle Y_{ik}}$. However,

$$\begin{array}{c}\hfill Y_{ik}={\mu }_{ik}+U_i+Z_{ik},i=1,\cdots ,N,k=1,\cdots ,n_i,\end{array}$$

(15)

where ${\displaystyle {\mu }_{ik}=E\left[Y_{ik}\right]}$, ${\displaystyle U_i}$ are mutually independent ${\displaystyle N(0,v^2)}$ random variables, ${\displaystyle Z_{ik}}$ are mutually independent ${\displaystyle N(0,t^2)}$ random variables, and ${\displaystyle U_i}$ and ${\displaystyle Z_{ik}}$ are independent of each other. We should mention that Equation (15) gives a simple interpretation of the uniform correlation model as one in which a linear regression model for the mean response incorporates a random intercept term which has variance ${\displaystyle t^2}$ between the subjects.

Theorem 1.

In the case of modeling the correlation between the same subject, we assume that ${\displaystyle P({ϵ}_{ik}\le 0,{ϵ}_{il}\le 0)=\delta }$ for any ${\displaystyle k\ne l}$ and the covariance matrix of ${\displaystyle S_i={(S_{i1},\cdots ,S_{i{n}_i})}^T}$ is given by

$$V_i=(\theta -{\theta }^2)[(1-\rho )I_{n_i}+\rho J_{n_i}],$$

(16)

where ${\displaystyle \rho }$ is the correlation coefficient of ${\displaystyle S_{ik}}$ and ${\displaystyle S_{il}}$ and equals ${\displaystyle (\delta -{\theta }^2)/(\theta -{\theta }^2)}$, ${\displaystyle I_{n_i}}$ is the ${\displaystyle n_i\times n_i}$ identity matrix, and ${\displaystyle J_{n_i}}$ is the ${\displaystyle n_i\times n_i}$ matrix of 1 s.

Proof. 

The form of the covariance matrix of ${\displaystyle S_i}$ is

$$V_i={\sigma }^2\left(\begin{array}{ccccc}1& \rho & \rho & \dots & \rho \\ \rho & 1& \rho & \dots & \rho \\ \dots & \dots & \dots & \dots & \dots \\ \rho & \rho & \rho & \dots & 1\end{array}\right),$$

(17)

because there is correlation between ${\displaystyle S_{ij}}$ and ${\displaystyle S_{i{j}^{\prime }}}$ with ${\displaystyle j\ne j^{\prime }}$${\displaystyle j,j^{{}^{\prime }}=1,..,n_i}$. We have

$$\begin{array}{c}\hfill \rho =Corr(S_{ij},S_{i{j}^{\prime }})=\frac{Cov(S_{ij},S_{i{j}^{\prime }})}{\sqrt{Var\left(S_{ij}\right)}\sqrt{Var\left(S_{i{j}^{\prime }}\right)}}=\frac{Cov(S_{ij},S_{i{j}^{\prime }})}{{\sigma }^2}.\end{array}$$

(18)

Moreover,

$$\begin{array}{c}\hfill Cov(S_{ij},S_{i{j}^{\prime }})=E\left[S_{ij}{S}_{i{j}^{\prime }}\right]-E\left[S_{ij}\right]E\left[S_{i{j}^{\prime }}\right]=\delta -{\theta }^2.\end{array}$$

(19)

Using the fact that ${\displaystyle P({ϵ}_{ik}\le 0)=\theta }$, we have

$$\begin{array}{cc}\hfill E\left[S_{ij}{S}_{i{j}^{\prime }}\right]& =E\left\{[\theta -I({ϵ}_{ij}\le 0)][\theta -I({ϵ}_{i{j}^{\prime }}\le 0)]\right\}\hfill \\ \hfill & ={\theta }^2-\theta E\left\{I({ϵ}_{ij}\le 0)\right\}-\theta E\left\{I({ϵ}_{i{j}^{\prime }}\le 0)\right\}+E\left\{I({ϵ}_{ij}\le 0)I({ϵ}_{i{j}^{\prime }}\le 0)\right\}\hfill \\ \hfill & =\delta -{\theta }^2,\hfill \end{array}$$

and

$$\begin{array}{c}\hfill E\left[S_{ik}\right]=E\left\{\theta -I({ϵ}_{ij}\le 0)\right\}=\theta -E\left\{I({ϵ}_{ij}\le 0)\right\}=0,\forall k.\end{array}$$

We use the fact that ${\displaystyle I({ϵ}_{ij}\le 0)}$ is a binary variable which takes the value 1 when ${\displaystyle {ϵ}_{ij}\le 0}$ and the value 0 otherwise with mean ${\displaystyle \theta }$ and variance ${\displaystyle \theta (1-\theta )}$. Similarly, the variable ${\displaystyle I({ϵ}_{ij}\le 0)I({ϵ}_{i{j}^{\prime }}\le 0)}$ is a binary variable with mean ${\displaystyle \delta }$ and variance ${\displaystyle \delta (1-\delta )}$. Then, we have that

$$\begin{array}{c}\hfill Var\left(S_{ik}\right)=Var[\theta -I(y_{ik}-x_{ik}^T\mathbf{\beta }\le 0)]=Var[\theta -I({ϵ}_{ik}\le 0)]=\theta (1-\theta ).\end{array}$$

(20)

From Equation (18), we take that the correlation coefficient is equal to ${\displaystyle \rho =\frac{\delta -{\theta }^2}{\theta -{\theta }^2}}$. Moreover, by Equations (17) and (20), the covariance matrix ${\displaystyle V_i}$ is

$$\begin{array}{cc}\hfill V_i& =(\theta -{\theta }^2)\left[(1-\rho )\left(\begin{array}{ccccc}1& 0& 0& .& 0\\ 0& 1& 0& ...& 0\\ ...& ...& ...& ...& ...\\ 0& 0& 0& ..& 1\end{array}\right)+\rho \left(\begin{array}{ccccc}1& 1& 1& ...& 1\\ 1& 1& 1& ...& 1\\ ...& ...& ...& ...& ...\\ 1& 1& 1& ...& 1\end{array}\right)\right]\hfill \\ \hfill & =(\theta -{\theta }^2)\left[(1-\rho )I_{n_i}+\rho J_{n_i}\right].\hfill \end{array}$$

 □

Now, let ${\displaystyle X_i={\{X_{i1},\cdots ,X_{i{n}_i}\}}^T}$. To obtain efficient estimators, we should incorporate an appropriate weighted function that takes into account the correlation for each subject. According to Jung (1996), based on the exchangeable correlation structure assumption

$$Corr(S_{ij},S_{ik})=\left\{\begin{array}{cc}1,\hfill & j=k,\hfill \\ 0\hfill & j\ne k,\hfill \end{array}\right.$$

(21)

the generalized least squares estimate of ${\displaystyle \mathbf{\beta }}$ obtained by minimizing

$$S_i{V}_i^{-1}{S}_i$$

(22)

and differentiating with respect to ${\displaystyle \mathbf{\beta }}$, we have the following weighted functions

$$U_{\theta }\left(\mathbf{\beta }\right)=\sum _{i=1}^N{X}_i^T{V}_i^{-1}{S}_i,$$

(23)

where ${\displaystyle V_i^{-1}}$ is the inverse matrix of ${\displaystyle V_i}$.

Proposition 1.

The inverse matrix of ${\displaystyle V_i}$ can be written as

$$\begin{array}{c}\hfill V^{-1}=\frac{1}{\theta -{\theta }^2}\left(W_i^{bet}+W_i^{wit}\right),\end{array}$$

(24)

where ${\displaystyle W_i^{bet}}$ and ${\displaystyle W_i^{wit}}$ are quantities related to information from different subjects and from the same subject, respectively

$$\begin{array}{c}\hfill W_i^{bet}=\frac{J_{n_i}}{n_i[1+(n_i-1)\rho ]}and{W}_i^{wit}=\frac{1}{1-\rho }\left(I_{n_i}-\frac{1}{n_i}{J}_{n_i}\right).\end{array}$$

(25)

Proof. 

Suppose ${\displaystyle A}$ is an invertible square matrix and ${\displaystyle u,w}$ are column vectors. Suppose furthermore that ${\displaystyle 1+w^T{A}^{-1}u\ne 0}$. Then, the Sherman–Morrison formula (Bartlett 1951) states that

$${(A+u{w}^T)}^{-1}=A^{-1}-\frac{A^{-1}u{w}^T{A}^{-1}}{1+w^T{A}^{-1}u}.$$

(26)

Starting from

$$V_i={\sigma }^2\left[(1-\rho )I_{n_i}+\rho J_{n_i}\right]$$

and supposing that ${\displaystyle \rho J_{n_i}=u{w}^T}$ where ${\displaystyle u=w={\{\rho ,\rho ,\cdots ,\rho \}}^T}$ is a ${\displaystyle n_i\times 1}$ vector, by Equation (26), we take

$$\begin{array}{cc}\hfill V_i^{-1}& =\frac{1}{{\sigma }^2}\left[\frac{1}{1-\rho }{I}_{n_i}-\frac{\left(\frac{1}{1-\rho }{I}_{n_i}\right)\rho J_{n_i}\frac{1}{1-\rho }{I}_{n_i}}{1+\frac{n_i\rho }{1-\rho }}\right]\hfill \\ \hfill & =\frac{1}{{\sigma }^2}\left[\frac{1}{1-\rho }{I}_{n_i}-\frac{1}{1-\rho }\left(\frac{\rho }{1+(n_i-1)\rho }\right)J_{n_i}\right]\hfill \\ \hfill & =\frac{1}{{\sigma }^2}\left[\frac{1}{1-\rho }{I}_{n_i}+\frac{1}{1-\rho }\left(\frac{n_i(1-\rho )-n_i-n_i(n_i-1)\rho }{(1+(n_i-1)\rho )n_i^2}\right)J_{n_i}\right].\hfill \\ \hfill & =\frac{1}{{\sigma }^2}\left[\frac{1}{1-\rho }{I}_{n_i}+\frac{1}{1-\rho }\left(I_{n_i}\frac{1-\rho }{[1+(n_i-1)\rho ]n_i}-\frac{1}{n_i}{I}_{n_i}\right)J_{n_i}\right]\hfill \\ \hfill & =\frac{1}{{\sigma }^2}\left[\frac{1}{1-\rho }{I}_{n_i}+\frac{J_{n_i}}{[1+(n_i-1)\rho ]n_i}-\frac{1}{n_i(1-\rho )}{I}_{n_i}\right]\hfill \\ \hfill & =\frac{1}{{\sigma }^2}\left[\frac{J_{n_i}}{[1+(n_i-1)\rho ]n_i}+\frac{1}{1-\rho }\left(I_{n_i}-\frac{1}{n_i}{J}_{n_i}\right)\right]\hfill \end{array}$$

that provides Equation (24).  □

If there is no correlation between the same subject, then the correlation coefficient ${\displaystyle \rho }$ is zero and the inverse matrix of ${\displaystyle V_i}$ is equal to

$$V_i^{-1}=\frac{1}{{\sigma }^2}{I}_{n_i},$$

and ${\displaystyle U_{\theta }\left(\mathbf{\beta }\right)}$ is equivalent to the estimating functions ${\displaystyle W_{\theta }\left(\mathbf{\beta }\right)}$. Furthermore, from Equation (23), using the result of Equation (24), we take

$$\begin{array}{cc}\hfill U_{\theta }\left(\mathbf{\beta }\right)& =\sum _{i=1}^N{X}_i^T{V}_i^{-1}{S}_i\hfill \\ \hfill & =\sum _{i=1}^N{X}_i^T\frac{1}{{\sigma }^2}\left[\frac{J_{n_i}}{n_i[1+(n_i-1)\rho ]}+\frac{1}{1-\rho }\left(I_{n_i}-\frac{1}{n_i}{J}_{n_i}\right)\right]S_i\hfill \\ \hfill & =\frac{1}{{\sigma }^2}\sum _{i=1}^n{X}_i^T\left[\frac{J_{n_i}}{n_i[1+(n_i-1)\rho ]}\right]S_i+\frac{1}{{\sigma }^2}\sum _{i=1}^N{X}_i^T\left[\frac{1}{1-\rho }\left(I_{n_i}-\frac{1}{n_i}{J}_{n_i}\right)\right]S_i\hfill \\ \hfill & =\frac{1}{{\sigma }^2}\sum _{i=1}^N{X}_i^T\left[\frac{1}{1+(n_i-1)\rho }\right]J_{n_i}\sum _{k=1}^{n_i}{S}_i/n_i+\frac{1}{(1-\rho ){\sigma }^2}\sum _{i=1}^N{X}_i^T\left(S_i-{\mathbf{1}}_{n_i}\sum _{k=1}^{n_i}{S}_i/n_i\right),\hfill \end{array}$$

(27)

where ${\displaystyle {\mathbf{1}}_{n_i}}$ is a ${\displaystyle n_i\times 1}$ vector of 1s. Then, from Equations (27) and (25), we can extract the following two estimating functions:

$$\begin{array}{cc}\hfill & U^{bet}\left(\beta \right)=\sum _{i=1}^N\frac{1}{1+(n_i-1)\rho }{X}_i^T{\mathbf{1}}_{n_i}\sum _{k=1}^{n_i}{S}_i/n_i=\sum _{i=1}^N{X}_i^T{W}_i^{between}{S}_i,\hfill \\ \hfill & U^{wit}\left(\beta \right)=\frac{1}{1-\rho }\sum _{i=1}^N{X}_i^T\left(S_i-{\mathbf{1}}_{n_i}\sum _{k=1}^{n_i}{S}_i/n_i\right)=\sum _{i=1}^N{X}_i^T{W}_i^{within}{S}_i.\hfill \end{array}$$

(28)

Remark 1.

Note that the estimating functions ${\displaystyle U^{wit}\left(\mathbf{\beta }\right)}$ indicate the differences within a subject while ${\displaystyle U^{bet}\left(\mathbf{\beta }\right)}$ indicate the information which comes from different subjects.

4.3. Parameters Estimation for QR Longitudinal Model

Generally, the most difficult issue when using quantile regression is the estimation of the covariance matrix of the parameter estimators because it involves the unknown density functions of the errors. Resampling methods have been proposed to estimate the covariance matrix (Parzen et al. 1994). These methods are useful because the parameter estimates can be easily obtained but the variance is difficult to be estimated. Moreover, there is no analytical proof for the validation of the traditional bootstrap technique for the quantile regression model (see Yin and Cai 2005). Fu and Wang (2012) extended the smoothing method of quantile regression with independent data proposed by Wang et al. (2009) and proposed a method for longitudinal data.

Suppose that ${\displaystyle \widehat{{\mathbf{\beta }}_u}}$ is the estimator which results from ${\displaystyle U_{\theta }\left(\mathbf{\beta }\right)}$. Then, under some regularity conditions, ${\displaystyle \widehat{{\mathbf{\beta }}_u}}$, is a consistent estimator of ${\displaystyle {\mathbf{\beta }}_0}$ and

$$\begin{array}{c}\hfill \sqrt{N}(\widehat{{\mathbf{\beta }}_u}-{\mathbf{\beta }}_0)\to N(0,\Lambda ).\end{array}$$

(29)

For the proof of the consistency of ${\displaystyle {\mathbf{\beta }}_u}$ and the asymptotic normality of ${\displaystyle {\mathbf{\beta }}_0}$, see the work by Fu and Wang (2012). For the definition of covariance matrix ${\displaystyle \Lambda }$, we refer to the works of Wang et al. (2009) and Koenker (2005).

Thus, the resulting estimator ${\displaystyle {\widehat{\mathbf{\beta }}}_u}$ from Equation (27) can be approximated by ${\displaystyle \mathbf{\beta }+{\Lambda }^{1/2}Z}$ where ${\displaystyle Z}$ is the standard normal distribution ${\displaystyle N(\mathbf{0},I_p)}$ and ${\displaystyle {\Lambda }^{1/2}Z}$ is a disturbance quantity to ${\displaystyle \mathbf{\beta }}$. Moreover, according to Equation (13), the estimating functions ${\displaystyle U_{\theta }\left(\beta \right)}$ can be defined as ${\displaystyle {\tilde{U}}_{\theta }\left(\beta \right)=E_Z\left\{U_{\theta }(\mathbf{\beta }+{\Lambda }^{1/2}Z)\right\}}$ where expectation is over ${\displaystyle Z}$. Nevertheless, the variance-covariance matrix ${\displaystyle \Lambda }$ is unknown, which means that the expectation cannot be computed. For that reason, Brown and Wang (2005) suggested the use of a known matrix ${\displaystyle \mathsf{\Gamma }}$ instead of ${\displaystyle \Lambda }$ and using appropriate iterative algorithms in order to estimate the matrix ${\displaystyle \Lambda }$. Thus, the objective function is ${\displaystyle {\tilde{U}}_{\theta }\left(\beta \right)=E_Z\left\{U_{\theta }(\mathbf{\beta }+{\mathsf{\Gamma }}^{1/2}Z)\right\}}$.

Note that

$$\begin{array}{cc}\hfill E\left\{L_{\theta }(\mathbf{\beta }+{\mathsf{\Gamma }}^{1/2}Z)\right\}& =\theta -P\{x_{ik}^T{\mathsf{\Gamma }}^{1/2}Z\ge b_{ik}\}=\theta -1+\mathsf{\Phi }\left[\frac{b_{ik}}{{\sigma }_{ik}}\right],\hfill \end{array}$$

(30)

where ${\displaystyle b_{ik}=y_{ik}-x_{ik}^T\mathbf{\beta }}$ and ${\displaystyle {\sigma }_{ik}^2=x_{ik}^T\mathsf{\Gamma }{x}_{ik}}$. Then,

$$\begin{array}{c}\hfill {\tilde{U}}_{\theta }\left(\beta \right)=\sum _{i=1}^N{X}_i^T{V}_i^{-1}{\tilde{S}}_i,\end{array}$$

(31)

where ${\displaystyle {\tilde{S}}_i=({\tilde{S}}_{i1},\cdots ,{\tilde{S}}_{i{n}_i})}$ with ${\displaystyle {\tilde{S}}_{ik}=\theta -1+\mathsf{\Phi }\left[\frac{b_{ik}}{{\sigma }_{ik}}\right]}$. Differentiating Equation (31) with respect to ${\displaystyle \mathbf{\beta }}$, we take

$${\tilde{D}}_{\theta }\left(\beta \right)=-\sum _{i=1}^N{X}_i^T{V}_i^{-1}{\tilde{\Lambda }}_i{X}_i,$$

(32)

where ${\displaystyle {\tilde{\Lambda }}_i}$ is a diagonal ${\displaystyle n_i\times n_i}$ matrix with diagonal element ${\displaystyle {\sigma }_{ik}^{-1}\varphi \left[\frac{b_{ik}}{{\sigma }_{ik}}\right]}$.

To produce the estimators and the corresponding covariance matrix, we need iterative methods. We adopt the algorithm of Fu and Wang (2012) who extended the induced smoothing method of Wang et al. (2009) and Pang et al. (2012). A similar algorithm is applied for the analysis of clustered data: a combined estimating equations approach by Stoner and Leroux (2002). The steps of the algorithm are the following:

• Step 1. Produce some initial values ${\displaystyle {\tilde{\mathbf{\beta }}}^0={\widehat{\mathbf{\beta }}}_I}$, which have been obtained by the independence working model and ${\displaystyle {\mathsf{\Gamma }}^0=n^{-1}{I}_p}$.
• Step 2. Given ${\displaystyle {\tilde{\mathbf{\beta }}}^{k-1}}$ and ${\displaystyle {\mathsf{\Gamma }}^{k-1}}$ from the ${\displaystyle k-1}$ step, update ${\displaystyle {\widehat{\delta }}^{k-1}}$, using the following equation:

  $$\begin{array}{c}\hfill {\widehat{\delta }}^{k-1}={\displaystyle \frac{{\sum }_{i=1}^N{\sum }_{k=1}^{n_i}{\sum }_{l\ne k}^{n_i}I[{\widehat{ϵ}}_{ik}\le 0,{\widehat{ϵ}}_{il}\le 0]}{{\sum }_{i=1}^N{n}_i(n_i-1)}}.\end{array}$$
• Step 3. Update the estimation parameters ${\displaystyle {\tilde{\mathbf{\beta }}}^k}$ and the matrix ${\displaystyle {\mathsf{\Gamma }}^k}$ using the equations

  $$\begin{array}{cc}\hfill & {\tilde{\mathbf{\beta }}}^k={\tilde{\mathbf{\beta }}}^{k-1}+{\left\{{\tilde{D}}_{\theta }({\tilde{\mathbf{\beta }}}^{k-1},{\mathsf{\Gamma }}^{k-1})\right\}}^{-1}{\tilde{U}}_{\theta }({\tilde{\mathbf{\beta }}}^{k-1},{\mathsf{\Gamma }}^{k-1},{\widehat{\delta }}^{k-1}),\hfill \\ \hfill & {\mathsf{\Gamma }}^k={\tilde{D}}_{\theta }^{-1}({\tilde{\mathbf{\beta }}}^{k-1},{\mathsf{\Gamma }}^{k-1})V({\tilde{\mathbf{\beta }}}^{k-1},{\widehat{\delta }}^{k-1}){\tilde{D}}_{\theta }^{-1}({\tilde{\mathbf{\beta }}}^{k-1},{\mathsf{\Gamma }}^{k-1}).\hfill \end{array}$$
• Step 4. Repeat Steps 2 and 3 until convergence.

Remark 2.

The final values of ${\displaystyle \tilde{\mathbf{\beta }}}$ and ${\displaystyle \mathsf{\Gamma }}$ (Step 3) are taken as the smoothed estimators of ${\displaystyle \mathbf{\beta }}$ and its covariance matrix, respectively. Under some regularity conditions, Fu and Wang (2012) established the consistency and asymptotic normality, i.e., ${\displaystyle n^{-1/2}\{{\tilde{U}}_{\theta }-U_{\theta }\}=o_p\left(1\right)}$ and the smoothing estimator ${\displaystyle {\mathbf{\beta }}_u\to {\mathbf{\beta }}_0}$ in probability, and ${\displaystyle \sqrt{N}({\mathbf{\beta }}_u-{\mathbf{\beta }}_0)}$ converges in distribution to ${\displaystyle N(\theta ,V_u)}$.

5. Numerical Illustrations

In this section, we present a numerical implementation of longitudinal quantile regression model with two correlated run-off triangles. The codes of this paper were implemented in R, using own routines, the “ChainLadder" (Gesmann et al. 2018) and the “quantreg" (Koenker 2018) packages.

5.1. Numerical Example Based on Average Premium Per Exposure

In this section, based on average premium per exposure, the loss reserving model is implemented by using the longitudinal quantile regression model. We suppose that we have two blocks of business for which we are trying to calculate reserve indications. Both companies operate in Greece. Company A mainly focuses on motor business and underwrites all vehicle categories apart from taxis and trucks while Company B underwrites all vehicle categories for motor business. Table 3 and Table 4 show the triangles of the incremental incurred claims (paid and outstanding claims) for both companies.

Table 3. Motor triangle and premiums for Company A.

Accident	Development Year
Year	1	2	3	4	5	6	7	8	9	10	Premium
2007	58,134	162,688	101,105	100,964	61,591	71,009	34,024	2746	646	10,190	1,051,637
2008	51,437	197,139	120,641	74,807	76,771	77,276	39,070	4396	13,809		1,190,965
2009	57,906	116,191	143,953	103,883	70,760	177,194	35,341	6088			1,327,568
2010	40,352	121,837	88,389	320,429	75,127	70,190	63723				1,418,348
2011	82,227	279,591	151,260	230,293	82,378	47,315					1,504,056
2012	196,417	119,755	228,499	99,894	44,266						1,580,233
2013	67,161	107,098	198,252	75,172							1,619,382
2014	78,293	141,865	106,150								1,727,540
2015	74,472	118,886									1,820,104
2016	43,281										1,883,017

Table 4. Motor triangle and premiums for Company B.

Accident	Development Year
Year	1	2	3	4	5	6	7	8	9	10	Premium
2007	63,078	143,002	144,235	75,007	60,775	70,804	27,508	4757	3172	6385	1,633,833
2008	65,567	177,292	107,870	137,305	72,741	68,708	102,864	4335	6107		1,675,707
2009	87,394	146,346	158,876	199,846	53,161	72,764	42,915	10,898			1,636,855
2010	70,017	153,893	119,028	93,771	49,600	185,689	28,331				1,689,715
2011	104,638	186,326	335,477	136,857	87,941	69,248					1,649,386
2012	76,390	190,629	192,606	121,704	66,297						1,712,587
2013	58,620	184,557	135,174	118,180							2,105,361
2014	87,845	166,511	145,385								2,265,432
2015	53,616	152,751									1,976,188
2016	62,904										1,351,719

In the sequel, we apply the following regression setting in a quantile longitudinal form,

$$\begin{array}{c}\hfill Y_{irj}={\mu }_i+a_{ir}+b_{ij}+e_{irj},fori=1,2;r=2,...,10;j=2,...,10,\end{array}$$

where, for the ${\displaystyle i}$ triangle, ${\displaystyle Y_{irj}}$ is the average premium per exposure of the r${\displaystyle th}$ accident year and of the j${\displaystyle th}$ development year, ${\displaystyle {\mu }_i}$ is the overall mean, ${\displaystyle a_{ir}}$ is the effect of the r${\displaystyle th}$ accident year, ${\displaystyle b_{ij}}$ is the effect of the j${\displaystyle th}$ development year, ${\displaystyle e_{irj}}$ is the error term, and the design matrix is of dimension ${\displaystyle (2\times 55)\times 18}$.

It is obvious that, for Company A, for the accident year 2007, a big claim has been paid 10 years after the accident date (the amount of this claim is embedded at the total incremental amount of 10,190) and could be represented as an outlier claim. This claim will dramatically change the development pattern of the payments in case of using the Chain Ladder method because the loss development factor for this year increases from 1.0117 to 1.0171 (see Table 5). This is commonly observed in motor business where claims are settled many years later, especially when accidents with large compensations (such as partial or total disability, deaths, etc.) are observed. This can also be observed in accident year 2008 where a large amount is observed at the last known development year (13,809). We have a similar situation for the run-off triangle for Company B, but not to that extent as for Company A. For Company B, the data of the triangle seem to be more stable. Moreover, the premiums of the companies by accident year are presented at the run-off triangles. For the implementation of the dataset, we divided the payments by exposures for each year of business before the analysis was carried out.

Table 5. Chain ladder: loss development factors.

Company	0–1	1–2	2–3	3–4	4–5	5—6	6-7	7–8	8–9
A	2.9324	1.6060	1.3737	1.1265	1.1491	1.0677	1.0068	1.0117	1.0171
B	3.2502	1.6822	1.3042	1.1188	1.1541	1.0782	1.0096	1.0069	1.0107

The number of exposures (counts of incurred losses) for each accident year is also provided (see Table 6 and Table 7) for each lines of business.

Table 6. Counts of incurred claims for Company A.

Accident	Development Year
Year	1	2	3	4	5	6	7	8	9	10
2007	118	272	241	169	103	106	71	4	3	5
2008	134	287	235	192	121	117	84	14	13
2009	129	254	267	193	110	136	80	16
2010	87	255	218	152	111	86	52
2011	148	285	277	212	127	94
2012	108	255	227	185	103
2013	129	215	220	150
2014	128	277	234
2015	122	236
2016	94

Table 7. Counts of incurred claims for Company B.

Accident	Development Year
Year	1	2	3	4	5	6	7	8	9	10
2007	139	286	276	170	137	140	74	15	8	6
2008	143	337	258	224	158	158	90	20	13
2009	151	273	310	239	145	135	81	11
2010	138	285	273	182	122	127	70
2011	161	372	349	282	185	129
2012	131	327	297	237	150
2013	144	345	284	222
2014	146	337	295
2015	130	301
2016	155

If we were trying to calculate the expected value of the reserve run-off, we could simply calculate the expected value for each line of business separately and add all the expectations together. However, when we quantify a value other than the mean, such as a quantile, we cannot simply sum across the lines of business. In such a case, we would overstate the aggregate reserve need.

Remark 3.

The only time the sum of a ${\displaystyle \theta }$th quantile would be appropriate for the aggregate reserve indication is when all the lines of business are fully correlated with each other which is of course a highly unlikely situation.

Figure 1 and Figure 2 show claims development charts of Companies A and B, respectively, with individual panels for each origin period. Chain Ladder loss development factors for each company are also presented in Table 5. According to the claims development chart, we observe that the patterns of Companies A and B appear similar (see Figure 3).

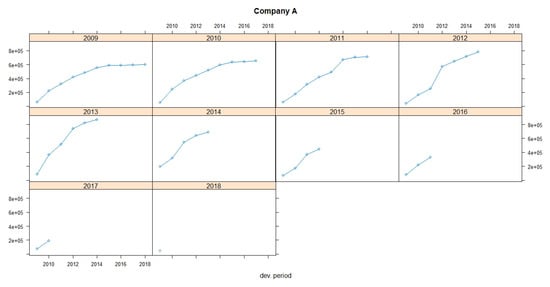
Figure 1. Claims development chart of Company A with individual panels for each origin period.

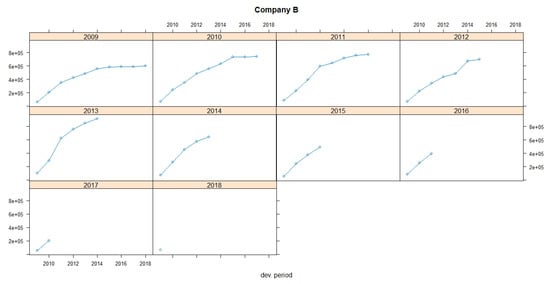
Figure 2. Claims development chart of Company B with individual panels for each origin period.

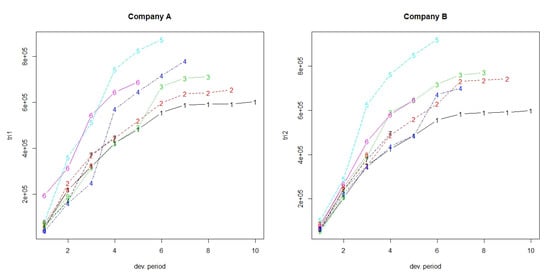
Figure 3. Claims development chart of the triangles with one line per origin period.

Table 8 and Table 9 display the values of reserves and ultimate paid claims based on individual quantile regression method, for Companies A and B, respectively, for different quantiles. Loss ratios for each quantile are also provided at the end of each of the Tables. Table 10 and Table 11 display the values of reserves and ultimate paid claims based on longitudinal quantile regression method, for Companies A and B, respectively, for different quantiles.

Table 8. Reserves and ultimate claims of Company A based on Individual Quantile Regression.

Accident	Quantile 50%		Quantile 60%		Quantile 75%		Quantile 90%		Quantile 95%		Quantile 99.5%
Year	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate
2007	0	603,097	0	603,097	0	603,097	0	603,097	0	603,097	0	603,097
2008	11,702	667,049	11,496	666,843	12,348	667,695	12,348	667,695	12,348	667,695	12,348	667,695
2009	25,522	736,838	25,770	737,085	30,734	742,050	30,734	742,050	30,734	742,050	30,734	742,050
2010	30,123	810,171	32,114	812,161	48,436	828,484	48,436	828,484	61,841	841,888	61,841	841,888
2011	84,962	958,027	86,226	959,291	102,917	975,981	102,917	975,981	102,917	975,981	102,917	975,981
2012	144,793	833,624	150,033	838,863	295,824	984,655	485,528	1,174,359	485,528	1,174,359	485,528	1,174,359
2013	218,293	665,976	223,617	671,300	222,374	670,057	485,688	933,370	485,688	933,370	485,688	933,370
2014	376,255	702,563	396,658	722,966	439,704	766,012	439,675	765,983	400,741	727,049	400,741	727,049
2015	433,878	627,236	514,291	707,648	547,762	741,119	519,185	712,542	482,151	675,508	482,151	675,508
2016	364,632	407,912	377,312	420,592	439,462	482,742	396,155	439,435	374,632	417,912	374,632	417,912
Total	1,690,161	7,012,491	1,817,516	7,139,846	2,139,562	7,461,893	2,520,666	7,842,996	2,436,579	7,758,909	2,436,579	7,758,909
LR	46.37%		47.21%		49.34%		51.86%		51.31%		51.31%

Table 9. Reserves and ultimate claims of Company B based on Individual Quantile Regression.

Accident	Quantile 50%		Quantile 60%		Quantile 75%		Quantile 90%		Quantile 95%		Quantile 99.5%
Year	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate
2007	0	598,722	0	598,722	0	598,722	0	598,722	0	598,722	0	598,722
2008	7915	750,705	8760	751,550	9338	752,128	7642	750,431	7642	750,431	7642	750,431
2009	15,633	787,833	15,012	787,213	14,631	786,831	20,011	792,211	20,011	792,211	20,011	792,211
2010	16,638	716,969	16,780	717,111	20,452	720,783	19,694	720,025	19,694	720,025	19,694	720,025
2011	64,164	984,651	77,249	997,735	156,940	1,077,426	232,413	1,152,900	232,413	1,152,900	232,413	1,152,900
2012	124,174	771,801	131,694	779,320	212,699	860,326	348,719	996,345	348,719	996,345	348,719	996,345
2013	184,956	681,488	196,298	692,830	270,111	766,642	413,334	909,865	413,334	909,865	413,334	909,865
2014	326,036	725,777	308,932	708,673	422,205	821,946	621,763	1,021,504	621,763	1,021,504	621,763	1,021,504
2015	398,134	604,501	382,772	589,139	477,907	684,274	614,736	821,104	614,736	821,104	614,736	821,104
2016	514,302	577,206	499,960	562,864	588,777	651,681	742,201	805,105	742,201	805,105	742,201	805,105
Total	1,651,953	7,199,653	1,637,457	7,185,156	2,173,060	7,720,759	3,020,513	8,568,213	3,020,513	8,568,213	3,020,513	8,568,213
LR	40.68%		40.60%		43.63%		48.42%		48.42%		48.42%

Table 10. Reserves and ultimate claims of Company A based on Longitudinal Quantile Regression.

Accident	Quantile 50%		Quantile 60%		Quantile 75%		Quantile 90%		Quantile 95%		Quantile 99.5%
Year	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate
2007	0	603,097	0	603,097	0	603,097	0	603,097	0	603,097	0	603,097
2008	10,465	665,812	13,163	668,509	14,614	669,961	14,998	670,344	16,354	671,701	14,284	669,631
2009	15,332	726,647	19,519	730,834	24,491	735,807	25,753	737,069	27,823	739,139	24,671	735,987
2010	18,773	798,820	24,548	804,595	30,472	810,519	33,114	813,161	36,000	816,047	31,594	811,641
2011	109,292	982,356	146,947	1,020,012	162,394	1,035,459	280,876	1,153,941	270,861	1,143,926	271,168	1,144,233
2012	142,717	831,548	195,409	884,240	227,356	916,187	388,819	1,077,650	534,912	1,223,743	535,184	1,224,015
2013	121,615	569,298	164,628	612,311	205,183	652,866	313,448	761,131	303,832	751,515	304,086	751,769
2014	143,793	470,101	216,128	542,436	274,426	600,734	369,152	695,460	398,023	724,331	624,747	951,055
2015	156,935	350,292	245,965	439,323	255,528	448,885	319,659	513,016	354,969	548,327	355,450	548,807
2016	108,851	152,131	205,266	248,546	205,286	248,567	211,902	255,182	211,842	255,123	211,977	255,257
Total	827,771	6,150,102	1,231,572	6,553,903	1,399,751	6,722,081	1,957,720	7,280,050	2,154,617	7,476,947	2,373,161	7,695,491
LR	40.67%		43.34%		44.45%		48.14%		49.44%		50.89%

Table 11. Reserves and ultimate claims of Company B based on Longitudinal Quantile Regression.

Accident	Quantile 50%		Quantile 60%		Quantile 75%		Quantile 90%		Quantile 95%		Quantile 99.5%
Year	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate	Reserves	Ultimate
2007	0	598,722	0	598,722	0	598,722	0	598,722	0	598,722	0	598,722
2008	14,812	757,602	19,390	762,179	21,292	764,082	21,818	764,608	23,573	766,363	20,865	763,655
2009	23,811	796,012	31,465	803,665	38,726	810,927	40,529	812,730	43,425	815,625	38,967	811,168
2010	31,032	731,363	42,019	742,349	51,128	751,459	54,931	755,262	59,120	759,451	52,655	752,985
2011	146,138	1,066,624	203,353	1,123,839	221,691	1,142,178	370,226	1,290,712	358,282	1,278,769	358,674	1,279,161
2012	220,915	868,541	313,593	961,219	357,766	1,005,392	589,509	1,237,135	806,340	1,453,966	806,747	1,454,373
2013	197,552	694,083	279,346	775,877	337,958	834,489	497,873	994,404	484,759	981,290	485,153	981,684
2014	217,454	617,195	342,324	742,065	418,633	818,374	541,538	941,279	583,882	983,622	899,021	1,298,762
2015	243,640	450,007	397,190	603,557	410,815	617,182	490,441	696,808	541,561	747,928	542,253	748,621
2016	189,118	252,022	356,630	419,534	356,665	419,569	368,159	431,063	368,056	430,960	368,290	431,194
Total	1,284,472	6,832,172	1,985,308	7,533,008	2,214,675	7,762,375	2,975,023	8,522,722	3,268,999	8,816,698	3,572,625	9,120,325
LR	38.61%		42.57%		43.86%		48.16%		49.82%		51.54%

Loss ratios (${\displaystyle LR}$) for motor car insurance typically range from 40% to 60%. In this case, insurance companies are collecting more premiums than the amount paid in claims. Loss ratio is considered as one of the tools which explains a company’s suitability for coverage. A high loss ratio means is considered bad, which leads to bad financial health because the insurance company may not collect enough premiums to pay claims and expenses while also making a reasonable profit.

Table 12 provides the values of reserves based on the individual quantile regression (IQR) and based on longitudinal quantile regression (LQR). To examine the role of dependence, it is important to calculate the reserves for each IQR, and then use the sum to compare it with the sum of the run-off triangles resulting from the LQR (last line of Table 12).

Table 12. Estimated reserves using Individual Quantile Regression (IQR) and the Longitudinal Quantile Regression (LQR).

	Quantile 50%	Quantile 60%	Quantile 75%	Quantile 90%	Quantile 95%	Quantile 99.5%
Company A IQR	1,690,161	1,817,516	2,139,562	2,520,666	2,436,579	2,436,579
Company B IQR	1,651,953	1,637,457	2,173,060	3,020,513	3,020,513	3,020,513
Company A LQR	827,771	1,231,572	1,399,751	1,957,720	2,154,617	2,373,161
Company B LQR	1,284,472	1,985,308	2,214,675	2,975,023	3,268,999	3,572,625
sumIQR-sumLQR	1,229,871	238,092	698,196	608,436	33,477	${\displaystyle -}$488,694

Applying individual quantile regression, a higher quantile leads to larger total reserve. Nevertheless, for Company A, quantiles over 95% provide equal values of reserves, while, for Company B, quantiles over 90% provide equal values of reserves. The longitudinal algorithm gives different estimations for each quantile. Applying longitudinal quantile regression, the estimated ultimate reserves for both Companies A and B are smaller than the sum of individual estimated reserves for each of Companies A and B based on individual quantile regression.

5.2. Comparison Criteria

For model comparison, four criteria, namely the root mean squared error (RMSE), the percentage total (PT), the mean absolute error (MAE), and the mean absolute percentage error (MAPE), were used.

RMSE is a measure of accuracy and is useful for comparing different models for a particular dataset (Hyndman and Koehler 2006). RMSE is the square root of the average of squared errors. The effect of each error on RMSE is proportional to the size of the squared error. Thus, larger errors have a disproportionately large effect on RMSE. Consequently, RMSE is sensitive to outliers (Pontius et al 2008; Willmott and Matsuura 2006).

RMSE for one triangle and for many run-off triangles is given, respectively, by

$$\begin{array}{c}\hfill RMSE={\left[{\displaystyle \frac{1}{m}}\sum _{i=1}^n\sum _{j=1}^{n-i+1}{(y_{ij}-{\widehat{y}}_{ij})}^2\right]}^{1/2}andRMS{E}^N={\left[{\displaystyle \frac{1}{mN}}\sum _{k=1}^N\sum _{i=1}^n\sum _{j=1}^{n-i+1}{(y_{ij}-{\widehat{y}}_{ij})}^2\right]}^{1/2},\end{array}$$

where ${\displaystyle m=\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)}$ represents the total number of the known incremental data (the left upper triangle) and ${\displaystyle k}$ is the counter for each triangle.

The percentage total (PT) was also a comparison criterion, which is defined for one and for many triangles, respectively, as

$$\begin{array}{c}\hfill PT={\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{j=1}^{n-i+1}{\widehat{y}}_{ij}}{{\sum }_{i=1}^n{\sum }_{j=1}^{n-i+1}{y}_{ij}}}andP{T}^N={\displaystyle \frac{{\sum }_{k=1}^N{\sum }_{i=1}^n{\sum }_{j=1}^{n-i+1}{\widehat{y}}_{ij}}{{\sum }_{k=1}^N{\sum }_{i=1}^n{\sum }_{j=1}^{n-i+1}{y}_{ij}}}.\end{array}$$

RMSE and PT measure the model-fit with respect to observations, where a PT value closer to 100 is accepted, while, for RMSE, we prefer the smallest values.

According to the comparison criteria, the longitudinal algorithm provides the smaller RMSE when using the 75% quantile, resulting to better fit of the data. Thus, a combination of different companies or lines of business provides a better estimation of the total reserve. In case of using the PT criterion, we take exactly the same results and the 75% quantile produces the best fit. If we make estimations separately, the suggested models for both triangles use quantiles below 75% which means weak prudence (Table 13).

Table 13. RMSE and PT for Individual and Longitudinal Quantile Regression.

	Root Mean Square Error (RMSE)			Percentage Total (PT)
Quantile	Company A	Company B	Longitudinal	Company A	Company B	Longitudinal
50%	457.52	248.60	398.07	82.78	90.37	84.02
60%	455.12	244.40	389.59	90.26	93.66	93.32
75%	511.97	263.43	388.36	123.37	106.04	106.02
90%	730.79	466.38	536.24	158.87	139.59	151.32
95%	693.67	466.38	762.02	158.87	139.59	185.72
99.5%	730.79	466.38	789.86	158.87	139.59	186.01

The MAE calculates the average amount of the errors by computing the absolute differences between prediction and actual observation divided by the total number of the observations. The lower the value of MAE is, the better the model fits.

Finally, the MAPE is the average of absolute percentage errors. MAPE has the significant disadvantage of producing infinite or undefined values when the actual values are zero or close to zero (Kim and Kim 2016). If the actual values are very small, then MAPE yields extremely large percentage errors (outliers).

The MAE criterion for single run-off triangle and the total MAE for ${\displaystyle N}$ run-off triangles is calculated, respectively, by

$$MAE=\frac{1}{m}\sum _{i=1}^n\sum _{j=1}^{n-i+1}\left[y_{ij}-\widehat{y_{ij}}\right]andMA{E}^N=\frac{1}{mN}\sum _{k=1}^N\sum _{i=1}^n\sum _{j=1}^{n-i+1}\left[y_{ij}^k-\widehat{y_{ij}^k}\right].$$

The MAPE criterion for single run-off triangle and the total MAPE for ${\displaystyle N}$ run-off triangles, is given, respectively, by

$$MAPE=\frac{100\%}{m}\sum _{i=1}^n\sum _{j=1}^{n-i+1}\left|\frac{y_{ij}-\widehat{y_{ij}}}{y_{ij}}\right|andMAP{E}^N=\frac{100\%}{mN}\sum _{k=1}^N\sum _{i=1}^n\sum _{j=1}^{n-i+1}\left|\frac{y_{ij}^k-\widehat{y_{ij}^k}}{y_{ij}^k}\right|.$$

For the MAPE and MAE criteria, the smallest values indicate the best fit. The computations of the values for each criterion are given in Table 14. According to the MAE criterion, the 60% quantile is the suggested value to be used, while, based on MAPE, the 50% quantile is the most appropriate. Nevertheless, the difference between the MAE values for 50% and 60% is not so big, which means that 60% could also be a good choice.

Table 14. MAE and MAPE for Individual and Longitudinal Quantile Regression.

	Mean Absolute Error (MAE)			Mean Absolute Percentage Error (MAPE)
Quantile	Company A	Company B	Combined	Company A	Company B	Combined
50%	272.30	158.31	212.53	38.00%	27.86%	31.99%
60%	274.38	155.00	210.89	39.13%	27.19%	32.60%
75%	375.69	178.86	233.63	62.06%	33.69%	39.49%
90%	521.73	336.46	441.93	93.37%	66.41%	84.37%
95%	520.07	336.46	610.00	92.54%	66.41%	83.07%
99.5%	522.96	336.46	614.50	93.53%	66.41%	84.38%

Figure 4 and Figure 5 display the reserve estimation for each accident year using the individual quantile regression and the longitudinal quantile regression. Each plot provides the reserve values in different quantiles for each accident year.

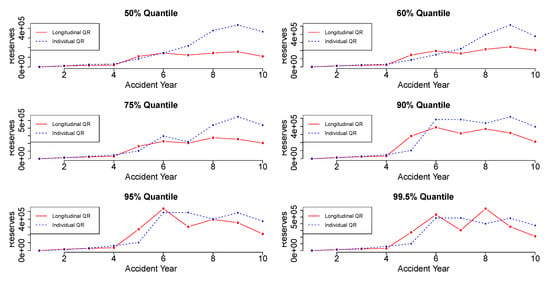
Figure 4. Reserves estimation for individual QR and longitudinal QR (Company A).

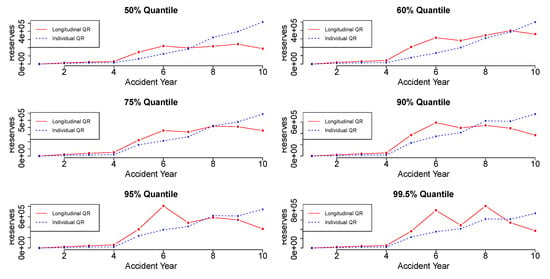
Figure 5. Reserves estimation for individual QR and longitudinal QR (Company B).

Figure 6 illustrates the values of the ultimate reserves, for different quantiles, based on the individual and the longitudinal quantile regression models, in comparison to the ultimate reserves based on the Chain Ladder method for Companies A and B. The ultimate reserves based on the Chain Ladder estimation for Company A is 1,624,721 and for Company B is 1,901,883. More specifically, for Company A, the Chain Ladder reserve value coincides with the individual quantile regression reserve value at 50-quantile, and with the longitudinal quantile regression reserve value around the 80-quantile. For Company B, the Chain Ladder reserve value coincides with the individual quantile regression reserve value around 50-quantile, and with the longitudinal quantile regression reserve value around the 60-quantile.

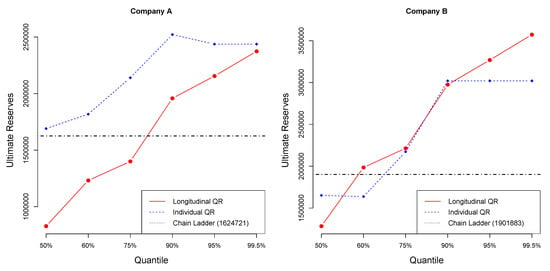
Figure 6. Ultimate reserves for individual QR and longitudinal QR.

6. Risk Capital Requirement and Risk Margin

Solvency II and IFRS bring some significant changes, particularly in relation to the estimation of insurance liabilities. Generally, the Probability of Sufficiency is a measure of solvency in liability valuation (DalMoro and Krvavych 2017):

• Probability of sufficiency below 50% indicates that the technical provisions are set below the central estimate, which leads to an under-reserved position.
• Probability of sufficiency with values between 50% and 60% indicates that the technical provisions are approximately at the level of central estimate, which leads to weak prudence.
• For values of probability of sufficiency around 75%, the technical provisions are above the central estimate, which leads to adequate prudence.
• Finally, if the probability of sufficiency is above 75%, the technical provisions are enough to lead to strong prudence.

Risk Margin

Based on Solvency II directive, risk margin represents the potential costs to transfer the insurance obligations to a third party and it is calculated based on the cost-of-capital (CoC) method. Solvency II considers risk over a one-year time horizon.

According to this approach, when the capital requirements for each future year are given, the risk margin is equal to the sum of the discounted costs of capital, which are the capital requirements multiplied by the cost-of-capital rate (6%). The risk margin (RM) is exclusively based on the solvency capital requirement (SCR) estimation and according to the cost-of-capital (CoC) methodology is calculated as follows (CEIOPS 2009):

$$\begin{array}{c}\hfill RM=\sum _{t\ge 0}\frac{SCR\left(t\right)}{{(1+r_t)}^{t+1}}\times CoC=\sum _{t\ge 0}\frac{Va{R}_{99.5\%}\left(R_t\right)-mean\left(R_t\right)}{{(1+r_t)}^{t+1}}\times CoC,\end{array}$$

where ${\displaystyle R_t}$ is the estimated reserve for the accident year ${\displaystyle t}$, ${\displaystyle r_t}$ is the risk-free rate for maturity, ${\displaystyle SCR\left(t\right)}$ is the Solvency Capital Requirement for the accident year ${\displaystyle t}$, and ${\displaystyle CoC}$ is the cost of capital rate. The solvency capital requirement is the difference between the 99.5% quantile and the 50% quantile of the reserves. The cost of capital is 6% (as Solvency II suggests) and we suppose that the risk-free rate for maturity is ${\displaystyle r_t=1\%}$ for all accident years (the real risk-free rate for maturity is given by EIOPA).

Along with the best estimate (BE), risk margin makes up the technical provisions and ensures that their value is equivalent to the amount that an (re)insurer would be expected to require in order to take over and meet the insurance obligations. Generally, risk margin increases the value of the technical provisions from the BE up to an amount which is equivalent to a theoretical level needed to transfer obligations to another (re)insurer. Risk margin represents what an (re)insurer would have to pay to the market to take on the BE liabilities. When the market takes on your BE liabilities, they will have to set aside capital to cover the SCR. Therefore, holding the SCR incurs a cost. Risk margin represents this cost. Dong et al. (2015) showed how one can provide an accurate estimation of risk margin and hence provision, instead of estimating the mean and then applying a risk margin. Their method is more robust when the data are heavy tailed. Their approach has been used for the univariate quantile regression model and is suitable for a simple line of business (single run-off triangle).

Table 15 presents the calculated risk margins for each individual line of business (Companies A and B), based on the univariate quantile regression model and Table 16 presents the corresponding risk margin for each individual line of business based on our longitudinal model.

Table 15. Risk Margin based on Individual Quantile Regression.

	Company A			Company B
Accident Year	SCR	Capital Charge 6%	Discounted Capital Charge	SCR	Capital Charge 6%	Discounted Capital Charge
			1% Discount Rate			(1% Discount Rate)
1	340,874	20,452	20,452	383,015	22,981	22,981
2	231,100	13,866	13,594	287,630	17,258	16,919
3	93,717	5623	5405	259,313	15,559	14,955
4	52,555	3153	2971	208,157	12,489	11,769
5	40,749	2445	2259	170,761	10,246	9465
6	55,963	3358	3041	57,434	3446	3121
7	5585	335	298	2310	139	123
8	3663	220	191	60	4	3
9	1672	100	86	0	0	0
Total	825,879	49553	RM = 48,297	1,368,680	82,121	RM = 79,337

Table 16. Risk Margin based on Longitudinal Quantile Regression.

	Company A			Company B
Accident Year	SCR	Capital Charge 6%	Discounted Capital Charge	SCR	Capital Charge 6%	Discounted Capital Charge
			1% Discount Rate			(1% Discount Rate)
1	389,957	23,397	23,397	511,493	30,690	30,690
2	321,754	19,305	19,114	436,219	26,173	25,914
3	244,764	14,686	14,396	368,081	22,085	21,650
4	118,911	7135	6925	162,896	9774	9486
5	73,566	4414	4242	116,999	7020	6746
6	12,598	756	719	19,949	1197	1139
7	1699	102	96	2103	126	119
8	554	33	31	550	33	31
9	0	0	0	0	0	0
Total	1,163,802	69,828	RM =68,921	1,618,289	97,097	RM = 95,774

Finally, Table 17 presents the calculated risk margins based on the bootstrap method and the resulting Figure 7 and Figure 8 illustrate: (a) the histograms of total simulated IBNRs; (b) the empirical cumulative distribution functions of IBNRs; (c) the simulated ultimate claim cost against ultimate claim cost; and (d) the latest actual incremental claims cost for the latest available calendar period against latest incremental claims, for Companies A and B, respectively.

Table 17. Risk Margin based on Bootstrap (Poisson).

	Company A			Company B
Accident Year	SCR	Capital Charge 6%	Discounted Capital Charge	SCR	Capital Charge 6%	Discounted Capital Charge
			1% Discount Rate			(1% Discount Rate)
1	2,79,592	16775	16775	369922	22195	12797
2	245258	14715	14570	362541	21752	11567
3	209005	12540	12293	287763	17266	9251
4	168286	10097	9800	213236	12794	7042
5	147734	8864	8518	215192	12912	6485
6	93559	5614	5341	142384	8543	4099
7	63681	3821	3599	80768	4846	2289
8	56266	3376	3149	75132	4508	1842
9	37758	2265	2092	69887	4193	1515
Total	1301139	78068	RM = 76138	1816825	109009	RM = 56886

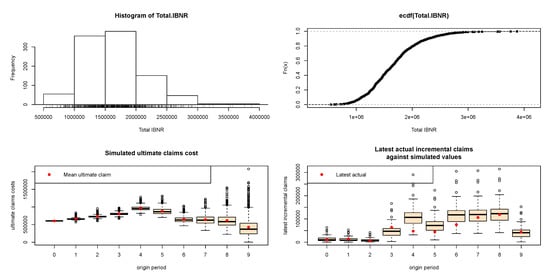
Figure 7. Bootstrap graphs for Company A.

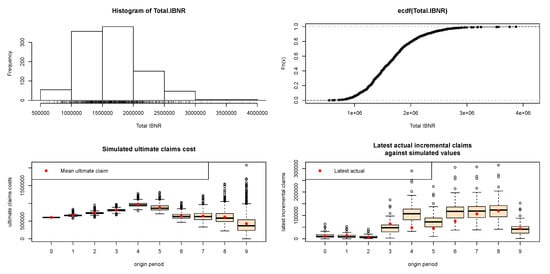
Figure 8. Bootstrap graphs for Company B.

From histograms and the empirical cumulative distribution functions, we observe that the IBNRs may follow distributions with positive skewness. We also observe that the simulated data may not follow the same trend as the actual data (specifically in Company B). It indicates that the original data might have some trends that are not reflected in the model.

Remark 4.

If the distribution of the reserves were known, then the mean of this distribution would be the BE, i.e., the amount to be paid as compensation to the beneficiaries. Nevertheless, this distribution is not known and for that reason many methodologies are used to estimate the BE such as the bootstrap method. In case of quantile regression models, a specific quantile, which provides estimations close to the mean, would be used to estimate the BE. For that reason, we use the 50% quantile, but a larger one could be used especially for long tail distributions.

7. Concluding Remarks

We propose quantile regression for longitudinal data in the framework of a general multivariate loss reserving model. Our model considers a combination of the between and within lines of business, taking into account the correlations and variation of run-off triangles. We investigated a general insurance portfolio that consists of two correlated subportfolios (two auto run-off triangles). The least squares estimators investigated only changes in the mean, while the quantile regression characterized a particular point of a distribution, which provides a more complete description of the entire shape of the claims distribution. According to Solvency II and IFRS, the solvency capital requirement (SCR) was provided based on the best estimate (BE) and, in the sequel, the overall risk margin (RM), based on the cost-of-capital (CoC) methodology, was calculated.