2.1. Bond Data
In order to establish rules to monitor risks of a bond portfolio over time, we analyse sovereign bond spreads of five European countries. We distinguish between short-term bonds with a maturity between three months and five years and long-term bonds with maturities between five and 30 years. We analyse sovereign bond data from Thomson Reuters Datascope (see (
Thomson Reuters DataScope 2018) for more details; a subscription is needed; therefore, our utilised datasets cannot be made openly available) and calculate spreads between the bond yields and the AAA-rated bond yield quoted from the European Central Bank (ECB). The spread series which we model is obtained as a spread referring to ECB AAA Svenson yields, see
Svensson (
1994) for more details.
Our analysis covers data from five European countries, namely Germany, Great Britain, Italy, Spain and France. For each country, we consider both short-term and long-term bonds issued by the countries between 2007 and 2017. The chosen countries reflect the diversity of European economies in that time period. Two of the analysed countries are from the PIIGS group (Portugal, Ireland, Italy, Greece and Spain) which were in the heart of the European debt crisis and exhibited economic downturn. Great Britain and France are considered more stable economies, but both dealt with relevant economic news events such as the Brexit Referendum or controversial elections during the considered time period. Finally, we analyse bonds issued by Germany which is handled as the most risk-free economy within the group. Therefore, our choice of countries reflects various economic situations, the analysis will show how news have adverse effects in different economic settings. The analysed bond data includes more than 300 bonds, and daily closing prices from Thomson Reuters Pricing are utilised. We focus on analysing spreads of single tradeable sovereign bonds, therefore concentrating on analysing a link between macroeconomic news and fixed income products. We would like to highlight that the obtained results can be utilised by risk management models in the Fixed Income domain.
2.2. Macroeconomic News Sentiment
We wish to analyse the effect news articles and macroeconomic announcements have on spreads of bond yields. In our study, macroeconomic sentiment comprised by RavenPack is employed (see (
RavenPack News Analytics 2018) for more details; a subscription is needed, therefore our utilised datasets cannot be made openly available). RavenPack News Analytics marks every macroeconomic news event in news items from various sources with a sentiment value called “ESS”—event sentiment score. This sentiment value lies between
and 1 and quantifies the sentiment of a particular news event for the chosen entity. In our case, we choose the bond issuer as the entity we would like to follow. We create daily news time series out of all sentiment values that stream in over a given day. Our work clearly distinguishes itself from other literature on sovereign bond spreads and their main determinants, since we do not take into account fiscal time series and fundamentals but rather try to analyse a connection between macro-economic news sentiment and bond spreads. One main advantage of this is that we are not limited to scheduled announcements, which are still covered in our news database, and quarterly or semi-annually releases of fundamental figures. On the contrary, news items are observed throughout the day and news sentiment signals are calculated before market closing time. By following these macro-economic news on a daily basis, we get daily macro-economic signals which can be included into daily trading decisions. Analysis on fundamentals can be an addition to our signals; however, in this work, we concentrate on daily macroeconomic news sentiment and its effect on sovereign bond spreads.
We follow macroeconomic news, which are bundled under the entities Germany, Great Britain, Italy, Spain and France, respectively, representing the issuer of the sovereign bonds. A typical macroeconomic news example from our database includes the time stamp, the relevance of the news with respect to the key word (entity) as well as the event sentiment score.
Depending on weekday and time, the news item is mapped to its relevant trading day. Weekend news are shifted to Monday and any news coming in after market closing time is shifted to the next working day. For each news item
, we have given a time stamp
which consists of the date and time of the release of the news item,
where
and
n denotes the number of news items in the data set. We map the time stamp of each news item to a trading day for that news item
where
We have that
and
and
m is the number of trading days in the given time interval
With
c denoting the market closing time, we set
We create nine different time series based on the relevance and sentiment value we receive from RavenPack’s database to build daily news sentiment values which are utilized as an input variable for our time series models. Firstly, we split the sentiment values into two sub-categories handling positive and negative news sentiment separately. We conduct a pre-analysis of our news sentiment data which allows us to consider all news after market closing time until market closing time on the following day for the daily news sentiment. We create
a mean news-sentiment value time series,
a volume of news time series,
a news-impact time series,
for the three categories
all news,
positive news,
negative news.
We build the volume of news time series
with
n denoting the number of news items and
t with
denoting the current trading day, as
The mean news-sentiment time series takes into account the event sentiment score “
ESS”, which is delivered with each news event,
. The mean overall sentiment scores are calculated for each trading day leading to a trading day mean news-sentiment time series. The mean news-sentiment value time series
is calculated as
The news-impact time series takes into account the potential influence decay of a news story. The news items for each working day are weighted keeping in mind that the most recent news item before closing has the highest effect on the closing yield. The other news items, which come in before that, have a decaying importance. The news-impact time series
with
c denoting the closing time of the market is given as
The calculation of the news-impact time series was introduced by (
Yu and Mitra 2016). The sentiment value
is multiplied by a decreasing exponential weight leading to the news impact score
The closing time of the market
c is the reference time,
measures the difference between news time
and market closing time and the decaying factor
is determined through
We choose a time span of 640 min, after which news stories only have half of their impact left.
Time series of volume of the news items are examined as well. We count the number of relevant news items for the entity considered for a given trading day. Again, weekend news and news after market closing are shifted to the next trading day. We count all incoming news items (neutral, positive and negative) to create the volume of all news time series and distinguish between positive and negative news sentiment to create a volume of positive and negative news time series.
Therefore, we create nine different time series observed throughout the time interval where the bond is active. All news time series are utilized as regressors in a regression model as well as external variables in an ARIMAX model. Furthermore, their correlation with the yield spread is calculated for the whole time period and through a rolling window approach.
When analysing correlations between bond yields and news-sentiment time series, we have to consider potential spurious correlations we might observe due to business cycle effects or common market microstructures. When analysing the volume of news times series, we cannot detect long-term business cycle trends, rather short-term news event effects are captured quite clearly. The news-impact time series put the highest weights to most recent news, news older than 10 h does not have a high weight in the daily time series anymore. Therefore, we focus on capturing short-term macroeconomic news effects and analyse the correlation between bond spreads and these derived macroeconomic news-sentiment series.
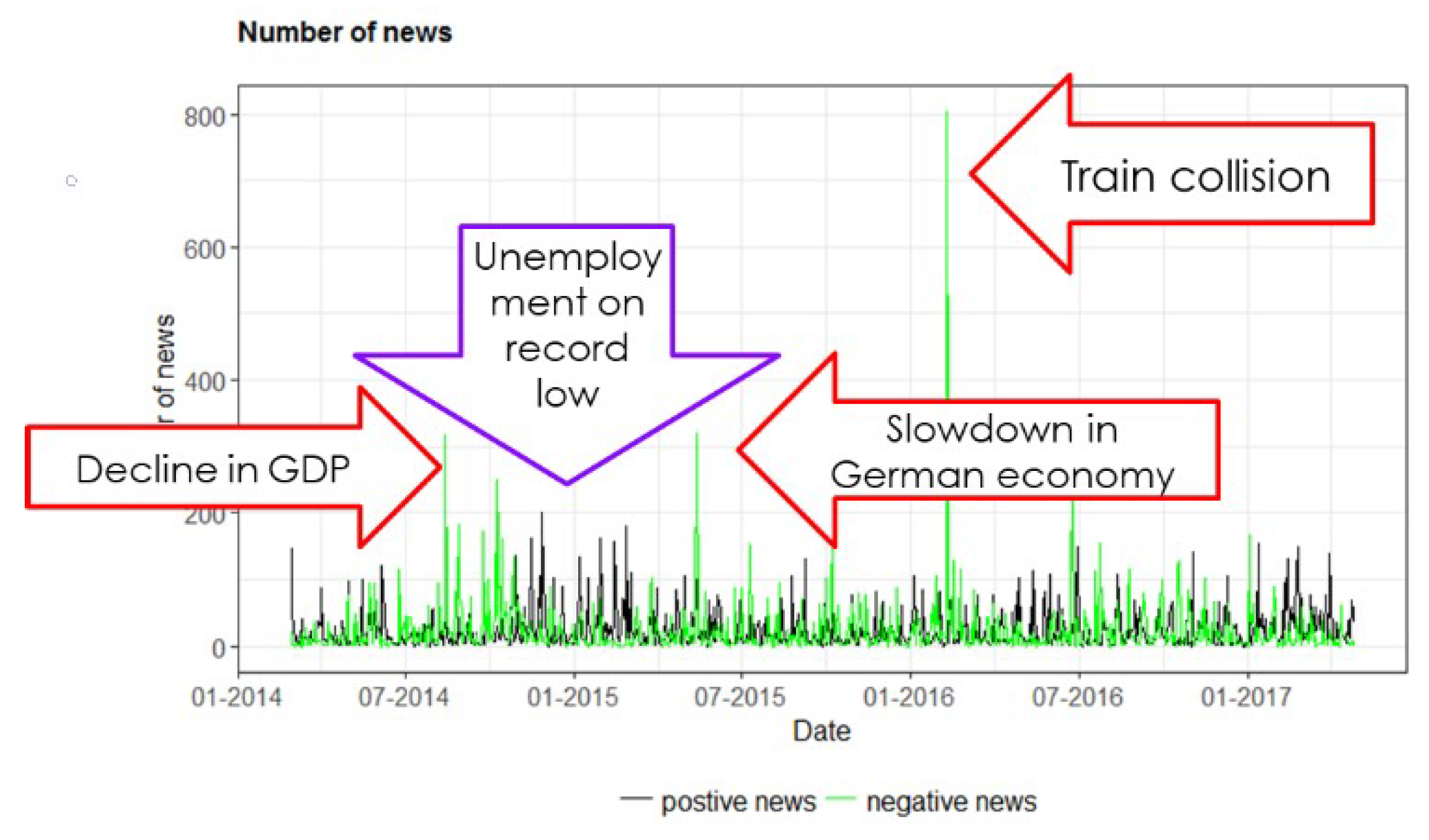
In
Figure 1, a typical time series of news volume is depicted. Here, we show a volume series for Germany, where we distinguish between positive and negative news items. We can see spikes in the positive and negative volume series, which are analysed in more detail to understand the reason for this dynamic. Increases in positive and negative news are triggered through various events, which might not all be relevant for movements of bond spreads. Since we would like to analyse effects of macroeconomic news on bond spreads, we are less interested in news collected under the topic “social”; instead, we concentrate in the following on news from the broad topics “politics” and “economics”.
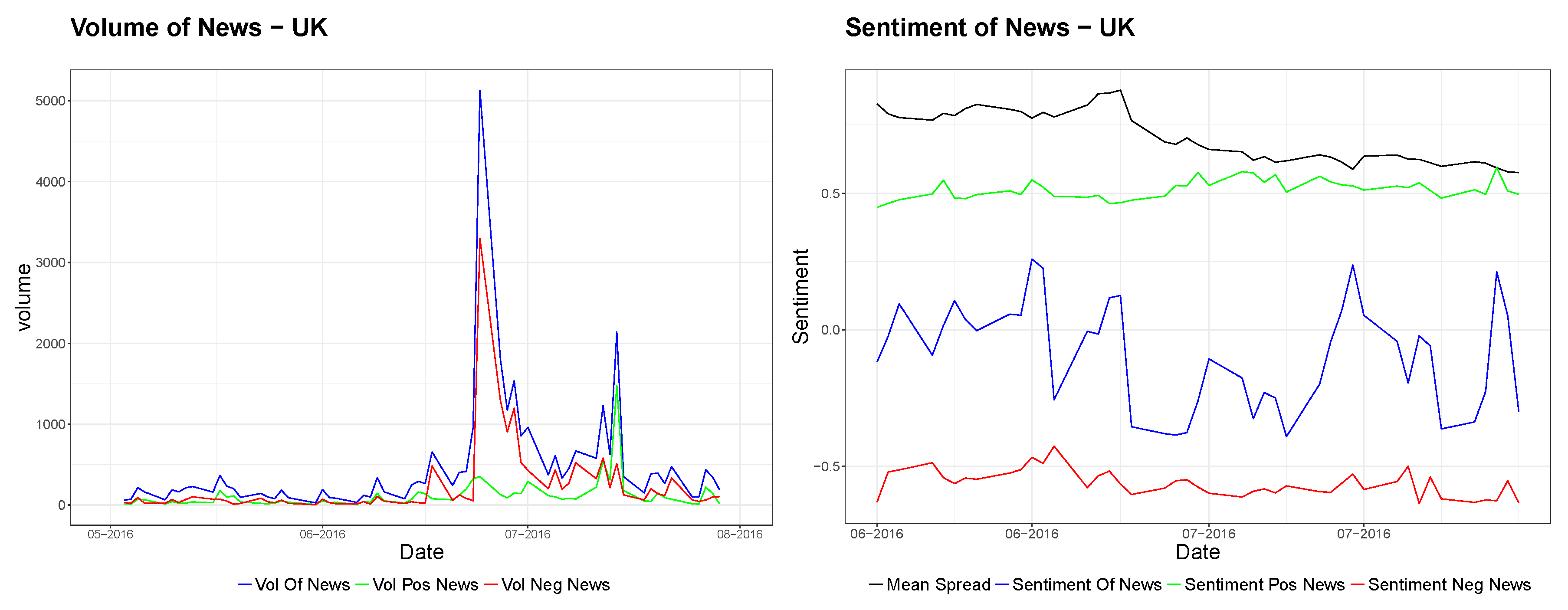
One important event that occurred in the covered time period has been the Brexit Referendum in the UK on 23 June 2016. In
Figure 2, we depict the volume and sentiment of news of positive, negative and overall news events for the entity UK between May and July 2016. A clear spike in the volume of news can be detected on and shortly after 23 June. In addition, the overall sentiment shows a decline in this period; however, the sentiment series exhibits less movement during the referendum period. Here, the volume of macroeconomic news is a stronger signal for events than the daily sentiment series. This example highlights the different features of the daily sentiment series, counting the occurring news events which are relevant for an entity is often a good indication of market movements.
2.3. Correlation and ARIMAX Models
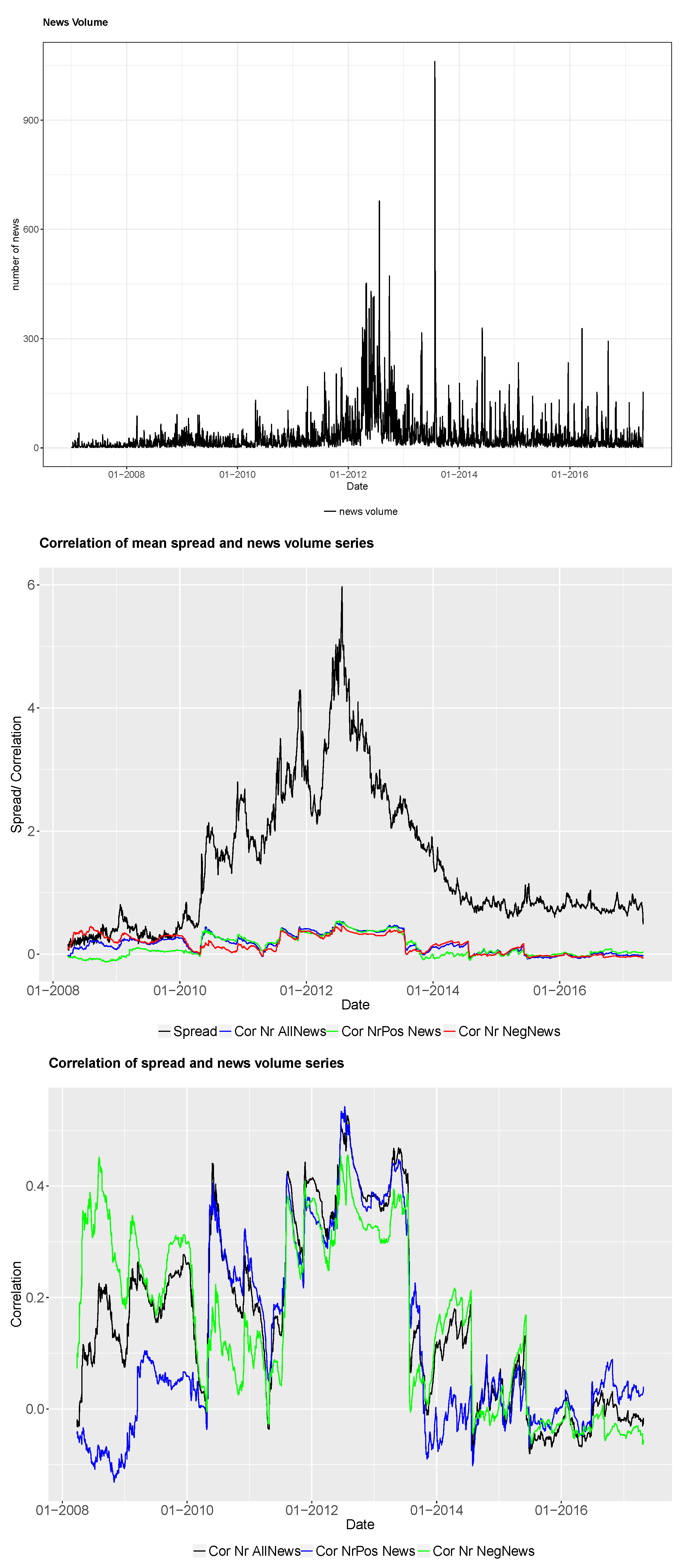
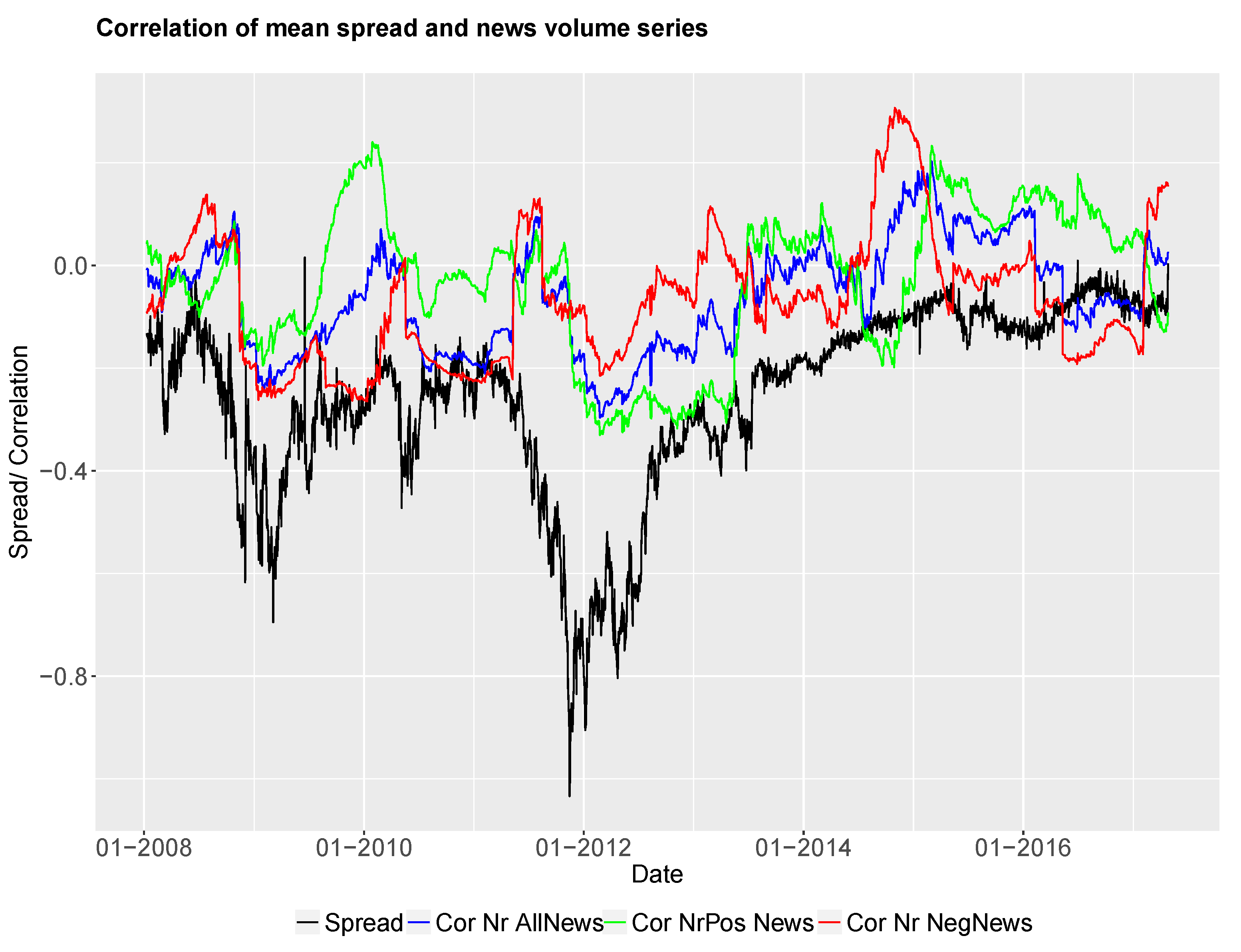
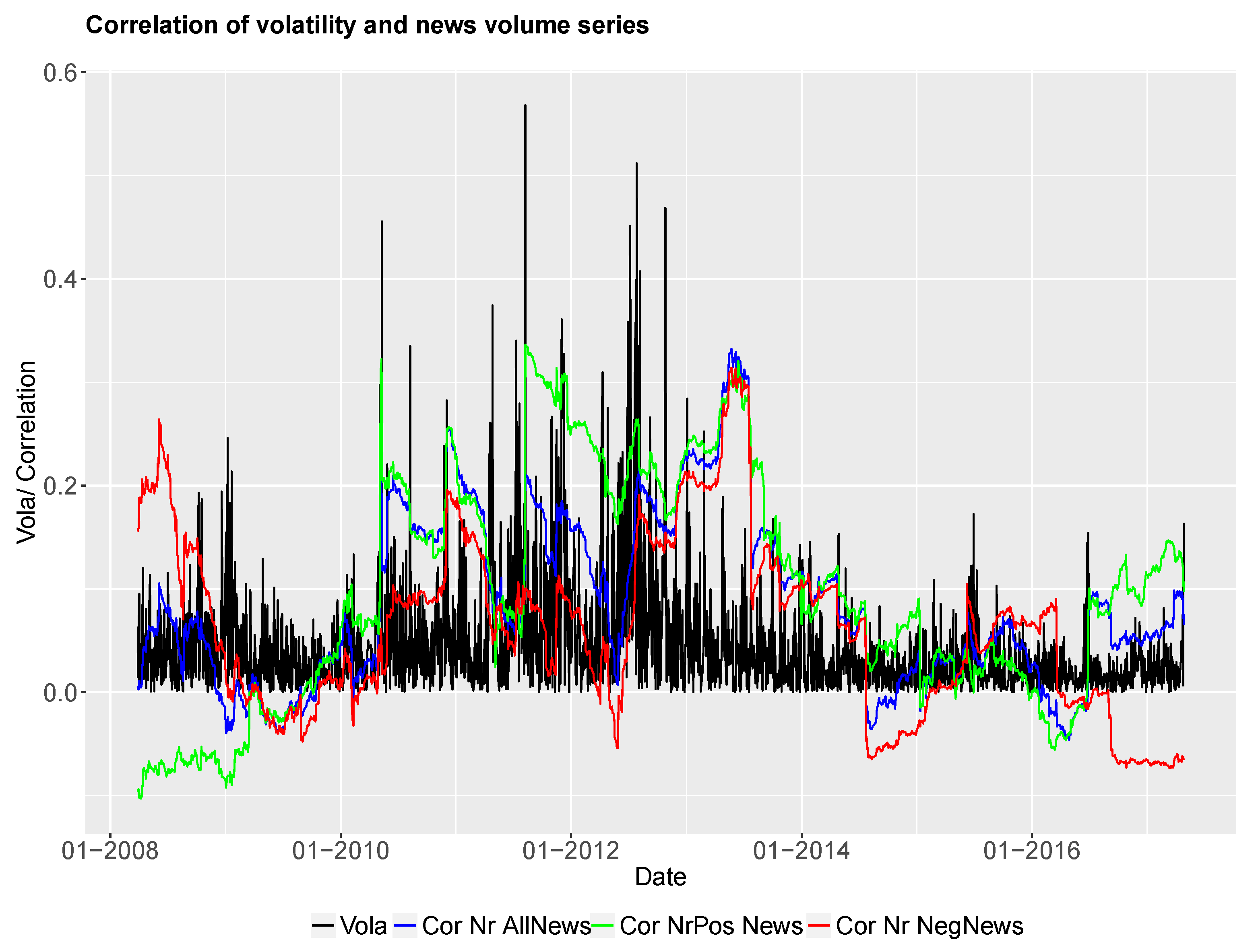
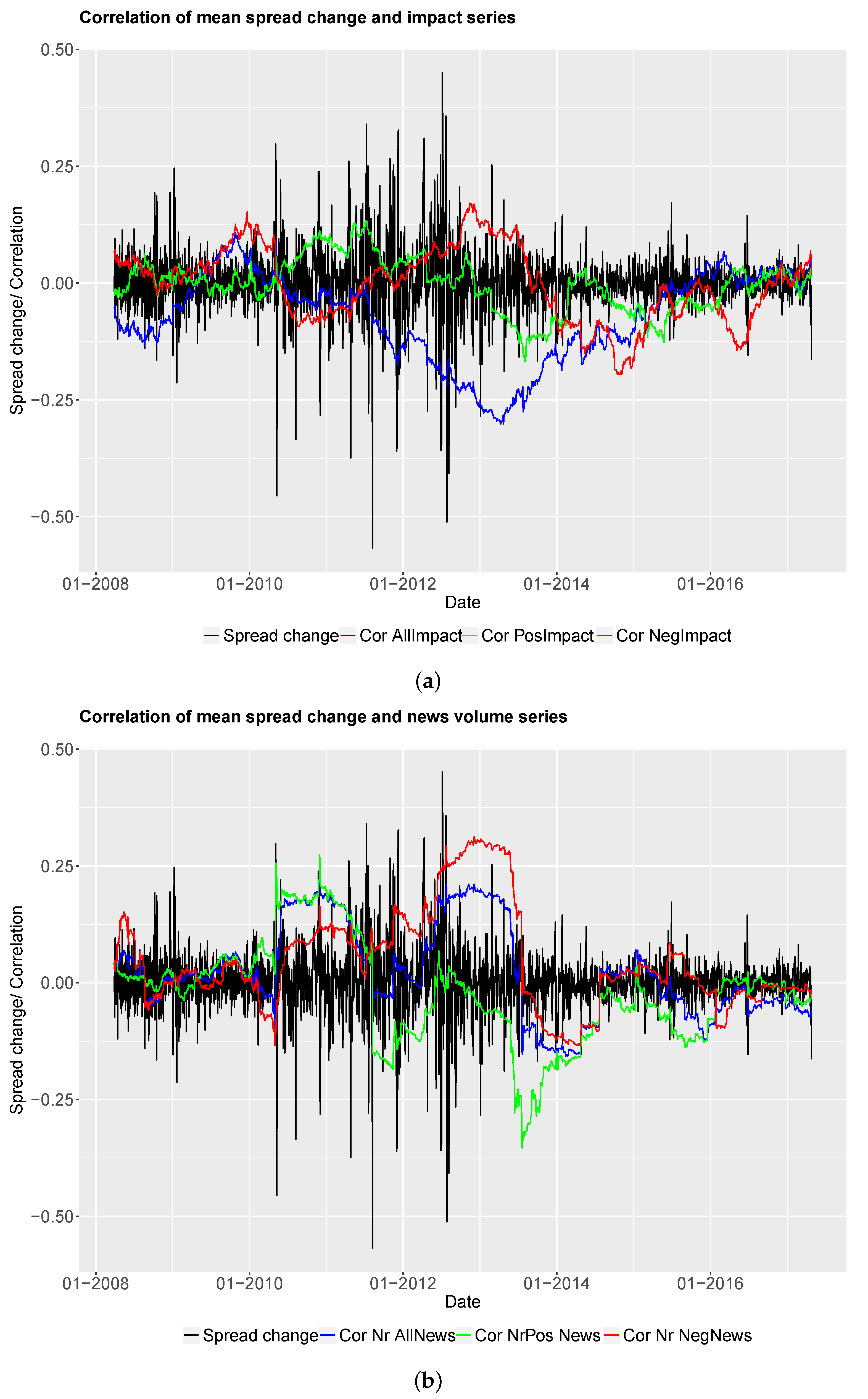
In order to establish whether a relation between the different news time series and the yield spread changes exists, we test for correlation between the daily spread change series and all nine news time series. We calculate Pearson’s correlation between the daily time series and test whether the correlation is significant. Furthermore, the correlation is estimated within a rolling window to see time-varying features of the correlation between time series. We would like to investigate stability and predictive accuracy over time.
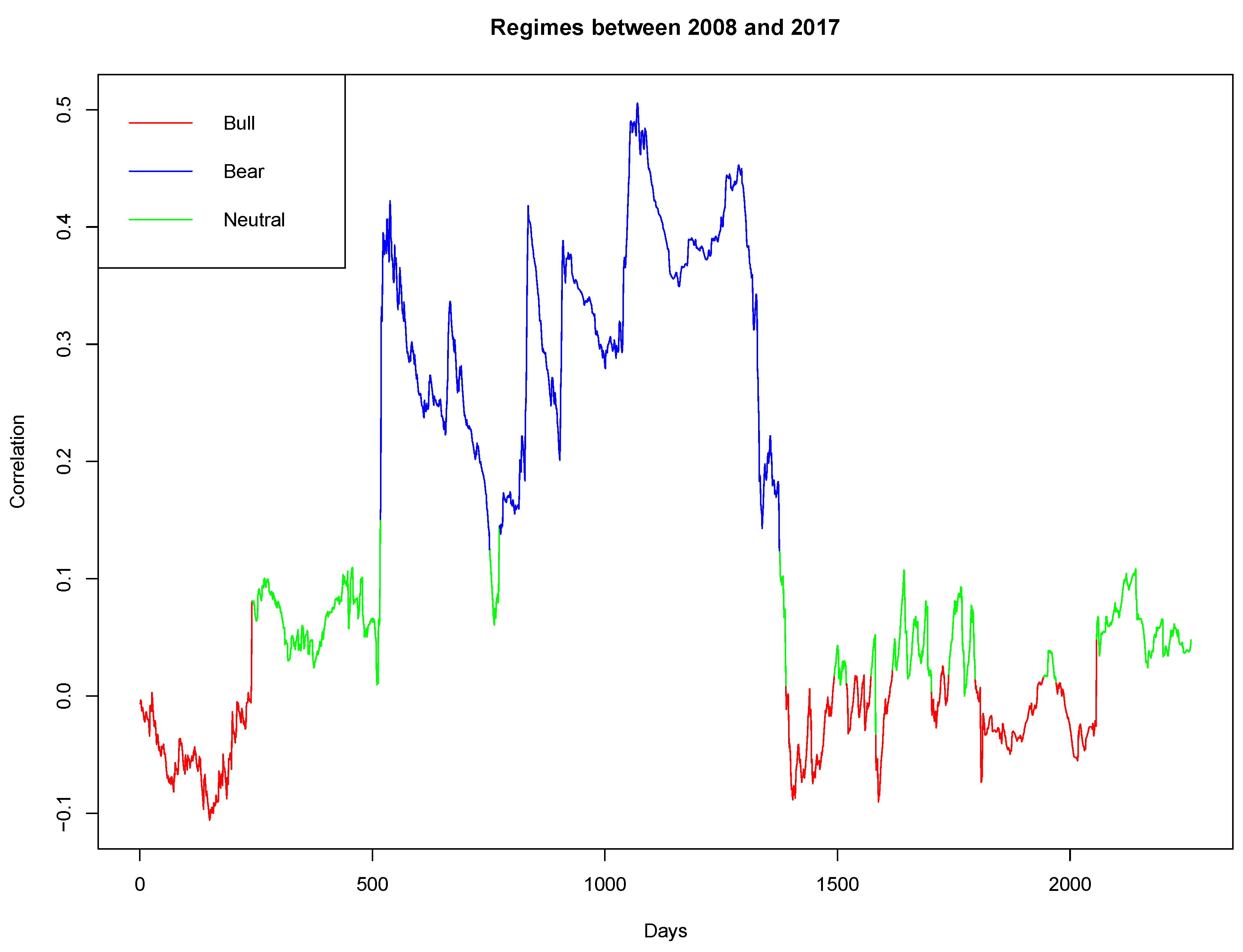
By calculating rolling correlations between daily news sentiment series and bond spread series, we establish the correlation through time. We would like to find out if the correlations are more or less stable over time or if we have large variations of correlation values. In particular, we are interested in investigating change points in the rolling correlation series. We assume that a significant change from positive to negative correlations indicates changes in the market environment. These changes can be captured in a regime-switching setting, where market states of the underlying bond spread can be filtered out by estimating the current state of the rolling correlation time series. In the literature, exogenous break points in sovereign bond spread series have been established in our considered time window between 2007 and 2017. The exogenous breaks often mark a division into pre- and post crisis periods (see, amongst others, (
Afonso et al. 2015;
Caggiano and Greco 2012)). Further methodologies to analyse a changing relationship between news time series and yield spreads over time include the Dynamic Conditional Correlation model by (
Engle 2002) and the specific model formulation for leptokurtic data analysed in (
Del Brio et al. 2011). In addition, a cointegration analysis can add further value, especially a threshold cointegration where adjustments occur when deviations reach a certain threshold (see, e.g., (
Stigler 2010) for an overview and (
Tsagkanos and Siriopoulos 2015) for a case study on asymmetric effects between markets and production in Northern and Southern Europe). These methodologies are promising alternatives and will be analysed in future work. We analyse our correlation findings further within a regime-switching setting, where hidden regime switches are estimated by filtering out information on the observed rolling correlation. News and their correlation to bond spreads are then analysed taking into account the current filtered market regime.
Secondly, a linear regression is performed to analyse the effects of news time series on the yield spread changes. All nine news time series are taken as regressors in a variety of combinations. We report here results for regression with three news series regressors, namely the Volume of All News, Positive Impact and Negative Impact.
Lastly, we apply an Integrated Autoregressive Moving Average (ARIMA) model (see (
Tsay 2010) for more details) to analyse and forecast bond yields. We additionally add external explanatory variables to the model, therefore fitting an ARIMAX(
p,
i,
q) model to yield spread changes. The ARIMAX(
p,
i,
q) model is given through
where
is the
i-th differenced series of the time series
is a white noise series and
is the
l-th external explanatory variable,
The explanatory variable are uni- or multivariate. An ARIMAX model was also successfully applied by
Apergis (
2015) to analyse Credit Default Swaps (CDS) spreads and newswire sentiments. His study results in improved forecast errors when external news time series were allowed. We model the spread changes firstly with an ARIMA(
p,
i,
q) model and compare the resulting in-sample and out-of-sample one-step ahead forecast errors to those which arise from ARIMAX(
p,
i,
q) model with various external regressors. In the following sections, we run a considerable amount of models on our daily yield spread series, taking into account uni- as well as multivariate external explanatory variables. We can improve the forecast errors of analysed bonds when sentiment is taken into consideration. This points to the fact that news sentiment has a value for bond yield modelling and risk assessment. Monitoring macroeconomic news sentiment series in addition to the actual yield spread can lead to early warning signs for unexpected changes in yields or structural changes visible in the yield spreads.