Generating VaR Scenarios under Solvency II with Product Beta Distributions
Abstract
1. Introduction
2. The Monte Carlo Algorithm
- Choose an index I randomly according to a uniform distribution over .
- Generate independently d random variables , …, where follows a Beta distribution with parameters and (product beta distribution).
- Set .
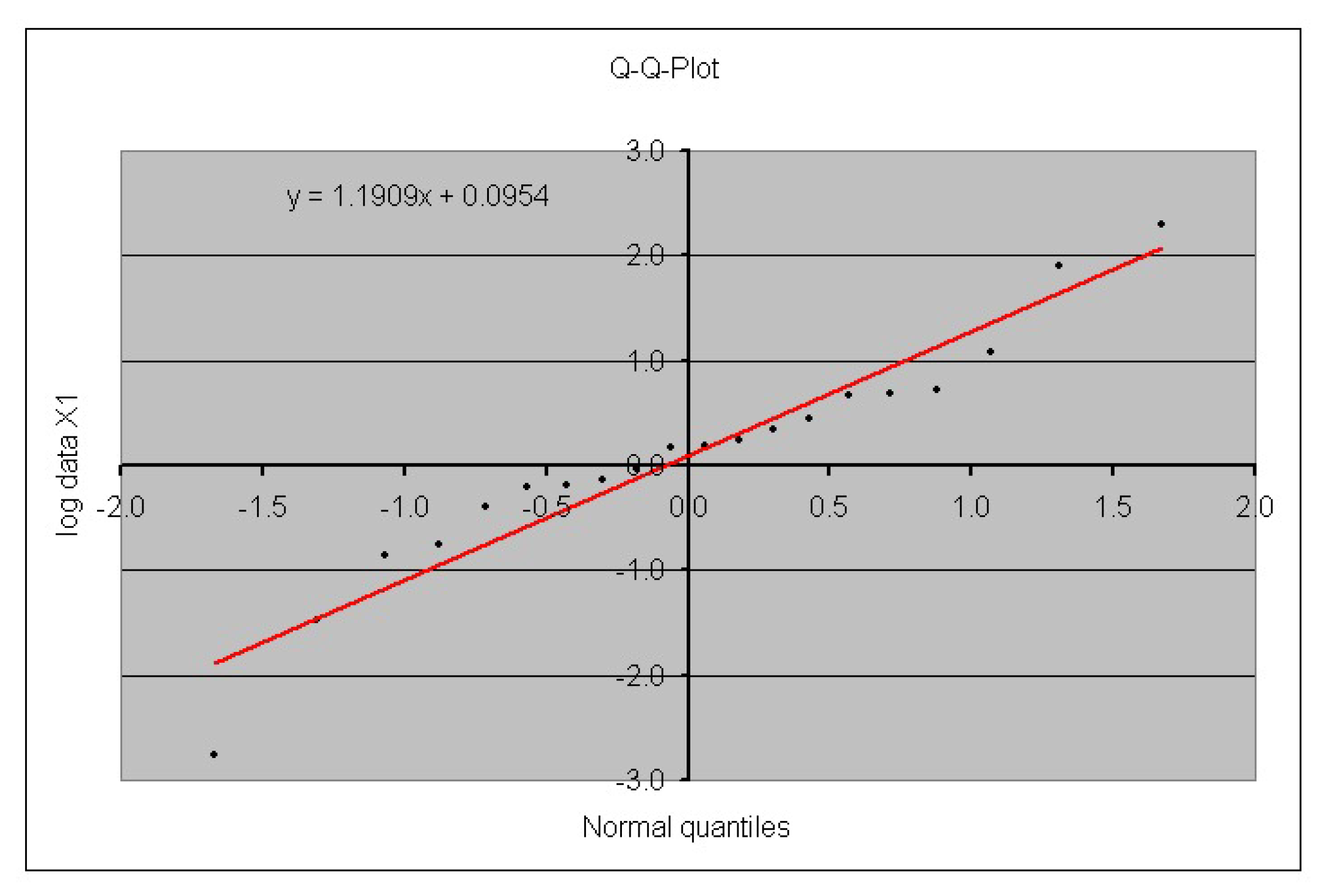
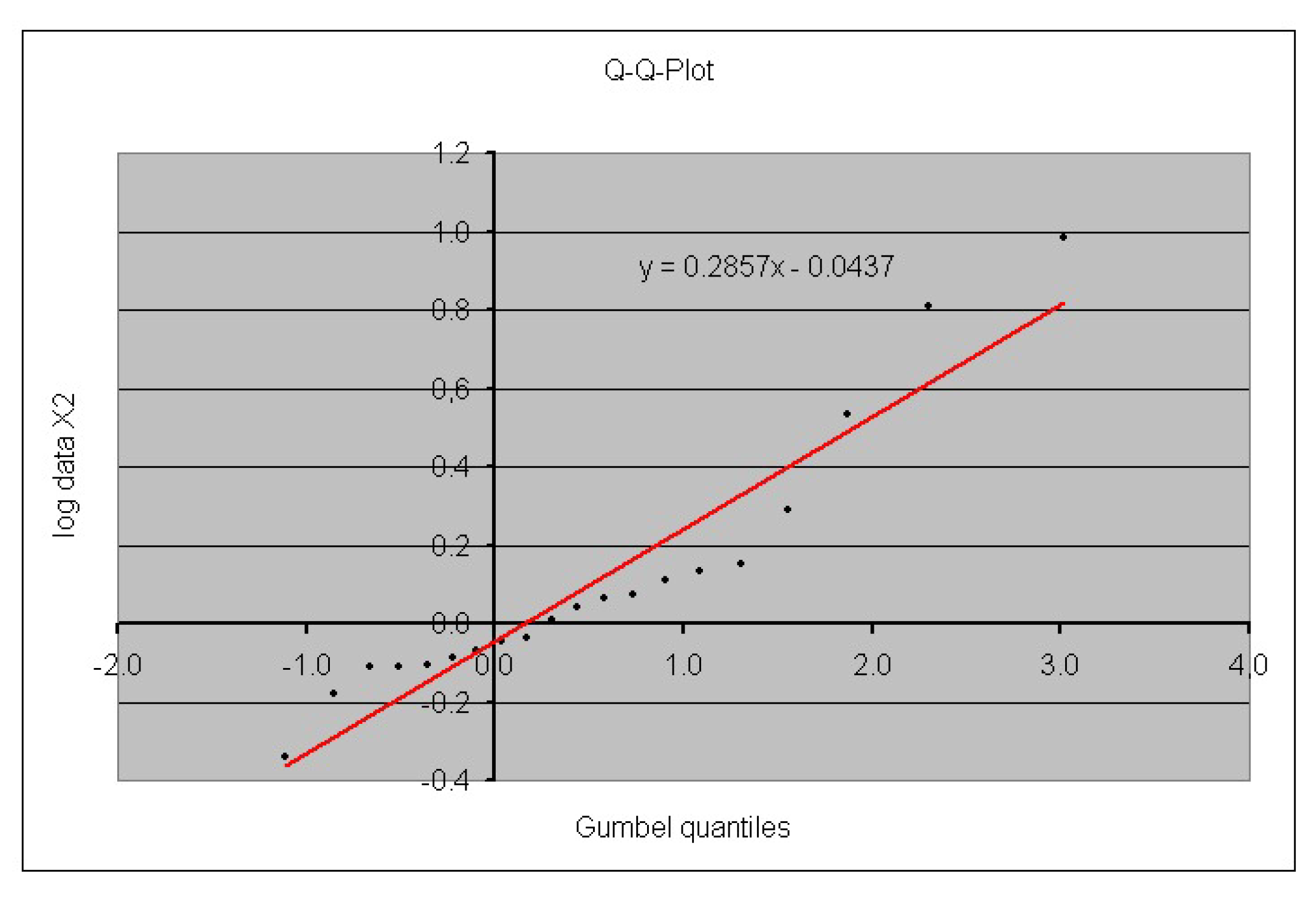
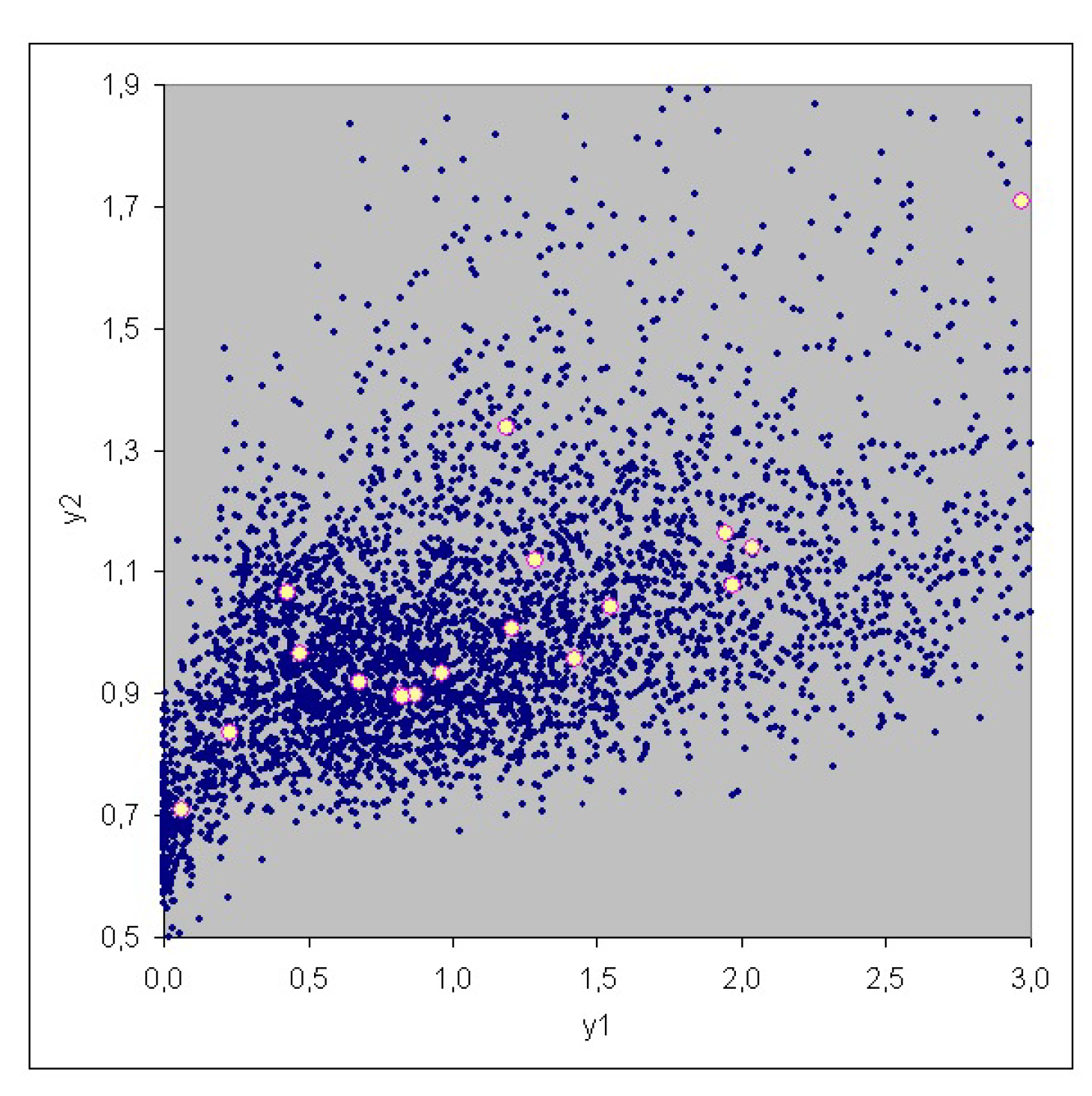
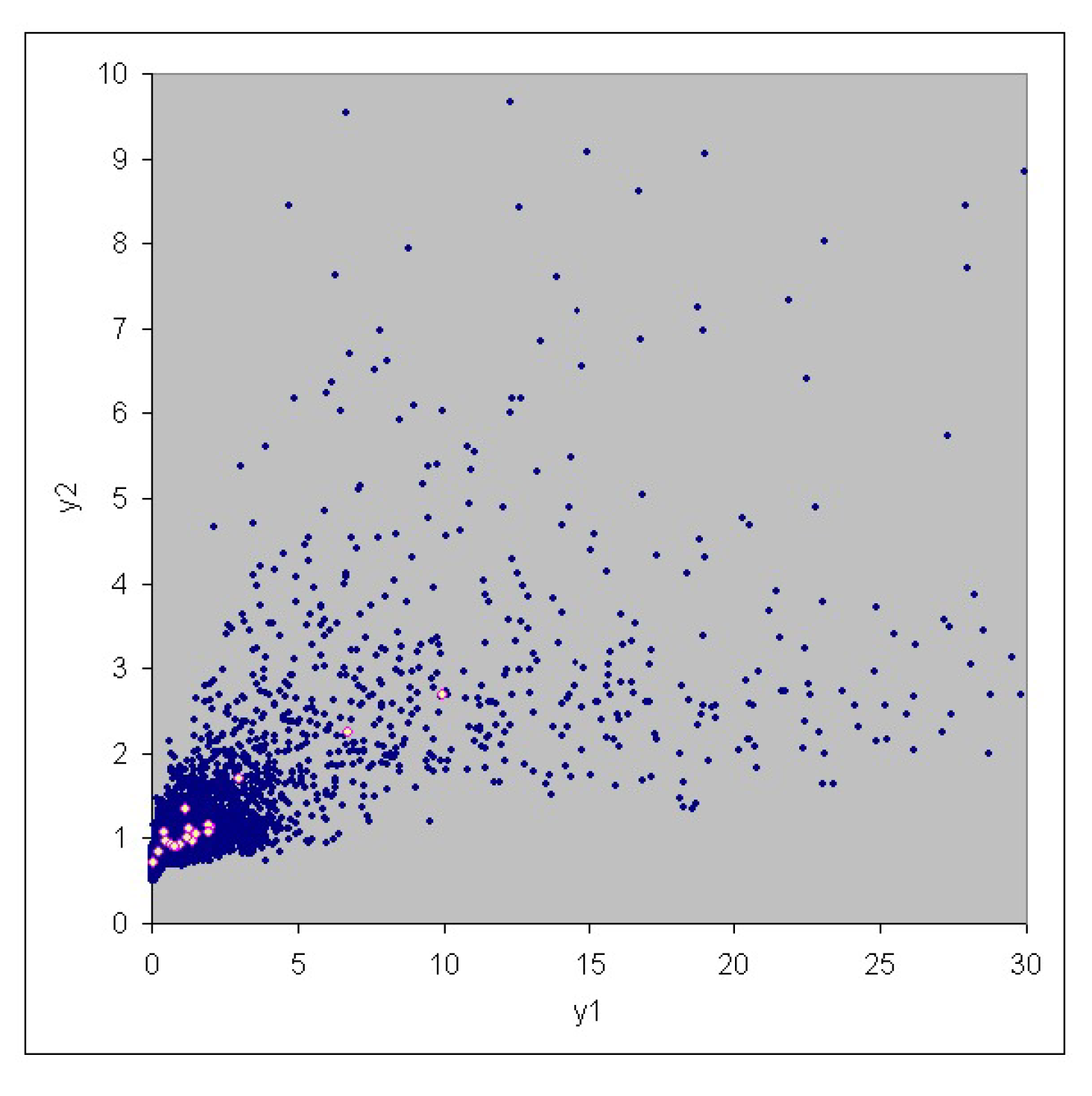
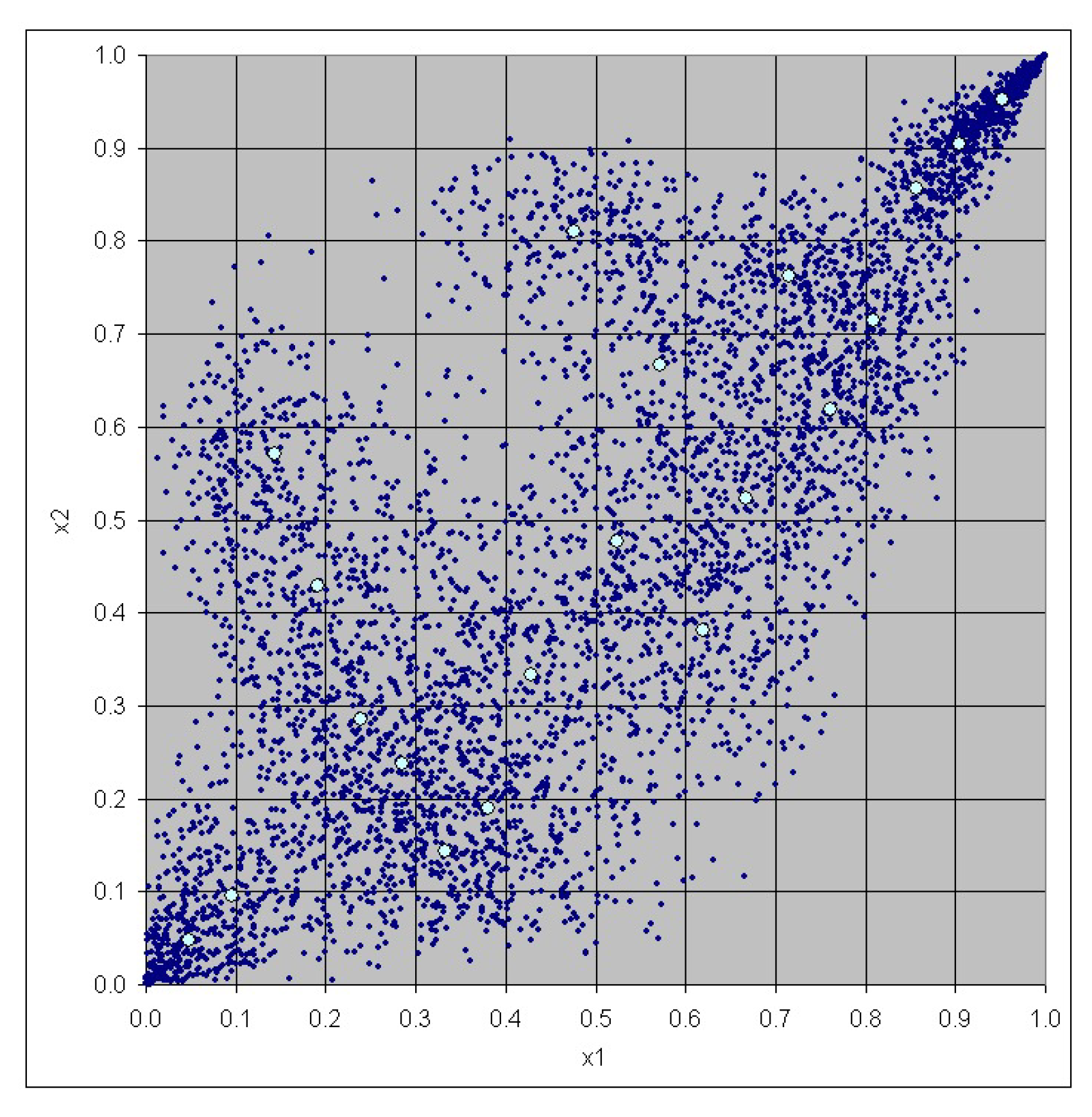
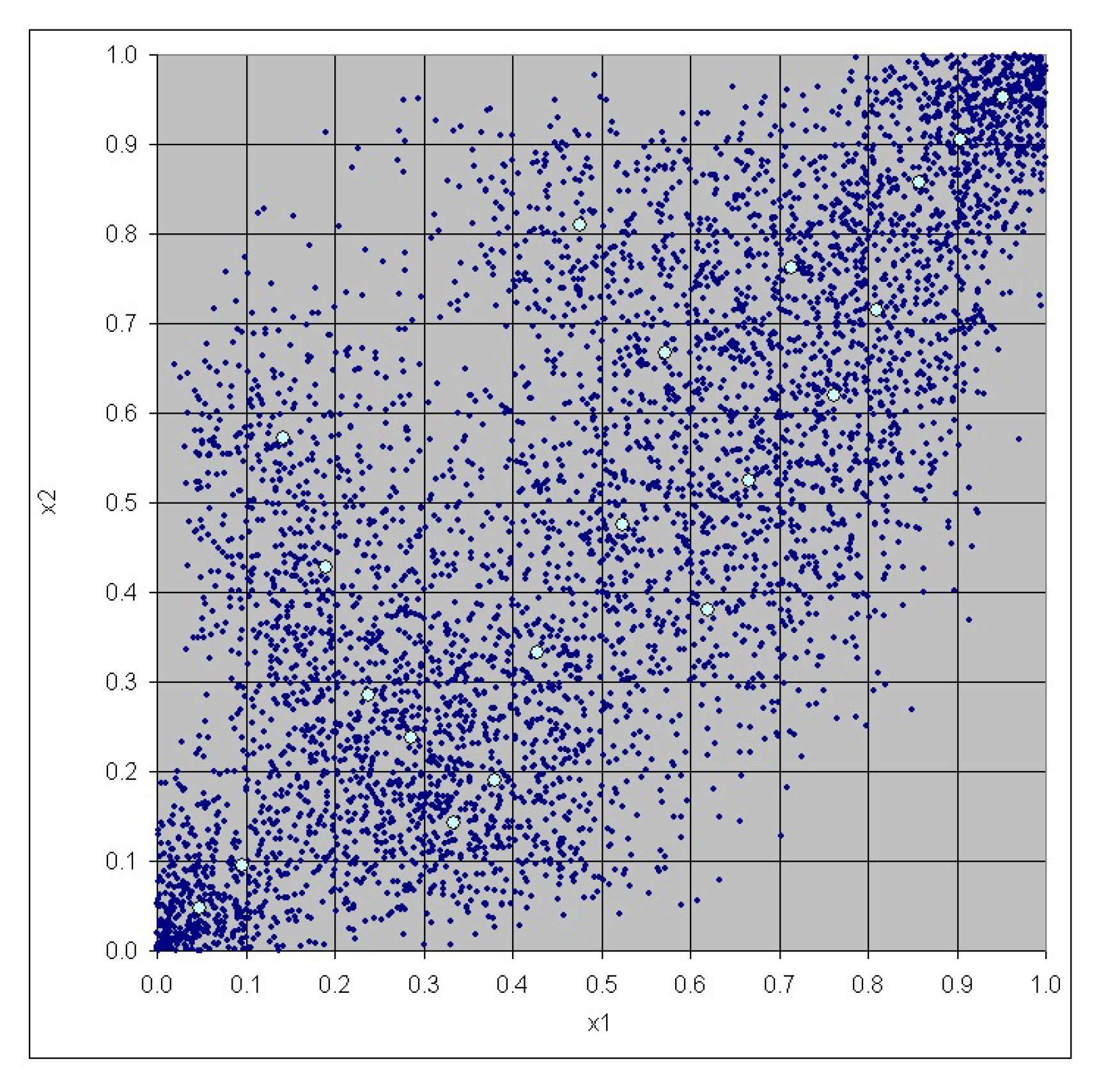
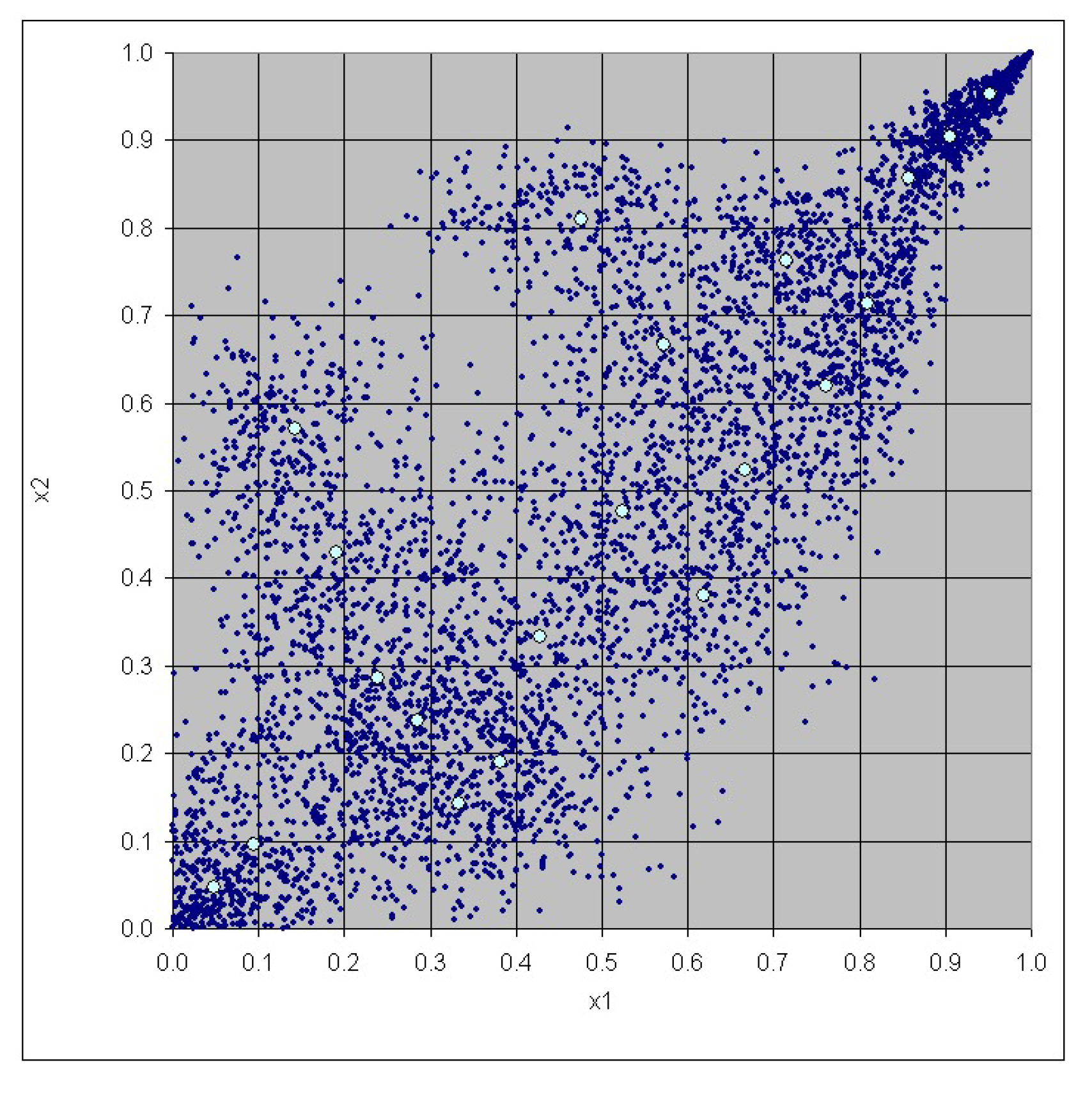
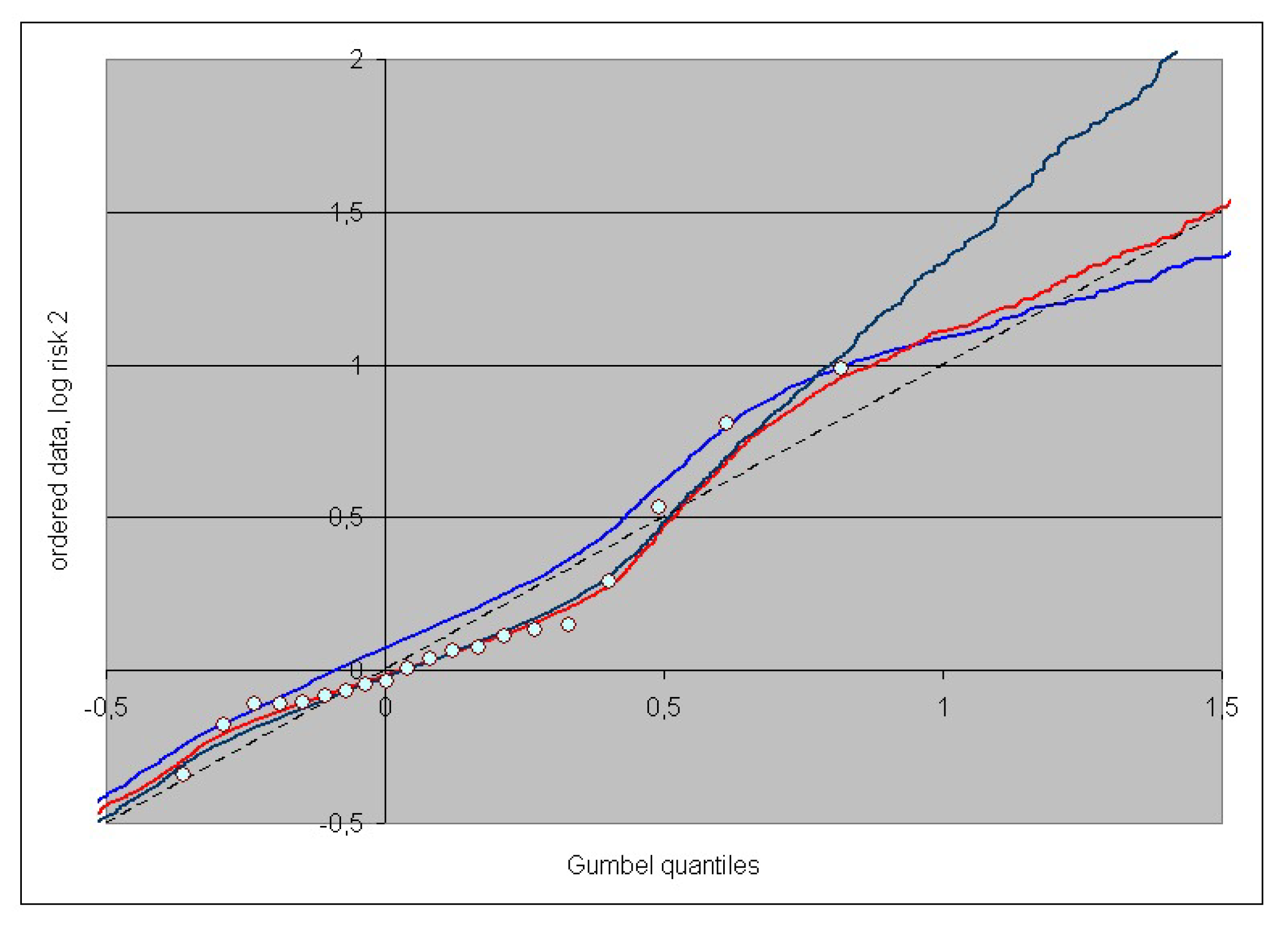
3. Case Study
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blumentritt, Thomas. 2012. On Copula Density Estimation and Measures of Multivariate Association. Reihe: Quantitative Ökonomie 171. Lohmar: Eul Verlag. [Google Scholar]
- Cadoni, Paolo, ed. 2014. Internal Models and Solvency II. From Regulation to Implementation. London: Risk Books. [Google Scholar]
- Cherubini, Umberto, Elisa Luciano, and Walter Vecchiato. 2004. Copula Methods in Finance. New York: Wiley. [Google Scholar]
- Cottin, Claudia, and Dietmar Pfeifer. 2014. From Bernstein polynomials to Bernstein copulas. Journal of Applied Functional Analysis 9: 277–88. [Google Scholar]
- Cruz, Marcelo, ed. 2009. The Solvency II Handbook. Developing ERM Frameworks in Insurance and Reinsurance Companies. London: Risk Books. [Google Scholar]
- Durante, Fabrizio, and Carlo Sempi. 2016. Principles of Copula Theory. Boca Raton: CRC Press. [Google Scholar]
- Embrechts, Paul, Giovanni Puccetti, and Ludger Rüschendorf. 2013. Model uncertainty and VaR aggregation. Journal of Banking and Finance 37: 2750–64. [Google Scholar] [CrossRef]
- European Union. 2015. Commission Delegated Regulation EU 2015/35 of 10 October 2014 supplementing Directive 2009/138/EC of the European Parliament and of the Council on the taking-up and pursuit of the business of Insurance and Reinsurance (Solvency II). Official Journal of the European Union 17.1: L12/1–L12/797. [Google Scholar]
- Ibragimov, Rustam, and Artem Prokhorov. 2017. Heavy Tails and Copulas. Topics in Dependence Modelling in Economics and Finance. Singapore: World Scientific. [Google Scholar]
- Joe, Harry. 2015. Dependence Modeling with Copulas. Boca Raton: CRC Press. [Google Scholar]
- Mai, Jan-Frederik, and Matthias Scherer. 2017. Simulating Copulas. Stochastic Models, Sampling Algorithms, and Applications, 2nd ed. Singapore: World Scientific. [Google Scholar]
- Mainik, Georg. 2015. Risk aggregation with empirical margins: Latin hypercubes, empirical copulas, and convergence of sum distributions. Journal of Multivariate Analysis 141: 197–216. [Google Scholar] [CrossRef]
- Malevergne, Yannick, and Didier Sornette. 2006. Extreme Financial Risks. From Dependence to Risk Management. New York: Springer. [Google Scholar]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2015. Quantitative Risk Management. Concepts, Techniques and Tools, 2nd ed. Princeton: Princeton University Press. [Google Scholar]
- Neumann, André, Taras Bodnar, Dietmar Pfeifer, and Thorsten Dickhaus. 2018. Multivariate multiple test procedures based on nonparametric copula estimation. Biometrical Journal, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Pešta, Michal, and Ostap Okhrin. 2014. Conditional least squares and copulae in claims reserving for a single line of business. Insurance: Mathematics and Economics 56: 28–37. [Google Scholar] [CrossRef]
- Pfeifer, Dietmar, Andreas Mändle, Olena Ragulina, and Côme Girschig. 2018. Continuous partition-of-unity copulas and their application to risk management. Advances in Statistical Analysis. [Google Scholar]
- Pfeifer, Dietmar, Andreas Mändle, and Olena Ragulina. 2017. New copulas based on general partitions-of-unity and their applications to risk management (part II). Dependence Modeling 5: 246–55. [Google Scholar] [CrossRef]
- Pfeifer, Dietmar, Hervé Awoumlac Tsatedem, Andreas Mändle, and Côme Girschig. 2016. New copulas based on general partitions-of-unity and their applications to risk management. Dependence Modeling 4: 123–40. [Google Scholar] [CrossRef]
- Rank, Jörn, ed. 2007. Copulas. From Theory to Application in Finance. London: Risk Books. [Google Scholar]
- Rose, Doro. 2015. Modeling and Estimating Multivariate Dependence Structures with the Bernstein Copula. Ph.D. thesis, Lincoln Memorial University, München, Germany. [Google Scholar]
- Sandström, Arne. 2011. Handbook of Solvency for Actuaries and Risk Managers. Theory and Practice. London: CRC Press, Taylor & Francis Group. [Google Scholar]
- Schumaker, Larry L. 2015. Spline Functions: Computational Methods. Philadelphia: SIAM. [Google Scholar]
- Scott, David W. 2016. Multivariate Density Estimation. Theory, Practice, and Visualization, 2nd ed. Hoboken: Wiley. [Google Scholar]
- Szegö, Giorgio, ed. 2004. Risk Measures for the 21st Century. Chichester: Wiley. [Google Scholar]
- Yang, Jingping, Zhijin Chen, Fang Wang, and Ruodu Wang. 2015. Composite Bernstein copulas. ASTIN Bulletin 45: 445–75. [Google Scholar] [CrossRef]
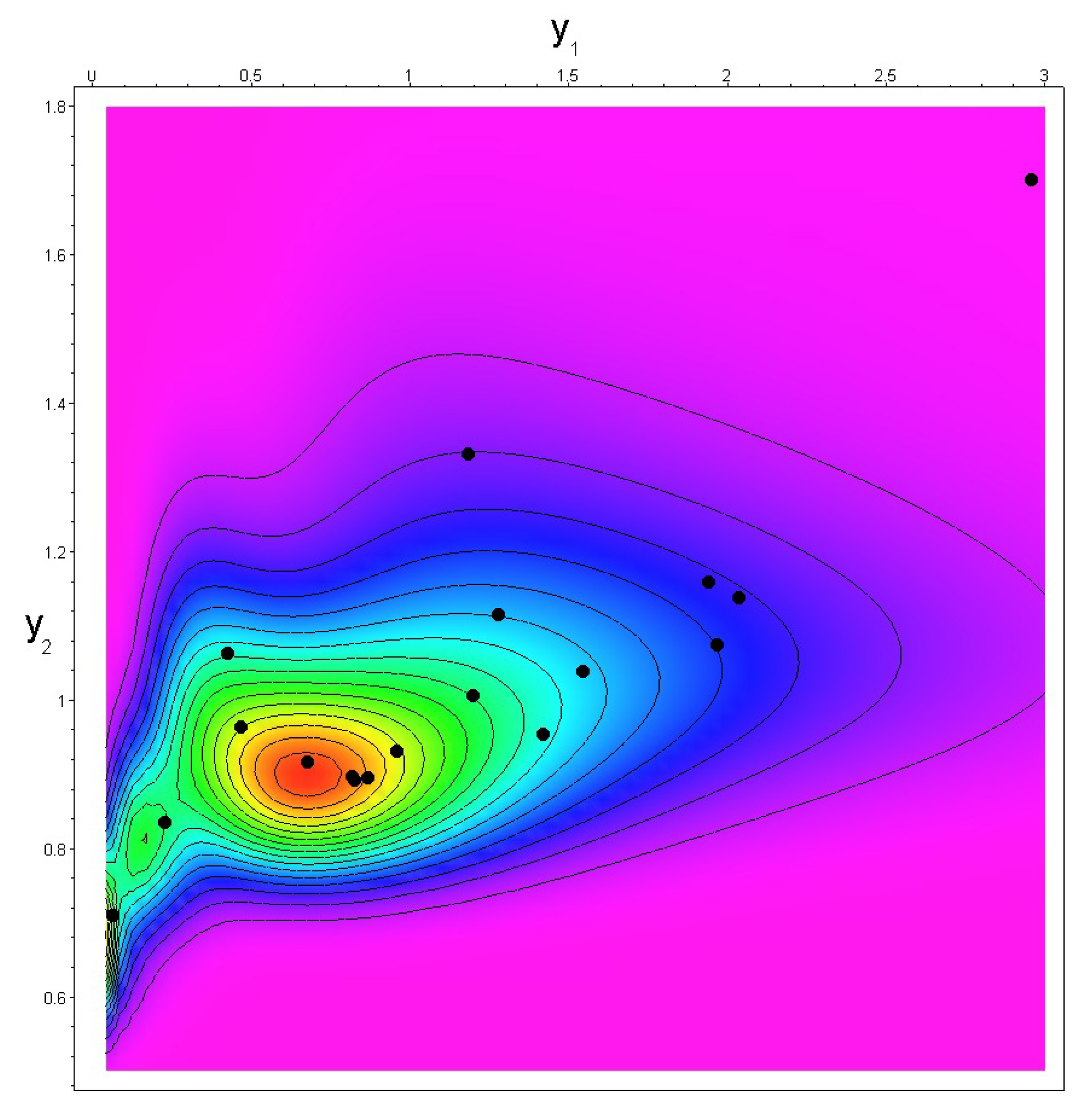
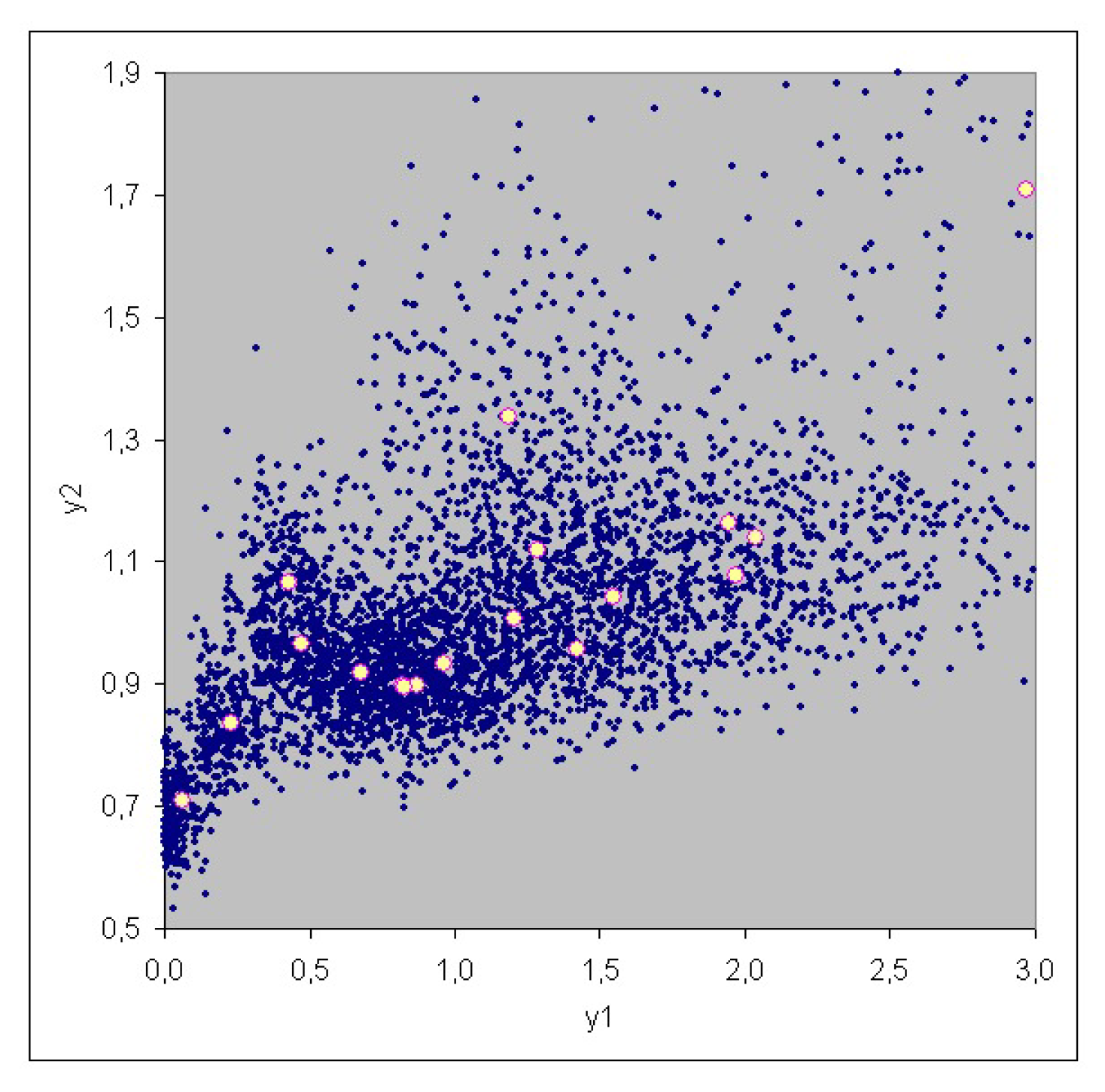
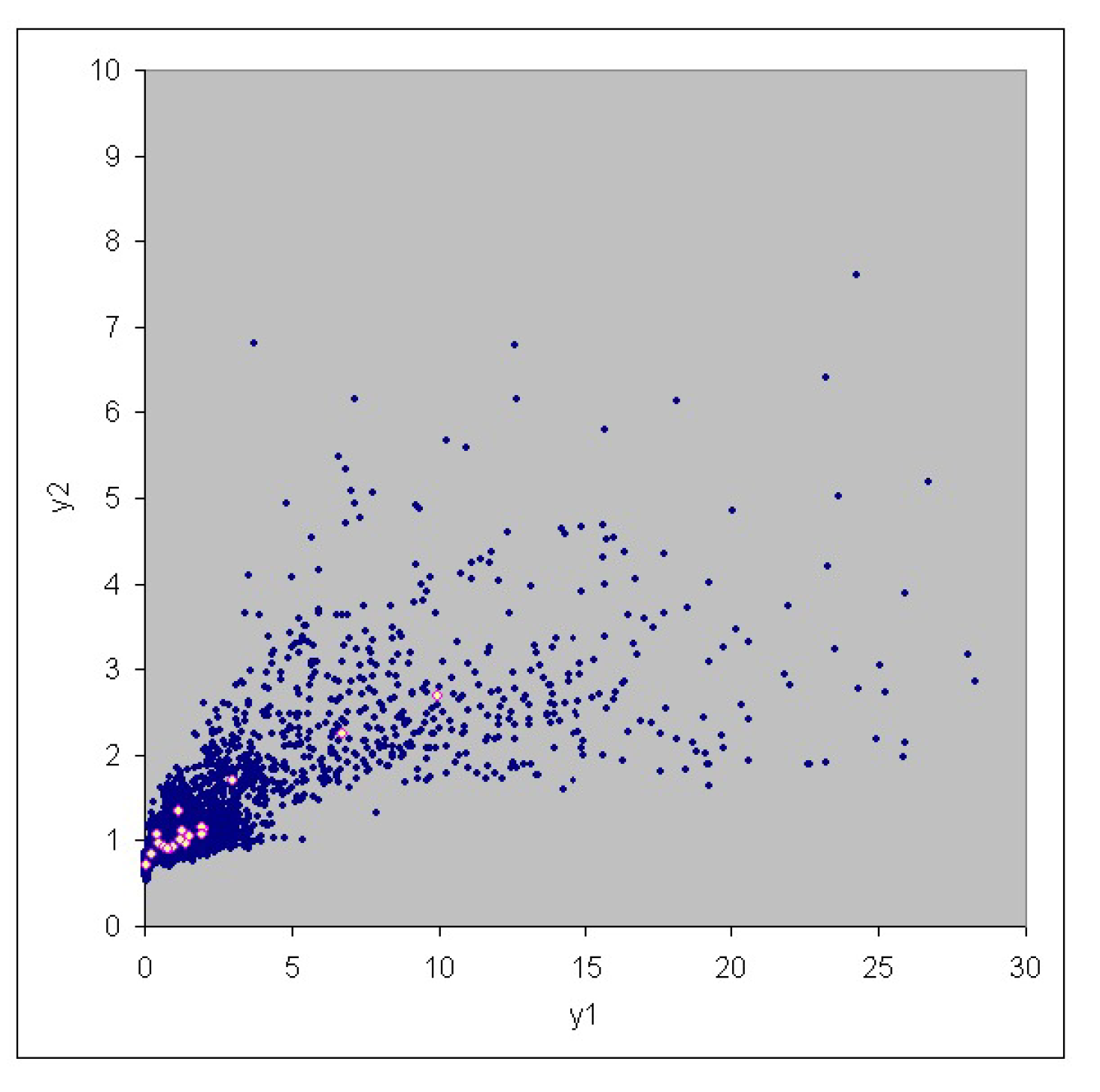

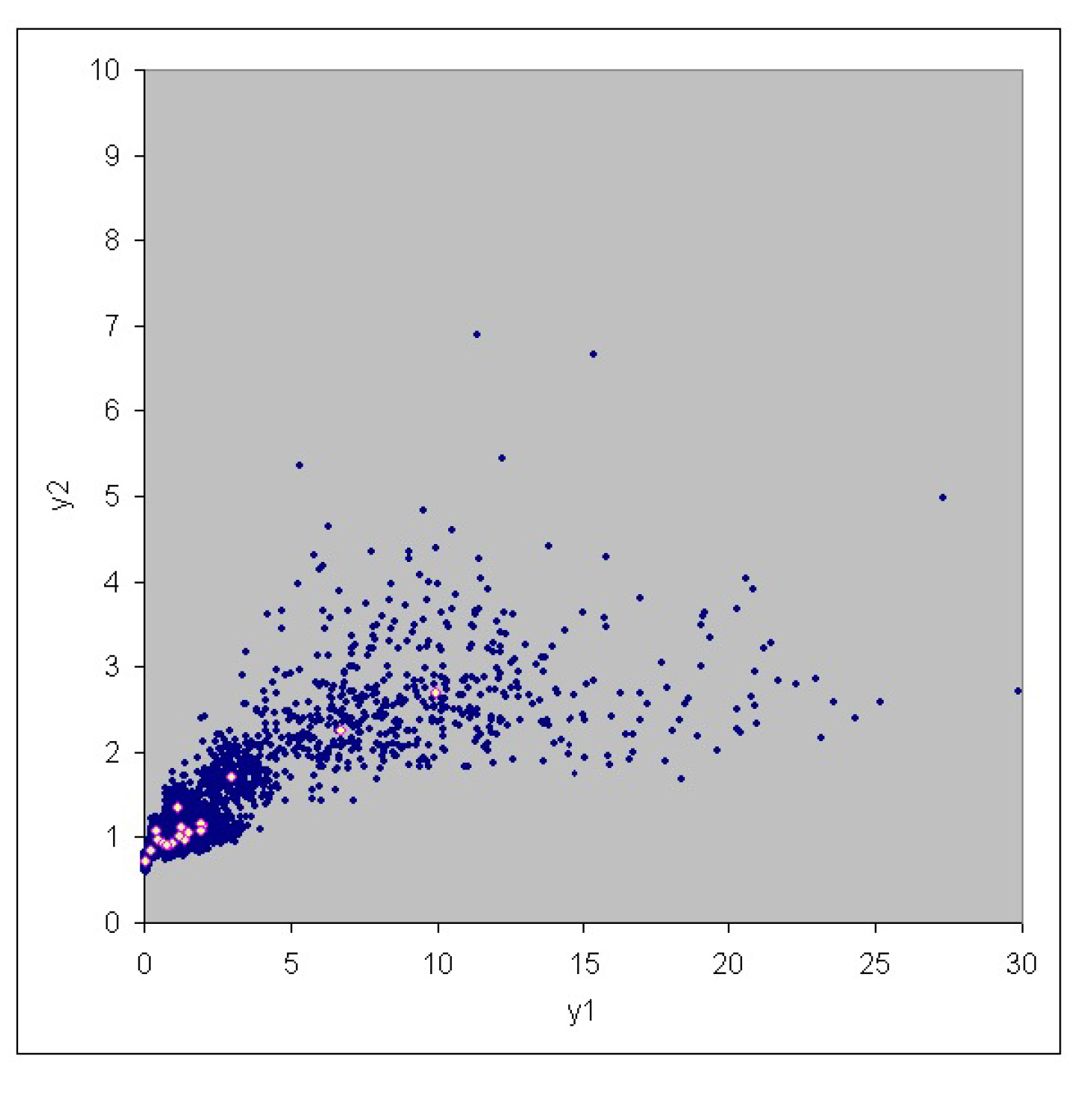
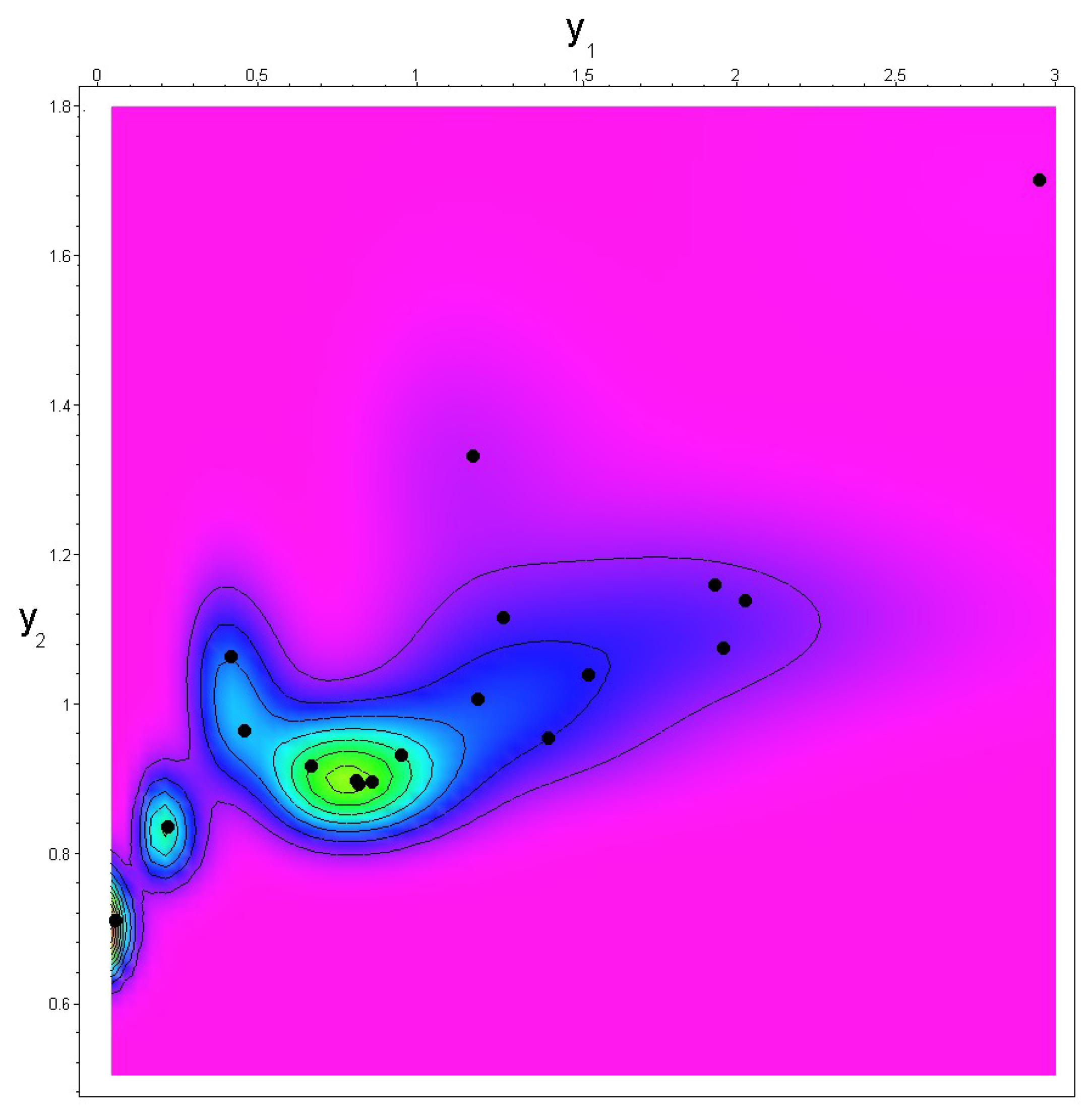
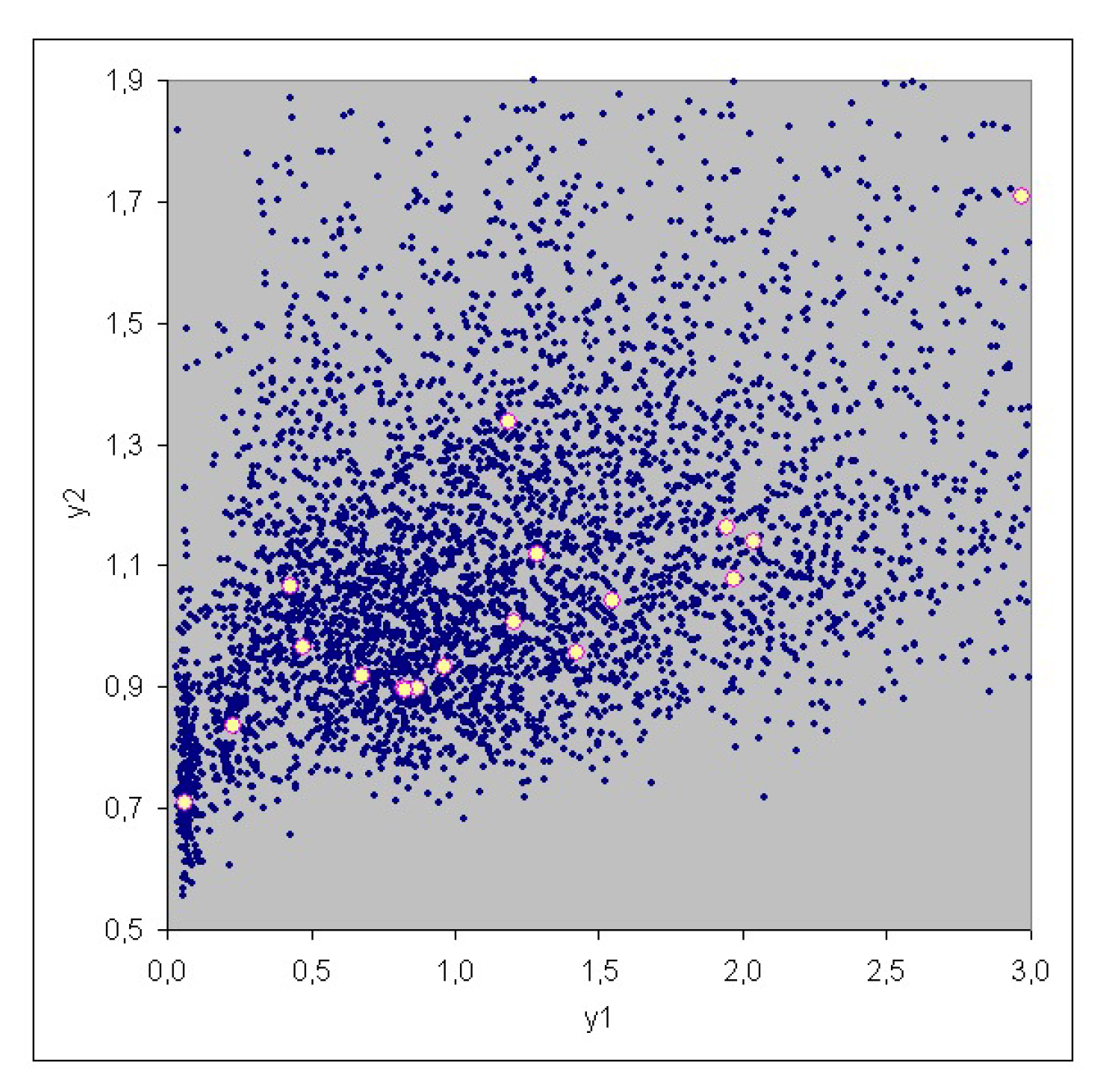

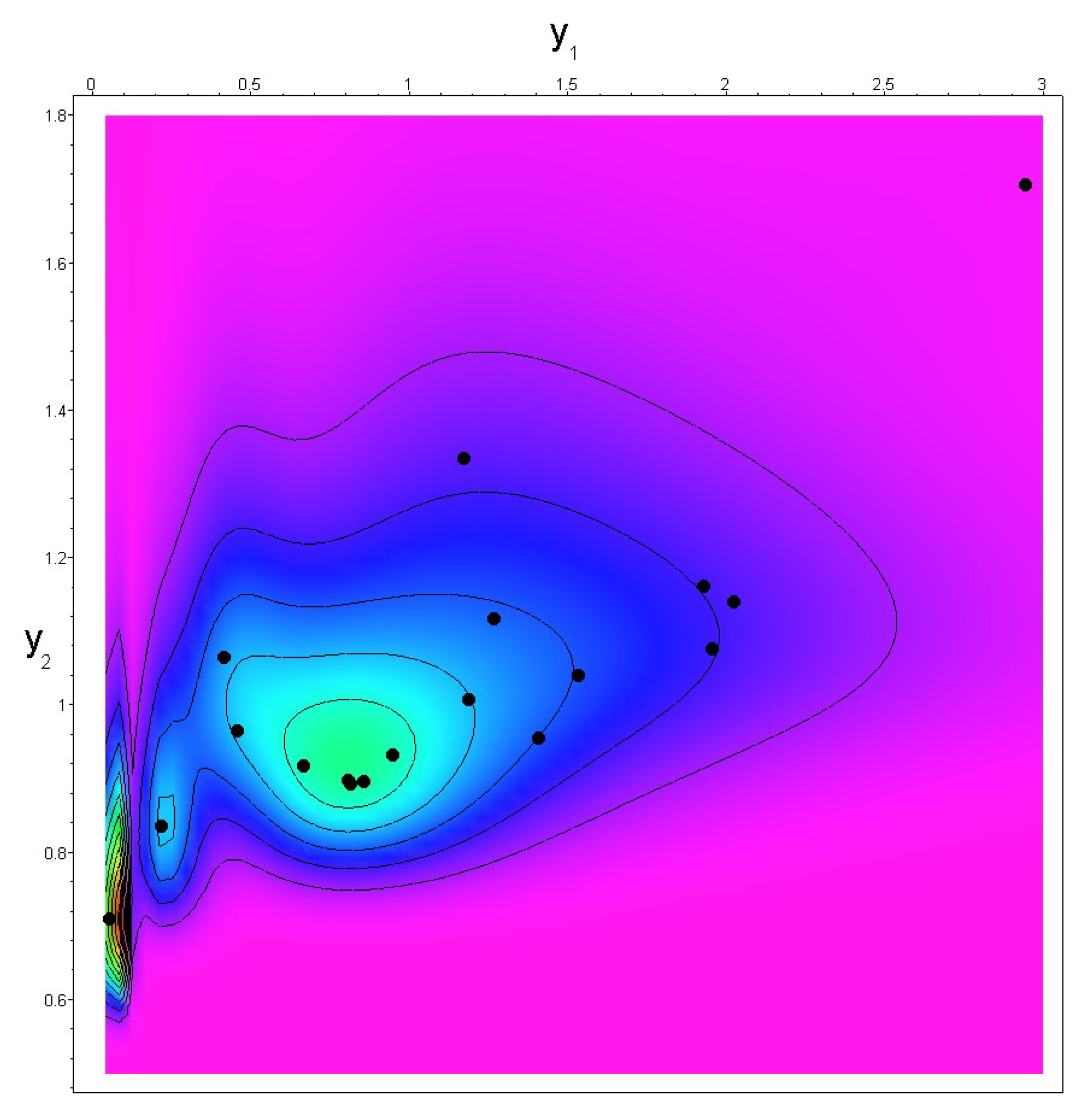
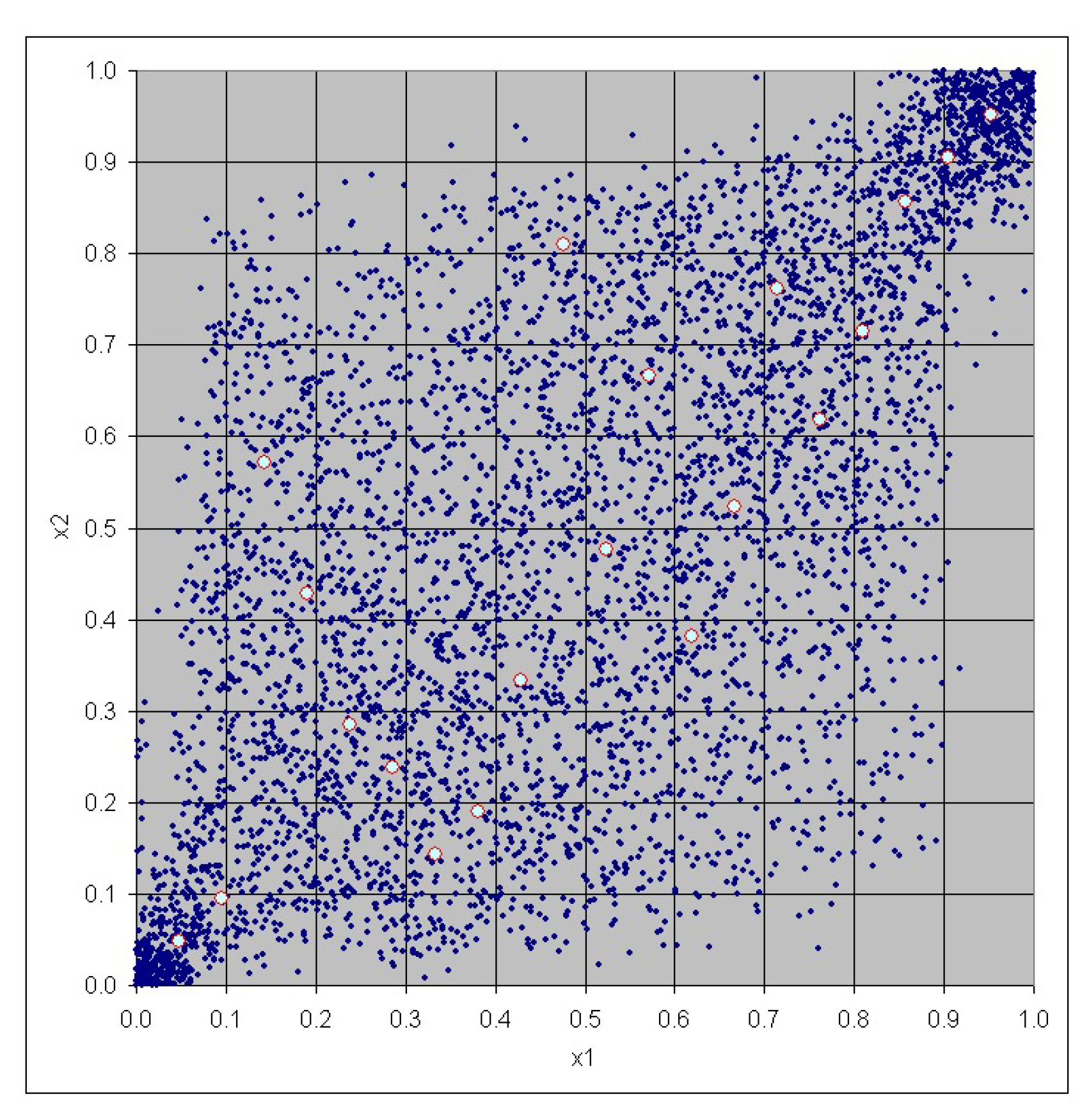
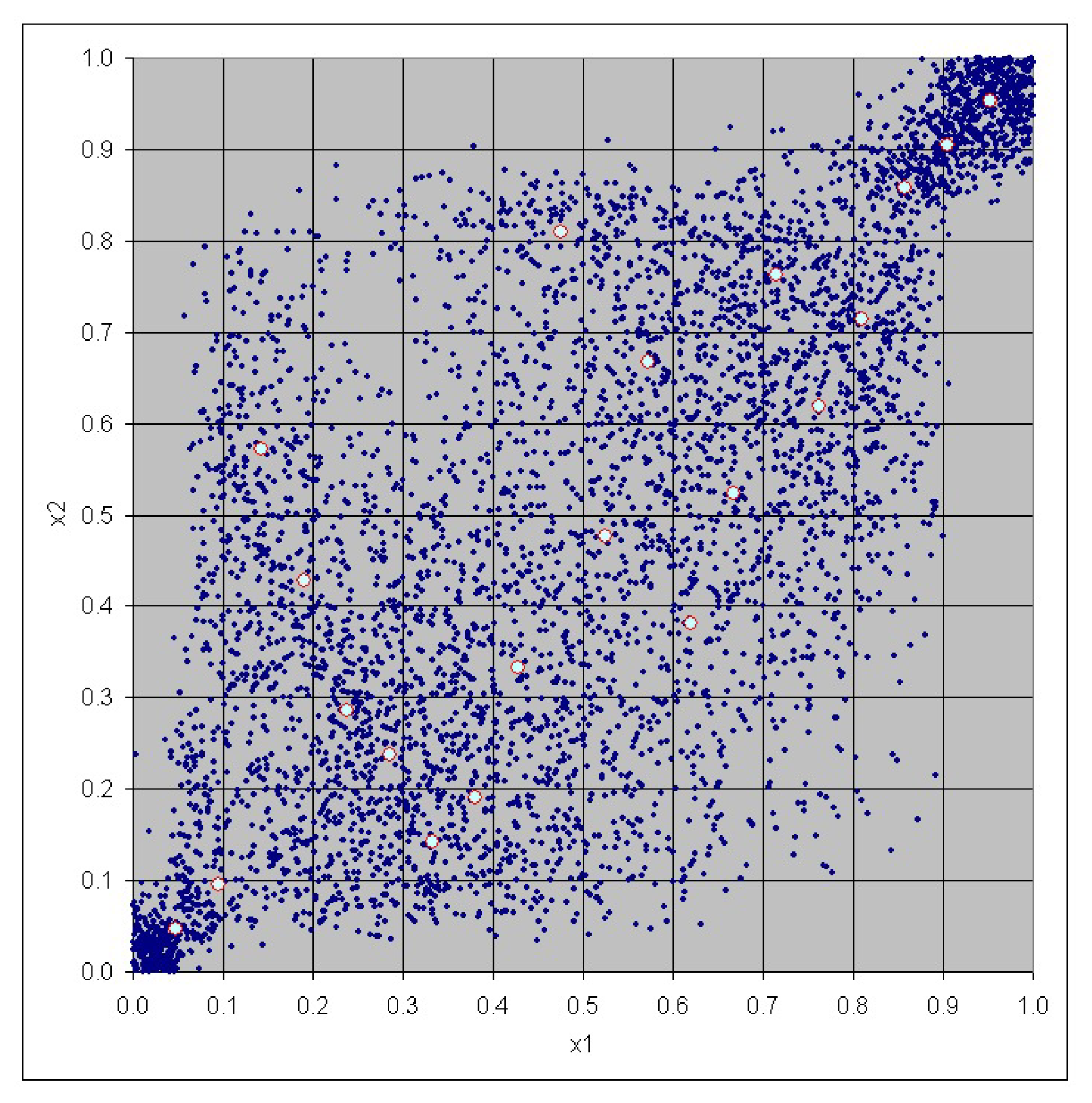
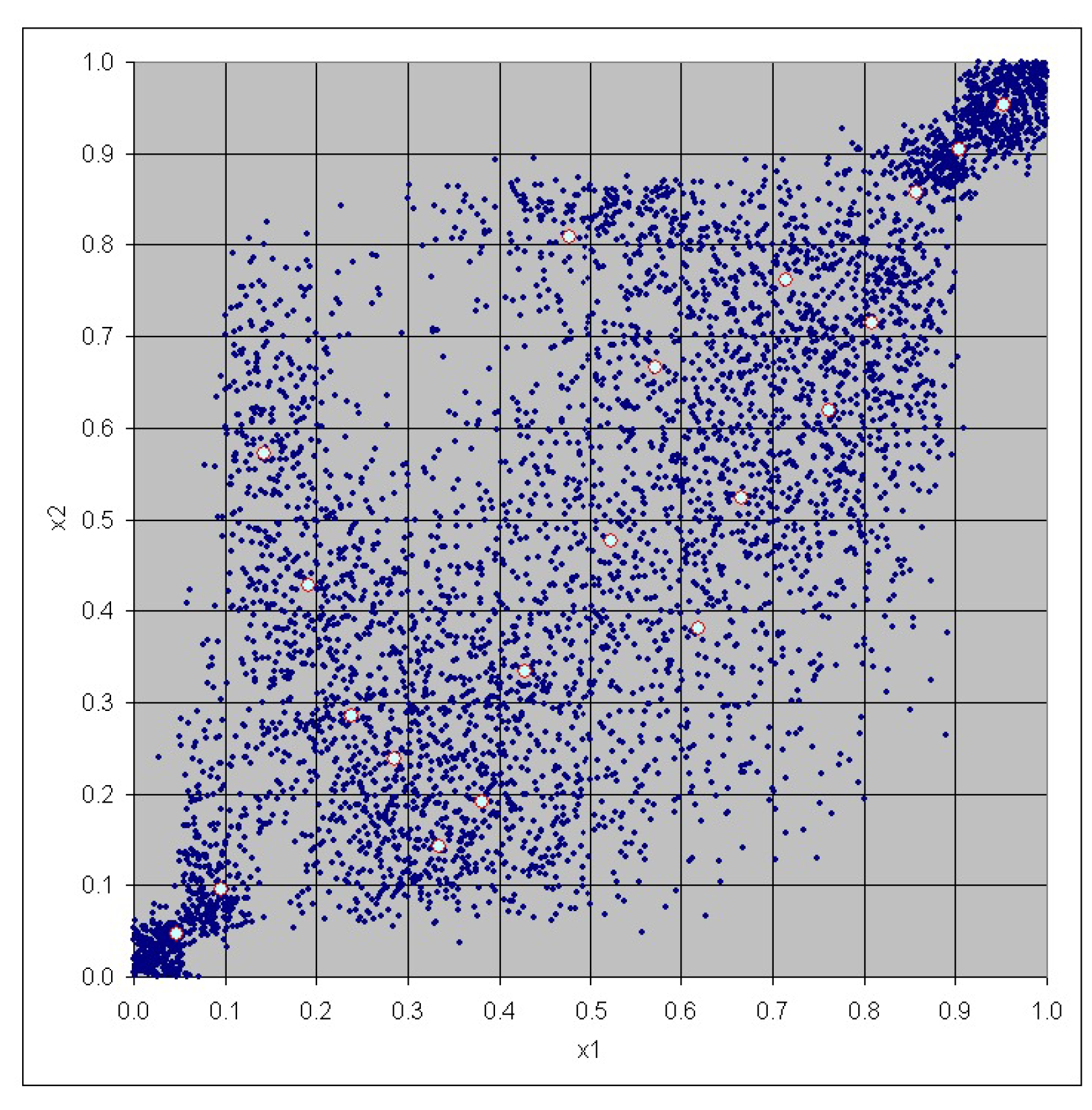
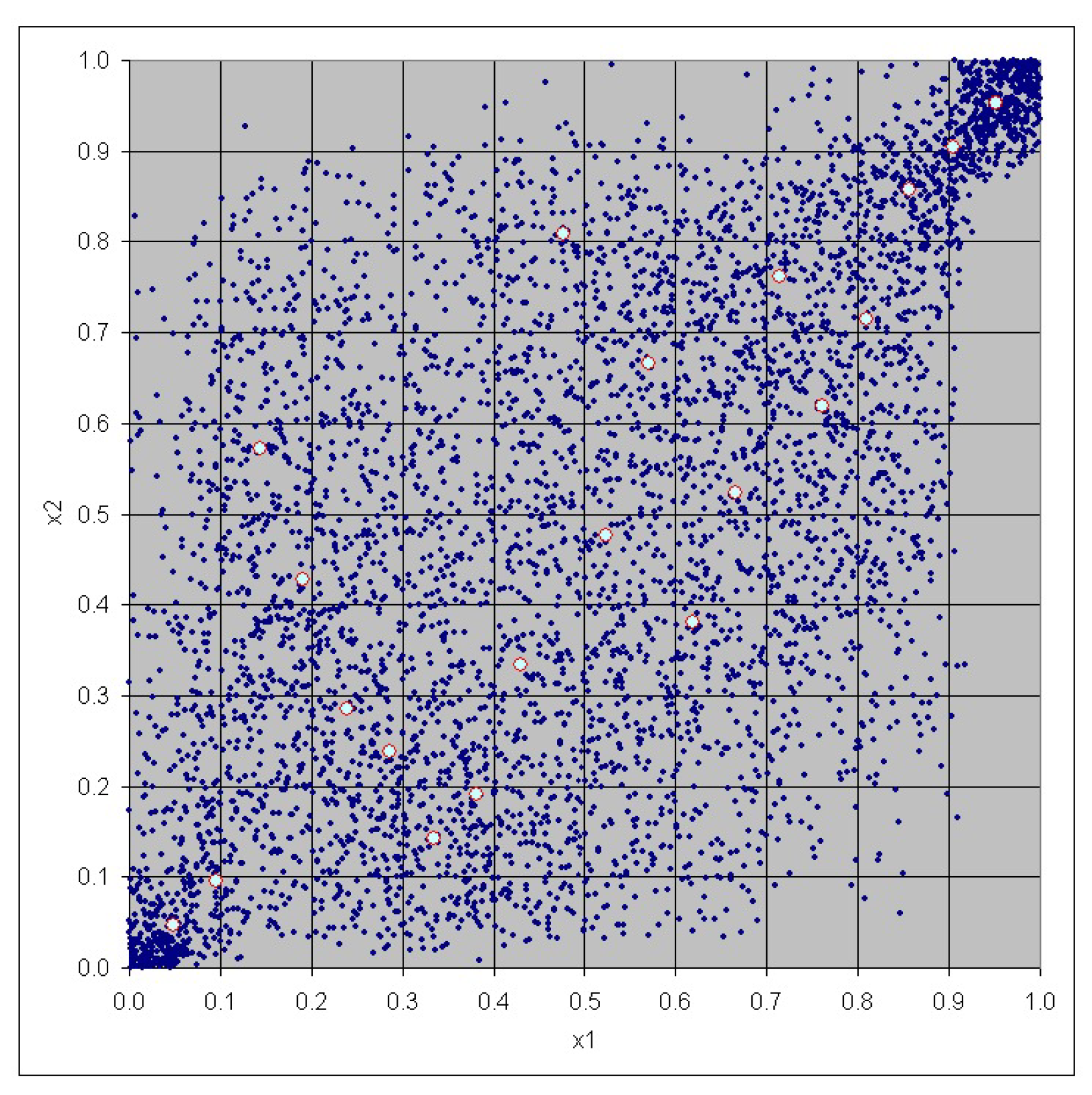



| No. | Risk | Risk |
|---|---|---|
| 1 | 0.468 | 0.966 |
| 2 | 9.951 | 2.679 |
| 3 | 0.866 | 0.897 |
| 4 | 6.731 | 2.249 |
| 5 | 1.421 | 0.956 |
| 6 | 2.040 | 1.141 |
| 7 | 2.967 | 1.707 |
| 8 | 1.200 | 1.008 |
| 9 | 0.426 | 1.065 |
| 10 | 1.946 | 1.162 |
| 11 | 0.676 | 0.918 |
| 12 | 1.184 | 1.336 |
| 13 | 0.960 | 0.933 |
| 14 | 1.972 | 1.077 |
| 15 | 1.549 | 1.041 |
| 16 | 0.819 | 0.899 |
| 17 | 0.063 | 0.710 |
| 18 | 1.280 | 1.118 |
| 19 | 0.824 | 0.894 |
| 20 | 0.227 | 0.837 |
| 0.0954 | 1.1909 | |
| –0.0437 | 0.2857 |
| m = 15 | m = 20 | m = 25 | m = 30 | m = 50 | m = 100 | Kernel Density | |
|---|---|---|---|---|---|---|---|
| 13.987 | 12.978 | 12.347 | 12.016 | 11.341 | 10.908 | 11.754 | |
| 40.637 | 31.235 | 26.989 | 23.966 | 19.498 | 16.580 | 17.272 | |
| 60.752 | 44.270 | 36.410 | 30.846 | 23.390 | 18.864 | 19.087 |
| Bernstein | NB Rook, a = 7 | NB UF, a = 7 | NB Rook, a = 15 | NB UF, a = 15 | |
|---|---|---|---|---|---|
| 7.166 | 6.885 | 7.016 | 6.974 | 7.155 | |
| 15.634 | 15.973 | 15.744 | 15.877 | 16.059 | |
| 21.105 | 20.801 | 21.311 | 20.256 | 21.733 |
| Gamma Rook, a = 7 | Gamma UF, a = 7 | Gamma Rook, a = 15 | Gamma UF, a = 15 | |
|---|---|---|---|---|
| 9.330 | 10.072 | 9.522 | 10.191 | |
| 18.113 | 21.224 | 18.550 | 21.428 | |
| 22.933 | 28.123 | 23.079 | 28.588 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pfeifer, D.; Ragulina, O. Generating VaR Scenarios under Solvency II with Product Beta Distributions. Risks 2018, 6, 122. https://doi.org/10.3390/risks6040122
Pfeifer D, Ragulina O. Generating VaR Scenarios under Solvency II with Product Beta Distributions. Risks. 2018; 6(4):122. https://doi.org/10.3390/risks6040122
Chicago/Turabian StylePfeifer, Dietmar, and Olena Ragulina. 2018. "Generating VaR Scenarios under Solvency II with Product Beta Distributions" Risks 6, no. 4: 122. https://doi.org/10.3390/risks6040122
APA StylePfeifer, D., & Ragulina, O. (2018). Generating VaR Scenarios under Solvency II with Product Beta Distributions. Risks, 6(4), 122. https://doi.org/10.3390/risks6040122





