1. Introduction
Insurance firms play an important role in the economy as providers of protection against financial and economic risks. In recent years, their contribution to systemic risk has increased.
1 According to the International Monetary Fund’s reports (see
IMF 2016 and
IMF 2017), this increase has been due to two main reasons. First, there has been a rise in insurers’ interest rate sensitivity (i.e., a growing common exposure to aggregate risk). This affected the asset side of insurers’ balance sheet by approximately 24 billion US dollars of investment (according to IMF estimates). Second, there is a significant growing exposure to other common sources of risk through cyber-insurance. A greater reliance on technology, combined with the interconnections of the global financial system, imply that cyber-threats can become systemic. The indirect exposure of insurance companies through their cyber-insurance risk underwriting may imply an important contribution to systemic risk. Highly correlated attacks could impact a large group of clients, and trigger multiple outstanding contracts simultaneously. In turn, the occurrence of a cyber-attack may significantly affect the asset side of insurance firms’ balance sheet because, for instance, it may trigger the fire sales of assets when all others are also selling. In such a case, insurers are unlikely to fulfill their role as financial intermediaries precisely when other parts of the financial system are failing to do so as well.
After the global financial crisis of 2007–2009, and with the aim of limiting systemic risk, some regulatory bodies have promoted the implementation of macro-prudential policies. Particularly, in the insurance sector, the Financial Stability Board (FSB) published a list of global systemically important insurers, and it intends to implement special policy measures for these institutions by January 2019.
2 In the same direction, the US regulatory reform, known as the Dodd–Frank Act, imposed on non-bank holding companies (including insurance companies) a new form of regulation for those deemed to be “Systemically Important Financial Institutions”. Despite these incipient attempts at macro-prudential policies, most insurance regulation remains micro-prudential in nature.
Systemic risk and reform proposals have led academics to focus on the extent to which insurance companies contribute to systemic risk (e.g.,
Acharya and Richardson 2014;
Bobtcheff et al. 2016;
Cummins and Weiss 2014). However, much less attention has been devoted to the analysis of the optimal way to regulate systemic insurers. Motivated by the observation that the insurance sector has been put on the map as a source of systemic risk, even though its regulation remains largely micro-prudential, this paper aims to fill the gap by studying the optimal regulation of the insurance sector when insurance companies are exposed to systemic risk.
More precisely, we propose a formal model of the insurance sector that, in the absence of systemic risk exposure, predicts that optimal regulation may be implemented by capital regulation (similar to what is observed in practice) and by actuarially fair technical reserve regulation. In the case of the failure of the insurer, an industry-managed solution may be enough. However, capital regulation and actuarially fair technical reserves are not enough when insurance companies are exposed to systemic risk. In such a case, prudential regulation should also add a systemic component to capital requirements that is non-decreasing in the insurer’s exposure to systemic risk. Hence, there is a rationale for the macro-prudential regulation of insurance companies, where capital requirements are linked to their contribution to systemic risk. Moreover, public intervention under the form of a bailout policy may be deemed necessary if a systemic event occurs. Implementing optimal regulation implies separating insurance firms in two categories, according to their exposure to systemic risk: those with relatively low exposure should be eligible for bailouts, while those with high exposure should not benefit from public support if a systemic event occurs.
This paper contributes to the growing body of literature analyzing the presence of systemic risk in the insurance industry (see
Eling and Pankoke 2016 for a recent review of the literature on this topic). Despite many methodological and empirical approaches aimed at the identification and measurement of systemic risk, to the best of our knowledge there is no theory providing a rationale for its regulation in the insurance sector. Some authors argue that traditional insurance activities do not create systemic risk (e.g.,
Cummins and Weiss 2014;
Harrington 2009 and
Tyler and Hornig 2009). The argument basically rests on the fact that traditional insurance activities wash out risks by diversification, therefore not generating systemic risk. However, this conclusion may not hold for non-traditional activities (e.g.,
Acharya and Richardson 2014 and
Bobtcheff et al. 2016). Based on descriptive statistics and a systemic risk measure,
Acharya et al. (
2011) argue that insurers with traditional business models pose low systemic risk in contrast to companies engaged in non-traditional insurance products. Similar to this strand of the literature, we argue that systemic risk may be generated if other activities are undertaken (e.g., cyber-insurance underwriting), or additional contractual clauses are attached to traditional insurance (e.g., minimum guarantees or early surrender options in the case of life insurance). Hence, we contribute by studying the optimal regulation for insurance companies under systemic risk.
Unlike the previous literature, we do not focus on the contribution of insurance companies to systemic risk. Our starting point is that insurance companies are exposed to a non-diversifiable (systemic) risk. We have in mind a severe but infrequent shock in which only the government is able to provide liquidity to stabilize the financial system.
3 In this case, government funding provision (i.e., bailout) of insurance companies responds to the very same rationale as emergency liquidity assistance in banking: to protect the system as a whole, by limiting the frequency and the cost of systemic crises. This is often referred to as a macro-prudential perspective. Hence, our contribution to the previous literature is to find a rationale for incorporating this macro-prudential component to insurance regulation.
A number of studies have addressed the issue of how to regulate insurance companies. However, the conclusions of this strand of literature are mixed and they are generally not supported by formal theory. On the one hand,
Acharya et al. (
2011) claim that institutions that are too interconnected to fail should pay a fee for the implicit guarantee of being bailed out in the case of a crisis. In the same direction,
Bach and Nguyen (
2012) offer a discussion about the need of prudential regulation in insurance. They claim that even though traditional insurance activities might not be systemically risky, macro-prudential regulation is necessary due to the economic cost of impaired insurance markets. We contribute by formalizing these results in a consistent theoretical model.
On the other hand,
Berry-Stolzle et al. (
2014) provide an empirical study of the consequences of raising capital in the insurance sector. They found that insurers had no difficulty in raising money during the 2007–2009 crisis. Based on this observation, they conclude that additional regulation for insurers is not needed. Similarly,
Grace (
2010) provides empirical evidence supporting the argument that insurers do not contribute to systemic risk, and he claims that no institution should be classified as systemically important, since this would create a moral hazard. Our results, however, are opposed to this strand of the literature: we formally find a rationale for capital surcharges and other regulation that are linked to the contribution of insurers to systemic risk.
To the best of our knowledge, we are the first to provide a formal theoretical model to justify the need of introducing a macro-prudential perspective to insurance regulation. We also propose concrete forms of implementing the optimal regulatory policy when systemic risk is an issue in the insurance industry, and discuss that implementing them would be feasible under realistic circumstances. Moreover, if systemic risk is not a concern, our model delivers similar results to previous work on insurance regulation (e.g.,
Plantin and Rochet 2007, and the references therein), which prescribe capital regulation similar to those observed in practice (e.g., Solvency II, a regulatory framework that aims to ensure that insurers hold enough capital and introduces a risk-based approach to regulation). Therefore, we complement this strand of the literature by extending the framework and showing how optimal regulation should be adapted to the consideration of systemic risk.
The rest of the paper is organized as follows.
Section 2 presents the basic model where systemic risk is not considered, and shows that optimal regulation can be implemented by capital regulation.
Section 3 extends the model to capture the occurrence of a systemic event that may lead to the failure of the system. Finally,
Section 4 summarizes our findings and concludes.
2. A Model without Systemic Risk
In this section we introduce a simple framework in order to study the optimal regulation of an insurance company when systemic risk is not an issue. The results in this section will serve as a benchmark to compare the effects of considering systemic risk exposures in the next section. More precisely, we propose a model that captures in the simplest possible way the risk and incentive trade-offs of an insurance company. In particular, we model the investment, technical reserve, and financing structure of the insurer’s balance sheet. We also restrict our attention to the interesting case where regulation is necessary because insurers and claimholders have opposite interests, and the former could take advantage of the nonexistence of sophisticated stakeholders.
2.1. Set Up
We propose a formal model inspired by
Rochet (
2004). Consider an economy with two dates (
), where insurers sell insurance contracts at
. These contracts will cover policyholders’ risks at
. This situation is the so-called “inversion of the production cycle” described in most insurance textbooks: insurance companies sell their products—and pocket insurance premium—for a very long time before settling claims. According to
Plantin and Rochet (
2007), this fact and the absence of a tough, sophisticated claimholder provide a rationale for the prudential regulation of insurance companies. Prudential regulation generally states that insurance companies (i) must estimate their outstanding liabilities toward policyholders in a sufficiently conservative way, and (ii) must finance an excess of investment in assets over such estimates with their own capital.
In order to capture these elements in a simple way, we work with the following balance sheet constraint of an insurance company at
:
where
A stands for risky assets whose return will be realized at
,
R stands for technical reserves representing the outstanding liabilities toward policyholders, and
E stands for equity capital.
At
, an insurance company will be able to cover its claims only if the returns generated by its risky investment portfolio are large enough. Investment returns are equal to
with probability
, and zero otherwise (
is the gross return rate on investment). This probability depends on how much effort an insurer exerts in monitoring its investments. That is, there is a classical moral hazard problem in the relationship between managers and other stakeholders. If the insurer exerts effort, the probability of success is
, whereas this probability decreases to
if the insurer shirks. The level of effort is unobserved by third parties, and exerting effort entails a private cost of
B (per unit of investment) to the insurer. Prudential regulation would impose minimum requirements to
R and
E. The timeline of the model is summarized in
Figure 1.
In order to study the interesting case in which moral hazard is an issue, we introduce the following assumptions:
Assumption 1: .
Assumption 1 implies that the investment portfolio has a positive net present value only when it is monitored by the insurer. Otherwise stated, if the insurer shirks, the return of the assets plus the private benefit from shirking is less than the invested amount. Without this assumption, the solution would be trivial since the interest of insurers and claimholders will be perfectly aligned.
Assumption 2: .
Assumption 2 implies that insurers need capital. If this were not satisfied, insurers could be 100% externally financed because moral hazard is not a concern. As before, this assumption puts the framework on the interesting case where prudential regulation is necessary.
We also introduce a simplifying assumption. The large, worldwide diversification, as well as the mutualization of risks performed by insurance companies through reinsurance mechanisms, suffice to perfectly diversify exogenous shocks away (see
Plantin and Rochet 2007, p. 95). Hence, we assume that from an ex ante perspective, technical reserves
R are equal to the expected value of future claims. This is equivalent to assuming that insurance companies perfectly fulfill an actuarially fair reserve requirement. We will show in the next section that optimal regulation without systemic risk may be implemented with actuarially fair reserves, so that there is no loss of generality by adopting this simplifying assumption at this stage.
2.2. Optimal Regulation
Optimal regulation in the absence of systemic risk would provide insurers with incentives to exert effort. In order for insurers to monitor their investment, the following incentive compatibility condition needs to be satisfied:
This condition implies an upper bound on technical reserves
. Otherwise stated, the equity financing of assets needs to be high enough for the insurer to have sufficient “skin in the game” in order to be willing to exert effort. More precisely, using the balance sheet constraint (given in Equation (
1)), we get that
.
Optimal prudential regulation in this case can be summarized in the following Proposition.
Proposition 1. In an economy without systemic risk, optimal prudential regulation can be implemented by a minimum capital requirement equal to: According to Proposition 1, the minimum capital requirement implementing optimal prudential regulation is independent of the way in which technical reserves are computed. Thus, there is no loss of generality by assuming that reserves are actuarially fair.
Optimal prudential regulation in Proposition 1 resembles what is currently applied in several jurisdictions. For example, in the United States, the solvency requirement follows a complex risk-based formula, of which Equation (
3) is a very simplified version. Insurance companies in Europe must meet the European solvency margin which, roughly speaking, states that the book value of a firm’s equity must exceed some threshold. More recently, the new Solvency II regime aims to ensure that insurers hold enough capital and introduces a risk-based approach to regulation: the riskier an insurer’s business, the more precautions it is required to take. This regulation has a parallel in Proposition 1, since the minimum capital requirement
is an increasing function of the riskiness of the insurance company, which is measured by
. Therefore, a first conclusion from these results is that current capital regulation of insurance companies (e.g., Solvency II) is appropriated to implement the optimal regulatory policy.
Despite prudential regulation, an insurance company may still fail, and its policyholders may not have their risks covered. Indeed, prudential regulation aims to reduce the probability of this event, but does not completely avoid it. In fact, aiming at zero failure would be unrealistic. From an ex ante perspective, this opens the question of whether claimholders would like to buy insurance in the first place. In practice, and absent systemic risk, there is a market solution whereby other insurance companies absorb the business of failing ones and cover (at least part) of their claims. This softens the participation constraint of policyholders. According to
Plantin and Rochet (
2007, p. 69), most countries have created guarantee funds indemnifying policyholders whose insurance company defaults. Moreover, they argue that the fund should raise premiums from insurance companies and must be owned and run by the industry. Formally, it is not difficult to see in the model that by pooling claims through a fund financed by actuarially fair premiums (i.e., with a premium
) on insurers, all policyholders will receive their claims.
3. Regulation with Systemic Risk
In this section, we extend the basic model setup by incorporating systemic risk exposures into the picture. Then, we study its implications for the optimal regulatory policy. In so doing, we highlight the limitations of the optimal policy derived in the previous section. We show how this optimal policy should be complemented with a macro-prudential component in order to address the problems imposed by systemic exposures. Moreover, we notice that market failures introduced by the presence of systemic risk imply a rationale for extending public intervention in the regulation of insurers. We conclude by analyzing ways of implementing the optimal policy and by discussing their feasibility.
3.1. Extended Set Up
The risks faced by insurance companies may be categorized into two types: (i) technical risks associated with the occurrence and magnitude of the insured losses, and (ii) financial risks associated with the return on the investment. The former are inherent in the insurance business, and have been largely covered by the actuarial literature. These risks are embodied in our model through the technical reserves, R. The latter risks affect the asset side of the balance sheet. Without the systemic component, we have modeled financial risks through the risky return , which occurs with probability p. Insurance firms typically invest in liquid, tradable, and diversified portfolios that match their liabilities much better than other intermediaries (e.g., bank loans and bank deposits). For this reason, insurance panics have not occurred, to our knowledge, in recent times.
Nevertheless, insurance firms are increasing their exposure to aggregate risk. This increase is largely due to a rise in insurers’ interest rate sensitivity and their participation in non-traditional activities (see
IMF 2016 and
Eling and Pankoke 2014). This systemic dimension of financial risk implies that several parts of the financial system, including all insurance companies, could be hit by the same shock. In such a case, insurance companies may be unable to seize assets to cover claims. In the words of the
IMF (
2016), “Thus, in the event of an adverse shock, insurers are unlikely to fulfill their role as financial intermediaries precisely when other parts of the financial system are failing to do so as well”.
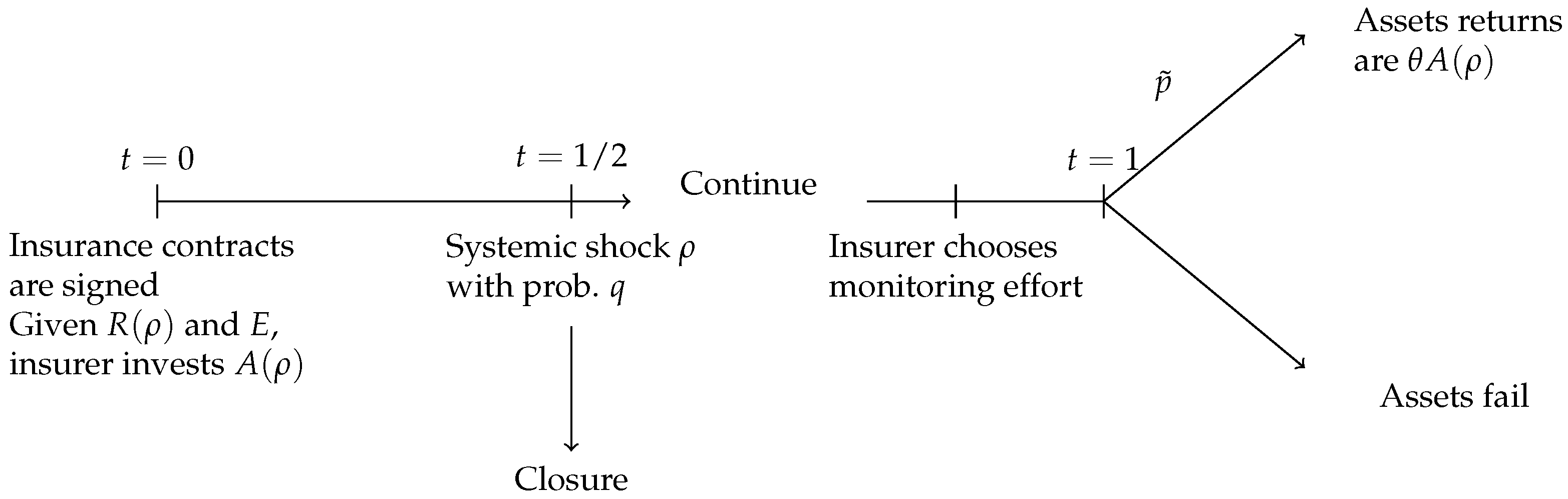
In order to model the systemic dimension of financial risk in insurance, we introduce an interim date () to the basic model, where a shock may occur with probability q. The exposure of an insurance company to the systemic risk is captured by a parameter . Should the systemic shock hit the industry, then an insurer would have to close activities unless it receives liquidity support for an amount . As stated before, we have in mind a severe and infrequent shock in which only the government is able to provide liquidity to stabilize the financial system.
We assume that the probability q of a systemic shock is small enough for the insurance company’s investment to be ex ante profitable, even if systemic risk is taken into account. This leads to the following assumption:
Assumption 3: .
Otherwise, there would be no reason for the insurance industry to exist.
There is a continuum of insurers that differ only in their exposure to systemic risk,
. This parameter is distributed according to a continuous distribution function
F. The regulator can perfectly observe the insurer’s exposure to systemic risk. Therefore, the regulation can be made contingent upon it. In particular, capital and reserve requirements may be functions of
. Moreover, let
be the probability that the regulator allows an insurance company with systemic risk
to continue operating (i.e., the probability of a bailout). If the insurance company is hit by a systemic shock and is not supported by the government, then it will close at
and its policyholders will no longer be insured.
Figure 2 shows the timeline of the model with systemic risk.
3.2. Optimal Regulation
Optimal prudential regulation will attempt to maximize the expected net surplus generated by the insurance activity. In this setting, optimal prudential regulation implies providing incentives for the insurer to exert effort, and minimizing the expected cost of public intervention.
As in
Section 2.2, Equation (
2) ensures effort because a moral hazard takes place after a systemic shock occurs. Taken with equality, the incentive compatibility constraint becomes:
Considering the expected cost of government bailouts, the insurer’s balance sheet constraint at
can be written as:
Note that
is the unconditional probability of continuation at
, and
is the size of the expected bailout in the case a systemic event materializes. Combining Equations (
4) and (
5), we get the following constraint:
Optimal prudential regulation is designed to maximize the expected net surplus generated by the insurance activity under the incentive compatibility constraint, considering the cost of bailouts. Formally, optimal regulation is the solution to maximize in
and
(which, given
E, implies a minimum capital requirement and a probability of bailout, conditional on the exposure to systemic risk) the following net surplus subject to Equation (
6):
The solution of the above programme leads to the following result.
Proposition 2. Given the exposure ρ of an insurance company to systemic risk, the optimal regulatory contract is such that:
Insurance companies with low exposure to systemic risk, , will be bailed out if the systemic shock occurs (i.e., ), and are subject to a capital requirement that increases in the level of the risky exposure: Insurance companies with high exposure to systemic risk, , will not be bailed out if the systemic shock occurs, and they are subject to a flat capital requirement:
Proposition 2 shows the optimal capital and bailout/closure regulation in the case where insurance companies are exposed to systemic risk. More precisely, optimal capital regulation introduces a capital requirement surcharge related to systemic risk. Note that . This surcharge is non-decreasing on the exposure. In the case of relatively low exposures (i.e., ), optimal regulation balances the trade-off between the cost of a bailout and the surplus generated by the insurance activity. However, if the exposure to systemic risk is too large, then bailouts are too costly compared to benefits. In such a case, should a systemic event materialize, it is optimal to close the insurance company down. Given that the insurer anticipates this situation, it is necessary to charge the highest capital requirement () in order to re-establish incentives toward exerting effort.
Interestingly, fair-priced reserve requirements are not enough from a normative point-of-view. It may be reasonable to price the systemic risk contribution and to require reserves for it. For example, in the case of systemic risk, the actuarially fair reserve requirements are:
, where
R represents the actuarially fair reserves due to the non-systemic risk component (as in
Section 2.2), and
represents the expected cost of a bailout due to a systemic event. Still, the provision of effort requires stronger incentives, which are given through non-decreasing capital requirements and are linked to the exposure to systemic risk.
From the results of the extended model, we can conclude that current regulatory efforts might be insufficient if the exposition of insurance companies to systemic risk continues to increase. A macro-prudential capital surcharge, non-decreasing on the exposition of the insurer to systemic risk, should be introduced. Still, this capital surcharge would not suffice if the insurer is highly exposed to systemic risk, and even fairly priced reserve requirements would not be enough from a normative point-of-view. There is still room for further public intervention in order to solve market failures when systemic risk is a concern.
3.3. Room for Further Public Intervention
We argued in
Section 2.2 that in the case where an insurance company fails when there is no systemic risk, there exists a market solution where other insurance companies absorb the business of the failed one and cover its claims. Furthermore, this solution may appear in the form of a private guarantee fund financed and run by the industry. In the case of systemic risk, however, market failures make it difficult to internalize the systemic risk component and to keep a fund of liquid assets so as to cover the materialization of this event.
Note that when the systemic shock hits, the maximum an insurer can pledge is equal to the continuation value of its assets while preserving incentive compatibility: . Hence, defining , those insurers with would not have enough pledgeable income to receive market assistance. Assumption 2 implies that . Thus, there is a mass of insurers with exposure to systemic risk between and that will be forced to close down in the event of a systemic shock, but should be bailed out from a welfare-maximizing perspective. Hence, a market-based solution fails to deliver an optimal guarantee scheme, and public intervention may be deemed necessary.
Another market failure that may prevent the success of an industry-based guarantee fund has to do with asymmetric information. We have assumed that systemic risk exposure is verified by a regulator. However, it is less obvious that other insurers are able to do such a verification due to, for example, their lack of access to supervisory information. If this is the case, systemic risk exposure () is not contractible, and adverse selection problems may appear, where high-exposure insurers would like to mimic low-exposure ones. This may also prevent the existence of an industry-managed fund, and provides a rationale for public intervention.
In order to price the premium for access to an insurance guarantee fund, one needs to consider the risk to be covered. First, as in the case without systemic risk, the insurance guarantee fund operates when the assets of the company fail at date
. A fair premium for this is
. Moreover, the expected cost of the bailout is equal to
. Hence, using Equation (
4) in order to preserve incentive compatibility, a fair price to access public support is equal to
, where
is the premium that breaks even with the cost of bailouts due to systemic risk events.
3.4. Implementation of Optimal Prudential Policy
In the previous sections, we took a normative perspective in order to study the optimal prudential regulation. Now, we assume a positive point of view in order to suggest a way in which this optimal policy may be implemented. Our findings are summarized in
Table 1.
One implication from the previous analysis is that technical reserves may be actuarially fair, no matter what the exposure of an insurance company is to systemic risk. Indeed, our previous results are independent of the value of the parameter R. Consequently, they are also independent of the way in which the level of technical reserves are computed. Thus, the way in which reserves are valued will not change anything regarding incentives, exposures, and other regulations.
Another implication is that the prudential authority should separate insurance companies according to their exposure to systemic risk in order to apply regulations. More precisely, low-exposure companies (i.e., those with ) should receive a regulatory menu different from high-exposure ones (i.e., those with ).
First, the minimum capital requirement should be increasing in for the low-exposure group of insurers, with . Instead, high-exposure companies should fulfill a flat capital requirement, . Hence, the capital requirement includes a macro-prudential component that is related to the exposure of insurance companies to systemic risk.
Second, as in the case without systemic risk, a guarantee fund managed and financed by the industry may be helpful in resolving non-systemic events. However, it is necessary to be complemented by a bailout mechanism managed by the prudential authority. Take the case of a low-exposure insurance company. The bailout mechanism should bail this company out in the case that a systemic event occurs, so that the company will continue serving customers. As we discussed previously, this mechanism may not be privately run by the industry, and the involvement of the prudential authority is required. The systemic event is then solved through the bailout mechanism. All companies in the market will anticipate this situation, because the prudential authority has classified the insurer in the low-exposure category and the bailout policy has been publicly announced. From an ex ante point of view, systemic risk has been completely covered in this case, so that an industry-managed guarantee fund with the premium would be implemented, as in the case without systemic risk. Of course, the prudential authority would need to finance bailouts. In order to do so in an actuarially fair manner, it could charge a premium equal to the expected cost of the bailout: .
High-exposure insurance companies should be declared as systemically important, and should not have access to the bailout mechanism. Hence, in the case of a systemic event, they will be forced to close down. Nevertheless, an industry-managed guarantee fund may still be suitable to resolve this situation, which occurs with probability q. Considering that high-exposure insurance companies’ claimholders also bear the risk that the assets of the company fail, which occurs with unconditional probability , an actuarially fair premium for this category of insurers in order to have access to the guarantee fund would be: .
The practical feasibility of implementing the optimal regulatory policy depends on a series pre-conditions, which correspond to assumptions in our model. First, in order for the regulator to be able to apply the optimal capital regulation, it must be able to verify the exposition of insurance companies to the systemic risk. This is also a pre-condition for structuring the bailout policy. In general, regulatory authorities access supervisory information from insurers, and also access aggregate information from markets, which allow them to assess the systemic risk contribution of individual institutions. In practice, several insurers have recently been declared “systemically important”, which is a form of separating insurers according to their exposure to systemic risk. Second, the regulator must commit not to bail out systemically important insurers. This capacity may vary across jurisdictions, depending on the relative strength and independence of their regulatory bodies.
4. Conclusions
In this paper, we propose a formal model to study the optimal regulation of insurance firms. When insurers face only idiosyncratic and diversifiable risk, we show that the optimal regulation can be implemented by a capital requirement and actuarially fair technical reserve regulation, akin to what is observed in practice. In particular, the regulatory Solvency II framework recently put in force may be seen as a form of implementing the optimal regulation. Solvency II aims to ensure that insurers hold enough capital and introduces a risk-based approach to regulation, which is in line with the results of our basic model where systemic risk is not an issue. This should improve the solvency of the insurance sector and, by extension, underpin the stability of the broader financial system.
Without systemic risk, the results from our theoretical model allow us to conclude that current capital regulation of insurance companies (e.g., Solvency II) are appropriate forms to implement the optimal regulatory policy. However, we argue that this (micro-)prudential approach may not be enough if insurance companies are exposed to systemic risk.
In practice, insurance firms are increasing their exposure to aggregate risk. This increase is largely due to a rise in insurers’ interest rate sensitivity and their participation in non-traditional activities (e.g., cyber-insurance). This paper contributes to the literature analyzing the presence of systemic risk in the insurance sector and provides a rationale for a macro-prudential approach to its regulation.
If systemic risk is a concern, our model shows that prudential regulation should also add a systemic component to capital requirements, where the minimum requirement is non-decreasing in the contribution of insurers to systemic risk. Moreover, public intervention may be deemed necessary if a systemic event occurs, because the externalities and the asymmetries of information prevent purely industry-managed solutions. Implementing an optimal policy implies complementing current (micro-prudential) measures with (i) a systemic capital surcharge, and (ii) the separation of insurance firms into two categories, according to their exposure to systemic risk: those with relatively low exposure should be eligible for bailouts by paying a premium to access this facility, while those with high exposure should be declared as “systemically important” and should not benefit from this public bailout mechanism.
From the results of the extended model, we can conclude that current regulatory efforts might be insufficient if the exposition of insurance companies to systemic risk continues to increase. Efforts to identify and declare certain insurers as systemically important go in the direction prescribed by our results. Nonetheless, other regulatory tools are far less developed. In particular, the creation of guarantee funds and bailout mechanisms, which according to our results should complement existing tools, need further development.
In summary, our results show that regulatory efforts along the lines of Solvency II go in the right direction towards the objective of improving the solvency and resilience of the insurance sector. Nonetheless, these efforts should be complemented with a macro-prudential approach to insurance regulation if, as expected, the insurance sector continues to be a source of systemic risk.