Market Equilibrium and the Cost of Capital with Heterogeneous Investment Horizons
Abstract
1. Introduction
2. Related Literature
3. Theoretical Results
- Preliminaries
- (1)
- First-degree Stochastic Dominance (FSD)
- (2)
- FSD among Investments with Normal Returns
- (3)
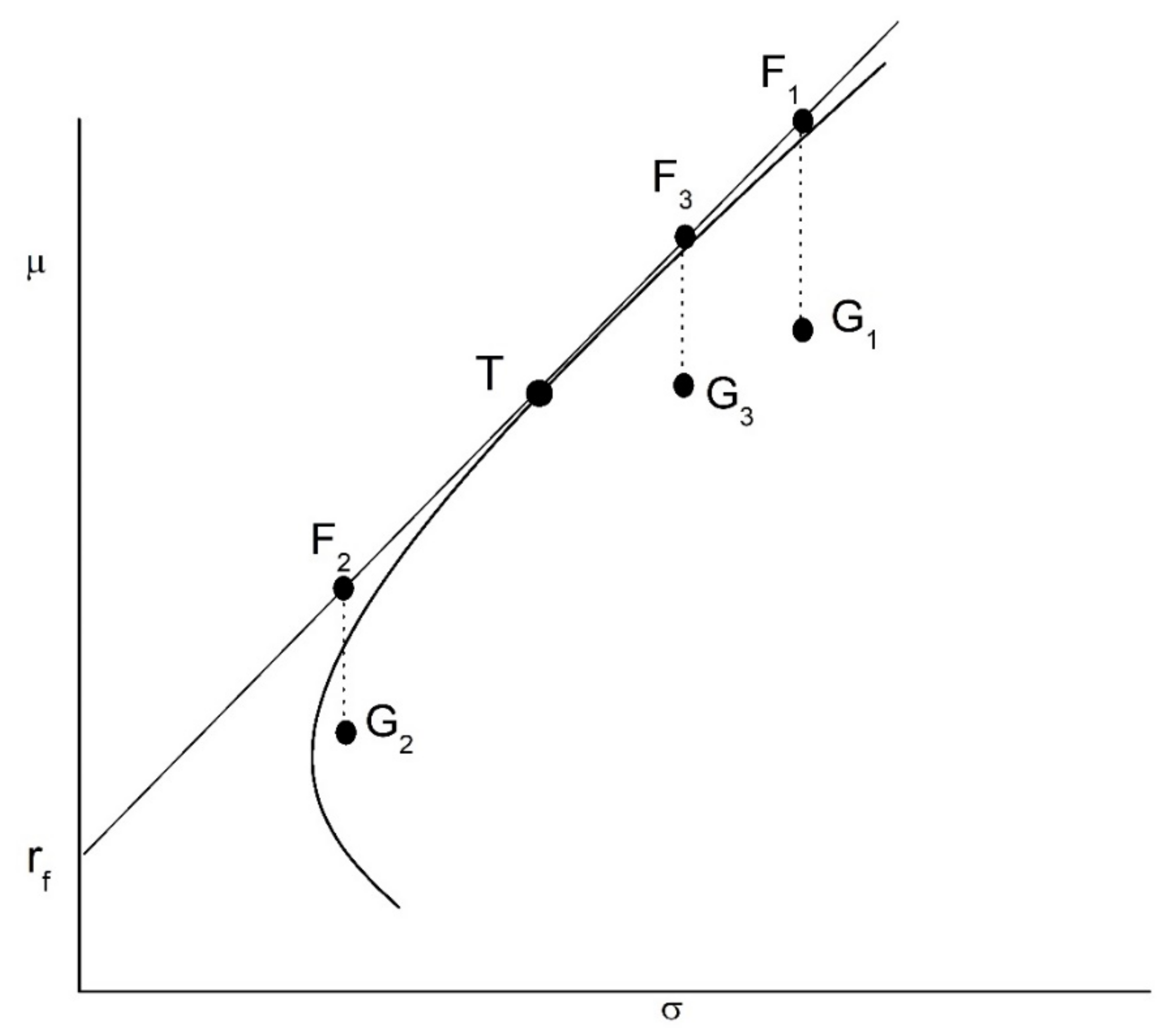
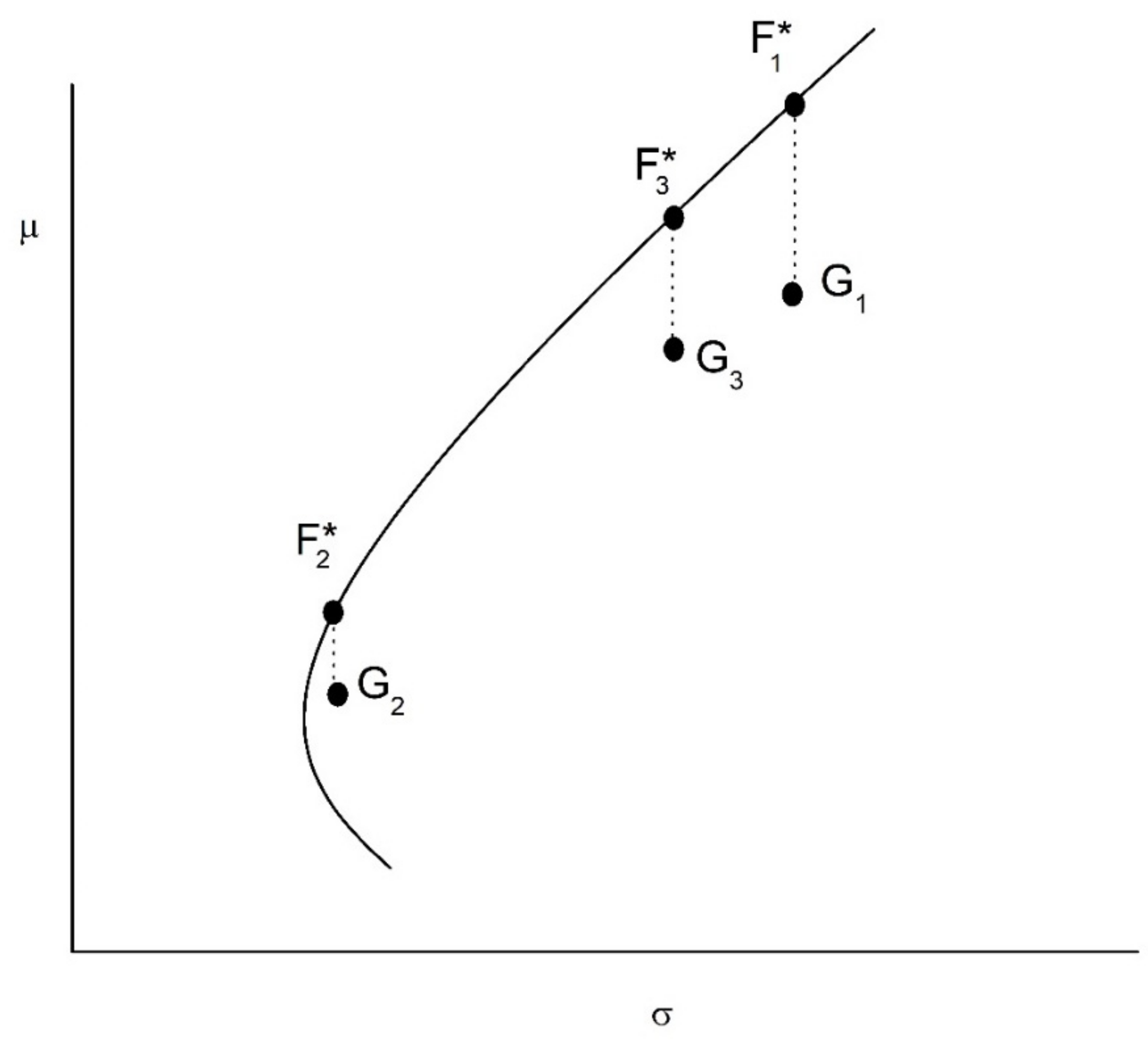
- Multi-Period FSD
- Extensions
- (i)
- Stochastic or Ambiguous Investment Horizons
- (ii)
- No Risk-Free Asset
- (iii)
- Time-Varying Return Parameters
- (iv)
- Intermediate Income and Consumption
4. Relaxing the Assumptions of 1-Period Normality and Serial Independence
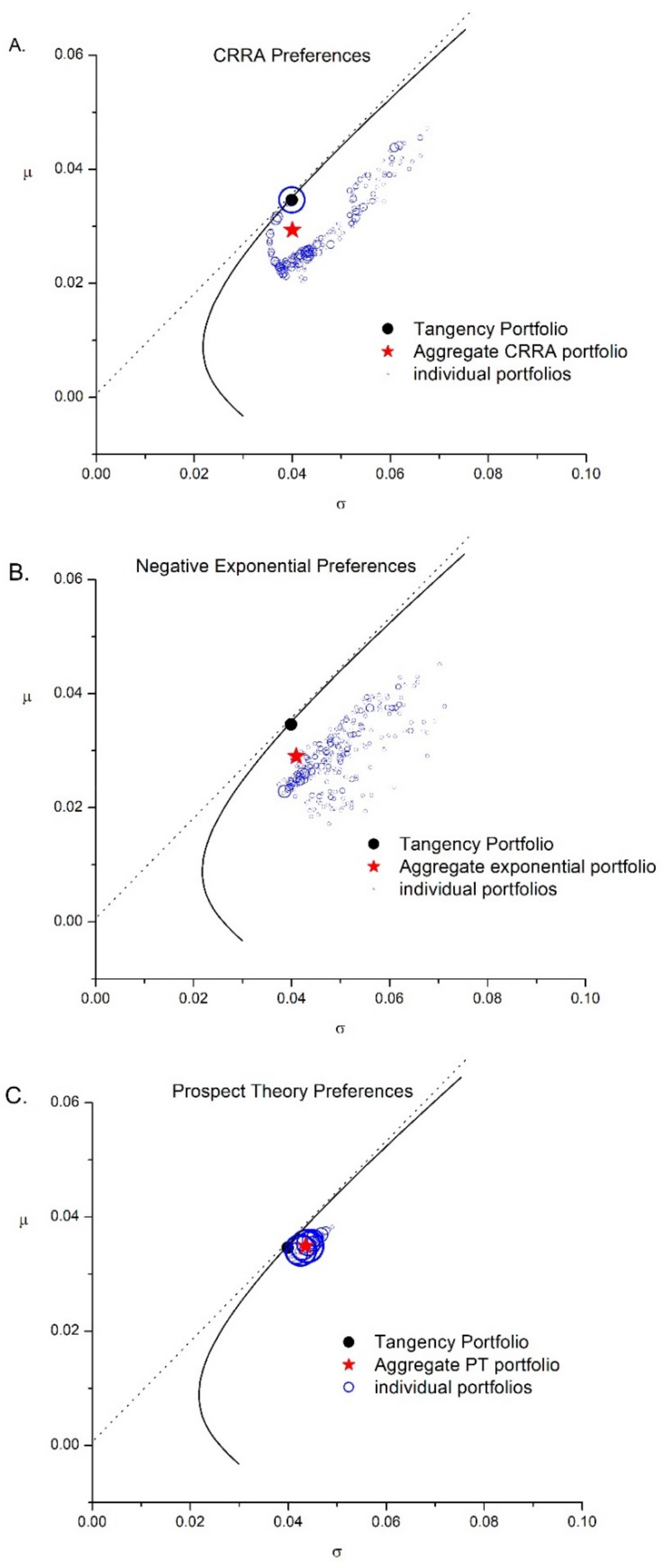
4.1. Methodology and Data
- (1)
- Constant relative risk aversion (CRRA): ;
- (2)
- Negative exponential preferences (or CARA): ; and
- (3)
- Prospect theory preferences, given by the following:where x denotes the change in wealth, rather than terminal wealth, i.e., (Tversky and Kahneman 1992).
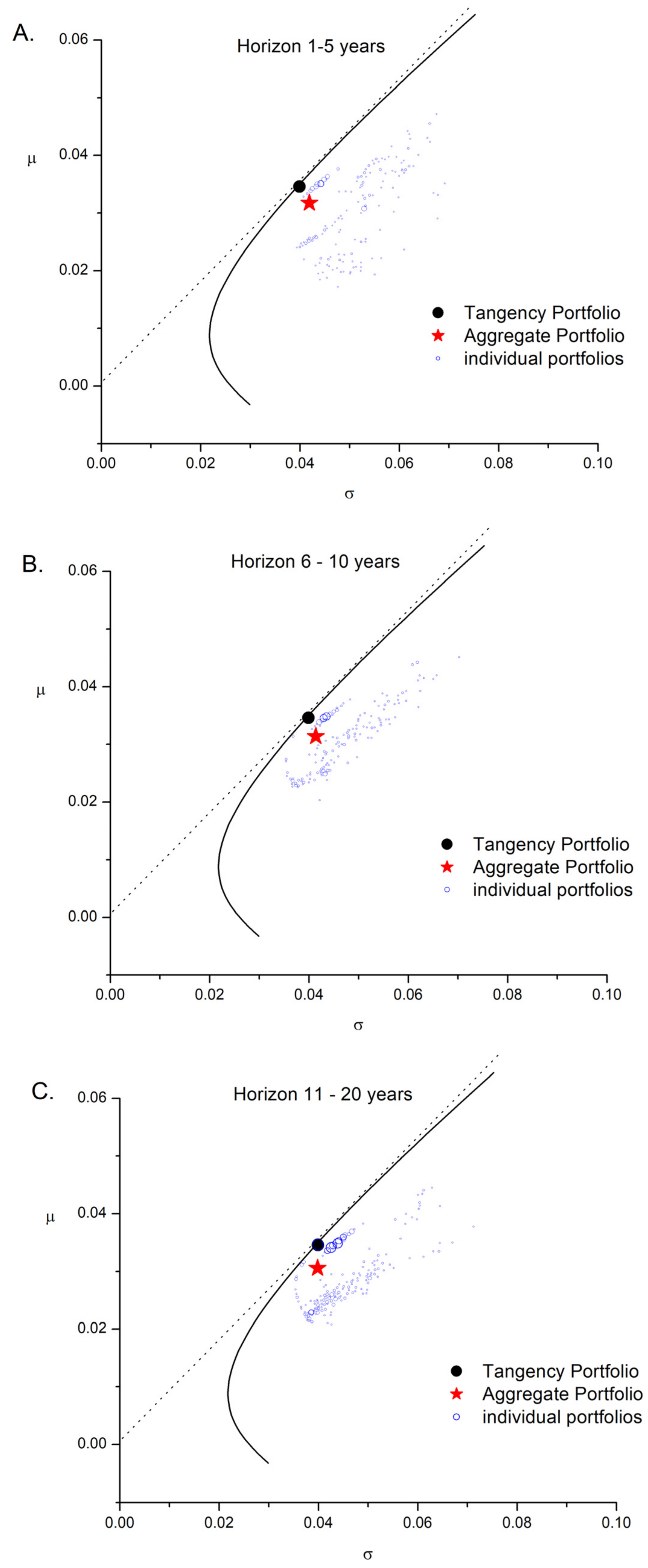
4.2. Results
5. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | A few of the studies in this vast literature are Shanken (1985), Kandel and Stambaugh (1987), Gibbons et al. (1989), MacKinlay and Richardson (1991), Zhou (1991), Fama and French (1992, 1993), Levy and Roll (2010), and Brennan and Zhang (2020). In a recent study, Dessaint et al. (2021) employed the CAPM to study the bidder return in M&As, where the purchased firms were classified by their CAPM betas. They are inconclusive concerning the empirical validity of the CAPM: “According to this view, our findings reflect temporary mispricing by the market, and managers are right to use the CAPM. An alternative view is that the market is efficient and the CAPM fails to explain expected returns, even in the long run” (see Dessaint et al. 2021, p. 39). |
| 2 | Jacobs and Shivdasani (2012, p. 120) report that “about 90% of the respondents in a survey conducted by the Association for Financial Professionals use the capital asset pricing model (CAPM) to estimate the cost of equity.” |
| 3 | Theorem 2 in Levy (1973) assumes that total returns are non-negative. This assumption does not hold for the normal return distributions considered here. However, one can safely truncate the normal return distributions at 0 without affecting the results. For example, for typical monthly return parameters of an expected rate of return of 1% and a standard deviation of 5%, a negative total return (i.e., rate of return < −100%) occurs only if the return deviates by more than 20 standard deviations to the left of the mean. The probability for such an event is about 10−89. Thus, truncating the total return distributions at 0 has virtually no effect on preferences. |
| 4 | The FSD rule is invariant to the initial wealth, and can be formulated either in terms of terminal wealth or change in wealth. In addition to risk-seeking over losses and risk-aversion over gains, prospect theory also includes the element of subjective probability weighting. In cumulative prospect theory, probability weighting is designed so that FSD is not violated. Namely, if F dominates G by FSD, all cumulative prospect theory investors prefer F, even under subjective probability weighting (Tversky and Kahneman 1992). |
| 5 | The special case of risk-averse investors was analyzed by Levy and Samuelson (1992). They did not analyze the effect of deviation from normality and the case of serial correlations, as discussed below. In general, additional restrictions may be necessary to avoid corner solutions. For example, if borrowing is unlimited and there is a risk-neutral investor, this investor will seek infinite leverage. While such corner solutions may arise with investors who are globally risk-neutral or globally risk-seeking, they will generally not arise for investors who are risk-seeking only over certain ranges. |
| 6 | This range is even larger than typically considered as realistic. See Mehra and Prescott (1985), and references within. |
| 7 | There is no natural calibration for b, and its value depends on the range of possible outcomes. For example, if the initial wealth is $100,000 and we take b = 1, we have , which is 0 for all practical or computational purposes. |
| 8 | Most estimates of the loss aversion parameter fall in this range; see Tversky and Kahneman (1992), Camerer and Ho (1994), Wu and Gonzalez (1996), and Abdellaoui et al. (2005). |
| 9 | The initial wealth is irrelevant for the optimization of CRRA investors, and PT investors with (Levy 2010). The empirical wealth distribution is very skewed, but this is not expected to have a systematic effect on the results. Indeed, we obtain similar results (not reported here) where the assumption of equal wealth across investors is replaced with a Pareto distribution of initial wealth. |
| 10 | The empirical return distributions are used to represent typical serial correlations and deviations from normality, so survivorship bias is not a concern in this study. When we randomly drew 100 firms, instead of taking the largest ones, very similar results were obtained—see Supplementary Materials Section S2. Recall that if the number of firms is close to the number of return observations, the covariance matrix becomes nearly singular. Thus, we could not include a much larger number of firms in our numerical analysis. |
| 11 | See, for example, Sharpe (1966, 1992), Jensen (1968), Samuelson (1989), Gruber (1996), Carhart (1997), French (2008), Fama and French (2008), and Levy (2023). There are, of course, many strategies suggested in the literature as being superior to the market index. However, overall, it seems that the market is close to optimal, as summarized by Bodie et al. (2020) in their classic textbook: “… a passive investor may view the market index as a reasonable first approximation to an efficient risky portfolio” (p. 267). |
References
- Abdellaoui, Mohammed, Frank Vossmann, and Martin Weber. 2005. Choice-based elicitation and decomposition of decision weights for gains and losses under uncertainty. Management Science 51: 1384–99. [Google Scholar] [CrossRef]
- Ang, Andrew, and Geert Bekaert. 2002. International asset allocation with regime shifts. The Review of Financial Studies 15: 1137–87. [Google Scholar] [CrossRef]
- Arditti, Fred D., and Haim Levy. 1975. Portfolio efficiency analysis in three moments: The multiperiod case. The Journal of Finance 30: 797–809. [Google Scholar]
- Arrow, Kenneth Joseph. 1971. Essays in the Theory of Risk-Bearing. Chicago: Markham Publishing Company. [Google Scholar]
- Barberis, Nicholas, Robin Greenwood, Lawrence Jin, and Andrei Shleifer. 2015. X-CAPM: An extrapolative capital asset pricing model. Journal of Financial Economics 115: 1–24. [Google Scholar] [CrossRef]
- Berk, Jonathan B., and Jules H. van Binsbergen. 2017. How Do Investors Compute the Discount Rate? They Use the CAPM. Financial Analysts Journal 73: 25–32. [Google Scholar] [CrossRef]
- Bessembinder, Hendrik. 2018. Do stocks outperform treasury bills? Journal of Financial Economics 129: 440–57. [Google Scholar] [CrossRef]
- Bessembinder, Hendrik, Michael J. Cooper, and Feng Zhang. 2021. What You See May Not Be What You Get: Return Horizon and Investment Alpha. SMU Cox School of Business Research Paper, (22-12). Available online: https://papers.ssrn.com/sol3/Papers.cfm?abstract_id=4096412 (accessed on 11 January 2024).
- Bessembinder, Hendrik, Michael J. Cooper, and Feng Zhang. 2023. Mutual fund performance at long horizons. Journal of Financial Economics 147: 132–58. [Google Scholar] [CrossRef]
- Black, Fischer. 1972. Capital market equilibrium with restricted borrowing. The Journal of Business 45: 444–55. [Google Scholar] [CrossRef]
- Bodie, Zvi, Alex Kane, and Alan Marcus. 2020. Investments. New York: McGraw Hill. [Google Scholar]
- Brennan, Michael J., and Yuzhao Zhang. 2020. Capital asset pricing with a stochastic horizon. Journal of Financial and Quantitative Analysis 55: 783–827. [Google Scholar] [CrossRef]
- Brennan, Thomas J., and Andrew W. Lo. 2010. Impossible frontiers. Management Science 56: 905–23. [Google Scholar] [CrossRef]
- Camerer, Colin F., and Teck-Hua Ho. 1994. Violations of the betweenness axiom and nonlinearity in probability. Journal of Risk and Uncertainty 8: 167–96. [Google Scholar] [CrossRef]
- Carhart, Mark M. 1997. On persistence in mutual fund performance. The Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Cutler, David, Angus Deaton, and Adriana Lleras-Muney. 2006. The determinants of mortality. Journal of Economic Perspectives 20: 97–120. [Google Scholar] [CrossRef]
- DeMarzo, Peter, and Costis Skiadas. 1998. Aggregation, determinacy, and informational efficiency for a class of economies with asymmetric information. Journal of Economic Theory 80: 123–52. [Google Scholar] [CrossRef]
- Dessaint, Olivier, Jacques Olivier, Clemens A. Otto, and David Thesmar. 2021. CAPM-based company (mis) valuations. Review of Financial Studies 34: 1–66. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1992. The cross-section of expected stock returns. Journal of Finance 47: 427–65. [Google Scholar]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2008. Mutual fund performance. Journal of Finance 63: 389–416. [Google Scholar]
- French, Kenneth R. 2008. Presidential address: The cost of active investing. The Journal of Finance 63: 1537–73. [Google Scholar] [CrossRef]
- Gibbons, Michael R., Stephen A. Ross, and Jay Shanken. 1989. A test of the efficiency of a given portfolio. Econometrica 57: 1121–152. [Google Scholar] [CrossRef]
- Graham, John R., and Campbell R. Harvey. 2001. The theory and practice of corporate finance: Evidence from the field. Journal of Financial Economics 60: 187–243. [Google Scholar] [CrossRef]
- Gruber, Martin J. 1996. Another Puzzle: The Growth in Actively Managed Mutual Funds. The Journal of Finance 51: 783–810. [Google Scholar] [CrossRef]
- Hadar, Josef, and William R. Russell. 1969. Rules for ordering uncertain prospects. The American Economic Review 59: 25–34. [Google Scholar]
- Handa, Puneet, Sagar P. Kothari, and Charles Wasley. 1989. The relation between the return interval and betas: Implications for the size effect. Journal of Financial Economics 23: 79–100. [Google Scholar] [CrossRef]
- Hanoch, Giora, and Haim Levy. 1969. The Efficiency Analysis of Choices Involving Risk. Review of Economic Studies 36: 335–46. [Google Scholar] [CrossRef]
- Jacobs, Michael T., and Anil Shivdasani. 2012. Do you know your cost of capital? Harvard Business Review 90: 118–24. [Google Scholar]
- Jensen, Michael C. 1968. The performance of mutual funds in the period 1945–1964. The Journal of Finance 23: 389–416. [Google Scholar]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An analysis of decision under risk. Econometrica 47: 263–92. [Google Scholar] [CrossRef]
- Kandel, Shmuel, and Robert F. Stambaugh. 1987. On correlations and inferences about mean-variance efficiency. Journal of Financial Economics 18: 61–90. [Google Scholar] [CrossRef]
- Lee, Cheng F., Chunchi Wu, and K. C. John Wei. 1990. The heterogeneous investment horizon and the capital asset pricing model: Theory and implications. Journal of Financial and Quantitative Analysis 25: 361–76. [Google Scholar] [CrossRef]
- Levhari, David, and Haim Levy. 1977. The capital asset pricing model and the investment horizon. The Review of Economics and Statistics 59: 92–104. [Google Scholar] [CrossRef]
- Levy, Haim. 1973. Stochastic dominance, efficiency criteria, and efficient portfolios: The multi-period case. The American Economic Review 63: 986–94. [Google Scholar]
- Levy, Haim. 2022. Stocks, Bonds, and the Investment Horizon: Decision-Making for the Long Run. London: World Scientific. [Google Scholar]
- Levy, Haim, and Harry M. Markowitz. 1979. Approximating expected utility by a function of mean and variance. The American Economic Review 69: 308–17. [Google Scholar]
- Levy, Haim, and Paul A. Samuelson. 1992. The capital asset pricing model with diverse holding periods. Management Science 38: 1529–42. [Google Scholar] [CrossRef]
- Levy, Haim, and Ran Duchin. 2004. Asset return distributions and the investment horizon. The Journal of Portfolio Management 30: 47–62. [Google Scholar] [CrossRef]
- Levy, Moshe. 2010. Loss aversion and the price of risk. Quantitative Finance 10: 1009–22. [Google Scholar] [CrossRef]
- Levy, Moshe. 2023. The deadweight loss of active management. The Journal of Investing 32: 17–41. [Google Scholar] [CrossRef]
- Levy, Moshe, and Richard Roll. 2010. The market portfolio may be mean/variance efficient after all: The market portfolio. The Review of Financial Studies 23: 2464–91. [Google Scholar] [CrossRef]
- Lintner, John. 1965. Security prices, risk, and maximal gains from diversification. The Journal of Finance 20: 587–615. [Google Scholar]
- Lintner, John. 1969. The aggregation of investor’s diverse judgments and preferences in purely competitive security markets. Journal of Financial and Quantitative Analysis 4: 347–400. [Google Scholar] [CrossRef]
- MacKinlay, A. Craig, and Matthew P. Richardson. 1991. Using generalized method of moments to test mean-variance efficiency. The Journal of Finance 46: 511–27. [Google Scholar]
- Markowitz, Harry. 1952. Portfolio selection. The Journal of Finance 7: 77–91. [Google Scholar]
- Martellini, Lionel, and Branko Urošević. 2006. Static mean-variance analysis with uncertain time horizon. Management Science 52: 955–64. [Google Scholar] [CrossRef]
- Mehra, Rajnish, and Edward C. Prescott. 1985. The equity premium: A puzzle. Journal of Monetary Economics 15: 145–61. [Google Scholar] [CrossRef]
- Merton, Robert C. 1971. Optimum consumption and portfolio rules in a continuous-time model. Journal of Economic Theory 3: 373–413. [Google Scholar] [CrossRef]
- Merton, Robert C. 1972. An analytic derivation of the efficient portfolio frontier. Journal of Financial and Quantitative Analysis 7: 1851–72. [Google Scholar] [CrossRef]
- Merton, Robert C. 1973. An intertemporal capital asset pricing model. Econometrica 41: 867–87. [Google Scholar] [CrossRef]
- Merton, Robert C. 1990. Continuous-Time Finance. Cambridge, MA: Basil Blackwell Inc. [Google Scholar]
- Mossin, Jan. 1966. Equilibrium in a capital asset market. Econometrica 34: 768–83. [Google Scholar] [CrossRef]
- Mukhlynina, Lilia, and Kjell G. Nyborg. 2016. The Choice of Valuation Techniques in Practice: Education versus Profession. University of Zurich Working Paper. Available online: https://ssrn.com/abstract=2784850 (accessed on 11 January 2024).
- Payne, John W. 2005. It is whether you win or lose: The importance of the overall probabilities of winning or losing in risky choice. Journal of Risk and Uncertainty 30: 5–19. [Google Scholar] [CrossRef]
- Payne, John W., Dan J. Laughhunn, and Roy Crum. 1980. Translation of gambles and aspiration level effects in risky choice behavior. Management Science 26: 1039–60. [Google Scholar] [CrossRef]
- Roll, Richard. 1977. A critique of the asset pricing theory’s tests Part I: On past and potential testability of the theory. Journal of Financial Economics 4: 129–76. [Google Scholar] [CrossRef]
- Samuelson, Paul A. 1989. The judgement of economic science on rational portfolio man. Journal of Portfolio Management 16: 4. [Google Scholar] [CrossRef]
- Shanken, Jay. 1985. Multivariate tests of the zero-beta CAPM. Journal of Financial Economics 14: 327–48. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance 19: 425–42. [Google Scholar]
- Sharpe, William F. 1966. Mutual fund performance. The Journal of Business 39: 119–38. [Google Scholar] [CrossRef]
- Sharpe, William F. 1992. Asset allocation: Management style and performance measurement. Journal of Portfolio Management 18: 7–19. [Google Scholar] [CrossRef]
- Shi, Lei. 2016. Consumption-based CAPM with belief heterogeneity. Journal of Economic Dynamics and Control 65: 30–46. [Google Scholar] [CrossRef]
- Tobin, James. 1958. Liquidity preference as behaviour towards risk. The Review of Economic Studies 25: 65–86. [Google Scholar] [CrossRef]
- Tversky, Amos, and Daniel Kahneman. 1992. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty 5: 297–323. [Google Scholar] [CrossRef]
- Williams, Joseph T. 1977. Capital asset prices with heterogeneous beliefs. Journal of Financial Economics 5: 219–39. [Google Scholar] [CrossRef]
- Wu, George, and Richard Gonzalez. 1996. Curvature of the probability weighting function. Management Science 42: 1676–90. [Google Scholar] [CrossRef]
- Zhou, Guofu. 1991. Small sample tests of portfolio efficiency. Journal of Financial Economics 30: 165–91. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levy, M.; Levy, H. Market Equilibrium and the Cost of Capital with Heterogeneous Investment Horizons. Risks 2024, 12, 44. https://doi.org/10.3390/risks12030044
Levy M, Levy H. Market Equilibrium and the Cost of Capital with Heterogeneous Investment Horizons. Risks. 2024; 12(3):44. https://doi.org/10.3390/risks12030044
Chicago/Turabian StyleLevy, Moshe, and Haim Levy. 2024. "Market Equilibrium and the Cost of Capital with Heterogeneous Investment Horizons" Risks 12, no. 3: 44. https://doi.org/10.3390/risks12030044
APA StyleLevy, M., & Levy, H. (2024). Market Equilibrium and the Cost of Capital with Heterogeneous Investment Horizons. Risks, 12(3), 44. https://doi.org/10.3390/risks12030044





