Time Restrictions on Life Annuity Benefits: Portfolio Risk Profiles
Abstract
:1. Introduction
2. Literature Review
3. Time Frames for the Policy and the Benefit Payment
3.1. Traditional Alternative Post-Retirement Income Solutions
- the immediate whole life annuity, purchased at the retirement time against a single premium (that is, the SPIA);
- the deferred life annuity, purchased during the working period, usually financed by a sequence of premiums (which constitute the so called “accumulation annuity”), with benefit payment commencing at the retirement time;
- the income drawdown, that is, a sequence of withdrawals from a fund, starting at the retirement time.
3.2. A Reference Scheme including Additional Alternatives
- an age within the working period (e.g., at the beginning of the accumulation period);
- the age at retirement;
- an age before retirement time (; e.g., the age at which the annuity rate is stated);
- the number of years of term annuity payments;
- the length in years of the delay period (e.g., in old-age life annuities).
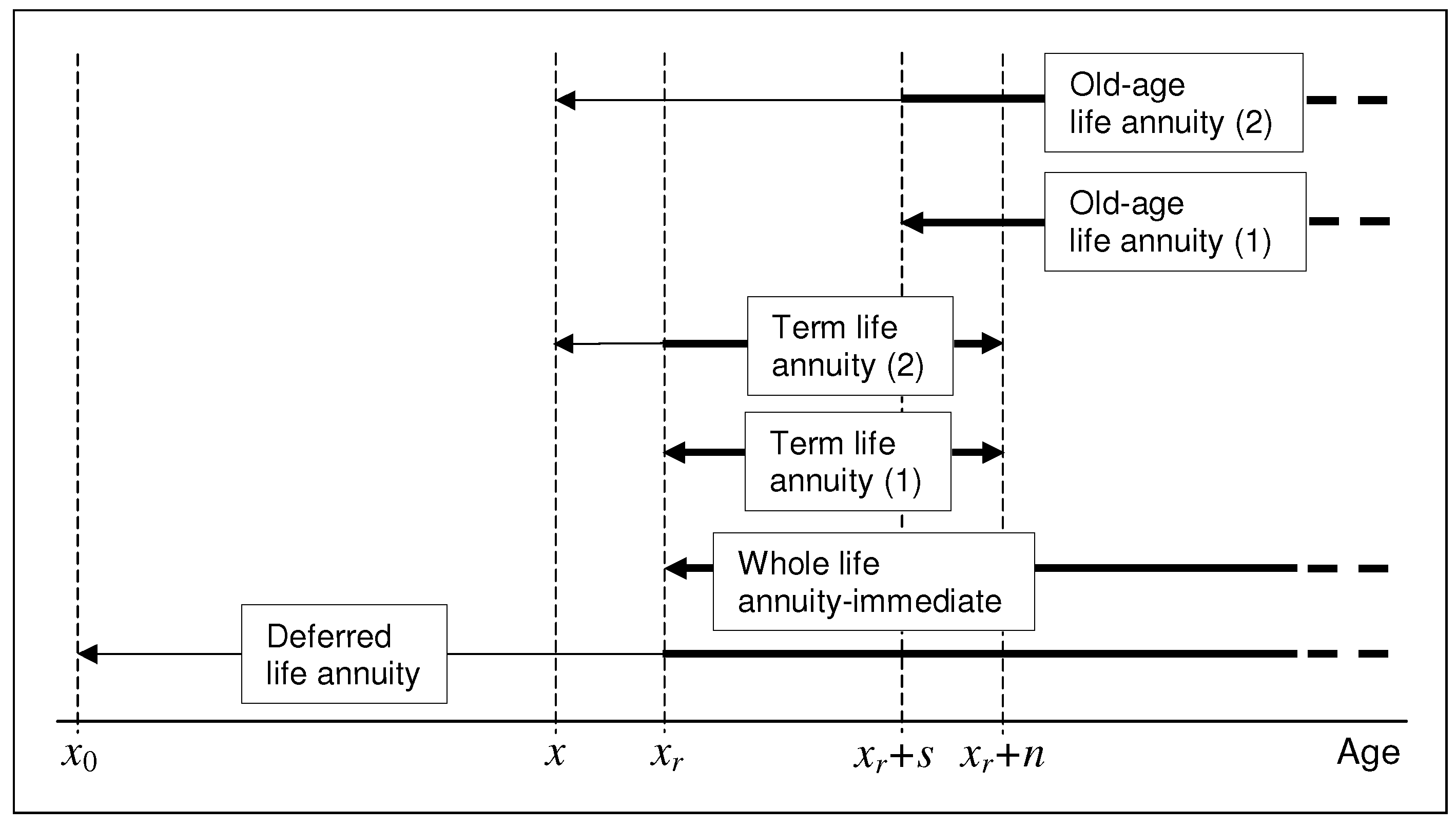
3.2.1. Deferred Life Annuities
3.2.2. Immediate Whole Life Annuity
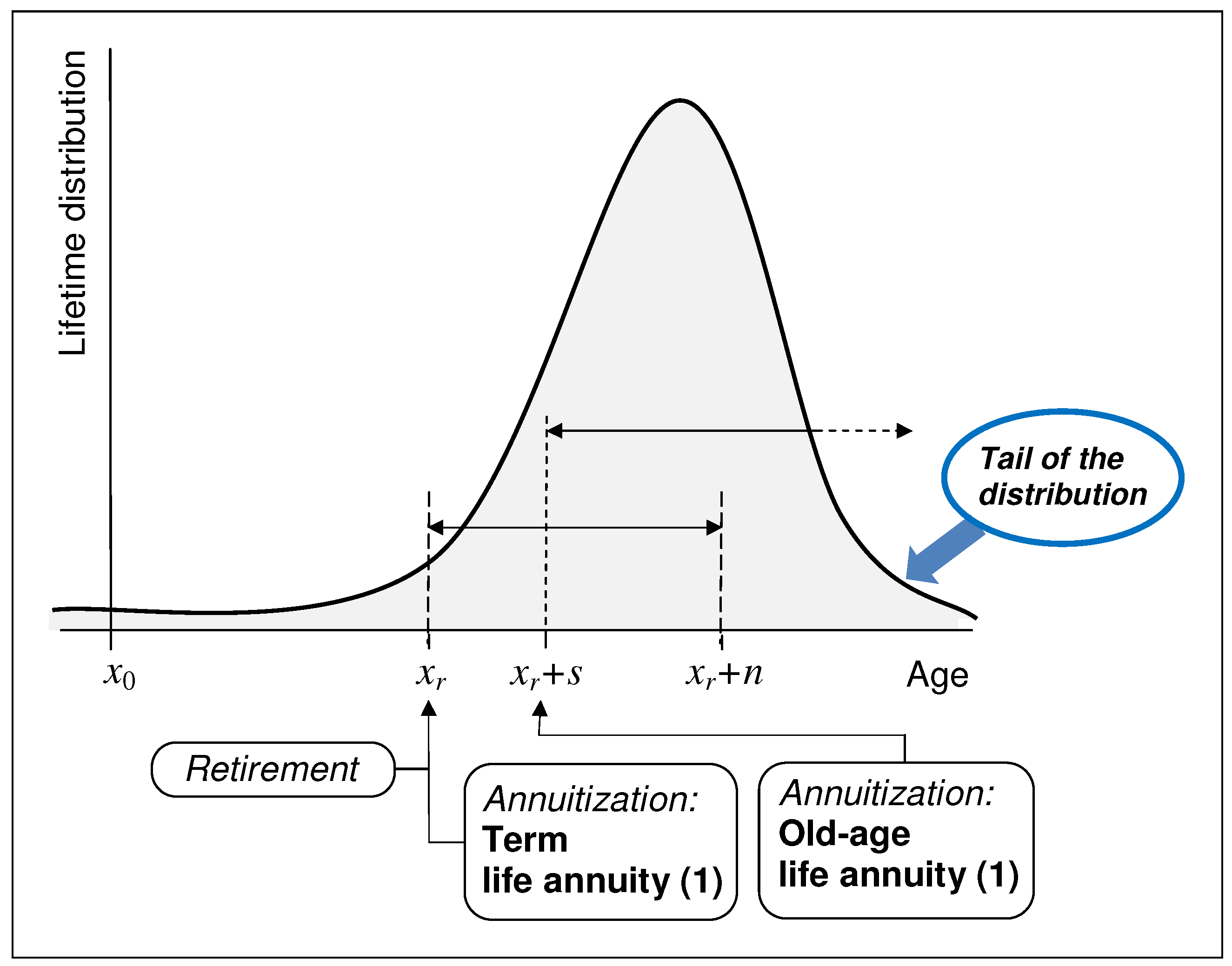
3.2.3. Term Life Annuities
3.2.4. Old-Age Life Annuities
3.3. Longevity Risk Transfers
4. Valuation Framework
4.1. Present Value of Future Benefits
4.2. Mortality Model
4.3. Financial Model
5. Portfolio Risk Profiles: Numerical Results
5.1. Arrangements
5.2. Parameters
5.3. Results and Discussion: Longevity Risk Only
5.4. Results and Discussion: Longevity and Financial Risk
5.5. Results and Discussion: Stress Test
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ANIA. 2014. Le Basi Demografiche per Rendite Vitalizie A 1900–2020 e A62. Relazione Tecnico-Metodologica. Available online: https://www.ordineattuari.it/media/246594/relazione_tecnica_a62_final.pdf (accessed on 29 March 2022).
- Bacinello, Anna Rita, An Chen, Thorsten Sehner, and Pietro Millossovich. 2021. On the market-consistent valuation of participating life insurance heterogeneous contracts under longevity risk. Risks 9: 20. [Google Scholar] [CrossRef]
- Biffis, Enrico. 2005. Affine processes for dynamic mortality and actuarial valuations. Insurance: Mathematics and Economics 37: 443–68. [Google Scholar] [CrossRef]
- Blackburn, Craig, and Michael Sherris. 2013. Consistent dynamic affine mortality models for longevity risk applications. Insurance: Mathematics and Economics 53: 64–73. [Google Scholar] [CrossRef]
- Blackburn, Craig, Katja Hanewald, Annamaria Olivieri, and Michael Sherris. 2017. Longevity risk management and shareholder value for a life annuity business. ASTIN Bulletin 47: 43–77. [Google Scholar] [CrossRef]
- Bowers, Newton L., Hans U. Gerber, James C. Hickman, Donald A. Jones, and Cecil J. Nesbitt. 1997. Actuarial Mathematics. Schaumburg: The Society of Actuaries. [Google Scholar]
- Boyle, Phelim, and Mary Hardy. 2003. Guaranteed annuity options. ASTIN Bulletin 33: 125–52. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A Poisson log-bilinear regression approach to the construction of projected lifetables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David P. Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Dickson, David C. M., Mary R. Hardy, and Howard R. Waters. 2020. Actuarial Mathematics for Life Contingent Risks, 3rd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Gerber, Hans U. 1995. Life Insurance Mathematics. Berlin and Heidelberg: Springer. [Google Scholar]
- Ghalehjooghi, Ahmad Salahnejhad, and Antoon Pelsser. 2021. Time-consistent and market-consistent actuarial valuation of the participating pension contract. Scandinavian Actuarial Journal 2021: 266–94. [Google Scholar] [CrossRef]
- Gong, Guan, and Anthony Webb. 2010. Evaluating the advanced life deferred annuity—An annuity people might actually buy. Insurance: Mathematics & Economics 46: 210–21. [Google Scholar]
- Hieber, Peter, Jan Natolski, and Ralf Werner. 2019. Fair valuation of cliquet-style return guarantees in (homogeneous and) heterogeneous life insurance portfolios. Scandinavian Actuarial Journal 2019: 478–507. [Google Scholar] [CrossRef]
- Huang, Huaxiong, Moshe A. Milevsky, and Thomas S. Salisbury. 2009. A different perspective on retirement income sustainability: The blueprint for a ruin contingent life annuity (RCLA). Journal of Wealth Management 11: 89–96. [Google Scholar] [CrossRef]
- Hunt, Andrew, and David Blake. 2021. On the structure and classification of mortality models. North American Actuarial Journal 25: S215–S234. [Google Scholar] [CrossRef]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar]
- Macdonald, Angus S. 2004. Annuities. In Encyclopedia of Actuarial Science. Edited by Josez L. Teugels and Bjørn Sundt. Hoboken: John Wiley & Sons. [Google Scholar]
- Milevsky, Moshe A. 2005. Real longevity insurance with a deductible: Introduction to advanced-life delayed annuities (ALDA). North American Actuarial Journal 9: 109–22. [Google Scholar] [CrossRef]
- Olivieri, Annamaria, and Ermanno Pitacco. 2009. Stochastic mortality: The impact on target capital. ASTIN Bulletin 39: 541–63. [Google Scholar] [CrossRef]
- Olivieri, Annamaria, and Ermanno Pitacco. 2015. Introduction to Insurance Mathematics. Technical and Financial Features of Risk Transfers, 2nd ed. EAA Series; Berlin and Heidelberg: Springer. [Google Scholar]
- Orozco-Garcia, Carolina, and Hato Schmeiser. 2019. Is fair pricing possible? An analysis of participating life insurance portfolios. Journal of Risk and Insurance 86: 521–60. [Google Scholar] [CrossRef]
- Pitacco, Ermanno. 2021. Life Annuities. From Basic Actuarial Models to Innovative Designs. London: Risk Books. [Google Scholar]
- Renshaw, Arthur E., and Steven Haberman. 2003. Lee–Carter mortality forecasting with age-specific enhancement. Insurance: Mathematics and Economics 33: 255–72. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the Lee–Carter model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
- Rocha, Roberto, Dimitri Vittas, and Heinz P. Rudolph. 2011. Annuities and Other Retirement Products. Designing the Payout Phase. Washington, DC: The World Bank. [Google Scholar]
- Schrager, David F. 2006. Affine stochastic mortality. Insurance: Mathematics and Economics 38: 81–97. [Google Scholar] [CrossRef]
- Stephenson, James B. 1978. The high-protection annuity. The Journal of Risk and Insurance 45: 593–610. [Google Scholar] [CrossRef]
| Annuity Type | Year of Birth | Entry Age | Deferment | Maximum Duration |
|---|---|---|---|---|
| Immediate whole life annuity | 1957 | 65 | 0 | ∞ |
| Deferred life annuity | 1972 | 50 | 15 | ∞ |
| Term life annuity (1) | 1957 | 65 | 0 | 25 |
| Term life annuity (2) | 1972 | 50 | 15 | 25 |
| Old-age life annuity (1) | 1942 | 80 | 0 | ∞ |
| Old-age life annuity (2) | 1957 | 65 | 15 | ∞ |
| Annuity Type | Benefit Payment Age Frames | |
|---|---|---|
| Immediate whole life annuity | 21.20 | |
| Deferred life annuity | 21.54 | |
| Term life annuity (1) | 19.23 | |
| Term life annuity (2) | 18.95 | |
| Old-age life annuity (1) | 9.47 | |
| Old-age life annuity (2) | 7.72 |
| Annuity Type | |||
|---|---|---|---|
| Immediate whole life annuity | 101.60% | 102.06% | 103.24% |
| Deferred life annuity | 101.76% | 102.26% | 103.55% |
| Term life annuity (1) | 100.96% | 101.24% | 101.92% |
| Term life annuity (2) | 101.06% | 101.35% | 102.10% |
| Old-age life annuity (1) | 102.65% | 103.38% | 105.40% |
| Old-age life annuity (2) | 103.65% | 106.66% | 107.42% |
| Annuity Type | |||
|---|---|---|---|
| Immediate whole life annuity | 105.28% | 106.83% | 110.71% |
| Deferred life annuity | 105.77% | 107.44% | 111.85% |
| Term life annuity (1) | 103.07% | 103.91% | 105.89% |
| Term life annuity (2) | 103.34% | 104.25% | 106.51% |
| Old-age life annuity (1) | 108.69% | 111.33% | 118.22% |
| Old-age life annuity (2) | 112.17% | 115.80% | 124.98% |
| Annuity Type | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Immediate whole life annuity | 103.24% (Age 65) | 104.14% (Age 70) | 105.43% (Age 75) | 107.42% (Age 80) | 110.64% (Age 85) | 116.13% (Age 90) | 124.69% (Age 95) | … (Age 100) | … (Age 105) | … (Age 110) |
| Deferred life annuity | 103.55% (Age 50) | 103.55% (Age 55) | 103.55% (Age 60) | 103.55% (Age 65) | 104.33% (Age 70) | 105.43% (Age 75) | 107.09% (Age 80) | 109.72% (Age 85) | 114.16% (Age 90) | 121.40% (Age 95) |
| Term life annuity (1) | 101.92% (Age 65) | 102.49% (Age 70) | 103.29% (Age 75) | 104.44% (Age 80) | 106.14% (Age 85) | - | - | - | - | - |
| Term life annuity (2) | 102.10% (Age 50) | 102.10% (Age 55) | 102.10% (Age 60) | 102.10% (Age 65) | 102.56% (Age 70) | 103.18% (Age 75) | 104.06% (Age 80) | 105.34% (Age 85) | - | - |
| Old-age life annuity (1) | 105.40% (Age 80) | 108.96% (Age 85) | 114.96% (Age 90) | 124.19% (Age 95) | … (Age 100) | … (Age 105) | … (Age 110) | … (Age 115) | … (Age 120) | |
| Old-age life annuity (2) | 107.42% (Age 65) | 107.42% (Age 70) | 107.42% (Age 75) | 107.42% (Age 80) | 110.64% (Age 85) | 116.13% (Age 90) | 124.69% (Age 95) | … (Age 100) | … (Age 105) | … (Age 110) |
| Annuity Type | Annuity Age Frames | Annuity Maximum Duration | Benefit Payment Age Frames | Maximum Number of Payments |
|---|---|---|---|---|
| Immediate whole life annuity | (65,121] | 56 | (65,121] | 56 |
| Deferred life annuity | (50,121] | 71 | (65,121] | 56 |
| Term life annuity (1) | (65,90] | 25 | (65,90] | 25 |
| Term life annuity (2) | (50,90] | 40 | (65,90] | 25 |
| Old-age life annuity (1) | (80,121] | 41 | (80,121] | 41 |
| Old-age life annuity (2) | (65,121] | 56 | (80,121] | 41 |
| Moderate Deviations in Mortality | Major Deviations in Mortality | ||||||
|---|---|---|---|---|---|---|---|
| Annuity Type | BE | ||||||
| Immediate whole life annuity | 16.60 | 102.24% | 102.87% | 104.45% | 104.64% | 105.98% | 109.86% |
| Deferred life annuity | 12.34 | 103.57% | 104.53% | 107.00% | 105.97% | 107.60% | 111.68% |
| Term life annuity (1) | 15.50 | 101.92% | 102.47% | 103.88% | 103.25% | 104.14% | 106.54% |
| Term life annuity (2) | 11.28 | 103.31% | 104.19% | 106.46% | 104.51% | 105.72% | 108.77% |
| Old-age life annuity (1) | 8.26 | 102.77% | 103.57% | 105.61% | 107.69% | 110.08% | 115.32% |
| Old-age life annuity (2) | 4.98 | 104.53% | 105.82% | 109.10% | 111.55% | 114.98% | 125.44% |
| Moderate Deviations in Mortality | Major Deviations in Mortality | ||||||
|---|---|---|---|---|---|---|---|
| Annuity Type | BE | ||||||
| Immediate whole life annuity | 14.85 | 103.72% | 104.75% | 107.36% | 105.26% | 106.78% | 111.02% |
| Deferred life annuity | 9.48 | 106.63% | 108.37% | 113.01% | 108.00% | 110.18% | 115.85% |
| Term life annuity (1) | 14.03 | 103.48% | 104.52% | 107.03% | 104.29% | 105.45% | 108.60% |
| Term life annuity (2) | 8.80 | 106.42% | 108.09% | 112.73% | 107.10% | 108.99% | 113.87% |
| Old-age life annuity (1) | 7.75 | 103.54% | 104.54% | 107.11% | 107.72% | 110.00% | 115.38% |
| Old-age life annuity (2) | 4.02 | 106.82% | 108.73% | 113.52% | 112.42% | 116.14% | 126.86% |
| Mortality Shock after 0 Years | Mortality Shock after 10 Years | |||
|---|---|---|---|---|
| Annuity Type | ||||
| Immediate whole life annuity | 109.41% | 111.75% | 107.38% | 109.93% |
| Deferred life annuity | 111.40% | 114.98% | 110.88% | 114.83% |
| Term life annuity (1) | 106.20% | 107.96% | 104.36% | 106.34% |
| Term life annuity (2) | 108.10% | 111.29% | 107.61% | 111.11% |
| Old-age life annuity (1) | 115.94% | 119.23% | 106.83% | 109.89% |
| Old-age life annuity (2) | 123.75% | 128.90% | 120.89% | 126.25% |
| Financial Shock after 0 Years | Financial Shock after 10 Years | |||
|---|---|---|---|---|
| Annuity Type | ||||
| Immediate whole life annuity | 107.10% | 109.47% | 103.96% | 106.17% |
| Deferred life annuity | 115.53% | 119.67% | 110.83% | 115.08% |
| Term life annuity (1) | 106.17% | 108.08% | 103.12% | 105.12% |
| Term life annuity (2) | 114.48% | 118.37% | 109.99% | 113.30% |
| Old-age life annuity (1) | 105.52% | 108.50% | 103.15% | 106.02% |
| Old-age life annuity (2) | 113.92% | 119.08% | 109.55% | 114.44% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivieri, A.; Pitacco, E. Time Restrictions on Life Annuity Benefits: Portfolio Risk Profiles. Risks 2022, 10, 164. https://doi.org/10.3390/risks10080164
Olivieri A, Pitacco E. Time Restrictions on Life Annuity Benefits: Portfolio Risk Profiles. Risks. 2022; 10(8):164. https://doi.org/10.3390/risks10080164
Chicago/Turabian StyleOlivieri, Annamaria, and Ermanno Pitacco. 2022. "Time Restrictions on Life Annuity Benefits: Portfolio Risk Profiles" Risks 10, no. 8: 164. https://doi.org/10.3390/risks10080164
APA StyleOlivieri, A., & Pitacco, E. (2022). Time Restrictions on Life Annuity Benefits: Portfolio Risk Profiles. Risks, 10(8), 164. https://doi.org/10.3390/risks10080164






