A Managed Volatility Investment Strategy for Pooled Annuity Products
Abstract
1. Introduction
2. Pooled Annuities and Investment Risk
3. Pooled Annuity Income Modelling Methodology
3.1. Pooled Annuity Product Features
3.2. Mortality Model
3.2.1. Systematic Longevity Risk
3.2.2. Idiosyncratic Longevity Risk
3.3. Economic Scenario Generator (ESG) Models
3.3.1. Economic Scenario Generator
3.3.2. Interest Rate Model
3.4. Equity Volatility Forecast Model
- To generate the series of residuals, subtract the path of realized equity returns by the mean simulated path, then take the square of each difference. Denote the residual at time t as , thenwhere is the realized equity return at time t, and is the mean equity return at time t.
- Assume an averaging period of n quarters, calculate the ‘realized variance’ by taking the moving average of residuals for the past n quarters. That is, the first realized variance is the average of the residuals from quarter 1 to quarter n; the second realized variance is the average of the residuals from quarter 2 to quarter , and so on. Denote the k-th realized variance as , then
- Take the square root of the realized variance to get the realized volatility. Denote the k-th realized volatility as , then
- Fit an AR(1) model to the series of realized volatility and test the significance of autoregression for prediction.
3.5. The Managed-Volatility Framework
3.6. Risk Measures
- Expected retirement income;
- Income variation;
- Access to underlying capital;
- Death benefit and reversionary benefits.
4. Investment Strategy Results
4.1. Simulation of Annuity Payments in the Pool
4.2. Balanced Fund with Target Volatility of 1.25 Historical Volatility
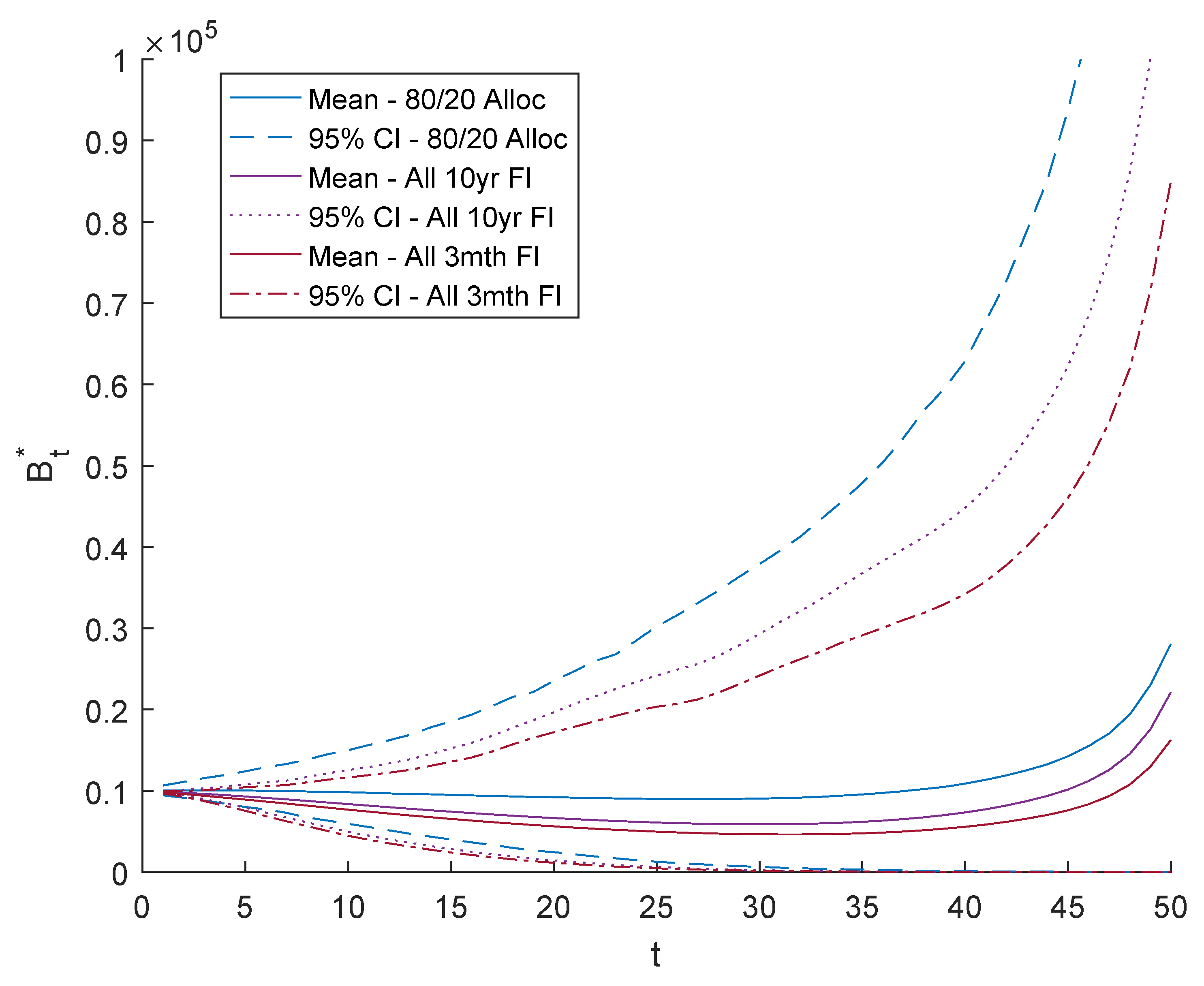
4.3. Equity Asset Allocation
- 100% 3-month fixed-income;
- 100% 10-year fixed-income;
- 80% fixed-income, 20% equity, without volatility management.
- 4.
- 80% fixed-income, 20% equity;
- 5.
- 65% fixed-income, 35% equity;
- 6.
- 50% fixed-income, 50% equity.
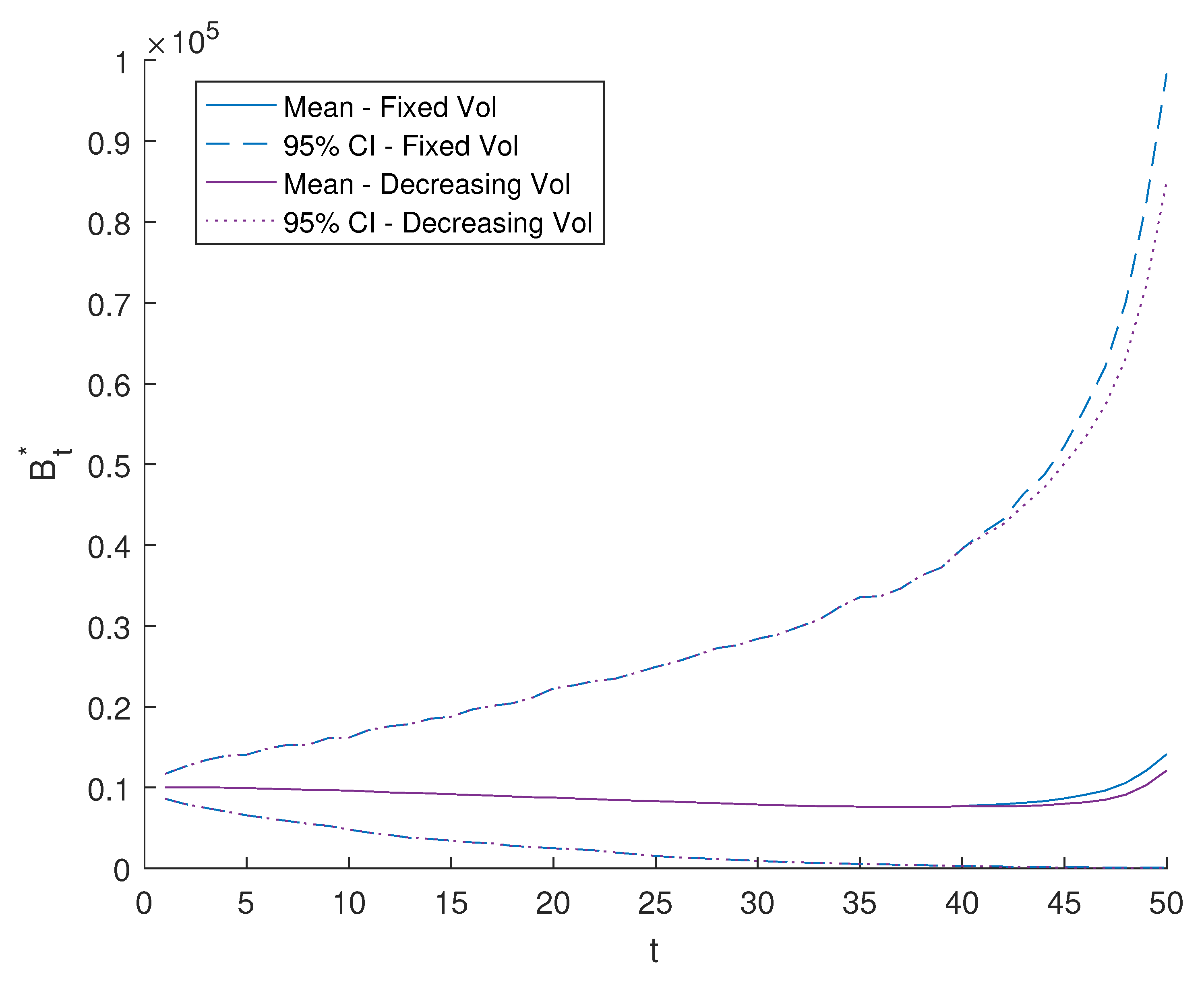
4.4. Varying the Level of Target Volatility
- Constant target volatility;
- Target volatility that decreases over time.
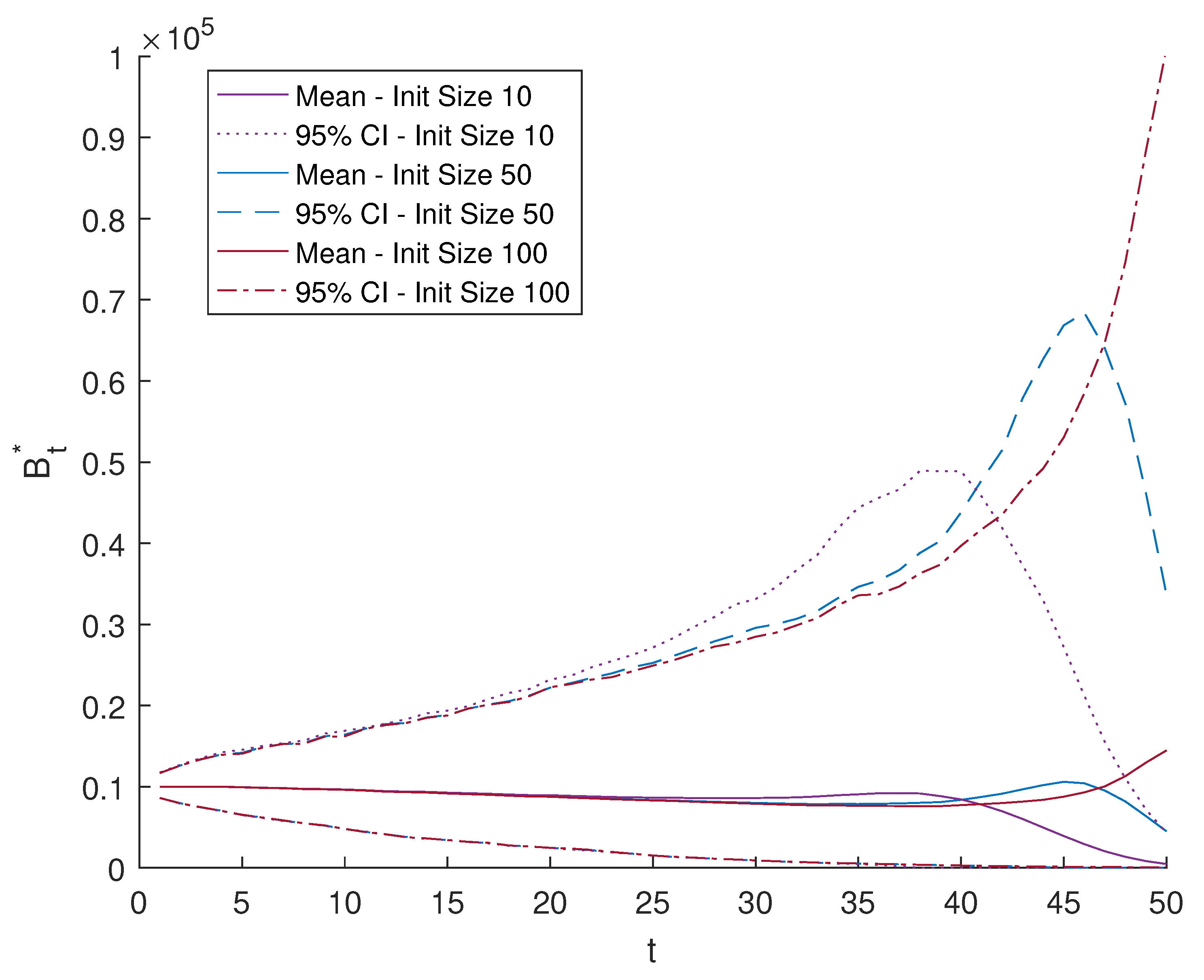
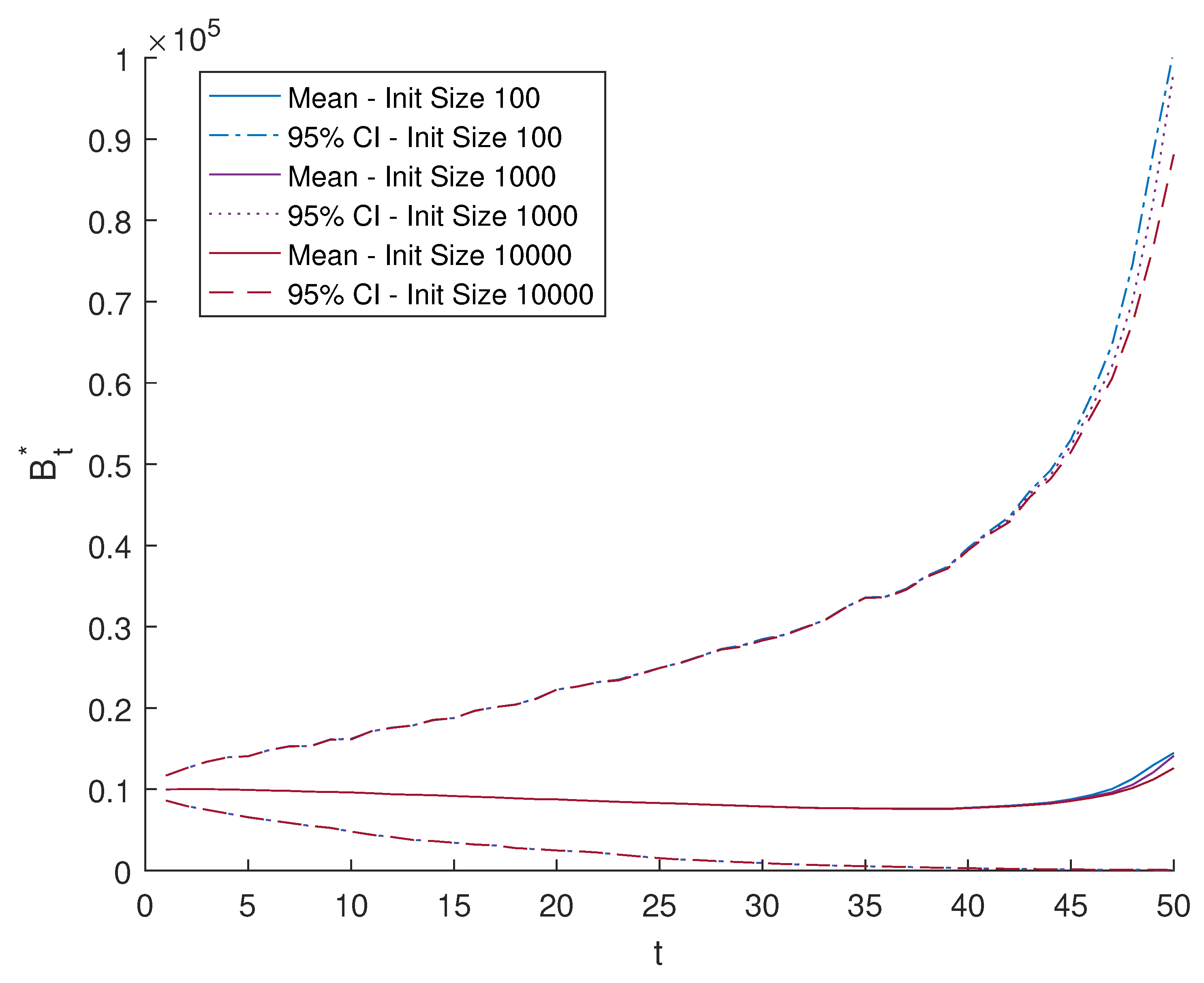
4.5. Pool Size with Equity Investments
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Mortality Model, Estimated Parameters and Simulation
| −0.1004 | −0.1347 | 1.4285 | 4.9659 |
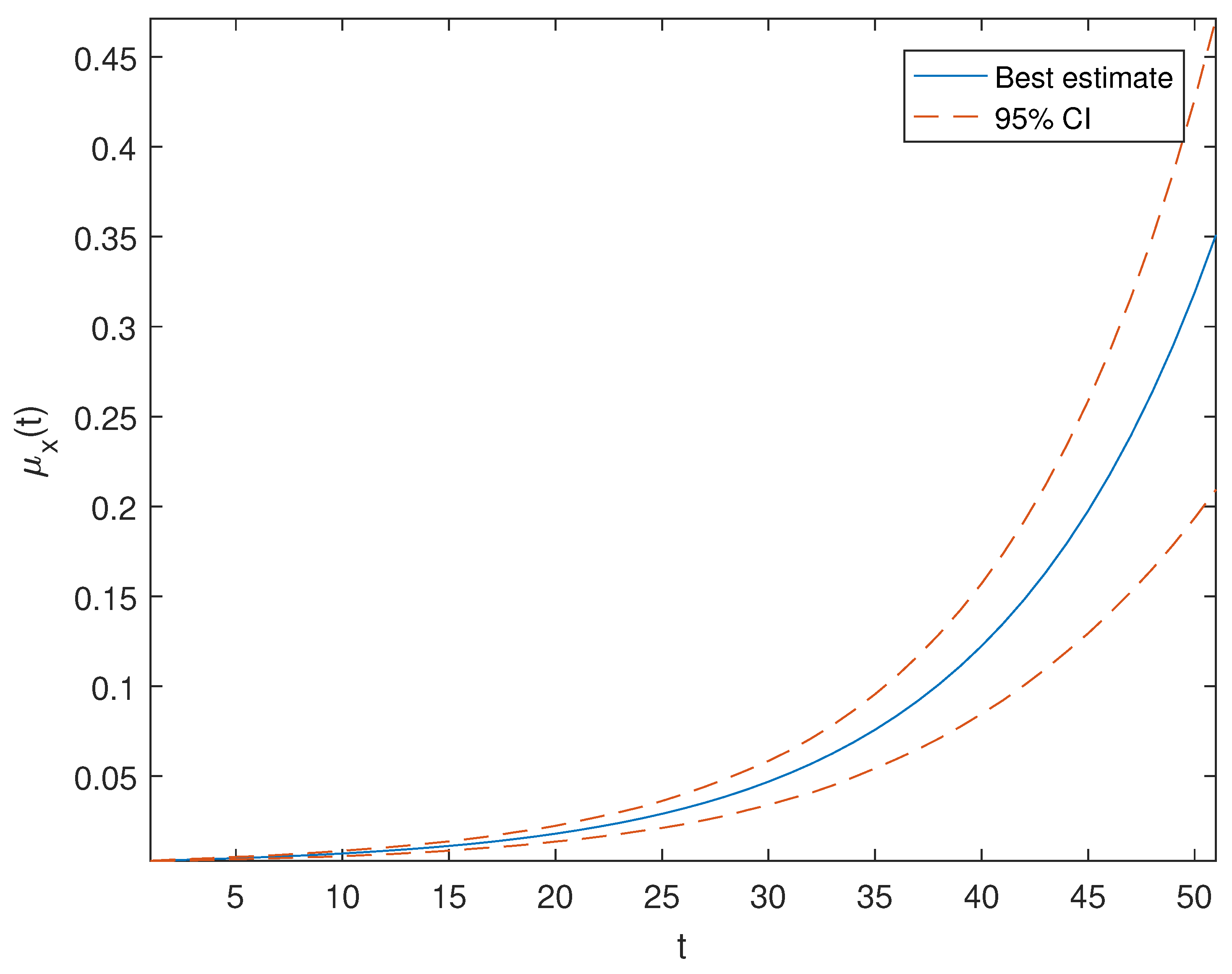
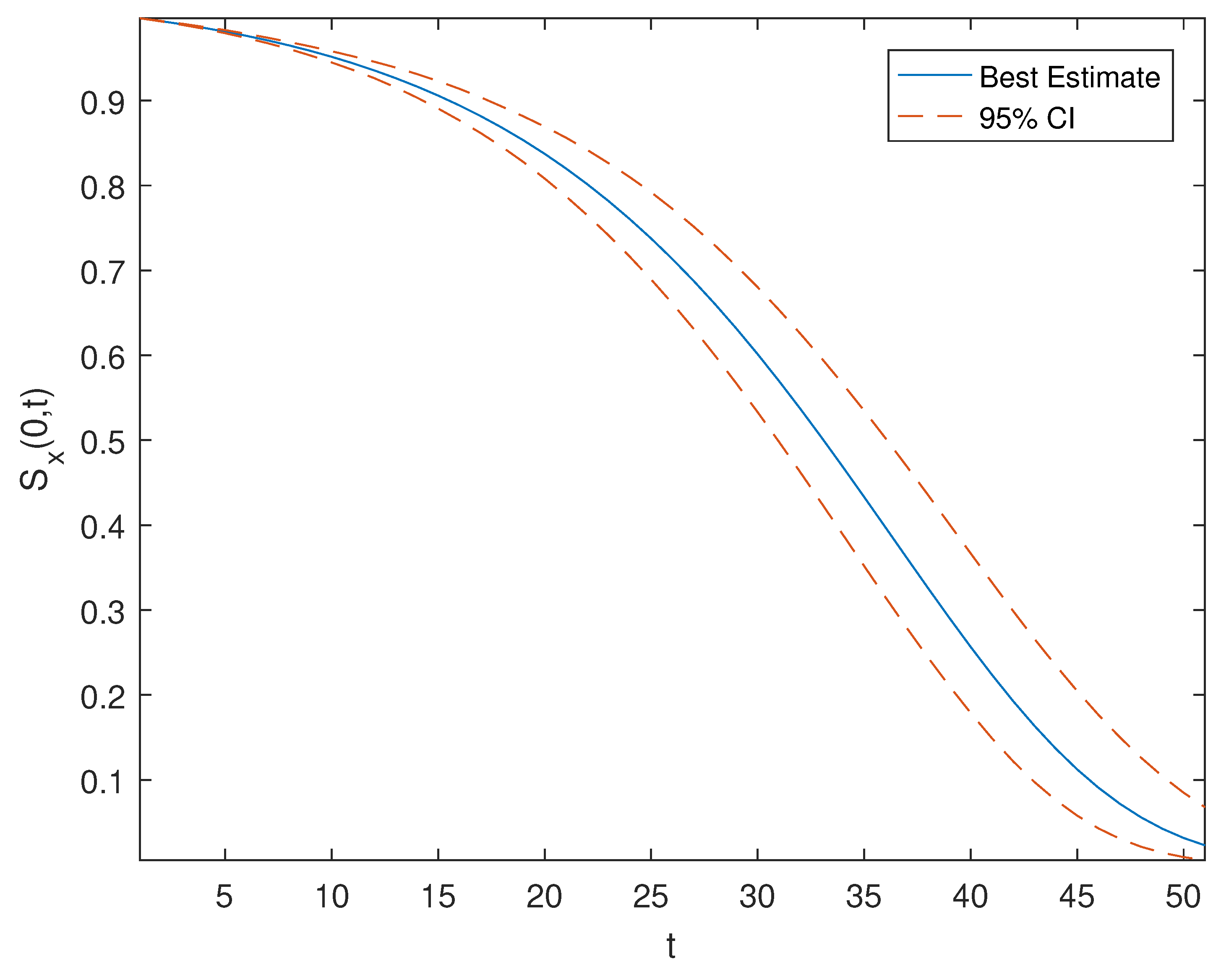
Appendix B. Economic Series Data, Estimation and Simulations
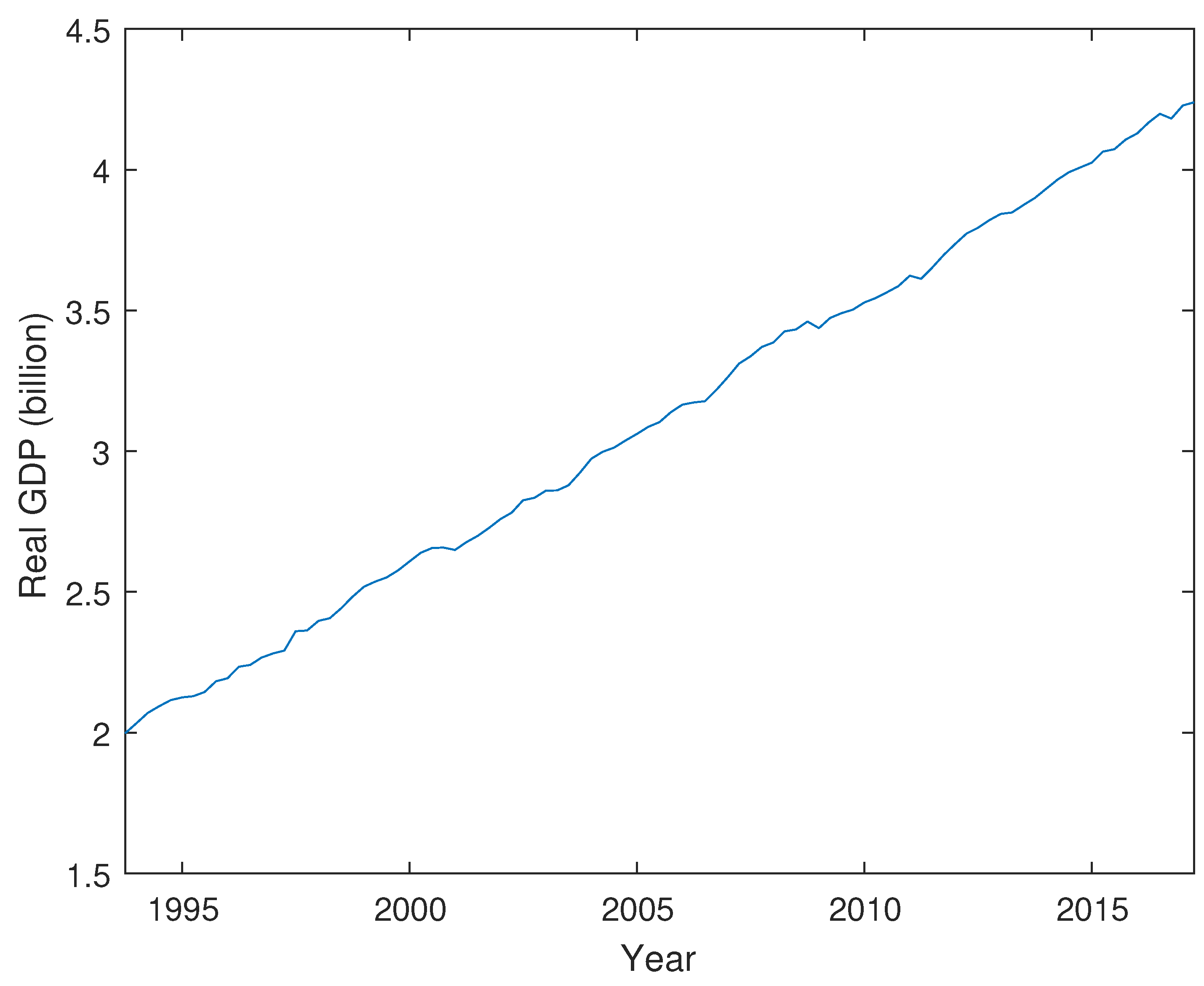
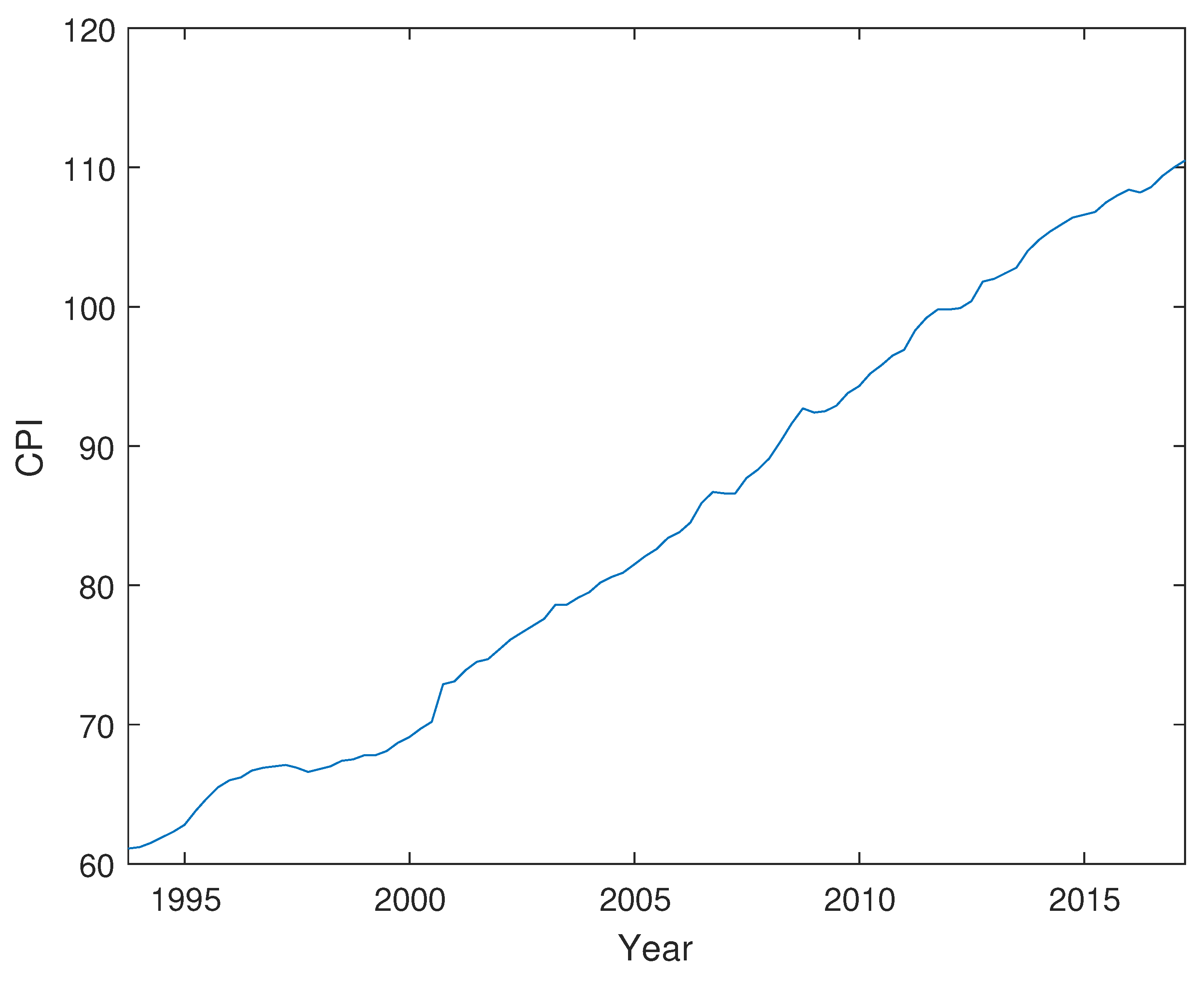
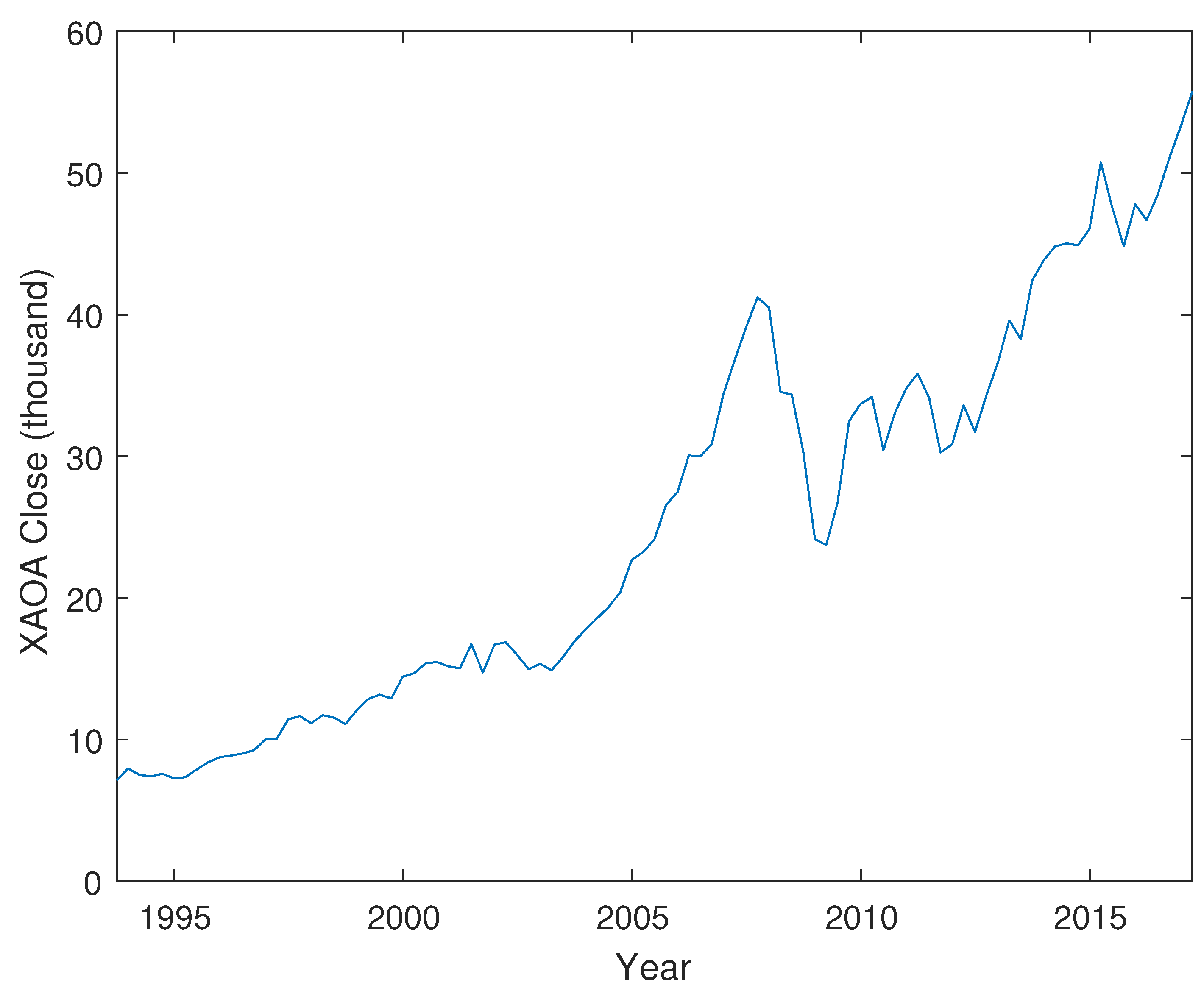


Appendix B.1. Cointegration Test for VAR Model
Appendix B.1.1. Stationarity at Level
| Aug D-F Test (at Level) | ||||
|---|---|---|---|---|
| P-Value | 0.9990 | 0.9990 | 0.9990 | 0.3199 |
| Null Hypothesis Result | not rejected | not rejected | not rejected | not rejected |
| Stationarity | no | no | no | no |
Appendix B.1.2. Johansen Test
| r | h | stat | cValue | pValue | eigVal |
|---|---|---|---|---|---|
| 0 | 0 | 46.0198 | 47.8564 | 0.0737 | 0.2351 |
| 1 | 0 | 24.8498 | 29.7976 | 0.1672 | 0.1396 |
| 2 | 0 | 12.9739 | 15.4948 | 0.1163 | 0.1142 |
| 3 | 0 | 3.3944 | 3.8415 | 0.0654 | 0.0421 |
Appendix B.2. Stationarity Test at First Difference for VAR Model
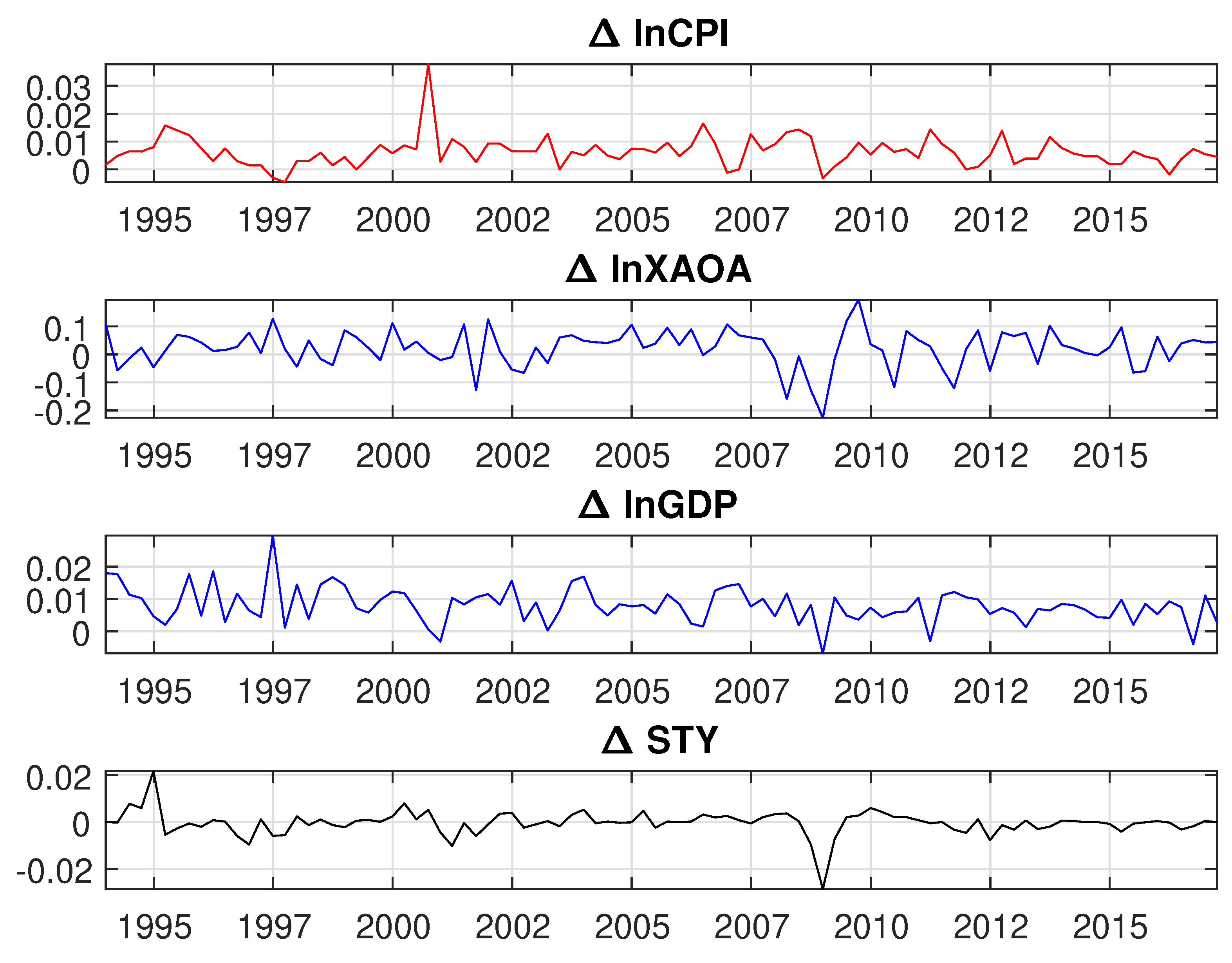
| Statistic | ||||
|---|---|---|---|---|
| Mean | 0.0066 | 0.0223 | 0.0079 | −0.0005 |
| Std Dev | 0.0057 | 0.0693 | 0.0055 | 0.0053 |
| Skewness | 1.9863 | −0.8634 | 0.5771 | −1.0974 |
| Kurtosis | 12.6015 | 4.6751 | 5.2732 | 14.2357 |
| First Quantile | 0.0030 | −0.0108 | 0.0047 | −0.0021 |
| Median | 0.0063 | 0.0273 | 0.0077 | 0.0001 |
| Third Quantile | 0.0091 | 0.0663 | 0.0112 | 0.0021 |
| Min | −0.0045 | −0.2256 | −0.0068 | −0.0286 |
| Max | 0.0377 | 0.1952 | 0.0296 | 0.0218 |
| Aug D-F Test (First Difference) | ||||
|---|---|---|---|---|
| p-value | 0.0010 | 0.0010 | 0.0010 | 0.0010 |
| Null Hypothesis result | rejected | rejected | rejected | rejected |
| stationarity | yes | yes | yes | yes |
Appendix B.3. Optimal Number of Legs for VAR Model
| VAR (1) | VAR (2) | VAR (3) | VAR (4) | |
|---|---|---|---|---|
| AIC | −2.1280 | −2.1154 | −2.0959 | −2.0854 |
Appendix B.4. Estimated Parameters for VAR Model
Appendix B.5. Simulation Versus Actual Results
| Simulation | Actual | |||||||
|---|---|---|---|---|---|---|---|---|
| Statistic | ||||||||
| Mean | 0.0067 | 0.0223 | 0.0080 | −0.0005 | 0.0066 | 0.0223 | 0.0079 | −0.0005 |
| Std Dev | 0.0001 | 0.0007 | 0.0001 | 0.0001 | 0.0057 | 0.0693 | 0.0055 | 0.0053 |
| Skewness | −0.2898 | −0.4418 | −0.3923 | −0.0616 | 1.9863 | −0.8634 | 0.5771 | −1.0974 |
| Kurtosis | 2.4385 | 3.5483 | 2.9874 | 4.0682 | 12.6015 | 4.6751 | 5.2732 | 14.2357 |
| First Quantile | 0.0066 | 0.0220 | 0.0080 | −0.0005 | 0.0030 | −0.0108 | 0.0047 | −0.0021 |
| Median | 0.0067 | 0.0224 | 0.0080 | −0.0005 | 0.0063 | 0.0273 | 0.0077 | 0.0001 |
| Third Quantile | 0.0067 | 0.0228 | 0.0080 | −0.0004 | 0.0091 | 0.0663 | 0.0112 | 0.0021 |
| Min | 0.0065 | 0.0203 | 0.0079 | −0.0006 | −0.0045 | −0.2256 | −0.0068 | −0.0286 |
| Max | 0.0068 | 0.0242 | 0.0081 | −0.0003 | 0.0377 | 0.1952 | 0.0296 | 0.0218 |
References
- Australia Government the Treasury. 2018. Retirement Income Disclosure Consultation Paper; Discussion Paper. Available online: https://treasury.gov.au/consultation/c2018-t347107 (accessed on 3 March 2022).
- Australia Government the Treasury. 2020. Retirement Income Review; Final Report. Available online: https://treasury.gov.au/publication/p2020-100554 (accessed on 3 March 2022).
- Blackburn, Craig, and Michael Sherris. 2013. Consistent dynamic affine mortality models for longevity risk applications. Insurance: Mathematics and Economics 53: 64–73. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–327. [Google Scholar] [CrossRef]
- Chen, An, Manuel Rach, and Thorsten Sehner. 2020. On the optimal combination of annuities and tontines. ASTIN Bulletin 50: 95–129. [Google Scholar] [CrossRef]
- Cox, John C., Jonathan E. Ingersoll, Jr., and Stephen A. Ross. 1985. A theory of the term structure of interest rates. Econometrica: Journal of the Econometric Society 53: 385–407. [Google Scholar] [CrossRef]
- Donnelly, Catherine. 2015. Actuarial fairness and solidarity in pooled annuity funds. Astin Bulletin 45: 49–74. [Google Scholar] [CrossRef]
- Donnelly, Catherine, Montserrat Guillén, and Jens Perch Nielsen. 2013. Exchanging uncertain mortality for a cost. Insurance: Mathematics and Economics 52: 65–76. [Google Scholar] [CrossRef]
- Donnelly, Catherine, Montserrat Guillén, and Jens Perch Nielsen. 2014. Bringing cost transparency to the life annuity market. Insurance: Mathematics and Economics 56: 14–27. [Google Scholar] [CrossRef]
- Duan, Jin-Chuan, and Jean-Guy Simonato. 1999. Estimating and testing exponential-affine term structure models by kalman filter. Review of Quantitative Finance and Accounting 13: 111–135. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. Econometrica: Journal of the Econometric Society 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert F., and Victor K. Ng. 1993. Measuring and testing the impact of news on volatility. The Journal of Finance 48: 1749–78. [Google Scholar] [CrossRef]
- Hainaut, Donatien, and Pierre Devolder. 2006. Life annuitization: Why and how much? ASTIN Bulletin 36: 629–54. [Google Scholar] [CrossRef]
- Harris, Glenn R. 1997. Regime switching vector autoregressions: A bayesian markov chain monte carlo approach. Paper presented at 7th International AFIR Colloquium, Cairns, Australia, August 13–15, Volume 1, pp. 421–451. [Google Scholar]
- Harris, Glen R. 1999. Markov chain monte carlo estimation of regime switching vector autoregressions. Astin Bulletin 29: 47–79. [Google Scholar] [CrossRef]
- Hocquard, Alexandre, Sunny Ng, and Nicolas Papageorgiou. 2013. A constant-volatility framework for managing tail risk. The Journal of Portfolio Management 39: 28–40. [Google Scholar] [CrossRef]
- Ignatieva, Katja, Andrew Song, and Jonathan Ziveyi. 2016. Pricing and hedging of guaranteed minimum benefits under regime-switching and stochastic mortality. Insurance: Mathematics and Economics 70: 286–300. [Google Scholar]
- James, Estelle, and Xue Song. 2001. Annuities Markets Around the World: Money’s Worth and Risk Intermediation. CeRP Working Papers 16/01. Turin: Center for Research on Pensions and Welfare Policies. [Google Scholar]
- Milevsky, Moshe A., and Thomas S. Salisbury. 2015. Optimal retirement income tontines. Insurance: Mathematics and Economics 64: 91–105. [Google Scholar] [CrossRef]
- Milevsky, Moshe A., and Thomas S. Salisbury. 2016. Equitable retirement income tontines: Mixing cohorts without discriminating. ASTIN Bulletin 46: 571–604. [Google Scholar] [CrossRef]
- Morrison, Steven, and Laura Tadrowski. 2013. Guarantees and Target Volatility Funds. Moody’s Analytics, September 2. [Google Scholar]
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica: Journal of the Econometric Society 59: 347–70. [Google Scholar] [CrossRef]
- OMeara, Taleitha, Aakansha Sharma, and Aaron Bruhn. 2015. Australia’s piece of the puzzle–why don’t australians buy annuities? Australian Journal of Actuarial Practice 3: 47–57. [Google Scholar]
- Papageorgiou, Nicolas A., Jonathan J. Reeves, and Michael Sherris. 2017. Equity Investing with Targeted Constant Volatility Exposure. FIRN Research Paper No. 2614828. Sydney: UNSW Business School. [Google Scholar]
- Pedersen, Hal, Mary Pat Campbell, Stephan L. Christiansen, Samuel H. Cox, Daniel Finn, Ken Griffin, Nigel Hooker, Matthew Lightwood, Stephen M. Sonlin, and Chris Suchar. 2016. Economic Scenario Generators: A Practical Guide. Practical Guide. Society of Actuaries: Society of Actuaries. [Google Scholar]
- Peijnenburg, Kim, Theo Nijman, and Bas J. M. Werker. 2016. The annuity puzzle remains a puzzle. Journal of Economic Dynamics and Control 70: 18–35. [Google Scholar] [CrossRef][Green Version]
- Piggott, John, Emiliano A. Valdez, and Bettina Detzel. 2005. The simple analytics of a pooled annuity fund. Journal of Risk and Insurance 72: 497–520. [Google Scholar] [CrossRef]
- Qiao, Chao, and Michael Sherris. 2013. Managing systematic mortality risk with group self-pooling and annuitization schemes. Journal of Risk and Insurance 80: 949–74. [Google Scholar] [CrossRef]
- Sherris, Michael, and Boqi Zhang. 2009. Economic Scenario Generation with Regime Switching Models. Research paper No. 2009ACTL05. Sydney: UNSW Business School. [Google Scholar]
- Stamos, Michael Z. 2008. Optimal consumption and portfolio choice for pooled annuity funds. Insurance: Mathematics and Economics 43: 56–68. [Google Scholar] [CrossRef]
- Ungolo, Francesco, Michael Sherris, and Yuxin Zhou. 2021. Multi-Factor, Age-Cohort, Affine Mortality Models: A Multi-Country Comparison. Working Paper, CEPAR. Kensington: UNSW. [Google Scholar]
- Valdez, Emiliano A., John Piggott, and Liang Wang. 2006. Demand and adverse selection in a pooled annuity fund. Insurance: Mathematics and Economics 39: 251–66. [Google Scholar] [CrossRef]
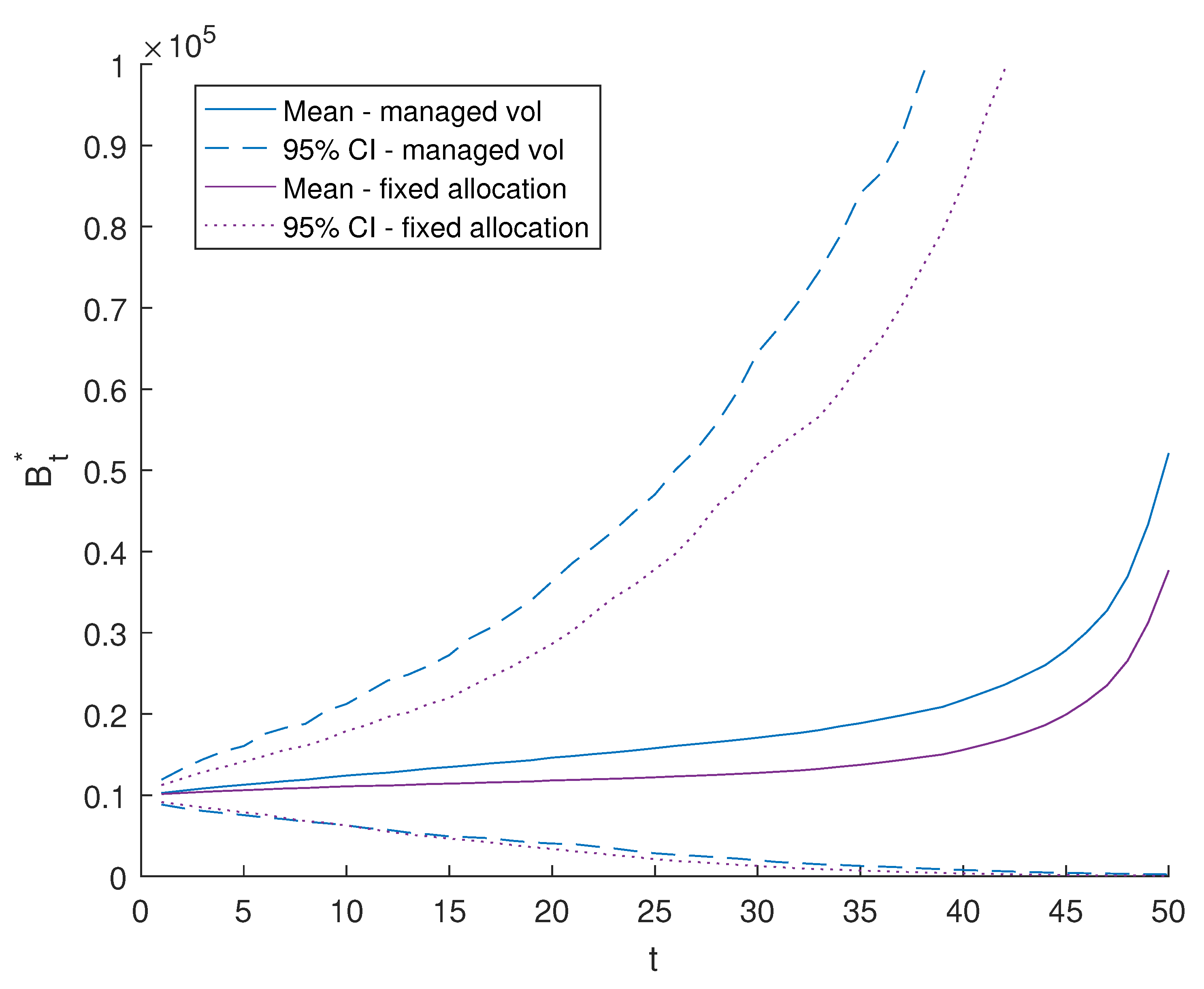
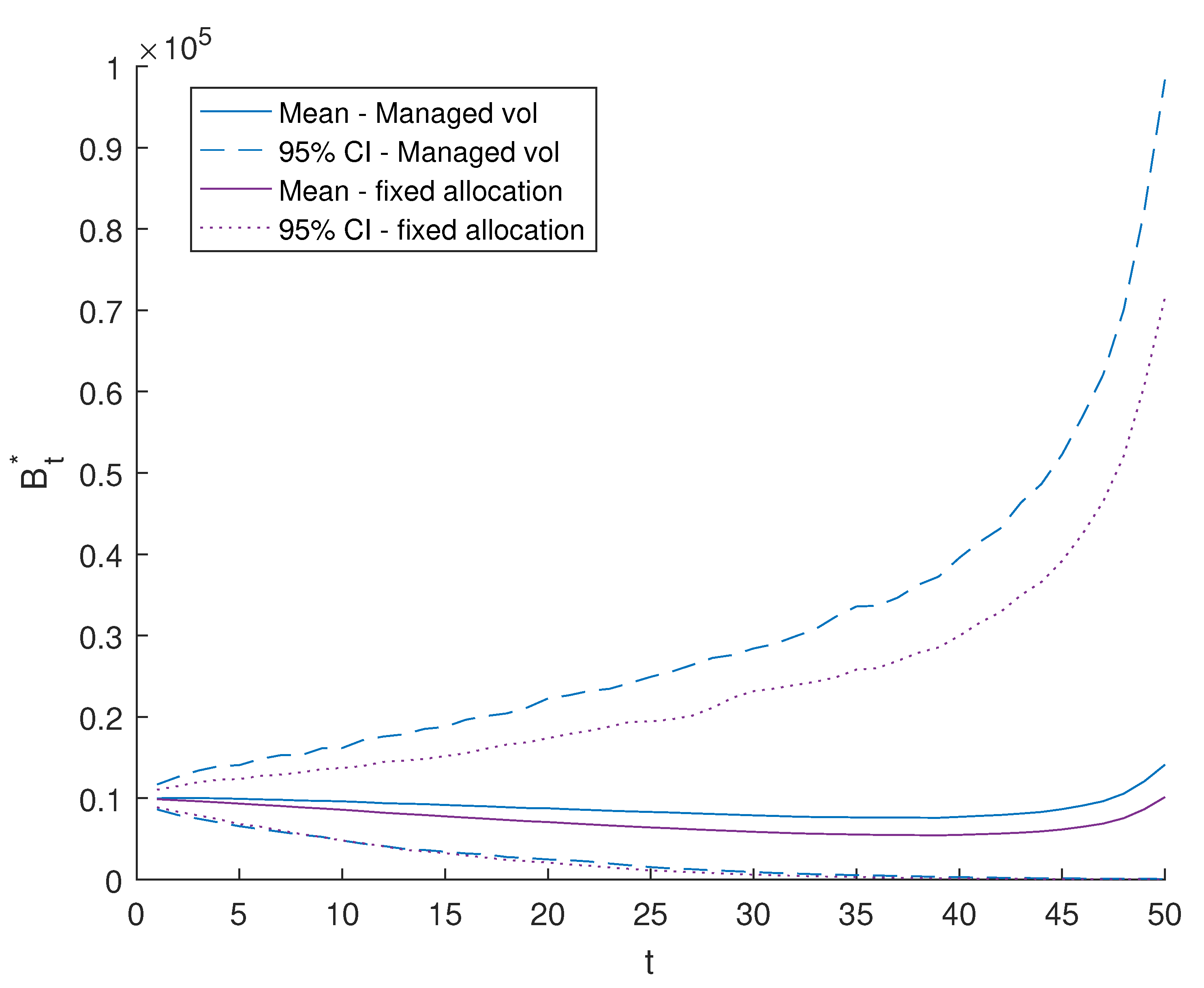


| 0.0345 | 0.0532 | 0.0542 | −0.0580 | 0.0088 | 0.0041 | 0.0000 | 0.0025 |
| Parameter | Value | Std Error | t-Statistic |
|---|---|---|---|
| a | 0.0028 | 0.0030 | 0.9436 |
| b | 0.9627 | 0.0390 | 24.6907 |
| 9.3195 |
| Annuity Payment | Mean | 2.5% | 25% | 50% | 75% | 97.5% |
|---|---|---|---|---|---|---|
| Age 80 | ||||||
| Managed-Volatility | 17,076 | 1979 | 6833 | 11,946 | 21,308 | 64,504 |
| Fixed Allocation | 12,741 | 1284 | 4472 | 8537 | 15,775 | 50,797 |
| Age 90 | ||||||
| Managed-Volatility | 21,732 | 790 | 4472 | 10,247 | 24,330 | 113,346 |
| Fixed Allocation | 15,574 | 364 | 2416 | 6149 | 15,849 | 85,344 |
| PV Annuity Payments | Mean | 2.5% | 25% | 50% | 75% | 97.5% |
|---|---|---|---|---|---|---|
| Nominal | ||||||
| Managed-Volatility | 362,034 | 122,504 | 204,108 | 278,783 | 411,766 | 1,118,248 |
| Fixed Allocation | 295,151 | 111,769 | 170,489 | 229,722 | 324,410 | 889,271 |
| Real | ||||||
| Managed-Volatility | 213,224 | 93,966 | 141,926 | 181,039 | 243,751 | 515,499 |
| Fixed Allocation | 180,308 | 89,340 | 124,175 | 155,512 | 199,716 | 426,634 |
| Nominal | ||||||
|---|---|---|---|---|---|---|
| Break Even Year | Mean | 2.5% | 25% | 50% | 75% | 97.5% |
| Managed-Volatility | 15 | NA | 19 | 16 | 14 | 11 |
| Fixed Allocation | 17 | NA | 21 | 17 | 15 | 12 |
| t | 1 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Managed-Volatility | 0.053 | 0.147 | 0.262 | 0.400 | 0.580 | 0.812 | 1.108 | 1.506 | 2.098 | 3.013 | 5.406 |
| Fixed Allocation | 0.077 | 0.198 | 0.307 | 0.432 | 0.587 | 0.784 | 1.005 | 1.289 | 1.704 | 2.349 | 4.160 |
| t | 1 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Managed-Volatility | 0.036 | 0.096 | 0.168 | 0.241 | 0.319 | 0.397 | 0.474 | 0.549 | 0.622 | 0.693 | 0.775 |
| Fixed Allocation | 0.052 | 0.128 | 0.194 | 0.256 | 0.322 | 0.387 | 0.450 | 0.516 | 0.582 | 0.650 | 0.736 |
| Age 80 | Age 90 | |||||
|---|---|---|---|---|---|---|
| Annuity Payment | Mean | 2.5% | 97.5% | Mean | 2.5% | 97.5% |
| All 3-mth FI | 4649 | 164 | 24,175 | 5571 | 15 | 34,202 |
| All 10-year FI | 5882 | 239 | 29,299 | 7340 | 26 | 44,811 |
| 80/20 10-year FI/Equity | 9045 | 638 | 37,899 | 10,885 | 121 | 62,853 |
| Annuity Payment | Age 80 | Age 90 | |||||
|---|---|---|---|---|---|---|---|
| FI/Equity | Asset Allocation | Mean | 2.5% | 97.5% | Mean | 2.5% | 97.5% |
| 80%/20% | Managed-Volatility | 10,596 | 894 | 42,687 | 12,806 | 199 | 71,993 |
| Fixed Allocation | 9045 | 638 | 37,899 | 10,885 | 121 | 62,853 | |
| 65%/35% | Managed-Volatility | 17,076 | 1979 | 64,504 | 21,732 | 790 | 113,346 |
| Fixed Allocation | 12,741 | 1284 | 50,797 | 15,574 | 364 | 85,344 | |
| 50%/50% | Managed-Volatility | 28,266 | 3822 | 100,717 | 40,403 | 2692 | 176,100 |
| Fixed Allocation | 18,244 | 2272 | 66,516 | 23,501 | 1044 | 120,537 | |
| PV Annuity Payments | Nominal | Real | |||||
|---|---|---|---|---|---|---|---|
| FI/Equity | Asset Allocation | Mean | 2.5% | 97.5% | Mean | 2.5% | 97.5% |
| 80%/20% | Managed-volatility | 264,253 | 104,840 | 774,528 | 165,073 | 85,286 | 376,239 |
| Fixed Allocation | 239,543 | 100,366 | 682,581 | 152,110 | 82,250 | 336,479 | |
| 65%/35% | Managed-volatility | 362,034 | 122,504 | 1,118,248 | 213,224 | 93,966 | 515,499 |
| Fixed Allocation | 295,151 | 111,769 | 889,271 | 180,308 | 89,340 | 426,634 | |
| 50%/50% | Managed-volatility | 535,537 | 149,816 | 1,647,287 | 292,319 | 105,250 | 748,161 |
| Fixed Allocation | 377,269 | 128,044 | 1,161,115 | 219,743 | 96,991 | 535,033 | |
| Break Even Year | Nominal | |||
|---|---|---|---|---|
| FI/Equity | Asset Allocation | Mean | 2.5% | 97.5% |
| 80%/20% | Managed-Volatility | 18 | NA | 13 |
| Fixed Allocation | 19 | NA | 14 | |
| 65%/35% | Managed-Volatility | 15 | NA | 11 |
| Fixed Allocation | 17 | NA | 12 | |
| 50%/50% | Managed-Volatility | 14 | 31 | 9 |
| Fixed Allocation | 15 | 41 | 11 | |
| Age 80 | Age 90 | |||||
|---|---|---|---|---|---|---|
| Mean | 2.5% | 97.5% | Mean | 2.5% | 97.5% | |
| Fixed Allocation | 12,741 | 1284 | 50,797 | 15,574 | 364 | 85,344 |
| 1 historical vol | 13,633 | 1415 | 53,270 | 16,798 | 422 | 91,590 |
| 1.25 historical vol | 17,076 | 1979 | 64,504 | 21,732 | 790 | 113,346 |
| 1.5 historical vol | 21,520 | 2733 | 77,124 | 28,697 | 1441 | 138,148 |
| Nominal | Real | |||||
|---|---|---|---|---|---|---|
| Mean | 2.5% | 97.5% | Mean | 2.5% | 97.5% | |
| Fixed Allocation | 295,151 | 111,769 | 889,271 | 180,308 | 89,340 | 426,634 |
| 1 historical vol | 310,310 | 113,091 | 945,729 | 188,229 | 89,956 | 447,627 |
| 1.25 historical vol | 362,034 | 122,504 | 1,118,248 | 213,224 | 93,966 | 515,499 |
| 1.5 historical vol | 429,562 | 133,505 | 1,319,962 | 244,708 | 98,498 | 604,932 |
| Nominal | |||
|---|---|---|---|
| Mean | 2.5% | 97.5% | |
| Fixed Allocation | 17 | NA | 12 |
| 1 historical vol | 16 | NA | 12 |
| 1.25 historical vol | 15 | NA | 11 |
| 1.5 historical vol | 15 | 36 | 10 |
| Nominal | Real | |||||
|---|---|---|---|---|---|---|
| Mean | 2.5% | 97.5% | Mean | 2.5% | 97.5% | |
| Fixed Target Vol | 362,034 | 122,504 | 1,118,248 | 213,224 | 93,966 | 515,499 |
| Trend Down Vol | 358,390 | 122,142 | 1,101,347 | 212,132 | 93,835 | 511,014 |
| Step Down Vol | 355,997 | 121,905 | 1,090,013 | 211,391 | 93,731 | 507,902 |
| Nominal | |||
|---|---|---|---|
| Mean | 2.5%-Tile | 97.5%-Tile | |
| Fixed Target Vol | 15 | NA | 11 |
| Trend Down Vol | 15 | NA | 11 |
| Step Down Vol | 15 | NA | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Labit Hardy, H.; Sherris, M.; Villegas, A.M. A Managed Volatility Investment Strategy for Pooled Annuity Products. Risks 2022, 10, 121. https://doi.org/10.3390/risks10060121
Li S, Labit Hardy H, Sherris M, Villegas AM. A Managed Volatility Investment Strategy for Pooled Annuity Products. Risks. 2022; 10(6):121. https://doi.org/10.3390/risks10060121
Chicago/Turabian StyleLi, Shuanglan, Héloïse Labit Hardy, Michael Sherris, and Andrés M. Villegas. 2022. "A Managed Volatility Investment Strategy for Pooled Annuity Products" Risks 10, no. 6: 121. https://doi.org/10.3390/risks10060121
APA StyleLi, S., Labit Hardy, H., Sherris, M., & Villegas, A. M. (2022). A Managed Volatility Investment Strategy for Pooled Annuity Products. Risks, 10(6), 121. https://doi.org/10.3390/risks10060121






