Analyzing How the Social Security Reserve Fund in Spain Affects the Sustainability of the Pension System

Abstract

Faced with the need to adjust public pension systems to meet changing demographic, economic and social conditions, most developed countries have created government reserve funds to ensure macroeconomic sustainability. This paper aims to study the importance that this reserve fund plays in the sustainability of the Spanish public pension system. Using data for the 2000 to 2019 period (20 observations) on the main variables impacting on the system, we calculate probabilities and other indicators of its unsustainability in relation to the reserve fund. Our model accurately reflects certain aspects of the data, and suggests that the probability of unsustainability is inversely associated with the size of the reserve fund, but that this relation is moderated by the heterogeneity of the members of the pension system. Moreover, the probability of unsustainability increases in line with the pension system deficit, the time elapsed until unsustainability is reached is shorter when the Reserve Fund balance falls, and the size of this fund at which the system becomes unsustainable diminishes with the probability of unsustainability.

1. Introduction

In response to changing demographic, economic and social conditions, most developed countries have reformed their public pension systems, seeking to maintain a decent standard of living for rising numbers of elderly citizens without imposing an excessive burden on public finances. More recently still, many countries have made unprecedented fiscal interventions to address the impact of the COVID-19 pandemic. These increased commitments strain governments’ fiscal capacity and may motivate further pension reforms in the future.

As well as introducing new pension formulas, adjusting traditional pay-as-you-go (PAYG) schemes and developing funded schemes with enhanced microeconomic features, some countries have set up government-backed reserve funds to ensure the macroeconomic sustainability of their pension systems. According to the latest annual OECD survey of public pension reserve funds, 23 countries have established reserves that are specifically designed to support PAYG public pension systems (OECD 2019).

Public pension reserve funds are classified as sovereign wealth funds by the IMF (2007). Like any trust fund, they accumulate resources that can potentially be freed up at any time, but are always subject to political intervention (Wang and Bohn 2019). These reserve funds contribute to pension sustainability by relaxing liquidity tensions, and thus constitute an element of protection for taxpayers, pensioners and society in general.

In this respect, Yermo (2008) examined the governance of public pension reserve funds and related investment issues, while Chen et al. (2017) reviewed important aspects of asset allocation. In another study, Holzmann et al. (2012) argued that public pension reserve funds cannot provide an absolute guarantee against intense economic risks, much less against demographic risks of a certain magnitude and duration. In this respect, too, Fall and Ferrari (2010) analysed the impact of demographic factors on pension systems, considering the role that should be played by a public pension reserve fund and the adjustments that might be needed to balance its accounts. Assuming a return on reserves in line with the average long-term return on bonds, these authors showed that the French pension reserve fund was able to optimise its returns for a given level of risk.

Viewing the Spanish system as a relevant example of the above issues, our paper assesses the sustainability of public pensions systems by applying probabilistic analysis to the situation of the Spanish Social Security Reserve Fund (henceforth, Reserve Fund). We are well aware that other statistical models may also be used for this purpose, but as (Hicks 1981, p. 232) argued, models are rays of light, illuminating a part of a whole, leaving the rest in darkness. Therefore, we consider it useful to employ various statistical models for this kind of analysis, to compare the results obtained and conclusions drawn and thus gain further insights.

This approach is especially valuable with respect to Spain, where the issues we address generate significant media coverage and public discussion. Our findings show that the approach adopted accurately reflects the situation reflected in the data.

The rest of this paper is organised as follows. Section 2 presents the key features of the Spanish pensions system and its Reserve Fund, and describes the data selected for analysis. Section 3 then offers a selective review of previous research conducted in this field. Section 4 describes the basic statistical model used and proposes some extensions. Section 5 empirically assesses the performance of the proposed model. Finally, Section 6 summarises the findings obtained and offers some concluding remarks. Details of additional analyses are given in the Appendix A and Appendix B.

2. The Spanish Public Pensions System and the Social Security Reserve Fund

The Spanish Social Security system is a complex structure, incorporating not only contributory pensions (retirement, permanent disability and survivors’ pensions), but also unemployment benefits and other contingencies (such as maternity allowances and temporal disability payments). In this paper, we focus on contributory pensions, because non-contributory ones are managed by the Autonomous Communities (self-governing regions) and are financed through general taxation, not from Social Security contributions.

The Reserve Fund is a sovereign investment fund that was set up in 2000 to meet the future needs of the Social Security system, with a special emphasis on its role as a corrector of budgetary and liquidity imbalances.

Following inter-party discussions and the political agreement known as the Toledo Pact, the Reserve Fund was established to stabilise and support the public pensions system, to avert possible imbalances between receipts and payments and thus ensure its ability to meet future needs, for both contributory and non-contributory benefits.

Table 1. Pension data in Spain.

Year (t)	Number of Contributors $\left(\mathit{N}\right(\mathit{t}\left)\right)$	Contributions $\left(\mathit{D}\right(\mathit{t}\left)\right)$	Reserve Fund $\left(\mathit{R}\right(\mathit{t}\left)\right)$	Total Annual Payment $\left(\mathit{X}\right(\mathit{t}\left)\right)$
2000	15,063	60,539.03	604	49,829
2001	15,650	63,466.69	2433	51,060
2002	16,126	65,132.58	6169	51,635
2003	16,614	67,624.07	12,025	53,077
2004	17,082	69,744.38	19,330	54,356
2005	17,835	72,177.67	27,185	55,930
2006	18,596	75,334.90	35,879	57,940
2007	19,152	78,846.55	45,716	59,585
2008	19,006	80,723.89	57,223	63,129
2009	17,917	79,447.23	60,022	67,158
2010	17,582	78,538.38	64,375	70,449
2011	17,326	78,420.62	66,815	73,891
2012	16,739	75,341.94	63,008	77,254
2013	16,228	72,926.41	53,744	80,710
2014	16,492	73,823.12	41,634	83,498
2015	17,017	74,438.01	32,481	85,503
2016	17,518	76,461.03	15,020	87,811
2017	18,127	79,485.10	8095	89,242
2018	18,701	82,836.57	5043	91,615
2019	19,189	88,057.37	2153	95,719

Notes: Number of contributors in thousands. Contributions, Reserve Fund and total annual payment in millions of euros at constant. 2000 prices using GDP deflator. Source: Number of contributors: Afiliación de trabajadores a la Seguridad Social (Boletin de Estadísticas Laborales). Contributions: Cuentas y Balances del Sistema de la Seguridad Social. Reserve fund: Fondo de Reserva de la Seguridad Social. 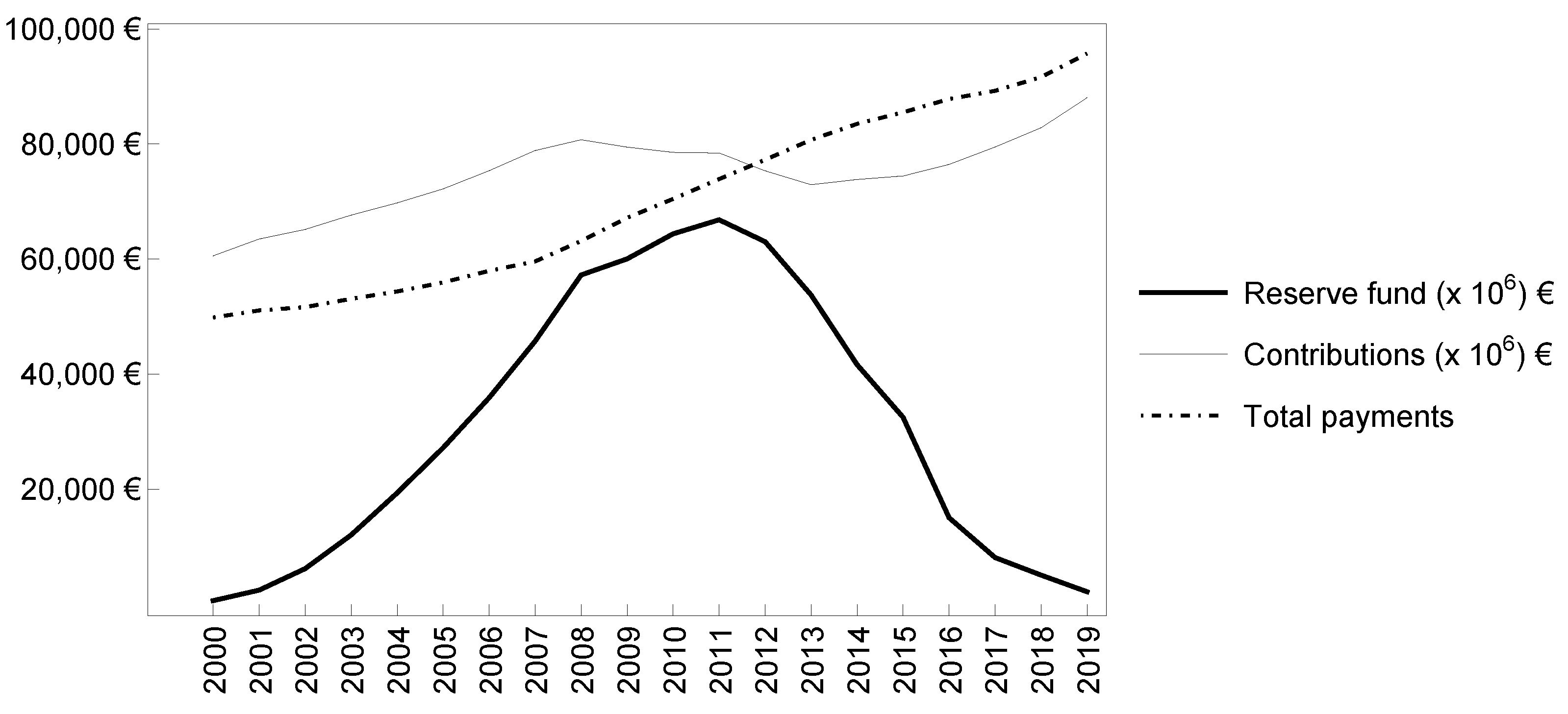Informe a las Cortes Generales.

shows the key data for the public pensions system in Spain from 2000 to 2019, with annual data for registered workers affiliated to the Social Security system ($N\left(t\right)$ where t is the time period), revenues from social security contributions ($D\left(t\right)$), the balance of the Reserve Fund ($R\left(t\right)$) and the total annual payment of (earnings-related) contributory pensions over the period 2000–2019 ($X\left(t\right)$).1 Adjustment is made for inflation by the GDP Implicit Price Deflator, to express the monetary variables in constant euros of 2000.

In 2001, the ratio between the number of social security affiliates and the number of pensioners receiving contributory and/or non-contributory pensions was 1.92 while in 2018 it was 1.75. In other words, in 2018 for every 1.75 contributors there was one pension system beneficiary (contributory and/or non-contributory). In view of the current Social Security deficit of over 18 billion euros per year, with a ratio of 1.75, the trend towards parity is worrying.

Figure 1 shows the evolution of total Social Security receipts and payments during the period 2001–2019. The abrupt inversion between these curves is inconsistent with a healthy economic system.

3. Literature Review

Analysis of the public pensions system in Spain has been undertaken from various directions. One such was taken by Bandrés-Moliné (2019), who reviewed the evolution of public accounts in this field, with special attention to benefit payments and the State aid that has been required to address the problems arising from contribution deficits. In a related analysis, García-Díaz (2019) examined the system’s current problems and prospects.

Moreover, since the seminal paper by Herce and Pérez-Díaz (1995), several papers have focused on system reform. In this respect, Bonin et al. (2001) evaluated the inter-generational impact produced by the 1997 Pensions Reform Act, using a Generational Accounting framework, and De la Fuente and Doménech (2013) considered the effects of the 2011 reform by analysing the determinant factors of spending on contributory pensions. In this respect, too, Díaz-Gimenez and J. Díaz-Saavedra (2017) applied an overlapping generations model with endogenous retirement in their analysis of the 2011 and 2013 reforms. Subsequently, Solé et al. (2019) employed a microsimulation behavioural model to assess the sustainability and adequacy of the Spanish pension system following the 2013 reform.

In a third approach, future scenarios have been mapped out and accounted for. For example, Herce (2003) examined the advantages of using ad hoc models for a better understanding of the fine structure of pensions programmes and formulae, while Hernández de Cos et al. (2017) analysed the recent evolution of the pensions system and predicted the impact of the latest reforms.

Fourthly, Roch-Casellas et al. (2017) assessed methodological aspects of the “sustainability factor” (i.e., linking the amount of new retirement pensions to changes in life expectancy) and the “annual revaluation index” (concerning the evolution of the Social Security balance, for all public pensions) which were introduced under the pension reform of 2013. In this area, too, Solé et al. (2019) used a dynamic, time-based, behavioural microsimulation model to analyse the impact of the same reform on the sustainability and adequacy of the system. These authors concluded that the introduction of these adjustment factors had had strongly negative effects on the adequacy of pensions, but represented a major step towards enhancing sustainability. Nevertheless, they warned that further support for the system would still be needed.

Pastor and Vila (2019) proposed an integrated framework of demographic, macroeconomic and institutional components and used these resources to explore the impact of reform alternatives. The results obtained suggest that reversing the 2011 reform and eliminating the sustainability factor would increase pensions system spending by 3.5 percentage points (p.p.) by 2048.

Finally, there exists a large, well-established body of literature on public debt sustainability, which bears close relation to the subject under study (see Vilariño et al. (2020) for a recent survey on this question with respect to Spain and Pamies and Reut (2020) regarding other European countries). For example, IAE (2019) claimed that the Spanish pension system lacked actuarial equivalence, which deprived the system of its primary source of sustainability. Moreover, it suffered from financial unsustainability in the medium term and actuarial unsustainability in every timeframe considered. Other studies in this area have analysed the effects of population aging on fiscal sustainability (see, for example, Ramos-Herrera and Sosvilla-Rivero 2020).

Turning now to the academic literature on other pension systems, Ka̧sek et al. (2008) examine the efficiency and sustainability of pension systems in the new member states of the European Union and Croatia. European Comission (2016) describes the main policy challenges faced by European pension systems, identifying levers to address these challenges and analysing the policies implemented in Member States. Gannon et al. (2020) develop a general model of Automatic Balance Mechanism based on the intertemporal minimization of a discounted quadratic loss function to analyse the sustainability of US pension schemes. Romp and Beetsma (2020) explore whether the intergenerational risk-sharing benefits that mandatory participation in pension arrangements offer suffice to ensure their survival when participation becomes voluntary. Lenney et al. (2021) explore the fiscal sustainability of US state and local government pension plans by analysing the fiscal cost of stabilizing pension debt as a share of the economy and examining the cost associated with delaying such stabilization into the future.

In this context, the analysis of our paper tries to shed more light on this little-explored and still open debate in the literature through the use of a probabilistic analysis for the Spanish case that allows us to unravel underlying trends that decisively influence the sustainability of the system. As (Granger 1990, chp. 1) claims “it is probably an advantage to have different groups looking at the same problem from different viewpoints so that their conclusions can be compared and possibly then form the basis for a new comprehensive model”. In this sense, we consider that our contribution can help to capture substantively relevant aspects that have been neglected in previous empirical modelling exercises.

4. An Alternative Statistical Model for Evaluating the Sustainability of the Pension System

This section describes the basic model (with some extensions) used to study the sustainability of the pension system. Like any economic model, ours is a simplified framework designed to illustrate complex processes. In this case, our main aim is to reflect and explain certain features of the Spanish public pensions system that have not been fully explored in previous research. For the sake of clarity, our model omits some factors that might also have been included, such as changes in system parameters (the substitutability rate, demographic factors, the evolution of employment, the generosity of the system, etc. See De la Fuente and Doménech (2013)).

In this analysis, we contemplate the system inputs(receipts in the form of workers’ contributions) and outgoings (the payments made to pensioners), and the Reserve Fund balance at the beginning of the year, from the standpoint of a Cramér-Lundberg process.

Let $R\left(t\right)$ be the reserves available at time $t\ge 0$ given by

$$\begin{array}{c}\hfill R\left(t\right)=R\left(0\right)+D\left(t\right)-X\left(t\right),\end{array}$$

where $R\left(0\right)$ is the initial Reserve Fund balance, a quantity which is known and nonnegative, $D\left(t\right)$ is the total system revenue in a given period and $X\left(t\right)$ is the total payment made to pensioners. We assume $D\left(t\right)=pt$, where p represents the total Social Security contributions made by workers.2

In the following subsection, we define the statistical model for $X\left(t\right)$.

4.1. A Statistical Model for the Total Payments Made from the Pensions System

The system by which the Spanish Social Security system obtains receipts and makes payments can be addressed by reference to the ruin theory, which is widely used in actuarial statistics (see for example Feller 1971; Rolski et al. 1999; Asmussen 2000). Since the applications of ruin probability are not restricted to the insurance setting, we can make use of classical risk process theory to consider the problems highlighted in our introduction.

Assume that the Reserve Fund balance at time $t\ge 0$ is determined by the following quantities: $\left(i\right)$ The initial reserve at time 0; $\left(ii\right)$ The receipts obtained up to time $t\ge 0$; $\left(iii\right)$ The payments made to pensioners up to time $t\ge 0$. Observe that only the third of these variables is random, and so we start by describing this process, denoted by ${\left\{X\left(t\right)\right\}}_{t\ge 0}$.

This process is written as:

$$\begin{array}{c}\hfill X\left(t\right)=\sum _{j=1}^{N\left(t\right)}{Y}_j,\end{array}$$

and it should be interpreted as the payments made from the Social Security System in the interval $(0,t]$, with the understanding that $X\left(t\right)=0$ if $N\left(t\right)=0$ and where $\left\{N\left(t\right),t>0\right\}$ denotes the number of pensioners in the time interval $(0,t]$, a counting process. $Y_j$ denotes the amount paid to the jth pensioner.

For our purposes, certain assumptions must be made. First: $\left(i\right)$$N\left(0\right)=0$; $\left(ii\right)$, $N\left(t\right)\in \mathbb{N}$; and $\left(iii\right)$$N\left(t\right)\le N(t+h)$. In this case, $N(t+h)-N\left(t\right)$ models the number of counts in the interval $(t,t+h]$.

Second, assume that $\left\{N\right(t),t\ge 0\}$ is a homogeneous Poisson process with intensity $\lambda$, thus $E\left[N\right(t\left)\right]=var\left[N\right(t\left)\right]=\lambda t$ for all $t\ge 0$ and $N\left(t\right)$ and $Y_j$ are two independent processes.

Third, assume that ${\left\{Y_j\right\}}_{j=1}^{\infty }$ is a sequence of independent and identically distributed random variables with a common distribution function $F(·)$ concentrated on $(0,\infty )$, with $F\left(0\right)=0$, mean $\mu <\infty$, variance ${\mu }_2<\infty$ and moment generating function (if any) $M_Y\left(\kappa \right)=\int exp\left(\kappa y\right)dF\left(y\right)$.

Finally, assume that the random variable $N\left(t\right)$ is independent of ${\left\{Y_j\right\}}_{j=1}^{\infty }$.

Under these assumptions, $X\left(t\right)$ is the variable of a compound Poisson process, i.e., $X(t+s)-X\left(t\right)$ over $(0,t]$ has the probability distribution given by

$$\begin{array}{c}\hfill Pr(X\left(t\right)\le x)=exp(-\lambda t)\sum _{j=0}^{\infty }\frac{{\left(\lambda t\right)}^j}{j!}{F}^{j*}\left(x\right),\end{array}$$

where $F^{j*}\left(x\right)$ is the jth convolution of the cumulative distribution function $F\left(x\right)$. That is,

$$\begin{array}{c}\hfill Pr(X\left(t\right)\le x|N\left(t\right)=n)=Pr\left(\sum _{j=1}^n{X}_j\left(t\right)\le x\right)=F^{n*}\left(x\right),\end{array}$$

with the assumption that $F^{0*}\left(x\right)=1$ for $x\ge 0$ and zero otherwise. Thus, the unconditional distribution of $X\left(t\right)$ is given by

$$\begin{array}{c}\hfill Pr(X\left(t\right)\le x)=\sum _{n=1}^{\infty }Pr(N\left(t\right)=n)F^{n*}\left(x\right).\end{array}$$

(1)

It can be shown that

$$\begin{array}{ccc}\hfill E\left[X\right(t\left)\right]& =& \mu E\left[N\right(t\left)\right],\hfill \\ \hfill var\left[X\right(t\left)\right]& =& {\mu }_{2}E\left[N\left(t\right)\right]+{\mu }^{2}var\left[N\left(t\right)\right].\hfill \end{array}$$

In practice, however, it is difficult to derive a closed-form expression for the distribution function given in (1). Therefore, numerical approximations based on the use of the normal and gamma distribution, among others, have been proposed. For example, the use of the normal approximation is straightforward, based on the idea that if the mean and the variance of $X\left(t\right)$ are known, (1) can be approximated by a normal distribution with the same mean and variance, because as the summands increase we would expect the distribution of this sum to tend to a normal distribution (according to the Central Limit Theorem). A disadvantage of this approach is that it is based only on the first two moments of $X\left(t\right)$, and so the approximation cannot capture the skewness of the true distribution. To overcome this problem, an alternative approximation, based on the use of the translated gamma distribution, has been proposed. Other approximations that have been considered are based on Edgeworth expansions and the Gram–Charlier series. Furthermore, if $N\left(t\right)$ has a Poisson, binomial or negative binomial probability function, an exact recursive expression for (1) can be found. This is known as Panjer’s recursion formula (see Panjer 1981; Rolski et al. 1999, chp. 4, among others). When X follows an exponential distribution and N follows a discrete distribution belonging to the exponential family of distributions, there exists a closed-form expression for (1). This, precisely, is the case we consider, in which N follows a Poisson distribution.

4.2. The Basic Model of Sustainability

The surplus at a future time t, $R\left(t\right)$ is unknown and treated as a continuous-time stochastic process.3 We assume that ${\left\{R\left(t\right)\right\}}_{t\ge 0}$ is a compound Poisson process with the Poisson parameter $\lambda >0$, which can be thought of as the expected number of pensioners per time unit and cumulative distribution function $F(·)$ of payments made to pensioners during the time unit with mean $\lambda >0$. In the present study, it is assumed that $p>E\left[N\right(t\left)\right]E\left[Y\right]$. By contrast, if this inequality is violated the system will without doubt be unsustainable. In practice, it is convenient to assume $p=(1+\tau )E\left[N\right(t\left)\right]E\left[Y\right]$, $\tau >-1$.4

T, the time at which the system becomes unsustainable, is defined as the minimum value of $t\ge 0$ at which unsustainability occurs. That is,

$$\begin{array}{c}\hfill T=min\left\{t>0:R\left(t\right)<0\right\}.\end{array}$$

Then, the probability of unsustainability in infinite time is given by

$$\begin{array}{c}\hfill \psi \left(x\right)=Pr\left\{{\cup }_{t\ge 0}\left(R\left(t\right)<0\right):R\left(0\right)=r\right\},\end{array}$$

(2)

which can be used to measure the probability that the capital available to the system responsible for the payment of pensions will fall below zero. This probability is defined in continuous time. We might also define it in a discrete time, but this case is not addressed in the present study.

Assuming the payments have a compound Poisson distribution, the probability of ultimate (2) is governed by the Volterra integral equation given in expression (A1) in the Appendix A.

4.3. Computing Probabilities of Unsustainability

In this subsection we present a specific model based on a distributional assumption which allows us to compute the probabilities given in (2). Assume that $Y_j$ follows an exponential distribution with cdf $F\left(y\right)=1-exp(-\sigma y)$, $\sigma >0$, that the nth-fold convolution of this exponential distribution has a closed form and that it is given by (see Rolski et al. 1999)

$$\begin{array}{c}\hfill f^{*n}\left(y\right)=\frac{{\sigma }^n}{(n-1)!}{y}^{n-1}{e}^{-\sigma y},n=1,2,\cdots \end{array}$$

i.e., it is an Erlang distribution with parameters n integer and $\sigma >0$. Now, the pdf corresponding to (1) is

$$\begin{array}{c}\hfill f\left(y\right)=\sqrt{\frac{\sigma \lambda }{y}}exp(-\lambda -\sigma y)I_1\left(2\sqrt{\lambda \sigma y}\right),y>0,\end{array}$$

(3)

with $f\left(0\right)=exp(-\lambda )$.

Here, $\lambda >0$ and $\sigma >0$ are the parameters of the Poisson and exponential distributions, respectively and $I_c\left(z\right)$ represents the modified Bessel function of the first kind shown in the Appendix B.5

Finally, under these assumptions (2) is an exponential function on r (see, for instance Gerber 1979; Willmot and Lin 2000; Konstantinides 2018) given by

$$\begin{array}{c}\hfill \psi \left(r\right)=\frac{\lambda }{\sigma p}exp\left[-\left(\sigma -\frac{\lambda }{p}\right)r\right].\end{array}$$

(4)

It is important to note that $\psi \left(r\right)$ is a function that depends on the variable r. Here, it is termed the unsustainability function, but in no case is it a probability density function. Observe that if the assumption $p>\lambda \mu$ is violated, then (4) can give values greater than 1. Furthermore, expression (4) increases with respect to parameter $\lambda$ and decreases with respect to r, $\sigma$ and p, which seems logical.

The probability function described in (4), assuming an exponential distribution for the payments made, is the simplest possible. Other models have been proposed in risk theory literature, based on exchanging the exponential distribution for others such as the gamma or the Pareto distributions. However, the expressions obtained for the probability of the function of interest are very complicated, although advances in computer technology now enable the probabilities to be calculated in a reasonable time. Other simple alternatives, considered natural extensions of the exponential distribution, can be found in Gómez-Déniz et al. (2016) and Gómez-Déniz et al. (2019). Thus, the simplest expression that can be derived from the integral Equation (A1) is that given in (4). However, a powerful tool, the Lundberg-de Finetti inequality, allows us to determine an upper bound for the probability given in (2) through $\widehat{\psi }\left(r\right)\le exp(-{\kappa }^{*}r),$ where ${\kappa }^{*}$ is the unique positive solution of the equation (details of this useful result can be found in Rolski et al. 1999; Willmot and Lin 2000; Konstantinides 2018) $\lambda M_Y\left(\kappa \right)-\lambda -p\kappa =0$, where $M_Y(·)$ is the moment generating function of Y.

4.4. Beyond Unsustainability

Let us now consider what happens if unsustainability does occur. That is, our attention is focused, not on the probability of the system becoming unsustainable, but on the amount, z, of the system’s deficit if and when unsustainability occurs. This situation can be formally defined as

$$\begin{array}{c}\hfill {\tilde{\psi }}_z\left(r\right)=Pr(T_r<\infty ,R\left(T_r\right)\ge z),\end{array}$$

that is, the probability of unsustainability and the amount of the system’s deficit at that moment. Observe that in this case, we have ${\tilde{\psi }}_z\left(r\right)\to \psi \left(r\right)$ when $z\to \infty$ and also that

$$\begin{array}{c}\hfill \frac{{\tilde{\psi }}_z\left(r\right)}{\psi \left(r\right)}=Pr\left(\right|R\left(T_r\right)|\le z:T_r<\infty )\end{array}$$

is a genuine cumulative distribution function. It can be shown that for exponential payments (see Kou and Wang 2003; Dickson and Waters 1992, among others) these probabilities are given by

$$\begin{array}{c}\hfill {\tilde{\psi }}_z\left(r\right)=\psi \left(r\right)\left[1-exp(-\sigma z)\right].\end{array}$$

(5)

This last result is related to the exact distribution of the overshoot in the first passage times of the jump diffusion process, due to the memoryless property of the exponential distribution (see Kou and Wang 2003 and references therein for details). Furthermore, note that if the system is unsustainable, i.e., $\psi \left(r\right)=1$, then the distribution of the deficit when unsustainability occurs is exactly the same as the distribution of payments. This property, too, is obviously related to the memoryless property of the exponential distribution.

4.5. Theoretical Extension of the Combination of Private and Public Pension Systems

In the preceding subsection, we explored the effect on the probability function given in (4) of a combination of two pension systems, one public and one private. If we assume that payments to pensioners are carried out independently from the two systems, within a Poisson distribution, we have, from (4)

$$\begin{array}{ccc}\hfill \psi (r_1+r_2)& =& \frac{\lambda }{\sigma p}exp\left[-\left(\sigma -\frac{\lambda }{p}\right)(r_1+r_2)\right]\hfill \\ & =& \frac{\lambda }{\sigma p}exp\left[-\left(\sigma -\frac{\lambda }{p}\right)r_1\right]exp\left[-\left(\sigma -\frac{\lambda }{p}\right)r_2\right]\hfill \\ & <& \psi \left(r_i\right),i=1,2,\hfill \end{array}$$

(6)

where the reserve funds for the public and private systems are denoted by $r_1$ and $r_2$, respectively. The immediate interpretation of (6) is that the unsustainability of the pension system decreases when the two modes, public and private, are considered jointly. In other words, solvency increases, which intuitively seems obvious. This consideration, as well as the effective calculation of the probabilities given in this case, warrant separate study, which might usefully be addressed in future research in this scenario.

5. Assessing the Performance of the Proposed Model

There is a long-standing debate on the intrinsic difficulty of determining the degree of realism of assumptions such as those made in this study. However, there is an implicit consensus that the criteria for evaluating economic models should be associated with their ability to provide accurate predictions. Given our eclectic approach, we follow Friedman (1953)’s recommendation and in this section we empirically assess the performance of the model.

Indeed, Friedman (1953) stresses more than once that science is about explanation, and that models must be judged by their simplicity and fruitfulness in the precision and scope of their predictions and in their ability to generate additional research lines.

5.1. Preliminary Analysis

The data used in this paper are summarised in Table 1 for values of $N\left(t\right)$, $D\left(t\right)$, $R\left(t\right)$ and $X\left(t\right)$, respectively.6

To calculate the theoretical density distribution of $X\left(t\right)$ given by (3), the probabilities of unsustainability using the expression given in (4), the system deficit, the expected time to unsustainability and the size of Reserve Fund required, we must first estimate not only $\lambda$ and $\sigma$, but also $\tau$.

Using the WinRATS econometric package, the following estimated parameters are obtained by maximum likelihood: $\widehat{\lambda }=43.172\left(13.222\right)$, $\widehat{\sigma }=0.00062\left(0.0002\right)$, obtained from (3) (the corresponding standard errors are shown in parentheses).

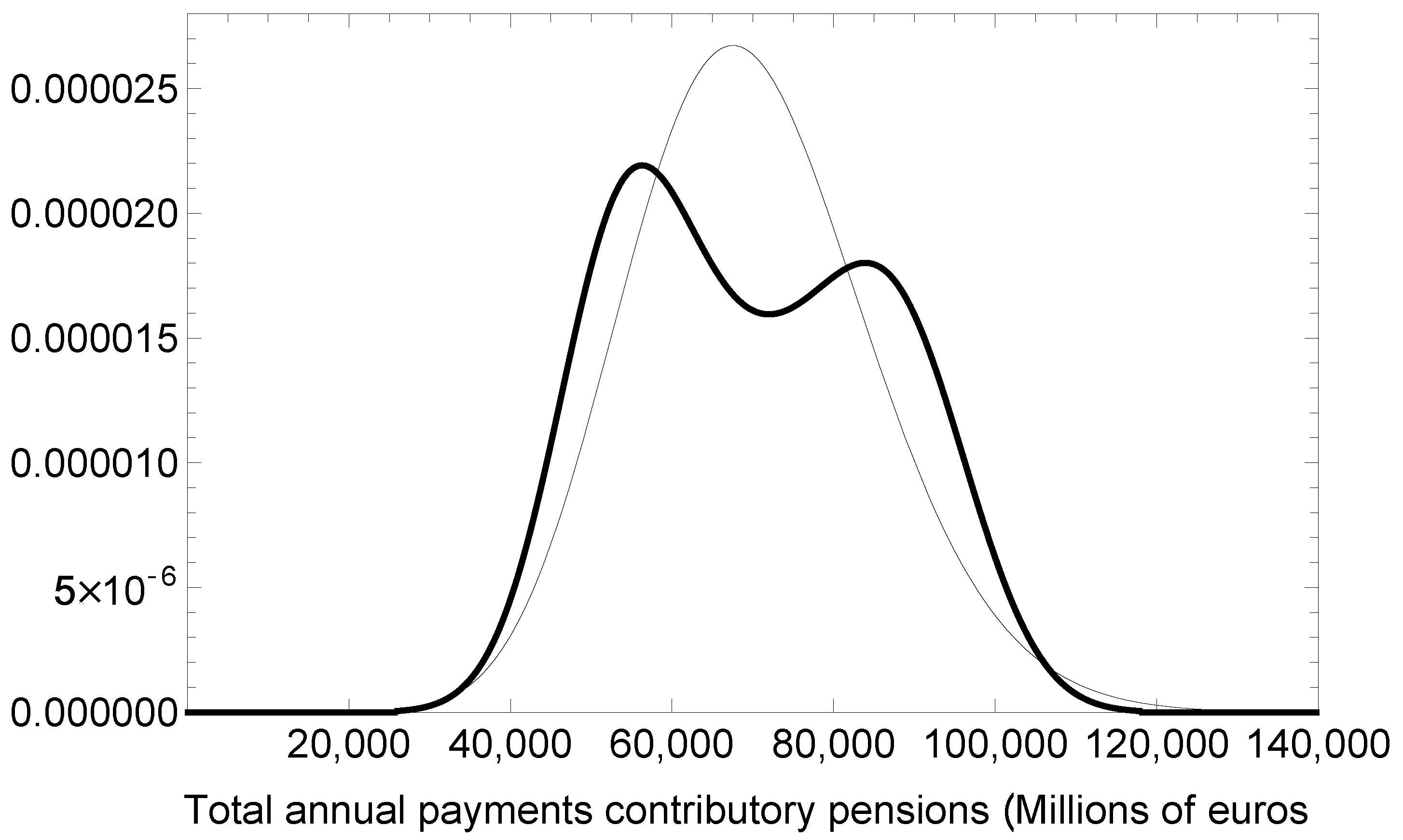
Figure 2 illustrates the empirical and theoretical distributions of the total annual payments, $X\left(t\right)$, which appear to be in reasonable agreement.

We estimate $\tau$ by equating $(1+\tau )E\left[N\right(t\left)\right]E\left(Y\right)$ to the total value of contributions (third column in Table 1).

Table 2. Estimated value of $\tau$ for the different years, t, considered.

Year	$\widehat{\mathit{\tau }}$
2000–2004	≈0
2005	0.031
2006	0.070
2007	0.126
2008	0.123
2009	0.135
2010	0.122
2011	0.121
2012	0.077
2013	0.042
2014	0.055
2015	0.064
2016	0.093
2017	0.136
2018	0.184
2019	0.258

shows the estimated $\tau$, $\widehat{\tau }$, obtained from

$$\begin{array}{c}\hfill \widehat{\tau }=\frac{D\left(t\right)\widehat{\sigma }}{\widehat{\lambda }}-1,\end{array}$$

for all t.

With the above information, we can construct probabilities and other indicators of unsustainability. We now proceed to analyse the probability of unsustainability, the time to unsustainability and the Reserve Fund required given the probability of unsustainability.

5.2. Probability of Unsustainability

In this section, we calculate the probability of unsustainability, distinguishing between that for homogeneous and heterogenous pensioners, and then calculate the probability of unsustainability and deficit.

5.2.1. Probability of Unsustainability with Homogeneous or Heterogeneous Pensioners

This subsection presents the calculated probability of unsustainability, assuming firstly homogeneity of the pensioners considered and then heterogeneity, using mixture models.

With Homogeneous Pensioners

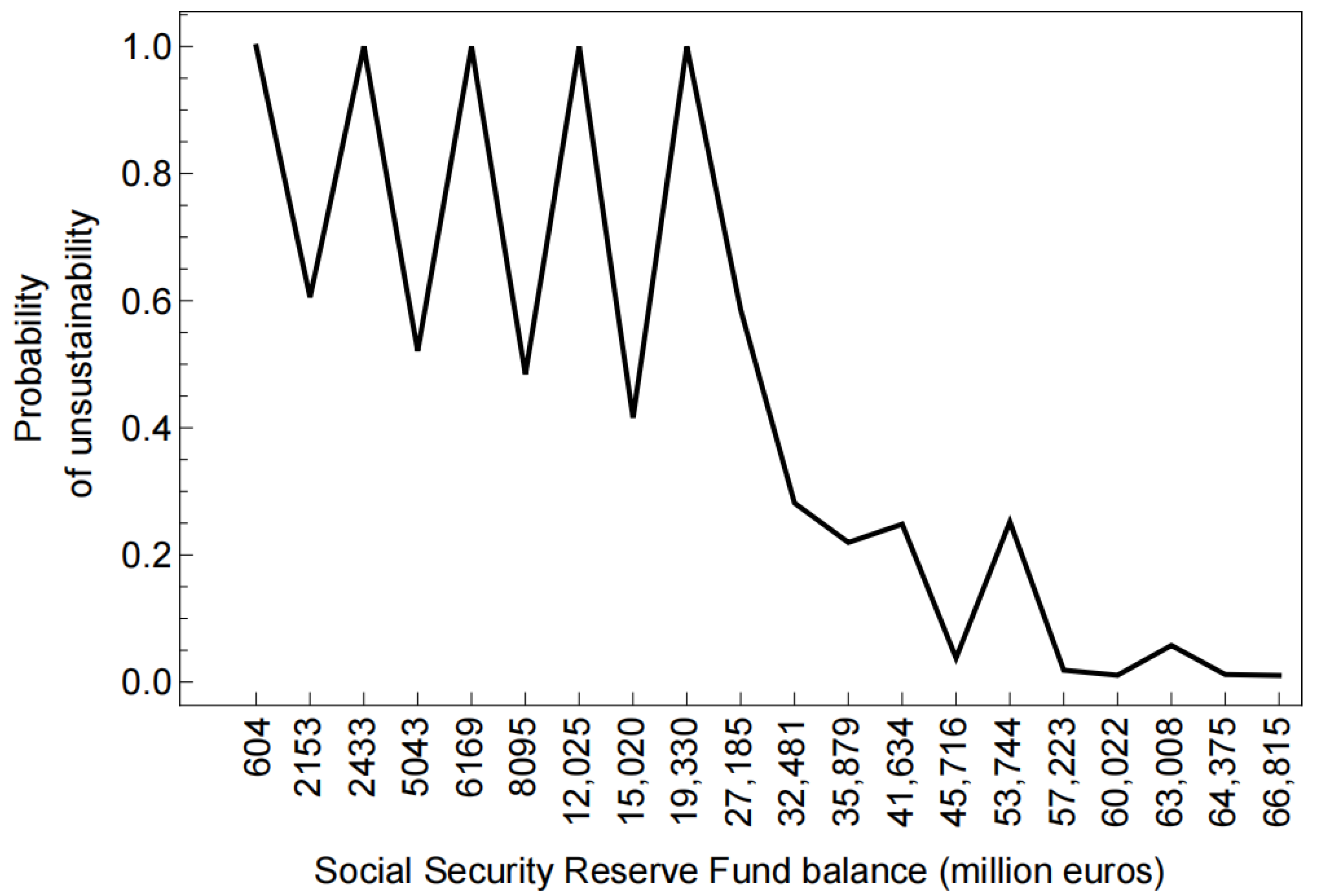
The probabilities of the unsustainability, $\widehat{\psi }\left(r\right)$, of the system, using the expression given in (4), can be obtained from the parameters reported in the Section 2, and are shown in Figure 3.

As can be observed, during the period under study, the estimated probabilities tended to decrease, which is in line with the data shown in Table 1. Indeed, due to the considerable surplus registered in the Social Security System, the Reserve Fund increased during the period from 2001 to 2011. However, the economic crisis of 2008 significantly affected the Social Security accounts and led to a sharp fall in the balance of the Reserve Fund. In other words, our model is capable of reproducing empirical regularities detected in the data, namely that the expected probability of unsustainability was lower when the system was in surplus and higher from 2012 onwards, when the deficit rose. The reduction in probabilities is more apparent when receipts are high. Thus, when the income scenario is very conservative, the probabilities are very high, and it is only when the estimated receipts are higher that $\widehat{\psi }\left(r\right)$ decreases significantly.

These results reflect strong dependence on the estimated system revenue, indicating that the impact on the probability of unsustainability is reduced when receipts are lower.

With Heterogeneous Pensioners

In Spain, Social Security spending on pensions depends on the total number of pensioners and the pension paid per person, among other aspects, while receipts are determined by the number of contributors. The latter quantity, in turn, depends on various factors, some relatively predictable (albeit scarcely controllable), such as demographics, and others less so, such as the performance of the labour market.

In other words, both the value of pension payments (represented by $\sigma$) and the number of pensioners (represented by $\lambda$) may be heterogeneous. Therefore, it would be desirable to consider both parameters as random variables, rather than fixed values. Albrecher et al. (2011) (see also Gómez-Déniz et al. 2019) offered a solution for this situation, in which both parameters or just one might be taken as random. Here, we consider only the case in which $\lambda$ is random and follows a distribution function (mixing distribution) $F\left(\lambda \right)$, $\lambda \in \Lambda$. In this case, the unconditional unsustainability function is given (see Albrecher et al. 2011) by

$$\begin{array}{c}\hfill \psi \left(r\right)={\int }_0^{{\lambda }_0}{\psi }_{\lambda }\left(r\right)d{F}_{\Lambda }\left(\lambda \right)+(1-F_{\Lambda }\left({\lambda }_0\right)),\end{array}$$

where ${\lambda }_0=p/E\left(X_1\right)$. For the special case in which the mixing distribution is gamma with shape parameter $\alpha >0$ and rate parameter $\beta >0$ the unconditional (mixture) unsustainability function is

$$\begin{array}{c}\hfill \psi \left(r\right)=\frac{{\left(p\beta \right)}^{\alpha }exp(-pr)}{\sigma {(p\beta -r)}^{\alpha +1}}\left[\alpha -\frac{\Gamma (1+\alpha ,\sigma (p\beta -r\left)\right)}{\Gamma \left(\alpha \right)}\right]+(1-F_{\Lambda }\left({\lambda }_0\right)).\end{array}$$

Here, $\Gamma (a,x)={\int }_x^{\infty }{\omega }^{a-1}exp(-\omega )d\omega$ is the incomplete gamma function.

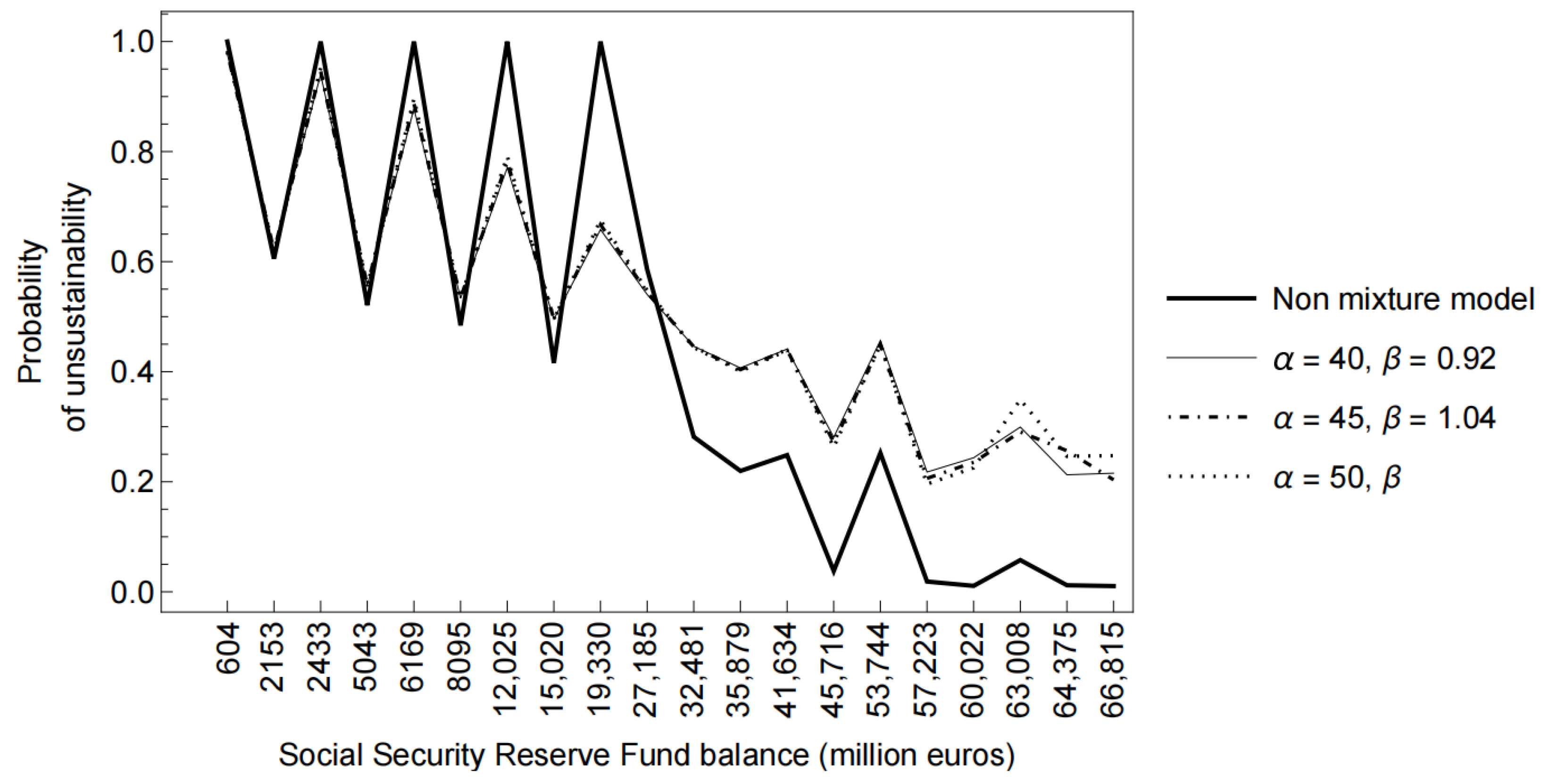
By using the estimated value of $\sigma$ we select $\alpha$ and $\beta$ such that the mean of $\Lambda$, given by $\alpha /\beta$, is equal to the estimated value of $\lambda$ computed previously. Observe that the larger the value of $\beta$, the lower the variance (given by $\alpha /{\beta }^2$) which helps explain the three scenarios considered in the mixture models under study. The corresponding results are shown in Figure 4.

In a comparable way to Figure 3, Figure 4 illustrates the probability of unsustainability by contrasting the non-mixture model with three heterogeneous models with different values of $\alpha$ and $\beta$. As can be seen, the results obtained when the pensioners are assumed to be heterogeneous are again consistent with the data in Table 1. These results indicate a smoothing of the curves and a decreased probability of unsustainability when the Reserve Fund increases. The results obtained by the heterogeneity model, for the three cases analysed, show similar patterns, with convergence to the non-mixture model when $r\to 0$.

5.2.2. Probability of Unsustainability and Deficit

Finally, we analyse the probability of unsustainability and of deficit at a fixed time, ${\tilde{\psi }}_z\left(r\right)$.

Figure 5 shows the value of the system deficit and various scenarios for the estimated value of $\tau$ on the Reserve Fund in 2016, 2017, 2018 and 2019, using the equation given in (5).

These results suggest that, in general, when the deficit increases, so does the probability. Notably, this occurs in all the revenue scenarios considered. However, the probability increase is more pronounced for lower levels of receipts, from which we surmise that when economic activity expands, the probability of unsustainability and deficit is much less than when it contracts.

5.3. Expected Time to Unsustainability

Since time is considered a random variable, we can compute its distribution function (although this is not studied here), the moments and, in particular, the expected time to unsustainability and its variance, assuming that unsustainability will eventually occur. In other words, we now focus on the distribution function $Pr(T_{r,p}\le t)=Pr(T\le t|T<\infty )$.

The expected time to unsustainability and the variance are given (see Dickson 2005, chp. 8) by

$$\begin{array}{ccc}\hfill E\left(T_{r,p}\right)& =& \frac{(1+\tau )+\sigma r}{\lambda \tau (1+\tau )},\hfill \\ \hfill var\left(T_{r,p}\right)& =& \frac{2(1+r\sigma )}{{\lambda }^2{\tau }^3},\hfill \end{array}$$

respectively. Recall that $p=(1+\tau )\lambda /\sigma$. Approximations of these and higher moments can be found in Dickson and Waters (2002). Here, we show that the conditional distribution of the time to unsustainability, given that unsustainability does occur, for the diffusion process $\tilde{R}\left(t\right)=D\left(0\right)+W\left(t\right)$ follows an inverse Gaussian distribution, where $W\left(t\right)$ is approximated by a normal distribution.

Figure 6 displays the expected time to unsustainability. As can be seen, this value increases when the Reserve Fund balance is high. On the contrary, when it is low, so is the expected time to unsustainability. Therefore, our model accurately reproduces certain patterns observed in the data. The highest expected time to unsustainability was around 18 years, which was recorded when the Reserve Fund balance peaked in 2013 as a result of the accumulated surpluses in the Social Security budget. However, the data presented in Table 1 show that unsustainability in fact arrived in 2017, only four years later. Similarly, although in 2017 the model estimated the system would take another three years to become unsustainable, this actually occurred in the same year (the Reserve Fund was 8.095, while the Social Security balance was 9.757). The lowest expected time to unsustainability is around one year, and is associated with the minimum balance of the Social Security Reserve Fund, which reflects drawdowns due to successive deficits in the contributory pension system.

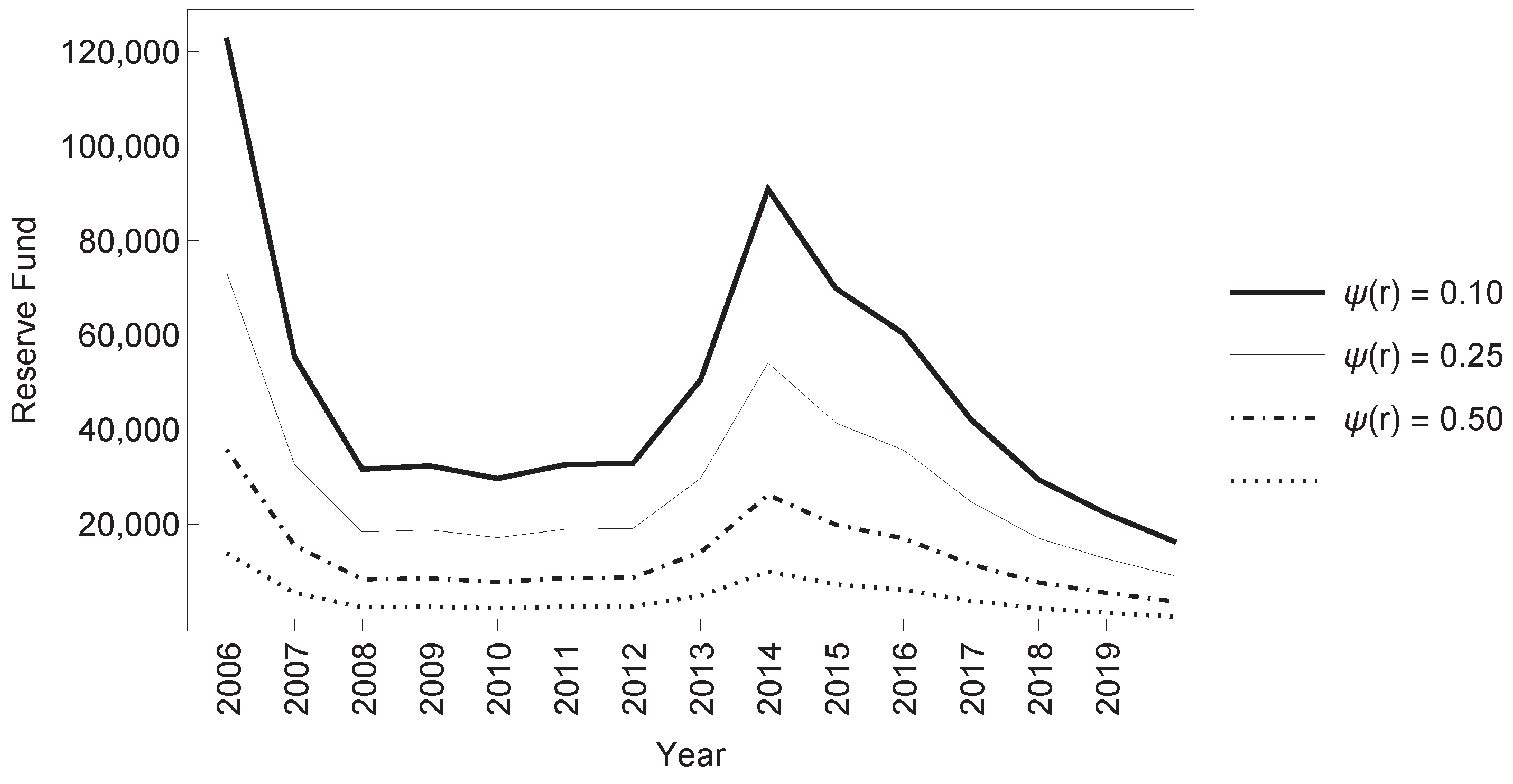
5.4. Size of the Reserve Fund Required for a Given Probability of Unsustainability

Finally, we compute the balance of the Reserve Fund $\tilde{r}$, at which the probability of the system becoming unsustainable, say $\tilde{\psi }$, is less than or equal to a given value. This value can be readily calculated by isolating r from the Equation (4), which gives

$$\begin{array}{c}\hfill \tilde{r}\ge \frac{p}{\lambda -\sigma p}log\left[\frac{\sigma p\tilde{\psi }}{\lambda }\right].\end{array}$$

The results obtained for probability values of 10%, 25%, 50% and 75% are shown in Figure 7.

Thus, the larger the probability value required, the smaller the size of Reserve Fund at which the system becomes unsustainable.

6. Concluding Remarks

With this paper, we contribute to the ongoing debate regarding the sustainability of public pension reserve funds and the impact of schemes to mitigate the demographic transition and to address the problem of sharply rising pension expenditure, focusing on the situation in Spain as a relevant example.

To this end, after examining the evolution of Spain’s Social Security Reserve Fund during the period 2001–2018, we apply the ruin theory that has been developed and widely used in actuarial statistics as a valuable analytical framework for computing the probability of system deficit and unsustainability. We also extend the theory by incorporating a combination of private and public pension systems, as suggested in the literature. In future research, we will explore the empirical implications of this extension to gain further insights into the redesign of the pension system. Another natural extension of the analysis presented in this paper would be to go beyond the static approach and adopt a dynamic modelling approach. This item is also in our future research agenda.

Structural pension reforms, motivated by long-run fiscal sustainability concerns, often come with significant implementation delays (Bi and Zubairy 2020). The future of the pension system is subject to the influence of many factors, including the ratio between the number of affiliated workers and the number of contributory and non-contributory pensioners, the relationship between pensions and wages, the birth rate and life expectancies. We also show that a contraction of economic activity, such as that caused by the COVID-19 pandemic, which reduced both wages and the total number of affiliated workers, decreases receipts to the system and so heightens the risk of deficit and unsustainability.

In this study, given the intrinsic difficulties derived from the complexity of the Spanish Social Security Pension System, we adopt a pragmatic approach, seeking a better understanding of the sustainability of the system and offering an alternative, complementary approximation of its reality. The findings obtained suggest that this approach accurately reflects certain observable facts that complement previous empirical modelling exercises, and may therefore help economists and policymakers understand the inner workings of the system in the current context where European pension systems are facing the dual challenge of remaining financially sustainable and being able to provide Europeans with an adequate income in retirement.

The main findings of this research can be summarised as follows. Firstly, we show that the estimated probability of unsustainability decreased in line with the Reserve Fund during the period 2000–2019. Second, we consider heterogeneity models and obtain smoother curves for the probability of long-term unsustainability, which rose significantly from 2005. Third, the estimated probability of unsustainability increases in line with the deficit. Fourth, the expected time to unsustainability decreases in line with the balance of the Reserve Fund. Finally, the required size of the Reserve Fund decreases in line with the probability of unsustainability.

As in every empirical analysis, the results we present should be taken with caution, since they are based on certain assumptions and on a particular framework of evaluation. Nevertheless, we believe these results form the basis for a tool that will help analysts assess possible reforms to the pension system, highlighting the level of the Reserve Fund as a key element in system sustainability.

Pension reforms require long-term strategies, and our findings can be used to inform the necessary deliberation on the future of the Reserve Fund and its role within the social protection system. The sharp fall in the Reserve Fund balance and the resulting political consequences have resulted in fresh loans being obtained from the State and in a Government commitment to supplement the system’s non-financial income, specifying that the transfers received should be used to ensure a return to budget equilibrium.

Of course, diverting tax revenues to reduce the Social Security deficit may not be the only solution. However, that is another question.