Common Factor Cause-Specific Mortality Model
Abstract
:1. Introduction
2. Methodology
2.1. Cause-of-Death Mortality
2.1.1. Crude Mortality
2.1.2. Net Mortality
2.2. Competing Risk
2.3. Model Estimation
2.4. Forecast
2.5. Old Ages
2.6. Population Dynamics
- : net migration for males and females (g) for age x (from 0 to 99 years old) in year t. We assume migration for ages 100 to 120 to be zero;
- : total life births for males and females (g) in year t;
- : the total crude mortality intensity for Dutch males and females (g) aged x in year t. This variable is obtained through Equation (3). We assumed mortality for individuals older than 120 in year t to equal that of a 120-year-old.
- : the exposure for males and females on the first day of 2016, aged x (from 0 to 99 years old). We assume the first period exposure for ages above 99 to equal zero.
3. Data
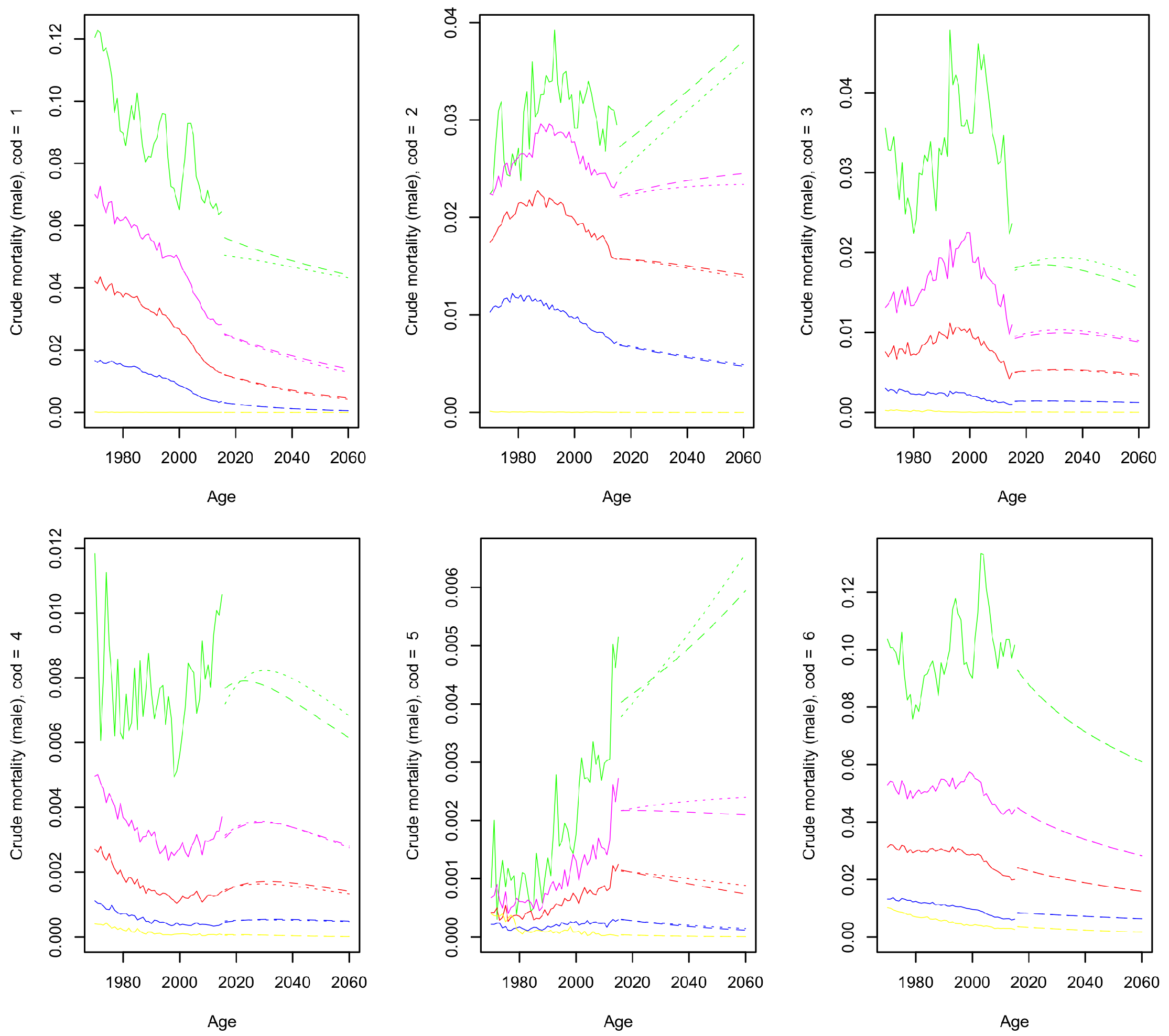
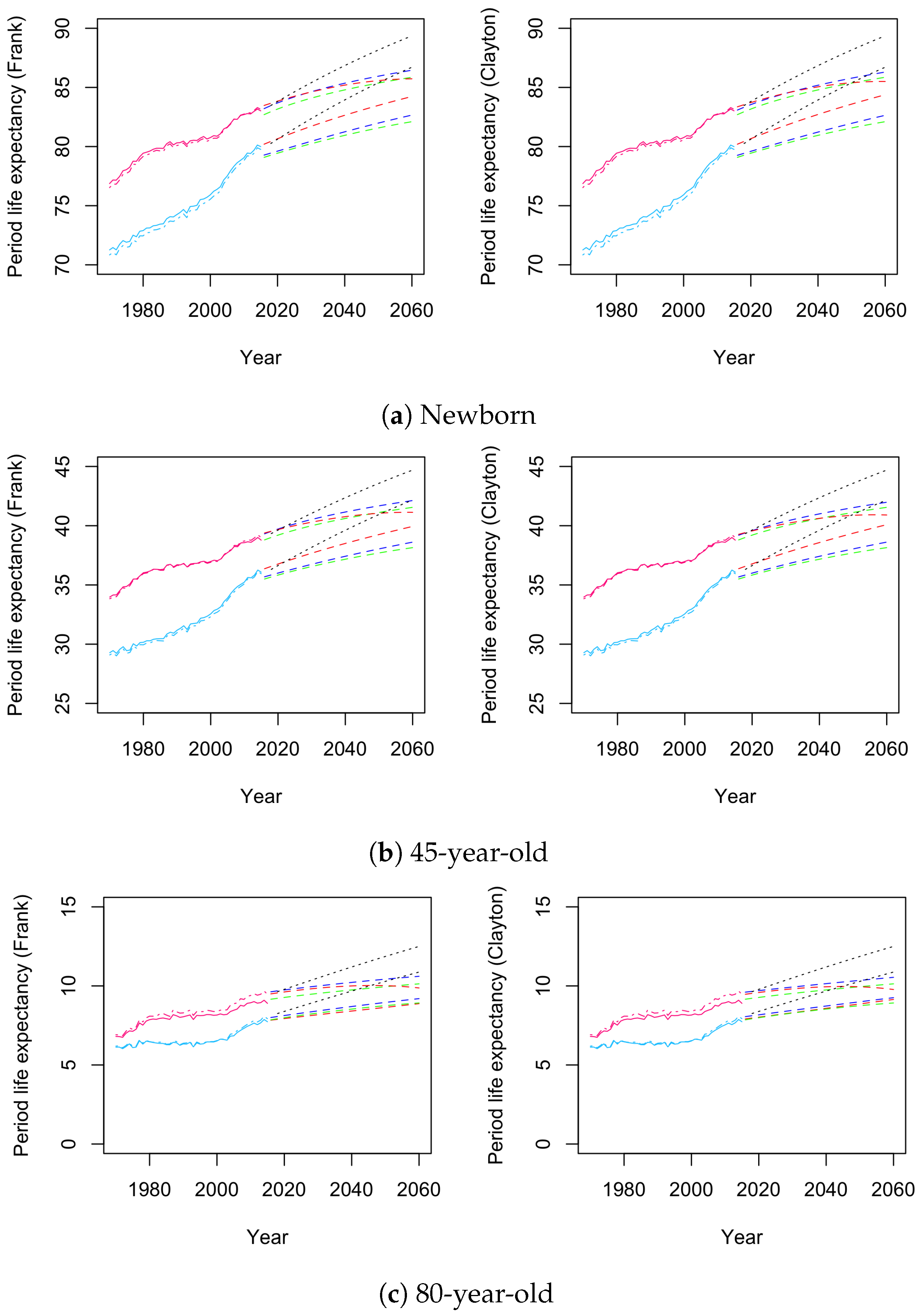
4. Numerical Results
4.1. Estimation
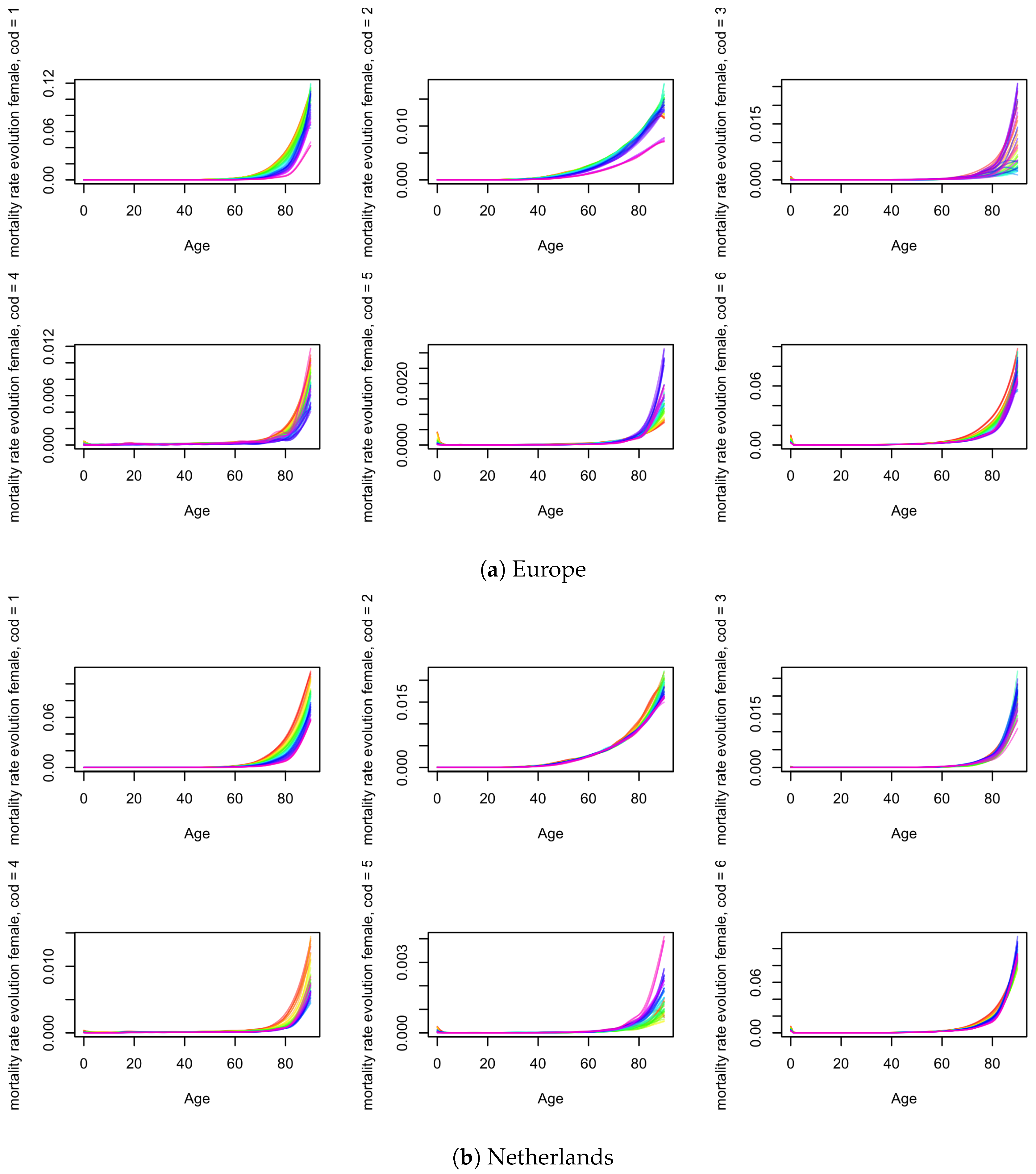
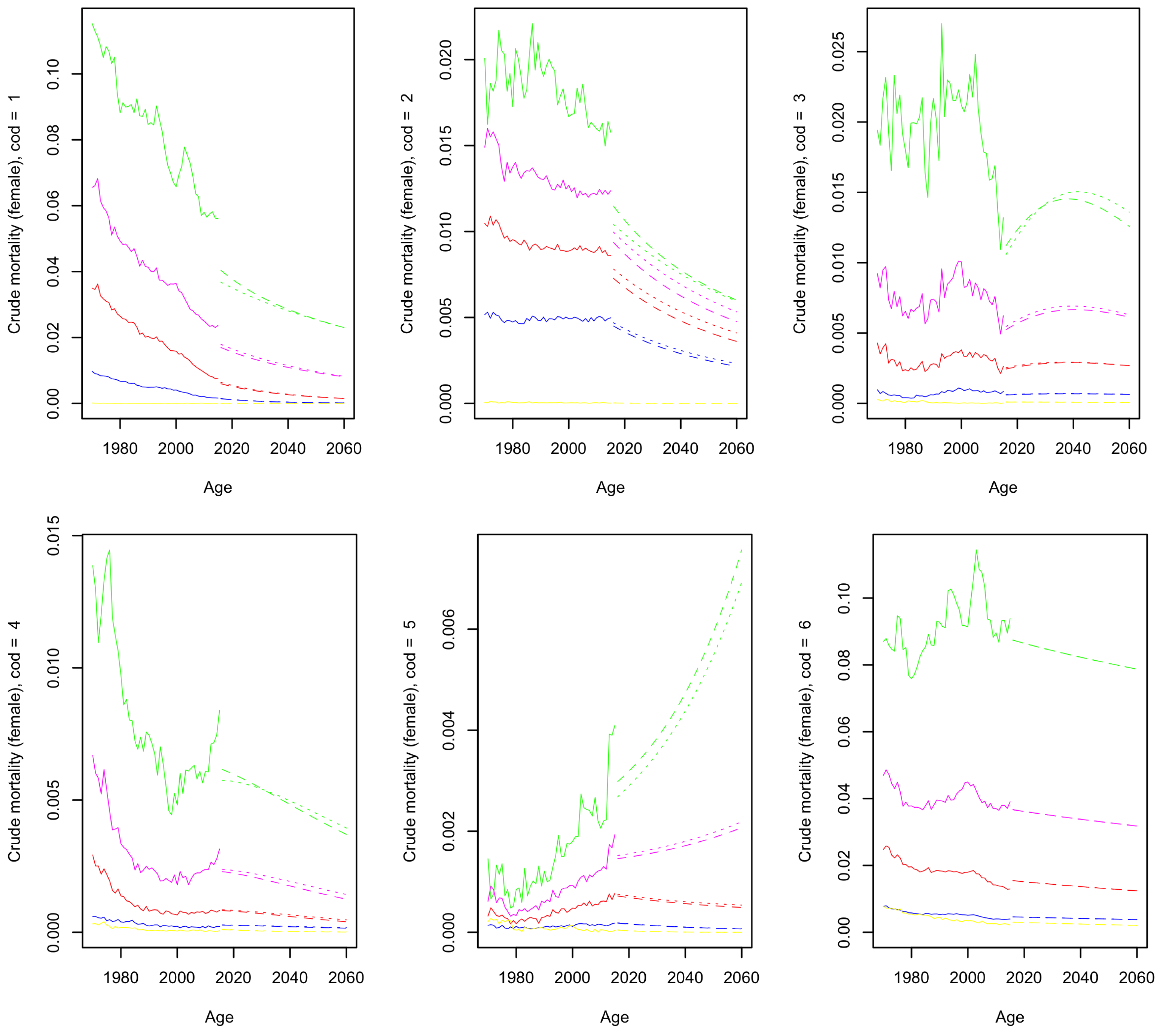
4.1.1. Crude Mortality
4.1.2. Net Mortality
4.2. Forecast Results
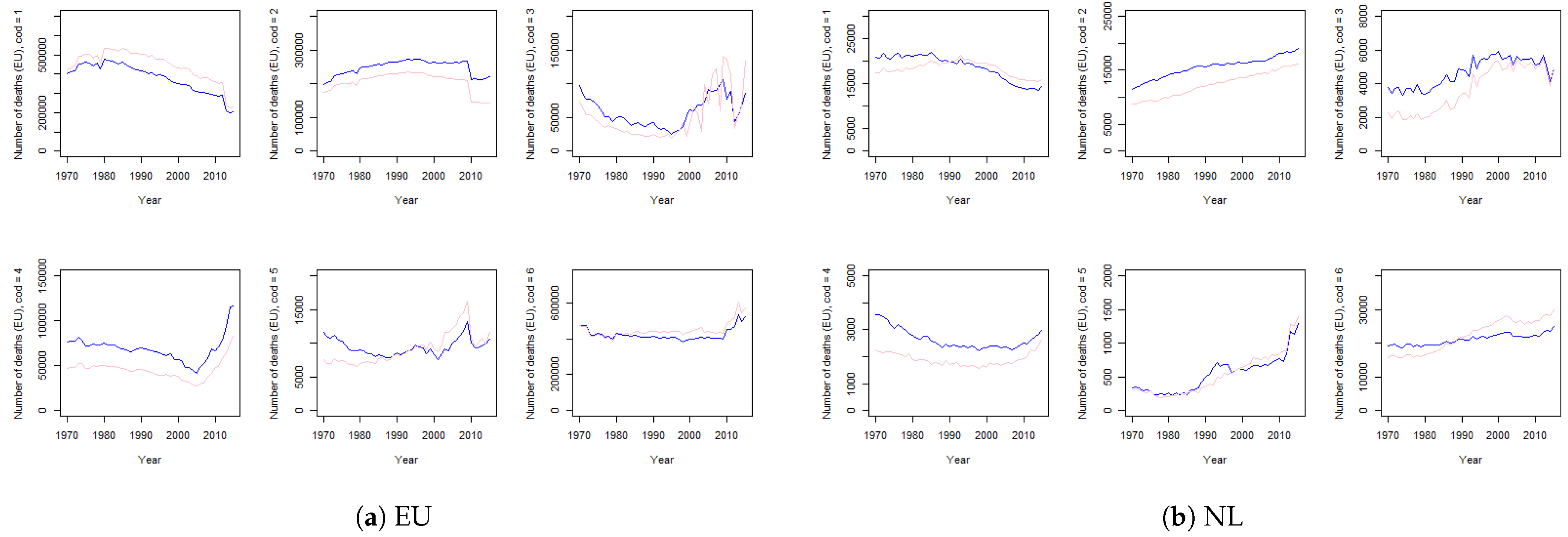
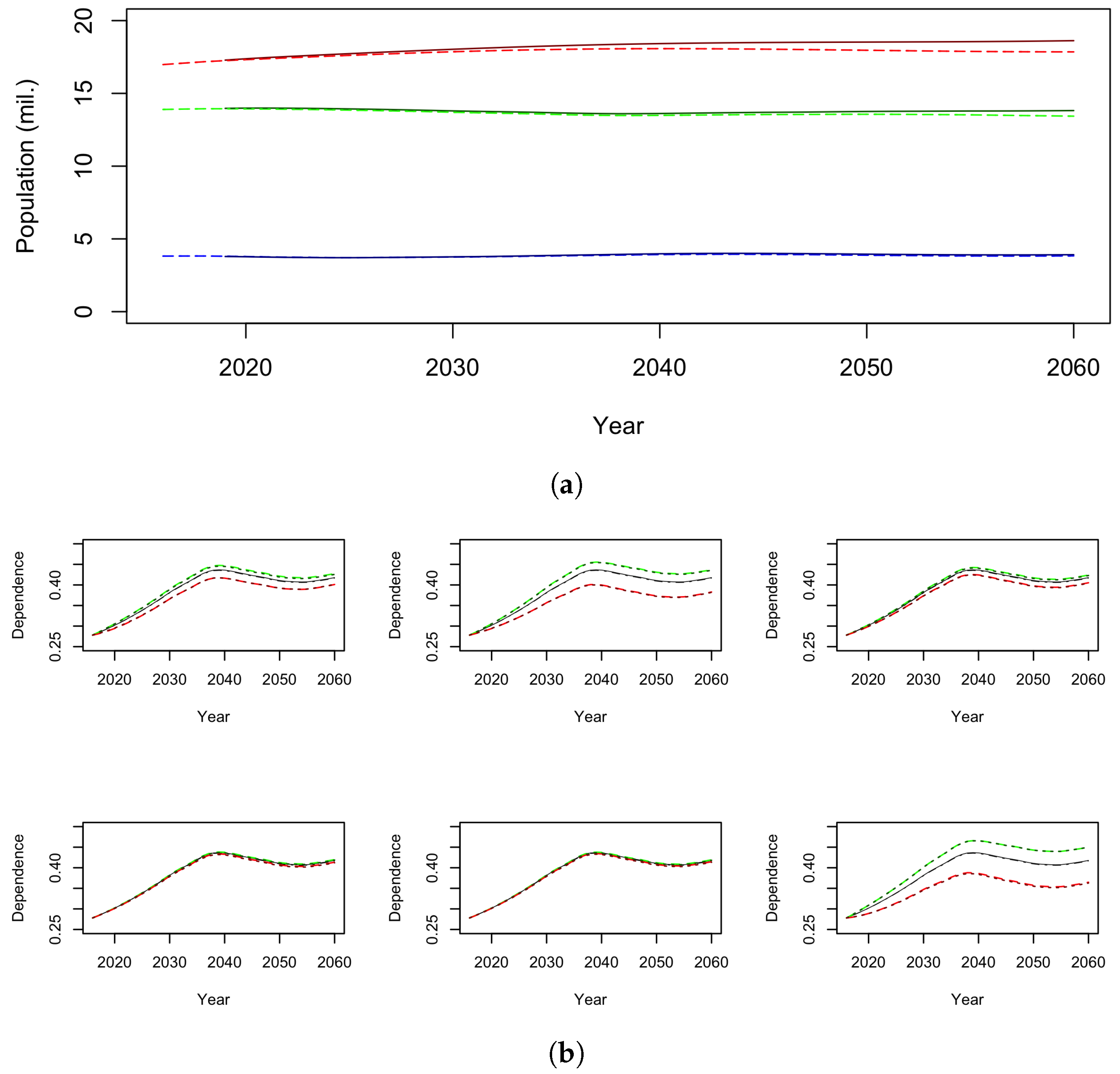
4.3. Population Dynamics
4.3.1. Model Outcomes
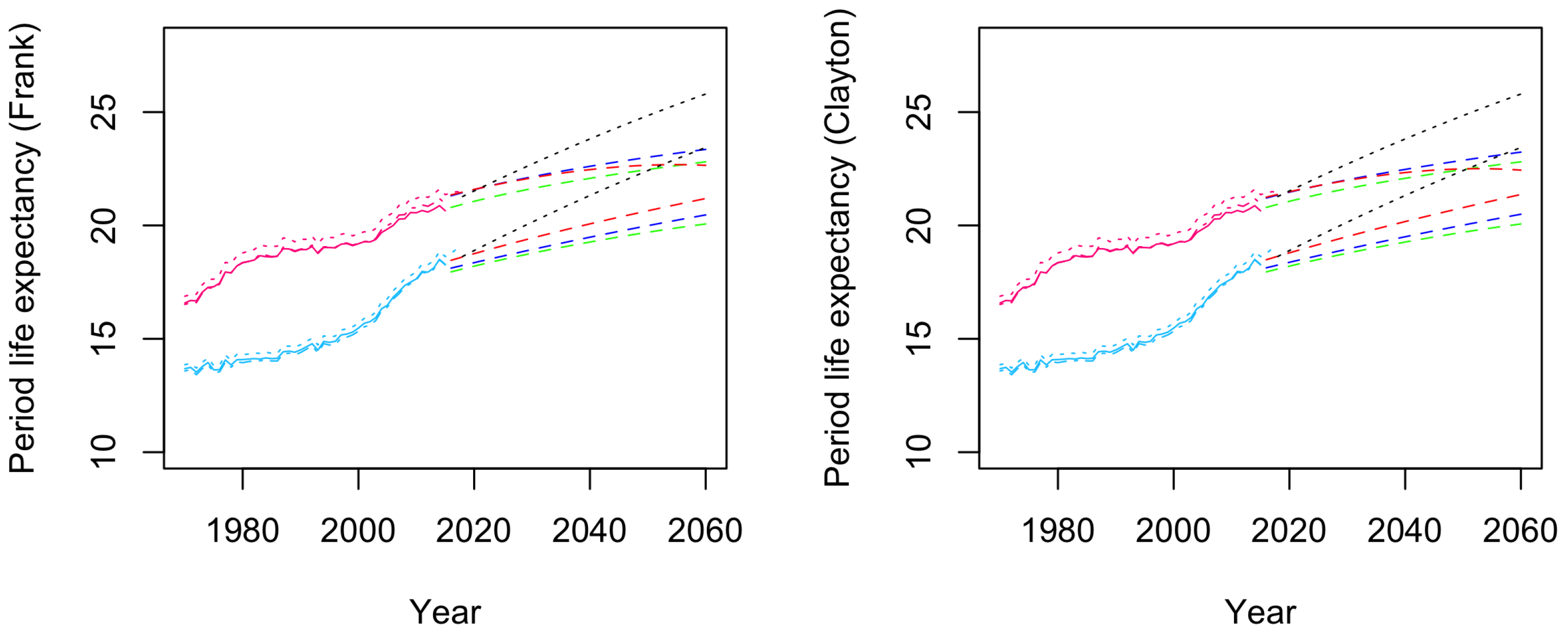
4.3.2. Model Comparison
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
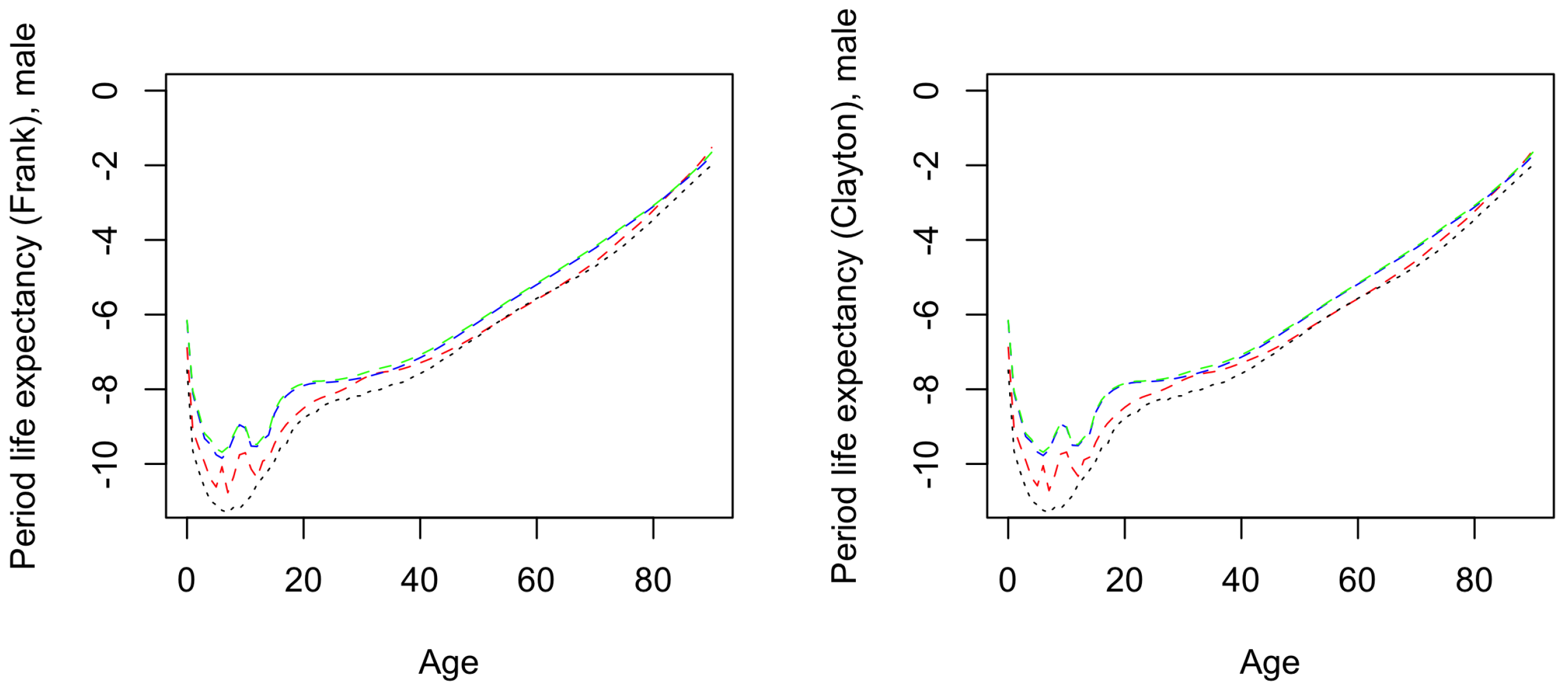
Appendix A. Frank and Clayton Copula Definition and Generator Function
Appendix B. Maximum Likelihood Estimation of (24)
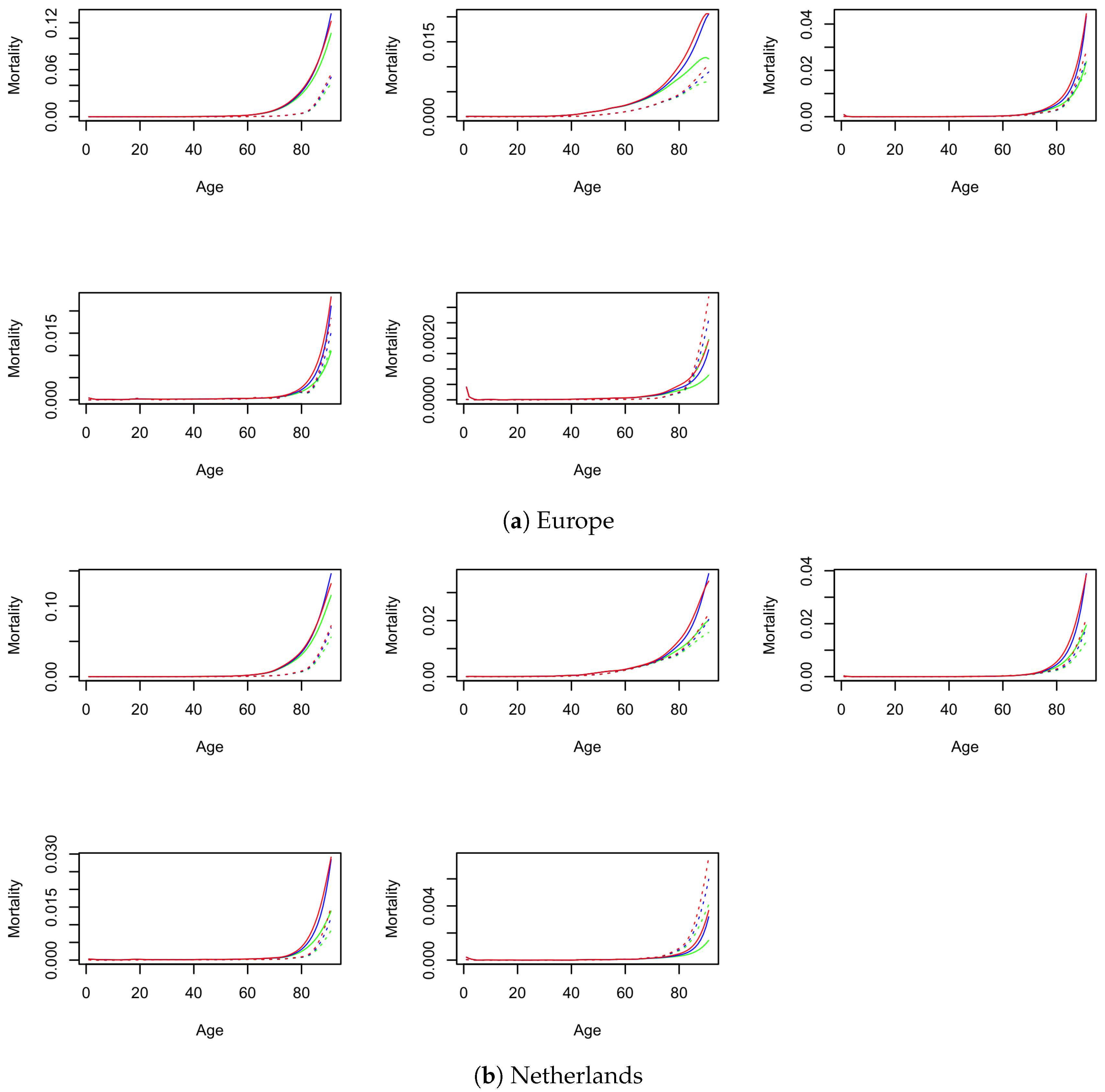
Appendix C. Crude and Net Mortality for Males
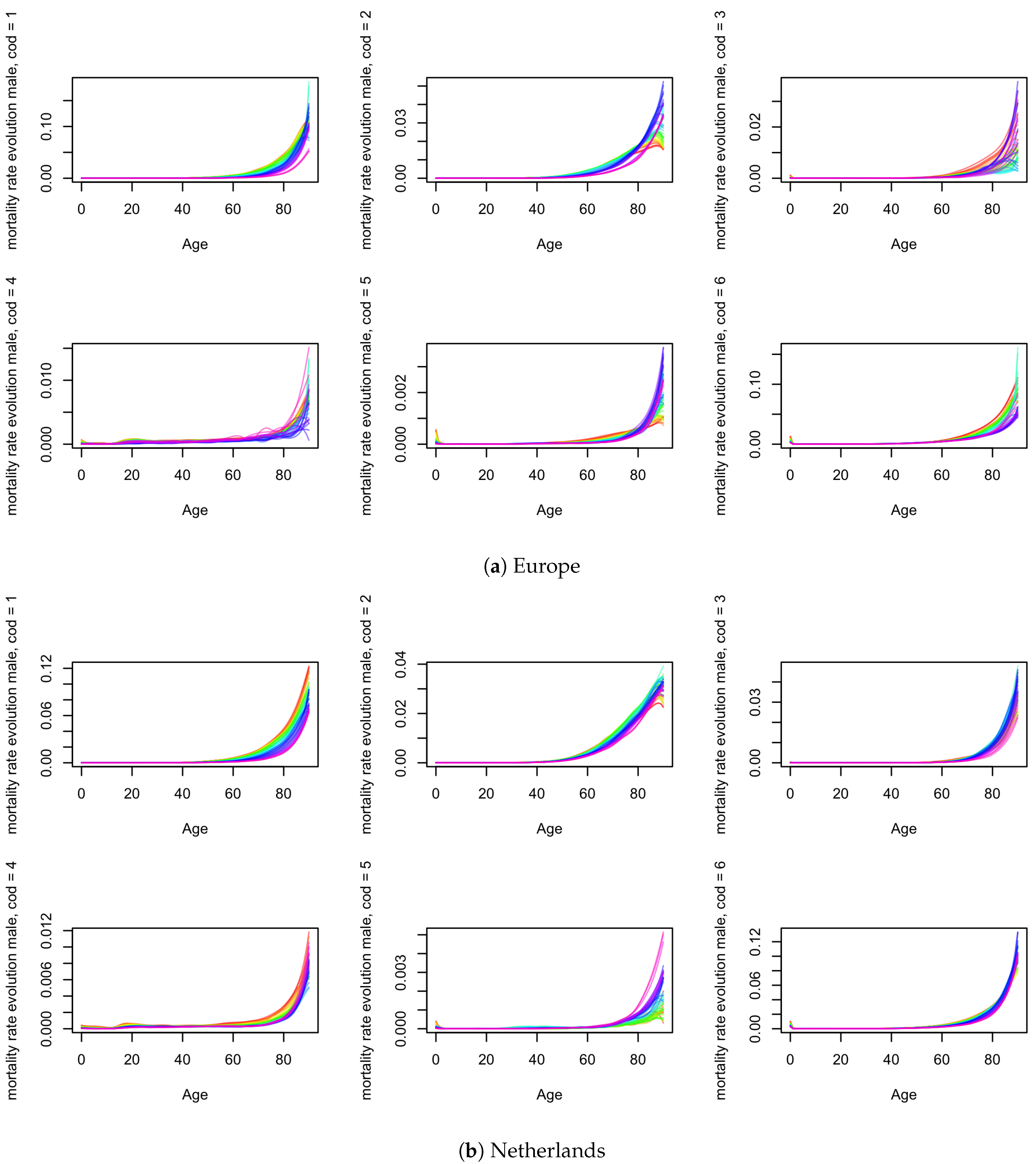
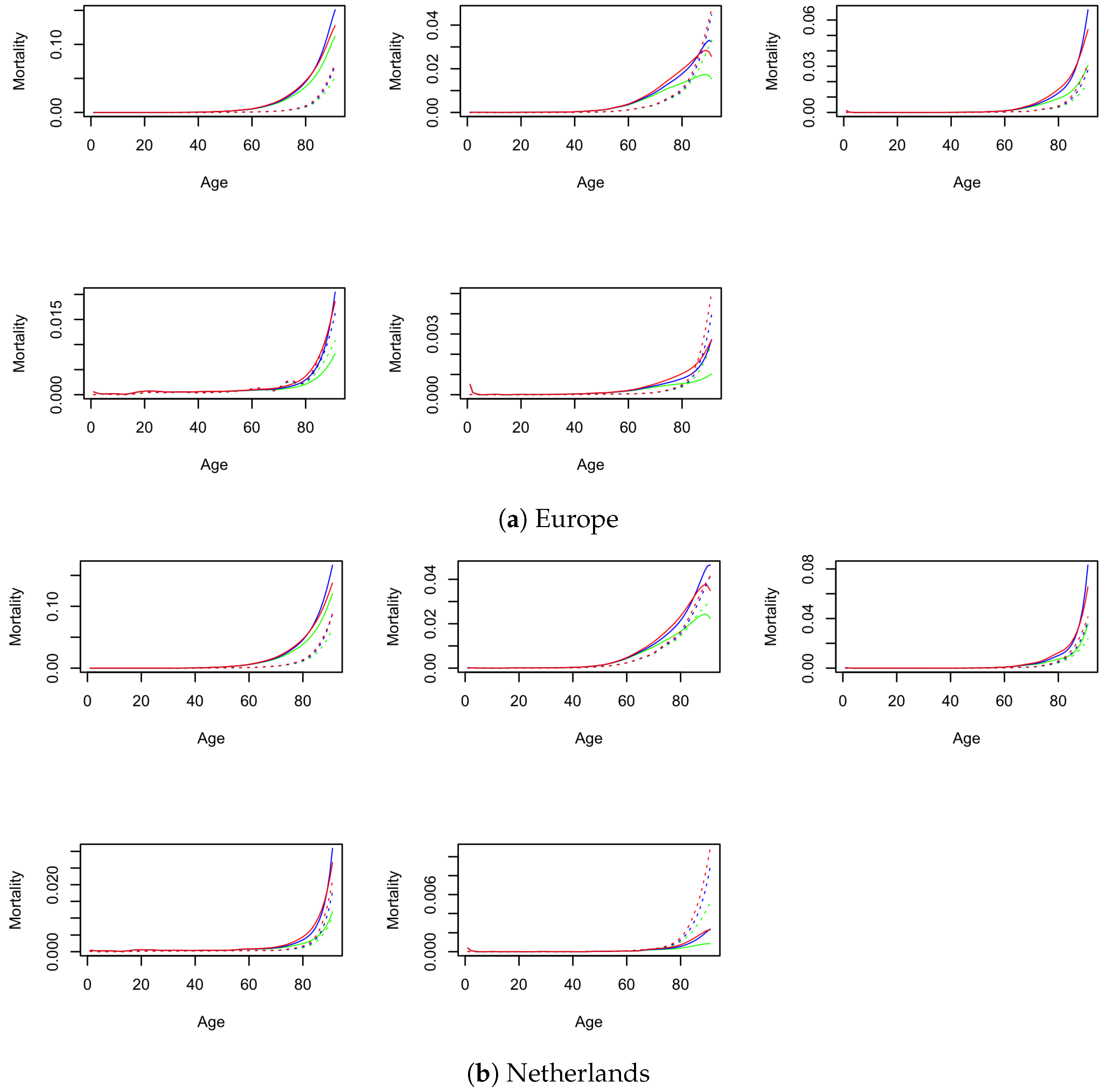
Appendix D. Robustness Checks
| Copula | r | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Independence | |||||||||||
| - | 0.292 | 0.397 | 0.376 | 18.21 | 20.07 | 21.07 | 22.81 | 18.83 | 21.70 | ||
| 0.5 | 0.294 | 0.404 | 0.384 | 18.51 | 20.46 | 21.32 | 23.15 | 19.19 | 22.02 | ||
| 2 | 0.288 | 0.383 | 0.361 | 17.64 | 19.35 | 20.59 | 22.18 | 18.18 | 21.11 | ||
| Frank | - | 0.292 | 0.397 | 0.377 | 18.22 | 20.15 | 21.20 | 22.92 | 18.86 | 21.81 | |
| 0.5 | 0.294 | 0.404 | 0.385 | 18.52 | 20.53 | 21.44 | 23.25 | 19.20 | 22.12 | ||
| 2 | 0.288 | 0.383 | 0.363 | 17.66 | 19.46 | 20.73 | 22.31 | 18.21 | 21.24 | ||
| Clay | - | 0.295 | 0.408 | 0.395 | 18.63 | 21.16 | 23.01 | 24.49 | 19.41 | 23.38 | |
| 0.5 | 0.296 | 0.411 | 0.397 | 18.79 | 21.21 | 23.08 | 24.60 | 19.53 | 23.50 | ||
| 2 | 0.292 | 0.401 | 0.391 | 18.15 | 21.01 | 22.84 | 24.25 | 19.09 | 23.14 | ||
| Frank | - | 0.292 | 0.398 | 0.379 | 18.25 | 20.25 | 21.31 | 23.05 | 18.89 | 21.93 | |
| 0.5 | 0.294 | 0.405 | 0.386 | 18.54 | 20.61 | 21.55 | 23.35 | 19.22 | 22.22 | ||
| 2 | 0.289 | 0.384 | 0.365 | 17.70 | 19.58 | 20.86 | 22.46 | 18.26 | 21.38 | ||
| Clay | - | 0.294 | 0.402 | 0.385 | 18.45 | 20.57 | 21.98 | 23.75 | 19.10 | 22.55 | |
| 0.5 | 0.295 | 0.407 | 0.389 | 18.68 | 20.78 | 22.14 | 23.97 | 19.34 | 22.76 | ||
| 2 | 0.291 | 0.392 | 0.375 | 17.96 | 20.16 | 21.66 | 23.33 | 18.62 | 22.13 | ||
| Frank | - | 0.293 | 0.400 | 0.383 | 18.36 | 20.46 | 21.58 | 23.36 | 19.01 | 22.22 | |
| 0.5 | 0.295 | 0.407 | 0.389 | 18.63 | 20.77 | 21.79 | 23.63 | 19.31 | 22.48 | ||
| 2 | 0.290 | 0.388 | 0.370 | 17.81 | 19.85 | 21.15 | 22.82 | 18.41 | 21.69 | ||
| Clay | - | 0.293 | 0.400 | 0.383 | 18.38 | 20.50 | 21.47 | 23.23 | 19.03 | 22.08 | |
| 0.5 | 0.295 | 0.407 | 0.390 | 18.64 | 20.81 | 21.68 | 23.51 | 19.33 | 22.34 | ||
| 2 | 0.290 | 0.388 | 0.371 | 17.86 | 19.90 | 21.06 | 22.71 | 18.45 | 21.57 | ||
| Frank | - | 0.298 | 0.416 | 0.399 | 19.16 | 21.25 | 22.53 | 24.27 | 19.79 | 23.19 | |
| 0.5 | 0.299 | 0.419 | 0.402 | 19.33 | 21.35 | 22.69 | 24.42 | 19.91 | 23.38 | ||
| 2 | 0.295 | 0.405 | 0.389 | 18.58 | 20.81 | 22.04 | 23.86 | 19.26 | 22.68 | ||
| Clay | - | 0.293 | 0.399 | 0.380 | 18.34 | 20.28 | 21.21 | 22.97 | 18.96 | 21.84 | |
| 0.5 | 0.295 | 0.406 | 0.387 | 18.63 | 20.64 | 21.45 | 23.29 | 19.29 | 22.14 | ||
| 2 | 0.290 | 0.386 | 0.366 | 17.82 | 19.61 | 20.76 | 22.39 | 18.34 | 21.28 | ||
| 1 | Source: Centraal Bureau voor de Statistiek. |
| 2 | For instance, the recent COVID-19 pandemic or an increase in the influenza virus-related deaths as observed by Actuarieel Genootschap (2018). |
| 3 | We refer to Enchev et al. (2017) for a survey and comparison of various multi-population models. |
| 4 | Enchev et al. (2017) analysed the ordinary Li–Lee model, two simplified versions of this model and the common age effect model of Kleinow (2015) and concluded that the regular Li–Lee model was the second-best performing model after the common age effect model. |
| 5 | Competing risks is the presence of censoring of the time of death from one cause in the event of death from another cause. |
| 6 | In addition to the clear extensions to the academic literature, we believe that the cause-specific extension is relevant for all practices which deal with longevity risk in the Netherlands and rely on the multi-population Antonio et al. (2017) model. |
| 7 | The LL model, as described in Antonio et al. (2017), is currently being used by Actuarieel Genootschap for the calculation of the Dutch life tables. |
| 8 | |
| 9 | The full definition of the survival functions as well as the first derivative and inverse of both corresponding generator functions are given in Appendix A, Equations (A1)–(A6). |
| 10 | Enchev et al. (2017) highlight the potential shortcomings in the re-estimation process of the time-dependent coefficient . They suggest a vector autoregressive model of order 1 (VAR(1)) instead of the AR(1) proposed by Li and Lee (2005). This is due to the sometimes diverging properties of the AR(1) model in a multi-population context. By the use of the VAR(1) model and its underlying covariance matrix, coherent forecasting can be retained. Moreover, this forecasting method does not significantly deviate from individual AR(1) forecasts (Enchev et al. 2017). |
| 11 | We acknowledge that we use a reduced variable set. A more comprehensive model could study all population flows with their own distinct functions, as can be seen in, e.g., Boumezoued et al. (2018). However, this is beyond the scope of our paper. |
| 12 | https://statline.cbs.nl/Statweb/ (accessed on 28 February 2019). |
| 13 | https://www.who.int/healthinfo/statistics/mortality_rawdata/en/ (accessed on 28 February 2019). |
| 14 | https://statline.cbs.nl/Statweb/ (accessed on 28 February 2019). |
| 15 | Keeping in mind the slim volume of cause-of-death data in many cases, we chose to include mortality numbers from Germany between 1970 and 1989, when the current country of Germany was split into the Federal Republic of Germany (West Germany/FRG) and the German Democratic Republic (East Germany/GDR). This is in contrast to the general mortality data used by Antonio et al. (2017). Moreover, in previous cause-of-death research by Arnold and Sherris (2015), mortality data of split Germany were not included, since no data were available for the German Democratic Republic before 1969. This does not pose a problem in our research, because the first year of our data set is 1970, and therefore, we accumulated the mortality knowledge of the German subsections to represent the total German mortality for the years preceding the fall of the Berlin Wall. |
| 16 | |
| 17 | For a full comprehensive display of the forecast, we refer to the illustrations in Figures S12–S15 of the Supplementary materials Section S.4. |
| 18 | This is not always the case, but results from our choice of dependence coefficient, as shown in Appendix D. |
| 19 | The sole difference is that in this case we have based the model on our acquired data set. |
References
- Actuarieel Genootschap. 2018. Prognose-Tafel 2018. Utrecht: Actuarieel Genootschap & Actuarieel Instituut. [Google Scholar]
- Alvarez, Jesús-Adrián, Malene Kallestrup-Lamb, and Søren Kjærgaard. 2021. Linking retirement age to life expectancy does not lessen the demographic implications of unequal lifespans. Insurance: Mathematics and Economics 99: 363–75. [Google Scholar] [CrossRef]
- Antonio, Katrien, Sander Devriendt, Wouter de Boer, Robert de Vries, Anja De Waegenaere, Hok-Kwan Kan, Egbert Kromme, Wilbert Ouburg, Tim Schulteis, Erica Slagter, and et al. 2017. Producing the dutch and belgian mortality projections: A stochastic multi-population standard. European Actuarial Journal 7: 297–336. [Google Scholar] [CrossRef]
- Arnold, Séverine, and Michael Sherris. 2015. Causes-of-death mortality: What do we know on their dependence? North American Actuarial Journal 19: 116–28. [Google Scholar] [CrossRef]
- Ayuso, Mercedes, Jorge M. Bravo, and Robert Holzmann. 2021. Getting life expectancy estimates right for pension policy: Period versus cohort approach. Journal of Pension Economics & Finance 20: 212–31. [Google Scholar]
- Boonen, Tim J., and Hong Li. 2017. Modeling and forecasting mortality with economic growth: A multipopulation approach. Demography 54: 1921–46. [Google Scholar] [CrossRef]
- Boumezoued, Alexandre, Héloïse Labit Hardy, Nicole El Karoui, and Séverine Arnold. 2018. Cause-of-death mortality: What can be learned from population dynamics? Insurance: Mathematics and Economics 78: 301–15. [Google Scholar] [CrossRef] [Green Version]
- Brillinger, David R. 1986. The natural variability of vital rates and associated statistics. Biometrics 42: 693–734. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A Poisson log-bilinear regression approach to the construction of projected lifetables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar] [CrossRef] [Green Version]
- Carriere, Jacques. 1994. Dependent decrement theory (with discussion). Transactions of the Society of Actuaries 46: 45–74. [Google Scholar]
- Chen, Hua, Richard MacMinn, and Tao Sun. 2015. Multi-population mortality models: A factor copula approach. Insurance: Mathematics and Economics 63: 135–46. [Google Scholar] [CrossRef]
- Deaton, Angus S., and Christina Paxson. 2004. Mortality, income, and income inequality over time in Britain and the United States. In Perspectives on the Economics of Aging. Chicago: University of Chicago Press, pp. 247–86. [Google Scholar]
- Enchev, Vasil, Torsten Kleinow, and Andrew J. G. Cairns. 2017. Multi-population mortality models: Fitting, forecasting and comparisons. Scandinavian Actuarial Journal 2017: 319–42. [Google Scholar] [CrossRef] [Green Version]
- Girosi, Federico, and Gary King. 2007. Understanding the Lee–Carter Mortality Forecasting Method. Technical Report. Available online: https://j.mp/2oTcxGt (accessed on 28 February 2021).
- Kannisto, Väinö. 1994. Development of Oldest-Old Mortality, 1950–1990: Evidence from 28 Developed Countries. Number 1. Odense: University Press of Southern Denmark. [Google Scholar]
- Kleinow, Torsten. 2015. A common age effect model for the mortality of multiple populations. Insurance: Mathematics and Economics 63: 147–52. [Google Scholar] [CrossRef] [Green Version]
- Lee, Ronald D., and Francois Nault. 1993. Modeling and forecasting provincial mortality in Canada. Paper presented at World Congress of the IUSSP, Montreal, QC, Canada, August 24–September 1. [Google Scholar]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting US mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar]
- Li, Han, Hong Li, Yang Lu, and Anastasios Panagiotelis. 2019. A forecast reconciliation approach to cause-of-death mortality modeling. Insurance: Mathematics and Economics 86: 122–33. [Google Scholar] [CrossRef]
- Li, Hong, and Yang Lu. 2019. Modeling cause-of-death mortality using hierarchical Archimedean copula. Scandinavian Actuarial Journal 2019: 247–72. [Google Scholar] [CrossRef]
- Li, Nan, and Ronald Lee. 2005. Coherent mortality forecasts for a group of populations: An extension of the Lee–Carter method. Demography 42: 575–94. [Google Scholar] [CrossRef] [Green Version]
- Ling, C. -H. 1965. Representation of associative functions. Publicationes Mathematicae Debrecen 12: 189–212. [Google Scholar]
- Lyu, Pintao, Anja De Waegenaere, and Bertrand Melenberg. 2020. A multi-population approach to forecasting all-cause mortality using cause-of-death mortality data. North American Actuarial Journal 25: S421–S456. [Google Scholar] [CrossRef] [Green Version]
- Marshall, Albert W., and Ingram Olkin. 1988. Families of multivariate distributions. Journal of the American Statistical Association 83: 834–41. [Google Scholar] [CrossRef]
- McNeil, Alexander J., and Johanna Nešlehová. 2009. Multivariate Archimedean copulas, d-monotone functions and ℓ1-norm symmetric distributions. The Annals of Statistics 37: 3059–97. [Google Scholar] [CrossRef]
- Newton, Isaac. 1833. Philosophiae Naturalis Principia Mathematica. Glasgow: G. Brookman, vol. 1. [Google Scholar]
- Oakes, David. 1989. Bivariate survival models induced by frailties. Journal of the American Statistical Association 84: 487–93. [Google Scholar] [CrossRef]
- OECD, ed. 2015. Pensions at a Glance 2015: OECD and G20 Indicators. Washington, DC: OECD Publishing. [Google Scholar]
- Oeppen, Jim, and James W. Vaupel. 2002. Broken limits to life expectancy. Science 296: 1029–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raphson, Joseph. 1702. Analysis Aequationum Universalis: Seu ad Aequationes Algebraicas Resolvendas Methodus Generalis, & Expedita, Ex Nova Infinitarum Serierum Methodo, Deducta ac Demonstrata. London: Typis TB Prostant Venales Apud A. & I. Churchill, vol. 1. [Google Scholar]
- Rivest, Louis-Paul, and Martin T. Wells. 2001. A martingale approach to the copula-graphic estimator for the survival function under dependent censoring. Journal of Multivariate Analysis 79: 138–55. [Google Scholar] [CrossRef] [Green Version]
- Sklar, M. 1959. Fonctions de repartition an dimensions et leurs marges. Publications de l’Institut de Statistique de l’Université de Paris 8: 229–31. [Google Scholar]
- Tsiatis, Anastasios. 1975. A nonidentifiability aspect of the problem of competing risks. Proceedings of the National Academy of Sciences 72: 20–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tuljapurkar, Shripad, Nan Li, and Carl Boe. 2000. A universal pattern of mortality decline in the G7 countries. Nature 405: 789. [Google Scholar] [CrossRef]
- Wang, Antai. 2012. On the nonidentifiability property of archimedean copula models under dependent censoring. Statistics & Probability Letters 82: 621–25. [Google Scholar]
- White, Kevin M. 2002. Longevity advances in high-income countries, 1955–96. Population and Development Review 28: 59–76. [Google Scholar] [CrossRef]
- Wilmoth, John R. 1995. Are mortality projections always more pessimistic when disaggregated by cause of death? Mathematical Population Studies 5: 293–319. [Google Scholar] [CrossRef]
- Zellner, Arnold. 1962. An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias. Journal of the American statistical Association 57: 348–68. [Google Scholar] [CrossRef]
- Zheng, Ming, and John P. Klein. 1995. Estimates of marginal survival for dependent competing risks based on an assumed copula. Biometrika 82: 127–38. [Google Scholar] [CrossRef]


| EU | NL | ||||
|---|---|---|---|---|---|
| Code | Causes of Death | Male (%) | Female * (%) | Male (%) | Female (%) |
| 1 | Circulatory system | 32.1 | 37.0 | 29.6 | 31.1 |
| 2 | Cancer | 20.8 | 17.1 | 24.6 | 20.9 |
| 3 | Respiratory system | 4.9 | 4.2 | 7.4 | 6.2 |
| 4 | External causes | 5.8 | 3.8 | 4.2 | 3.2 |
| 5 | Infectious and parasitic diseases | 0.8 | 0.8 | 0.8 | 0.9 |
| 6 | Other | 35.6 | 37.2 | 33.4 | 37.7 |
| Gender | COD | Trend | Approx. | Model Comparison |
|---|---|---|---|---|
| Transition Age | (/) | |||
| Male | 1 | - | - | = |
| 2 | +/− | 80–85 | , | |
| 3 | - | - | ||
| 4 | - | - | ||
| 5 | +/− | 70–80 | , | |
| 6 | - | - | = | |
| Female | 1 | - | - | |
| 2 | - | - | ||
| 3 | = | - | ||
| 4 | - | - | , | |
| 5 | +/− | 70–80 | ||
| 6 | - | - | = |
| Copula | r | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Independence | |||||||||||
| - | 0.292 | 0.397 | 0.376 | 18.21 | 20.07 | 21.07 | 22.81 | 18.83 | 21.70 | ||
| 0.5 | 0.294 | 0.404 | 0.384 | 18.51 | 20.46 | 21.32 | 23.15 | 19.19 | 22.02 | ||
| 2 | 0.288 | 0.383 | 0.361 | 17.64 | 19.35 | 20.59 | 22.18 | 18.18 | 21.11 | ||
| Frank | - | 0.000 | 0.000 | 0.001 | 0.01 | 0.08 | 0.13 | 0.11 | 0.03 | 0.11 | |
| 0.5 | 0.000 | 0.000 | 0.001 | 0.01 | 0.07 | 0.12 | 0.10 | 0.01 | 0.10 | ||
| 2 | 0.000 | 0.000 | 0.002 | 0.02 | 0.11 | 0.14 | 0.13 | 0.03 | 0.13 | ||
| Clay | - | 0.003 | 0.011 | 0.019 | 0.42 | 1.09 | 1.94 | 1.68 | 0.58 | 1.68 | |
| 0.5 | 0.002 | 0.007 | 0.013 | 0.28 | 0.75 | 1.76 | 1.45 | 0.34 | 1.48 | ||
| 2 | 0.004 | 0.018 | 0.03 | 0.51 | 1.66 | 2.25 | 2.07 | 0.91 | 2.03 | ||
| Frank | - | 0.000 | 0.001 | 0.003 | 0.04 | 0.18 | 0.24 | 0.24 | 0.06 | 0.23 | |
| 0.5 | 0.000 | 0.001 | 0.002 | 0.03 | 0.15 | 0.23 | 0.20 | 0.03 | 0.20 | ||
| 2 | 0.001 | 0.001 | 0.004 | 0.06 | 0.23 | 0.27 | 0.28 | 0.08 | 0.27 | ||
| Clay | - | 0.002 | 0.005 | 0.009 | 0.24 | 0.50 | 0.91 | 0.94 | 0.27 | 0.85 | |
| 0.5 | 0.001 | 0.003 | 0.005 | 0.17 | 0.32 | 0.82 | 0.82 | 0.15 | 0.74 | ||
| 2 | 0.003 | 0.009 | 0.014 | 0.32 | 0.81 | 1.07 | 1.15 | 0.44 | 1.02 | ||
| Frank | - | 0.001 | 0.003 | 0.007 | 0.15 | 0.39 | 0.51 | 0.55 | 0.18 | 0.52 | |
| 0.5 | 0.001 | 0.003 | 0.005 | 0.12 | 0.31 | 0.47 | 0.48 | 0.12 | 0.46 | ||
| 2 | 0.002 | 0.005 | 0.009 | 0.17 | 0.50 | 0.56 | 0.64 | 0.23 | 0.58 | ||
| Clay | - | 0.001 | 0.003 | 0.007 | 0.17 | 0.43 | 0.40 | 0.42 | 0.20 | 0.38 | |
| 0.5 | 0.001 | 0.003 | 0.006 | 0.13 | 0.35 | 0.36 | 0.36 | 0.14 | 0.32 | ||
| 2 | 0.002 | 0.005 | 0.01 | 0.22 | 0.55 | 0.47 | 0.53 | 0.27 | 0.46 | ||
| Frank | - | 0.006 | 0.019 | 0.023 | 0.95 | 1.18 | 1.46 | 1.46 | 0.96 | 1.49 | |
| 0.5 | 0.005 | 0.015 | 0.018 | 0.82 | 0.89 | 1.37 | 1.27 | 0.72 | 1.36 | ||
| 2 | 0.007 | 0.022 | 0.028 | 0.94 | 1.46 | 1.45 | 1.68 | 1.08 | 1.57 | ||
| Clay | - | 0.001 | 0.002 | 0.004 | 0.13 | 0.21 | 0.14 | 0.16 | 0.13 | 0.14 | |
| 0.5 | 0.001 | 0.002 | 0.003 | 0.12 | 0.18 | 0.13 | 0.14 | 0.10 | 0.12 | ||
| 2 | 0.002 | 0.003 | 0.005 | 0.18 | 0.26 | 0.17 | 0.21 | 0.16 | 0.17 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zittersteyn, G.; Alonso-García, J. Common Factor Cause-Specific Mortality Model. Risks 2021, 9, 221. https://doi.org/10.3390/risks9120221
Zittersteyn G, Alonso-García J. Common Factor Cause-Specific Mortality Model. Risks. 2021; 9(12):221. https://doi.org/10.3390/risks9120221
Chicago/Turabian StyleZittersteyn, Geert, and Jennifer Alonso-García. 2021. "Common Factor Cause-Specific Mortality Model" Risks 9, no. 12: 221. https://doi.org/10.3390/risks9120221
APA StyleZittersteyn, G., & Alonso-García, J. (2021). Common Factor Cause-Specific Mortality Model. Risks, 9(12), 221. https://doi.org/10.3390/risks9120221






