1. Introduction
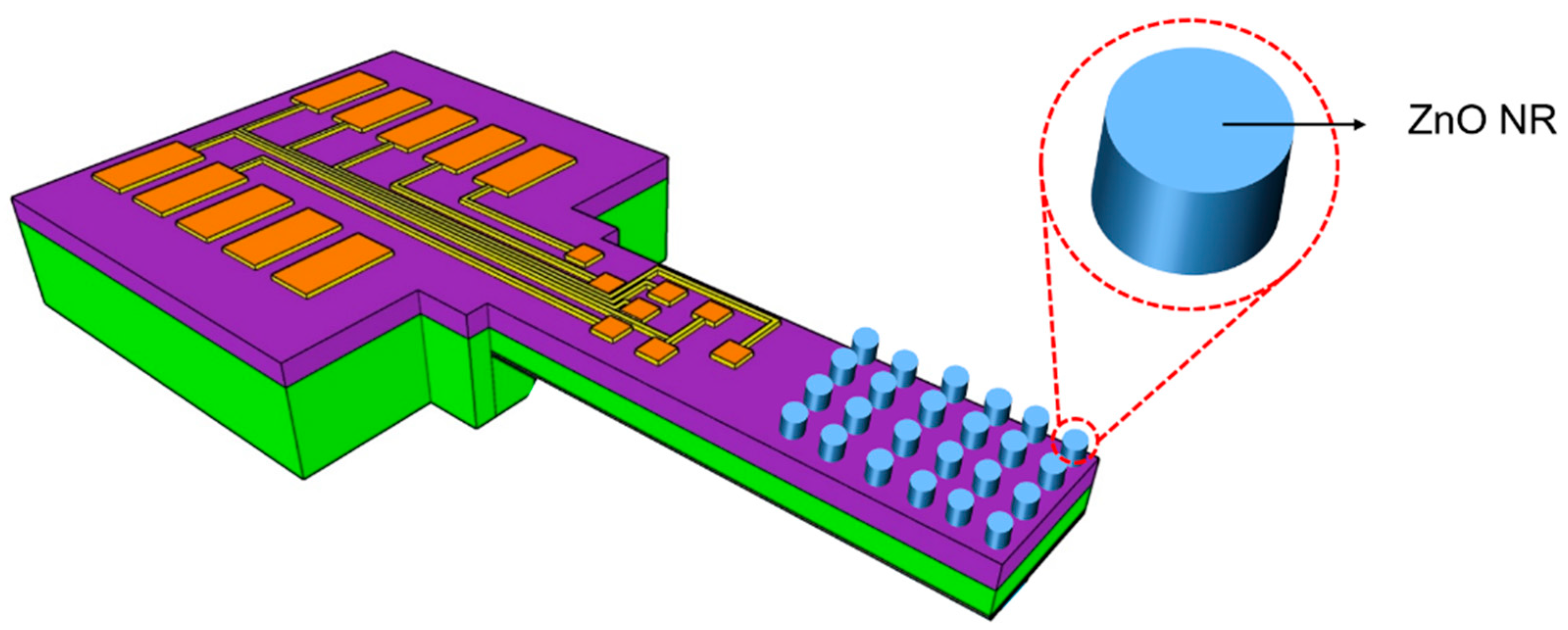
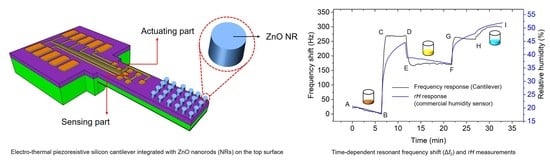
Silicon micro-electro-mechanical system (MEMS)-based cantilevers combined with nanorod arrays are a versatile platform integrating micro and nano-components (
Figure 1), which can be used in multiple sensing applications of physical, chemical, and biological targets [
1]. Due to their capability to detect small amounts of mass, they can be used as sensitive sensors with high resolution (e.g., for monitoring humidity, toxic gases, and airborne nanoparticles) [
2,
3,
4]. In dynamic mode operation, MEMS cantilever sensors have normally been operated as micro-resonators, in which their resonant frequency shift (∆
f0) can be monitored as their mass changes due to the adsorption/desorption of analytes on/from the sensitive layer. Sensor characterization by frequency sweeping is one of the most common methods used to figure out the amplitude and phase responses, and finally identify the resonant frequency [
5,
6,
7]. However, regardless of the set frequency interval during sweeping, this technique is not feasible for fast real-time measurement of resonance shifting. Therefore, a robust real-time system, which is capable of measuring the resonance shifts of microcantilever sensors continuously, is required.
Phase-locked loop (PLL)-based systems have been broadly used to realize continuous real-time frequency tracking of resonant sensors [
8,
9,
10], which principally employ the excitation frequency as a means to control the phase difference between excitation signal and sensor output. In the case of cantilever sensors, the phase difference in resonance is ideally independent of the resonant frequency. Therefore, the resonant frequency can be monitored by tracking the resonance phase. When the resonance phase has reached the desired phase difference, the output frequency of the PLL stays constant. This is commonly referred to as frequency lock and is interpreted as the resonant frequency in this work. Here, the resonance phase becomes an essential parameter for detecting the resonant frequency.
In this study, we implemented a PLL-based system for tracking the resonance shifting of an electro-thermal piezoresistive silicon cantilever resonator, which is subsequently called an electro-thermal piezoresistive cantilever sensor. This cantilever was covered by zinc oxide nanorod (ZnO NR) arrays that were modified with self-assembled monolayers of chitosan (see
Figure 1). Nevertheless, PLL systems do not function properly in electro-thermal piezoresistive cantilever sensors due to their reversed phase response. Low thermal-mechanical coupling and parasitic direct thermal coupling [
3] are inhibitive to an ideal phase response. Resonance tracking cannot work properly then, because there is an ambiguity in the phase response, which subsequently leads to instabilities during the locking process of the resonant frequency. Therefore, there is a need to develop a technique that can guarantee an utmost suppression of parasitic effects on electro-thermal piezoresistive cantilever sensors. Some work uses dual sensor systems that are fabricated in the same chip for cancelling the parasitic effects [
11,
12,
13]. However, implementation of dual sensor systems will enlarge the sensor size and increase its power consumption. In the case of electro-thermal piezoresistive cantilever sensors, realizing the similar effect of direct thermal-parasitic coupling between two cantilevers is complicated as the heat supply and the boundary condition, which cause the temperature distribution in the cantilever body, are not easily controlled precisely. Therefore, hereby we apply an external reference signal in order to obtain a symmetric amplitude shape and a monotonic phase response by subtracting it from the outputs of the electro-thermal piezoresistive cantilever sensor [
14]. By using an external circuit, the amplitude and phase of the reference signal can be controlled at a given frequency to obtain a suitable signal for eliminating the direct thermal-parasitic effect. We expect that the implementation of reference signal subtraction can expedite resonance tracking based on the PLL technique and reduce instabilities during the locking process of the resonant frequency. As proof-of-concept measurements, we investigated the resonance tracking of electro-thermal piezoresistive cantilever sensors under different levels of relative humidity (
rH). MEMS cantilever sensors with ZnO NRs and a chitosan layer are highly sensitive to
rH, and can most conveniently be used for sensing volatile organic compounds (VOCs) [
15,
16] and gases [
17,
18].
2. Self-Actuating and Self-Sensing
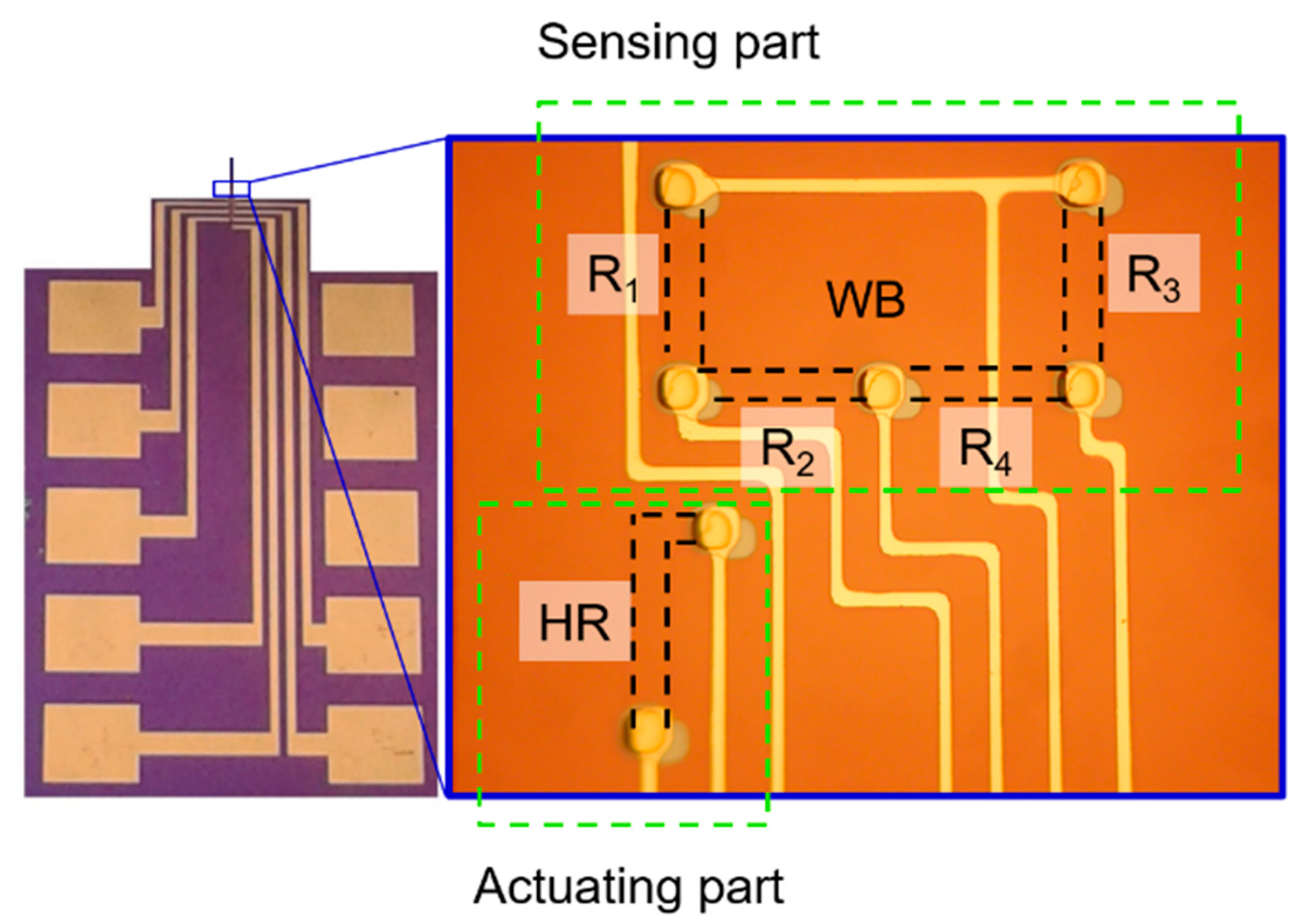
Electro-thermal piezoresistive cantilever sensors were fabricated using bulk silicon wafers and a bulk micromachining technique, leading to lower cost of materials and fabrication processes with respect to surface micromachining [
19]. This cantilever sensor design comprises two main parts, i.e., for mechanical actuation and electrical sensing. Both are realized in the form of diffused
p-type silicon resistors (
Figure 2). A heating resistor (HR) and piezoresistors in a U-shaped full Wheatstone bridge (WB) configuration act as actuating and sensing components, respectively [
20]. The HR, located at the cantilever clamped end, triggers an in-plane actuation of the cantilever beam. Subsequently, this deflection is sensed by the WB that is located about 33 µm away from the HR. The average size of the diffused resistors is around 60 µm × 10 µm. The cantilever beam has a total length of 1000 µm, a width of 170 µm, and a thickness of 12 µm. Details of the fabrication procedure of the electro-thermal piezoresistive cantilever sensors covered by ZnO NRs and chitosan layer were described previously in [
2,
21,
22].
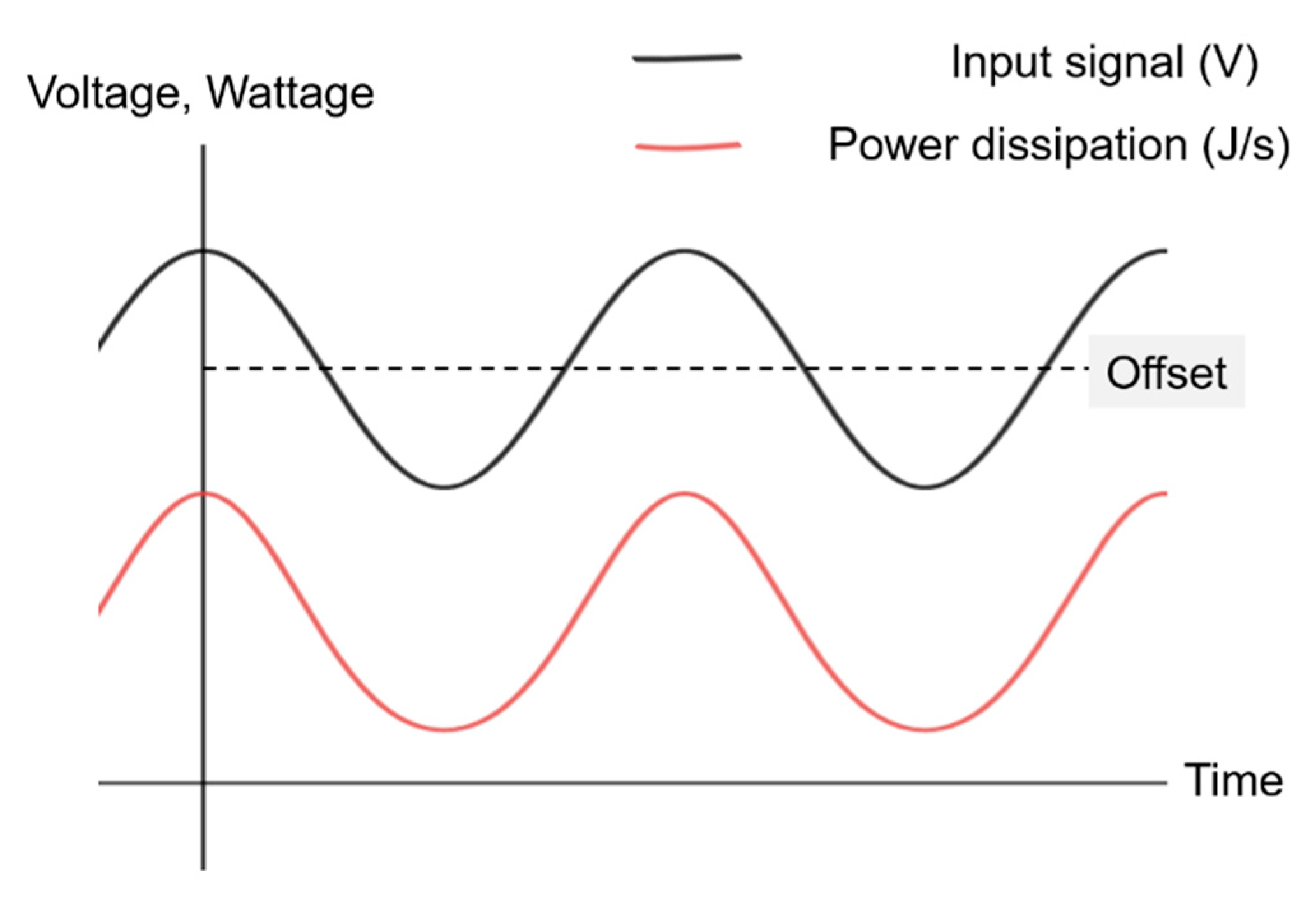
Mechanical actuation is obtained by applying an alternating current (AC) voltage
Vaccos(
2πft) superimposed on a direct current (DC) voltage
Vdc to the HR (
Figure 3, in black line). The electrical current passing through the HR is converted into heat by the Joule heating effect. Consequently, the electrical power (
P) is dissipated leading to a temperature field around the HR [
9,
23]. By inserting the AC and DC components into Equation (1), the resulting power loss (dissipation energy)
P can be illustrated by a waveform, which is indicated by the red curve in
Figure 3. In order to avoid an additional oscillation with double period in the red curve, the amplitude of the third summand on the right side of Equation (1) should be much higher than the fourth.
Here, R is the resistance of the HR, Vdc and Vac are the DC and AC voltage amplitudes, respectively, f is the excitation frequency, and t is time.
Thermal energy is mostly generated due to the loss of kinetic energy of the current carrying electrons by collisions among themselves and with the lattice atoms [
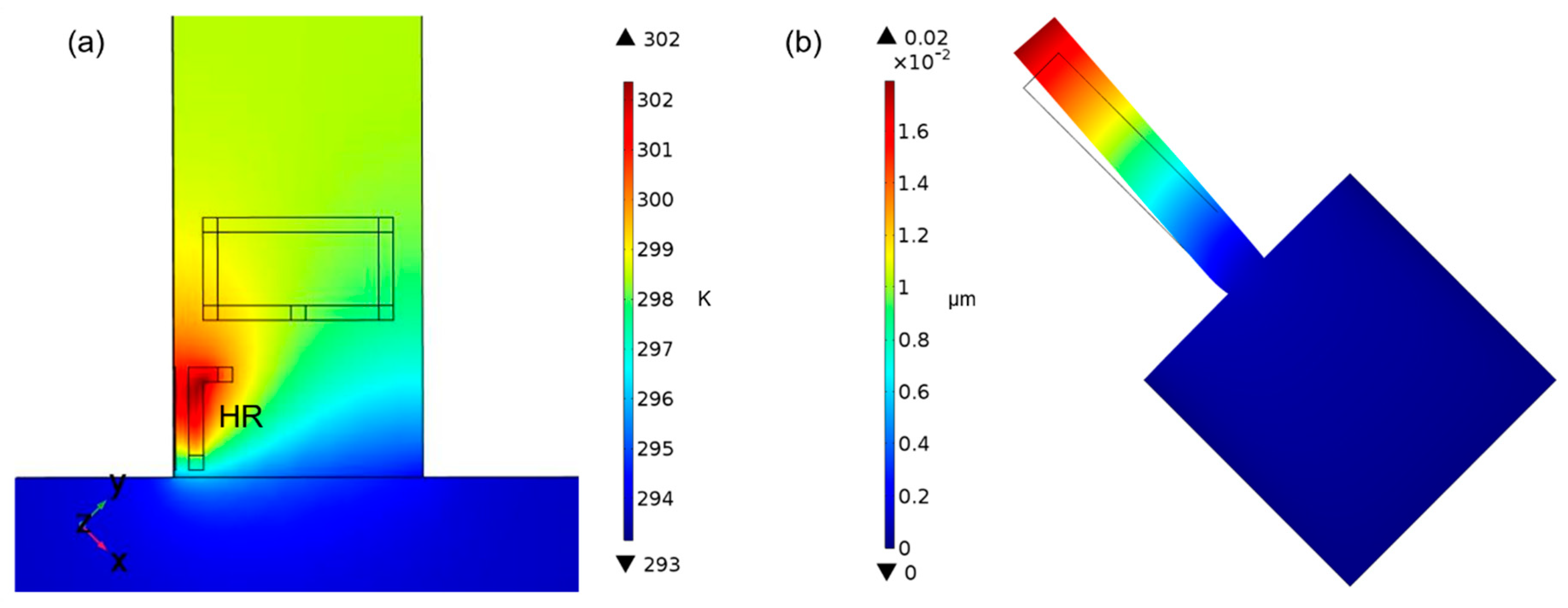
24]. The thermal energy subsequently results in static and dynamic temperature distributions in the cantilever. To further analyze the temperature distribution and the thermally induced deflection of the microcantilevers due to the Joule heating, finite element modelling (FEM) by COMSOL Multiphysics 4.4b was performed using a 5 V DC voltage at the input of the HR. FEM shows that there is a temperature gradient in the vicinity of the HR, with a maximum temperature of 302.4 K observed around the center of the HR (
Figure 4a). This local temperature increase yields an expansion of the cantilever around the HR leading to a bending of the cantilever in the lateral (in-plane) direction. A total static displacement at the free end of approximately 17.8 nm is observed (
Figure 4b).
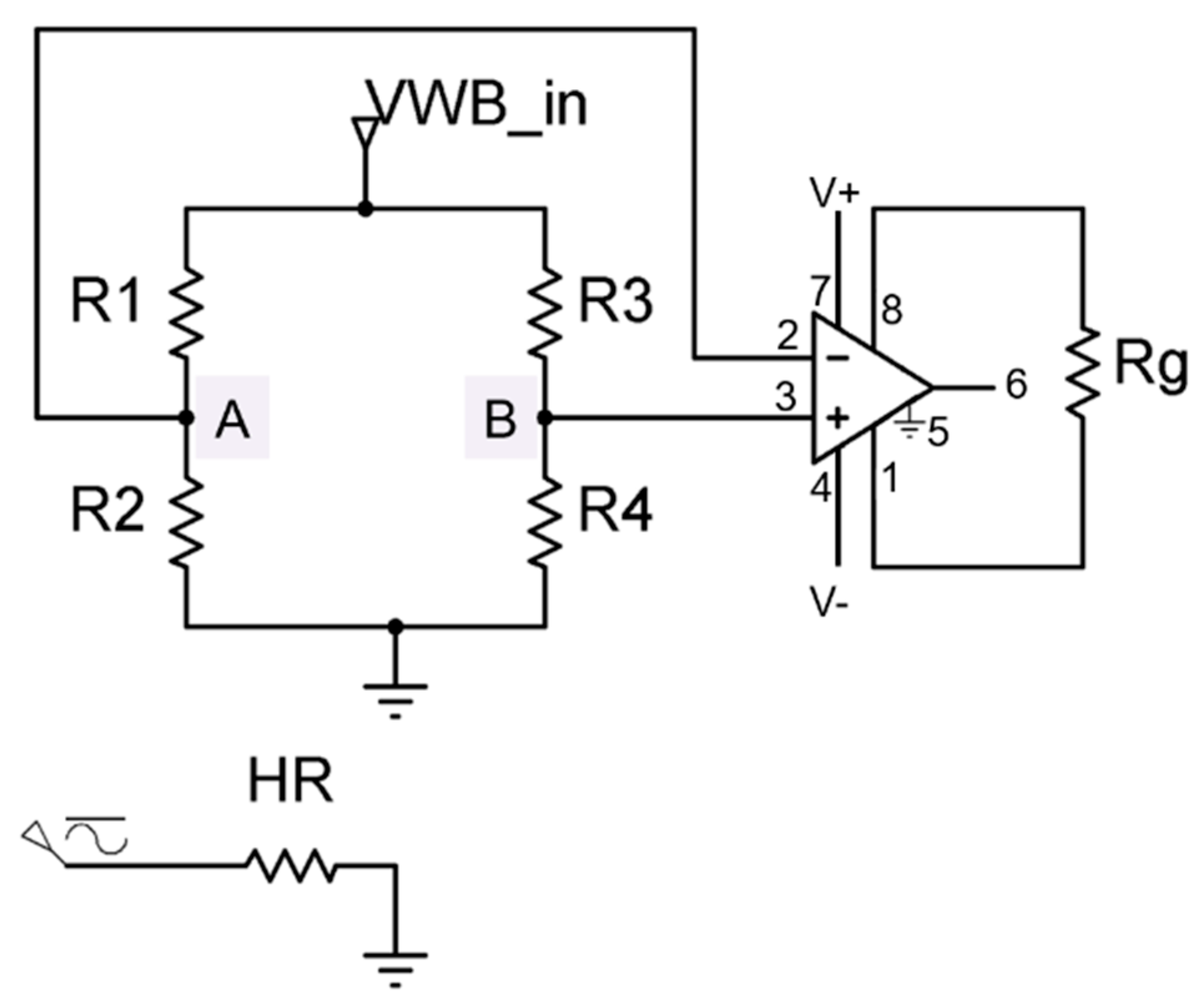
As discussed before, the response due to the electro-thermal actuation is sensed by four piezoresistors configured in a U-shaped WB. The WB was designed for adapting the strain distribution induced in the cantilever due to its lateral bending. Because of the dependence of resistivity on the applied strain ε, the resistors
Ri (
i = 1, …, 4) of the WB experiences relative resistance changes Δ
Ri according to:
where
πl/t and
σi are, respectively, the longitudinal/transverse piezoresistive coefficient of
p-type silicon along the (110) crystal direction and the stress along the cantilever axis at the position of the resistor
Ri. By applying a supply voltage (
VWB_in) to the full WB circuit, the cantilever bending leads to an integral bridge resistance change Δ
R, which can be recorded via the (transverse) output voltage (
VWB_out) of the WB.
Basically, a WB is a parallel combination of two voltage dividers (shown in
Figure 5), which subdivide a large voltage into smaller ones. The WB configuration can be used to measure very low values of resistances down to the milli-ohms range. This is done by detecting a voltage difference between the two output terminals (A and B). These two outputs are subsequently fed into an instrumentation amplifier (INA217) that detects their differences. In the case of a DC signal input (
VA,
VB), the amplifier subtracts and amplifies the input voltages according to
Vout =
G(
VB −
VA), where
G is an amplification factor. Nevertheless, the WB on the cantilever generates
VA and
VB in the form of voltage oscillations. Therefore, in the differential amplifier output we obtain a sinusoidal signal having the same frequency as the actuation signal.
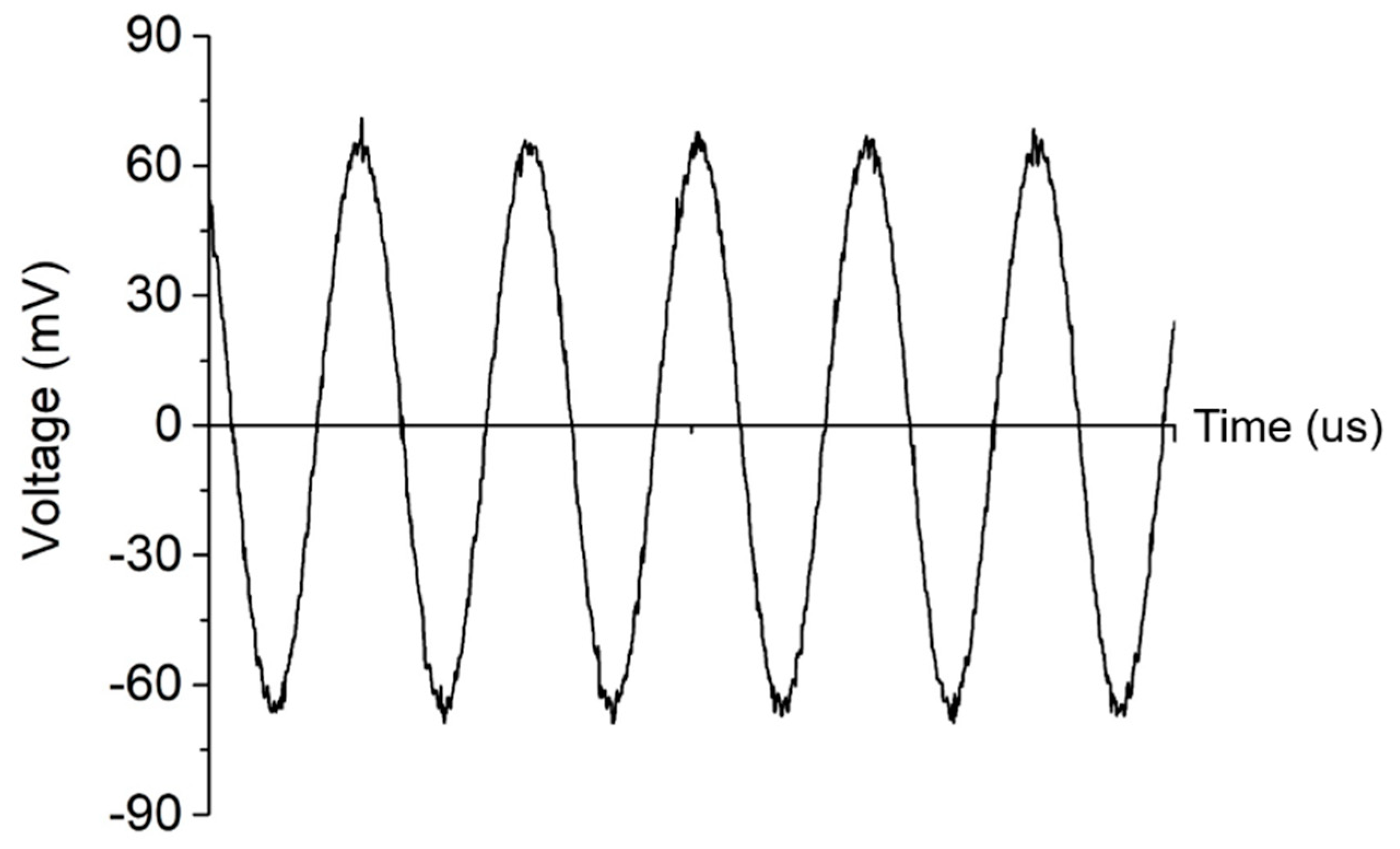
Figure 6 shows the amplified output voltage in the time domain at resonance with an output signal to noise ratio (SNR) of 31.6 dB.
3. Reference Signal Subtraction
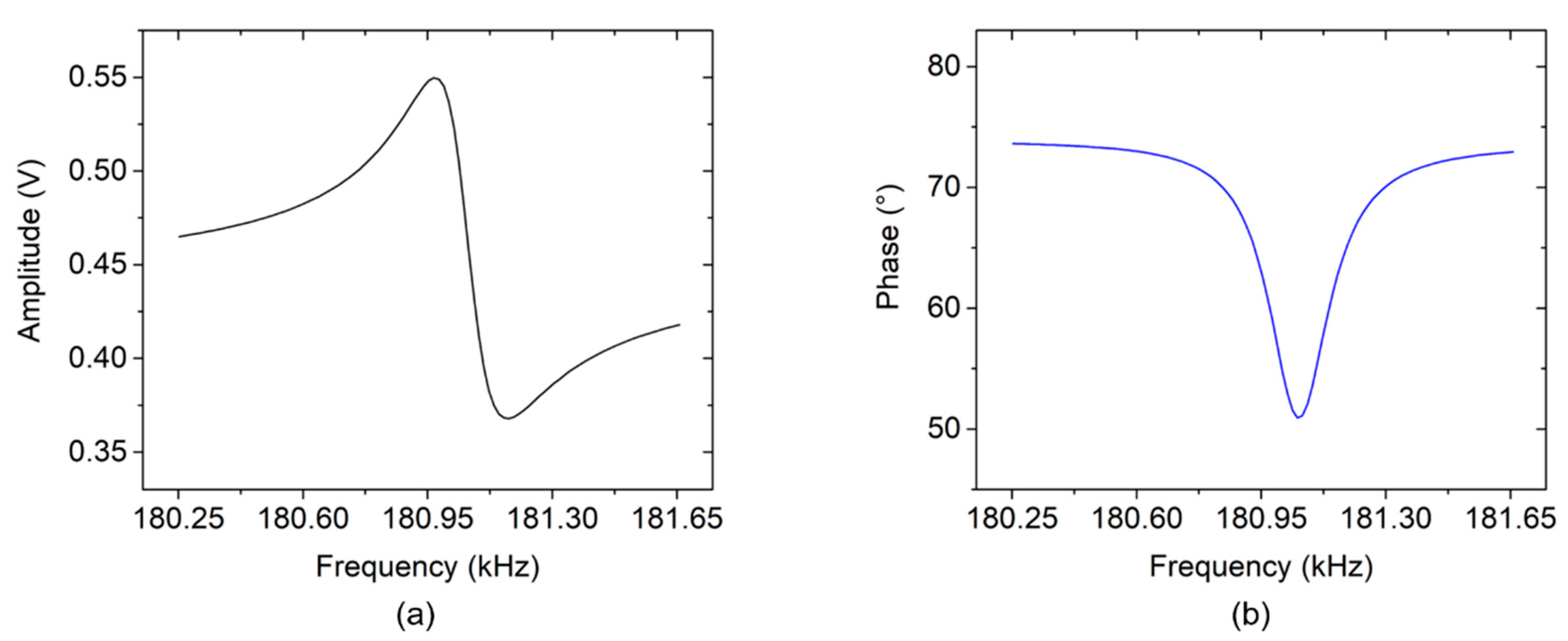
The amplified WB output signal (
VWB_out) shows an asymmetric spectral amplitude line shape (
Figure 7a) and a reversed phase response (
Figure 7b) in the same frequency domain. An asymmetric amplitude shape that occurs concurrently with a reversed phase characteristic is called Fano resonance. It is yielded by mixing a discrete state (Lorentzian line shape) with a constant continuum background [
25]. Therefore, in order to obtain a symmetric amplitude shape (Lorentzian line shape), elimination of the continuum background should be done by subtracting a corresponding characteristic. Simultaneously, the symmetric amplitude shape should then be accompanied by a monotonic phase response.
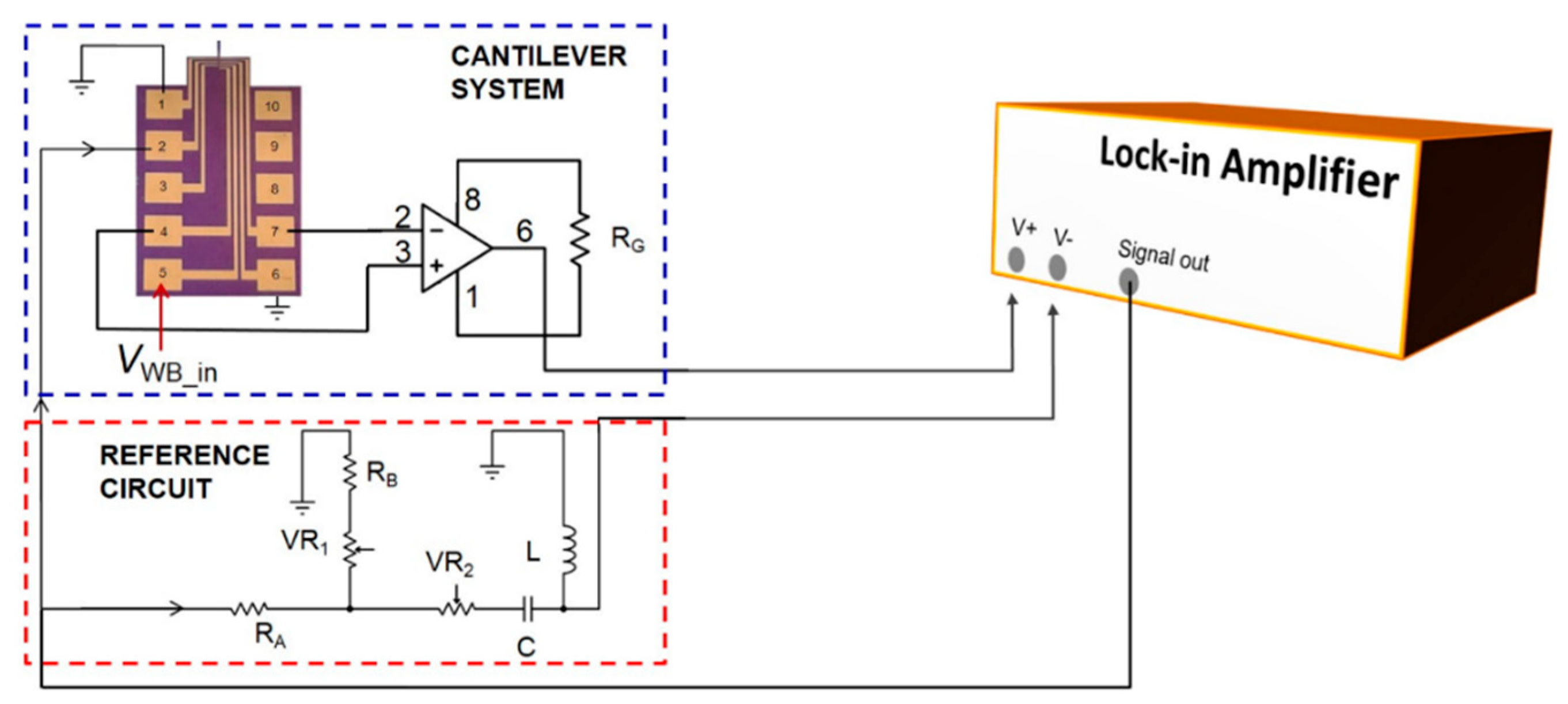
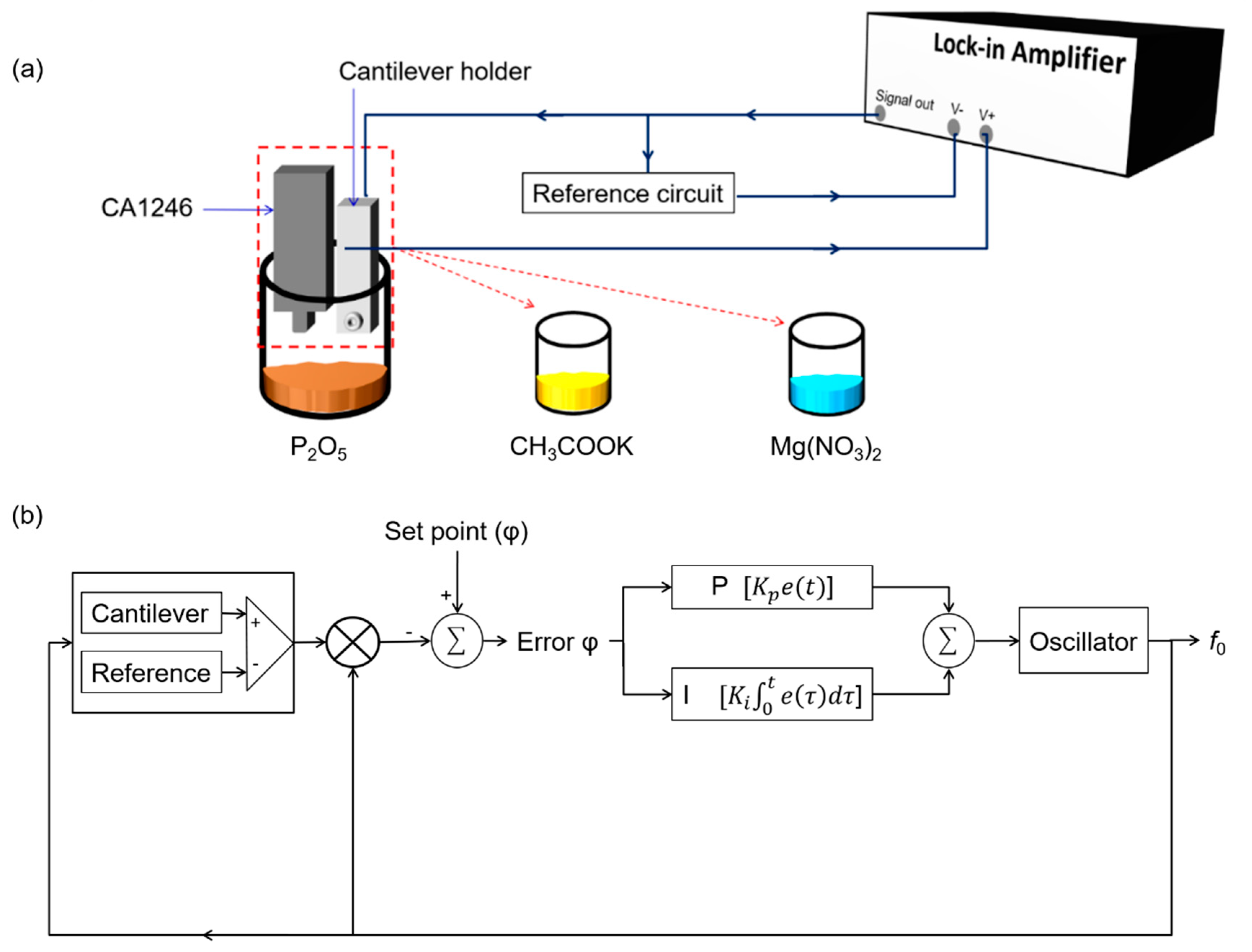
The setup of reference signal subtraction is shown in
Figure 8. An AC signal (2 V) with offset voltage (5 VDC), generated by a lock-in amplifier (MFLI, Zurich Instruments, Zurich, Switzerland), actuates the cantilever through contact pad 2. The vibrations are then detected by the WB, which is supplied with 1 V DC through contact pad 6. Contact pads 1 and 5 act as common ground (GND). The voltage difference at the WB outputs, picked-up at contact pads 7 and 4, are then fed into the instrumentation amplifier through pin 2 and pin 3, respectively. Furthermore, the signal output of reference circuit was subtracted from the signal output of the instrument amplifier (pin 6). This subtraction was performed using both positive (
V+) and negative (
V−) voltage input terminals of the MFLI lock-in amplifier. The
V+ and
V− terminals were connected to the output signal of the instrumentation amplifier and the reference circuit, respectively, and the resultant output voltage (
VO) was then calculated internally in the MFLI lock-in amplifier. The reference circuit was designed and fabricated to provide a controlling mechanism for the reference amplitude and phase signal through
VR1 and
VR2. It was intended to generate and provide a suitable characteristic reference signal, which could then be subtracted from signal of cantilever system. In order to yield a symmetric line shape at the differential output, the amplitude and phase of reference signal should be placed close to the baselines of the asymmetric amplitude and the reversed phase, respectively, of the electro-thermal piezoresistive cantilever.
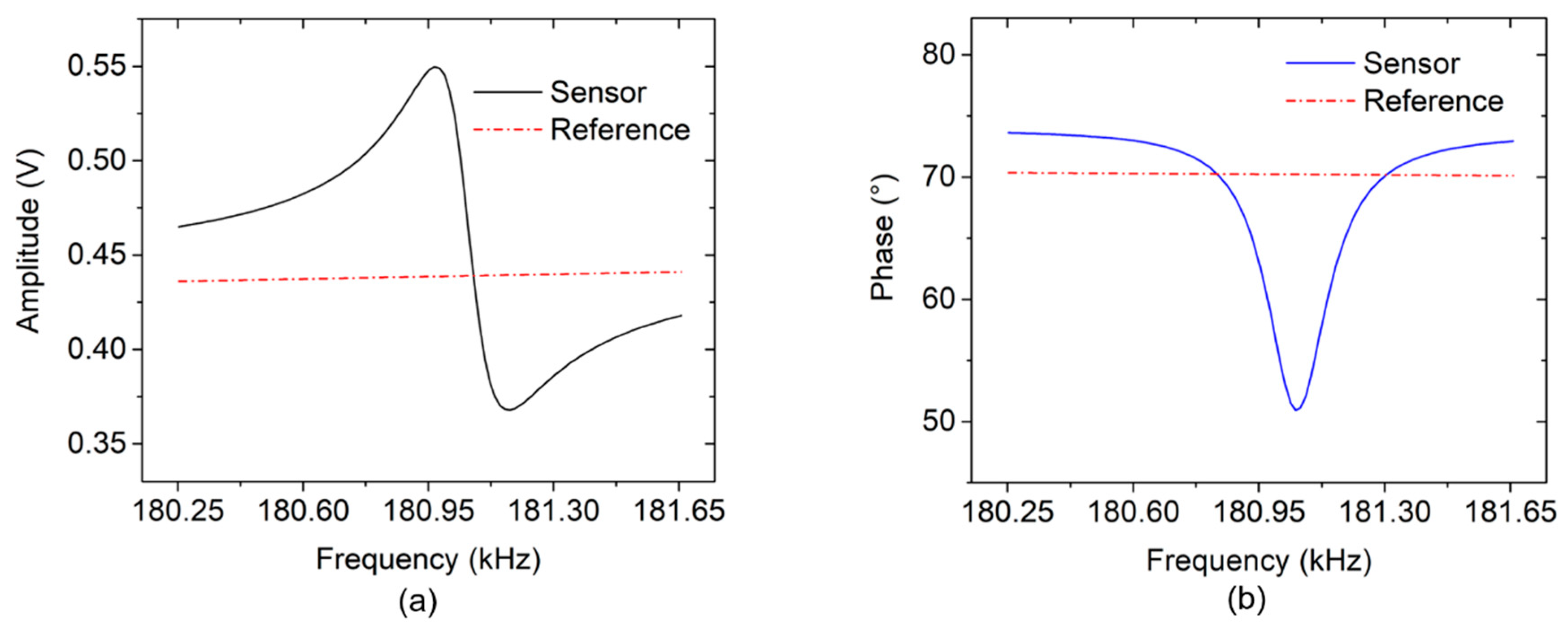
The signals of electro-thermal piezoresistive cantilever sensor and reference circuit, during measurement, are depicted in
Figure 9. The sensor amplitude (
Figure 9a, black full line) has a baseline between ~0.466 V and ~0.418 V whilst the baseline of the phase (
Figure 9b, blue full line) ranges from ~73.60° to ~72.93° in the same frequency band, i.e., from 180.25 to 181.65 kHz. The reference signal was then adjusted to the baseline of the sensor signal by
VR1 and
VR2 (see
Figure 8), which resulted in a measured reference amplitude increasing from ~0.436 V to ~0.441 V and a phase response decreasing from ~70.35° to ~ 70.12° in the examined frequency range (shown in red dash-dot line). The slight sloping behavior is caused by the inductance of the RCL circuit.
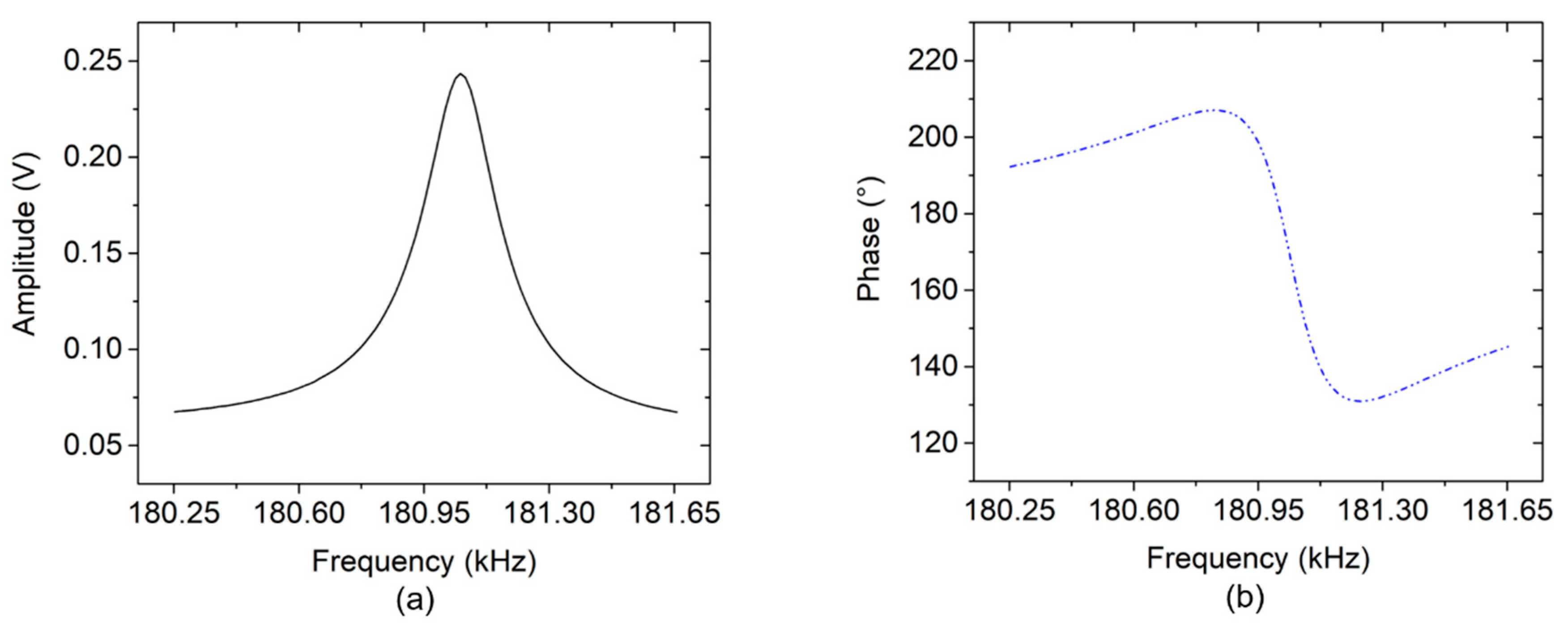
Subtracting the reference from the sensor signal yields the required symmetric amplitude shape (
Figure 10a, full line) and an extended frequency range of monotonic phase response (
Figure 10b, dash-dot-dot line). The resonant frequency is measured at
f0 = 181.052 kHz, the stop band rejection of amplitude response increases from 83 mV to 173 mV, while the phase response range increases from 21.82° to 75.61°.
To evaluate the measured resonant frequency (obtained by the reference subtraction method), a Fano fitting approach [
25] was used to extract the resonant frequency
f0 and the quality factor
Q of the asymmetric signal. The
f0 and
Q are the most relevant parameters of the resonant-mode line shape, which have a main influence on the sensitivity and detection limit of added substances on the cantilever. In the Fano fitting approach, the signal amplitude
σ is modeled by Equation (3) to extract the resonant frequency
f0, and
Q is calculated using Equation (4).
where
q,
f,
g,
H are the asymmetry factor, the frequency, curve width, and gain parameters respectively. An offset
σ0 and a term varying linearly with frequency (
c × f) represent a frequency-dependent part of the baseline. In the calculation of
Q, the term (
c × f) is neglected, because it has only a small influence on the resonance line shape.
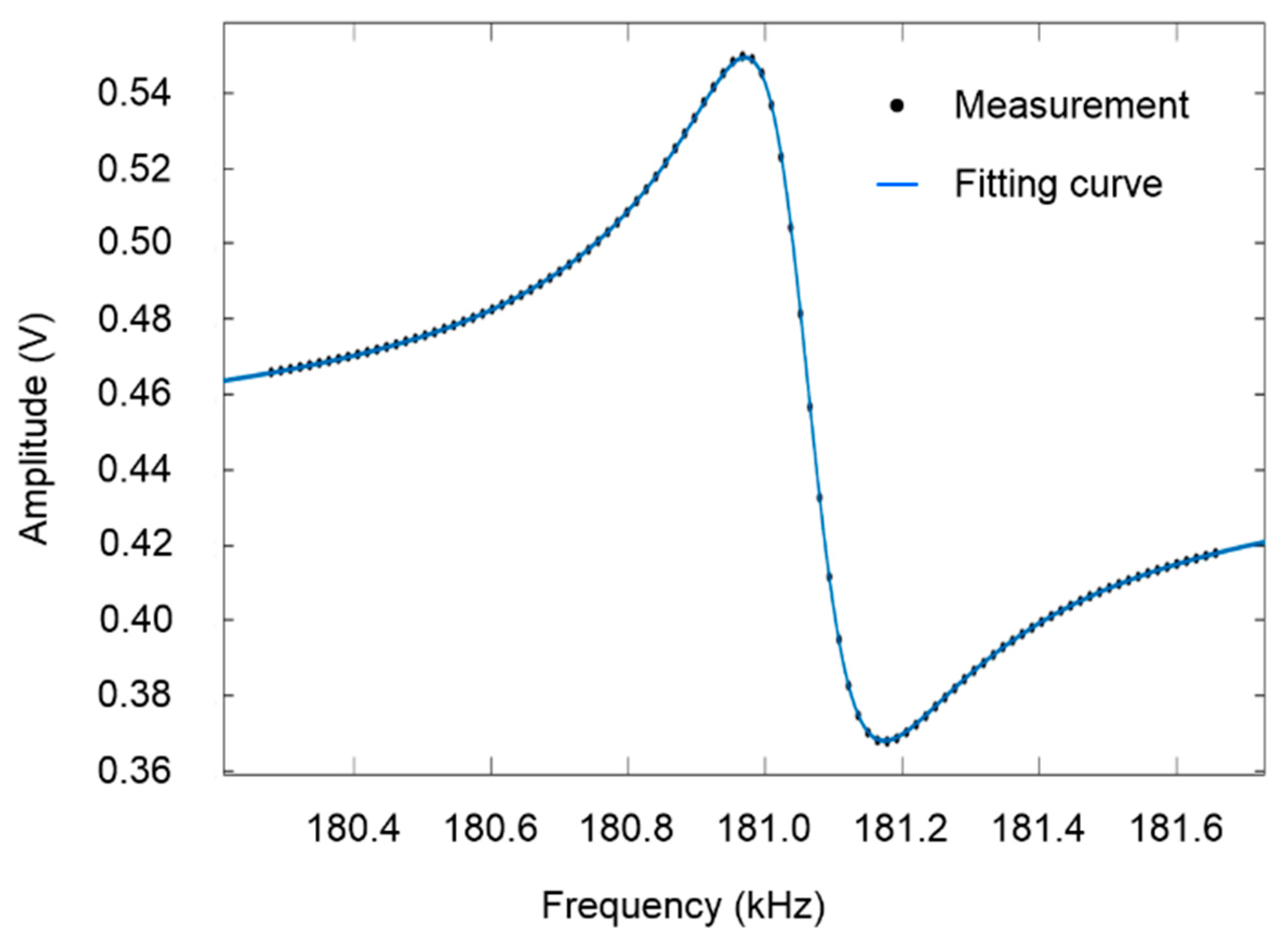
The measured asymmetric amplitude response (cf. black full line of
Figure 9a) and the corresponding amplitude Fano fitting curve of an electro-thermal piezoresistive cantilever sensor are depicted in
Figure 11. For fitting the curve, we implement a nonlinear least squares method with 95% confidence interval, thereby resulting in
f0 ≈ 181.055 kHz and
Q ≈ 936. By fitting the simple harmonic oscillator (SHO) formula to the data of
Figure 10a, we obtain
f0 = 181.052 kHz and
Q = 858 from the measured differential resonance signal. The obtained results from the two approaches indicate that the resonant frequencies are comparable and similar. The observed lower
Q-factor obtained from the measured differential resonance signal are caused by non-perfect reference signal.
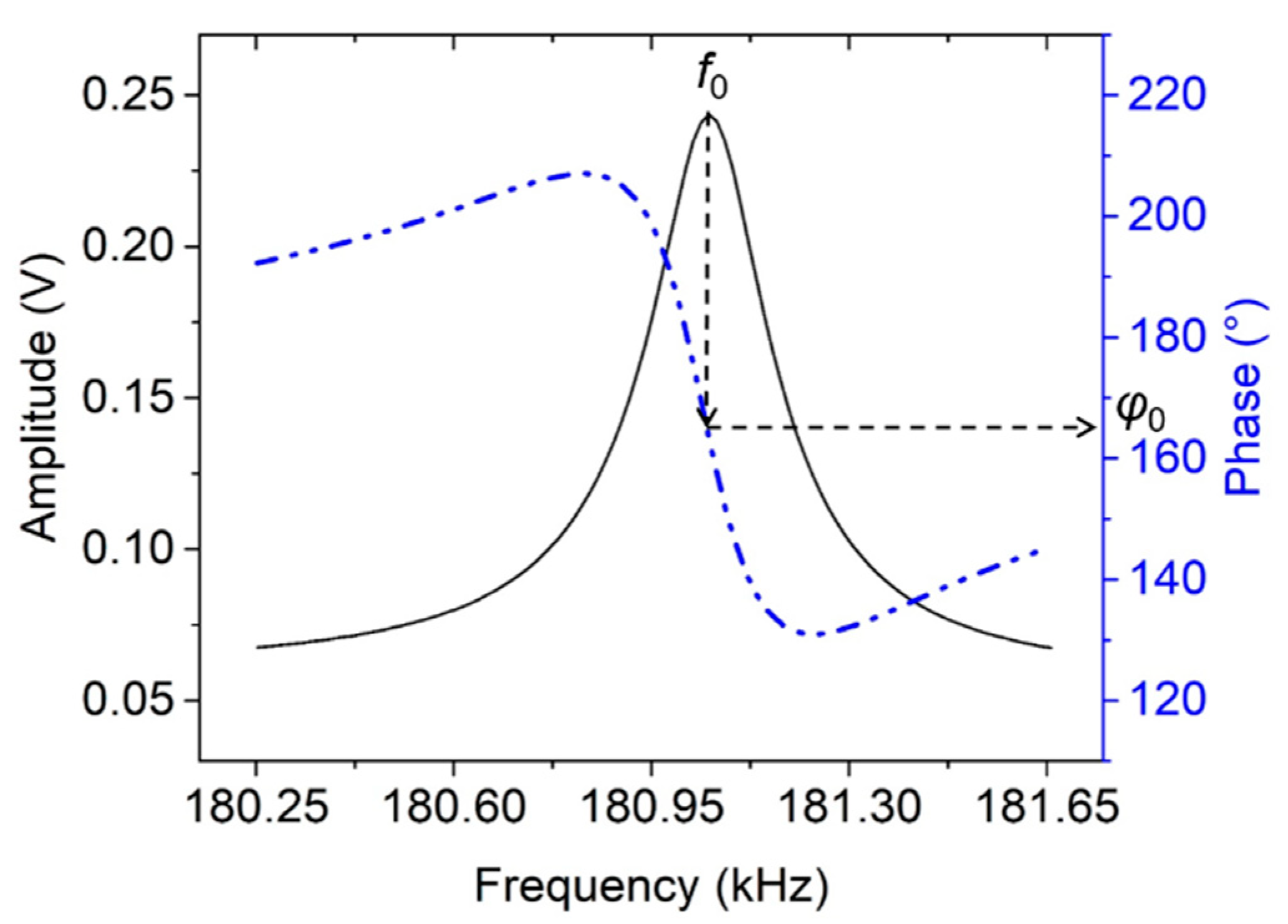
4. Real-Time Resonant Frequency Tracking
Tracking of the resonance frequency is performed by implementing the PLL technique, as shown in
Figure 12. Applying sensor and reference signals at differential mode results in a symmetric amplitude shape (black full line) and an extended range of monotonic phase response with no ambiguity in the phase response (blue dash-dot-dot line), as depicted in
Figure 13. The monotonic phase response is applicable in the PLL-based system for resonant frequency tracking. From the highest peak of amplitude, the resonance phase
φ0, is determined. It is subsequently used as a set point of phase. In the PLL, this set-point value is subtracted from the measured phase difference (resulted from mixing process of differential output and oscillator), generating a current error signal
e(
t). A proportional controller (P-controller) results in an output that is proportional to
e(
t). The response time of the P-controller is adjusted by a proportional gain
Kp which, however, never reaches the steady state condition and thus maintains the steady-state error. Due to this limitation, an integral controller (I) is used in addition to eliminate the steady-state error. It integrates the current error
e(
t) with the previous errors at every sampling time
τ and then sums a cumulative error
e(
τ) over a certain time until it approaches zero. The controller speed can be increased by enlarging the integral gain
Ki and the proportional gain
Kp. Once the error signal is zero, the resonance frequency
f0 is determined and can be tracked henceforth. These two PI parameters are set to achieve the highest precision possible, while still accurately tracking the resonant frequency.
The experiment setup shown in
Figure 12 is used to confirm the performance of the monotonic phase response that is obtained by subtracting the reference signal from the sensor output. The resonant frequency tracking under changing relative humidity (
rH) has been realized by using a lock-in amplifier with an integrated PLL system (MFLI, Zurich Instruments). For comparison,
rH was simultaneously measured using a commercial thermohygrometer (CA 1246, Chauvin Arnoux, Paris, France). In these experiments, we investigated if the resultant nearly monotonic phase response would yield an improved response during the resonance frequency tracking. Therefore, the test configuration involved an assessment of the resonance response and
rH using both the electro-thermal piezoresistive cantilever sensor (coated with ZnO NRs and chitosan) and the commercial
rH sensor under identical conditions. Both sensors were simultaneously placed in a bottle filled with a chemical solution that defined a certain
rH level. Different chemical solutions were used, including phosphor pentoxide (P
2O
5), potassium acetate (CH
3COOK), and magnesium nitrate (Mg(NO
3)
2). The sensors measured
rH (thermohygrometer) and the corresponding frequency shift (cantilever sensor) in the bottle over time, and were then removed and stabilized at ambient air before sequentially transferring them to another bottle-filled chemical solution.
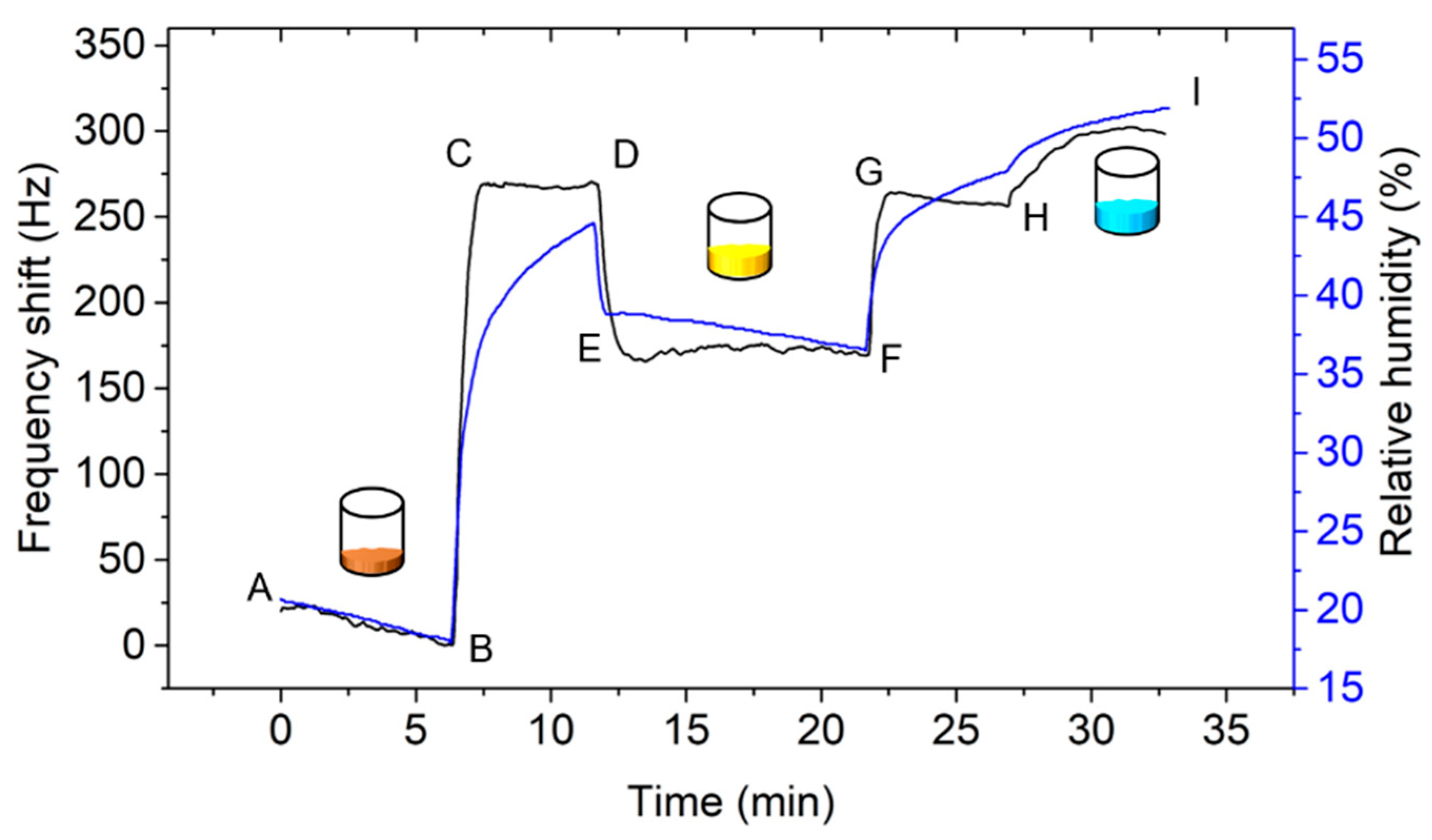
The experimental results (
Figure 14) showed the resonant frequency shifts (cantilever sensor) and relative humidity (thermohygrometer, commercial sensor) over time. The
rH levels measured by the thermohygrometer were 19.37 ± 0.77%, 37.88 ± 0.70%, and 50.68 ± 0.97% for P
2O
5, CH
3COOK, and Mg(NO
3)
2, respectively. In the P
2O
5 and CH
3COOK solutions, the electro-thermal piezoresistive cantilever sensor presents large frequency changes Δ
f0, i.e., ~268.8 Hz (region B–C) and ~99.9 Hz (region D–E). Moreover, this cantilever sensor also stabilizes faster than the commercial sensor at ambient conditions as shown in regions of C–D and G–H. Obviously, the ZnO NRs and chitosan on the cantilever more directly interact with the ambient air by absorbing and desorbing of water molecules thereby yielding a fast response during changes of ambient conditions compared with the commercial sensor, which uses capacitive-based sensing technique. In this case, the water molecules should first pass through the conductor plate before reaching the dielectric material, which then modifies its capacitance value. Therefore, it takes some time to stabilize during the absorption phase for every
rH level. From here, we can conclude that the electro-thermal piezoresistive cantilever sensor with ZnO NRs and chitosan layer shows a better response time during the absorption process compared to the commercial
rH sensor.
At higher
rH level, i.e., Mg(NO
3)
2 solution, however, the electro-thermal piezoresistive cantilever sensor exhibits a slower response time (see
Figure 14 (region H–I)) compared to P
2O
5 and CH
3COOK solutions. This is supposedly caused by a non-ideal configuration between the sensor and reference signals at higher concentration of the water molecules. This condition is expected due to the change of the baselines of the amplitude and phase responses of the sensor output. Moreover, the
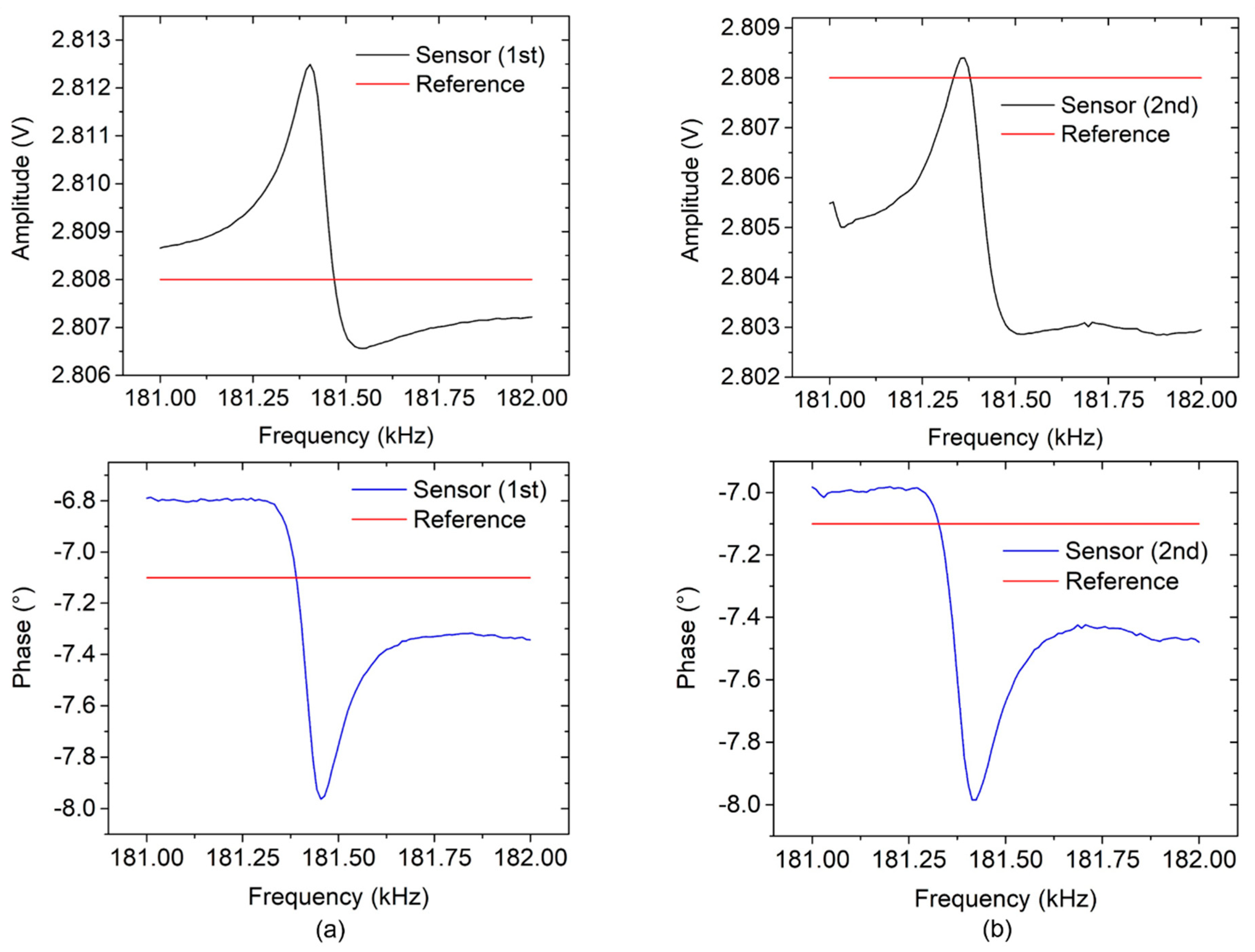
Q-factor changes with
rH level as well. By applying a fitting curve method on the sensor amplitude responses,
Q-values of about 1893 and 1779 were respectively obtained at low (
Figure 15a, 1st condition) and high (
Figure 15b, 2nd condition)
rH levels. This is an improvement compared to the previously reported
Q-values for a ZnO-covered cantilever at different
rH levels, in which it was observed to decrease from 514 ± 18 (
rH = 30%) to 437 ± 15 (
rH = 60%) [
26].
The illustrations in
Figure 15 explain how a non-ideal configuration between sensor and reference signals can gradually occur after extended operation and a corresponding increase of added mass on the electro-thermal piezoresistive cantilever sensor. At the beginning (1st condition), we have an ideal configuration as shown in
Figure 15a, i.e., the reference signals (red) are put in balanced positions between the baselines of amplitude and phase, respectively, of the sensor signal. In the 2nd condition, the mass added to the cantilever had increased. In this case, we have a non-ideal configuration of sensor and reference signals. Amplitude and phase values shifted downwards to the reference signal as shown in
Figure 15b. This condition is expected to reduce the symmetry of amplitude line shape and to thus yield a reversed phase response again. As previously explained, a reversed phase response leads to signal instability in resonance locking. Development of an adaptive reference signal is therefore required to ensure a monotonic phase response during real-time measurement and to overcome this issue.