Carbon Futures Trading and Short-Term Price Prediction: An Analysis Using the Fractal Market Hypothesis and Evolutionary Computing
Abstract
:1. Context, Background and Structure
1.1. Context
1.2. Background
1.3. Structure
2. The EU ETS: An Efficient or a Fractal Market View?
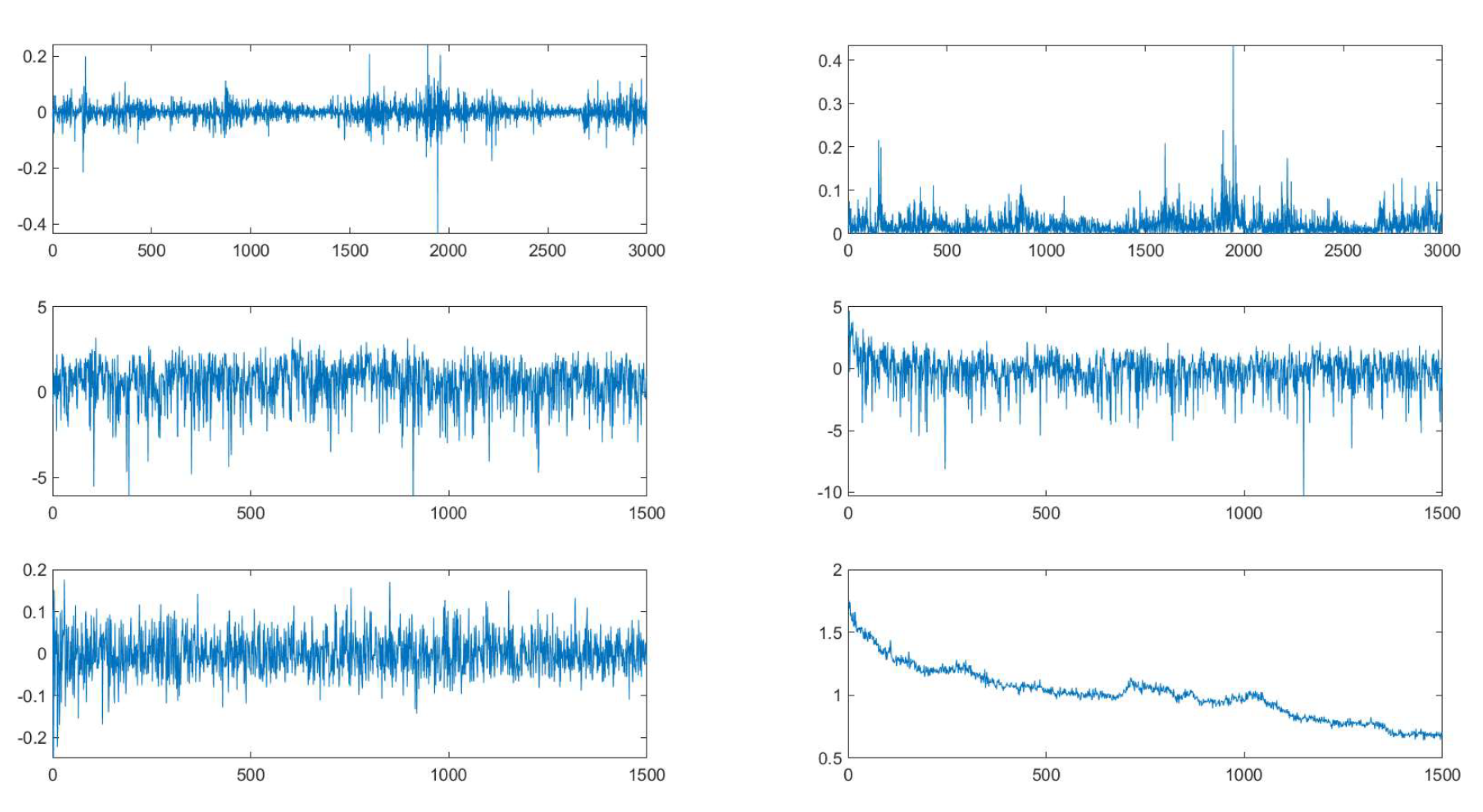
3. Examining the Behaviour of the EUA Carbon Futures Market
4. Stochastic Field Theory and the Determination of an Investment Index
4.1. Einstein’s Evolution Equation
4.2. The Approach to Predicting Market Trends
- The RWH is compounded in the case when ; therefore, EEE is reduced to the simple form
- The EMH is compounded in the case when for a real constant c, i.e., when the PDF is a Gaussian function. In Fourier space, we can write EEE as
- The FMH is compounded in the case when where is the Lévy Index for a real constant c, i.e., when the PDF is Lévy distributed. In Fourier space, the evolution equation is then given byThe Lévy distribution has a Characteristic Function (CF) which is a generalisation to the form
4.3. The Lyapunov Exponent, Volatility, and the Lyapunov-to-Volatility Ratio (LVR)
5. Carbon Futures Trading
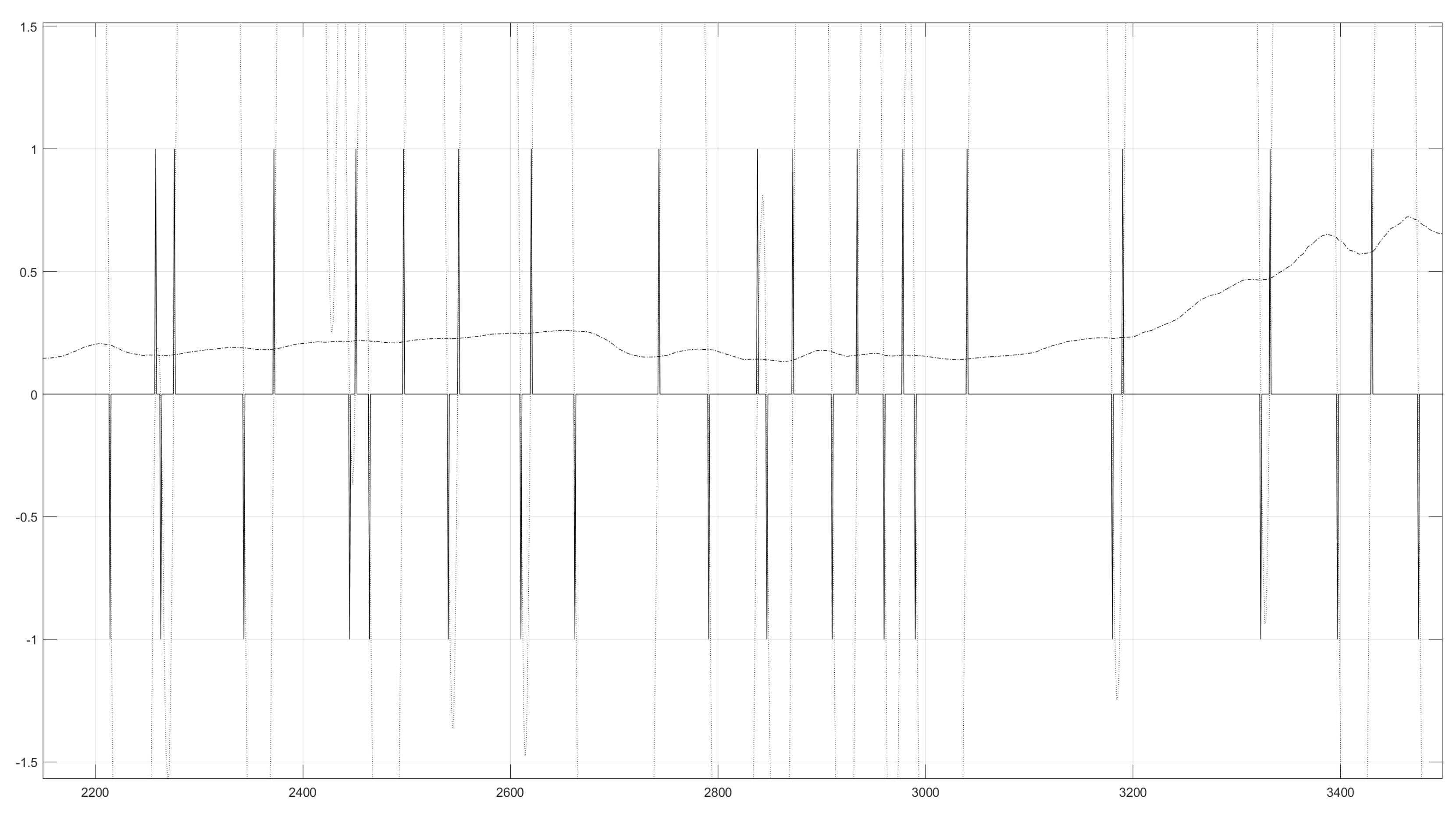
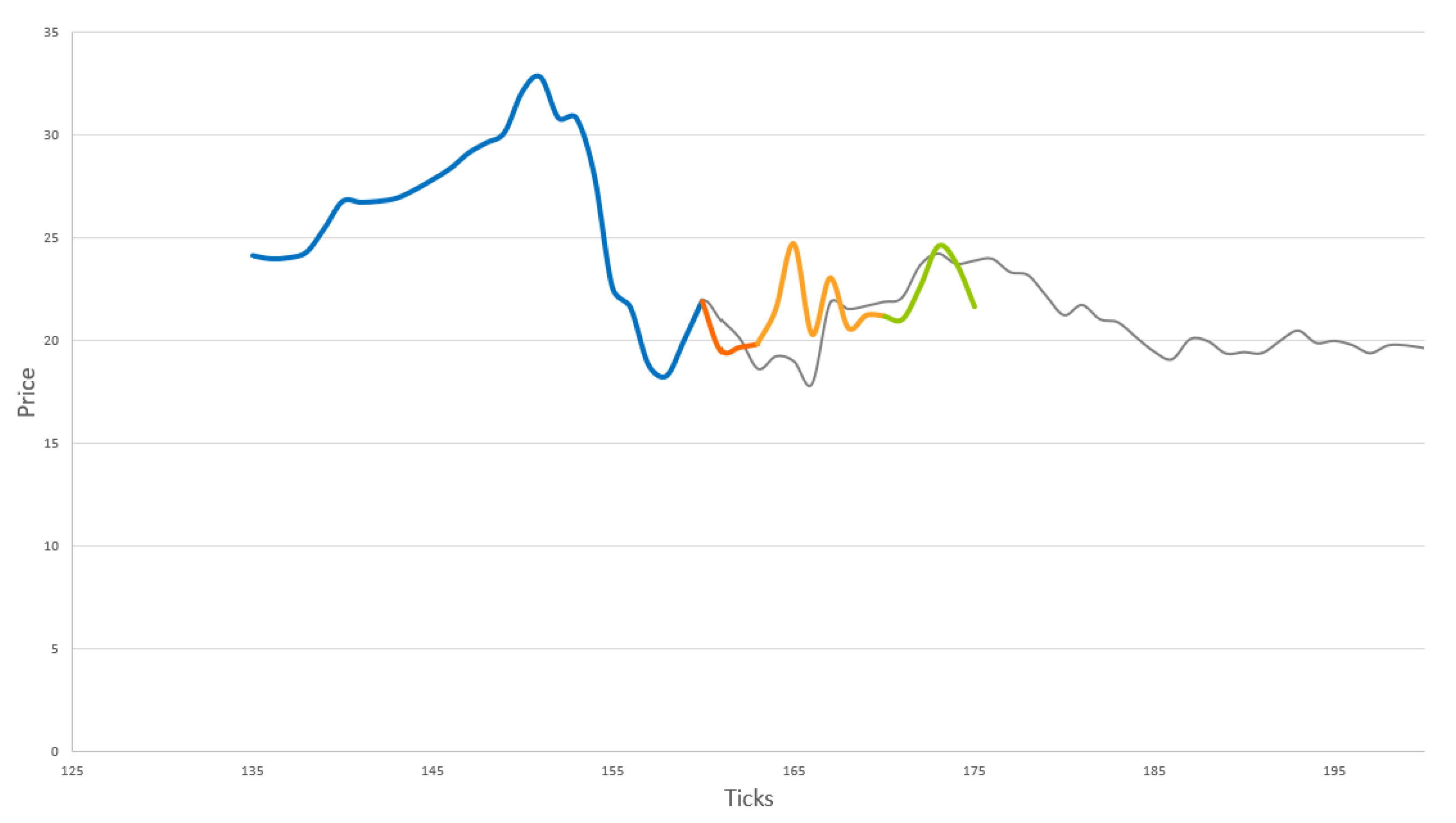
6. Future Price Prediction
7. Summary of Results and Comparison with Other Approaches
- (i)
- an EC (or other) solution to trade execution timing is required (at least for commercially viable levels of return);
- (ii)
- reductions in the value of W (along with the LVR amplitude to support trading decisions) supports a more profitable return (in most cases) than a value of W optimised for trend prediction alone (without EC). To evaluate the benefit (or otherwise) of EC, analysis was carried out to compare the returns using EC against those achieved from the various approaches outlined previously. This was carried out using the 2005–2019 time series and Table 5 presents the comparative returns.
- (i)
- there is validity in using EC in the LVR EC Periods;
- (ii)
- trading using this approach improves returns by overcoming the issue of lag and noise around the trade execution points within a trend;
- (iii)
- this approach may provide ROI expectations well above that otherwise expected in the market and/or comparable with wider benchmarks, even while overall market performance was substantially lower.
8. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. M-Code Used for Data Analysis
Appendix A.1. Function Lyapunov
Appendix A.2. Function Volatility
Appendix A.3. Function Movav
Appendix A.4. Function Evaluator
Appendix A.5. Function Backtester
References
- Tvinnereim, E. The Global Carbon Market in 2020. 2013. Available online: http://www.worldcommercereview.com/publications/article_pdf/109 (accessed on 7 August 2013).
- Reuters, Carbon Market Value Rises. 2019. Available online: https://www.reuters.com/article/us-global-carbontrading-report/ (accessed on 3 November 2019).
- Mandelbrot, B. The Variation of Certain Speculative Prices. J. Bus. 1963, 35, 394–419. [Google Scholar] [CrossRef]
- Fama, E. The Behaviour of Stock Market Prices. J. Bus. 1965, 38, 105. [Google Scholar] [CrossRef]
- Engle, R.F. Auto-Regressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 1007. [Google Scholar] [CrossRef]
- Daskalakis, G.; Markellos, R. Are the European Carbon Markets Efficient? Rev. Future Mark. 2008, 17, 103–128. [Google Scholar]
- Seifert, J.; Uhrig-Homburg, M.; Wagner, M. Dynamic Behaviour of CO2 Spot Prices. J. Environ. Econ. Manag. 2008, 56, 180–194. [Google Scholar] [CrossRef]
- Paolella, M.S.; Taschini, L. An Econometric Analysis of Emission Allowance Prices. J. Bank. Financ. 2008, 32, 2022–2032. [Google Scholar] [CrossRef] [Green Version]
- Benz, E.; Truck, S. Modelling the Price Dynamics of CO2 Emission Allowances. Energy Econ. 2009, 31, 4–15. [Google Scholar] [CrossRef]
- Daskalakis, G.; Psychoyios, D.; Markellos, R. Modelling CO2 Emission Allowance Prices and Derivatives: Evidence from the European Trading Scheme. J. Bank. Financ. 2009, 33, 1230–1241. [Google Scholar] [CrossRef]
- Montagnoli, A.; de Vries, F.P. Carbon Trading Thickness and Market Efficiency. J. Energy Econ. 2010, 32, 1331–1336. [Google Scholar] [CrossRef]
- Paul, E.; Frunza, M.C. Derivative Pricing and Hedging on Carbon Market. In Proceedings of the 2009 International Conference on Computer Technology and Development, Kuala Lumpur, Malaysia, 3–5 April 2009. [Google Scholar]
- Hiroyuki, M.H.; Jiang, W. An ANN-Based Risk Assessment Method for Carbon Pricing; Department of Electronics and Bioinformatics, Meiji University: Tokyo, Japan, 2008. [Google Scholar]
- Sanin, M.; Violante, F.; Bataller, M. Understanding volatility dynamics in the EU-ETS market. Energy Policy 2015, 82, 321–331. [Google Scholar] [CrossRef] [Green Version]
- Fosso, O.B.; Gjelsvik, A.; Haugstad, A.; Mo, B.; Wangensteen, I. Generation Scheduling in a Deregulated System: The Norwegian Case. IEEE Trans. Power Syst. 1999, 4, 75–80. [Google Scholar] [CrossRef]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A.J. ARIMA Models to Predict Next-Day Electricity Process. IEEE Trans. Power Syst. 2004, 19, 366–374. [Google Scholar]
- Garcia, R.C.; Contreras, J.; van Akkeren, M.; Garcia, J.B. GARCH Forecasting Model to Predict Day Ahead Electricity Prices. IEEE Trans. Power Syst. 2005, 20, 867–874. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural Networks for Short-term Load Forecasting: A Review and Evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Szkuta, B.R.; Sanabria, L.A.; Dillon, T.S. Electricity Price Short-Term Forecasting Using Artificial Neural Networks. IEEE Trans. Power Syst. 1999, 14, 851–857. [Google Scholar] [CrossRef]
- Gao, F.; Guan, X.; Cao, X.R. Papalexopoulos, Forecasting Power Market Clearing Price and Quantity Using a Neural Network Method. In Proceedings of the IEEE PES Summer Meeting, Seattle, WA, USA, 18 July 2000; pp. 2183–2188. [Google Scholar]
- Broomhead, D.S.; Lowe, D. Multivariable Functional Interpolation and Adaptive Networks. Complex Syst. 1988, 2, 321–355. [Google Scholar]
- Box, G.E.P.; Jenkins, G. Time Series Analysis: Forecasting and Control (Holden-Day series in time series analysis); Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Feng, Z.H.; Zou, L.L.; Wei, Y.M. Carbon Price Volatility - Evidence from the EU ETS. Appl. Energy 2010, 88, 590–598. [Google Scholar] [CrossRef]
- Marina, F.; Mauer, E.M.; Pahle, M.; Tietjen, O. From Fundamentals to Financial Assets: The Evolution of Understanding Price Formation in the EU ETS, Working Paper. 2019. Available online: https://www.econstor.eu/handle/10419/196150 (accessed on 10 February 2020).
- Lamphiere, M. An Econophysics and Evolutionary Computing Based Approach to Carbon Futures Trading and Price Prediction. Ph.D. Thesis, Technological University Dublin, Dublin, Ireland, 2021. [Google Scholar]
- Ljung, G.M.; Box, G.E. On a Measure of a Lack of Fit in Time Series Models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Box, G.E.; Pierce, D.A. Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Durbin, J.; Watson, G.S. Testing for serial correlation in least squares regression. Biometrika 1971, 58, 1–19. [Google Scholar] [CrossRef]
- Charles, A.; Darne, O. Variance ratio tests of random walk: An overview. J. Econ. Surv. 2009, 23, 503–527. [Google Scholar] [CrossRef] [Green Version]
- Hurst, H. Long-term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Robustness of the Rescaled Range R/S in the Measurement of Noncyclic Long Run Statistical Dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Statistical Methodology for Non-periodic Cycles: From the Covariance to R/S Analysis. Ann. Econ. Soc. Meas. 1972, 1, 259–290. [Google Scholar]
- Wei, Y.M.; Liu, L.C.; Fan, Y.; Wu, G. China Energy Report 2008: Carbon Emissions Research; Beijing Science Press: Beijing, China, 2008. [Google Scholar]
- Blackledge, J.M. The Fractal Market Hypothesis: Applications to Financial Forecasting. Centre for Advanced Studies, Warsaw University of Technology: Warsaw, Poland, 2010; ISBN 978-83-61993-01-83. [Google Scholar]
- Blackledge, J.M.; Kearney, D.; Lamphiere, M.; Rani, R.; Walsh, P. Econophysics and Fractional Calculus: Einstein’s Evolution Equation, the Fractal Market Hypothesis, Trend Analysis and Future Price Prediction. Mathematics 2019, 7, 1057. Available online: https://www.mdpi.com/2227-7390/7/11/1057/htm (accessed on 7 November 2020). [CrossRef] [Green Version]
- Einstein, A. On the Motion of Small Particles Suspended in Liquids at Rest Required by the Molecular-Kinetic Theory of Heat. Ann. Phys. 1905, 17, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Nutonian, Eureqa: The A.I.-Powered Modelling Engine. 2020. Available online: www.nutonian.com (accessed on 29 January 2020).
- Schmidt, M.; Lipson, H. Distilling Free-form Natural Laws from Experimental Data. Science 2009, 324, 81–85. Available online: https://science.sciencemag.org/content/324/5923/81 (accessed on 24 June 2020). [CrossRef] [PubMed]
- Dubcakova, R. Eureqa: Software Review. Genet. Program. Evolvable Mach. 2011, 12, 173–178. [Google Scholar] [CrossRef] [Green Version]
- The Coming Global Carbon Price Boom. 2015. Available online: http://grenatec.com/the-coming-global-carbon-price-boom/ (accessed on 4 December 2020).
- Climate Cap. World Carbon Fund Executive Summary-Generating Absolute Returns from Global Carbon Markets. 2021. Available online: https://www.carbon-cap.com/uploads/vzgdKwr4/WorldCarbonFundExecutiveSummary.pdf (accessed on 17 February 2021).
- Chevallier, J. Macroeconomics, Finance, Commodities: Interactions with Carbon Markets in a Data-Rich Model. Econ. Model. 2011, 28, 557–567. [Google Scholar] [CrossRef] [Green Version]















| Product | From | To | Data Points |
|---|---|---|---|
| EUA Dec 2008 | 15-09-05 | 15-12-08 | 831 |
| EUA Dec 2009 | 14-12-06 | 14-12-09 | 774 |
| EUA Dec 2010 | 13-08-07 | 31-12-10 | 865 |
| EUA Dec 2013 | 03-01-10 | 17-12-13 | 1012 |
| EUA Dec 2014 | 02-01-09 | 16-12-14 | 1494 |
| EUA Dec 2015 | 06-08-10 | 16-12-14 | 1085 |
| Product | L | W, T | Accuracy | Trades |
|---|---|---|---|---|
| EUA Dec 2008 | 831 | 48, 11 | 100% | 11 |
| EUA Dec 2009 | 774 | 48, 11 | 100% | 11 |
| EUA Dec 2010 | 865 | 48, 11 | 80.35% | 16 |
| EUA Dec 2013 | 1012 | 48, 11 | 81.25% | 17 |
| EUA Dec 2014 | 1494 | 48, 11 | 77.74% | 29 |
| EUA Dec 2015 | 1085 | 48, 11 | 77.78% | 20 |
| Product/ Time Series | Length (Ticks) | Long Accuracy | Short Accuracy | Combined Accuracy |
|---|---|---|---|---|
| EUA (2005–2019) | 3572 | 81.48% | 82.14% | 81.82% |
| EUA (2005–2019) | 2000 | 81.25% | 87.50% | 84.37% |
| EUA (2005–2019) | 1000 | 100% | 100% | 100% |
| EUA Dec 2008 | 831 | 100% | 100% | 100% |
| EUA Dec 2009 | 774 | 100% | 100% | 100% |
| EUA Dec 2010 | 865 | 75.00% | 85.71% | 80.35% |
| EUA Dec 2013 | 1012 | 87.50% | 75% | 81.25% |
| EUA Dec 2014 | 1494 | 76.92% | 78.57% | 77.74% |
| EUA Dec 2015 | 1085 | 77.78% | 77.78% | 77.78% |
| Product | ROI (%) () | ROI (%) () | Buy and Hold Change (%) |
|---|---|---|---|
| EUA Dec 2008 | −43.27% | 4.6% | −46.40% |
| EUA Dec 2009 | −4.8% | 22.12% | −38.04% |
| EUA Dec 2010 | −19.66% | −12.81% | −43.86% |
| EUA Dec 2013 | −49.58% | −59.03% | −332.97% |
| EUA Dec 2014 | −47.87% | −46.98% | −335.43% |
| EUA Dec 2015 | −35.60% | −31.88% | −284.33% |
| Zero-Crossings ROI (%) | ROI (%) | ROI (%) | with EC ROI (%) |
|---|---|---|---|
| −23% | −19% | +23% | +36% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamphiere, M.; Blackledge, J.; Kearney, D. Carbon Futures Trading and Short-Term Price Prediction: An Analysis Using the Fractal Market Hypothesis and Evolutionary Computing. Mathematics 2021, 9, 1005. https://doi.org/10.3390/math9091005
Lamphiere M, Blackledge J, Kearney D. Carbon Futures Trading and Short-Term Price Prediction: An Analysis Using the Fractal Market Hypothesis and Evolutionary Computing. Mathematics. 2021; 9(9):1005. https://doi.org/10.3390/math9091005
Chicago/Turabian StyleLamphiere, Marc, Jonathan Blackledge, and Derek Kearney. 2021. "Carbon Futures Trading and Short-Term Price Prediction: An Analysis Using the Fractal Market Hypothesis and Evolutionary Computing" Mathematics 9, no. 9: 1005. https://doi.org/10.3390/math9091005
APA StyleLamphiere, M., Blackledge, J., & Kearney, D. (2021). Carbon Futures Trading and Short-Term Price Prediction: An Analysis Using the Fractal Market Hypothesis and Evolutionary Computing. Mathematics, 9(9), 1005. https://doi.org/10.3390/math9091005






