1. Introduction
The principal purpose of this paper is to provide a review of the Fractal Market Hypothesis (FMH) which is a hypothesis for analysing financial time series based on the principles of fractal geometry, specifically the self-affine properties of stochastic fields. However, this paper has also been composed for readers who have no or little prior knowledge of fractal geometry or the principles of financial time series modelling, risk assessment analysis and future price prediction. For this reason, this paper provides a short introduction to fractal geometry and an overview on the mathematical modelling of financial signals. These elements are then combined to explain the principles of the FMH and how and why it can be used to model financial times series data. The FMH is part of the continuing evolution of ‘technical’ market theory, and, in this section, we provide a contextual overview of some of the basic concepts relating to the study of market risk, presenting the ideas that lie behind the developments in the field that have led to the FMH and its applications.
Following a brief introduction on how probability theory was first introduced to the study of market movements and the analysis that went before, we introduce some of the major theoretical developments in the modelling of financial times series. It is these underlying theories that have proved to be the driving force for the development of the various market analysis methods over the past 100 years, starting with Louis Bachelier’s ‘Théorie de la Spéculation’ [
1]. In the following sections, a review is provided without recourse to any mathematical details associated with the concepts. The foundations for the mathematical models associated with these concepts are considered later on in the paper.
1.1. On the Study of Risk
There are many ways of trying to predict and manage market risk. In financial markets, the oldest and perhaps the simplest approach is termed ‘fundamental analysis’ [
2]. This involves an investigative analysis of a company, industry, or market, and/or the economy, around a proposed investment or trade, which can reveal the cause of stock price changes. The results are then used to try and predict a stock’s next move. This type of fundamental analysis assumes an underlying cause. The price, bond, derivative or commodity is taken to move because of some event or fact, which, more often than not, comes from another external event. The implicit assumption in this approach, is that if one can understand the underlying cause early enough, then one can forecast the event and take the appropriate action to manage the risk or investment. In the real world, however, causes are often obscure or imperceptible. Critical information is often unknown, indeterminable, concealed or even misrepresented (such as in the Enron or Parmalat corporate scandals, for example [
3]). In addition to this, information can simply be misunderstood by some or even all of the market participants.
Major trading houses still employ large numbers of fundamental analysts to find discernible patterns [
4] which are, at times, quite accurate. For example, certain exchange rates can approach a level as described by a fundamental view, before falling back, or trending upwards. However, on an open market, this type of analysis can be severely limited. The precise sentiment, or mechanism, that links news to price is often inconsistent, and is open to individual interpretation. In hindsight, fundamental analysis can often be reconstituted so as to reveal exact predictions of events. However, before the fact, two diametrically opposed outcomes may have seemed equally likely. Thus, although validity may be perceived from time to time, it is not necessarily the best foundation to build a risk management system. In response to this, the financial industry has and continues to develop other forms of data analysis using more quantitative tools.
The second oldest form of analysis is termed ‘technical analysis’ [
5]. This concerns the recognition of patterns (real or perceived), and the study of price, volume and indicator charts, in search of clues as to whether to buy or sell. After falling out of favour in the 1980s, the discipline expanded again in the 1990s as the public took to the internet to trade stocks and shares online. It is from this evolution in communications technology that ‘modern finance theory’ was born, involving analysis methods that emerged from the mathematics of chance, probability theory, statistical analysis, and stochastic field modelling. The basic concept is that while it is not possible to predict the exact value of a future price, the (short term) fluctuations of such future values can be assessed, provided that the statistical characteristics of the fluctuations do not change in time. In this context, risk may be considered to be a measurable quantity, and is therefore manageable. It is upon this assumption that modern day market analysis has been developed. The FMH is arguably an inevitable consequence of the fact that financial time series are non-Ergodic, i.e., they are statistically non-stationary stochastic fields.
1.2. Basic Technical Issues in Financial Analysis
The majority of specific trading strategies rarely appear in the academic literature or are publicly available [
6]. Some research suggests, however, that traders today rely on technical analysis more so than fundamental analysis, in particular, for short-term forecasting, [
7,
8]. Within the realm of technical trading, there are several basic approaches that can be categorised [
9]. These include:
The Price Filter Approach where the strategy is to buy or sell after some price increases or decreases by some pre-defined percentage.
Moving Average Approach, where a buy or sell is generated after the price moves above or below a longer-term rolling average.
Support and Resistance Approach, which is based upon the principle that most trends begin when a price of a commodity breaks out from a fixed price range. This type of strategy seeks to buy or sell when the price rises above or below a local maximum.
Channel Breakout Approach, which is defined as a region within which a high price (taken over a number of periods) is within a pre-defined percentage of the corresponding low price (over the periods considered).
Many of the above approaches originated from stock trading, and not commodities, where much less research is available. This is mainly due to the fact that, historically, commodities were more ‘specialist’ than stocks. With the expansion of electronic and algorithmic-trading, and the way in which this has changed investments, the ways in which commodity and stock-market assets are traded have become more and more similar. Thus, many of the financial principles developed relating to stock markets can also be considered in terms of commodities (at least at a basic theoretical level).
Published articles outlining technical trading approaches date back to the 1960s, where a trading strategy was proposed for Copper futures, for example [
10]. In 1988, a study was undertaken to apply technical trading rules to twelve futures markets which obtained returns of up to 5.6% over a period of six years [
11]. In 2007, an extensive review of technical trading strategies applied to options and futures markets was carried out [
12]. It was found that the average annual profit for almost 100 different approaches was between 4% and 6%.
In 2008, Marshall et al. [
13] posed the question as to whether a basic-rules-type approach could successfully be applied to commodities and determined that, while some traders could make attractive returns using these principles, the strategies did not improve the average market returns when assessed across 15 different sets of commodities. Thus, based on publicly available strategies, it can be concluded that a basic rule-based approach to future trading may not be able to ‘beat the market’, and we can assume circa 4–6% as a benchmark for returns on ‘commercial’ trading strategies. This is especially attractive in the era of low interest rates, as broadly experienced since the financial crisis of 2008.
1.3. Financial Time Series Analysis
A financial time series is essentially a digital signal that, most commonly, consists of a uniformly sampled set of discrete values for the price of a commodity. The time intervals between the sequential price values can vary significantly, from seconds and minutes to days and months. For this reason, many applications developed for processing signals in general can be applied. Financial signal processing relies on the application of numerous algorithms that compute a range of statistical measures, for example, in an attempt to quantify various aspects of the price movements as data are streamed into a trading centre, for example.
The focus of of such signal processing algorithms is based on outcomes that are specific to issues in economics and market analysis. Consequently, such algorithms focus on processing financial signals that yield metrics that are of specific interest to the financial traders. The principal goal of such algorithms is to provide a quantitative analysis that allows a best estimation of movements in financial markets, such as stock prices, options prices, or other types of derivatives. These are typically applied on a moving window basis to produce ‘metric signals’, i.e., signals that are a sequential time series of specific metrics computed from a sample of the original data. Examples of such metrics include the Volatility and the Lyapunov Exponent, which are considered later in this paper. For a series of
N (positive only) price values
, these metrics are given by [
14]
Further, such metrics can be combined into parameters such as the Lyapunov-to-Volatility Ratio (LVR) given by . Metrics such as these are relatively easy to compute (they do not involve regression, for example) and are representative of the time evolution of a financial signal when computed on a moving window basis. In this case, the metrics are related, given that they both include the log difference between two price values (i.e., ) but where, unlike the Lyapunov Exponent , the Volatility is a positive only quantity, i.e., . In addition to developing different ad hoc algorithms to assess the characteristics of a financial signal, it is often desirable to attempt to produce a more physically relevant model which unifies the known properties of the signal, subject to a specific application. This is a desire that is equally applicable to the development of models for financial signals.
An underlying model for a signal
(as a function time
t) is compounded in the equation
where ⊗ denotes the convolution integral,
is the ‘Impulse Response Function’,
is the ‘Information Function’ and
is a random viable of time, i.e., a stochastic function of time that is often referred to as the system ‘Noise’ [
15]. This is a linear stationary model for a signal where the noise is taken to be additive, and where we can define a Signal-to-Noise Ratio (SNR) given by
An underlying problem in signal processing is as follows: given
, and, with knowledge of the deterministic function
and the statistical characteristics of the stochastic function
, solve Equation (
3) for
. This is the deconvolution problem which is usually an ill-conditioned problem and sometimes an ill-posed problem. Either way, it is concerned with the extraction of information from noise for which only an estimation for the information function
is usually possible.
Financial signal processing is, in a sense, also concerned with the extraction of information from noise. However, it often attempts to achieve the impossible, at least in a deterministic sense. This is to extrapolate the signal into the future, to estimate the actual short-term future price of an investment and/or the longer-term trends of that price. Moreover, it is often of importance to predict future changes in the SNR that may occur. This is required to estimate the extent of future price variation in an investment—the future volatility of the signal.
In the field of cryptography, Equation (
3) can be used as a basic model in which
is replaced with
. The ciphertext signal is then given by [
16]
where
c is a measure of the ‘Ciphertext-to-Cipher Ratio’. This form of encrypting a plaintext signal
using a cipher
is predicated on convolutional encoding in which decryption requires the deconvolution problem to be solved exactly. However, unlike signal processing in general, including financial signal processing, in cryptography, the computation of
is under the control of the cryptographer through the application of a cryptographically strong pseudo-random number generator, for example.
In signal processing,
is a naturally occurring noise field and it is usually only possible to determine the statistical characteristics of the background noise by recording a signal when
. This is consistent with the processing of financial signals in which the level of noise (usually attributed to market volatility) is a naturally occurring feature of the signal and needs to be quantified through the computation of the volatility. Moreover, financial signals are intrinsically non-stationary and so Equation (
3) can only be applied to a segment of data over which stationary behaviour can be assumed. It is then of value to obtain suitable models for the stochastic behaviour of these (short-time) financial signals. In this context, and, as will be discussed later, the Fractal Market Hypothesis is based on considering a model for a financial signal given by Equation (
4) for
and where
In this case, the function represents a price for some commodity or stock. On a theoretical level, it is taken to be the ‘density function’ associated with a canonical ensemble of random-walk interactions, relating to the financial transactions that take place in a free market. In the sections that follow, a short history on the rationale for developing fundamental physical models to describe the stochastic behaviour of a financial signal is addressed.
1.4. Structure of the Paper
The structure of this extended work reflects its focus to serve primarily as a review paper which is inclusive of an extensive list of references. The basic aim of this paper is to provide an overview on the history of the development of financial time series modelling and to review the literature associated with the development of such models.
Section 2 and
Section 3 introduces the reader, through a review of the relevant literature, to the Random Walk and the Efficient Market Hypotheses (inclusive of the Black–Scholes model), respectively. The reason for this, is to set the scene and provide a historical background to the evolution of the FMH.
Section 4 introduce the reader to the basic principles of fractal geometry, which is then followed by an introduction, and and review, of the FMH, as given in
Section 5.
Section 6 provides a mathematical model that unifies all the hypotheses considered under the FMH, focusing on the basic differential equations and associated scaling laws associated with the models. In
Section 7, a case study is given which explains (with reference to prior research published by the authors) how the FMH can be used to provide long-term market price predictions using the ‘Lyapunov-to-Volatility Ratio’ and/or the ‘Beta-to-Volatility Ratio’. The purpose of these long-term predictions is to provide a risk assessment on short-term price predictions obtained using a technique in machine learning known as Evolutionary Computing. The ‘TuringBot Symbolic Regression Software’ is used for this purpose, working with cryptocurrency data, specifically Bitcoin (BTC–USD exchange) market prices by way of an example. The work reported in
Section 7 represents the principal original contributions to the field, predicated on a review of the FMH that is provided.
2. The Random Walk Hypothesis
In 1654, Blaise Pascal and Pierre de Fermat first conceived the notion of probability to assist aristocrats gambling on the throw of a dice [
17]. This work helped lay the groundwork for the development of the theory of probability. There was, however, a prevailing perception during the time that ‘real’ mathematicians did not touch money. As a result, work in the field of market analysis and risk did not progress significantly further until the early 1900s when, in France, Louis Bachelier began to study French government bonds [
1].
Bachelier recognised that trying to understand the causes and effects of market movements was futile. He passed over the conventional ‘fundamental’ and ‘charting’ type analysis that had gone before, and instead, attempted to estimate the ‘odds’ that prices would move. This was a unique approach at the time. He undertook this approach by observing the ‘strange and unexpected’ analogy between the diffusion of heat through a substance and market price trends [
1]. He observed that in both cases, it is not possible to make a precise forecast. Whether it be the diffusion of particles in matter, or the activities of individuals in a free market, the dynamics of their behaviour are so complicated, that one can never analyse every factor, and how they interrelate, before any result is itself superseded. However, in both fields, it is possible to observe the broad pattern of probabilities that describes the whole system. Bachelier, therefore, adapted the principles of one field (thermodynamics) to the problems of another (market dynamics).
The Bachelier model starts by looking at the markets in terms of what Bachelier called a ‘fair game’. This is analogous to a simple coin toss: it is as likely to come up heads as it is tails. Moreover, each time you toss a coin, the odds remain 50–50 regardless of what happened in the prior toss. In other words, Bachelier assumed that there was no market memory. While it is possible to see extended runs of heads or tails, with each toss of the coin, the trend is as likely to end as it is to continue. In effect, what Bachelier referred to was what we today know as a ‘random walk’. This term was first introduced by Karl Pearson in 1905 [
18] and can be defined as a ‘mathematical formalisation of a path that consists of a succession of random steps’.
In the context of financial markets, the concept was later developed into what can be termed the Random Walk Hypothesis (RWH), e.g., [
19,
20]. An example of a three-dimensional random walk is given in
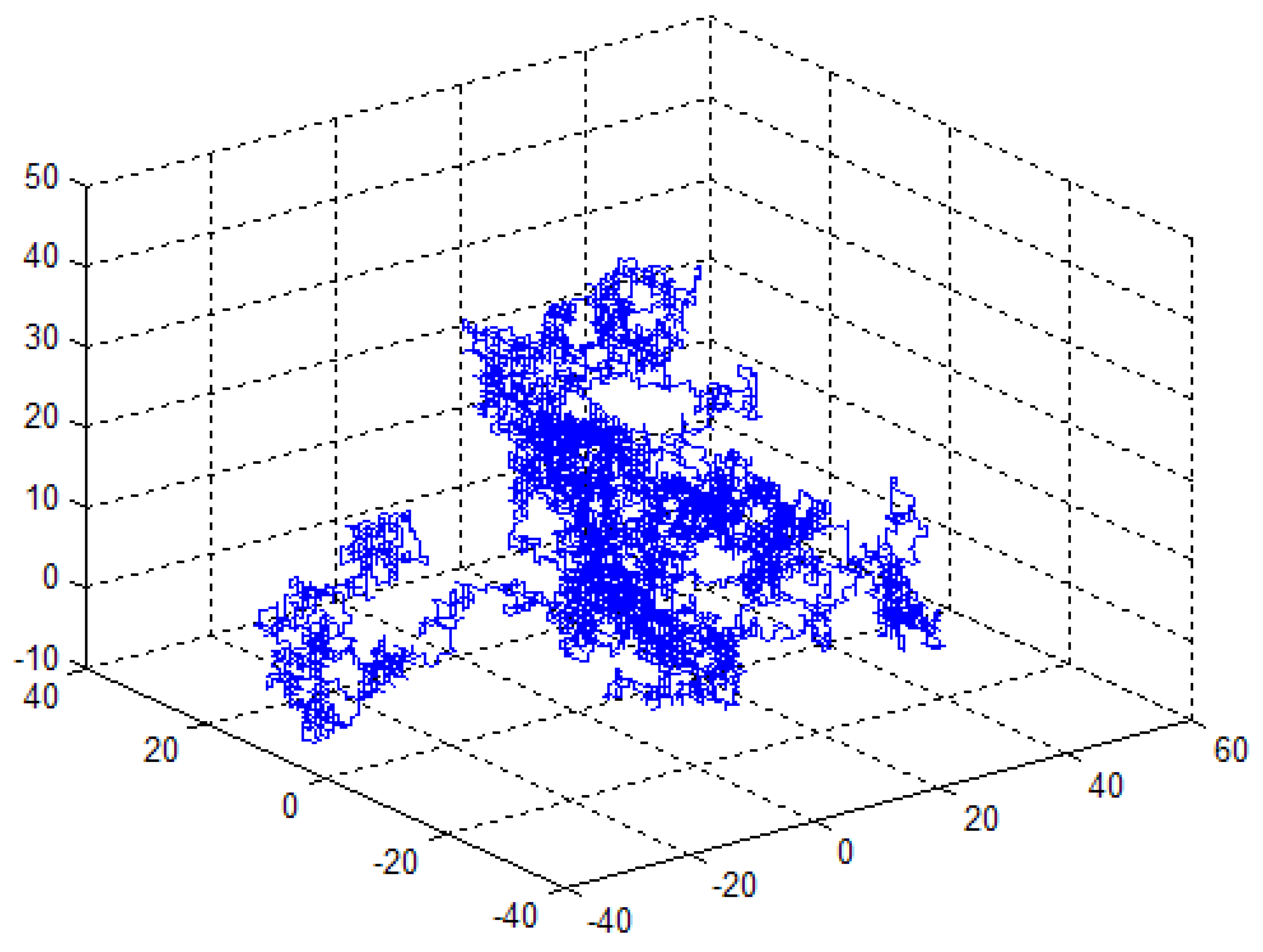
Figure 1 [
21]. Models of this type are used in many applications where they help to explain the observable characteristics of fields that are known to be the result of stochastic processes, i.e., where the spatial and temporal characteristics of a physical system are non-deterministic.
Before Bachelier, Jean Claude Fourier had devised the heat equation to describe the way heat (specifically, the temperature) spreads through a material [
22]. Bachelier adopted this equation to calculate the probability of government bond prices rising up and down, in a technique that he called the ‘Radiation of Probability’. Because the Scottish botanist Robert Brown [
23] was the first to comment on the erratic way in which tiny pollen grains moved in water, random walks are often referred to as Brownian motion, a phenomenon that was first investigated theoretically by Albert Einstein in 1905 [
24]. This led to the development of a field equation—the ‘Evolution Equation’—which was similar to that used by Bachelier to explain the characteristics of random motion. Einstein’s evolution equation is an equation for the density function (a function of space and time) which represents the number of particles per unit dimension undergoing random walks. In doing so, Einstein was able to use his evolution equation to derive the diffusion equation, which has the same basic properties as Fourier’s heat equation, when the density function is taken to describe temperature.
Using the rationale associated with a random walk, Bachelier argued that the best estimate of tomorrow’s price is the price of today. In other words, market prices behaved as a ‘martingale’ (i.e., today’s price seems to be yesterday’s price plus some random component). Moreover, he argued that each and every price variation is unrelated to the previous one (or the next one), a result that occurs through the same unchanging processes that drive the markets. In other words, he proposed that market changes were a sequence of independent and identically distributed variables. In this context, Bachelier’s opening lines in his ‘Théorie de la Spéculation’ are as follows [
1]: ‘The factors that determine activity on the Exchange are innumerable, with events, current or expected, often bearing no apparent relation to price variation. In addition to the somewhat natural causes for variation, come artificial causes: the Exchange reacts to itself, and the current trading is a function, not only of prior trading, but also of its relationship to the rest of the market. The determination of this activity depends on an innumerable number of factors: it is thus to hope for mathematical forecasting. Contradictory opinions about these variations are so evenly divided that at the same instant buyers expect a rise, a sellers expect a fall’. Bachelier later added [
1]: ‘The calculus of probability can doubtless never be applied to market activity, and the dynamics of the Exchange will never be an exact science. But it is possible to study mathematically the state of the market at a given instant; that is to say, to establish the laws of probability for price variation which the market at that instant dictates’.
Bachelier’s proposal suggested that if all of the price changes of French government bonds were plotted as a time series, then they will spread out across the paper in a familiar bell-type-shape curve (a normal or Gaussian distribution) with many small changes clustered in the centre, and fewer large changes in the tails. An original approach at the time, this idea conveniently paved a way for using the statistical methods that had been developed earlier by Carl Fredrick Gauss for the description and analysis of normal or ‘Gaussian’ distributions coupled with the Central Limit Theorem, i.e., that the continued addition of different and independent stochastic fields with different characteristic statistical distributions will produce a stochastic field that is normally distributed. In the context of this theorem (the combination of stochastic systems tend to reduce to one that is Gaussian distributed), Gauss’s famous distribution came to be applied to the analysis of financial and commodity markets. This distribution is taken to describe the price differences (and not the price) of a financial time series, a distribution with a mean of zero. Moreover, in financial time series analysis, it is the underlying statistical model that forms the basis for the so-called Efficient Market Hypothesis, as shall be discussed in the following section.
3. The Efficient Market Hypothesis
Bachelier’s economic insight went unnoticed for many years; indeed, he was roundly criticised by his peers at the time [
25]. However, after the 1929 Wall Street crash, more economists and mathematicians began trying to understand financial markets and the stigma that had previously existed in regard to Bachelier’s ideas began to disappear. In 1956, the work of Bachelier was acknowledged by Paul A. Samuelson and the idea of ‘fair game’ and ‘random walks’ caught on. Economists began to recognise the advantages of describing markets based on the principles of Brownian motion. In the 1960s and 1970s, these concepts were developed further into a broader framework through the work of Eugene Fama, for example, who studied market dynamics and developed Bachelier’s ideas beyond the model of independent increments. He subsequently formed the basis of a financial model that would later come to be known as the Efficient Market Hypothesis (EMH) [
26].
The EMH asserts that financial markets are efficient, specifically, ‘informationally efficient’. In this sense, it is not possible to consistently achieve any returns that are in excess of the average market returns, at least, on a risk-adjusted basis, given the information that is available at the time the investment is made. In other words, an efficient financial market is a market where the price always fully reflects the information that is available.
The idea that all market information is instantaneously available is not physically reasonable and is as philosophically irrational as the principle of instantaneous action at a distance, which underpins Newtonian mechanics, for example. The reality is that, as with the propagation of any physical field which occurs at a finite speed, market information is not obtained instantaneously, but takes a finite period of time to percolate through the global financial system, even though that system is constructed from an increasingly efficient information network and communications infrastructure.
Eugene Fama went on to detail two crucial concepts that effectively define the nature of efficient markets. He proposed three types of efficient markets; strong, semi-strong and weak forms. Each of these forms is related to what information is factored into the market—the price of a specific commodity. Weak-form efficiency reflects all publicly available information on the price of a commodity. Semi-strong efficiency requires that the markets react quickly to new public information, whether it relates to trading activity or new market information. Finally, strong-form efficiency assumes that all knowable information about a company or stock is already embedded in the price of the security, both public and private. However, since new information enters the market randomly, asset price movements must also therefore be random [
27]. Thus, the more efficient the market is, the more random the sequence of price changes becomes. This eliminates any potential opportunities for price prediction (i.e., with returns over and above the ‘random walk’ model) as no investment pattern should be discernible [
28].
The EMH demonstrates that the notion of market efficiency can, in principle, be rejected, unless the accompanying model of market equilibrium is also rejected, i.e., the price setting mechanism. This concept is known as the ‘Joint Hypothesis Problem’, which states that when a theoretical model yields returns that are significantly different from the actual return, then it is not possible to be fully certain if there exists an imperfection in the model, or if the market is inefficient. In this context, traders are only able to modify their models by introducing different factors in order to eliminate any anomalies. This is justified in terms of explaining, as completely as possible, the actual returns associated with a financial model. The anomalies then function as flags to the model maker in terms of whether it can predict returns from the factors that have been introduced into the model. However, as long as there exists an anomaly, then neither the conclusions relating to a flawed model or the issue of market inefficiency can be fully rationalised.
In the 1970s and 1980s, Fama’s hypothesis came to be the guiding principle for many standard tools of modern finance, especially on how to value securities. Critics, however, subsequently blamed Fama’s belief in rational markets for the dot-com crash between 1999 and 2001 [
29]. In response to this criticism, in 2012, Fama, along with other proponents of the EMH, stated that market efficiency does not mean that there is no uncertainty in regard to the future, and that market efficiency is but a simplification of the financial system, which may not always be the case [
30]. This is certainly true, and, moreover, scientifically prudent. It is within this context that the Fractal Market Hypothesis becomes a natural successor of the EMH.
3.1. The Modern Portfolio Theory
In 1952, Markowitz introduced ‘Modern Portfolio Theory’ (MPT) [
31], which would later simply became known as ‘Portfolio Theory’. This is a model for the inclusion of diversification in investment, with the aim of determining a grouping of investment assets that collectively has a lower risk than any individual asset. Markowitz’s hypothesis grew out of earlier work by John Williams in the late 1930s, where Williams argued that to estimate a stock’s value, one should start by forecasting how much in dividends it will pay; then, one should adjust the prediction for inflation, foregoing interest, and other factors which make the forecast uncertain. In considering Williams’ earlier work, Markowitz noted that investors do not only look at their potential profit, but also look for diversification. They think about risks as well as reward, fear as well as greed. They buy many stocks, not just one and thereby build portfolios. This is a form of ‘spread betting’.
Markowitz pondered on how to translate these two concepts (i.e., risk and reward), into models that market practitioners could work with. Risk, Markowitz thought, depends on how much the stock price swings up or down around a mean—in other words, the odds that you guessed wrongly in regard to the final price. Markowitz was, in effect, proposing that the prospects for every stock can be described by just two numbers, the reward and risk. These numbers are related to the mean and the variance, the variance being the average squared deviations from the mean, which in turn, is related to the ‘Volatility’ of a stock price over time. Each possible combination of stocks will give a different return and a different overall risk profile. In addition, stock prices have a tendency to move up and down together, which Markowitz likened to the simple coin tossing game that had gone before. If the market was uncorrelated, it was a ‘fair’ game and one could expect to come out even. However, if correlated, there would be a biased tendency. Markowitz’s theory, therefore, was to mix stocks so that one could lower the overall risk profile of the portfolio. If this was achieved efficiently, Markowitz argued, one would not sacrifice too much profit.
As a result of this hypothesis, Markowitz and his contemporaries became credited with transforming investment from a game of stock tips and hunches to the engineering of means, variances, and ‘risk aversion’ indices. Indeed, the term ‘financial engineering’ first became popular on Wall Street, with the introduction of Markowitz’s Modern Portfolio Theory. There was, however, and still are, problems with this theory. As Markowitz points out in [
32], ‘it is not certain that assuming a normal distribution is necessarily suitable for the measurement of market risk’.
To build an efficient portfolio, one need accurate forecasts of earnings, share prices, and the volatility associated with thousands of stocks; otherwise, the predictive results may become wildly inaccurate. Further, for any stock, it is necessary to calculate its ‘covariance’ (a measure of the joint variability of two random variables) for every other stock and/or how it fluctuates against all other stocks. For any major market, this amounts to millions of calculations. Moreover, because of constant price changes, this exercise needs continual repetition to up-date the result in time. It was this very need that became the primary driving force behind the development of the mainframe computer on Wall Street in the 1960s.
MPT is essentially concerned with a trade-off between risk and return, where investment advisers focus on returns with the occasional caveat ‘subject to risk’. Most modern portfolio theories assumes that the exists a risk-free investment, that there will be a return from depositing funds in a sound financial institute or investing in equities. In order to increase the profit, the investor must accept greater risk. Why should this be so?
Suppose there exits an opportunity to have a guaranteed return greater than that from a conventional bank deposit. In this case, no (rational) investor will invest any money with a bank. Moreover, if the investor could borrow money at less than the return on an alternative investment, then they would borrow as much money as possible to invest in an opportunity with a higher yield. In this case, and, in response to the pressure of supply and demand, the banks would raise their interest rates. This would attract money for investment with the bank, and reduce the profit made by investors who have borrowed money from the bank. And if such opportunities did arise, the banks would probably be the first to invest our savings in them. This argument exhibits elasticity because of various ‘friction factors’ such as transaction costs, differences in borrowing and lending rates, liquidity laws and so on. However, in general, the principle is sound, because the market is saturated with arbitrageurs whose purpose is to seek out and exploit irregularities or miss-pricing.
Problems arise with MPT due to the fact that the market is considered to be ‘rational’. In other words, all investors are assumed to aim to maximise economic efficiency alone (i.e., to make as much money as possible, regardless of any and all other personal, environmental, strategic, or even social considerations) [
31,
32]. It simply attempts to maximise risk-adjusted returns, without regard to other consequences or thought.
Since being proposed, there has been widespread criticisms in regard to both the theoretical concepts and practical applications of MPT. These include the observations that:
financial returns do not follow Gaussian distributions;
correlations between asset classes are not fixed, but instead, vary depending on external events, especially in times of crises.
Moreover, there is growing evidence that investors are not rational and that the markets are not efficient [
33].
In MPT, no attempt is made to explain the underlying structure of price changes. Various outcomes are simply given in terms of probabilities. Thus, if a history exists of a particular system-level event, such as the liquidity crisis experienced following the crash of 2008, then there is no way to compute the odds of it occurring. In this respect, the reliance of MPT on asset prices means that it is vulnerable to all the typical and past modes of market failure. It can therefore be argued that MPT will break down, precisely when investors are most in need of protection from risk [
34].
3.2. The Black–Scholes Model
The Black–Scholes model considers a financial market which contains certain derivative investment instruments. The model was first articulated by Fischer Black and Myron Scholes in their 1973 paper,
‘The Pricing of Options and Corporate Liabilities’ [
35]. They derived a (nonlinear) partial differential equation, now known as the Black–Scholes equation. This equation governs the price of an option
as a function of stock price
S over time
t and is given by
where
r is the risk-free interest rate, and
is the volatility of the stock. Solutions to this equation require that
r and
are known, for which only estimates are possible, as gauged at some future point in time. In practice, it is this issue that can lead to solutions of the Black-Scholes equation becoming inaccurate.
The principal idea associated with the derivation of this equation is that one can hedge an option perfectly by buying and selling the underlying asset in just the right way. Consequently, this eliminates risk. However, the principal assumption is that the options markets are ‘frictionless’ (efficient). Robert Merton would later be the first to publish material expanding on the mathematical understanding and basis of the options pricing model. This type of hedge is now commonly referred to as ‘delta hedging’. Since its introduction, it has became the basis of many of the hedging strategies used on Wall Street and other major investment companies around the world. The acceptance of the model led to a rapid increase in options trading worldwide and legitimised the options markets. The model still remains widely used today, although often with bespoke adjustments and market correction factors.
The original model incorporates constant price variations of a stock, the time value of money, the option’s strike price, and the time for the option to expire. In order for the model to be applicable in practice, it also has to ‘assume away all kinds of complications’ [
36]. For example, Black and Scholes, like Bachelier and Markowitz before them, assumed that a stock’s risk (i.e., its volatility or ‘Vol’) can be gauged by a normal distribution. From these underlying assumptions, they showed that ‘it is possible to create a hedged position, consisting of a long position in the stock and a short position in the option, whose value will not depend on the price of the stock’ [
36]. Within just a few years, traders had incorporated the Black–Scholes terminology of ‘Vol’s’ (estimates of the Volatility at a point in time), for example, into their daily language. An entire industry grew up, and with the help of the Black–Scholes model (and its many subsequent variations), corporate financiers bought insurance, debt portfolios, and hedged against unwanted market problems more than ever before [
37].
The Black–Scholes model permitted an entirely new type of trading; not just in the actual stocks or currencies themselves, but in their volatility. Traders could construct elaborate combinations of options, so that they could cash in; not at a specific price, but when the price swung more wildly up or down than normal. Alternatively, they could design option packages that paid off only if prices were steady.
The conceptual leap associated with the development of the Black–Scholes model is that traders are not estimating the price of an asset in the future. Rather, they are gambling on how risky the market will be at some point in that future. In other words, they are considering how volatile the markets will be at a later date. This, of course, requires a good estimate of the future volatility and it is in this respect that Black–Scholes analysis is based on a ‘random walk’ model, in which price changes are taken to be independent and conform to a normal or Gaussian distribution.
As a result of this key underlying assumption, the Black–Scholes model has shown a fundamental inability to explain the proven characteristics of financial markets, such as Kurtosis (long tails), skewness, clustering, flights, the volatility smile (i.e., where graphing implied volatilities against strike prices for a given expiry, yields a curved ‘smile’ instead of the expected straight line) [
38], or to explain major market crashes in the past that have led to recession. In fact, the widespread use and heavy reliance on the Black–Scholes model is now considered as a significant contributor to the 2008 global economic crash [
39].
3.3. Value and Limitations of the Efficient Market Hypothesis
Aside from the schools of thought on financial market behaviour already discussed, there are a variety of significant articles that also advocate an ‘efficient market’ approach. Other publications have tried to summarise the history of the EMH and categorise the spectrum of views on it, for example, [
40,
41].
In 1959, Osborne [
42] showed that the logarithm of stock prices follows Brownian motion. This is the basis for the so-called ‘log normal model’, where price variations in time denoted by the function
is given by the equation
where
reflects the average rate of growth of an asset, and
is taken to be a normally distributed stochastic field. In regard to this equation, the relative log-price change of an asset at a point in time
t is taken to be determined by some random value
whose amplitude is determined by the volatility
with the sum of an underlying trend component determined by the value of
. Thus, when
, the price value may exhibit long-term trends characterised by an exponential growth or exponential decay, depending upon whether
is positive or negative, respectively. This model is an example of a (continuous) log-normal random walk and includes the following properties:
- (i)
price increments exhibit statistical stationarity in which samples of data taken over equal time increments can be superimposed onto each other in a statistical sense;
- (ii)
the scaling of prices can be suitably re-scaled such that they too, can be superimposed onto each other in a statistical sense;
- (iii)
price changes are statistically time independent.
In 1961, Muth introduced a hypothesis that makes the case that current expectations strongly influence future performance [
43]. In other words, a trader may make a prediction based on available information and past experience, and because this prediction is based on rational reasons, and the market does not waste useful information, the prediction is likely to come true, save for a random error. In this context, Malkiel [
44] published
‘A Random Walk Down Wall Street’ in 1973, a book which has proven to be one of the most popular publications on the theory of random walks, and is subsequently cited by many in support of an efficient market assumption.
In 1978, Ball collected what was regarded as ‘scattered pieces of anomalous evidence regarding market efficiency’ in an attempt to review the acceptance of the EMH [
45]. He believed that ‘there is no other proposition in economics which has more solid empirical evidence supporting it, than the Efficient Market Hypothesis’. Despite drawing this conclusion, he also referred to a number of papers that found anomalies with the hypothesis. In summary, he stated that: ‘the studies provide a powerful stimulus and serve to highlight the fact that there are inadequacies in our current state of knowledge’.
Eun and Shim, in 1989 [
46], used auto-regressive analysis (i.e., a stochastic process model used to capture the linear inter-dependencies among multiple time series) to study nine international stock markets. They found interdependence amongst national stock markets, and noted that this was consistent with informationally efficient markets. In 1991, Jackson [
47] wrote a paper that considered a detailed model of the price formation process, assuming that agents are not price takers and concluded that it is possible to have an efficient market.
In 1990, Lo [
48] wrote a paper entitled
‘Long Term Memory in Stock Market Prices’. He used a modification of Mandelbrot’s Re-Scaled Range Analysis (to be discussed later on in this work) that accounted for short-term dependence to find that there is ‘little evidence of long-term memory in historical US stock market prices’. He further edited two volumes that combined the most influential articles on the EMH at the time [
49]. However, in 1999 Lo and MacKinlay [
50] published
‘A Non-Random Walk Down Wall Street’, in which the authors put the EMH to the test, and concluded that ‘markets are not completely random after all, and that predictable components do exist in recent stock and bond returns’.
Metcalf and Malkiel [
51] studied a number of Wall Street Journal contests, and found that experts failed to consistently beat the market. In 2001, Rubinstein [
52] re-examined some of the significant claims made in the literature against the EMH, and concluded that markets are rational. Similarly, Malkiel [
29] continued the defence of the EMH by examining some of its criticisms. He concluded that markets are far more efficient but less predictable than many academic papers have reported on, arguing that when anomalies have been noted and published, practitioners tend to implement strategies in such a way that the anomalies subsequently weaken or disappear, thereby evolving market efficiency.
In 2004, Timmermann [
53] published a paper entitled
‘Efficient Market Hypothesis and Forecasting’ in which non-stationary behaviour in a financial time series is considered that arise due to the number of investors who discover a technique that has been trading/forecasting successfully, and subsequently utilise the technique themselves. The end result is that the success of the strategy is short lived as it is eventually incorporated into all market prices. In 2005, Malkiel [
54] analysed the performance of professional investment managers and concluded that in general, there is no out-performance of index benchmarks. The paper also provided evidence that large market prices tend to reflect all information. In this context, Toth and Kertesz, in 2006 [
55], produced evidence of growing efficiency on the New York Stock Exchange and Yen and Lee [
56] produced a survey paper in 2008, concluding that ‘the EMH is here to stay’.
In 2009, Ball [
57] addressed the global financial crisis and argued that the collapse of large institutions such as Lehman Brothers reflects a failure to heed the teaching of efficient markets. He responds to a number of criticisms that were levelled at the EMH around the time of the crisis, such as the view that the EMH should have predicted the crisis, or predicted the stock price bubble. Ball lays the blame at the feet of actors in financial institutions for the stock price bubble, claiming that not enough empirical calculations were carried out on the stock prices to identify that a bubble had been created. Further, he offers the random walk argument in response to the EMH predicting the crash. If indeed a crash was predictable, then the very essence of the EMH would be untrue, stating that: ‘if anything, the hypothesis predicts that we should not be able to predict crises... if we could predict a market crash, current market prices would be inefficient because they would not reflect the information embodied in the prediction’. This statement reflects the intrinsic limitations of the EMH and is indicative of the way in which financial models based on the FMH have evolved since the crash of 2008. This is in keeping with the psychology of judgment and decision-making, as well as behavioural economics in regard to prospect theory, for example, as considered by Daniel Kahneman [
58]. In order to appreciate the FMH, it is useful to first review the underlying principles of fractal geometry. For this reason, a short overview of the subject is given in the following section.
4. An Overview of Fractal Geometry
The term fractal geometry was first coined by Benoit Mandelbrot [
33]. The term
fractal is derived from the Latin adjective
fractus. The corresponding Latin verb
frangere means ‘to break’, to create irregular fragments. Moreover, in addition to the term ‘fragmented’,
fractus also means ‘irregular’. Both meanings are preserved in the term
fragment. Thus, the term ‘fractal’ is well suited to describing the study of geometric objects that exhibit scale invariance or self-similarity.
Self-similar objects are an intrinsic feature of the geometry of nature, where natural objects have a fundamental and universal geometric feature. This feature is that they tend to look the same at different scales, a property known as ‘self-similarity’. Otherwise, they tend to at least have an affinity at different scales; they are self-affine. However, it is not just the shape or geometry of natural objects that exhibit self-affinity, but the time evolution of such objects. Financial time series are examples of the latter case, i.e., the time evolution of a self-affine stochastic field. The Fractal Market Hypothesis is a result of noting that a financial time series looks the same over different time scales, at least in a statistical sense, i.e., the distribution of price values over a day, for example, is similar to the distribution for a month, which is similar to the distribution for a year and so on (assuming that there are enough data over each time scale to make the distribution—the computed histogram—statistically significant).
The mathematical roots of fractal geometry can be traced back to published works starting in the 17th Century with notions of recursion—the process of repeating things in a self-similar way. This discovery was complemented with studies undertaken primarily in the 19th Century, on classes of continuous functions that were not differentiable functions in the usual sense [
59].
In 1904, Helge von Koch, extending the ideas of Poincaré (the first to discover a chaotic deterministic system) gave a definition for a self-similar function [
60]. The principles of self-similarity were considered further by Paul Lévy. In his 1938 paper
‘Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole’, new self-similar curves were described such as the ‘Lévy C Curve’ [
61].
In the 1960s, Benoit Mandelbrot considered the basis for a self-similar geometry in papers such as
‘How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension’ [
62]. In 1975, he consolidated the ideas and results of hundreds of years of mathematical development by coining the word ‘fractal’. By 1982, he had expanded these ideas in his book
‘The Fractal Geometry of Nature’ [
33], a work which introduced fractal geometry into the mainstream of professional and popular mathematics.
4.1. Self-Similar Functions
For a one-dimensional function
, say, the property called self-similarity is compounded in the result
where
is the scale length (for all dilations) and
is some exponent which determines the amplitude over which the function exhibits self-similar properties. If, for example,
, then the function is exactly self-similar.
The term self-affinity is used to describe objects that have a distorted self-similarity. An object is self-similar if is scales by the same amount in all directions. In terms of Equation (
5), this would mean the
is a constant for all values of
x. A self-affine object does not necessarily scale identically in all directions; in terms of Equation (
5),
may vary with
x so that
becomes a non-stationary self-similar function. Thus, the term self-affinity is a more general description of the fractal geometry of nature as it is rare for natural objects to exhibit scale invariance in all directions, i.e., the Fractal Geometry of nature is a non-stationary phenomenon.
From the scaling theorem (or similarity theorem) of the Fourier transform, the spectrum
of a function defined by Equation (
5) is given by
where
is the Fourier transform, defined by
This relationship is important in the (spectral) analysis of stochastic functions that are statistically self-affine, financial time series being examples of statistically self-affine (digital) signals.
4.2. Self-Affine Structures
Self-affine structures generate objects which we often perceive in terms of ‘texture’. As Manelbrot states, ‘texture is an elusive notion which mathematicians and scientists tend to avoid because they can not grasp it... and... much of fractal geometry could pass as an implicit study of texture’ [
33]. In addition to the fractal geometry of (time-invariant) objects or fields, the time evolution of such fields also exhibits a self-affine behaviour. This includes the ‘complexity’ associated with dynamical systems that are nonlinear for which there is a definable connectivity between the nonlinearity of the system undergoing feedback (iteration) and the self-affine characteristics that the system exhibits.
Quantifying this ‘connectivity’ is compounded in the Feigenbaum diagram [
63] which is used to graph the chaotic properties of a nonlinear feedback system, specifically, an iteration applied to a nonlinear function
. The Feigenbaum diagram is a display of the values obtained or approached asymptotically for fixed points, periodic orbits or chaotic attractors, as a function of the ‘bifurcation parameter’
a, say. A standard example of this, is the Logistic Map, which is based on the iteration
. All chaotic systems of this type bifurcate at the same rate, a discovery first made by Mitchell Feigenbaum in 1975 and published in 1978 [
64]. For a single-parameter map based on the iteration
, the bifurcation rate is quantified by the Feigenbaum constant which is the limiting ratio of each bifurcation interval to the next and is given by 4.669201609... Although it is believed that this number is transcendental, there is, to date, no known proof of this or whether the Feigenbaum constant is irrational.
Most fractals are scale invariant entities relating to a discrete set of scaling values
L where a sequence of translations and/or rotations are applied in order to match the fractal with itself at different (discrete) scales. Deterministic fractals are typically of this, and are based on a sequence of systematic iterations that produces consecutive repetitions of an original object (its initial shape). This process produces a number of scaled-down copies of the object. For each iteration, if the scale length is reduced by a factor
L, and
N copies of the object are generated (being re-assembled in a coordinated way that is the same at each iteration), then, the resulting pattern can be taken to adhere to the equation
, where
D is the fractal dimension. This dimension is then determined by the equation
Figure 2 provides a simple example of such an iterative process to produce a so-called ‘Cantor Set’ [
59]. Starting at the top of the graphic, a line of length 1 unit is cut into three lines of equal length, one of which is discarded. In the case of
Figure 2, the line that is discarded is the central component, but it could also be the line to the left or right hand side. Repeating this process again and again (as illustrated in
Figure 2 for six iterations), at each iteration,
and
from which it follows that
. Thus, in the case of this iteration, the fractal dimension is less than 1, i.e.,
. A Cantor set of this type is an example of so called ‘Fractal Dust’ (a distribution of points, at least, for a large number of iterations). This is because it has a fractal dimension that is less than the topological dimension
n, that, for a line is
. In this respect, if the line at each iteration is retained instead of deleted, then at each iteration
and the original topological dimension is recovered. It is for this reason that fractals are considered to be space-filling objects when
for topological dimensions
.
Having introduced the exponent
in Equation (
5) and dimensions
n and
D, it is of value to consider the relationship between them. This is given by [
59]
The range of values of is then determined by the value of the topological dimension n and the corresponding range in values of D, i.e., and ; and For the applications of fractal geometry in financial analysis (the Fractal Market Hypothesis), we are typically interested in a time series, specifically a digital signal of time, which has a topological dimension of . In this case, , and the relationship between the fractal dimension and the scaling exponent is .
4.3. The Mandelbrot Set
In addition to the Cantor set considered in the previous section, there are numerous examples of fractal objects that can be used to further introduce the principles associated with the study of fractal geometry. It is arguable that the most iconic of these is the Mandelbrot set [
65]. This a fractal that emerges from an analysis of the iteration of nonlinear functions in the complex plane. It is a structure that arises from an iteration of the type
where
f is a nonlinear function but where we consider the iteration to take place in the complex plane. In this case, we consider a complex function
where
is the independent complex variable with real and imaginary components
x and
y, respectively. Complex plane analysis then involves the iteration
for some initial condition
. This iteration represents the application of a map which is denoted by
.
The behaviour of for increasing values of n provides a trajectory or ‘orbit’ (in the complex plane). This is given by the sequence of complex values that are produced by an iteration which depends on the function and the initial condition . If is a linear function, then the iteration may or may not converge depending upon the characteristics of the function. However, if the function is nonlinear, then the iteration may produce a range of different orbits in the complex plane. Such orbits may be characterised by divergence, convergence, periodicity or chaos.
The Mandelbrot set is a set which is specifically concerned with a study of the orbits produced when is a quadratic, i.e., when where c is a complex constant for some initial condition . There are two approaches that can be considered in this respect. We can analyse the iteration for a fixed value of c and different values of the initial condition . Alternatively, we can analyse the iteration for different values of c for the same initial condition . The Mandelbrot set is based on considering an iteration for different values of c for the initial condition . Hence, we can formally define the Mandelbrot set as that set of complex numbers c for which the complex function does not diverge when iterated from alone.
Figure 3 shows a (standard) Mandelbrot set for
and
, a
grid and
iterations [
66]. The central region of the image (the black area) represents those regions in the complex plane when the obits converge. The grey level components of the image (through to white components) are those regions in the complex plane where the orbits ‘escape to infinity’ (diverge) as the iterations proceed. The rate at which this happens determines the grey levels that are displayed. In the practice of computing a set of this type, the numerical floating point values obtained after a finite number of iterations are normalised, quantised and then presented on an grey 8-bit level scale (as given in
Figure 3) or using a specific pseudo-colour map.
While the Mandelbrot set is an icon of Fractal Geometry, it is only one of many such nonlinear complex function iterations that can be considered. In each case, by default,
. A study of the non-standard Mandelbrot set for case when
is given in [
66], a publication that includes the prototype Matlab functions used to conduct the study.
Figure 3 shows the difference between the Mandelbrot sets for
, illustrating that there is a radical difference between a self-similar object (the Mandelbrot set for
) and a Euclidean object (a square for
) in the complex plane.
As illustrated in
Figure 3, unlike the Mandelbrot set, the Euclidean square is symmetric with respect to both the imaginary axis and the real axis shifted to the left of
, a quantification of this result being given in [
66]. Just as the topological dimension of this Euclidean object (a nonstandard Mandelbrot set) is 2, the fractal dimension (specifically, the Hausdorff Dimension) of the boundary of the (standard) Mandelbrot set is also 2. Clearly, this is a case where the fractal dimension is the same for two very different complex plane sets. It is an extreme example of the fact that the fractal dimension alone can not necessarily be used to differentiate between two different fractals (or a fractal and non-fractal set). In other words, two different fractals can have exactly the same fractal dimension. In order to make such a differentiation, it is necessary to use multi-fractals as briefly addressed in the following section.
4.4. Multi-Fractals
There are a wide variety of deterministic and stochastic fractals for all topological dimensions. However, the fractal dimension alone, is not always sufficient to characterise a fractal, and, the fractal dimension is only one of a number of generalised dimensions that can be defined. These dimensions are derived via a measure theoretic analysis in ‘real space’. By way of an example, consider a fractal curve C with a fractal dimension to be the sum of two fractal curves and , with fractal dimensions and , respectively. In this case, , i.e., C is characterised by the larger of the fractal dimensions for the two curves. Thus, if the same value of fractal dimension is found for the merged curve C and .
The need for multi-fractal measures can be appreciated by considering a point-set with a large but finite number of points
N embedded in fractal dimensional space which is then covered a uniform grid of hypercubes of size
and then counting the number
of nonempty boxes. This provides an approach to computing the Fractal Dimension of an arbitrary self-affine object—specifically the ‘Box Dimension’ [
59].
A computational strategy of this type, does not include information concerning the distribution of the number of points in the nonempty boxes. To quantify this issue, suppose there are
points in the
hypercube and let
. The similarity (box-counting) dimension (which only takes account of the total number of nonempty boxes
and not
) is then given by
However, we can also define another metrics such as the the information dimension given by
Similarly, other dimensions can also be considered, leading to a hierarchy of generalised dimensions given by (for
) [
59]
These dimensions have a synergy with the statistical moments for a stochastic field (self-affine or otherwise). Along with other metrics, they form the basis of multi-fractal financial analysis and can be used to develop fuzzy inference systems based on generating a feature vector (whose elements are the values of the elements of the vector) from which a multi-parametric probability space is evolved using training data from which financially significant events are known to occur. In this way, a decision is made based on a fuzzy inference, on the likelihood of a event occurring based on the financial time series. However, as with other techniques in Artificial Intelligence, the key to this approach is the quality and quantity of relevant data which may not always available, especially in a field of study when future events can not necessarily be fully categorised [
67]. Another issue is the number of elements (multi-fractal parameters or otherwise) used to construct the feature vector. Such elements might, for example, include information entropy based metrics, designed to differentiate between order and disorder in a financial signal, when represented as a binary string [
68].
4.5. Self-Affine Functions and Fractional Calculus
Although the concept of a fractional calculus (the calculus of noninteger derivatives and integrals) has been known about for some time (dating back to the work of Niels Abel in the 1820s, which led to the birth of the subject, [
69]), it has only relatively recently experienced a rapid increase in the number of mathematicians who are now contributing to its development and the applications thereof, e.g., [
70,
71]. Even so, the connectivity between fractal geometry and fractional calculus is not always made clear and is therefore worthy of quantification. As this issue will be discussed later in regard to developing a model for a financial signal that is based on the use of fractional calculus under the FMH, we briefly consider a simple quantification of this connectivity.
Let
be a random function of time with a white noise spectrum
where we introduce the notation
, indicating that
and
are Fourier transform pairs, i.e., using the non-unitary definitions,
where
k is the (spatial) frequency. The term ‘white noise spectrum’ used here implies that
has an amplitude spectrum
and thereby a power spectrum
that is uniformly distributed across all frequencies
k.
Suppose we consider filtering
with the function
giving the spectrum
What is the effect of doing this on the scaling properties of the inverse Fourier transform
? The key to answering this question is based on noting that
where
is the Gamma function. Then, using the convolution theorem, we can write the inverse Fourier transform of
as
where ⊗ denotes the convolution integral as given. This expression for
is a model for a linear stationary process, where the sum of
is subject to an inverse scaling by
.
The convolution integral given in Equation (
9) has an important and relevant scaling relationship which is obtained by considering the convolution of the kernel
with the function
when we can write (with
)
The result illustrates that this particular convolution integral exhibits the scaling characteristics defined by Equation (
5).
So what is the relationship between this result and fractional calculus? It is a consequence of noting the generalisation of
to
Thus, if we consider the fractional differential equation (for
)
then upon Fourier transformation, we obtain Equation (
7), which, in turn, can be written as Equation (
9) and has the scaling properties compounded in Equation (
5). Moreover, assuming that
is a dimensionless function, and, given that
x has dimensions of length, then by induction
, in Equation (
10), must have a dimension of
- a fractional dimension. In this context, we can consider the solution to a fractional differential equation to be a solution that describes a self-affine function. The function
is given by the anti-derivative of
which can be written as
Note that, from Equation (
9), if
, then, given that
, we obtain
thereby retaining the standard relationship between a first-order derivative and the anti-derivative or integral of the function
. Further, given that
, to obtain higher-order fractional derivatives, we can first fractionally integrate the function
, say, and then differentiate the result. Thus, for example,
Unlike a standard differential, which defines the gradient of a function at some value
x that is independent of previous values less than
x, a fractional differential of the same function at the same value of
x is dependent on the history of the function due to the convolution of the function with the kernel
. Hence, unlike an integer derivative, a fractional derivative has ‘memory’. This is an important aspect in the approach to analysing financial signals under the FMH because financial signals should be assumed to be influenced by the memory of past financial conditions and decisions. Thus, it may be said that unlike other financial hypotheses such as the EMH as discussed in
Section 3, which do not consider financial systems to have memory, the FMH is intrinsically memory associative. This issue is explored later in
Section 6.3.1 in terms of the form of a memory function that is a characteristic of the Generalised Kolmogorov–Feller Equation.
The analysis considered above is predicated on Equation (
7) which, strictly for a white noise spectrum
, implies that the amplitude spectrum
of a self-affine function
is characterised by the scaling relationship
This is a fundamental ‘signature’ for all self-affine functions, albeit being limited to the one-dimension case. Thus, the exponent is a fundamental parameter for characterising the fractal properties of a financial signal. The analysis of a financial signal in terms of changes in (on a moving window basis) is therefore a primary issue in the characterisation of a financial signal under the FMH.
Equation (
9) is a common example of a fractional integral of order
, the anti-derivative of a fractional differential of the same order. However, there are numerous other definitions for a fractional integral, and, consequently, a fractional differential. Some example of this are presented in [
72], which develops a generic definition of a fractional differo-integral given by
where
Using different Sigmoid-type functions to approximate the sign function , it is then possible to derive a number of different definitions for a fractional derivative. It is also conjectured (with a justification) that there is no limit to the number of self-consistent definitions that can be derived for a fractional differo-integral. Thus, one of the interesting issues in the applications of fractional calculus is the apparent lack of any definition for a fractional differo-integral that can be said to be unique. This has implications for both analytical and numerical procedures that are applicable when modelling a system in terms of a fractional differential equation, for example.
5. The Fractal Market Hypothesis
The Fractal Market Hypothesis emerged in the 1990s with the work of Edgar Peters [
73] (an asset manager) and Benoit Mandelbrot [
33] (a mathematician), for example. This was a natural consequence of the work of mathematicians and others to develop the subject of fractal geometry, an icon of which is Mandelbrot’s famous book
‘The Fractal Geometry of Nature’ first published in 1982 [
33]. The hypothesis states that financial time series exhibit stochastic self-affine structures. This means that variations in prices are still taken to be random walks, but crucially, random walks whose statistical distribution is similar over different scales in time. This principle was actually first conceived by Ralph Elliott who was a professional accountant and reported on the apparent self-affine properties of financial time series data in 1938 [
74]. He was the first to observe that different sized windows of financial time series data could be scaled in such a way that they were statistically similar, i.e., the histogram of the data was (approximately) the same shape. This discovery led to the idea that financial signals were characterised be so called ‘Elliot Waves’ [
75].
The principle of Elliott waves developed in the 1930s and the Fractal Market Hypothesis that evolved in the late 1990s provides a self-consistent financial time series model for the interpretation and analysis of financial signals and investment theory. The key to this is that fractal time series have an inherent memory and thus, the price of a commodity tomorrow is determined in some way by the characteristics of the past. The importance of this observation in financial analysis is self-evident and has been the subject of research over the past few decades. This has, more recently, included the connectivity between memory, self-similarity and fractional calculus, when the fractional derivative of a function depends on the ‘history’ of that function.
One of the reasons that financial time series, and other financial data have emerged to have self-affine properties is due to the innate complexity of the world economic system. This includes the (in)stabilities that have become evident in more recent times. The dynamics of market prices have become a reflection of the multitude of interactions between agents with different investment horizons and different views on the interpretation of information, leading to disruptions, and to crashes when these interactions are broken. In this sense, the sophistication and complexity of the global financial systems that have evolved in recent times, within the context of a genuinely free global market, has led to the development of a self-organised system and self-organised systems tend to exhibit self-affine properties. This property has led to a new approach to modelling financial times series for trading and investment and for the evaluation of financial (in)stability [
76].
5.1. Nonlinear Dynamics and Chaos Theory
Chaos theory is a field of applied mathematics which has found numerous applications in many diverse disciplines including, control engineering, biology and economics, for example. It considers the behaviour of dynamical systems that are highly sensitive to initial conditions (e.g., nonlinear differential equations) and explores the transitions between order and disorder. This is where small and seemingly insignificant differences in initial conditions (due to rounding errors in numerical computations, for example), produce significantly different outcomes, rendering the idea of producing reliable deterministic long-term predictions an impossibility [
77].
It is important to note that this can happen even when dynamical systems are considered to be deterministic. This means that their dynamic behaviour is taken to be fully determined, subject to the initial conditions that are applied, and that there are no random elements or functions involved such as a stochastic source function, for example [
78]. In other words, the determinism associated with these systems does not necessarily make them predictable. This includes simple rule-based trajectories such as the ‘
algorithm’ [
79] which leads to the ‘Collatz’ Conjecture’. In this case an irregular sequence of numbers is generated subject to an initial value (a positive integer). The conjecture is concerned with whether every sequence will always reaches 1 when starting from any positive integer; a conjecture for which there is currently no proof [
80]. In terms of the seemingly irregular stream of numbers that the
algorithm can produce, the stream is an example of ‘Geometric Brownian Motion’.
Systems often become chaotic when there is feedback present, such as in the case of financial and commodity markets. For example, as the value of a commodity rises or falls, traders are inclined to buy or sell. This, in turn, further impacts the asset price, causing it to rise or fall irregularly - ‘chaotically’. Whilst there remains some controversy over the existence of chaotic dynamics in economics, this behaviour has been verified in a variety of systems including fluid dynamics and mechanics, for example. One of the more generic aspects of chaotic systems is that they tend to be the result of a feedback in regard to a nonlinear function and that they are characterised by self-affine structures, as briefly discussed in
Section 4.2.
A study of chaotic stochastic fields was initially carried out by Andrey Kolmogorov [
81,
82,
83,
84], amongst many others. Kolmogorov published his book
‘Foundations of the Theory of Probability’ in 1933, which provided the basis for a modern axiomatic approach to probability theory [
85]. In 1938, he also established the basic theorems for ‘smoothing’ and predicting stationary stochastic processes. Kolmogorov’s work also focused on turbulence, where his publications significantly influenced the field. He also developed, and is considered a founder of the field of algorithmic complexity theory, which is now commonly referred to as Kolmogorov complexity theory and has application in the developments and assessment of encryption algorithms, for example. From this work, Kolmogorov found that there are two kinds of continuous time Markov processes (i.e., stochastic processes with no memory), depending on the assumed behaviour over small intervals of time [
82]. If you assume that ‘in a small time interval there is an overwhelming probability that the state will remain unchanged, then, if it changes, the change may be radical’. This leads to what is called the phenomenon of ‘jump processes’. The other case, Kolmogorov surmised, leads to processes such as those ‘represented by classical diffusion and by Brownian motion’.
In addition to Kolmogorov, William Feller studied the relationship between Markov chains and differential equations. His theory on generators of stochastic processes, gave rise to the theory of ‘Feller Operators’ (i.e., a Markov process with a Feller transition function). As a result of these relationships, the diffusion and jump type properties associated with the Kolmogorov, Fokker–Planck [
86] and Kolmogorov–Feller [
87] equations makes such equations appropriate for modelling stochastic functions, and, in particular, nonstationary dynamic behaviour. In this context, the Generalised Kolmogorov–Feller Equation is introduced later on in this work in regard to developing a rate equation for a financial signal which incurs a so-called ‘memory function’.
Despite initial insights in the early part of the 20th Century, chaos theory only really became formalised after the 1950s, when it started to become evident that linear systems theory (the prevailing systems theory of the time), could not explain the observed behaviour of many dynamic systems. The most widely known research of this time was that of Edward Lorenz in 1961, which was concerned with the behaviour of weather systems [
88]. It was in this study that he first coined the term the ‘butterfly effect’. In a similar fashion to Modern Portfolio Theory, the main catalyst for the wider development and acceptance of chaos theory was the digital computer which allowed repeated iterations of mathematical formulae to be carried out in more detail and to a greater accuracy than ever before.
Another important development (and one of particular relevance), was the introduction of the ‘Lyaponuv exponent’, e.g., [
89,
90,
91]. The Lyapunov exponent of a dynamical system, characterises a property of the system that is concerned with the rate of separation of infinitesimally close trajectories [
92]. In other words, the exponent characterises the extent of a systems sensitivity to its initial conditions. The rate at which this separation occurs can be different for different assumptions of the initial phase, and thus, a spectrum of Lyapunov exponents are possible. As a result of this, it is most common to refer to the largest exponent (i.e., the maximal Lyapunov exponent). This is because it can be used to define the overall predictability of a system. A positive maximal Lyapunov exponent is taken as an indication that the system is chaotic. The Lyapunov exponent has many uses in analysing systems for their chaotic behaviour, or their transition from non-chaotic to chaotic behaviour for a non-stationary process. The exponent can therefore help to determine the short-term predictability of a given (chaotic) system. This makes it of value in financial forecasting as shall be considered later in this work.
5.2. Fractals and Finance
Benoit Mandelbrot initially spent many years developing his ideas and applying the theoretical concepts of Lévy and Pareto (amongst others) for his research into cotton price movements. He observed that the changes in the price of cotton (the price differences) did not conform to a normal distribution, but rather a Lévy distribution [
61] with a Lévy index (
) equal to
[
93]. Lévy distributions have an undefinable variance, but, as shall be discussed later on, when
, a Lévy distribution reduces to a normal distribution which has a finite variance. In this respect, Mandelbrot reasoned that, in the markets, correlations may exist between past and future prices; and that the statistically independent random walk model was in fact an incorrect general assumption. This lead Mandelbrot to look at the phenomena of long-term dependence. Using the original principle of Brownian motion applied to an asset price, one can determine how far it is should be expected for that price to move. However, what happens if the price changes further than the square root of time law forecasts (i.e., the random walk model)? How could this happen? Mandelbrot reasoned that if the market exhibits long-term dependence, then a rate move in one direction will tend to continue on the next day and again a few days later. Here, the coin tossing game is no longer operating on the blind form of chance. Mandelbrot went on to develop a metric for estimating this tendency called the Hurst exponent
H, after the hydrologist, Harold Edwin Hurst [
94].
In 1906, Edwin Hurst was charged with a major infrastructural development on the river Nile that was entitled the ‘Century Storage’. His task was to stockpile water for the Egyptians against the worst of possible droughts. Hurst was therefore faced with the dilemma of estimating how much the Nile flooded from one year to the next. Sometimes the flood ran high, sometimes the levels ran low. Much like in predicting financial markets, either prosperity or poverty could hang on the estimation [
37]. The obvious solution was to build a dam that was high enough to hold back the waters of several wet years in a row. How high should that be?
Engineers of the day assumed that the flood variations from one year to the next were statistically independent (as with Bachelier’s coin tossing game). Hurst concluded, however, that this assumption was inaccurate. He found that the variance from highest to lowest increased over time faster than one would expect. Thus, it was not only single floods that Hurst needed to considered. Looked at individually, a Gaussian distribution fitted the data for each year’s flooding reasonably well, but it was the runs, the back-to-back floods or droughts, that he realised mattered most in engineering a successful solution.
Hurst looked at Nile flood data and similar data across the world and found a similar scenario. Specifically, he found that the range of highs to lows widened not by a square root power law as per a ‘fair game”, but as a fractional power law of the form
as a function of time
t, where
for the case of the Nile river [
94]. After solving the dilemma at hand, Hurst constructing the dam to such success that he was named the ‘Father of the Nile’. He found that his theory could also be applied to a broad range of other phenomena, including the way clay patterns accumulated on a lake bed, annual rainfall in New York and the growth rings of trees, for example.
In this context, the Hurst exponent is a measure of the long-term memory of a time series. It is an index of long-range dependence, which quantifies the relative tendency of a time series either to regress strongly to the mean or to cluster in a direction—to provide a trend. For , a time series is characterised by anti-persistent behaviour in which the values are uncorrelated in time. This is where any data point in the time series with a relatively high value is most likely to be followed be a low value in adjacent pairs, and that this behaviour, which reflects large differences in the values of such pairs, will last for a long time into the future. For , the opposite is true, which is where a high value in the time series will most likely be followed by another and similarly, a low value by another low value. In other words, for this range in values of the Hurst exponent, a run of similar values may be expected, leading to a certain trend in the times series. For , it can be expected that the series is neither persistent nor anti-persistent, but is characterised by a stream of data that is completely uncorrelated in terms any definable behaviour (persistence .v. anti-persistence). In this respect, knowledge of the value of H can be valuable in terms of qualifying the underlying dynamics of a signal and its possible future behaviour, i.e., is it trending or otherwise .
Picking up on the work of Hurst in the 1960s, Mandelbrot discovered the same pattern in many other contexts; the oddest of all of these was how financial markets fluctuated. He reasoned that there was a power law at play and likened big floods and droughts, to price jumps and boom to bust cycles. Thus, what Mandelbrot termed the Hurst exponent (
H) is essentially a measure of ‘persistence’ for
or ‘anti-persistence’ for
and is related to the fractal dimension
D (and Topological dimension
n) via the equation
[
59]. Methods of computing
H from a time series (financial or otherwise) are considered in [
37], for example, and references therein.
Where a long-term dependence exists, the price change is not necessarily proportional to the time elapsed. Instead of the power law being specific to the case when , it could actually be any fraction between 0 and 1. Each produces a completely different type of price series or trajectory. For example, if H approaches 1, the price will roam far; its dynamic will be ‘persistent’ over a given period, producing an upward or downward price trend. If H is equal to , then the series is completely uncorrelated. However, if H is smaller than , the price will roam less in the sense that each step will tend to be followed by another reversing direction in a narrow sawtooth type wave pattern. This is a characterisation of ‘ anti-persistence’.
To evaluate the impact of the Hurst exponent
H and the associated Lévy index
, Mandelbrot developed a statistical test called ‘Re-Scaled Range Analysis’ (RSRA) [
37,
94]. This is simply the range divided by the standard deviation. It is a type of test known to statisticians as ‘non-parametric’ testing. It makes no simplifying assumptions about how the data are organised and so does not try to reduce everything down to such common metrics as the mean and variance, that presumes a normal distribution. The results of RSRA testing, provides an indication of long-term dependence. Under some circumstances, these two factors are so interrelated that
H is simply equal to
. For example, in the case of a fair coin tossing game, the Hurst exponent is
and
.
This type of financial modelling is now referred to as the ‘Multi-Fractal Model of Asset Returns’. Although not without its criticisms, the validity of this model has been independently tested on the Dollar–Deutschmark exchange, for example, where, in 1997, Calvet and Fisher [
95] concluded that price changes in the market do scale as the model predicts and that volatility clusters in a classic multi-fractal pattern. Later research in 2009 [
96], also tested the theory across other stocks such as Lockheed and Motorola, all of which were subsequently found to have multi-fractal characteristics. The power of this form of fractal analysis is its unique ability to express a great deal of complicated and irregular data sets in a few simple formulae for specific metrics such as the Hurst exponent, the Lévy index and the Lyapunov exponent. This power is especially clear in the case of multi-fractal fields, which is fundamental to the study of turbulence and is therefore of significant value in the analysis of financial time series and other market data. It is for this reason that the principles of Fractal Geometry has and continues to be used in the study of how financial markets work, a principle that is a central component of the Fractal Market Hypothesis.
5.3. Black Swans
The term ‘Black Swans’ primarily relates to the work of Nassim Taleb who focused on problems concerned with randomness, probability and uncertainty in finance. Taleb heavily criticised the risk and investment management methods used by the global finance industry and was one of the few who warned specifically of the impending financial crisis to come (in 2007). He advocated what he called a ‘black swan’ robust society. This is a society that can withstand difficult to predict events [
97].
The phrase ‘black swan’ itself derives from a Latin expression, loosely translated to ‘a rare bird in the lands, very much like a black swan’. When the phrase was coined in English, a black swan was presumed not to exist. However, following the discovery of black swans in Western Australia in 1697 by Dutch explorer Willem Hesselsz de Vlamingh, the term metamorphosed to connote that a perceived impossibility might later be disproven [
98]. Thus, it is proposed that ‘anti-fragility’ should be built into financial systems; that is, an ability to benefit and grow from random events, errors, and volatility, as well as ‘convex tinkering’ (where experimentation outperforms a purely theoretical approach).
As a trader, Taleb’s strategy was to safeguard an investment portfolio against a crises, while, at the same time, reaping rewards from rare events (short term market persistence). As a result, he incurred a number of jackpots, which were then followed by lengthy ‘dry spells’. Consequently, he became a pioneer of tail risk hedging, which is now also referred to as ‘black swan protection’, whereby investors are insured against extreme market movements.
A black swan is an event which typically has three main attributes:
- (i)
it is an outlier which lies outside the realm of regular expectations, where nothing in the past points to its possibility;
- (ii)
it carries an extreme impact;
- (iii)
in spite of its unlikelihood, human nature leads to the concoction of explanations after the fact, thereby attempting to make an event explainable and predictable [
99].
A major problem which has been labelled by the term ‘Ludic Fallacy’ by Taleb is the belief that the randomness found in life, resembles the artificial randomness that we can simulate. Any modelling then stems from the assumption that an unexpected event may be predicted by making an extrapolation from past observations. Such accuracy is even more unlikely when these statistics are presumed to conform to Gaussian distributions alone.
The principal idea is not to attempt to predict black swan events. Instead, it is to build robustness against ‘black events’ when they do occur, and, further, to be able to exploit such events when they do occur. Banks and trading firms are overly vulnerable to black swan events and are ‘exposed to losses significantly beyond those predicted by their defective models’ [
100]. In particular, one must be critical of the widespread use of the normal distribution models as the basis for calculating risk, despite much evidence to the contrary. While other distributions such as the the Lévy distribution are not usable with exact precision, they are at least more descriptive of reality. The Lévy distribution is one of a number of non-Gaussian distributions that are relevant to the analysis of financial signals as reviewed in the following section.
5.4. Non-Gaussian Distributional Analysis
In 1962, Cootner’s research [
101] indicated that the stock market is not a random walk, and, in 1974, Alexander [
102] also concluded that Standard and Poor’s (S&P) 500 industrial signals do not follow a random walk. Further, in 1971, Kemp and Reid [
103] determined that share price movements were ‘conspicuously non-random’, while in 1977, Beja [
104] showed that efficiency in a real market is impossible. A similar result would be found by Grossman and Stiglitz [
105] in 1980, who proposed that the market can never be perfectly efficient. Moreover, in 1965, Mitchell [
106] proposed that the distributions of price changes were too ‘peaked’, relative to Gaussian distributions, to be normally distributed. This phenomenon would come to be known as Leptokurtosis, the same characteristic also being separately observed by M. Olivier [
107], F. C. Mills [
108], and B. Mandelbrot [
93].
Example forms of Kurtosis are shown in
Figure 4. The studies described above are but a few examples of the fact that the non-normal distribution of price changes have and continue to be observed in a wide range of financial time series data.
In 1978, Ball [
45] examined persistent excess returns after public announcements of a firms’ earnings. A similar study would be made by Roll [
111] in 1984, when he examined trading futures. De Bondt and Thaler [
112] continued with this theme of market overreaction. The authors tested the reaction of both winning and losing stock portfolios. They found that losing portfolios later went on to outperform the market average, while stocks that had previously been successful went on to drop below the market average.
In 1982, Engle [
113] found empirically that distributions of asset returns had longer tails than those from normal distributions and appeared negatively skewed, with examples of such skewed distributions being given in
Figure 4. Fischer Black [
114] introduced the idea of traders who try to make a profit on the spread within a trade (i.e., arbitrageurs) and French and Roll [
115] published a study on market volatility during the hours in which the trading ‘pit’ is open as opposed to when it is closed. They found that prices are more volatile during market opening hours as opposed to hours when the trading exchange is closed. The authors thus concluded that ‘private information is the key factor behind high trading-time variances’ (i.e., market inefficiency).
In 1989, Cutler [
116] produced a paper that investigated the impact of news on a market and found that price movement is not adequately explained by news alone. In 1988, Fama and French [
117] found large negative auto-correlations in stock market data beyond a year. In the same year, Poterba and Summers [
118] found similar results, in that they observed negative correlations over a long period, with positive correlations over a short period. Schiller [
119] considered ‘Market Volatility’ where his conclusions challenged the EMH. At the same time Lehmann [
120] found reversals in weekly stock market returns and therefore rejected the EMH. Elsewhere, Jegadeesh [
121] demonstrated evidence of predictable behaviour of returns and thus rejected the Random Walk Hypothesis. Chopra et al. [
122] published further evidence of stocks overreacting, while Bekaert and Hodrick [
123] described predictable components in excess returns on equity and Forex markets. In 1993, Jegadeesh and Titman [
124] investigated the abnormal gains achieved by trading strategies that have found success/failure (i.e., excess market returns on a risk adjusted basis should not be possible in an efficient market).
In 1994, Huang and Stoll [
125] produced new evidence of micro-structures in stock market return predictions. Later, Haugen [
126] published a book that showed how short-run over-reaction may lead to long-term reversals when the market realises its error. In 1996, Cambell et al. [
127] produced a popular book that looked at ‘momentum strategies’. The implication of this was that markets respond gradually to new information— a contradiction to the EMH. Mifre and Rallies [
128] and Shen et al. [
129,
130] found momentum in commodity markets specifically. This concurs with research around the ‘Momentum Strategy’, where momentum (i.e., past ‘winners’ outperforming past ‘losers’) was found through an empirical analysis in the study of stock returns.
These papers have challenged the prior assumptions of Fama, in that, the exceptional returns provided by these strategies appear to contradict the EMH. In this respect, Shleifer [
131] published ‘Inefficient Markets: An Introduction to Behavioural Finance’ which questioned the assumptions of investor rationality as well as perfect arbitrage. Attempts at modelling inefficient markets have been undertaken through the application of the (time) fractional Black–Scholes equation for European options [
132], which is an example of the use of fractional calculus to model markets that appear to conform to the FMH and has become a primary issue in financial time series modelling. A short introduction to this is provided in
Section 6.3.
In 2010, Lee et al. [
133] investigated the stationarity of stock market prices across 32 developed and 26 developing countries from 1999 to 2007. In this work, it was concluded that the markets examined were not efficient. Eastman and Lucey considered a study relating to the shape and volume of the distribution of futures contract returns in 2008 [
134]. A wide variety of contracts were analysed from major futures exchanges with agricultural, industrial and foreign exchange being included, amongst others. Tests of normality indicated that daily returns and daily volumes were not normally distributed. Monthly returns and volumes displayed mixed results, with the majority of products considered to be non-normal. Nonparametric tests were also used to assess whether returns and volumes were symmetric about the mean. The research concluded that daily returns and volumes are asymmetric, with mixed results for monthly data.
In 2018, research by Morales and Hanly [
28] evaluated efficiency across European power markets. They concluded that electricity markets across Europe exhibited inefficiency (the European power generation sector, of course, being a key driver of EU ETS market pricing). Stationarity tests found prices did not follow a random walk process, a result that was supported by auto-correlation analysis and joint variance ratio tests which showed evidence of correlated returns. This suggests the potential of predictable patterns on electricity prices, which is not a characteristic that should be evident in an efficient market. In this context, Hanly [
135], when investigating energy price risk using futures contracts, noted that participants carry a significant level of price risk given the innate volatility and susceptibility of energy products to political, economic and weather events.
Research across oil and natural gas markets has shown that energy commodities tend to be significantly riskier than the majority of assets traded; and that this can be related to the existence of long tails, asymmetry and long memory in energy markets [
136,
137]. In this respect, more recent studies have considered extreme risk events that are often accompanied by a sudden plummeting of liquidity (effects that do conform to the EMH). For example, Zhang et al. [
138] study the nonlinear fluctuation characteristics and causes of contracts with different maturity periods in the China stock index futures market, under a framework of the FMH, using a multi-fractal de-trending fluctuation model.
The work that has and continues to be undertaken in the statistical analysis of price differences for a wide range of markets indicates that the assumption that price differences are normally distributed with a zero mean is an increasingly inadequate description of a fundamental statistical characteristic. It would appear that financial time series are characterised by price differences that are:
- (i)
peaked with long-tails—Leptokurtic;
- (ii)
non-symmetric—skewed;
- (iii)
statistically non-stationary in regard to both (i) and (ii).
It is in this context that a review of the underlying mathematical bases for the RWH, EMH and FHM and the corresponding financial times series models that can be evolved is now considered, as given in the following section.
6. Mathematical Models for Financial Hypotheses
Having reviewed the background to the Fractal Market Hypothesis (and other market hypotheses), the aim of this section is to derive the basic mathematical models (in particular, those that are characterised by an intrinsic scaling relationship) associated with the Random Walk, Efficient Market and the Fractal Market Hypothesis. The purpose of this is to provide the mathematical modelling framework to complement the review that has been given so far. In this context, it is shown how each of the financial hypotheses discussed in this review can be unified in terms of the Generalised Kolmogorov–Feller Equation as provided in [
14].
6.1. The Random Walk Hypothesis
As discussed earlier, Louis Bachelier stated that the best estimate of the price of a commodity tomorrow is the price of today plus some random value (which may be positive or negative) [
1]. In this context, he concluded that there is no useful information contained in the historical price movements of securities. In other words, the dynamics of historical financial time series has no bearing on future price movements.
The apparent random behaviour of commodity prices was also noted by the economist Holbrook Working in 1934 [
19] in his analysis of financial time series. Further, and, as discussed earlier, in the 1950s, Maurice Kendall attempted to find periodic cycles in the financial time series [
20]. Studying various securities and commodities for the time, he did not observe any. In all cases, prices appeared to be yesterday’s price plus some random change (up or down). He therefore suggested that price changes were independent and followed random walks. Thus, having looked for some cyclic behaviour in financial time series, Kendall came to the same conclusions as Louis Bachelier.
This conclusion is the basis for the ‘Random Walk Hypothesis’ (RWH), which is the simplest of financial times series models. Conceived to try and interpret price variations, it can be conceived in terms of the difference equation
where
is the price of a commodity today,
is the price tomorrow and
is some random number which may be positive or negative, subject to some initial condition
.
In the context of the Bachelier’s statement that the price estimate of a commodity tomorrow is the price of today plus (or minus) some random value, the variable represent the daily price value for day n. This could be the open or close values on that day, or the high and low values during the same day. However, the value of does not have to represent a daily price value alone, but any value that changes over an interval of time in which price movements are quantified and for which data are available.
Similarly, the value of
may represent any trading commodity, including energy commodities such as gas and oil, precious metals and currency exchange (the Forex markets) and more recent additions to free-market trading such as Carbon trading and Cryptocurrencies. However, it is well known that the time series for each commodity is different in terms of scale and irregularity. In terms of the model compounded in Equation (
12), the only variable that can account for any difference in the time series
(subject to some initial condition
) is the random variable
. This variable may have a different scaling value, effecting the amplitude of the variable relative to
. Moreover, the random variable will change according to the histogram which characterises the distribution of values it possesses.
Equation (
12) assumes that the times series is stationary; what ever distribution
adheres to, it does not change in time. It is therefore a statistically stationary model and describes a digital signal that is characterised by an Ergodic system [
139]. An Ergodic system is one, such that any collection of random samples taken from a process will represent the average statistical properties of the entire process. In other words, regardless of what the individual samples are, the samples taken provide a broad overview representing the whole process.
In terms of Bachelier’s hypothesis,
describes the price differences which are taken to be normally distributed. In this respect,
Figure 5, provides an example simulation for a financial time series based on Equation (
12), for
where
is obtained through application of the Matlab Gaussian random number generator
randn.
Equation (
12) is a simple example of a discrete random walk model. Its counterpart continuous time model can be derived if we write
where
is an arbitrary constant interval of time. It is then clear that we can cast the RWH in terms of the first-order differential equation (as
)
In this context, the function
becomes the sum (the integral) of independent random variations. This is referred to as Brownian motion which is the basis upon which the Efficient Market Hypothesis is predicated. We also note that the spectrum of
is given by
where
and
is the (angular) temporal frequency. Thus, for a white noise spectrum
the amplitude spectrum of a financial signal (according to the Random Walk Hypothesis) is characterised by the frequency scaling law
.
6.2. The Efficient Market Hypothesis
The Random Walk Hypothesis is the basis of the Efficient Market Hypothesis (EMH). The EMH states that random price movements indicate a well-functioning or efficient market. This is a concept which emerged in the mid-1960s. The hypothesis assumes that there is a rational and unique way to use available information. It assumes that all agents possess this knowledge and that any chain reaction produced by a ‘shock’ happens instantaneously. This is intuitively not physically possible. Thus, it is arguable that financial models that are based on the EMH have and will continue to fail.
Form the point of view of developing a financial time series model, the EMH is the manifestation of assuming that the random price movements are a consequence of a system that is characterised by Gaussian distributed deviations and that the time series are a product of the process of (classical) diffusion. In order to explain this, it is of value to cast the problem in terms of the the Generalised Kolmogorov–Feller equation, which, for a one-dimension density field evolving in space
x and time
t and denoted by
is given by [
14]
where
is a memory function,
is the Probability Density Function (PDF) that is characteristic of the stochastic system where
and
is a random variable (a stochastic source function) as a function of both space and time. The symbol
denotes the convolution integral in time
t and
denotes convolution in a one-dimensional space
x. This equation is essentially a version of Einstein’s evolution equation [
24] modified to include a memory function
. It is obtained by applying a Taylor series in time to the evolution equation
and expressing this series in terms of the convolution of the function
with memory function
, i.e.,
Equation (
14) provides the basis for developing all the time series models that are considered in this paper. The time dependence of the density field
is taken to be a description of a continuous financial signal where
represents the density field as a function of time (a continuous random walk model). In this context, it is informative to first show how Equation (
13), for example, can be derived from Equation (
14). Let
and
. Then, Equation (
14) reduces to the form
Thus, if we integrate over
x and let
then Equation (
13) is recovered. In this respect, the original RWH considered by Bachelier is a manifestation of Equation (
14) for the case when both the memory function and the PDF are delta functions. This is clearly a very elementary model, as it assumes that the system has no memory and that the system PDF is concentrated at
.
In regard to Equation (
14), the EMH model can be formulated by considering a system which is memory independent so that
and has a zero-mean Gaussian-distributed PDF. Thus, let us assume that for variance
,
is given by the normalised Gaussian distribution
where
is the characteristic function—the Fourier transform of
. Fourier transforming Equation (
14), and using the Convolution Theorem, we can write
where
and
. Further, if we consider the case when
, then
and we can write
Noting that
then in real space, the Diffusion Equation is obtained, given by
In the infinite domain, and, for the initial condition
, the Green’s function solution to this diffusion equation is given by [
140]
where
is the Green’s function [
140]
Writing
in terms of the Taylor series
we consider the spatial convolution for the first term of this series alone. In this case,
and it is then clear that as
,
Further, noting that
we can consider a (non-causal) model for
whose frequency spectrum is given by
In this context, and, compared to the RWH where , under the EMH the amplitude spectrum scales according to the scaling relationship .
6.3. The Fractal Market Hypothesis
Given the analysis provided in the previous section, a model for the FMH can be developed as follows. The EMH is based on assuming that
is Gaussian distributed. The FMH is based on assuming that
is Lévy distributed with a characteristic function given by
where
is the Lévy index and the constant
a has dimensions of
. Clearly, when
and
the Characteristic Function reduces to that for a normal distribution. For
,
is a Cauchy distribution, but for arbitrary values of the Lévy index, the distribution has the asymptotic form [
141]
There are two fundamental issues to be considered in this case. The first is that by repeating the analysis given in the previous section, we obtain a equation for
which describes fractional diffusion compounded in the fractional diffusion equation
where
The second important aspect associated with this distribution is that compared to a normal distribution, the Lévy distribution has longer tails. An example of this is illustrated in
Figure 6 which compares the two distributions for
.
Figure 6 also provides an example of the distribution for the daily price difference of a financial signal. It compares the distribution of this data with a normal distribution. In this case, the histogram is characteristic of the time series for the Bitcoin–USD daily exchange rates. The overlying red line shows a normal distribution with a mean and standard deviation taken from the empirical Bitcoin–USD exchange rates. The blue line shows a Gaussian kernel-density best-fit estimator to the histogram, revealing a substantial deviation from the normal distribution [
142]. Bitcoin–USD exchange rates are considered later on in this work in regard to long- and short-term forecasting using the FMH based on the assumption that the system is Lévy distributed.
The relative long tails of a Lévy distribution are characteristic of a stochastic process in which extreme events can occur. Moreover, their occurrence is, on a statistical basis, significantly more likely compared to a stochastic process characterised by a Gaussian distribution. In terms of a financial time series, this includes fast-evolving trends. The length of the tails of a Lévy distribution is determined by the value of the Lévy index. The larger the value of the index, the shorter the tail becomes. Unlike the Gaussian distribution which has finite statistical moments and short tails, the Lévy distribution has infinite moments and ‘long tails’.
In the statistical analysis of (conventional) systems, it is expected that the stochastic fields the system generates have PDFs where (at least) the first two moments (the mean and variance) are well defined and finite. For systems that exhibit Lévy distributions, we are required to consider a statistical analysis subject to the condition that all the moments (starting with the mean) are infinite. Thus, unlike a stochastic signal that is Gaussian distributed and can be characterised by the mean and variance (the first two statistical moments), for example, a Lévy distributed signal cannot be characterised in the same way.
Instead, the way to quantify such a stochastic signal is through the Lévy index itself. If this is undertaken on a moving window basis for a given financial time series, a Lévy index signal can be generated. In effect, such a signal is a measure of the variations in the length of the tail associated with the signal as a function of time. In turn, this function provides an indication of the likelihood of a trend taking place when it decreases in value and the length of the distribution tail increases. This requires a solution to Equation (
17) to be formulated, as shall now be considered.
Following the approach given in [
14], a solution to Equation (
17) for
can be obtained, given by
where
, and
Thus, as
we obtain a spectral model given by
and a time series model given by
which reduces to Equation (
15), when
with
, given that
.
In terms of the scaling relationship for the Random Walk and Efficient Market Hypotheses, it is immediately apparent that the scaling law for the FMH is a generalisation. Thus, the RWH is consistent with
, the EMH assumes that
and the FMH, for any values of
. Unlike the RWH and EMH in which the values of
is assumed to be a constant, any time variations in the Lévy index,
, provides an indication of the dynamic behaviour of a financial signal. This can be achieved by repeatedly applying regression methods to the signal (amplitude) spectrum on a moving window basis. The rationale for this is that as
deviates away from 2, there is a greater likelihood of a rare but extreme event taking place, a so-called ‘Lévy flight’ or a ‘Black Swan’.
Figure 7 shows a comparison for the cases when
,
and
, for the same zero-mean Gaussian-distributed stochastic function
, based on applying the filter
to the white noise spectrum
.
Another approach to estimating this index is to approximate Equation (
18) by (ignoring scaling by
and for
)
under the condition that
, a condition which, in practice, is equivalent to modelling the data over a window of a times series where scaling stationarity can be assumed and the finite integral over
is a constant. A ‘
-index’ can then be estimated using regression methods (a least squares fit, for example, orthogonal linear regression or singular value decomposition) based on the times series data itself rather than the spectrum of the data, the Lévy index being given by
.
In the context of the asymptotic analysis presented to formulate the time series models for
as given, and, ignoring scaling factors, it is possible to state the differences between the three hypotheses considered in terms of the heuristic fractional differential equation:
Then, for
we obtain the RWH; with
we obtain the EMH and with
we have the FMH. If, for each case,
is a zero-mean Gaussian distribution, then, for
, the price differences also conform to this distribution. However, for
, the distribution of the price differences associated with a solution for
given by
will not necessarily conform to that of
. Moreover, this representation of price differences in terms of
assumes that the model for
is stationary and is therefore only valid for short time periods, given that financial signals are intrinsically non-stationary. Thus, over longer time scales,
can be expected to vary in time and the distribution of price differences will change accordingly. The concatenation of such
-varying stochastic fields will then lead to a price difference time series whose overall distribution is taken to be consistent with that of a real financial signal. In other words, the distribution of the price changes over a long period is the combination of different distributions over shorter periods of time due to the time variations in
as shall be illustrated later in
Section 7.1. It is this difference that is fundamental to the application of the FMH for time series modelling, given that the price differences of financial time series do not conform to a normal distribution compounded in the statistical distribution for
alone. In this context, we may quantify the FMH in terms of a non-stationary heuristic model for the price of a commodity as compounded in the equation
6.3.1. Memory Function for the FMH
Another approach to developing the basic random scaling fractal model where the amplitude spectrum of a financial signal is taken to be characterised by a
scaling law is to consider a specific memory function
in Equation (
14). Noting that
if we approximate
by the Taylor series
then, provided
is a symmetric distribution so that
, we can write
and Equation (
14), reduces to the form
In Fourier space,
and for
to be characterised by a self-affine scaling law, we require that
. Thus, since
we infer that
Given the FMH model for a financial signal where
then the price approaches zero if
. This is because
as
. In turn, this implies that the memory function approaches
, given that
, meaning that the ‘system’ has a constant memory, i.e.,
. This is not a physically significant interpretation because it indicates that there is no time evolution of the density field in Equation (
14) given that
On the other hand, as
,
becomes the integral of
(the basis for the RWH) and the memory function approaches zero. For the FMH model compounded in Equation (
21), by estimating the value of
for a time series
, one can produce an estimate for the memory function
given by Equation (
20) for that time series.
6.3.2. Asymptotic Rate Equation
Another variation on a theme of the rate equation concerns the asymptotic case, when the characteristic function
as
. In this case, if we consider Equation (
14) in Fourier space, we have
from which we obtain the rate equation
The rationale for this asymptotic result, in terms of the behaviour of a PDF
when
, can be formulated as follows:
Now, if the PDF is such that
as
, as is the case with the Lévy distribution given by Equation (
16), for example, then,
In addition to the Lévy distribution, it may be expected that all stable PDF’s approach zero as
. In this sense, the rate equation given by Equation (
22) applies for any case when
. However, it may be argued that Equation (
22) is especially applicable for any distribution that can only be defined in an asymptotic form as given in Equation (
16). This is the case in the application of Equation (
16) to formulate an FMH-based mathematical model.
Applying the memory function given by Equation (
20), in the solution to Equation (
22), we obtain
where
and
Equation (
22) and solutions thereof have been studied further in [
72], which includes a method of computing the index
by applying the same regression algorithms used to compute this index when
.
7. Case Study: Trend Analysis and Price Forecasting of Cryptocurrencies
The first application of using the FMH for trend analysis and long-term price forecasting coupled with the use of machine learning for short-term forecasting was undertaken in 2021 for the case of carbon trading [
143]. This study implemented the models, methods, algorithms and Matlab functions published in [
14]. In this section, we consider the application of the same approach for cryptocurrency trading, using, by way of an example, the Bitcon–US dollar (BTC–USD) exchange rates.
Cryptocurrencies have become a standard trading commodity, along with other currencies traded as part of Forex [
144], which is similar to buying and selling other types of securities and commodities. When a Forex trade is undertaken, one currency is sold and another currency is bought. A profit is then made if the value of the currency that has been bought increases with respect to the currency that has been sold.
The global cryptocurrency market size was USD 827 million in 2020 and is projected to grow from USD 910M in 2021 to USD 1903M in 2028 at a compound annual growth rate of 11.1% in forecast period, 2021–2028 [
145]. The market cap of the stable coins sector is ∼USD 110B, representing a 5.17% of the total cryptocurrency market cap. The primary factor that is driving this phenomenal market growth is the development of distributed ledger technology, the rising digital investments in venture capital and the growth in price values of cryptocurrencies such as Bitcoin [
146]. Further, developing countries have started using digital currencies as a financial exchange medium and the increasing popularity of digital assets such as Bitcoin is likely to drive market growth in the forthcoming years [
147]. This is predicated on the utilisation and integration of blockchain technology to attain decentralisation and controlled efficient transactions which offers decentralised, fast, transparent, secure, and reliable transactions.
As a result of these advantages, companies and central banks of developing countries are investing in cryptocurrencies and collaborating with other companies to deliver efficient services to cryptocurrency users. In this respect, the target market is very lucrative, especially at this point in time when, 2021 witnessed a sustained and stable increase in cryptocurrency valuation. It is in this context, that this case study focuses on the application of the algorithms presented in [
14] for Bitcoin trading, specifically the daily BTC–USD opening values using data available at [
148] from 17 December, 2020 to 30 November, 2021.
7.1. Long-Term Prediction
Figure 8 shows the result of applying a backtest for daily opening Bitcoin price values from 7-12-2020 to 30-11-2021. The figure provides a trend analysis obtained for a moving window, based on repeatedly computing the Lyapunov-to-Volatility Ratio (LVR) using Equations (
1) and (
2), and the Beta-to-Volatility Ratio (BVR). In the latter case, it is assumed that the short time windowed data scales as
, i.e., for any windowed section of data,
, where
c is a constant. A least squares method is then used to compute
. The results are based on using the Matlab function ‘Backtester’ and related functions presented in [
14]. They are based on optimising the computational parameters for this process (window sizes), following the adaptive filtering approach presented in [
143].
The results given in
Figure 8 are of the pre-filtered and normalised BTC–USD data after application of a moving average filter (red lines) of period 40 and the post-filtered BVR and LVR signals (green lines) for a period of 35. The zero-crossing positions for these signal (blue line ‘spikes’) indicate the points in time where a change in the trend of the filtered data stream takes place. Apart from a difference in the amplitudes of these signals, the LVR and BVR perform the same function. In both cases (i.e., in the computation of the BVR and LVR signals), a combined accuracy 100% is obtained for predicting the long-term trends for the daily BTC–USD time series considered, i.e., when to ‘go long’ (to buy BTC–USD and for how long—100% accuracy) and when to switch to going short (when to sell and/or stop buying BCS-USD and ‘hold the position’—100% accuracy). These accuracies are based on comparing the predicted trends with those that actually occur (the basic principle of all ‘back-testing’) as provided in the ‘Backtester’ Matlab function given in [
14].
A complementary analysis of the data is given in
Figure 9 which shows the filtered and normalised BTC–USD data stream (red line), together with the Volatility (green line) and the Lévy index (blue line). The data is moving average filtered using a period of 5. The Volatility and Lévy index are then computed using another moving window for a period of 5. The Lévy index
is computed from
, given that
. From
Figure 9, it is noted (strictly in the context of the numerical procedures that are applied), that the variations in
have a mean value
(the actual value for the data is 0.9838). For
, the PDF
of the system described by Equation (
14) is given by the Cauchy distribution when
Thus, it may be surmised that the current daily BTC–USD exchange rate time series is characterised by a variable Lévy index with a mean
. Further, on the basis of Equation (
18),
implies that
Comparing this result with Equation (
13), the dynamic behaviour of BTC–USD prices appears to be similar to a random walk but not identical to it, given that
fluctuates above and below its mean value
.
While this approach can complement trend prediction methods in financial signal analysis, and, in this sense, provide a long-term forecast, it is not suitable for generating short-term predictions of actual price values. A relatively new and novel approach to doing this is to revert to the application of Evolutionary Computing as discussed in [
14,
143].
The confidence level associated with these predictions is determined by the value and continuity of the BVR and LVR signals. This is because the amplitude of these signals is a measure of the volatility, i.e., the lower the volatility, the greater the signal amplitude. Thus, in the application of the short-term forecasting method considered in the following section, the BVR-LVR signals provide not only an indication of the price trend and whether a trader should go long, go short or hold the position, but also a risk management indicator in terms of when short-term predictions can be trusted. This occurs when the amplitude of the BVR-LVR signals is high and continuous.
7.2. Short-Term Market Price Prediction
The method of short-term predictions considered in this section follows directly from that reported in [
14,
143]. This is predicated on the application of evolutionary computing to simulate a financial signal, specifically to evolve formulas (based on a window of price values) that can then be used to predict future values. In the previous publication the ‘Eureqa’ modelling engine was used [
149]. Originally created by the University of Cornell’s Artificial Intelligence Lab and later commercialised by Nutonian Inc. [
150], the software uses an evolutionary search to determine mathematical equations that describe sets of data in their simplest form. In this paper, a complementary system is used, namely, the ‘TuringBot Symbolic Regression Software’ [
151]. Like Eureqa, this is a software package that uses symbolic regression to find mathematical formulas from data values.
In regard to using such systems, a critical issue is the length of the data window or period that should be chosen for formula evolution. This question is ultimately data dependent and ideally relates to the sequence of data points that may be assumed to be dynamically interrelated in the short term. For a financial signal characterised by a memory function given by Equation (
20), this may be considered to be determined by the time period over which the memory function is influential, the short time period over which the data may be considered to be dynamically related. In this case, the ‘influence’ is related to the value of
, where it is noted that when
,
(no memory) and when
,
(constant memory). The use of a memory function that is consistent with the fractal scaling law for a financial signal therefore provides a useful reference to qualify the window size that may be used. This requires an accurate estimate of
to be computed from the data stream.
The choice of the period, depends on the type of data, and specifically, the volatility which will typically very in time. As the volatility increases, one can expect to increase the period. However, in regard to this case study, and, given that the long-term predictions discussed in the previous section are the basis for evaluating the accuracy of a short-term prediction, the period is set to the same value as that used to generate the results given in
Figure 8, i.e., 40 days.
Figure 10 shows the 10 daily future price predictions from 21 November, 2021 to 30 November, 2021 of the BTC–USD, using sequential historical data on a moving window basis for a period of
days. In each case, a simulation formula is evolved through the application of the TuringBot to produce
M functions
using a moving window consisting of
N price values. In practice, and, for each case (i.e. for each window of data), the formula is evolved from price values
where
,
, …,
. The one-day future price prediction is then given by
. For the one-day ahead predictions given in
Figure 10,
and
.
The evolution process is halted when the relative mean error between the data and the evolved formula simulation of the data is ∼1%. All the basic operations are used (addition, multiplication and division), and all trigonometric, exponential and hyperbolic functions. These functions are used so that the evolved formulae are easily translated into Matlab to process and plot the data. For example,
Figure 11 shows a screen shot of the TuringBot system after having evolved the nonlinear formula or ‘Function’, as highlighted, based on the BTC–USD daily (open) price data from 21-10-2021 to 29-11-2021 (40-days). These data, and the 40-point function evolved, (i.e.,
), is provided in the plot shown in
Figure 11, the function itself being given by (for
)
This formula is then used to predict the opening price value for 30-11-2021, which yields
= USD 54236, the actual price on this date being USD 58266 as shown in
Figure 10. There are or course, and, as to be expected, differences between the actual and predicted price values as shown in
Figure 10. The relative mean error between the predicted and actual values for this case is 2.4%
Comparing the predicted price values with those that actually occurred on a day-by-day basis, it is clear that the price predictions are within a definable tolerance zone. This is because both the BVR and the LVR are relatively high (and stable) as indicated by the amplitudes of these signals (and the continuation of this amplitude) given in
Figure 8 over the same period of time, when the volatility is relative low. However, there are a number of significant variations on a theme that can be applied to the basic methodology considered, in order to assess the performance and accuracy of the predictive power. These variations include issues such as the following:
the inclusion of a larger number of the functions available with the TuringBot, for example, including ‘Other functions, Logical functions and History functions’;
the effect of varying the period (window size) used to compute the formulae, and the accuracy of future predictions for a varying number of future projections;
the correlation between the predictive accuracy, and the memory function, based on an estimate of for different sets of price data;
the effect of smoothing the data (for a specific period) prior to formulae evolution on the predictive accuracy of the formulae.
In regard to the issue of data smoothing, the method may be expected to provide forecasts over intermediate time scales, which yield a greater level of accuracy than are possible with the longer-term forecasts using the approach discussed in
Section 7.1. Such a study lies beyond the scope of this publication.
8. Conclusions
The crash of 1987 took many by surprise when, in just one day, the Dow Jones plunged 29.2% [
152]. The financial models of the day stated that it should never have happened and theorists supposed that it was a ‘once in an age’ statistical anomaly. Carefully designed investment portfolios ‘blew up’ and options-based insurance portfolios failed. Financial turmoil in the dot-com bubble of the late 1990s reinforced the fact that something may not be quite right in financial theory, while the more recent global economic crash in 2008 only serves to demonstrate this fact still further. The likelihood of witnessing several of these ‘once in an age’ events in just a few decades is improbable in the extreme, yet it is a trend we see repeated across the history of global markets.
Most financiers continue to disagree as to where the real truth lies with respect to the actual efficiency of markets. It can be concluded that, in reality, a financial market cannot be considered to be completely efficient (according to the EMH) or entirely inefficient. In reality, financial markets are a mixture of both. Sometimes the market will provide fair returns on an investment; at other times, investors can generate higher-than-anticipated profits, or even significant losses. While there are many others, the innovations of the Modern Portfolio Theory and the Black–Scholes Model, are perhaps the most significant developments in recent financial orthodoxy. These models are the principle building blocks from which the world of modern financial engineering has been constructed.
In more recent times, many have tried to fix the underlying flaws in the formulae with patches and work-arounds, but nonetheless, the underlying principles continue to rest primarily upon the foundations laid down by Bachelier over a century ago. The whole edifice of financial orthodoxy, appears valid only if one assumes that Bachelier and his latter day counterparts are correct, when the Gaussian distribution (for price differences) correctly assumes how prices move. Conventional financial theory assumes that the variation of prices can be modelled by random processes, which in effect follow the simplest ‘mild’ pattern, as if each upward or downward movement were determined by the toss of a coin.
While at times this can indeed be correct, it is perhaps comparable in fluid dynamics to applying a model for laminar flow; even though we know a flow can become turbulent (at least at times). This analogy is representative of the ambiguities in financial modelling, given that the existence and smoothness problem associated with the Navier–Stokes fluid equations of motion was one of the Millennium Prize Problems stated by the Clay Mathematics Institute in 2000, and, to date, has still not been solved [
153]. This is because a theoretical understanding of the solutions to the Navier–Stokes equations (which are nonlinear equations) is incomplete. Additionally, these solutions include turbulence, which is a major unsolved problem in physics. Thus, by analogy, the issue of market turbulence is an unsolved problem in Econophysics.
Where the consideration of non-Gaussian behaviour is relevant, fractal geometry can help in financial modelling analysis. This is the basis for the Fractal Market Hypothesis, and is most relevant when price movements do not fully follow ‘mild’ or ‘laminar’ assumptions, and where we determine that there is long-term dependence or market ‘memory’. In this scenario, a more accurate non-Gaussian model of price movements can pave the way for a new, more reliable type of financial theory, one that takes account of both ‘mild’ and ‘wild’ markets.
The underlying issues associated with the FMH is that the distribution of price differences is more centrally peaked with longer tails than those associated with a normal distribution. In this context, the Lévy distribution is consistent with such a distribution. Moreover, by considering such a non-Gaussian distribution, it is possible to formulate a fractional diffusion equation for the density field whose solution is characterised by a scaling law (where is the Lévy index). This scaling law underpins the self-affine structure of a financial time series. In this respect, the Lévy index can be used to characterised the ‘tail length’ of the local distribution of price changes in a financial time series, and hence, the possibility of predicting the onset of extreme price changes.
Another important feature of the FMH is that a financial signal is taken to be memory associative. This is because the basic model for a self-affine signal involves the convolution of a white noise stochastic field with the kernel . In this context, a memory function where , (as defined through the Generalised Kolmogorov–Feller Equation) exhibits a scaling relationship in time that is the inverse the scaling relationship for the Hurst exponent where . In this respect, and H play a similar role.
In continuous random walk theory, the density function
represents the number of particles per unit length due to the random motion (random walking) of a canonical ensemble of particles whose most likely travel distance from a source after time
t is proportional to
. While the acknowledgement of such properties can not bring certainty of results in terms of financial forecasting, this approach to market analysis at least faces up to the empirical facts relating to the non-Gaussian properties found in today’s global markets, due to the complexity and self-organisation of these markets upon which the FMH is based. It is in this context, and, the example case study given in
Section 7, that this review paper has been composed.