A Review on Initialization Methods for Nonnegative Matrix Factorization: Towards Omics Data Experiments

Abstract

Nonnegative Matrix Factorization (NMF) has acquired a relevant role in the panorama of knowledge extraction, thanks to the peculiarity that non-negativity applies to both bases and weights, which allows meaningful interpretations and is consistent with the natural human part-based learning process. Nevertheless, most NMF algorithms are iterative, so initialization methods affect convergence behaviour, the quality of the final solution, and NMF performance in terms of the residual of the cost function. Studies on the impact of NMF initialization techniques have been conducted for text or image datasets, but very few considerations can be found in the literature when biological datasets are studied, even though NMFs have largely demonstrated their usefulness in better understanding biological mechanisms with omic datasets. This paper aims to present the state-of-the-art on NMF initialization schemes along with some initial considerations on the impact of initialization methods when microarrays (a simple instance of omic data) are evaluated with NMF mechanisms. Using a series of measures to qualitatively examine the biological information extracted by a given NMF scheme, it preliminary appears that some information (e.g., represented by genes) can be extracted regardless of the initialization scheme used.

1. Introduction

Low-rank matrix dimensionality reduction mechanisms represent a class of unsupervised mathematical techniques dedicated to the principle of parsimony, capable of revealing the low-dimensional structure embedded in the original data while preserving as much information as possible. Relevant information stored in data is often non-negative, and this positive sign is strictly related to a physical entity (examples include pixels in images, the probability of a particular topic occurring in a linguistic document, the amount of pollutants emitted by a factory, and so on). Taking into account this non-negativity constraint could bring some advantages in terms of interpretability and visualization of big data, while better preserving physical feasibility. In the biomedical field, the availability of big omic data (genomics, transcriptomics, proteomics, etc.) has led to the emergence of the application of specific numerical mechanisms capable of extracting valuable and interpretable information about complex interactions between data to achieve a better understanding of the underlying biological processes.

Omic data analysis represents a very active research area in the biomedical field and recent advances in technologies have allowed the simultaneous measurement of long sequential molecules, the expression levels of a large numbers of genes and proteins, genetic variants, molecules, bio-markers, cells, tissue samples and individuals [1,2]. One way to manage these data is to investigate their natural representation in terms of a data matrix $X\in {\mathbb{R}}_{+}^{n\times m}$, of which the nonnegative elements $X_{ij}$ measure some biological values (expression counts, protein concentrations, gene expression level, etc.) in its i-th row and an individual sample in its j-th column [3,4,5].

Low rank reduction mechanisms can be fruitfully used to better understand complex biological processes: in the early 2000s, they were first used in the analysis of microarray data [6,7,8,9]; gradually, they emerged in the literature as useful mechanisms to explore high-throughput omics data (i.e., uncovering their low-dimensional structure, such as groups of similar genes, interpretable subspaces, critical dimensions) and identifying in them new and known specific biological pathways [3,10,11,12,13,14,15,16].

A matrix factorization approximates a given pre-processed omic data matrix X to a low-dimensional space of dimension r as the product of two matrices $W\in {\mathbb{R}}^{n\times r}$ and $H\in {\mathbb{R}}^{r\times m}$, i.e., $X\approx WH$, where the first factor W describes the embedded structure between features, and the second matrix H quantifies the structure between samples. Generally speaking, each pair of a column in W and the corresponding row of H represents an ideal source of biological, experimental and technical variation and their relative roles in each sample (which is actually known as a “complex biological process” [3]). From a mathematical point of view, each original sample (one column vector $X(:,j)$ in X) is a linear combination of new column features $W\left(:,k\right)$, ($k=1,\dots ,r$) weighted with coefficients $H_{kj}$ so that

$$X(:,j)\approx \sum _{k=1}^{r}W(:,k)H_{kj},$$

(1)

for $j=1,\cdots ,m$ and $r<nm/(n+m)$.

Various matrix factorizations have proven their effectiveness in handling omic data; the best known are: Singular Value Decomposition (SVD) [8,17], Principal Component Analysis (PCA) and its sparse and probabilistic variants [14], Independent Component Analysis (ICA) [18] and Nonnegative matrix factorizations (NMF) [3,19,20,21,22,23]. Each of these techniques is based on different constraints that characterize the final properties of the matrix factors, leading to different optimization problems and numerical algorithms that must be used. PCA is based on a convex quadratic optimization problem with a unique global minimum that leads to orthogonal matrix factors that determine the proportion of explained variance in the omic data. ICA and NMF are based on nonconvex optimization problems, so the numerical algorithms used to solve them provide solutions that depend on the initialization mechanism in question. ICA factors derive from the minimization of mutual information between data components. On the other hand, when dealing with omic data, NMF algorithms minimize the generalized Kullback–Leibler divergence (KL) under the non-negativity of the elements in W and H factors. This constraint produces an approximation of the omic data matrix as a nonnegative linear combination of the columns in W (commonly called metagenes), weighted by elements $H_{kj}$ in H, and is compatible with the intuitive notion of combining parts into a whole [24]. Note that each $H_{kj}$ describes the effect that the kth metagene has on the jth sample, so that a low value $H_{kj}$ indicates that the corresponding kth metagene has reduced importance in approximating the jth sample. NMF allows to reveal interpretable latent factors (unlike PCA or ICA, which also have negative entries without obvious biological significance) and to identify genes belonging to multiple pathways or biological processes [20,22,23,25]. As these reasons lead to a much more intuitive and interpretable representation, NMF is quite often preferred to other techniques.

As previously observed, the NMF optimization problem

$$\underset{W,H\ge 0}{min}KL(X;WH),$$

(2)

where $KL(X;WH)$ is the KL objective function

$$KL(X,WH)=\sum _{ij}(X_{ij}log(\frac{X_{ij}}{{\left(WH\right)}_{ij}})-X_{ij}+{\left(WH\right)}_{ij})$$

(3)

has to be solved. However, this nonlinear objective function is nonconvex in both W and H, so iterative numerical algorithms had to be used. These algorithms guarantee to converge to some local minima (more precisely, stationary points), but require initialization mechanisms that can greatly affect their convergence rate and often the “biological” quality of the obtained solution factors W and H.

Despite that several different initialization schemes for NMF have appeared in the literature (we direct the reader to [26] for a recent review of theoretical and practical aspects of NMF), very often, only studies on the performance of NMF algorithms with respect to the residual of the cost function are presented. Qualitative behavior of NMF factors with respect to the initialization mechanism has been studied when large text data or images are processed. On the contrary, when NMF algorithms are used to analyze omic data, random initialization is the most commonly used method, although this does not guarantee good quality of the extracted matrix factors from a biological point of view. A very preliminary study regarding the influence of some initialization techniques on a particular NMF algorithm appeared in [27]. Here, it is suggested that there might be some biological information strictly related to the microarray data under analysis that can be extracted independently of the initialization scheme in question.

In this paper, we have proposed a revised taxonomy of initialization methods for NMF, starting from the one presented in [28], highlighting which schemes are used in the analysis of omic data by NMF algorithm, together with their main advantages and disadvantages. Using a specific NMF algorithm and a selected subset of initialization schemes belonging to different types, we also analyzed a pair of benchmark microarray data matrices, showing that the relevance of the extracted information cannot be immediately understood as it is the case for text or image data, indicating that the influence of initialization and its impact on the extracted biological information are worth further investigation.

The remainder of the paper is organized as follows. In Section 2 we briefly highlight the importance of initialization for feeding iterative NMF algorithms. In Section 3 we illustrate the iterative algorithms for NMF, and we describe in detail the initialization schemes that have appeared in the literature panorama to date. Section 4 deals with the brief presentation of some results obtained when a selection of initialization schemes was used to feed a specific NMF algorithm for the analysis of two microarray datasets: the qualitative measurement showed how a core of information strictly related to the analyzed dataset (i.e., some genes) can be extracted independently of the particular initialization scheme used.

2. How Important Are Initializations for NMF?

The task of nonnegative low-rank approximation of a given omic data matrix X can be formulated as a constrained (under the condition of nonnegativity of the factor matrices) optimization problem using the nonlinear KL-divergence (3). The lack of convexity of each NMF objective function in W and H simultaneously means that no closed-form solution exists and thus convergence to global optima of (2) is not necessarily achieved [29].

Numerical methods for solving (2) include: multiplicative update rules (MU) [9,24,30,31], which are characterized by good theoretical convergence properties [32], alternating nonnegative least squares [33,34,35], and projected gradient descent methods [36]. The iterative nature of each of these numerical methods requires the use of an initialization of W or both W and H to matrices (of appropriate size) with only nonnegative elements.

However, the choice of initial values affects not only the convergence property of the algorithm but, in particular, the quality of the solution to which it converges. An illustrative example of the influence of initialization on the “quality” of the final factors is the Swimmer dataset presented in [37]. This image dataset consists of 256 black and white images, each representing some stick figures (with a fixed torso of 12 pixels) and four moving parts (four limbs of 6 pixels) positioned in four different ways. An extraction of this dataset is shown in Figure 1.

This dataset highlights the importance of good initial values when solving the NMF task correlated with these images. As discussed in [38], when applying, for example, multiplicative updating rules and the projected gradient algorithm with a random initialization, the final NMF factors fail to properly extract the latent parts (torso and limbs) embedded in the figures, thus mixing the ghostly appearance of the torso with some of the other parts. Due to nonconvexity, iterative algorithms are not guaranteed to converge to the global optimum, and they are equally dependent on initialization. For a simple image dataset satisfying the separability rule theorized in [37], random initialization has been shown to lead to solutions that are not fully satisfactory in terms of interpretability and NMF part-based decomposition [24]. Other types of structured initialization algorithms might give better results in some cases [38].

Nevertheless, comparisons between the results obtained when using different initialization methods have been under-researched. Some initialization schemes have been qualitatively compared to demonstrate the best clustering performance for different face and text datasets [39], others improved face component separation [40], or better separation performance in the audio source separation task [41].

However, when NMFs are used to analyze microarrays or more general omic data, the problem of choosing an appropriate initialization becomes more complicated because the data have special meanings, and very often, only random initialization mechanisms are chosen. In [42], an integrative approach for disease subtype classification based on NMF was proposed. Here, the most appropriate final NMF factors were chosen as those that produce the smallest value of the objective function among numerous local minima obtained by multiple random initializations of W and H. In particular, a random initialization of W was obtained from a uniform distribution or using the SVD-based initialization algorithm [43]. However, final comparisons were made only in terms of the performance of the objective function. In [44], the proposed hierarchical alternating least squares algorithm for solving NMF tasks was initialized with respect to single cell datasets using either a random method and a selection of r columns randomly sampled from the corresponding input data. Comparisons accounting for the variations due to these two different initializations showed that they performed similarly, although the qualitative representations of the final solutions revealed some differences between them. In [45], clustering of multiple types of genomic data was approached via an nNMF algorithm that initialized the factors Ws with (i) a uniformly randomly generated matrix and (ii) a nonnegative matrix decomposition technique with respect to each piece of data. However, no comparisons were reported on the final results with respect to the different initializations. Some comparisons of the impact of three specific initialization methods on the solutions obtained by the multiplicative NMF update algorithm applied to problem (2) appeared in [27] and refer to two benchmark cancer datasets. This preliminary study suggests the existence of latent biological information that can be extracted by NMF algorithms regardless of the initialization mechanisms used, but these observations need further investigation.

As the preceding discussion suggests, there are a number of research questions and shortcomings in the existing literature that need to be addressed. In particular, to our knowledge, the question “Do initialization mechanisms affect the final results of NMF for omic data analysis?” still remains open. To pave the way for in-depth research in this context, we present a complete taxonomy of initialization schemes for NMF algorithms, highlighting their mathematical aspects, advantages and possible weaknesses.

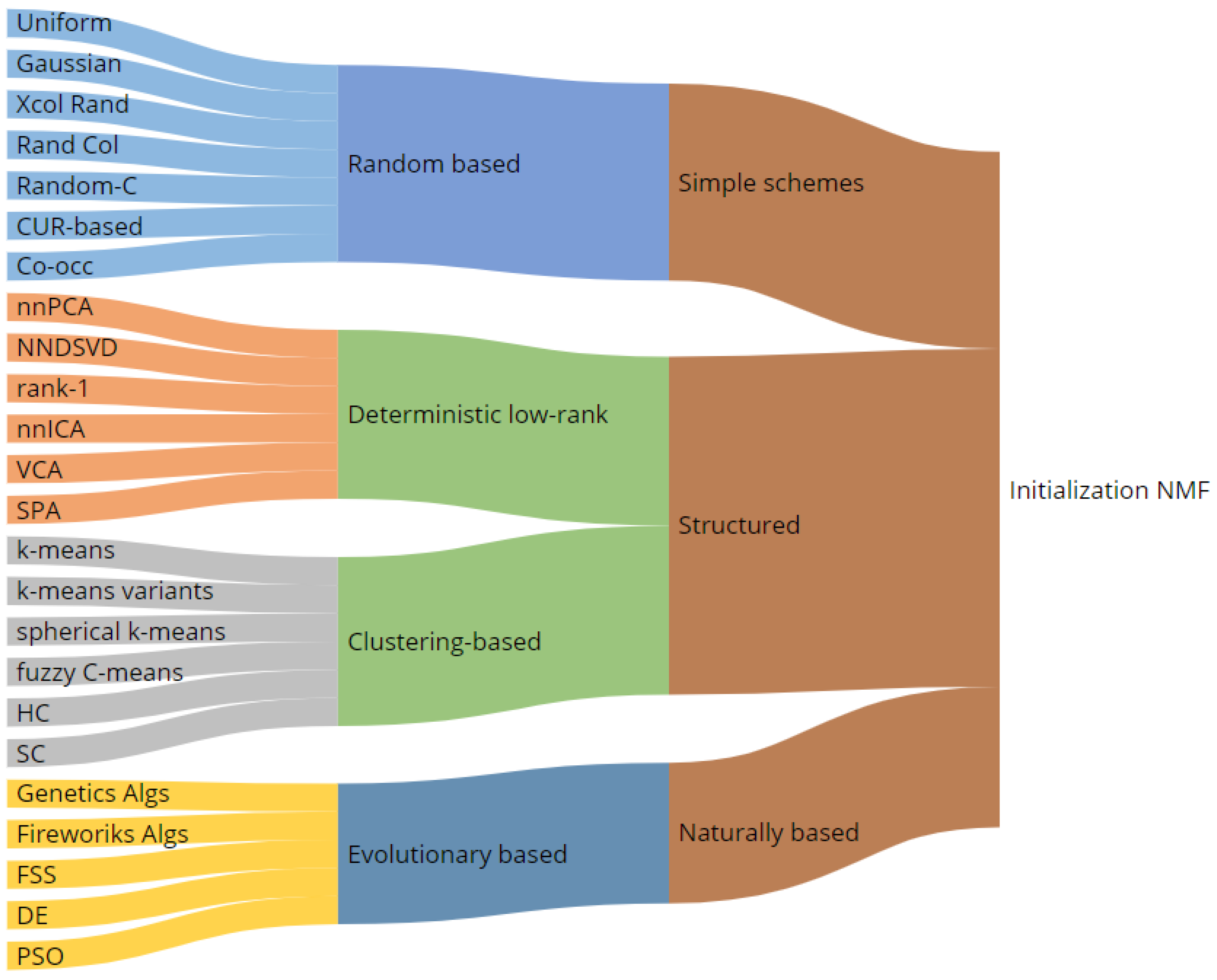
3. NMF Iterative Algorithms and a Complete Taxonomy of Initialization Mechanisms

In this section, we present iterative algorithms for NMF of alternating least squares type. These include the majorize–minimize (MM) algorithms, coordinate descent and gradient descent methods, expectation–maximization algorithms, and cone projection approaches [46,47]. We focus on the general constrained nonlinear optimization NMF problem, which is a more comprehensive version of (2) defined as follows:

$$\underset{W,H\ge 0}{min}{D}_{\beta }(X;WH)$$

(4)

where the cost function is the general $\beta$-divergence,

$$D_{\beta }(X;WH)=\sum _{i=1}^n\sum _{j=1}^m{d}_{\beta }(X_{ij};{\left(WH\right)}_{ij});$$

with $d_{\beta }$ is commonly defined for each $x,y$ as

$$d_{\beta }(x;y)=\left\{\begin{array}{cc}\frac{1}{\beta (\beta +1)}(x^{\beta }+(\beta -1)y^{\beta }-\beta x{y}^{\beta -1})\hfill & \beta \in \mathbb{R}-\{0,1\};\\ xlog\left(\frac{x}{y}\right)-x+y\hfill & \beta =1;\\ \frac{x}{y}-log\frac{x}{y}-1\hfill & \beta =0.\end{array}\right.$$

Different values of the parameter $\beta$ allow to take into consideration the Euclidean distance, the Kullback–Leibler divergence (3) and the Itakura–Saito divergence as special cases $(\beta =2,1,0$, respectively).

Alternating least squares type algorithms sequentially update H given W and then W given H, as

-

Set $k=0$ and W equals to any nonnegative $W_0$;

-

With fixed $W_k$, update $H_{k+1}=argmi{n}_{H\ge 0}{D}_{\beta }(X;W_k{H}_k)$;

-

With fixed $H_{k+1}$, update $W_{k+1}=argmi{n}_{W\ge 0}{D}_{\beta }(X;W_k{H}_{k+1})$;

-

Iterate until a stopping criteria is satisfied.

These two steps are essentially identical because of the symmetry of the factorization. Indeed, from $X\approx WH$ we have $X^{\top }\approx H^{\top }{W}^{\top }$, where we reverse the roles of W and H and make no assumptions on the data dimensions n and m. Writing the derivative of the cost function $\nabla D_{\beta }(X;WH)$ with respect to H (resp. W) as the difference of two nonnegative functions (see [48] for details), the update rules of alternating least squares algorithms can be written as functions of the ratio of the nonnegative terms.

For example, the updating rules for Frobenius and KL-divergence (3) for factors H and W can be expressed in the following matrix forms:

$$\begin{array}{c}H\leftarrow H.\ast \frac{\left(W^{\top }X\right)}{\left(W^{\top }WH\right)},\hfill \\ W\leftarrow W.\ast \frac{\left(X{H}^{\top }\right)}{\left(WH{H}^{\top }\right)}\hfill \end{array}$$

(5)

and

$$\begin{array}{c}W\leftarrow W.\ast \frac{\left(X./\left(WH\right)\right)H^{\top }}{{\mathbf{1}}_n\ast {\left(\sum _{j=1}^m{H}_{:j}\right)}^{\top }}\hfill \\ \\ H\leftarrow H.\ast \frac{W^{\top }\left(X./\left(WH\right)\right)}{{\left(\sum _{i=1}^n{W}_{i:}\right)}^{\top }\ast {\mathbf{1}}_m}\hfill \end{array}$$

(6)

where $.\ast$ denotes the Hadamard product, the ratio is referred to element-wise division and ${\mathbf{1}}_m$ is a m dimensional vector of ones.

As mentioned earlier, algorithms for computing NMF must be initialized with an initial left factor W (or both factors W and H) to begin with.

We propose to classify the initialization mechanisms for iterative NMF algorithms (which have appeared in the literature panorama so far) into three classes, indicating the main idea on which the initialization is based. In particular, we can identify: (i) random-based schemes, (ii) structured initializations, (iii) evolutionary and nature-based mechanisms. Figure 2 illustrates the three main classes and their subclasses.

3.1. Random Based Initializations

The simplest way to choose the initial factors W and H is to construct them as matrices (of dimensions $n\times r$ and $r\times m$, respectively) with random numbers. Random initializations were used early in [30], while a discussion of their goodness in terms of algorithm performance and other variants of randomization methods can be found in [49]. Random-based initializations generally construct dense factors, require low computational cost and processing time for their computations, and are the benchmark mechanisms used in the majority of NMF studies, especially when analyzing omic data. However, the quality and reproducibility of the NMF result are rarely questioned. To ensure robust and reproducible results, users should run NMF with random initialization a sufficient number of times and finally select the best result based on some quantitative and qualitative criteria [43]. Different mechanisms of random matrix generation are:

• Uniform random: the elements in the matrix W (and in H) are chosen as uniformly distributed numbers in the interval $[0,1]$ or in the same range as the entries of the target matrix.
• Gaussian random: the elements in the matrix W (and in H) are chosen as $max\{g,0\}$, where the number $g\in \mathbb{R}$ is a Gaussian values.
• Random $Xcol$: the factor matrix W is obtained by averaging over r randomly selected columns of the data matrix X. This scheme is very inexpensive and has the advantage of yielding a sparser factor when the data matrix is already sparse. When dealing with omic data, selected columns of X can be considered as a kind of a priori information that can influence the following update process.
• Random-C initialization: this mechanism is based on a double random selection of columns in the data matrix X as follows:

  -

  Identify p of the longest (in the 2-norm sense) columns of X;

  -

  Randomly choose q columns from the previous p longest;

  -

  Construct each column of W as the average of these q columns.

  This scheme is inspired by the C-matrix of the CUR decomposition and produces the densest W, in which column vectors are closed with the centroids of the data matrix (see spherical-k means initialization) [49].
• CUR-based initialization: the factor matrix W is constructed as a submatrix (with a small number of actual columns) of the data matrix X. In this way, values are obtained that are more interpretable from a biological point of view (and usually to the same extent as the original data) [50,51]. CUR-based mechanisms differ in the “statistical” way of selecting columns (or rows, if we refer to the initialization of the factor H) from the matrix X. This selection is based on computing an “importance score” for each column (row) of X and randomly selecting r of these columns (rows) using this score as the probability distribution for importance sampling. The scoring values of a column $X_{:j}$ in X can be calculated as: normalized statistical leverage score [50], spectral angular distance, or symmetrized KL-divergence [52].
• Co-occurrence initialization: firstly the data co-occurrence matrix (i.e., $X{X}^{\top }$) is formed and then r of its columns are selected by the algorithm proposed in [53] to form the factor W. The data co-occurrence matrix contains information about hidden relationships between columns and rows in the data matrix X, but the computational costs required for this make this initialization mechanism expensive and often impractical for use in the context of biomedical data analysis where large datasets are considered.

3.2. Structured Initialization

Schemes belonging to the structured initialization class are based on the idea of applying low-rank factorizations, well-known clustering mechanisms on the data matrix X to generate initial factors for NMF, or very specific data-driven schemes such as semantic harmonic initialization when audio data are involved ([54,55,56]). These specifically structured initializations for NMF were mainly designed to improve their performance either in terms of computational complexity or for preserving the particular data structure.

Initialization schemes based on low-rank decomposition algorithms do not require a randomization step, so they can also be classified in the subclass of “deterministic” structured initialization methods. They include schemes using the Singular Value Decomposition and the Nonnegative Double Singular Value Decomposition (NNDSVD) [43,57,58] and its variants [59], rank-1 decomposition [39,60] [61], nonnegative PCA [62,63], nonnegative ICA [64], Vertex Component Analysis [65,66,67], Successive Projection Algorithm [68].

On the other hand, schemes based on clustering algorithms reduce to the minimum use of random numbers (only some hyperparameters need to be randomly set up before the clustering data matrix [69]) avoiding the application of multi-start random initializations [70]. The subclass of “clustering based” initializations includes: k-means [71] and its variant [72], spherical k-means methods [73,74], fuzzy C-Means clustering [40,75], Hierarchical Clustering [76] and Subtracting Clustering [28].

Table 1. Structured Initialization schemes for NMF algorithms with their main references and an indication if they have been applied in the context of microarrays or omic data analysis.

	Method	Main References	Omic Data
Deterministic low-rank	NNDSVD	[43,57,58]	yes
	NNDSVD variant	[59]	no
	nonnegative PCA	[62,63,71,75]	no
	rank-1	[39]	no
	nonnegative ICA	[41,64,77]	yes
	Vertex Component Anal.	[65,66,67]	no
	Successive Projection Alg.	[68]	no
Clustering-based	k-means	[72]	no
	k-means variant	[57,71]	yes
	spherical k-means	[73,74]	no
	fuzzy C-Means	[40,75,78,79]	no
	Hierarchical Clustering	[76]	no
	Subtracting Clustering	[28]	no

summarises these mechanisms, their related references and if they have or have not been used when microarrays and generally omic data are involved.

In the following, we take a closer look at the structured initializations for NMF, some of which are used for microarrays or omic data in general.

3.2.1. Non-Negative Double Singular Value Decomposition

NNDSVD described in [43] is based on two processes of SVD, and it constructs both factors W and H in NMF as the positive parts of rank-1 matrices obtained by the left and right singular vectors of the SVD decomposition of X.

Let $X={\sum }_{i=1}^k{\sigma }_i{u}_i{v}_i^{\top }$ be the SVD representation of the data matrix X, with rank k and ${\sigma }_i$,$u_i,v_i$ as the nonzero singular values and the left and right singular vectors of X, respectively. Then, for every $r<k$, the optimal rank-r approximation of X is given by

$$X\approx \sum _{i=1}^r{\sigma }_i{C}_i,$$

where $C_i=u_i{v}_i^{\top }$ are the rank-1 matrix formed by the first $i=1,\dots ,r$ singular vectors. Each matrix $C_i$ can be written as the sum of two nonnegative components $C_i=C_i^{+}-C_i^{-}$, being the positive and the negative section of $C_i$, respectively. Approximating each $C_i$ by $C_i^{+}$, by its nonnegativeness from Perron–Frobenius theory, its maximum left and right singular vectors will also be nonnegative. The dominant singular triplets can be used as initial vectors and rows to W and H.

The main phases of this algorithm are described in the following [43]:

-

Compute the largest r singular triplets of X (first SVD process);

-

Initialize the first column and row vectors in W and H as the nonnegative dominant singular vectors of X weighted by $\sqrt{{\sigma }_i}$;

-

Compute the positive section of each $C_i$;

-

Compute the largest r singular triplets of $C_i^{+}$ (second SVD process);

-

Initialize the j-th columns and rows in W and H, for $j=2,\dots ,r$ as the singular dominant vectors of each $C_i^{+}$, weighted by the $\sqrt{{\sigma }_i\left(C_i^{+}\right)}$ and normalized.

NNDSVD is composed of two processes of SVD and this justifies its name. There are some variants of it, namely NNDSVDA and NNDSVDAR, which involve a replacement of the zero value on the result $(W,H)$ by the average of all elements in the matrix X and by a very small random value, respectively. This initialization scheme is included in the main tools for NMF analysis of biological data [80,81], moreover, its deterministic properties make NNDSVD the most commonly used initialization scheme together with random approaches.

3.2.2. Nonnegative ICA Initialization

Independent component analysis is a mechanism used to extract a set of statistically independent source variables from a collection of mixed signals without having information about the data source signals or the combination process. It has been used as a knowledge extraction mechanism in various biological and omic data analysis tasks. A modified nonnegative version of ICA (nnICA) was proposed in [64] to feed NMF algorithms, and such initialization has been shown to be effective in speeding up the learning process and obtaining desired solutions.

The main phases of this algorithm are:

-

Compute the ICA on the observed data matrix X;

-

Initialized the factor W as the absolute of the independent components source matrix obtained from ICA.

3.2.3. k-Means Initialization

Another structured initialization sometimes used in biological contexts is the (spherical) k-means clustering [74]. In this scheme, the columns of W are initialized with the centroids ${\left\{c_j\right\}}_j$ of the best k (spherical) clusters of data, i.e., the center points of k disjoint subsets ${\left\{{\Pi }_j\right\}}_{j=1}^k$ of the columns of X that are closest with respect to a distance function (generally the Euclidean norm when spherical-k means clustering is required).

The main phases of this algorithm are described below, adopting the notation introduced in [74].

-

Initialize k centroids ${\left\{c^{\left(0\right)}\right\}}_{j=1}^k$ randomly choosing some columns in X and set $t=0$ (this is the initial iteration) ;

-

Compute $d_{ij}^{\left(t\right)}=\frac{c_j^{\left(0\right)}{X}_{*i}^{\top }}{\parallel c_j^{\left(0\right)}\parallel \parallel X_{*i}\parallel }$, $j=1,\dots ,k$ and $i=1,\dots ,m$;

-

Define the new partition of clusters ${\Pi }_j^{(t+1)}=\{X_{:i}|argma{x}_l(d_{il}^{\left(t\right)})\}$;

-

Recompute each centroid as: $c_{j=1}^{(t+1)}=\frac{{\sum }_{X_{:i}\in {\Pi }_j^{(t+1)}}{X}_{:i}}{\parallel {\sum }_{X_{:i}\in {\Pi }_j^{(t+1)}}{X}_{:i}\parallel }$;

-

Initialize the columns of the factor W as the final cluster centroid vectors.

This initialization scheme expects the initial matrix H to be chosen randomly or as the matrix in which the elements are the absolute values of the elements in $W^{\top }X$. A variant allows to compute the elements of the factor H as the membership degrees of each data point using the (spherical) k-means clustering [71].

3.3. Evolutionary and Natural Based Initialization

Schemes based on stochastic global search and evolutionary optimization methods have recently appeared in the literature panorama as feeding schemes for NMF algorithms, but they have not been used in the analysis of omic data.

Under this class, we can enumerate a number of different population-based algorithms: Genetic Algorithms, Particle Swarm Optimization, Fish School Search, Differential Evolution and Fireworks Algorithm [82,83], which have been proposed as new initialization variants for NMF multiplicative algorithms. All these population-based methods sequentially initialize individual rows of W or individual columns of H to minimize the NMF objective function before factorization. These methods were compared experimentally, and some of them showed a reduction in the number of NMF iterations required to achieve a given accuracy. They also allow parallel/distributed computation by splitting the initialization into several partially independent subtasks.

Another Genetic Algorithm approach was proposed in [84] to estimate the factor W by first generating a population of individuals (representing potential solutions for NMF optimization, i.e., estimates of the matrix W), then selecting individuals according to the value of a specific fitness function and reproducing them by applying a specific genetic operator. This process leads to the evolution of individuals within the population that better solve the optimization problem.

Nevertheless, these approaches suffer from difficulties in their applicability due to the large number of hyperparameters that need to be fixed and tuned a priori [69].

4. How Many Initializations Influence NMF Results for Omic Data Analysis?

The preceding literature review illustrates the existence of various initializations that can be used to feed iterative NMF processes and the fact that their impact on the NMF final has been largely considered only in terms of the performances (convergence rates and/or final relative error of the objective function) of the specific algorithm adopted. Some initialization schemes were qualitatively compared to demonstrate the best clustering performance for multiple face and text datasets [39], others improved the separation of face components [40], while initialization based on ICA proved better separation performance in the audio source separation task [41]. In the context of omic data analysis, only some random initializations and NNDSVD are used, but no comparisons have been made on how such a scheme affects the final results from a biological point of view. It should be noted that any initializations can implicitly encode prior knowledge into the NMF that may focus the resulting factors to reflect valid biological information embedded in the data [3]. Because there is a lack of information in the literature about comparing initialization methods and how these can be interpreted concerning the influence of biological results achieved by NMF, we decide to focus on this aspect by testing some techniques on real datasets. We start a preliminary study to inspect how some seeding approaches can affect the results in omic data analysis, hoping to put the basis of new theoretical and experimental studies in this direction.

Here, we briefly illustrate a preliminary study of ours using three different types of initializations with the KL-based MM algorithm to study two benchmark microarray datasets: MCF7 and Golub data derived from breast cancer cells and leukemia microarray studies, respectively.

Table 2. Description of datasets analyzed by the NMF KL-based algorithm fed by a subset of initialization schemes. The MCF7 data matrix consists of 10,331 genes extracted by a cell cycle microarray from breast cancer cells and 434 compounds linked to arachidonic acid. The data matrix was pre-processed, as described in [25]. The Golub data matrix consists of 5000 genes and 38 tumor samples: 27 patients with acute lymphoblastic leukemia and 11 patients with acute myeloid leukemia [9,85].

Dataset	no. Rows	no. Columns	Type	References
	(Genes)	(Compounds/Patients)
MCF7	10,331	434	breast cancer	[25]
Golub	5000	38	leukemia	[9,85]

contains information about these data.

We performed some numerical experiments (in R project environment [81] on an I-7 Core machine with a memory capacity of 12 GB RAM) using the KL-based update rules initialized with: random initialization with randomly generated elements in the interval $[0,1]$, nnICA and NNDVSD. According to previous studies, the hyperparameter rank value was set to $r=4$ and a stopping value of 3000 iterations (at most) was considered. Different executions were performed for initialization with randomness (10 random and 10 nnICA initializations have been saved).

We focused our attention on the columns of the basis matrices obtained for each dataset and initialization, relying on the assumption that all the knowledge extracted from the process is hidden into these latent factors. The obtained $W_{dataset}\in {\mathbb{R}}^{10331\times 84}$ matrices (concatenating all the basis from experiments for both MCF7 and Golub datasets) were compared in terms of information embedded, exploiting cosine similarity criterion. Particularly, the matrix $cos{W}_{dataset}\in {\mathbb{R}}^{84\times 84}$, defined as:

$${\left(cos{W}_{dataset}\right)}_{ij}=\frac{W_{dataset}{(:,i)}^{\top }{W}_{dataset}(:,j)}{\parallel W_{dataset}{(:,i)\parallel }_2{\parallel W_{dataset}(:,j)\parallel }_2}.$$

(7)

for $i,j=1,\cdots ,84$ collects the cosine values among columns of the basis matrix $W_{dataset}$, for both MCF7 and Golub datasets.

To demonstrate metagenes strictly related from a geometrical point of view (according to the cosine similarity), we filter values in the cosine similarity matrices, considering only pairs of metagenes with similarity values in the range $[0.8,1]$. Figure 3 and Figure 4 show a pseudo-binary version of the heatmaps for $cos{W}_{MCF7}$ and $cos{W}_{Golub}$, respectively.

Despite the large number of relevant metagenes that have appeared, some of them (85.24% and 86.43% from the MCF7 and Golub datasets, respectively) are repeated. Among the latter, those with higher and lower frequency seem to be qualitatively coherent among themselves, and, moreover, they share a common behavior pattern. On the other hand,

Table 3. Number of metagenes with a high similarity degree for the MCF7 and Golub datasets.

		Initialization
Dataset	Random	nnICA	NDVSD
MCF7	18	15	10
	24	25	10
	2	4	0
Golub	19	30	10
	10	25	10
	1	3	0

gives the number of metagenes that occur only once in each initialization scheme for the two datasets MCF7 and Golub.

Similarities and common behavior were investigated by also performing PCA on the $W_{dataset}$ matrices for both datasets.

Table 4. Percentage of variance explained for the two microarray datasets.

Percentage of Variance	PC1	PC2	PC3	PC4
MCF7	$79.8372$	$10.5284$	$4.4372$	$2.4361$
Golub	$63.2523$	$14.9335$	$12.4118$	$9.4001$

gives the percentage of variance explained by four principal components. As can be observed for both datasets, the information contained in the data seems to be mainly collected in the first components. High geometric relationships for all extracted metagenes and a high percentage of variance explained in the first components of PCA strongly suggest that metagene groups seem to be quantitatively related. In addition, the similar behavior in the cosine-filtered heatmap and relatively repeated metagenes suggests their qualitative similarity and that metagenes extracted with different initializations share common latent knowledge.

The experimental results in this section are focused on analyzing the information embedded into the column of the basis matrices achieved by several runs of different seeding methodologies. Quantitative and qualitative comparisons have been made on these results to provide evidence and form a geometrical, statistical and visual point of view (with cosine similarities, PCA and explained variances, counting frequencies and heatmap representations) that some shared knowledge is present between the different runs. Furthermore, as explained at the beginning of this section, this is a preliminary study, which needs to be further investigated and extended. We hope that this will provide the basis for future direction and collaboration between the mathematical and biological world.

5. Conclusive Remarks

Various matrix factorizations prove to be effective tools for the analysis of omic data. Among them, Nonnegative Matrix Factorization is able to reveal interpretable latent factors and identify genes belonging to multiple pathways or biological processes. However, the algorithms for calculating NMF need to be initialized. The current literature has not yet considered the question of the possible influence of the particular initialization methods on the final results of NMF for omic data analysis. In order to pave the way for a deeper investigation of this aspect, in this paper, we have completely reviewed the NMF initialization schemes appearing in the literature, pointed out their main characteristics and when they have been used for omic data. Moreover, we briefly illustrated some preliminary results obtained when three selected initialization schemes were used to feed the KL-based algorithm when two benchmark cancer datasets were considered. The experimental results obtained in this biological context seem to indicate that interpretable information strictly related to the data matrix under analysis can be extracted regardless of the particular initialization scheme used in the iterative NMF algorithm. The results presented in this work are from a preliminary study and part of a future project that aims to provide the basis for a deep collaboration between the theoretical-numerical mathematical aspect of these techniques and the biomedical world. Even if, from a mathematical point of view, the alternate algorithmic nature of NMF achieves local minimum, this is quite often sufficient in data analysis applications to extract useful knowledge from real datasets. For these reasons, future analysis in this direction should be devoted to different aspects: to the comparison of particular objective functions adopted in the minimization process and to construct a biological dataset with some a priori knowledge to better interpret the results. It is of the authors opinion that this could help researchers connect how the particular minimization process adopted is hiddenly related to the extracted biological information embedded in the data. Further analysis is needed, and a massive controlled experimental session with multiple datasets and some a priori biological knowledge of them are required to finally assess the actual influence of initialization produced on the final information extracted by NMF from omic data.