Abstract
In this paper, an advanced computational technique has been presented to compute the error bounds and subdivision depth of quaternary subdivision schemes. First, the estimation is computed of the error bound between quaternary subdivision limit curves/surfaces and their polygons after kth-level subdivision by using order of convolution. Secondly, by using the error bounds, the subdivision depth of the quaternary schemes has been computed. Moreover, this technique needs fewer iterations (subdivision depth) to get the optimal error bounds of quaternary subdivision schemes as compared to the existing techniques.
Keywords:
quaternary subdivision scheme; subdivision models; inequalities; convolution; error bound; subdivision depth; curves and surfaces MSC:
65D17; 65D05; 65U07
1. Introduction
Subdivision schemes are major tools in Geometric Modeling. These tools are mainly used to produce curve and surface models. The schemes are categorized into binary, ternary, quaternary,…, n-ary schemes. Presently, thousands of schemes have been introduced in each category. All these schemes help the technologist to produce the refine models to meet the requirements of the investors in the area of engineering. The initial sketch and subdivision rules are the main ingredients of these schemes. The estimation of the error bounds of the limit models from its initial sketch is one of the important tasks. Another task is to find the number of subdivision steps (depth) required to get the user-defined tolerable error. These two tasks are also called the distance/error between the limit model & its kth level model and subdivision depth, respectively. In this paper, we address these tasks for quaternary schemes. First, we give an overview of quaternary subdivision schemes (QSS) before addressing these tasks.
In general, QSS has four rules to refine each edge of the initial polygon (sketch). These rules are the affine combination of the points of the polygon, and they produce successively refined sketches. In the limiting case, we get the limiting model. Initially, Mustafa and Faheem [1] introduced 4-point approximating QSS which produces models. The generalized idea of m-point approximating QSS is given by Siddiqi and Younis [2]. They also introduced interpolating QSS in the same year [3]. A 4-point QSS is presented by Pervaiz [4] in 2018. Moreover, the QSS also belongs to the classes of the schemes introduced by [5,6,7,8,9,10,11,12,13] in different years. So, the importance of the QSS cannot be denied. Furthermore, the tasks of finding the error bounds and subdivision depth of models produced by QSS are meaningful.
The first technique was introduced by Mustafa et al. [14] in 2006, then its generalized version for QSS was presented by Mustafa et al. [15] in 2010. The further generalization has also been done for other categories of the schemes [16]. This technique is not suitable to use for some subdivision schemes. We also mention the drawback of this technique in this paper. The second technique is introduced by Deng et al. [17]. It is not mature enough. It only works for binary interpolating schemes. Its generalization to the cases of n-ary subdivision schemes needs to be investigated.
The third technique is introduced by Moncayo and Amat [18] and Shahzad et al. [19]. It works for binary class of schemes. Its generalization for the ternary class of schemes was introduced by Faheem et al. [20]. In this work, we are interested in generalizing the technique for QSS.
The remaining part of the work is configured as follows: In Section 2 and Section 3, we present general inequalities to compute the error bound and subdivision depth of curve and surface models produced by QSS, respectively. In Section 4 and Section 5, we offer the applications of these inequalities for curve and surface models, respectively. The conclusion will be drawn in Section 6.
2. The Error Bounds and Subdivision Depth for Curve Models
If the sequence of points show a succession in , where and the index represents the subdivision level (number of iterations) then the configuration of the th level points computed by QSS is shown in Figure 1. A generalized mathematical form of the QSS is presented as the affine combination of the points [15],
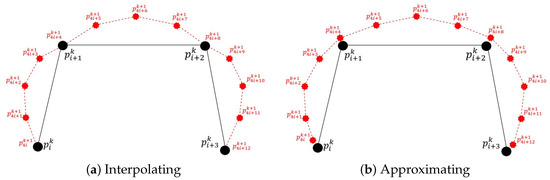
Figure 1.
The configuration of new points for the interpolating and approximating QSS for curves; the solid lines are the control polygon, and the dotted lines are the refined polygon.
Since the combination is affine it holds
The adjustment of the coefficients for the computation of error bound and subdivision depth is
along with the strict condition (See [15])
Here, we introduce some new notations, for , as follows
Furthermore, to be more specific, update the track defined in [20] for the computation of error bounds and subdivision depth. Let, at the kth level of resolution, the vector represents the approximation coefficients. Then the approximation coefficients of two consecutive stages k and in the reconstruction process of QSS is defined as
where shows the resolution level and shows the convolution product. If and are finite vectors with length and respectively then
Now we move forward and present some results of successive convolutions for one-dimensional array of vectors based on QSS.
Lemma 1.
Let and with for be finite one-dimensional arrays of vectors. Then for QSS, the one-dimensional convolution of these vectors satisfies the following inequality
where
and
Proof.
See Appendix A.1. □
Lemma 2.
For QSS, the term defined by (9) satisfies the following equality
Proof.
See Appendix A.2. □
Corollary 1.
The term involved in the inequality (8) satisfies the following equality
Proof.
See Appendix A.3. □
Now, we present the inequalities to compute the error bound and subdivision depth for the curve models produced by QSS.
Theorem 1.
If is the initial polygon and is the polygon obtained by QSS at subdivision level. Then the error bound between two successive levels is
where defined in (13),
and
We omit the proof since it is similar to the one given in [15].
Theorem 2.
If we assume the same conditions as in the Theorem 1 with the limiting curve model then the error bounds between the limiting curve model and its level polygon satisfies the inequality
where , such that .
By looking at the proof of Theorem 2.1 of [15] one may lead to prove of Theorem 2.
Given a user tolerable error , the subdivision depth of limiting model generated by QSS concerning for is a positive integer k such that the error bound . In the following theorem, we compute the subdivision depth.
Theorem 3.
If we assume the same conditions as in the Theorem 2 with the user tolerable error and
then .
3. The Error Bounds and Subdivision Depth for Surface Models
In this work, we first generalize the results presented in Lemma 1 to Lemma 2 and Corollary 1 for two-dimensional arrays then we generalize the inequalities of Theorems 1–3 to compute the error bound and subdivision depth of the limiting tensor product surface models generated by QSS.
For this, let be the polygon made by the sequence of points in , where and the polygon be obtained by the tensor product of the scheme (1). The graphical representation of the points at kth and th levels is shown in Figure 2 whereas the mathematical form of tensor product QSS is described as
where and satisfies (2).
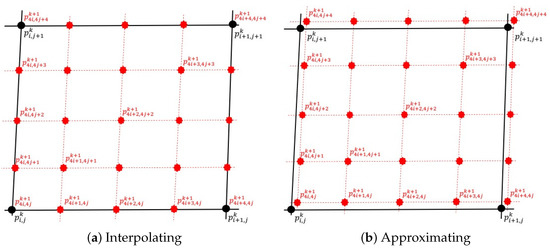
Figure 2.
The configuration of new points for the interpolating and approximating QSS for the surface. The solid lines show one face of coarse polygon while the dotted lines show the faces of the refined polygon.
Here we introduce new notations , for such that
Since the extension of some of the results from one dimension array of vectors to two-dimensional array is straight forward (See [15]), therefore we skip the trivial explanations and directly come to the following result.
Lemma 3.
Let be a finite two-dimensional array of vectors and , with for are one-dimensional arrays of vectors. Then, for QSS, the two-dimensional convolution satisfies the following inequality
Here
and
where
Proof.
See Appendix A.4. □
Now, we present the inequalities to compute the error bound and subdivision depth for the surface models produced by QSS. By using a similar approach of [15], one can easily prove the Theorems 4 and 5.
Theorem 4.
If is the initial polygon and is the polygon obtained by (17). Then the error bound between two successive levels is
Here for is defined in (20) and (21) and where and for are defined in [15].
Theorem 5.
If we assume the same conditions as in the Theorem 4 with the limiting surface model then the error bound between the limiting surface model and its kth level polygon is defined by the inequality
where , such that .
In the following theorem, we present the subdivision depth for the surface model.
Theorem 6.
If we assume the same conditions as in the Theorem 5 with the user tolerable error and if
then .
4. Numerical Applications for Curve Models
In this section, we demonstrate the performance of our inequalities to compute error bound and subdivision depth of the curve models. First, we compute defined in (13) at different values of .
Example 1.


If the curve model is produced by a 3-point approximating QSS [2] with coefficients , , , , , , , , , , , . Then for , we have
For , we get
Using (5) and Lemma 1, we have with for . Hence
Now consider
This implies
For , we get
This implies
This further implies
Since , for all , therefore we have
Now using (25), we acquire
This implies that
Similarly, we can compute the values of for . For convenience, we have computed the values up to , which are shown in Table 1. The subdivision depth k by Theorem 3 at different values of are given in Table 2.

Table 1.
Values of for

Table 2.
Depth of a 3-point approximating QSS curve model.
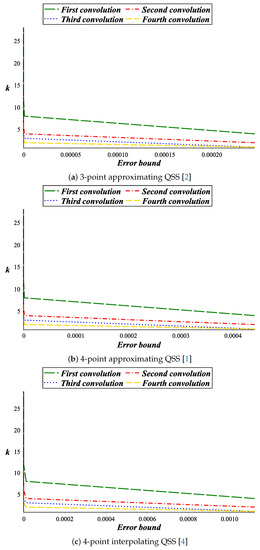
In this work, for is equal to defined in [15]. If , then the error bound of QSS cannot be computed. However, in the proposed approach, if we increase the value of , the values of decreases until becomes less than one. The main advantage of this approach also to compute error bounds of those QSS, whose is greater or equal to one. As in Table 2, twenty-eight iterations are needed to achieve a given error tolerance by technique given in [15], but by our technique, it needs only seven iterations corresponding to . The graphical comparison between the results at first and fourth convolutions are demonstrated in Figure 3a.

Figure 3.
The comparison between various convolutions for curve case.
Example 2.

The subdivision depth of the curve model produced by a 4-point approximating QSS [1] are given in Table 3. The graphical view of these depths is shown in Figure 3b.

Table 3.
Depth of a 4-point approximating QSS curve model.
Example 3.

The subdivision depths of the curve model produced by a 4-point interpolating QSS [4] for (see Table 1) are shown in Table 4. From Table 4, we can observe that the number of iterations k (subdivision depth) decreases with the increase of (order of convolution) to obtain a user given error tolerance. This is the main reason for the reduction of computational cost as compared to the technique given by [15]. The graphical analysis can be seen in Figure 3c.

Table 4.
Depth of a 4-point interpolating QSS curve model.
5. Numerical Applications for Surface Models
Now we demonstrate the performance of our results to compute error bound and subdivision depth of the surface models. First, we compute the term for by using (20) and (21). These are shown in Table 5. We see that the values of decrease with the increase of . This is the advantage of our approach.

Table 5.
The values of for .
Example 4.

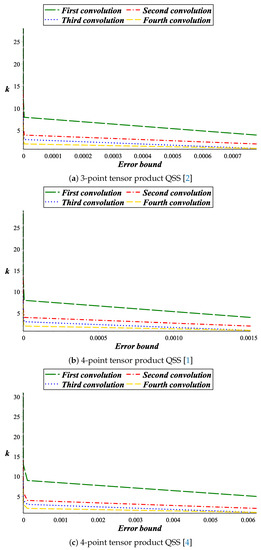
The subdivision depths of the surface model produced by the tensor product of a 3-point approximating QSS [2] are given in Table 6. The values are computed by using the Theorem 6. The graphical representation is shown in Figure 4a.

Table 6.
Depth of the 3-point approximating QSS surface model.

Figure 4.
The comparison between different convolutions for the surface case.
6. Conclusions
An advance computational technique has been developed to compute the error bounds of the quaternary subdivision model from its control polygon at level. This technique also predict the number of iterations (subdivision depth) which are required to reach user-defined error tolerance. This technique is the modified version of the technique presented in [15]. When the technique of [15] fails to work then the proposed technique can work by increasing the convolution steps. Moreover, we need fewer iterations to get the optimal subdivision depth as compared to the existing techniques.
Appendix A
Appendix A.1. Proof of Lemma 1
Proof.
To prove this result, we start with the case of and convolutions then a general case will be derived.
- Case
Then
where . Thus
- Case
From (A1), we acquire
This implies
where
So
This implies
- The general case
Applying the same argument, we acquire the reformulations for convolution as follows
where is defined recursively by
Hence
□
Appendix A.2. Proof of Lemma 2
Proof.
similarly
Here, we start from an induction process over .
- Case l0 = 1
From (A3), we have
Using (A8)
We suppose that it is true for an integer that is
Now, we will prove the statement for
- Case
Consider
By using (A9), we acquire
Now, replace n by
Similarly we can prove
Hence
This completes the proof. □
Appendix A.3. Proof of Corollary 1
Appendix A.4. Proof of Lemma 3
Proof.
To prove the proposed result, we start with the case of th and th convolutions then we discuss the general case.
- Case
Consider an arbitrary sequence of vectors . Then we have
where we are taking and for c and d. Thus
This implies
- Case
Now, after applying two time convolution, we obtain
This implies
This again implies that
Which implies
Now
Consider
and
then we get
- The general case
By the same strategy, we acquire reformulations for th convolutions given in the following
This implies
where
and
Thus
□
Author Contributions
Conceptualization, F.K. and S.-W.Y.; Formal analysis, M.I. and S.A.; Methodology, A.G. and S.-W.Y.; Supervision, A.G.; Writing—original draft, A.S., F.K. and M.I.; Writing—review & editing, A.G. and F.K. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (No. 71601072), Key Scientific Research Project of Higher Education Institutions in Henan Province of China (No. 20B110006) and the Fundamental Research Funds for the Universities of Henan Province.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data for implementation of the result are included in the paper.
Acknowledgments
The author A. Shahzad thanks to University of Sargodha, Pakistan for providing facilities and support.
Conflicts of Interest
The authors declare no conflict of interest in this paper.
References
- Mustafa, G.; Faheem, K. A new 4-point C3 quaternary approximating subdivision scheme. Abstr. Appl. Anal. 2009, 9, 1–14. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Younis, M. The m-point quaternary approximating subdivision schemes. Am. J. Comput. Math. 2013, 13, 6–10. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Younis, M. The quaternary interpolating scheme for geometric design. ISRN Comput. Graph. 2013, 13, 1–8. [Google Scholar] [CrossRef]
- Pervaiz, K. Shape preservation of the stationary 4-point quaternary subdivision schemes. Commun. Math. Appl. 2018, 9, 249–264. [Google Scholar]
- Deslauriers, G.; Dubuc, S. Symmetric iterative interpolation processes. In Constructive Approximation; DeVore, R.A., Saff, E.B., Eds.; Springer: Boston, MA, USA, 1989; pp. 49–68. [Google Scholar]
- Zheng, H.C.; Song, Q. Designing general p-ary n-point smooth subdivision schemes. Appl. Mech. Mater. 2014, 472, 510–515. [Google Scholar] [CrossRef]
- Conti, C.; Romani, L. Dual univariate a-ary subdivision schemes of de Rham-type. J. Math. Anal. Appl. 2013, 407, 443–456. [Google Scholar] [CrossRef]
- Lian, J.-A. On a-ary subdivision for curve design III. 2m-point and (2m + 1)-point interpolatory schemes. Appl. Appl. Math. Int. J. 2009, 4, 434–444. [Google Scholar]
- Siddiqi, S.S.; Ahmad, N. A new five-point approximating subdivision scheme. Int. J. Comput. Math. 2008, 85, 65–72. [Google Scholar] [CrossRef]
- Pan, J.; Lin, S.; Luo, X. A combined approximating and interpolating subdivision scheme with C2 continuity. Appl. Math. Lett. 2012, 25, 2140–2146. [Google Scholar] [CrossRef]
- Hussain, S.M.; Aziz, U.R.; Baleanu, D.; Nisar, K.S.; Ghaffar, A.; Karim, S.A.A. Generalized 5-point Approximating Subdivision Scheme of Varying Arity. Mathematics 2020, 8, 474. [Google Scholar] [CrossRef]
- Aslam, M.; Abeysinghe, W.P. Odd-ary approximating subdivision schemes and RS strategy for irregular dense initial data. ISRN Math. Anal. 2012, 2012, 745096. [Google Scholar] [CrossRef][Green Version]
- Deng, C.; Li, Y.; Xu, H. Repeated local operations for m-ary 2N-point Dubuc–Deslauriers subdivision schemes. Comput. Aided Geom. Des. 2016, 44, 10–14. [Google Scholar] [CrossRef]
- Mustafa, G.; Chen, F.L.; Deng, J.S. Estimating error bounds for binary subdivision curves/surfaces. J. Comput. Appl. Math. 2006, 1, 596–613. [Google Scholar] [CrossRef][Green Version]
- Mustafa, G.; Hashmi, S. Estimating error bounds for quaternary subdivision schemes. J. Math. Anal. Appl. 2009, 10, 159–167. [Google Scholar]
- Mustafa, G.; Hashmi, S. Subdivision depth computation for n-ary subdivision curves/surfaces. Vis. Comput. 2010, 26, 841–851. [Google Scholar] [CrossRef]
- Deng, C.; Jin, W.; Li, Y.; Xu, H. A formula for estimating the deviation of a binary interpolatory subdivision curve from its data polygon. Appl. Math. Comput. 2017, 304, 10–19. [Google Scholar] [CrossRef]
- Moncayo, M.; Amat, S. Error bounds for a class of subdivision schemes based on the two-scale refinement equation. J. Comput. Appl. Math. 2011, 236, 265–278. [Google Scholar] [CrossRef][Green Version]
- Shahzad, A.; Faheem, K.; Ghaffar, A.; Mustafa, G.; Nisar, K.S.; Baleanu, D. A novel numerical algorithm to estimate the subdivision depth of binary subdivision schemes. Symmetry 2020, 12, 66. [Google Scholar] [CrossRef]
- Khan, F.; Mustafa, G.; Shahzad, A.; Baleanu, D.; Al-Qurashi, M.M. A computational method for subdivision depth of ternary schemes. Mathematics 2020, 8, 817. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).