Research on Optimization of Array Honeypot Defense Strategies Based on Evolutionary Game Theory
Abstract
1. Introduction
- Bounded rationality: People are facing an uncertain world, and their computing and cognitive abilities of the environment are limited. To simulate a more realistic offensive and defensive process, we need to use the game theory of bounded rationality to reason about the offensive and defensive process of array honeypot system.
- Dynamic: The biggest feature of array honeypot is dynamic changes. Considering that traditional game theory may not be able to simulate the dynamic characteristics of array honeypot but only a static representation. Therefore, it is necessary for us to find a game theory that can truly interpret the offensive and defensive process of array honeypot.
- Multi-party game: When people use game theory to infer the process of network attack and defense, they usually only consider attackers and defenders. However, actual participants are the defender, the attacker and the legitimate user for array honeypot. Consequently, we need to find a three-party game method to deduce the offensive and defensive process of array honeypot.
- We design a three-party evolutionary game model of array honeypot. Then we formally describe strategies and revenues of both players in the game, and the payoff matrix of the three-party evolutionary game is constructed.
- We obtain the Jacobian matrix from the partial derivatives of the Replicator Dynamics. The evolutionarily stable strategies can be obtained by analyzing the eigenvalue matrix, which is got from the Jacobian matrix.
- We use the simulation function of MATLAB and Gambit system to verify the effectiveness of our scheme. The experimental results prove that the deduced defense strategies will become stable after population evolution, and it can effectively resist attacks from attackers.
2. Related Work
- We deduce the defense strategies of array honeypot based on evolutionary game theory of bounded rational, which can be more in line with real offensive and defensive scenarios.
- We use evolutionary game theory to deduce the defense strategies of array honeypot, then the evolution process can truly reflect the dynamic characteristics of array honeypot.
- The evolutionarily stable strategy we inferred can make all game participants reach a stable state of existence, and it will not change the existing stable state even if the sudden change of a certain population.
3. Overview of Game Theory
3.1. Game Theory
- Static game: The problem of simultaneous decision-making by various players or different players in a sequence of decisions, but the latter decision-making person does not know the decision made by the former.
- Dynamic game: All problems except the conditions of static game.
- Complete information game: In this game, players know all opponents and understand opponent revenue, behavior strategy, etc. On the contrary, it is an incomplete information game.
- Perfect information game: In this game, players only know all the decisions that the opponent has made and the payoffs obtained. On the contrary, it is a game of imperfect information.
3.2. Evolutionary Game Theory
3.2.1. Key Concepts
3.2.2. Evolutionarily Stable Strategy
- Balance, .
- Stability, .
3.2.3. Replicator Dynamic
3.2.4. Evolutionary Stable Equilibrium
4. System Model and Evolutionary Game Analysis
4.1. Evolutionary Game Model of Array Honeypot
4.1.1. Model Assumptions
- It is assumed that the defender, the attacker, and the legitimate user are bounded rationally. That is, these three parties do not have ‘omnipotent and omniscience’, and they cannot obtain the optimal results instantly.
- We suppose that the information among the defender, the attacker, and the legitimate user are not completely public. In other words, the three parties cannot accurately understand the status, payment functions and game strategies of other players.
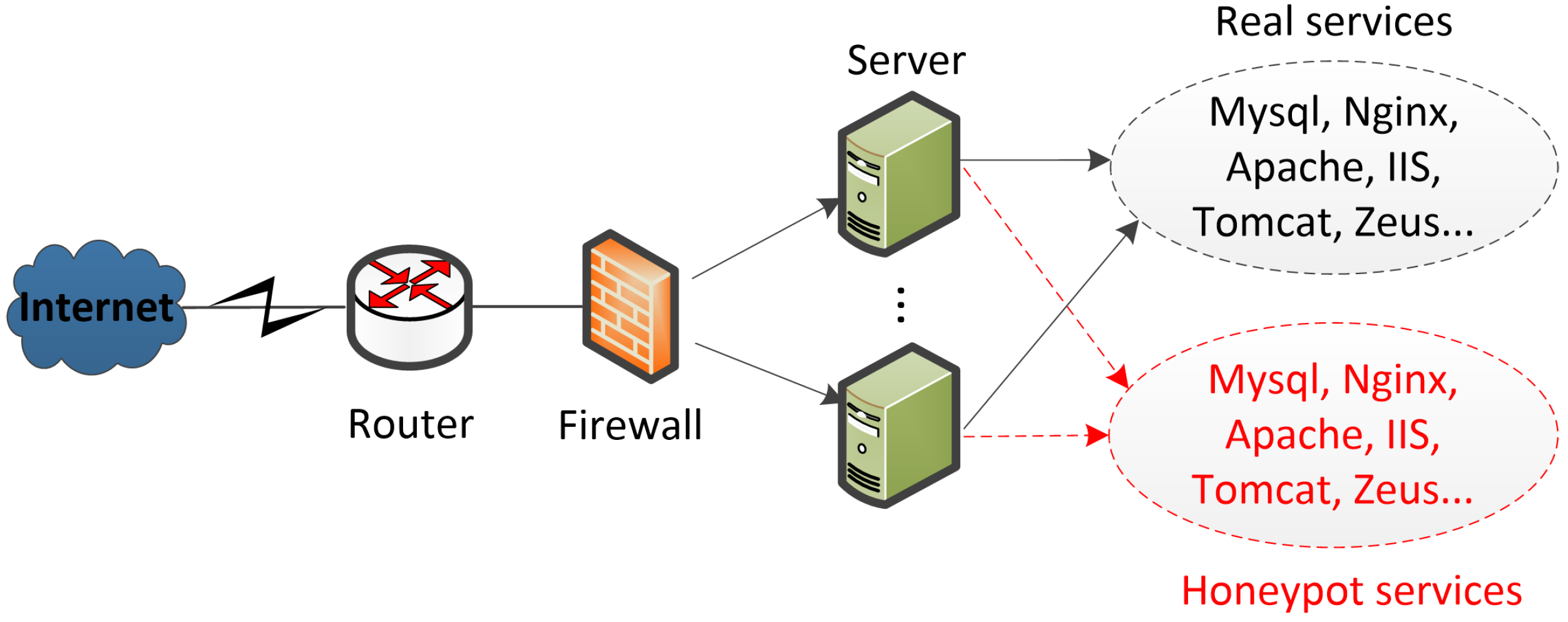
- We presume that attackers and legitimate users can only access one service at a time. Since array honeypot can provide honeypot services and real services at the same time, visitors may access the honeypot service or the real service when they access the server.
- Assume that the success rate of hackers accessing the honeypot system is 100%, legitimate users will access the honeypot system and the real system, and defenders can predict real-time attacks.
4.1.2. Model Description
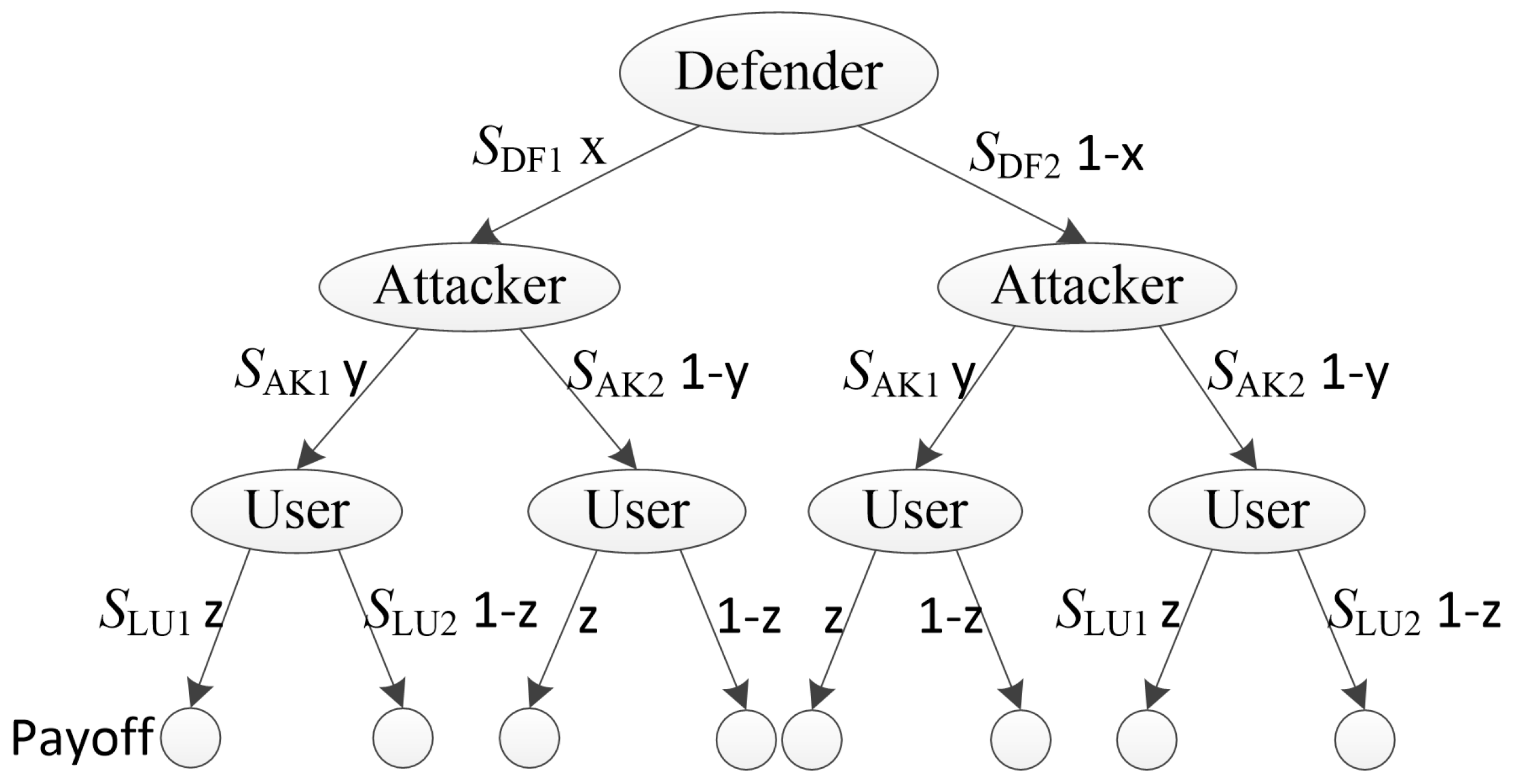
- For the defender, we suppose that the array honeypot system executes the strategy with probability x. Correspondingly, the strategy is executed with probability .
- For the attacker, it is assumed that the array honeypot system executes the strategy with probability y. And the strategy is executed with probability .
- For legitimate users, we presume that the array honeypot system executes the strategy with probability z. In turn, the system executes the strategy with probability .
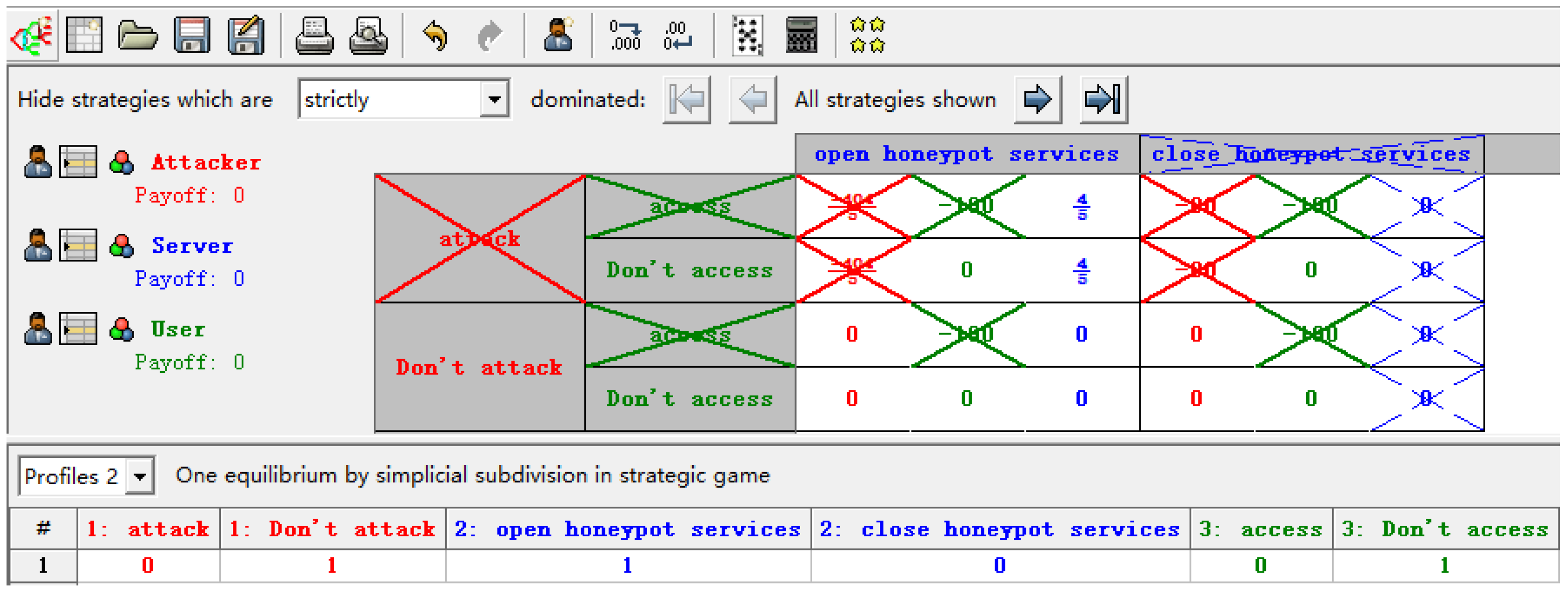
- Opening honeypot services. If an attacker attacks the server and a legitimate user accesses the server, the revenues are for . Since the role of deploying honeypot services is to identify illegal intrusions, attackers who access the services will suffer losses as and legitimate users who incorrectly access the service will be damaged as a. Conversely, when the attacker does not attack the service, no matter whether the user accesses it or not, the payoff is 0 for the defender.
- Closing honeypot services. When the attacker attacks the server and the legitimate user accesses the server, the payoffs are for . It means that when they cannot access the service, they will suffer losses.
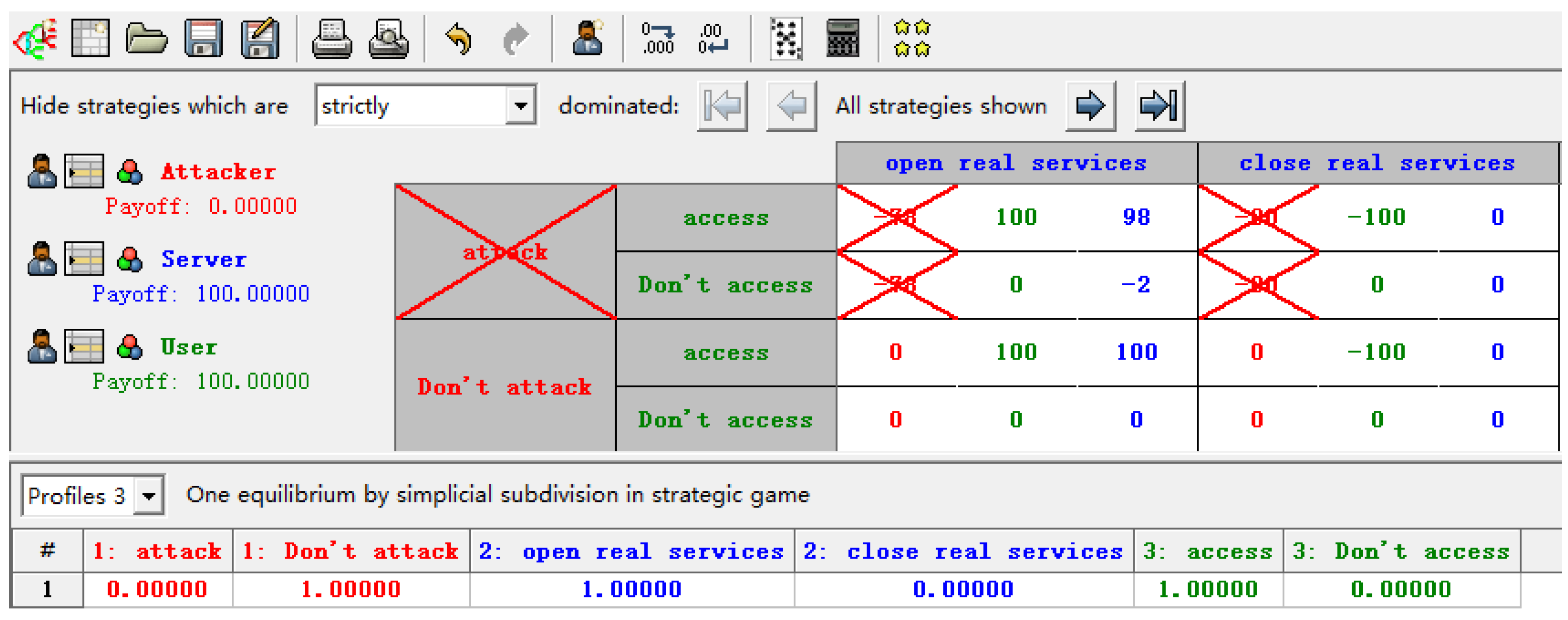
- Opening real services. If an attacker attacks the server and a legitimate user accesses the server, the payoffs are for . Attackers who access the real services will gain revenue as and legitimate users who access the real service will gain revenue as a. However, defenders will suffer losses as . Conversely, when the attacker does not attack the service and the user accesses the service, the benefits are for .
- Closing real services. Same as closing honeypot services, the attacker and the user will suffer losses, and the defender has no revenue.
4.2. Evolutionary Game Analysis of Array Honeypot
4.2.1. Honeypot Services
4.2.2. Real Services
5. Simulation
5.1. Gambit Simulation Results
5.1.1. Honeypot Services
5.1.2. Real Services
5.2. MATLAB Simulation Results
6. Conclusions and Outlook
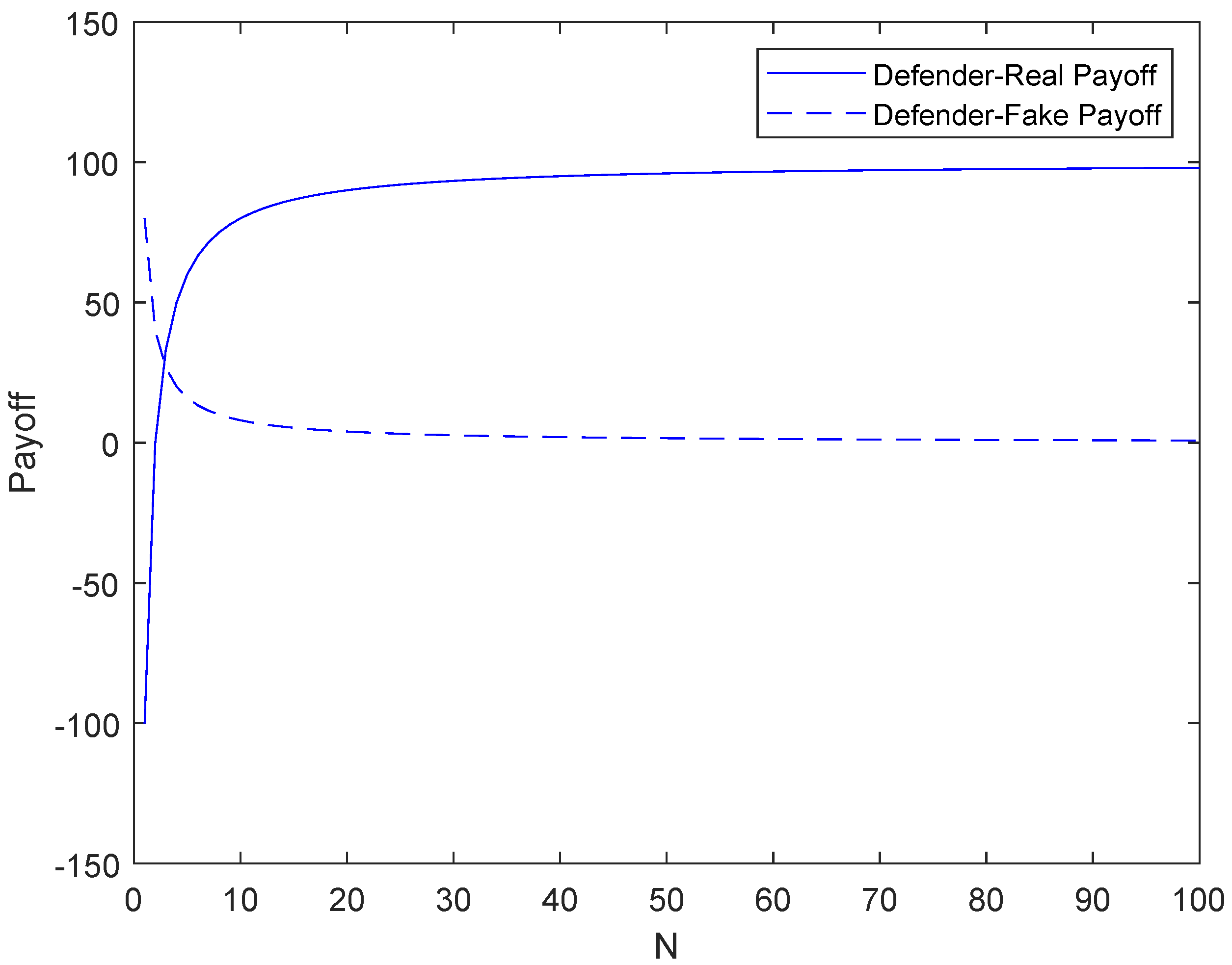
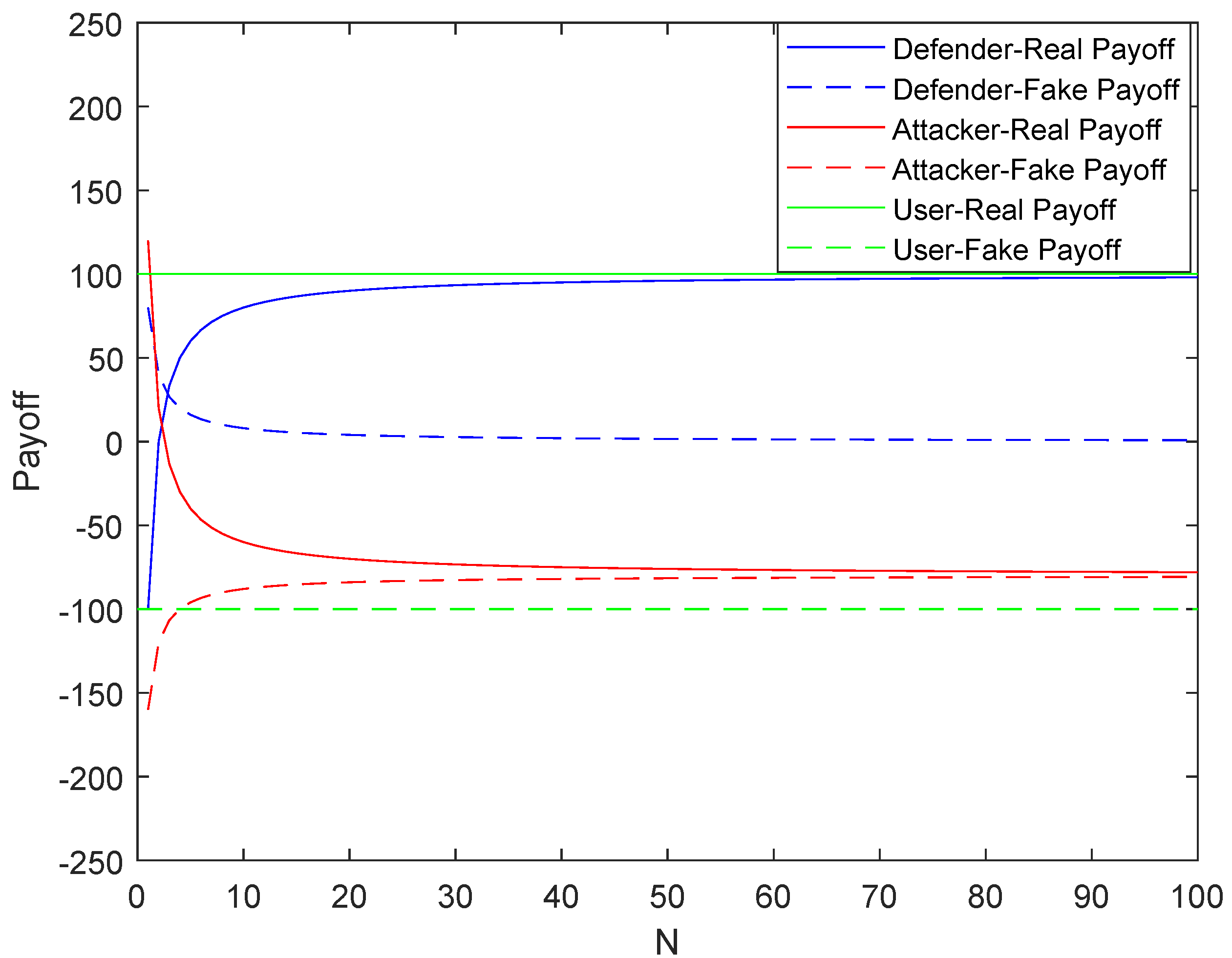
- In array honeypot systems, real services and honeypot services are randomly assigned. Hence, the attacker has a high probability of accessing the honeypot service. At this time, it will bring great losses to the attacker. When attackers access a real service, the attack cost of the attacker will multiply rapidly and the revenue will decrease to a negative level with the increase of N. Therefore, the defender can adjust the number of servers N to make the evolution stable equilibrium change in favor of the defender, to resist malicious attacks and protect the network system security.
- In the array honeypot defense system, the server will always open the honeypot service. For real services, when , the optimal strategy for the three-party is . When , the optimal strategy for the three-party is . When , the optimal strategy for the three-party is .
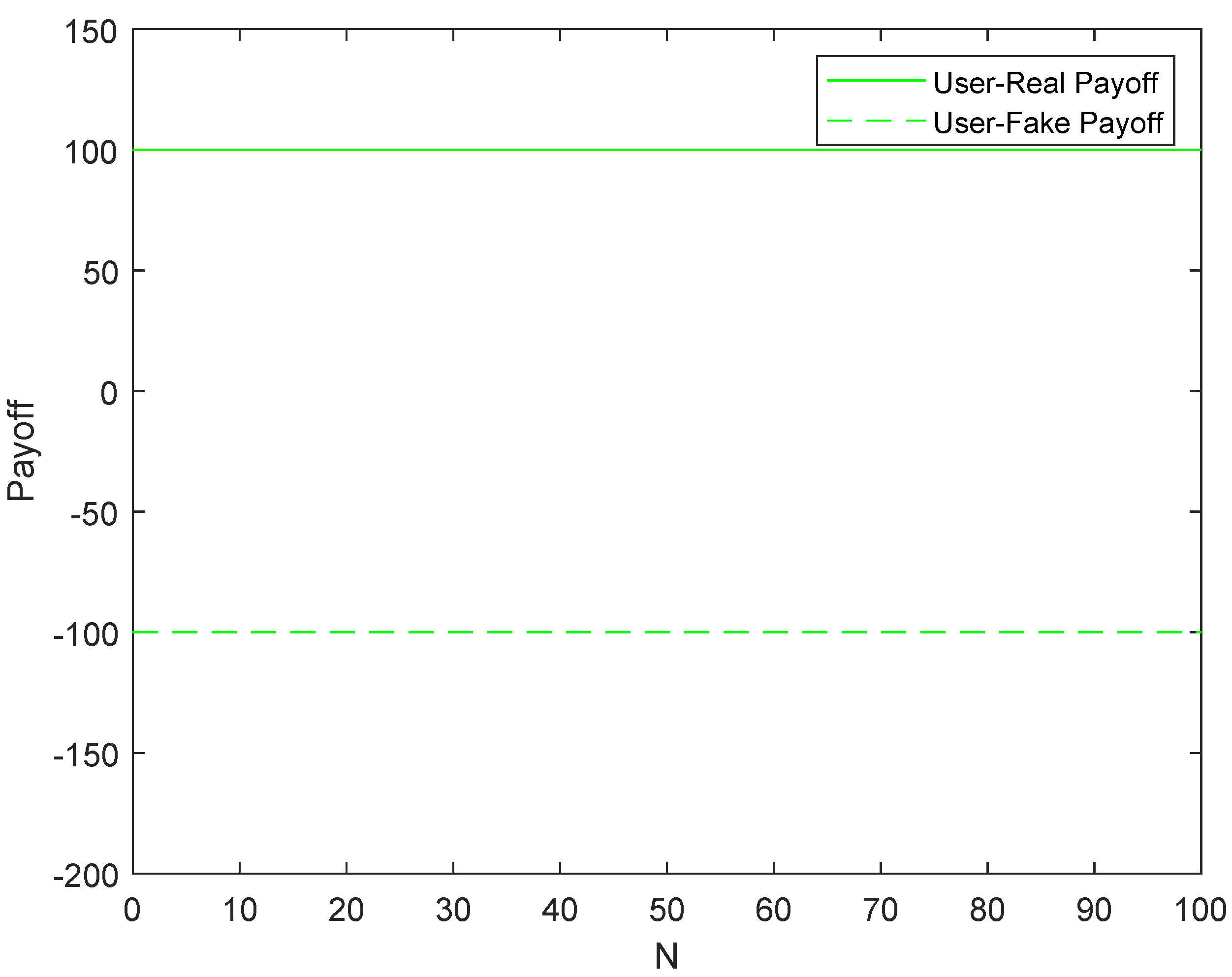
- When a legitimate user accesses a real service, the revenue is always 100. On the contrary, if the user accesses the honeypot service, the revenue is −100. Therefore, legitimate users will definitely access the real service and only access the real service.
- In the array honeypot system, identifying hackers and legitimate users is a very important part. If the system recognizes incorrectly, irreversible losses will occur. This paper is based on the ideal situation that the system must be able to identify visitors. Therefore, we can consider using algorithms to identify system visitors in future research.
- This paper simply states that defenders will be able to resist various types of attacks. However, we do not consider how the defender predicts the risk level of the attack. Therefore, it is necessary to establish the risk prediction mechanism to keep the risk level at an acceptable level in the future work.
- The conclusion of our scheme is that the purpose of defending against hackers can be achieved by increasing the number of servers. However, the number of servers cannot be increased indefinitely, and the defense effect of the system will certainly be affected by the cost. Moreover, hackers may only attack the system in a flash, and the system cannot have unlimited response time. Therefore, future research needs to consider the impact of budget and response time on system defense.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Miao, Y.; Yang, Y.; Chen, Z.; Hu, J. The Construction and Application of Network Attack Graph. China Commun. 2009, 6, 71–74. [Google Scholar]
- Shi, L.; Jiang, L.; Jia, C.; Wang, X. A Game Theoretic Analysis for the Honeypot Deceptive Mechanism. J. Electron. Inf. Technol. 2012, 34, 1420–1424. [Google Scholar] [CrossRef]
- Spitzner, L. Honeypots: Catching the insider threat. In Proceedings of the 19th Annual Computer Security Conference, Las Vegas, NV, USA, 8–12 December 2003; pp. 170–179. [Google Scholar]
- Provos, N. A virtual honeypot framework. In Proceedings of the 13th USENIX Security Symposium, San Diego, CA, USA, 9–13 August 2004; pp. 1–14. [Google Scholar]
- Spitzner, L. Honeypots: Tracking Hackers; Addison-Wesley: Reading, UK, 2003. [Google Scholar]
- Kuwatly, I.; Sraj, M.; Al Masri, Z.; Artail, H. A dynamic honeypot design for intrusion detection. In Proceedings of the IEEE/ACS International Conference on Pervasive Services, Beirut, Lebanon, 19–23 July 2004; pp. 95–104. [Google Scholar]
- Krawetz, N. Anti-honeypot technology. IEEE Secur. Priv. 2004, 2, 76–79. [Google Scholar] [CrossRef]
- Shi, L.; Zhao, J.; Jiang, L.; Xing, W.; Gong, J.; Liu, X. Game Theoretic Simulation on the Mimicry Honeypot. Wuhan Univ. J. Nat. Sci. 2016, 21, 69–74. [Google Scholar] [CrossRef]
- Shi, L.; Li, J.; Han, X.; Jia, C. Design and Implementation of Distributed Self-Election Dynamic Array Honeypot System. China Commun. 2011, 8, 109–115. [Google Scholar]
- Shi, L.; Li, J.; Liu, X.; Jia, C. Research on dynamic array honeypot for collaborative network defense strategy. J. Commun. 2012, 33, 159–164. [Google Scholar]
- Shi, L.; Li, Y.; Liu, T.; Liu, J.; Shan, B.; Chen, H. Dynamic Distributed Honeypot Based on Blockchain. IEEE Access 2019, 7, 72234–72246. [Google Scholar] [CrossRef]
- Herbert, G. Game Theory Evolving; Priceton University Press: Boston, MA, USA, 2015. [Google Scholar]
- Edwards, A.W.F.; Anthony, W. The genetical theory of natural selection. Genetics 2000, 154, 1419–1426. [Google Scholar]
- Cincotti, A. Three-player partizan games. Theor. Comput. Sci. 2005, 332, 367–389. [Google Scholar] [CrossRef][Green Version]
- Cincotti, A. N-player partizan games. Theor. Comput. Sci. 2010, 411, 3224–3234. [Google Scholar] [CrossRef]
- Manshaei, M.; Zhu, Q.; Alpcan, T.; Basar, T.; Hubaux, J. Game Theory Meets Network Security and Privacy. ACM Comput. Surv. 2013, 45. [Google Scholar] [CrossRef]
- Zhang, C.; Bin, N. Game Theory and Information Economics; Posts And Telecom Press: Beijing, China, 2015. [Google Scholar]
- La, Q.; Quek, T.; Lee, J.; Jin, S.; Zhu, H. Deceptive Attack and Defense Game in Honeypot-Enabled Networks for the Internet of Things. IEEE Internet Things J. 2016, 3, 1025–1035. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Liu, Y. Research on Optimal Selection of Moving Target Defense Policy Based on Dynamic Game with Incomplete Information. Acta Electron. Sin. 2018, 46, 82–89. [Google Scholar]
- Ge, X.; Zhou, T.; Zang, Y. Defense Strategy Selection Method for Stackelberg Security Game Based on Incomplete Information. In Proceedings of the 2019 International Conference on Artificial Intelligence and Computer Science, Shanghai, China, 12 November 2019. [Google Scholar]
- Guan, R.; Li, L.; Wang, T. A Bayesian Improved Defense Model for Deceptive Attack in Honeypot-Enabled Networks. In Proceedings of the 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; IEEE 5th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Zhangjiajie, China, 10–12 August 2019; pp. 208–214. [Google Scholar]
- Boumkheld, N.; Panda, S.; Rass, S.; Panaousis, E. Honeypot type selection games for smart grid networks. In Proceedings of the International Conference on Decision and Game Theory for Security, Stockholm, Sweden, 30 October–1 November 2019; pp. 85–96. [Google Scholar]
- Zhang, H.; Li, T. Optimal Active Defense Based on Multi-stage Attack-Defense Signaling Game. Acta Electron. Sin. 2017, 45, 431–439. [Google Scholar]
- Shandilya, V. On a Generic Security Game Model. arXiv 2018, arXiv:1801.05958. [Google Scholar] [CrossRef][Green Version]
- Du, M.; Wang, K. An SDN-Enabled Pseudo-Honeypot Strategy for Distributed Denial of Service Attacks in Industrial Internet of Things. IEEE Trans. Ind. Inform. 2020, 16, 648–657. [Google Scholar] [CrossRef]
- Shi, L.; Jiang, L.; Liu, X.; Jia, C. Game Theoretic Analysis for the Feature of Mimicry Honeypot. J. Electron. Inf. Technol. 2013, 35, 1063–1068. [Google Scholar] [CrossRef]
- Tian, W.; Ji, X.; Liu, W.; Liu, G.; Zhai, J. Prospect Theoretic Study of Honeypot Defense Against Advanced Persistent Threats in Power Grid. IEEE Access 2020, 8, 64075–64085. [Google Scholar] [CrossRef]
- Cheng, D.; He, F.; Qi, H.; Xu, T. Modeling, Analysis and Control of Networked Evolutionary Games. IEEE Trans. Autom. Control 2015, 60, 2402–2415. [Google Scholar] [CrossRef]
- Zhu, J.; Song, B.; Huang, Q. Evolution game model of offense-defense for network security based on system dynamics. J. Commun. 2014, 35, 54–61. [Google Scholar]
- Huang, J.; Zhang, H.; Wang, J.; Huang, S. Defense strategies selection based on attack-defense evolutionary game model. J. Commun. 2017, 38, 168–176. [Google Scholar]
- Li, Y.; Shi, L.; Feng, H. A Game-Theoretic Analysis for Distributed Honeypots. Future Internet 2019, 11, 65. [Google Scholar] [CrossRef]
- Smith, J. Evolution and the theory of games. Am. Sci. 1976, 64, 41–45. [Google Scholar] [PubMed]
- Smith, J. Game theory and the evolution of behaviour. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1979, 205, 475. [Google Scholar] [CrossRef]
- Wang, X.; Gu, C.; Zhao, J.; Quan, J. A Review of Stochastic Evolution Dynamics and Its Cooperative Mechanism. J. Syst. Sci. Math. Sci. 2019, 39, 1533–1552. [Google Scholar]
- Huang, J.; Zhang, H.; Wang, J. Markov Evolutionary Games for Network Defense Strategy Selection. IEEE Access 2017, 5, 19505–19516. [Google Scholar] [CrossRef]
- Huang, J.; Wang, J.; Zhang, H.; Wang, N. Network Defense Strategy Selection Based on Best-response Dynamic Evolutionary Game Model. In Proceedings of the 2nd IEEE Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 2611–2615. [Google Scholar]
- Zhang, H.; Huang, J. Defense Strategies Selection Method Using Non-cooperative Game. In Proceedings of the 2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14–17 October 2016; pp. 1325–1330. [Google Scholar]
- Taylor, P.T.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Selten, R. A note on evolutionarily stable strategies in asymmetric animal conflicts. J. Theor. Biol. 1980, 84, 93–101. [Google Scholar] [CrossRef]
- Deng, C. Three-Party Evolutionary Game Analysis of P2P Network Lending Based on Nonlinear System Stability Theory. Chin. J. Manag. Sci. 2020. [Google Scholar] [CrossRef]
- Zhou, T.; Zhou, S.; Liu, L. Dynamic Evolution and Stability Strategy Analysis of Game AmongGovernment, Bicycle Sharing Enterprise and Consumer. J. Manag. 2020, 33, 82–94. [Google Scholar]
- Cheng, L.; Yang, R.; Liu, G.; Wang, J. Multi-population Asymmetric Evolutionary Game Dynamics and Its Applications in Power Demand-side Response in Smart Grid. Proc. CSEE 2021. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, G.; Huang, H.; Wang, X. Equilibrium analysis of general N-population multi-strategy games for generation-side long-term bidding: An evolutionary game perspective. J. Clean. Prod. 2020, 276, 124123. [Google Scholar] [CrossRef]



| Honeypot Services | Real Services | ||||
|---|---|---|---|---|---|
| Parameters | Conditions of Establishment | Characterizations of Establishment |
|---|---|---|
| a | Basic benefit of users or servers. | |
| b | Attack costs. | |
| c | Basic benefit of honeypots. | |
| The break factor of attackers. | ||
| The bait factor of honeypots. |
| Balance Node | Conditions for Progressive Stability | Stability Conclusion | ||
|---|---|---|---|---|
| 0 | Unstable | |||
| 0 | Unstable | |||
| Unstable | ||||
| Unstable | ||||
| Unstable | ||||
| Indeterminate | ||||
| Unstable | ||||
| Indeterminate | ||||
| Parameter | Values |
|---|---|
| a | 100 |
| b | 80 |
| c | 80 |
| 2 | |
| 1 | |
| N | 1, 2, 3, 10, 100 |
| Payoff | N | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 10 | 100 | |
| Stable Strategy (x,y,z) | ( | ||||
| Payoff | N | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 10 | 100 | |
| Stable Strategy (x,y,z) | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, L.; Wang, X.; Hou, H. Research on Optimization of Array Honeypot Defense Strategies Based on Evolutionary Game Theory. Mathematics 2021, 9, 805. https://doi.org/10.3390/math9080805
Shi L, Wang X, Hou H. Research on Optimization of Array Honeypot Defense Strategies Based on Evolutionary Game Theory. Mathematics. 2021; 9(8):805. https://doi.org/10.3390/math9080805
Chicago/Turabian StyleShi, Leyi, Xiran Wang, and Huiwen Hou. 2021. "Research on Optimization of Array Honeypot Defense Strategies Based on Evolutionary Game Theory" Mathematics 9, no. 8: 805. https://doi.org/10.3390/math9080805
APA StyleShi, L., Wang, X., & Hou, H. (2021). Research on Optimization of Array Honeypot Defense Strategies Based on Evolutionary Game Theory. Mathematics, 9(8), 805. https://doi.org/10.3390/math9080805






