A Singularly P-Stable Multi-Derivative Predictor Method for the Numerical Solution of Second-Order Ordinary Differential Equations
Abstract
1. Introduction
- Methods with unknown constant coefficients,
- Methods with variable coefficients (coefficients are a function of the frequency of the problem).
2. Preliminaries
3. Development of the New Scheme
3.1. Development
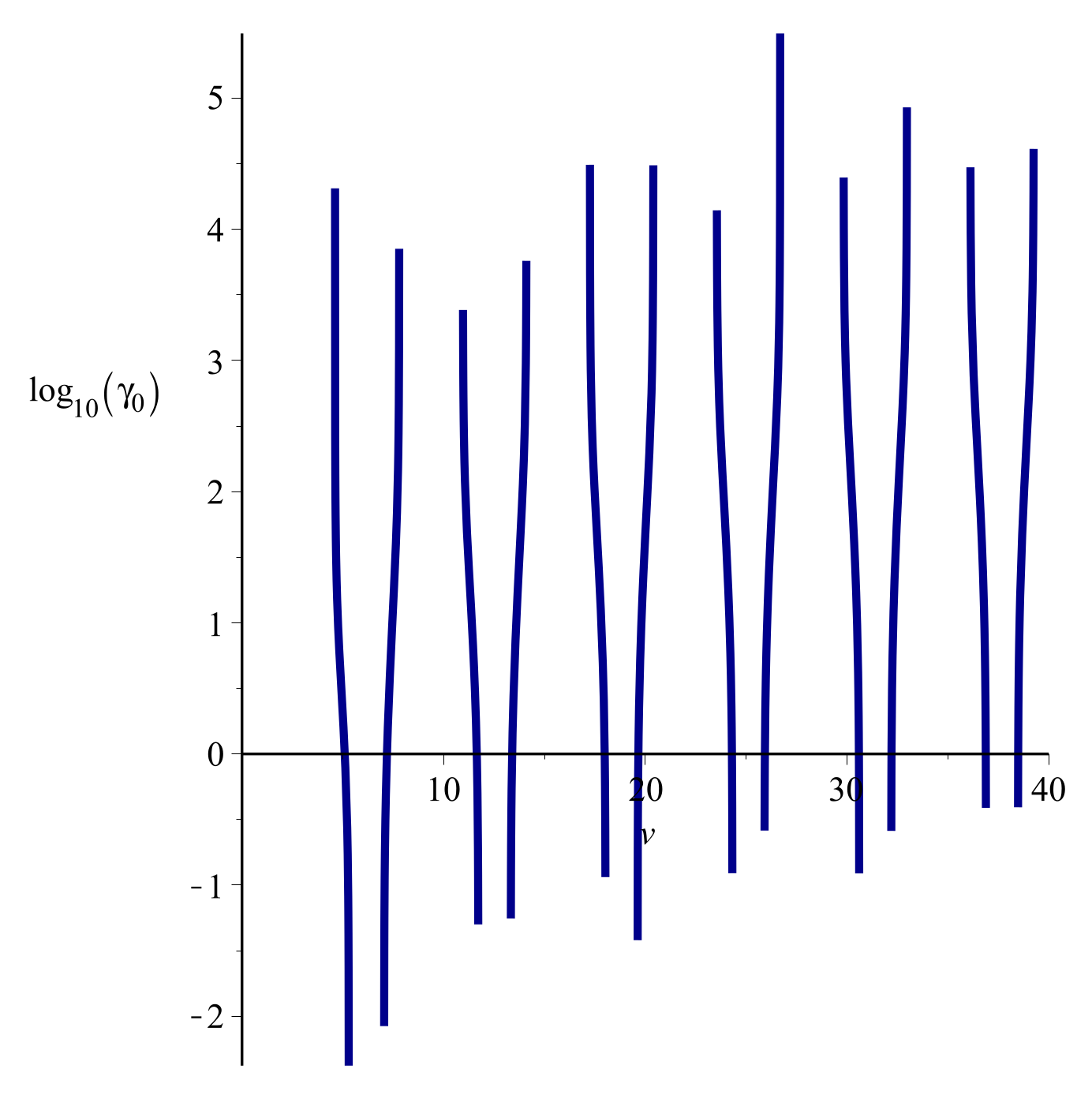
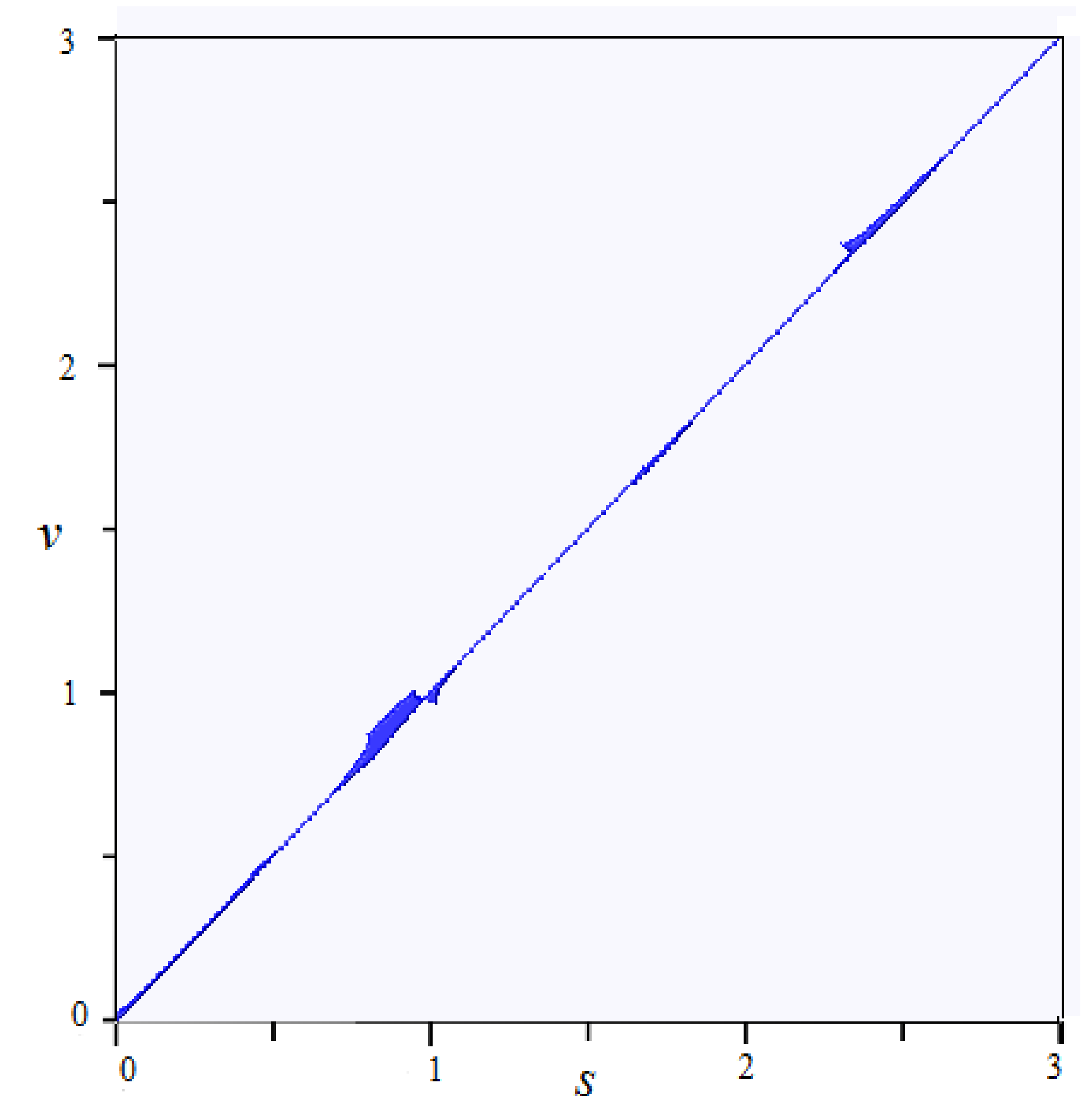
3.2. Periodicity Analysis
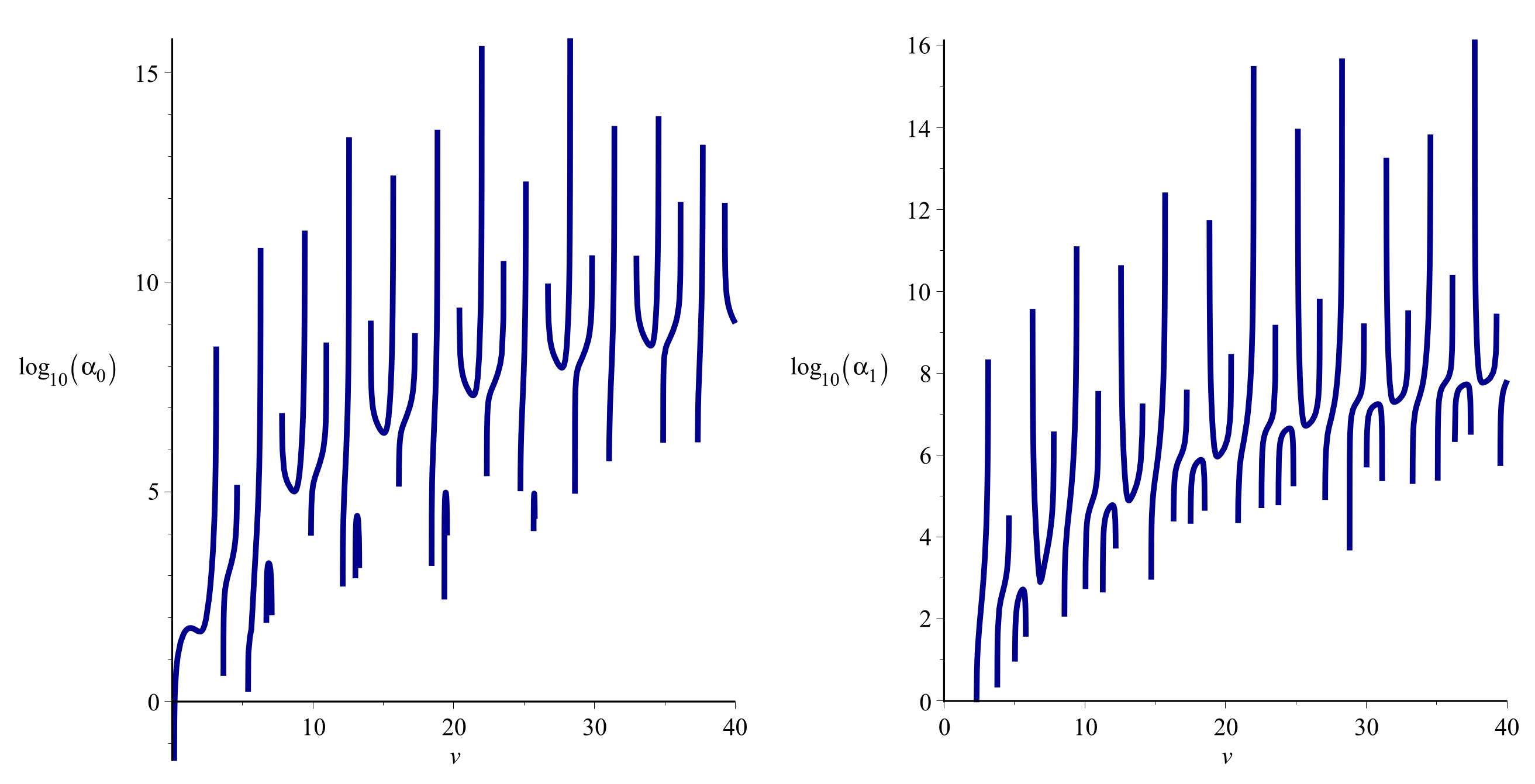
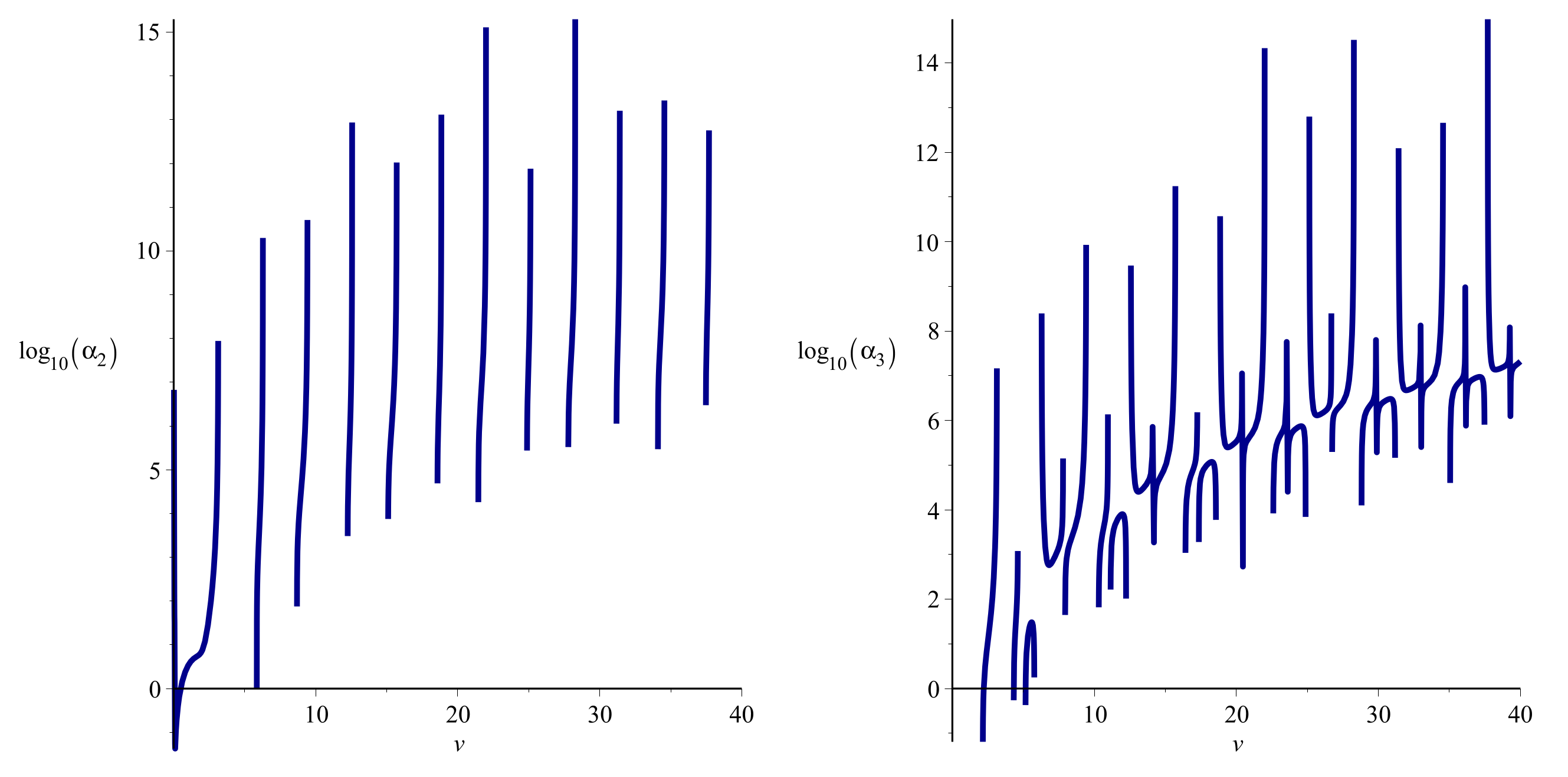
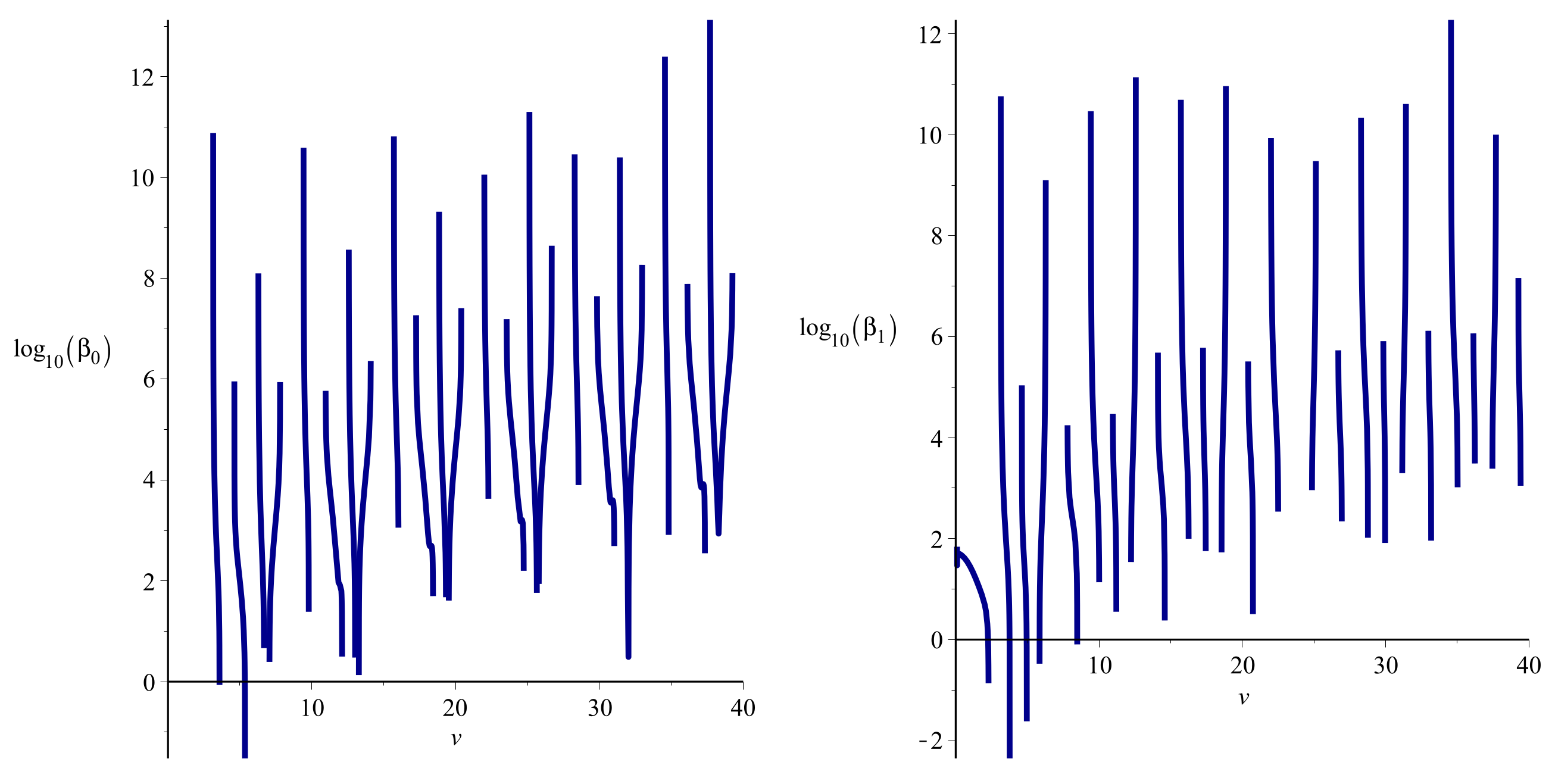
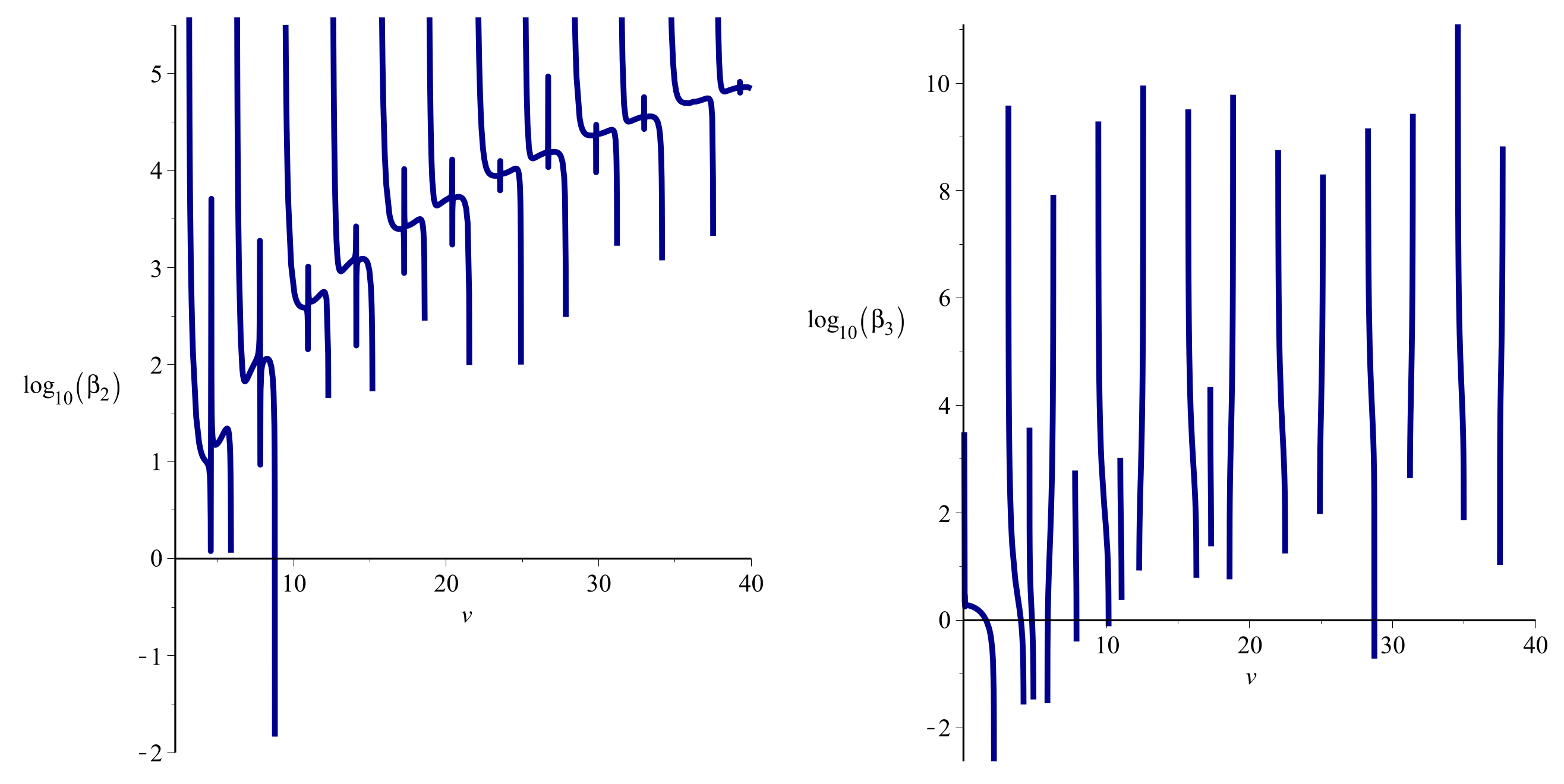
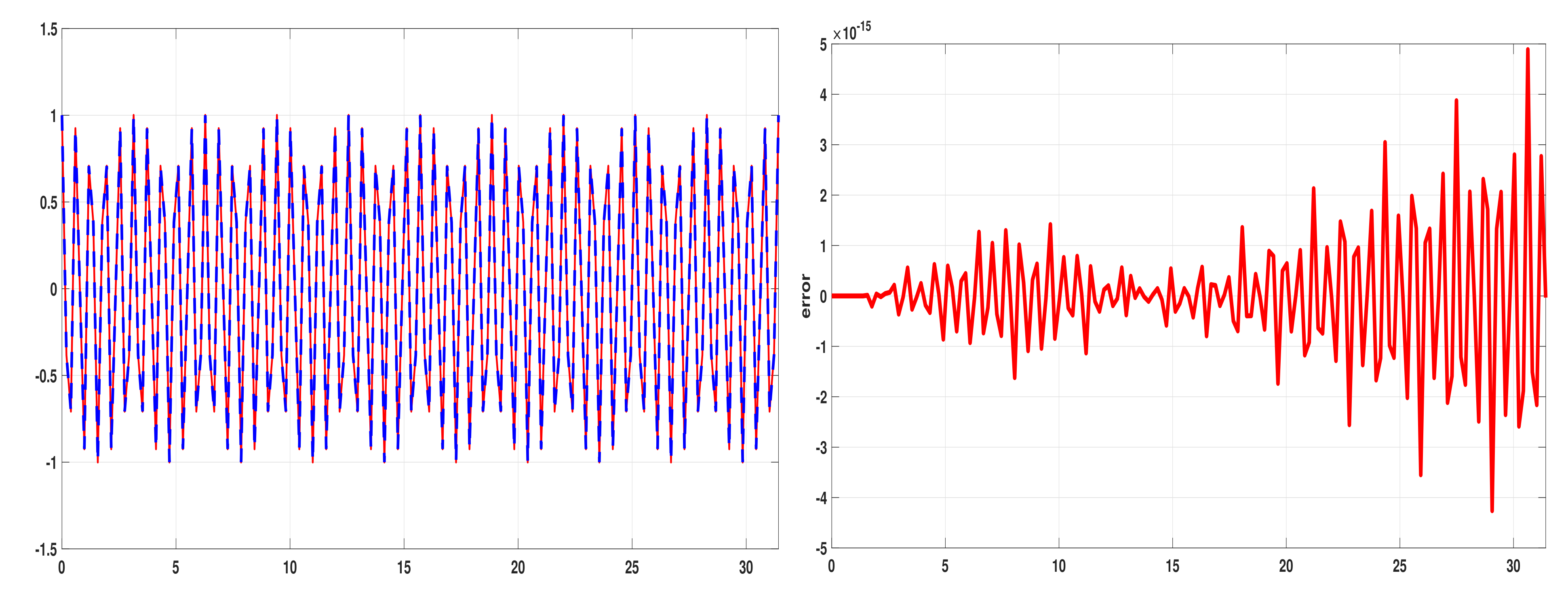
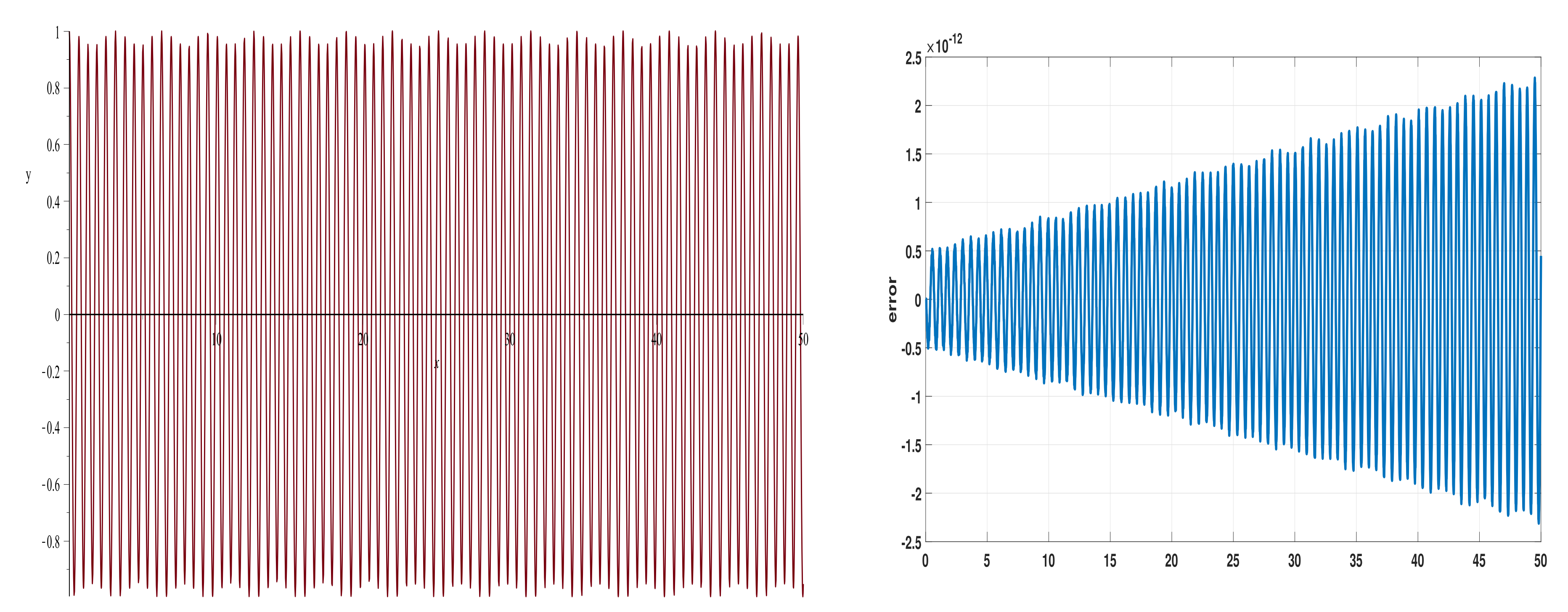
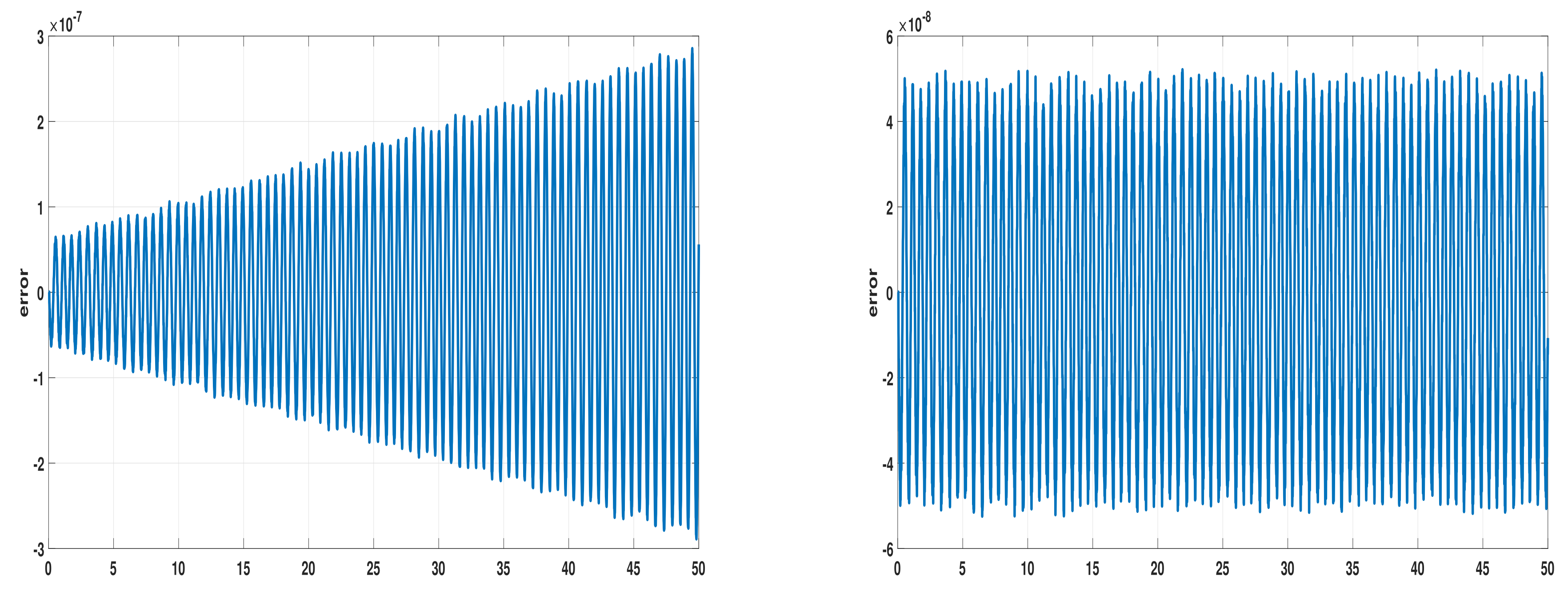
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Aliev, F.A.; Aliev, N.A.; Mutallimov, M.M.; Namazov, A.A. Algorithm for solving the identification problem for determining the fractional-order derivative of an oscillatory system. Appl. Comput. Math. 2020, 19, 415–422. [Google Scholar]
- Aliev, F.; Aliev, N.; Safarova, N.; Mamedova, Y. Solution of the problem of analytical construction of optimal regulators for a fractional order oscillatory system in the General case. J. Appl. Comput. Mech. 2021, 7, 970–976. [Google Scholar]
- Aliev, F.; Aliev, N.; Velieva, N.; Safarova, N. Larin parameterization to solve the problem of analytical construction of the optimal regulator of oscillatory systems with liquid dampers. J. Appl. Comput. Mech. 2020, 6, 1426–1430. [Google Scholar]
- Alolyan, I.; Simos, T.E.; Tsitouras, C. Interpolants for sixth-order Numerov-type methods. Math. Methods Appl. Sci. 2019, 42, 7349–7358. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M.; Hamidi, N.; Nieto, J.J. Hilfer and Hadamard fractional differential equations in Fréchet spaces. TWMS J. Pure Appl. Math. 2019, 10, 102–116. [Google Scholar] [CrossRef]
- Ananthakrishnaiah, U. P-stable Obrechkoff methods with minimal phase-lag for periodic initial-value problems. Math. Comput. 1987, 49, 553–559. [Google Scholar] [CrossRef]
- Ashyralyev, A.; Erdogan, A.S.; Tekalan, S.N. An investigation on finite difference method for the first order partial differential equation with the nonlocal boundary condition. Appl. Comput. Math. 2019, 18, 247–260. [Google Scholar]
- Chen, W.; Wu, W.X.; Teng, Z.D. Complete dynamics in a nonlocal dispersal two-strain SIV epidemic model with vaccinations and latent delays. Appl. Comput. Math. 2020, 19, 360–391. [Google Scholar]
- Chun, C.; Neta, B. Trigonometrically-Fitted Methods: A Review. Mathematics 2019, 7, 1197. [Google Scholar] [CrossRef]
- Henrici, P. Discrete Variable Methods in Ordinary Differential Equations; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Jeon, Y.; Bak, S.; Bu, S. Reinterpretation of Multi-Stage Methods for Stiff Systems: A Comprehensive Review on Current Perspectives and Recommendations. Mathematics 2019, 7, 1158. [Google Scholar] [CrossRef]
- Guliyev, V.S.; Akbulut, A.; Celik, S.; Omarova, M.N. Higher order Riesz transforms related to Schrödinger type operator on local generalized Morrey spaces. TWMS J. Pure Appl. Math. 2019, 10, 58–75. [Google Scholar]
- Gürbüz, B.; Sezer, M. Laguerre polynomial solutions of a class of initial and boundary value problems arising in science and engineering fields. Acta Phys. Pol. A 2016, 130, 194–197. [Google Scholar] [CrossRef]
- Lambert, J.D.; Watson, I.A. Symmetric multistep methods for periodic initial value problems. J. Inst. Math. Appl. 1976, 18, 189–202. [Google Scholar] [CrossRef]
- Martin-Vaquero, J.; Vigo-Aguiar, J. Exponential fitting BDF algorithms: Explicit and implicit 0-stable methods. J. Comput. Math. Anal. 2006, 192, 100–113. [Google Scholar] [CrossRef][Green Version]
- Franco, J.M. A class of explicit two-step hybrid methods for second-order IVPs. J. Comput. Appl. Math. 2006, 187, 41–57. [Google Scholar] [CrossRef]
- Franco, J.M.; Palacios, M. High-order P-stable multistep methods. J. Comput. Appl. Math. 1990, 30, 1–10. [Google Scholar] [CrossRef]
- Gautschi, W. Numerical integration of ordinary differential equations based on trigonometric polynomials. Numer. Math. 1961, 3, 381–397. [Google Scholar] [CrossRef]
- Hairer, E. Unconditionally stable methods for second-order differential equations. Numer. Math. 1979, 32, 373–379. [Google Scholar] [CrossRef]
- Harikrishnan, S.; Kanagarajan, K.; Elsayed, E.M. Existence and stability results for differential equations with complex order involving Hilfer fractional derivative. TWMS J. Pure Appl. Math. 2019, 10, 94–101. [Google Scholar]
- Lin, C.; Hsu, C.W.; Simos, T.E.; Tsitouras, C. Explicit, semi-symmetric, hybrid, six-step, eighth order methods for solving y″ = f(x,y). Appl. Comput. Math. 2019, 18, 296–304. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Shokri, A. The new classes of high order implicit six-step P-stable multiderivative methods for the numerical solution of Schrödinger equation. Appl. Comput. Math. 2020, 19, 59–86. [Google Scholar]
- Moshtaghi, N.; Saadatmandi, A. Numerical solution for diffusion equations with distributed-order in time based on Sinc-Legendre collocation method. Appl. Comput. Math. 2020, 19, 317–355. [Google Scholar]
- Neta, B. P-stable symmetric super-implicit methods for periodic initial value problems. J. Comput. Math. Appl. 2005, 50, 701–705. [Google Scholar] [CrossRef][Green Version]
- Neta, B.; Ford, C.H. Families of Methods for Ordinary Differential Equations Based on Trigonometric Polynomials. J. Comput. Appl. Math. 1984, 10, 33–38. [Google Scholar] [CrossRef][Green Version]
- Neta, B.; Fukushima, T. Obrechkoff versus super-implicit methods for the solution of first- and second-order initial value problems, Numerical methods in physics, chemistry, and engineering. Comput. Math. Appl. 2003, 45, 383–390. [Google Scholar] [CrossRef]
- Odibat, Z. Fractional power series solutions of fractional differential equations by using generalized Taylor series. Appl. Comput. Math. 2020, 19, 47–58. [Google Scholar]
- Ozyapici, A.; Karanfiller, T. New integral operator for solution of differential equations. TWMS J. Pure Appl. Math. 2020, 11, 131–143. [Google Scholar]
- Qalandarov, A.A.; Khaldjigitov, A.A. Mathematical and numerical modeling of the coupled dynamic thermoelastic problems for isotropic bodies. TWMS J. Pure Appl. Math. 2020, 11, 119–126. [Google Scholar]
- Ramos, H.; Jator, S.N.; Modebei, M.I. Efficient k-step linear block methods to solve second order initial value problems directly. Mathematics 2020, 8, 1752. [Google Scholar] [CrossRef]
- Ravangard, A.R.; Momayez, L.; Rashidi, M. Effects of geometry on simulation of two-phase flow in microchannel with density and viscosity contrast. J. Therm. Anal. Calorim. 2020, 139, 427–440. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Rabiei, F.; Nia, S.N.; Abbasbandy, S. A review: Differential transform method for semi-analytical solution of differential equations. Int. J. Appl. Mech. Eng. 2020, 25, 122–129. [Google Scholar] [CrossRef]
- Shokri, A.; Vigo-Aguiar, J.; Mehdizadeh Khalsaraei, M.; Garcia-Rubio, R. A new implicit six-step P-stable method for the numerical solution of Schrödinger equation. Int. J. Comput. Math. 2020, 97, 802–817. [Google Scholar] [CrossRef]
- Simos, T.E. A P-stable complete in phase Obrechkoff trigonometric fitted method for periodic initial-value problems. Proc. R. Soc. A 1993, 441, 283–289. [Google Scholar]
- Simos, T.E.; Tsitouras, C. 6th order Runge–Kutta pairs for scalar autonomous IVP. Appl. Comput. Math. 2020, 19, 392–401. [Google Scholar]
- Simos, T.E.; Williams, P.S. A finite-difference method for the numerical solution of the Schrödinger equation. J. Comput. Appl. Math. 1997, 79, 189–205. [Google Scholar] [CrossRef]
- Sommeijer, B.P.; Van der Houwen, P.J.; Neta, B. Symmetric linear multistep methods for second order differential equations with periodic solutions. Appl. Numer. Math. 1986, 2, 69–77. [Google Scholar] [CrossRef]
- Stiefel, E.; Bettis, D.G. Stabihzation of Cowell’s method. Numer. Math. 1969, 13, 154–175. [Google Scholar] [CrossRef]
- Tunc, T.; Sarikaya, M.Z.; Yaldiz, H. Fractional hermite Hadamards type inquality for the co-ordinated convex functions. TWMS J. Pure Appl. Math. 2020, 11, 3–29. [Google Scholar]
- Van Daele, M.; Vanden Berghe, G. P-stable Obrechkoff methods of arbitrary order for second-order differential equations. Numer. Algor. 2007, 44, 115–131. [Google Scholar] [CrossRef]
- Vigo-Aguiar, J.; Ramos, H. A family of A-stable Runge–Kutta collocation methods of higher order for initial value problems. IMA J. Numer. Anal. 2007, 27, 798–817. [Google Scholar] [CrossRef]
- Vigo-Aguiar, J.; Ramos, H. On the choice of the frequency in trigonometrically-fitted methods for periodic problems. J. Comput. Appl. Math. 2015, 277, 94–105. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, D.; Dai, Y.; Wu, D. An improved trigonometrically fitted P-stable Obrechkoff method for periodic initial-value problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2005, 461, 1639–1658. [Google Scholar] [CrossRef]
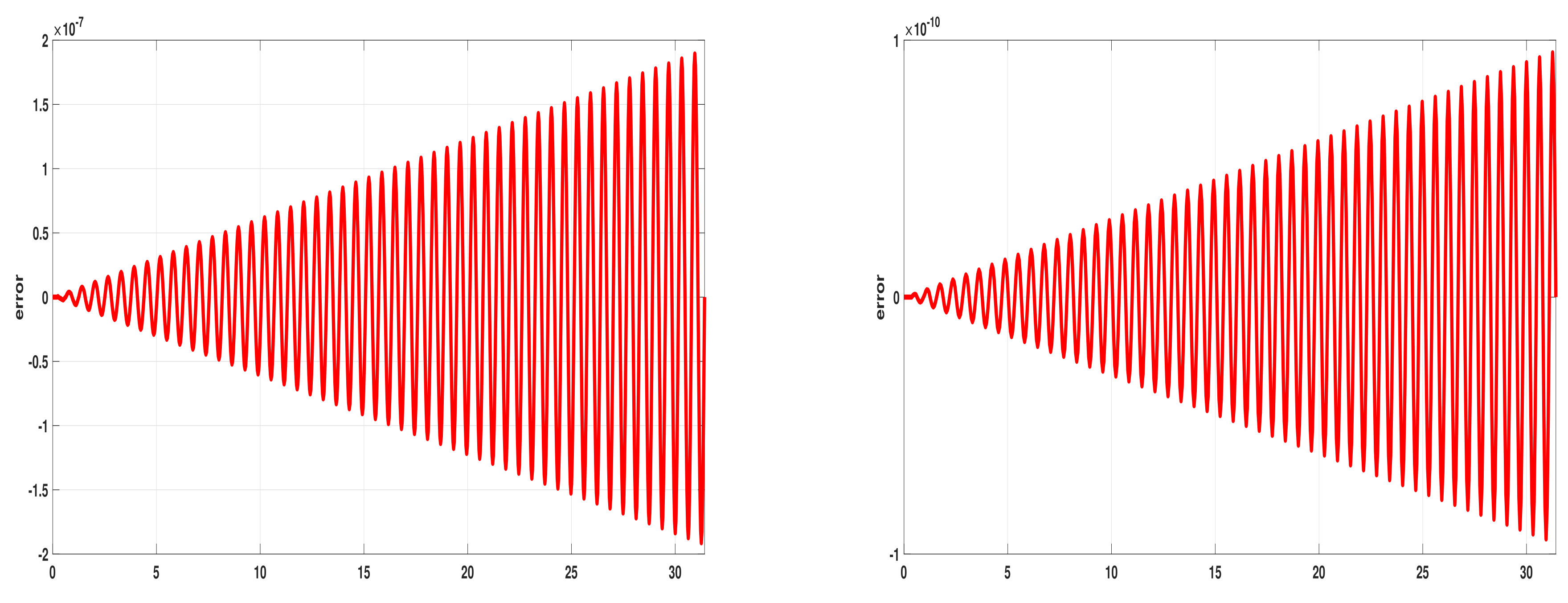
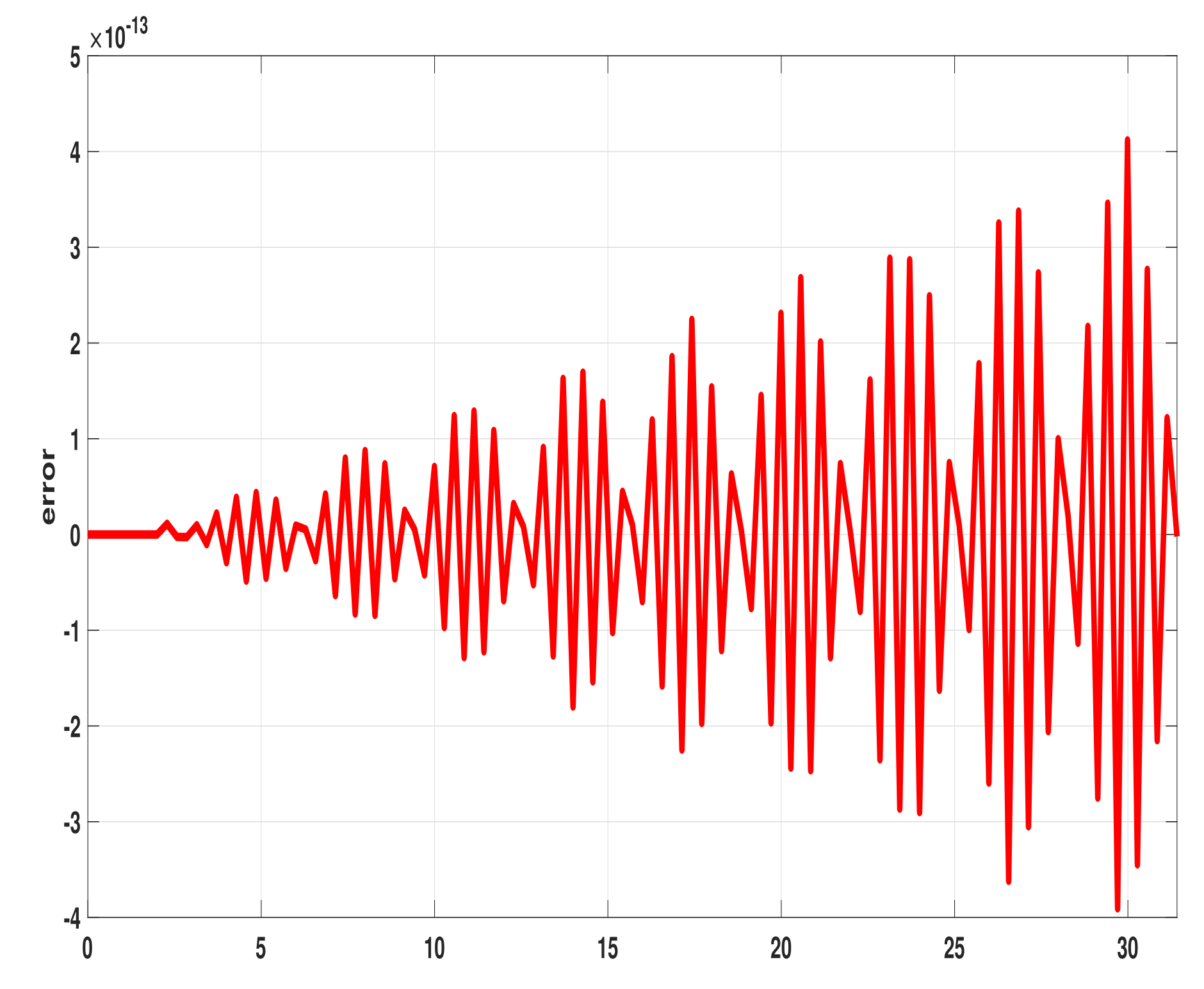
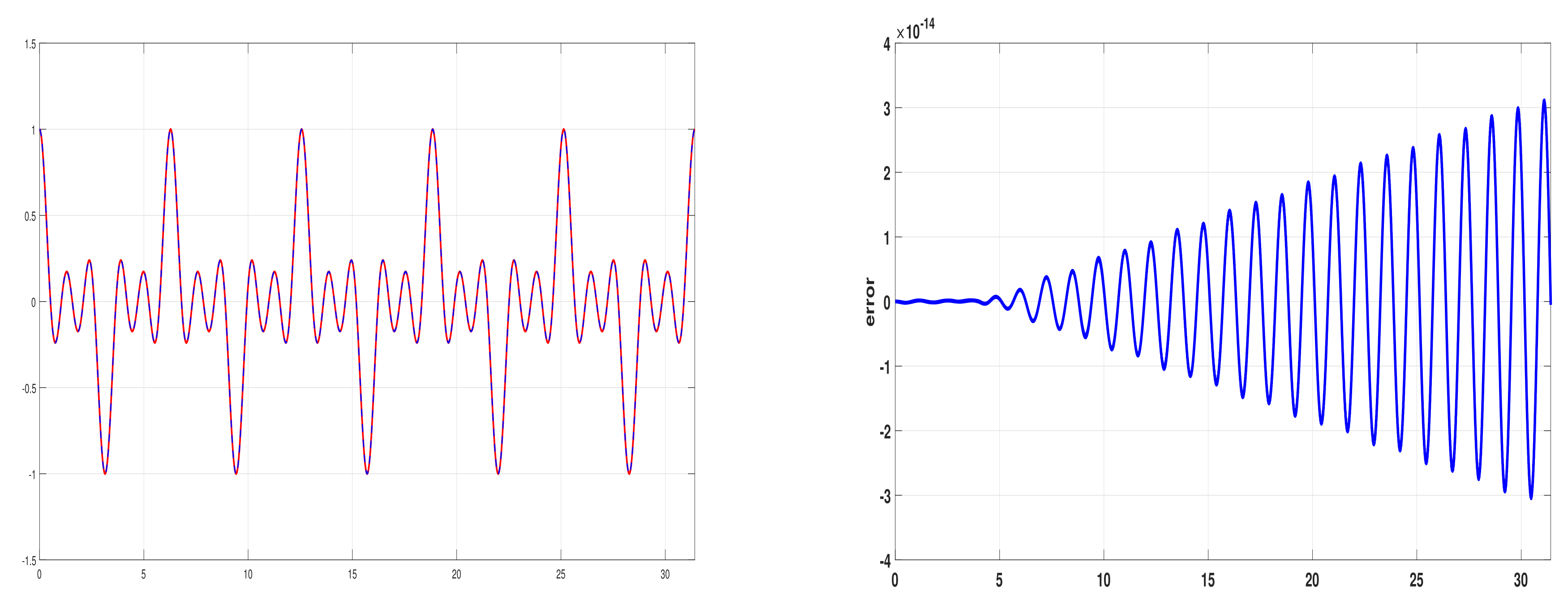
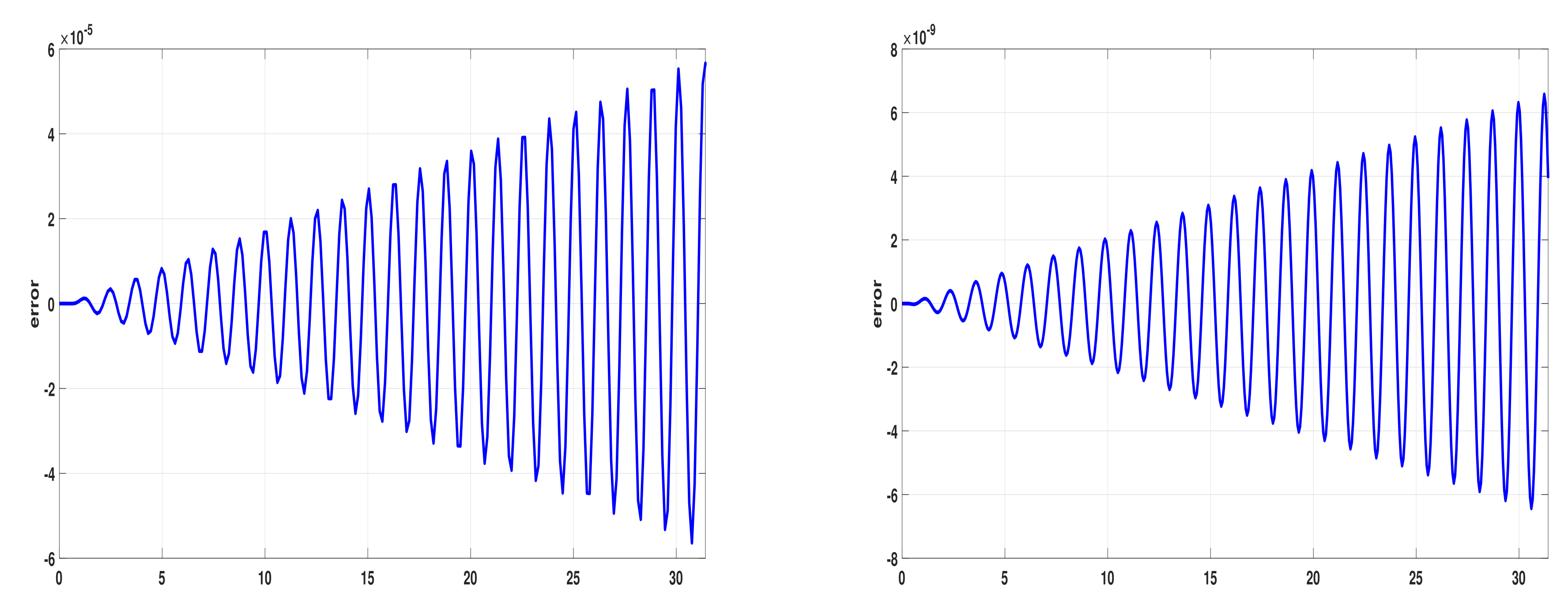
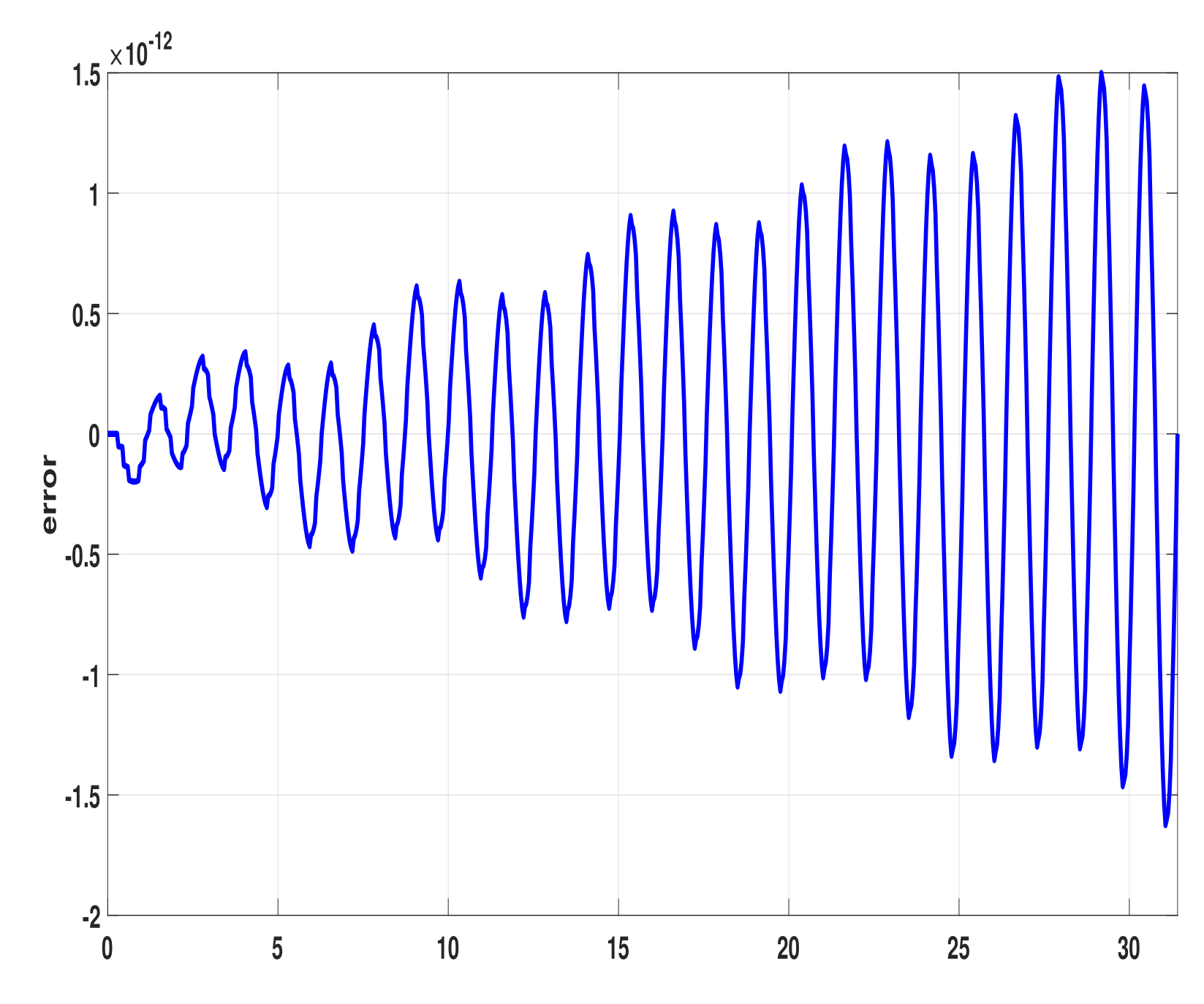

| h | Ananthakrishnaiah | Simos | Wang | New |
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shokri, A.; Neta, B.; Mehdizadeh Khalsaraei, M.; Rashidi, M.M.; Mohammad-Sedighi, H. A Singularly P-Stable Multi-Derivative Predictor Method for the Numerical Solution of Second-Order Ordinary Differential Equations. Mathematics 2021, 9, 806. https://doi.org/10.3390/math9080806
Shokri A, Neta B, Mehdizadeh Khalsaraei M, Rashidi MM, Mohammad-Sedighi H. A Singularly P-Stable Multi-Derivative Predictor Method for the Numerical Solution of Second-Order Ordinary Differential Equations. Mathematics. 2021; 9(8):806. https://doi.org/10.3390/math9080806
Chicago/Turabian StyleShokri, Ali, Beny Neta, Mohammad Mehdizadeh Khalsaraei, Mohammad Mehdi Rashidi, and Hamid Mohammad-Sedighi. 2021. "A Singularly P-Stable Multi-Derivative Predictor Method for the Numerical Solution of Second-Order Ordinary Differential Equations" Mathematics 9, no. 8: 806. https://doi.org/10.3390/math9080806
APA StyleShokri, A., Neta, B., Mehdizadeh Khalsaraei, M., Rashidi, M. M., & Mohammad-Sedighi, H. (2021). A Singularly P-Stable Multi-Derivative Predictor Method for the Numerical Solution of Second-Order Ordinary Differential Equations. Mathematics, 9(8), 806. https://doi.org/10.3390/math9080806









